Estimating the Single Shear Strength Performance of Joints Using Screws and Nails with Decayed Wood
Abstract
1. Introduction
2. Calculation Methods
2.1. Overview of the Proposed Model and Calculation Method of the Yield Strength
2.2. Modeling Multiple Layers for Decayed Wood
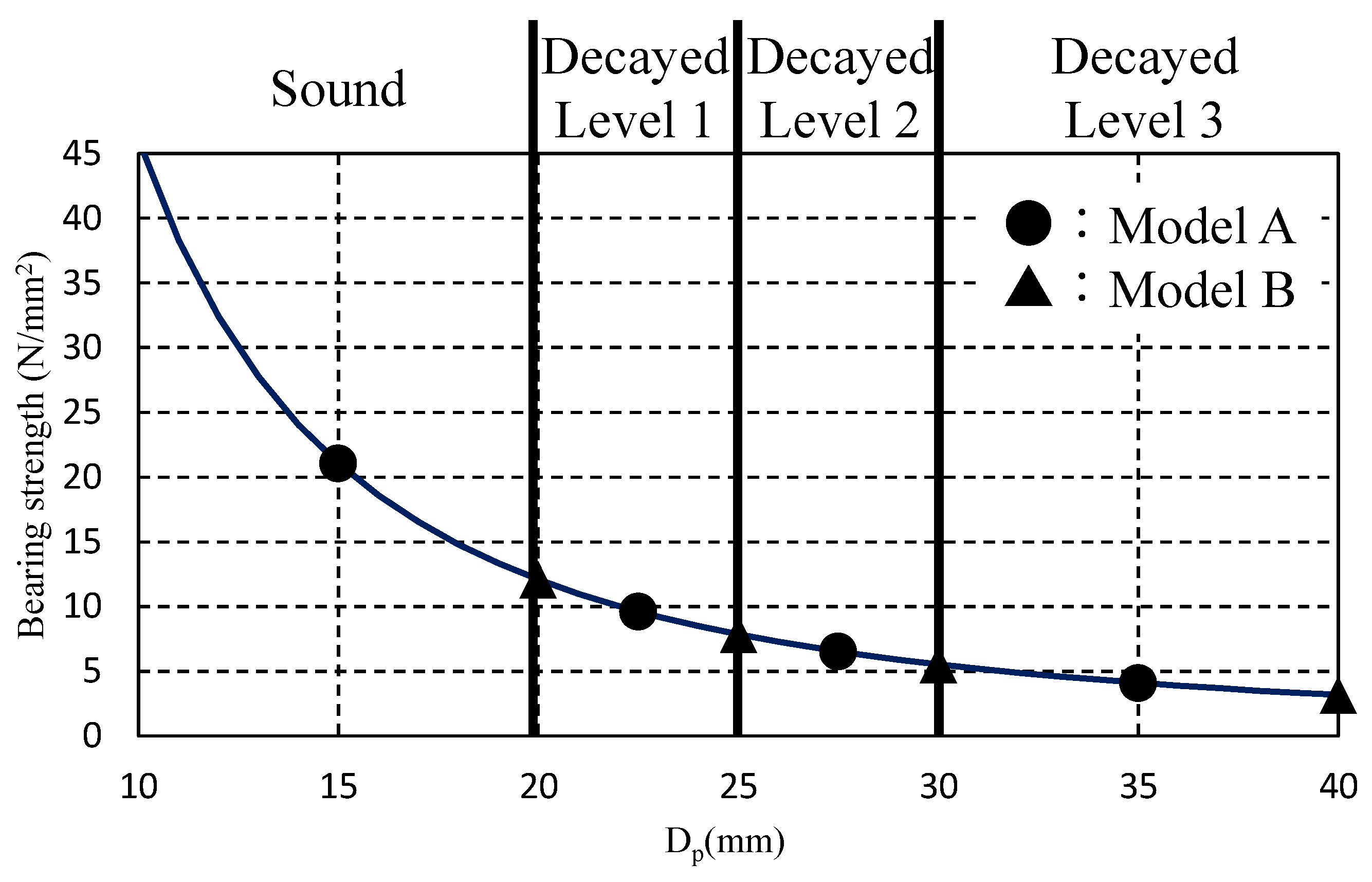
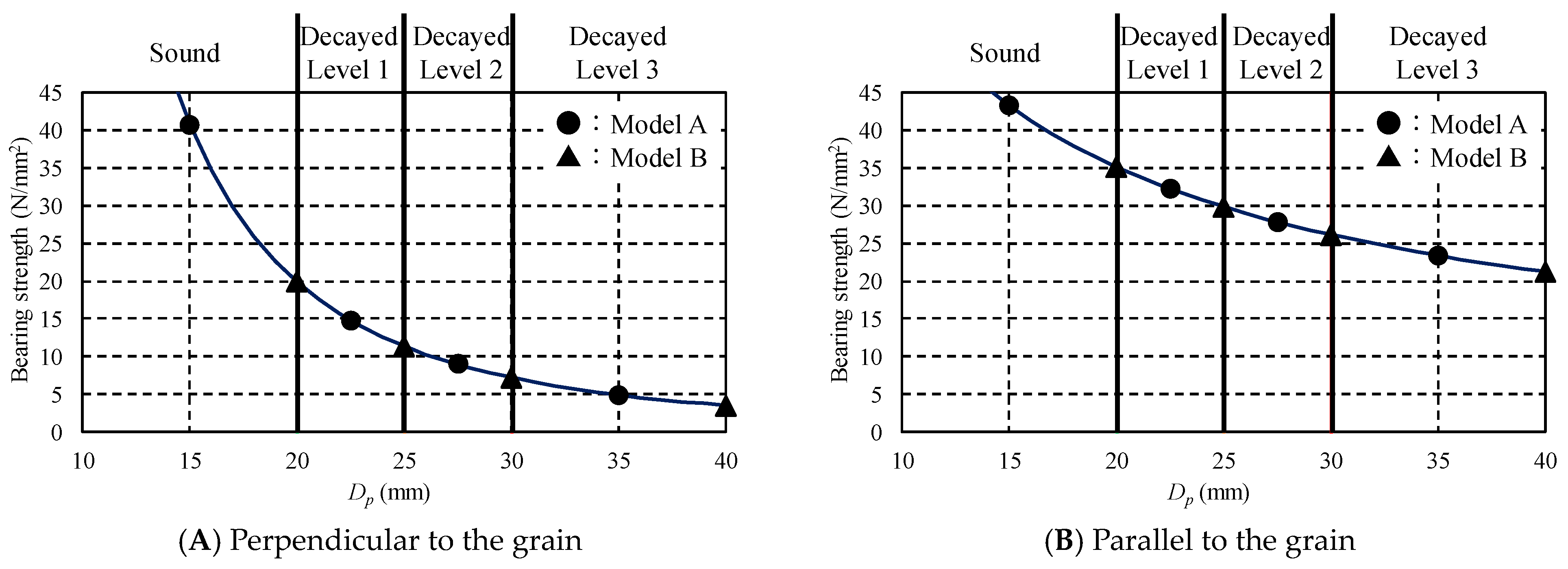
2.3. Calculation of Single Shear Yield Strength for Sugi and Todomatu with Decay
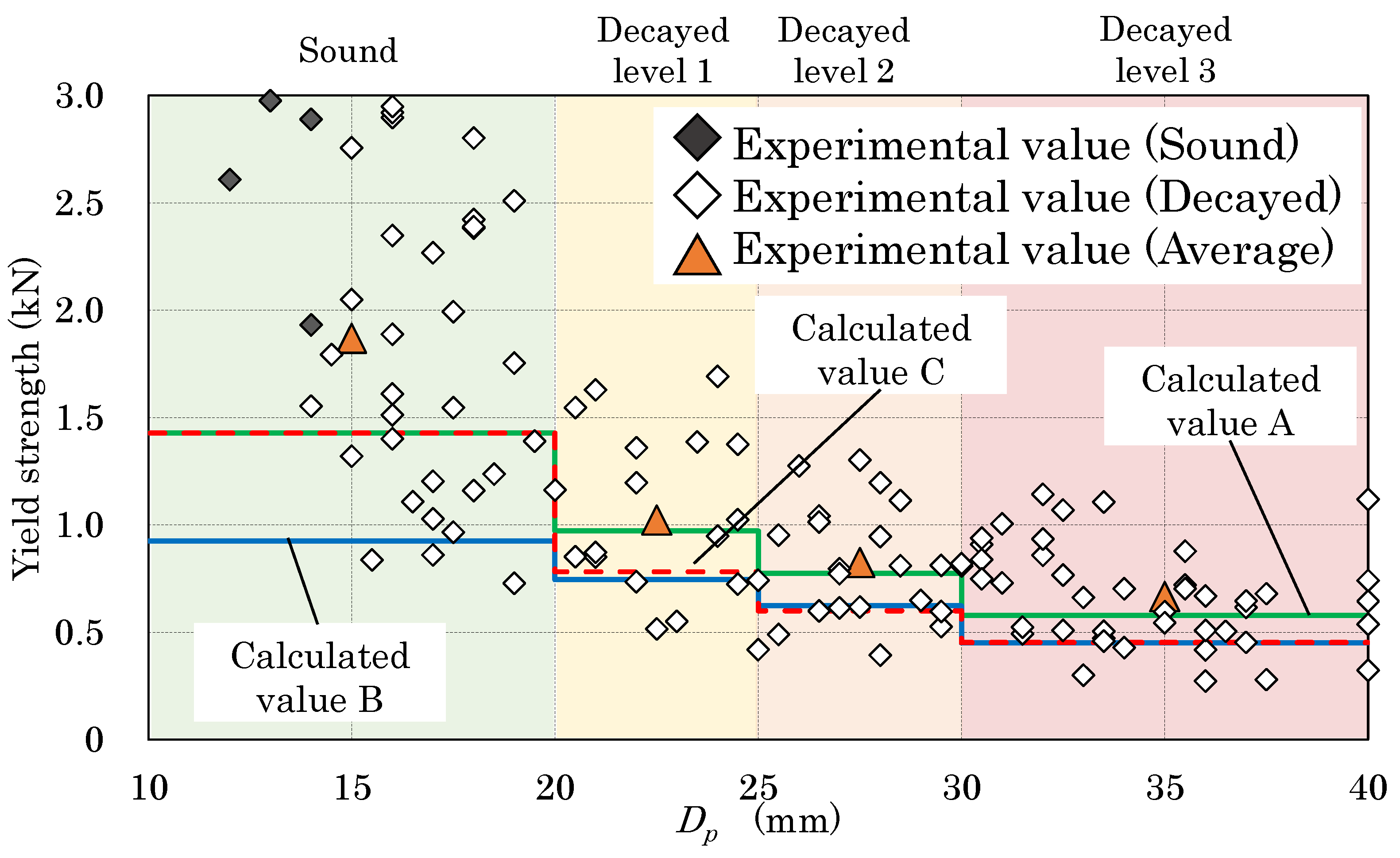
2.3.1. Estimation of Yield Strength for Decayed Todomatsu
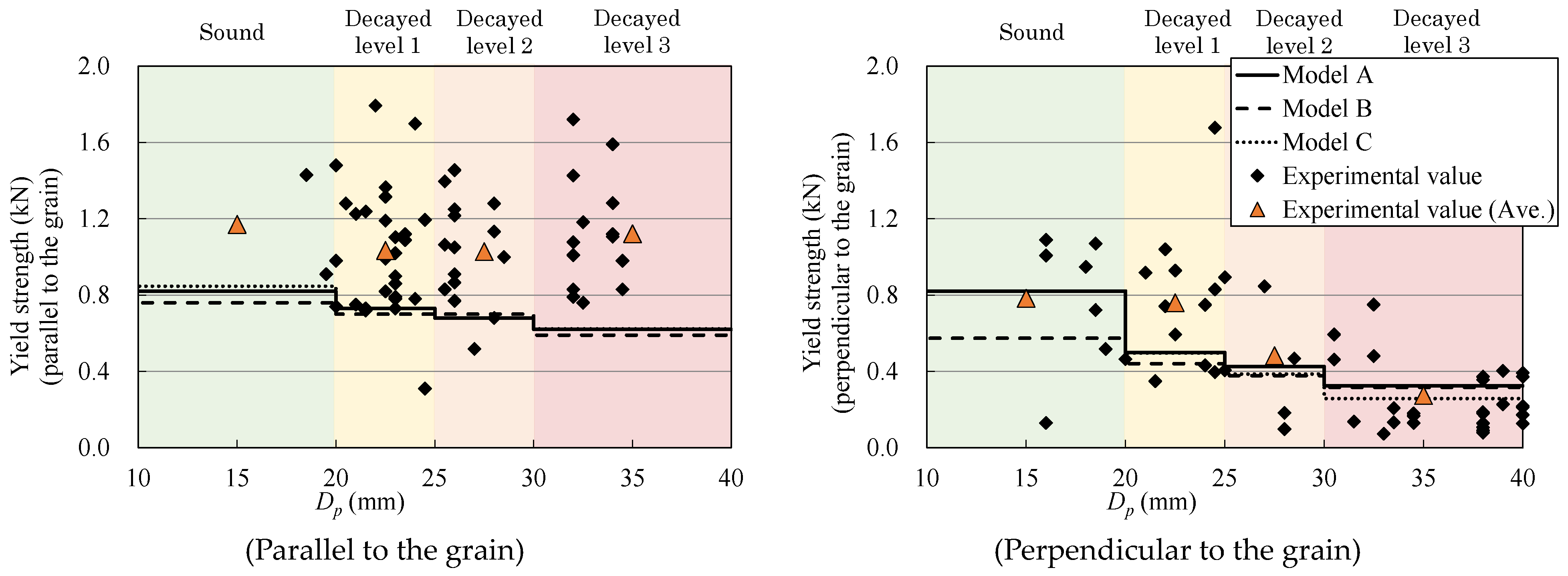
2.3.2. Estimation of Yield Strength for Decayed Sugi
3. Results and Discussion
3.1. Estimated Value versus Experimental Value of Decayed Todomatsu
3.2. Estimated Value versus Experimental Value of Decayed Sugi
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akyildiz, H.M. Screw-nail withdrawal and bonding strength of paulownia (Paulownia tomentosa Steud.) wood. J. Wood Sci. 2014, 60, 201–206. [Google Scholar] [CrossRef]
- Cappellazzi, J.; Konkler, J.M.; Sinha, A.; Morrell, J.J. Potential for decay in mass timber elements: A review of the risks and identifying possible solutions. Wood Mater. Sci. Eng. 2020, 15, 351–360. [Google Scholar] [CrossRef]
- Ota, Y.; Ishiyama, H.; Okamoto, S. Study on the structural performance of plywood bearing wall the rusted nail and decayed wood. Proc. World Conf. Timber Eng. 2023, 2023, 2617–2626. [Google Scholar]
- Olaf, S. Indoor wood-decay basidiomycetes: Damage, causal fungi, physiology, identification and characterization, prevention and control. Mycol. Prog. 2007, 6, 261–279. [Google Scholar]
- Frederick, G.T.; Terry, L.H. Brown-rot wood decay—Insights gained from a low-decay isolate of Postia placenta. Plant Pathol. 1997, 1, 1–17. [Google Scholar]
- Harada, M.; Hayashi, Y.; Hayashi, T.; Karube, M.; Ohgawa, T. Effect of moisture content of members on mechanical properties of timber joints. J. Wood Sci. 2005, 51, 282–285. [Google Scholar] [CrossRef]
- Hijikuro, K.; Ono, Y. Field survey into deterioration degradation states for structural member of wooden house. AIJ J. Technol. Des. 1999, 9, 41–44, In Japanese. [Google Scholar] [CrossRef]
- Sonoda, S.; Nakatani, H.; Hasegawa, M.; Shiba, K.; Hata, M. Damage to wooden houses by the niigataken Chuetsu-oki Earthquake in 2007. Bull. Toyama Prefectural. Agric. For. Fish. Res. Cent. 2009, 1, 6–17. (In Japanese) [Google Scholar]
- Wilcox, W. Review of literature on the effects of early stages of decay on wood strength. Wood Fiber 1978, 9, 252–257. [Google Scholar]
- Gilfillana, J.R.; Gilbertb, S.G. Development of a technique to measure the residual strength of woodworm infested timber. Constr. Build. Mater. 2001, 15, 381–388. [Google Scholar] [CrossRef]
- Gao, S.; Wang, X.; Wiemann, C.M.; Brashaw, K.B.; Ross, J.R.; Wang, L. A critical analysis of methods for rapid and nondestructive determination of wood density in standing trees. Ann. For. Sci. 2017, 74, 27. [Google Scholar] [CrossRef]
- Mäkipää, R.; Linkosalo, T. A non-destructive field method for measuring wood density of decaying logs. Silva Fenn. 2011, 45, 1135–1142. [Google Scholar] [CrossRef]
- Thaler, N.; Lesar, B.; Humar, M. Correlation between brown rot decay Pilodyn measurements. Eur. J. Wood Prod. 2012, 70, 893–895. [Google Scholar] [CrossRef]
- Takanashi, R.; Sawata, K.; Sasaki, Y.; Koizumi, A. Withdrawal strength of nailed joints with decay degradation of wood nail corrosion. J. Wood Sci. 2017, 63, 192–198. [Google Scholar] [CrossRef]
- Sawata, K.; Sasaki, T.; Doi, S.; Iijima, Y. Effect of decay on shear performance of dowel-type timber joints. J. Wood Sci. 2008, 54, 356–361. [Google Scholar] [CrossRef]
- Kent, S.; Leichti, R.; Rosowsky, D.; Morrell, J. Effects of wood decay by postia placenta on the lateral capacity of nailed oriented strandboard sheathing and Douglas-fir framing members. Wood Fiber Sci. 2004, 36, 560–572. [Google Scholar]
- Kent, S.M.; Leichti, R.J.; Rosowsky, D.V.; Morrell, J.J. Effects of decay on the cyclic properties of nailed connections. J. Mater. Civ. Eng. 2005, 17, 579–585. [Google Scholar] [CrossRef]
- Sawata, K.; Sasaki, Y. Lateral strength of nailed timber connections with decay. J. Wood Sci. 2018, 64, 601–611. [Google Scholar] [CrossRef]
- Ueda, R.; Sawata, K.; Takanashi, R.; Sasaki, Y.; Sasaki, T. Degradation of shear performance of screwed joint caused by wood decay. J. Wood Sci. 2020, 66, 42. [Google Scholar] [CrossRef]
- Nishino, S.; Shibao, M.; Nagami, T.; Taki, Y.; Mori, T.; Tanaka, K. Propose on Database for Evaluation Method of Residual Performance of Wooden Structure with Bio-deterioration. In Summaries of Technical Papers of Annual Meeting of AIJ, Sendai, Japan 2018; Architectural Institute of Japan: Tokyo, Japan, 2018; pp. 609–610. (In Japanese) [Google Scholar]
- Mori, T.; Tanaka, K.; Mouri, Y.; Yanase, Y.; Inoue, M.; Isoda, H. Study on survival strength of wood screwed joint after termite attack. J. Struct. Constr. Eng. AIJ 2016, 81, 1113–1120. [Google Scholar] [CrossRef][Green Version]
- Mori, T.; Tanaka, K.; Kawano, K.; Nakahata, T.; Yanase, Y.; Kurisaki, H. Estimation of shear strength of nail driven into decayed wood of Japanese cedar sugi. J. Soc. Mater. Sci. Jpn. 2014, 63, 314–319, In Japanese. [Google Scholar] [CrossRef]
- Maeda, K.; Ohta, M.; Momohara, I. Changes of Cross Sectional Area and Density of the Decayed Wood. Wood Ind. 2015, 70, 153–157. (In Japanese) [Google Scholar]
- Tomitaka, R.; Toda, M. Application of European Yield Theory to Laminated Timber composed of Lumber with any Thickness and Bearing Strength. Summ. Tech. Pap. Annu. Meet. AIJ 2018, 72, 555–556. (In Japanese) [Google Scholar]
- Architectural Institute of Japan. Standard for Structural Design of Timber Structures; Maruzen: Tokyo, Japan, 2006; p. 31. (In Japanese) [Google Scholar]
- Mori, T.; Noda, Y.; Azuma, T.; Mori, M.; Toda, M.; Isoda, H. Evaluation of Single Shear Strength Performance of Wood Screw Joint Driving into Compulsive Decayed Wood. J. Struct. Eng. B 2015, 61B, 237–242. (In Japanese) [Google Scholar]
- Toda, M.; Mori, M.; Ohashi YMHirai, T. Effects of Wood Decay on the Shear Performance of Nailed Timber Joint. Mokuzai Gakkaishi 2010, 56, 41–47, In Japanese. [Google Scholar] [CrossRef]
- Sawata, K.; Yasumura, M. Determination of embedding strength of wood for dowel-type fasteners. J. Wood Sci. 2002, 48, 138–146. [Google Scholar] [CrossRef]
- Kawano, K.; Nakahata, T.; Mouri, Y.; Mori, T.; Tanaka, K.; Inoue, M. Surviving Strength Properties of Japanese Softwood with Biodeterioration Part.3 Estimation of shear strength of nail joint into decayed wood of Japanese cedar. In Summaries of Technical Papers of Annual Meeting of AIJ, Kobe, Japan, 2014; Architectural Institute of Japan: Tokyo, Japan, 2014; pp. 387–388. (In Japanese) [Google Scholar]

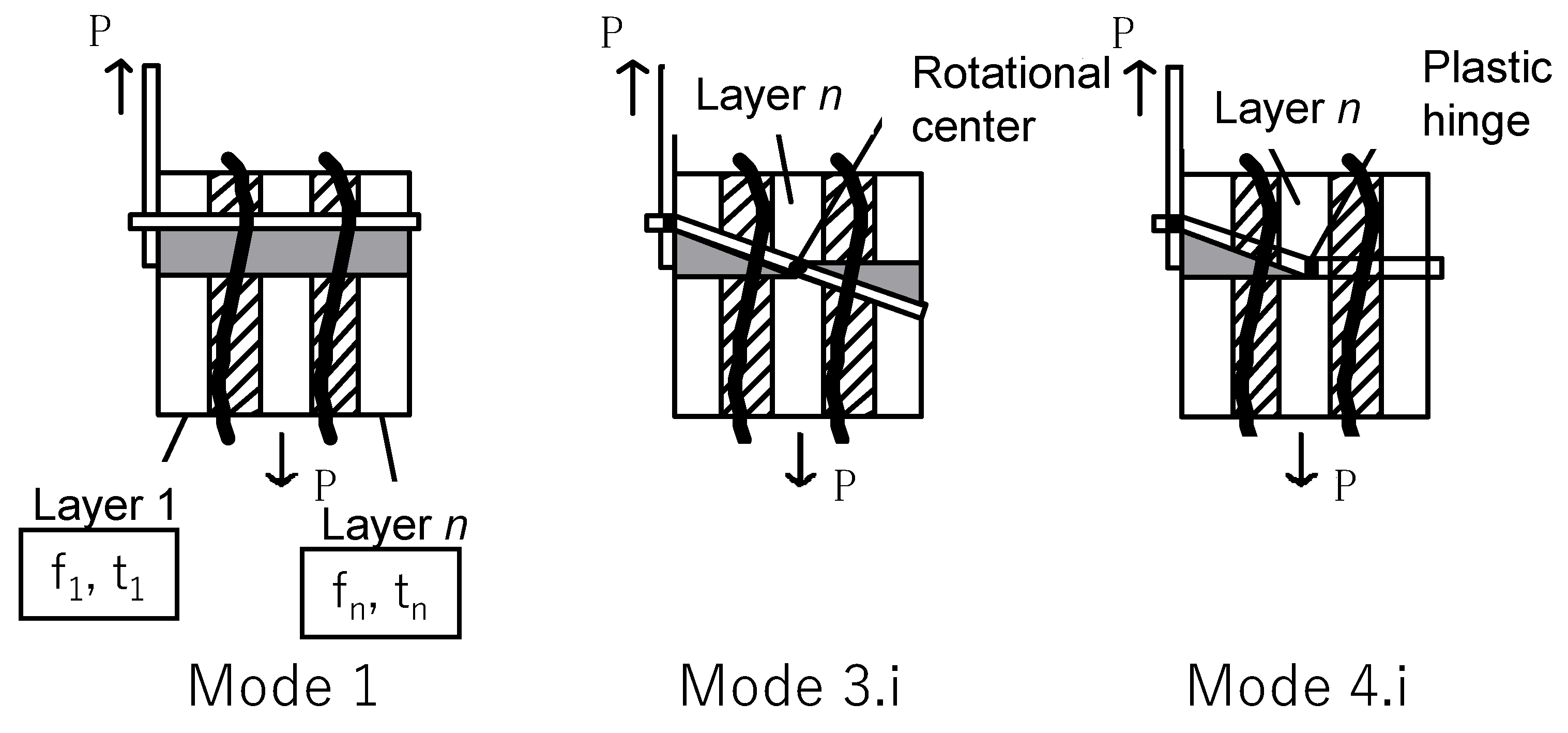
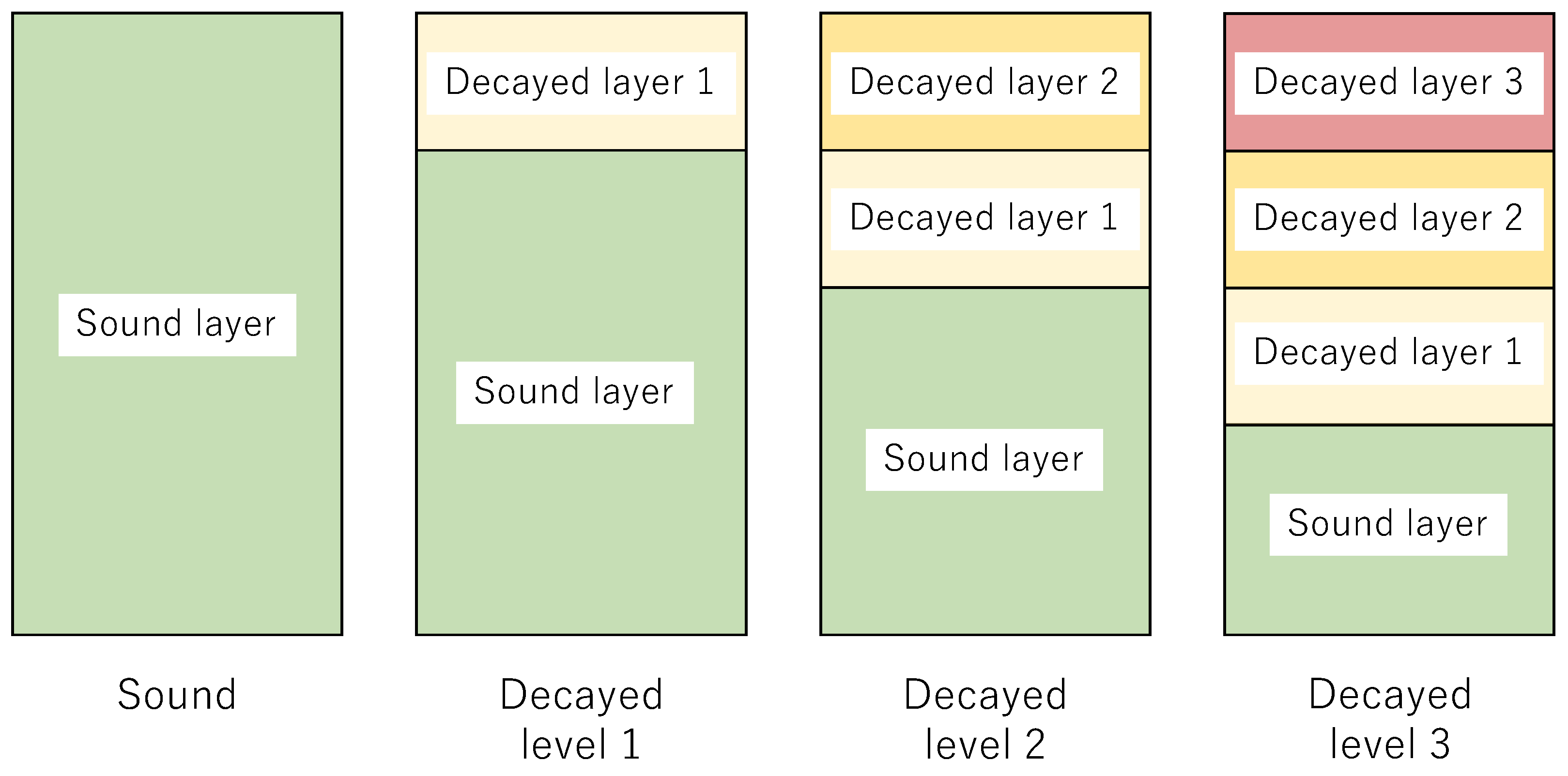
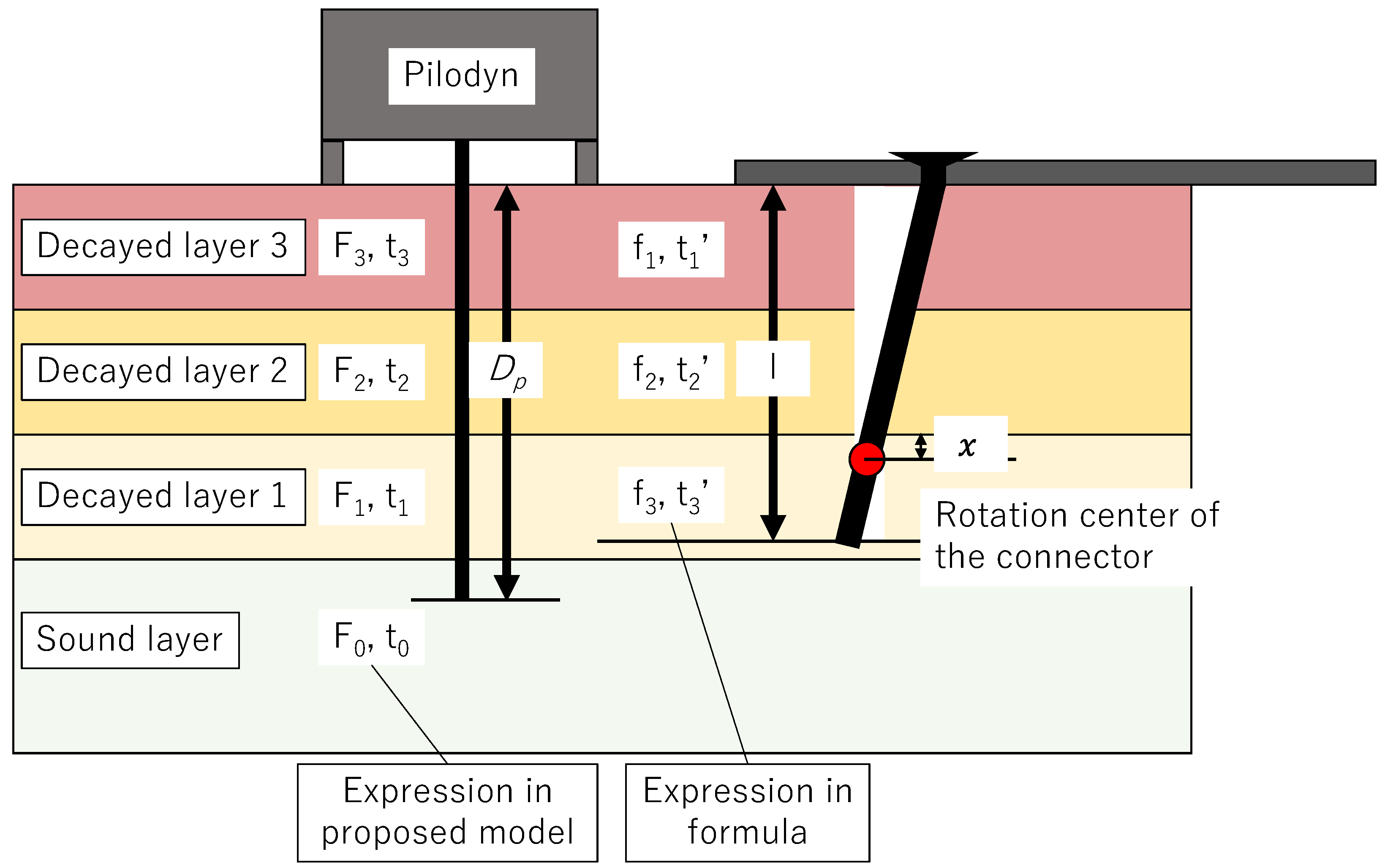

| Character in the formula | t1′ (f1) | t2′ (f2) | t3′ (f3) | t4′ (f4) | |
| Character to be assigned to formulas | Decayed level 1 | t1 (F1) | t0 (F0) | - | - |
| Decayed level 2 | t2 (F2) | t1 (F1) | t0 (F0) | - | |
| Decayed level 3 | t3 (F3) | t2 (F2) | t1 (F1) | t0 (F0) | |
| Fm (N/mm2) | |||
|---|---|---|---|
| Model A | Sound layer | F0 | 21.05 |
| Level 1 layer | F1 | 9.62 | |
| Level 2 layer | F2 | 6.53 | |
| Level 3 layer | F3 | 4.10 | |
| Model B | Sound layer | F0 | 12.08 |
| Level 1 layer | F1 | 7.85 | |
| Level 2 layer | F2 | 5.52 | |
| Level 3 layer | F3 | 3.17 | |
| Decayed Level | Dp (mm) | Thickness of Sound Layer and Each Decayed Layer (mm) | ||||
|---|---|---|---|---|---|---|
| Model A | Sound | 15.0 | 0 | 0 | 0 | 15.00 |
| Level 1 | 22.5 | 0 | 0 | 13.82 | 8.68 | |
| Level 2 | 27.5 | 0 | 7.25 | 13.82 | 6.43 | |
| Level 3 | 35.0 | 9.32 | 7.25 | 13.82 | 4.62 | |
| Model B | Sound | 20.0 | 0 | 0 | 0 | 20.00 |
| Level 1 | 25.0 | 0 | 0 | 14.29 | 10.71 | |
| Level 2 | 30.0 | 0 | 9.21 | 14.29 | 6.50 | |
| Level 3 | 40.0 | 13.56 | 9.21 | 14.29 | 2.94 | |
| Fm (N/mm2) | |||
|---|---|---|---|
| Perpendicular to the Grain | Parallel to the Grain | ||
| Model A | Sound layer | 40.73 | 43.22 |
| Level 1 layer | 14.82 | 32.22 | |
| Level 2 layer | 8.99 | 27.85 | |
| Level 3 layer | 4.93 | 23.39 | |
| Model B | Sound layer | 19.88 | 35.09 |
| Level 1 layer | 11.40 | 29.85 | |
| Level 2 layer | 7.24 | 26.15 | |
| Level 3 layer | 3.53 | 21.23 | |
| Decayed Level | Dp (mm) | Thickness of Sound Layer and Each Decayed Layer (mm) | ||||
|---|---|---|---|---|---|---|
| Model A | Sound | 15.0 | 0.00 | 0.00 | 0.00 | 15.00 |
| Level 1 | 22.5 | 0.00 | 0.00 | 11.79 | 10.71 | |
| Level 2 | 27.5 | 0.00 | 6.42 | 11.79 | 9.29 | |
| Level 3 | 35.0 | 8.53 | 6.42 | 11.79 | 8.26 | |
| Model B | Sound | 20.0 | 0.00 | 0.00 | 0.00 | 20.00 |
| Level 1 | 25.0 | 0.00 | 0.00 | 11.72 | 13.28 | |
| Level 2 | 30.0 | 0.00 | 7.86 | 11.72 | 10.42 | |
| Level 3 | 40.0 | 12.16 | 7.86 | 11.72 | 8.26 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mori, T.; Inoue, R.; Tanaka, K. Estimating the Single Shear Strength Performance of Joints Using Screws and Nails with Decayed Wood. Buildings 2024, 14, 1924. https://doi.org/10.3390/buildings14071924
Mori T, Inoue R, Tanaka K. Estimating the Single Shear Strength Performance of Joints Using Screws and Nails with Decayed Wood. Buildings. 2024; 14(7):1924. https://doi.org/10.3390/buildings14071924
Chicago/Turabian StyleMori, Takuro, Ryo Inoue, and Kei Tanaka. 2024. "Estimating the Single Shear Strength Performance of Joints Using Screws and Nails with Decayed Wood" Buildings 14, no. 7: 1924. https://doi.org/10.3390/buildings14071924
APA StyleMori, T., Inoue, R., & Tanaka, K. (2024). Estimating the Single Shear Strength Performance of Joints Using Screws and Nails with Decayed Wood. Buildings, 14(7), 1924. https://doi.org/10.3390/buildings14071924







