A Practical Approach to Alignment and Error Feedback Control for Long-Span Arch Bridges
Abstract
:1. Introduction
2. Mathematical Model
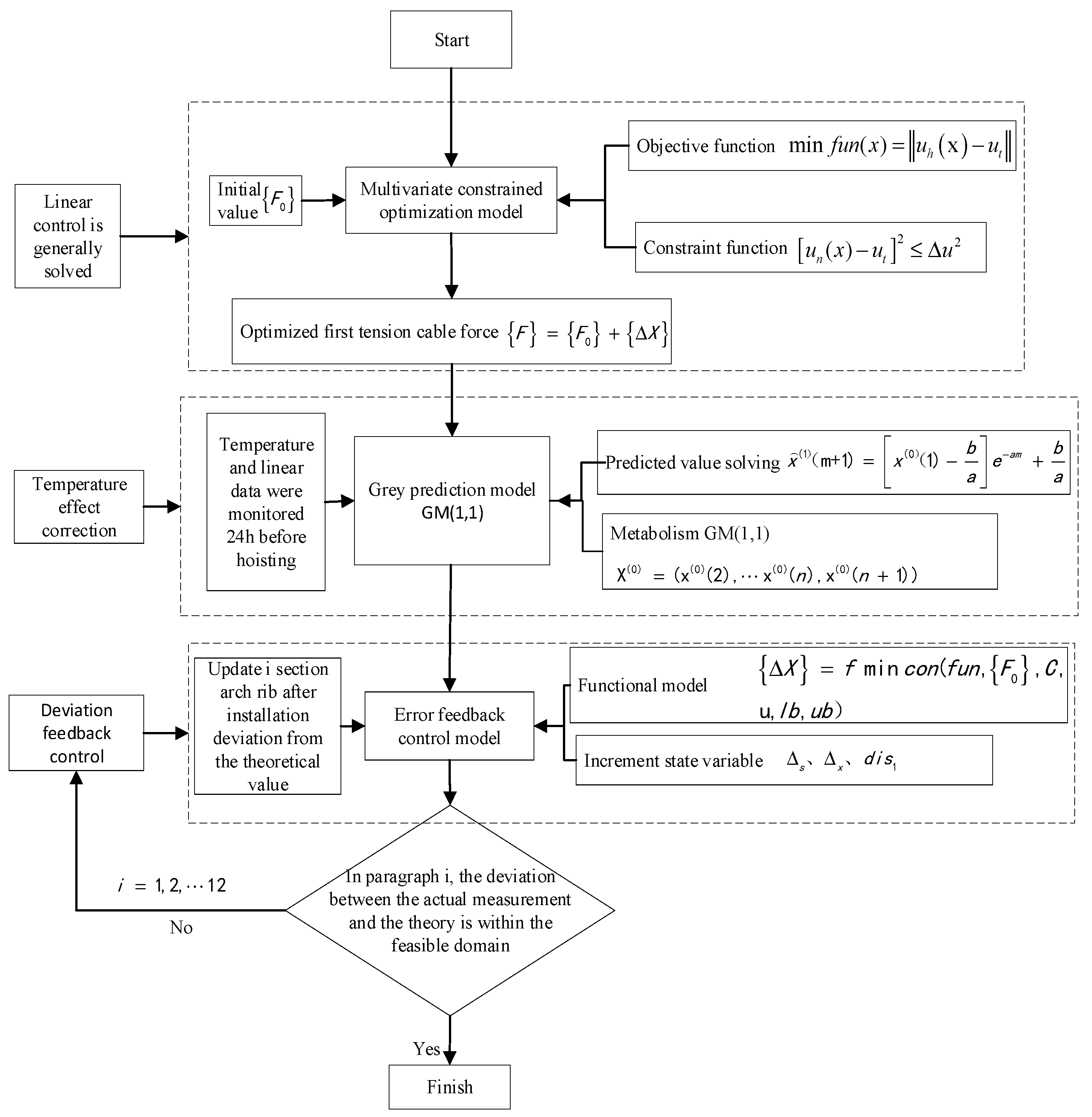
2.1. General Solution of Alignment Control
2.2. Alignment Control Optimization
2.3. Alignment Control Considering Temperature Influence
2.4. Feedback Control of Parameter Errors
- (1)
- The initial cable force is obtained after the final optimization. Based on the material characteristics, geometric characteristics, boundary conditions, and external load information of concrete-filled steel tube arch bridges, a finite element model is established. According to Equations (2) and (3), the initial tensile force of a group of buckles during construction is solved and optimized.
- (2)
- According to Equation (4), the cable force of a single unadjusted cable under control objectives, such as tower deviation, arch rib alignment, and cable force uniformity, is obtained.
- (3)
- In order to improve the accuracy of the grey prediction model GM(1, 1), the grey model GM(1, 1) with a fixed median is established, where is taken as the latest information, and the previous information is replaced with . The model built with is called the metastatic GM(1, 1) model.
- (4)
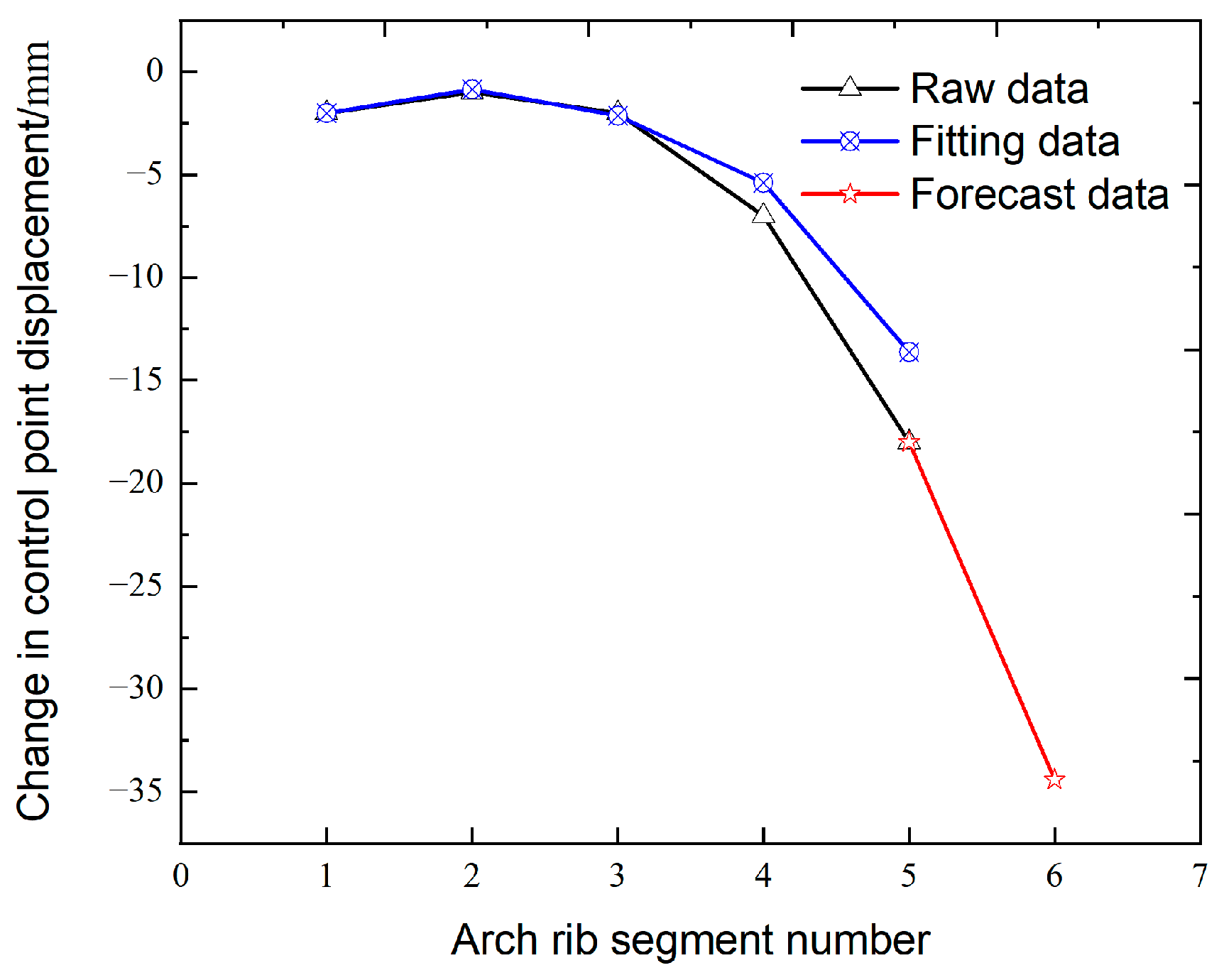
- The original data are fitted, and the segment arch rib under the prediction is affected by temperature through a comprehensive consideration of metastatic GM(1, 1) and the fitting results. Then, the prediction data and the trend of the original data are used to judge whether it is reasonable and reliable.
- (5)
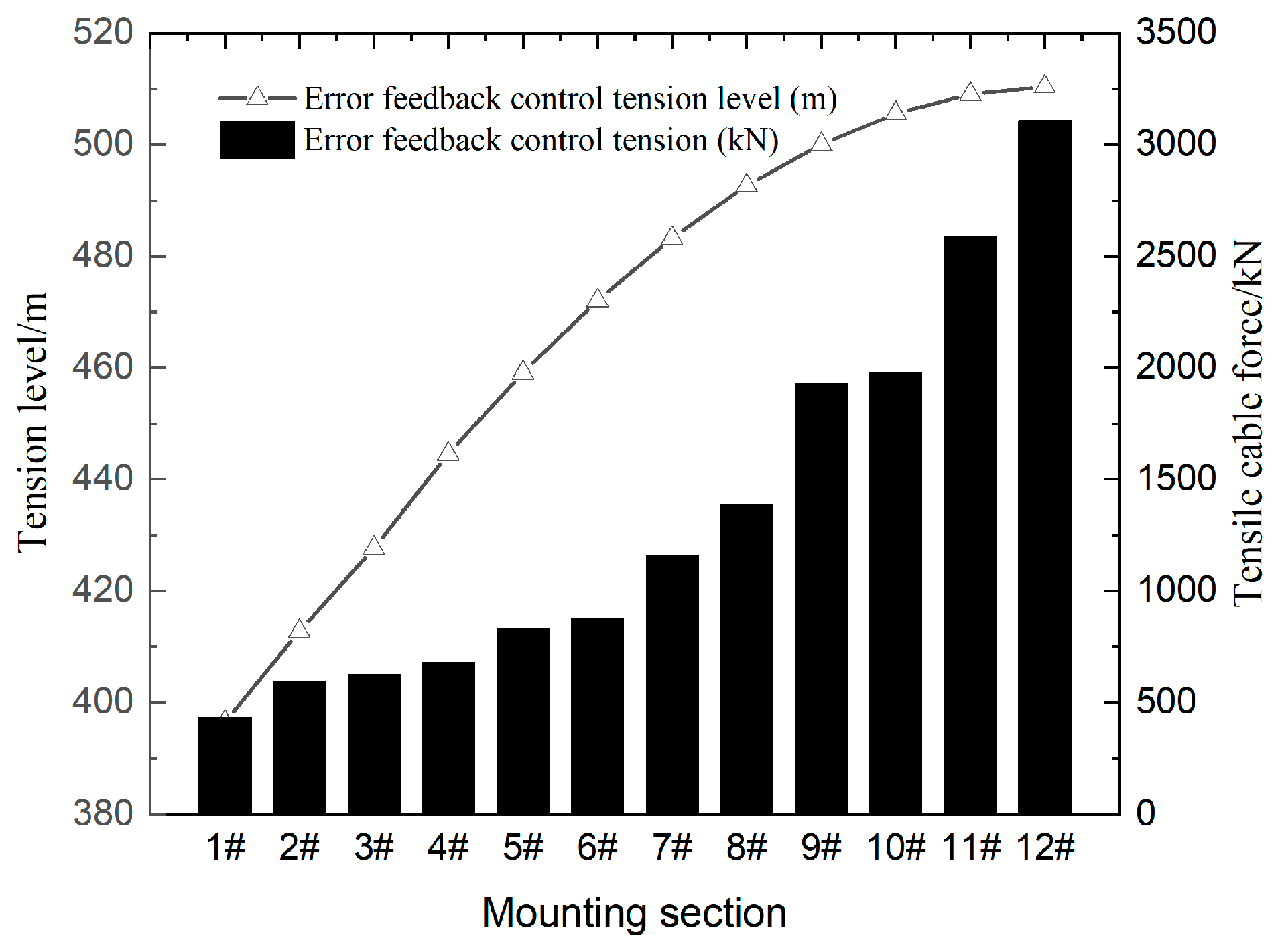
- and are the upper and lower limits of the current segment alignment caused by various error factors. Approximating the practical value of the current segment after installation using and , and optimizing the mathematical model (2), results in the feedback control characterizing various parameter errors and environmental interferences.
- (6)
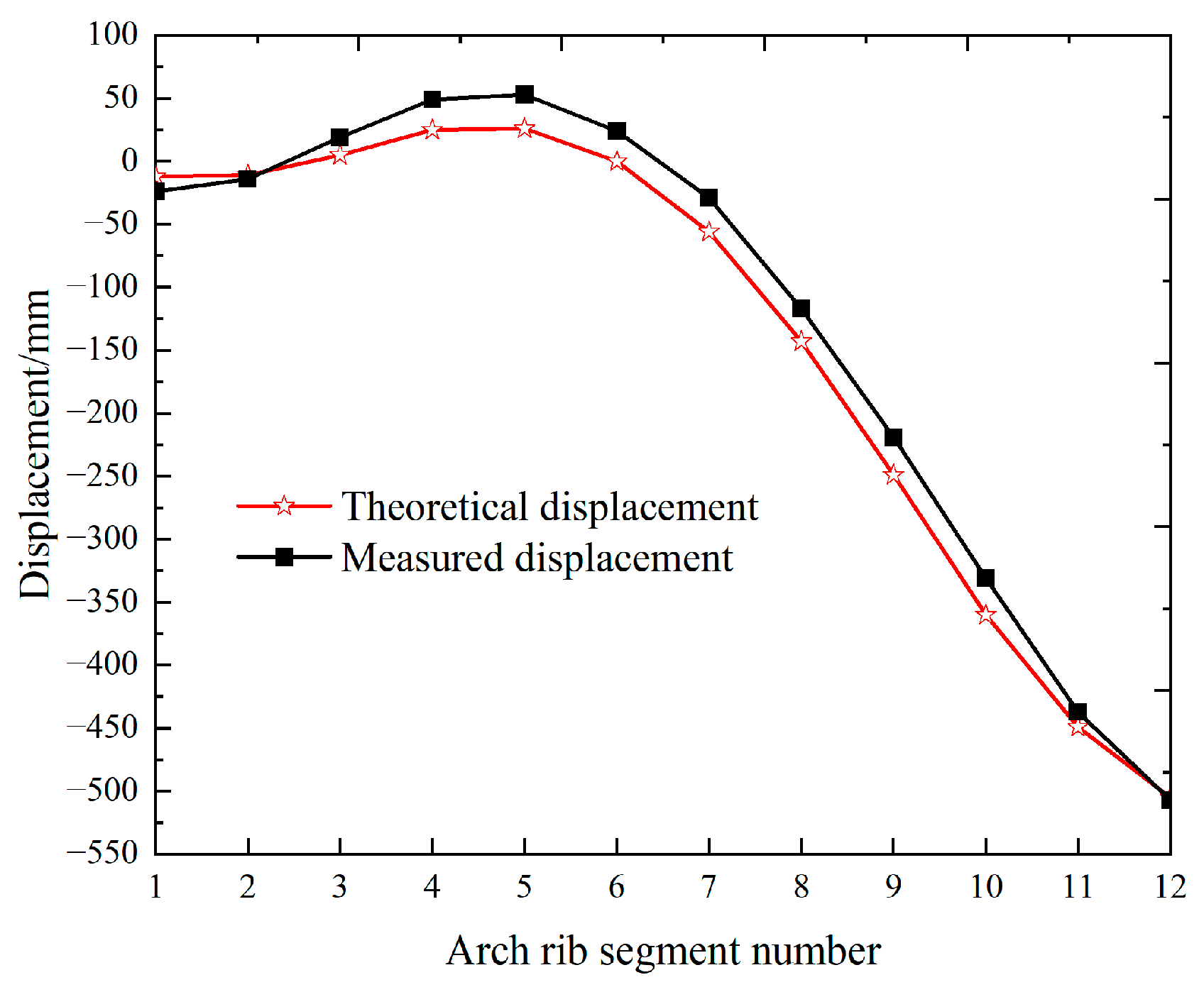
- Through error feedback control, various parameter errors and environmental interferences in the bridge construction process are corrected. If the deviation between the measured value and the theoretical value is within a feasible region, the iteration is completed. If the requirements are not met, one should return to step (5) and adjust the tunable parameters to realize the model output, offset-free-tracking practical arch rib structure.
3. Practical Application
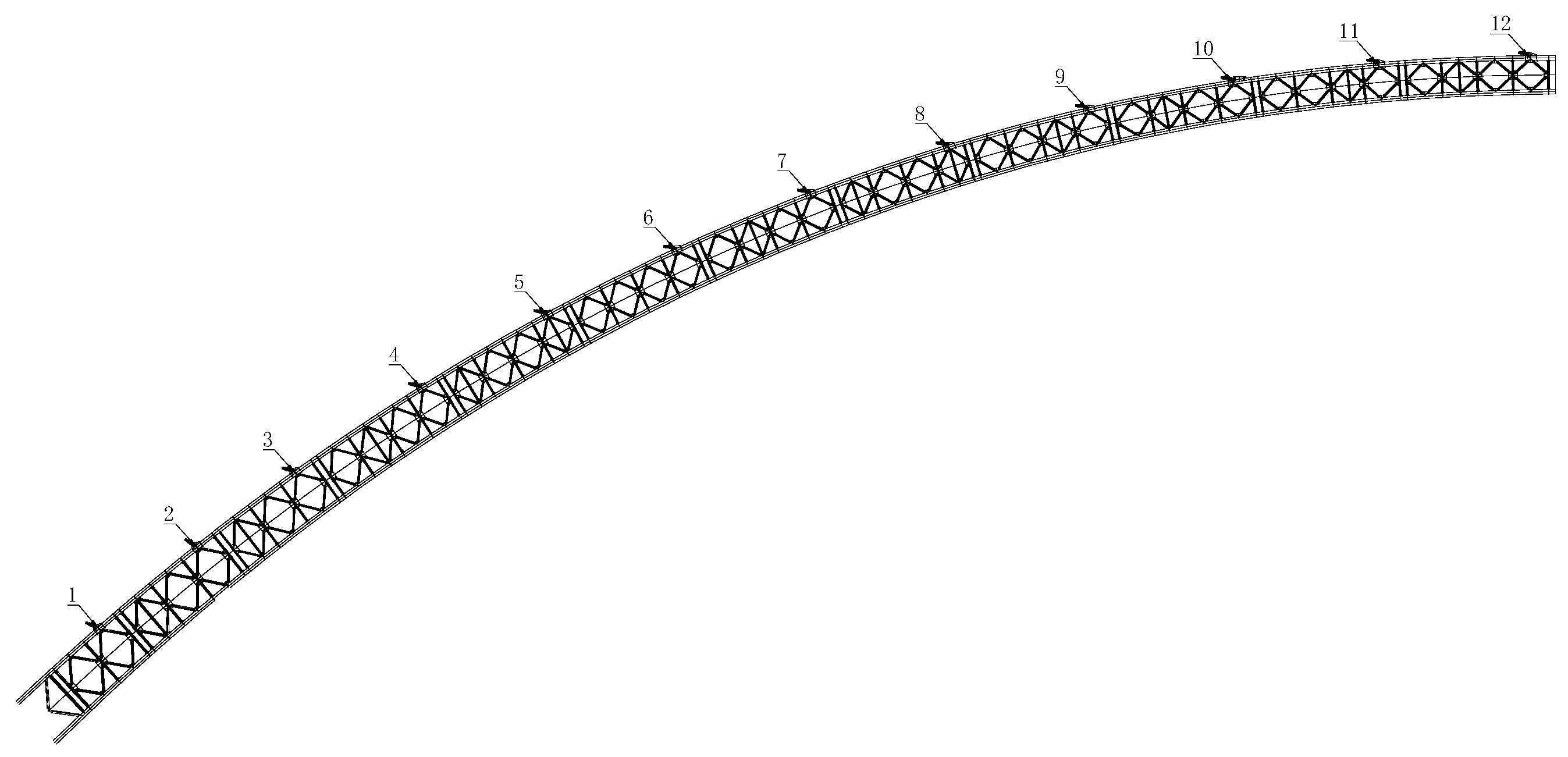
3.1. Project Background and Finite Element Model
3.2. Application of the Practical Approach to Alignment Control and Error Feedback
3.2.1. General Solution and Optimization of Alignment Control
3.2.2. Alignment Control Considering Temperature
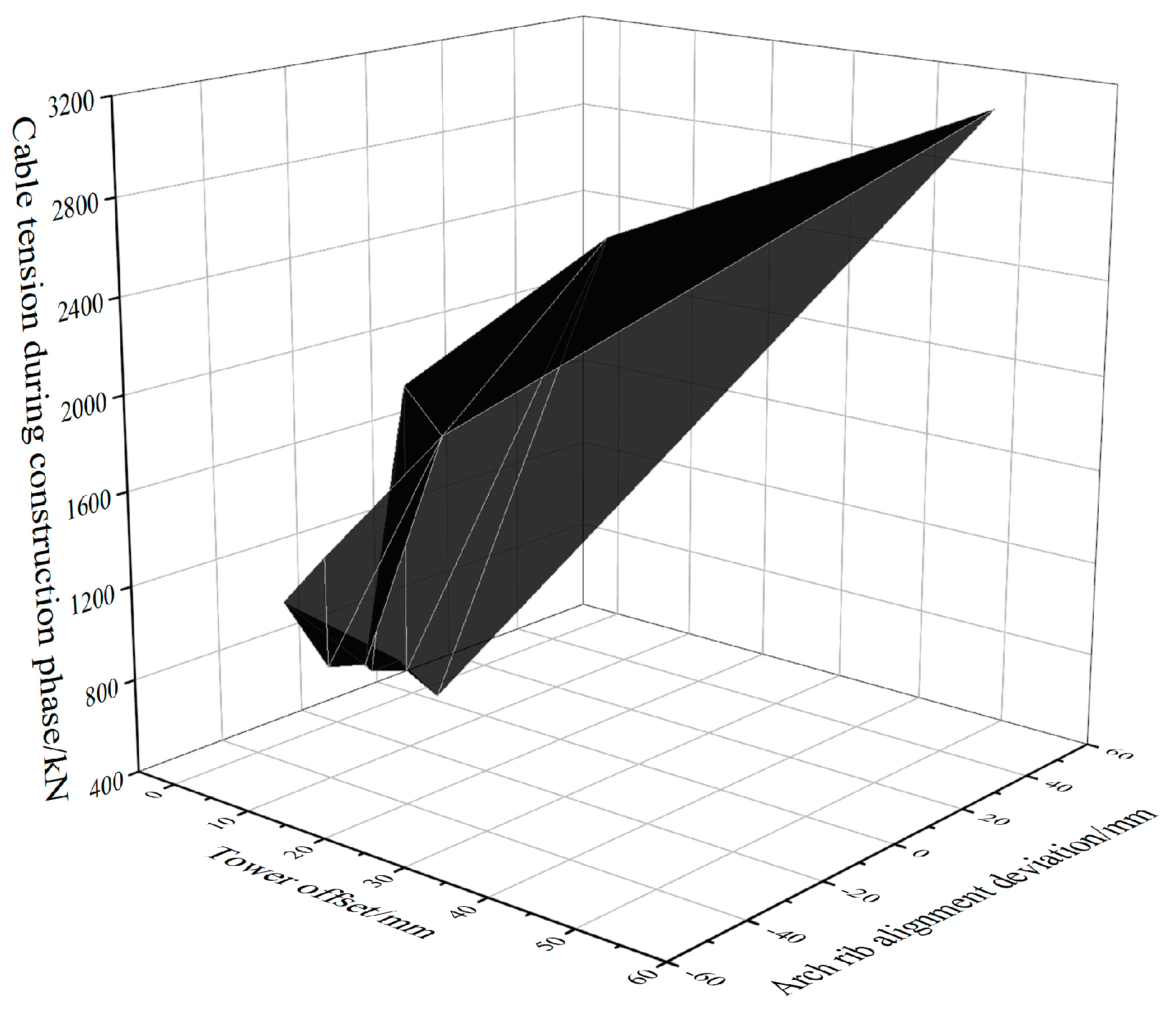
3.2.3. Error Feedback Control and Control Effect Evaluation
4. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, R.; Zhang, Z. A Summary of Development of Concrete-Filled Steel Tube Framed Arch Bridges in China. Bridge Constr. 2016, 46, 45–50. [Google Scholar]
- Zhou, Q.; Feng, P.; Zhou, J.; Xin, J.; Wang, J. Analysis of concrete emptying in concrete-filled steel tube arch bridge under uneven temperature field. J. Bridge Constr. 2024, 54, 103–109. [Google Scholar] [CrossRef]
- Mou, T.; Fan, B.; Zhao, Y.; Li, S. Application and Development of Steel Pipe Concrete Bridges in China. Highway 2017, 62, 161–165. [Google Scholar]
- Zhou, Y.; Wang, Y.; Zhou, J. Arch calculation and control method of 500 m class steel pipe arch bridge. China Highw. J. 2022, 35, 60–72. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Li, J. The calculation method of the whole process cable force optimization of the long-span concrete-filled steel tube arch bridge constructed by cable-stayed suspension method. Prog. Build. Steel Struct. 2019, 21, 33–39. [Google Scholar] [CrossRef]
- Xie, K.; Wang, H.; Guo, X.; Zhou, J. Study on the safety of the concrete pouring process for the main truss arch structure in a long-span concrete-filled steel tube arch bridge. Mech. Adv. Mater. Struct. 2021, 28, 731–740. [Google Scholar] [CrossRef]
- Zhen, J.; Wang, J.; Feng, Z.; Han, Y.; Qin, D. Test on vacuum auxiliary filling technology of concrete-filled steel tube arch section. China Highw. J. 2014, 27, 44–50. [Google Scholar] [CrossRef]
- Han, Y. Test and application of vacuum assisted filling of concrete in tubular arch bridge. Bridge Constr. 2015, 45, 19–25. [Google Scholar]
- Zhou, D.; Deng, N.; Shi, T. Test and numerical simulation analysis of large scale hydration temperature field of concrete-filled steel tube arch bridge. J. Guangxi Univ. 2021, 46, 51–59. [Google Scholar] [CrossRef]
- Sun, J.; Xie, J. Simulation analysis of the hydration heat of large diameter CFST arch and its effects on loading age. Appl. Therm. Eng. 2019, 150, 482–491. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, J.; Zhang, J.; Zhang, L. Self-regulating loading pouring method of long span CFST arch bridge. J. Harbin Inst. Technol. 2020, 52, 82–89. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, J. Chinese steel tube concrete arch bridge. Engineering 2018, 4, 306–331. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, C.; Zhu, Y.; Wang, C. Improved Iteration Algorithm for Determination of Tension of Fastening Stays for Cantilever Construction of Arch Bridge. Bridge Constr. 2016, 46, 65–69. [Google Scholar]
- Qin, D.; Zheng, J.; Du, H.; Han, Y.; Zheng, J.; Wei, L. Optimization Calculation Method for Stayed-Buckle Cable Force under One-Time Tension by Fastening Stay Method and Its Application. China Railw. Sci. 2020, 41, 52–60. [Google Scholar]
- Han, Y.; Qin, D.; Zheng, J. Optimization calculation method for CFST arch bridge cable-stayed suspension construction. Highway 2018, 63, 100–104. [Google Scholar]
- Zhou, J.; Liu, J.; Zhou, W.; Yan, R.; Yan, T. Analysis of the influence of temperature changes on the pre lifting value of cable-stayed buckle and the main arch ring shape of steel tube concrete arch bridges. J. China Foreign Highw. 2017, 37, 62–66. [Google Scholar] [CrossRef]
- Chen, B.; Wei, J.; Zhou, J.; Liu, J.P. Application of concrete-filled steel tube arch bridges in China: Current status and prospects. China Civ. Eng. J. 2017, 50, 50. [Google Scholar] [CrossRef]
- Yu, M.; Deng, N.; Wang, L.; Hao, T.; Zhang, Z. Study on Sunshine Temperature Effect in Concrete-filled Steel Tubes Arch Rib of Extra-Large Arch Bridge. Highw. Eng. 2021, 46, 99–104. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, G.; Qiu, Y. Optimal Polynomial Time-varying Parameters Discrete Grey Model and Its Applications. Stat. Decis. 2022, 38, 31–36. [Google Scholar] [CrossRef]
- Li, X.; Wang, C. STI prediction based on metabolic GM (1, 1) Copula BP neural network. Stat. Decis. 2021, 37, 158–161. [Google Scholar] [CrossRef]
- Vasques, J.F.; Gonalves, R.G.D.J.; Silva-Junior, A.J.D.; Martins, R.S.; Gubert, F.; Mendez-Otero, R. Gangliosides in nervous system development, regeneration, and pathologies. Neural Regen. Res. 2023, 18, 81–86. [Google Scholar] [CrossRef]
- Li, C.; Huang, J.; Li, X. Consider the sunshine temperature field of concrete-filled steel tube arch. Sino-Foreign Highw. 2020, 40, 102–107. [Google Scholar]


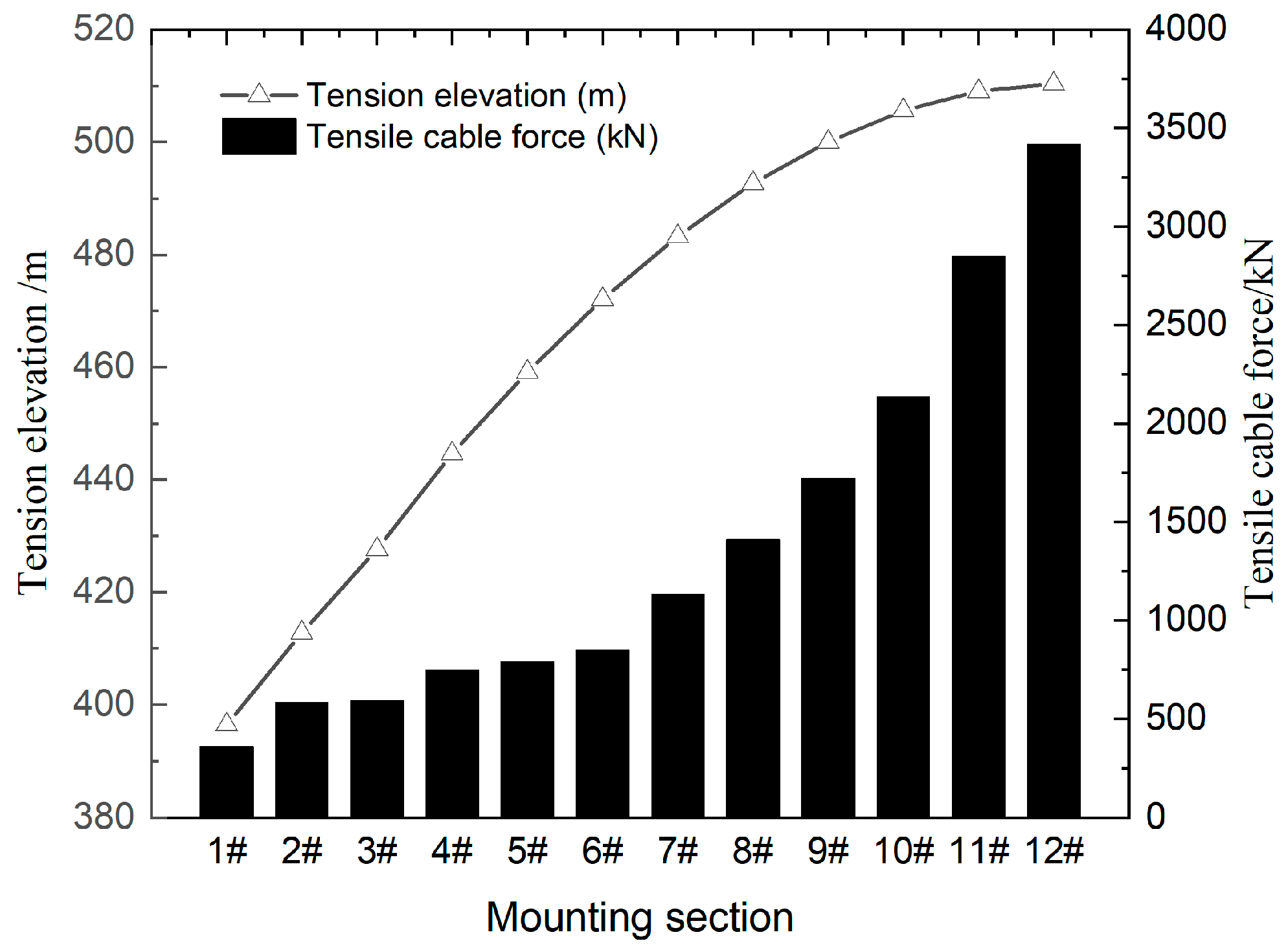

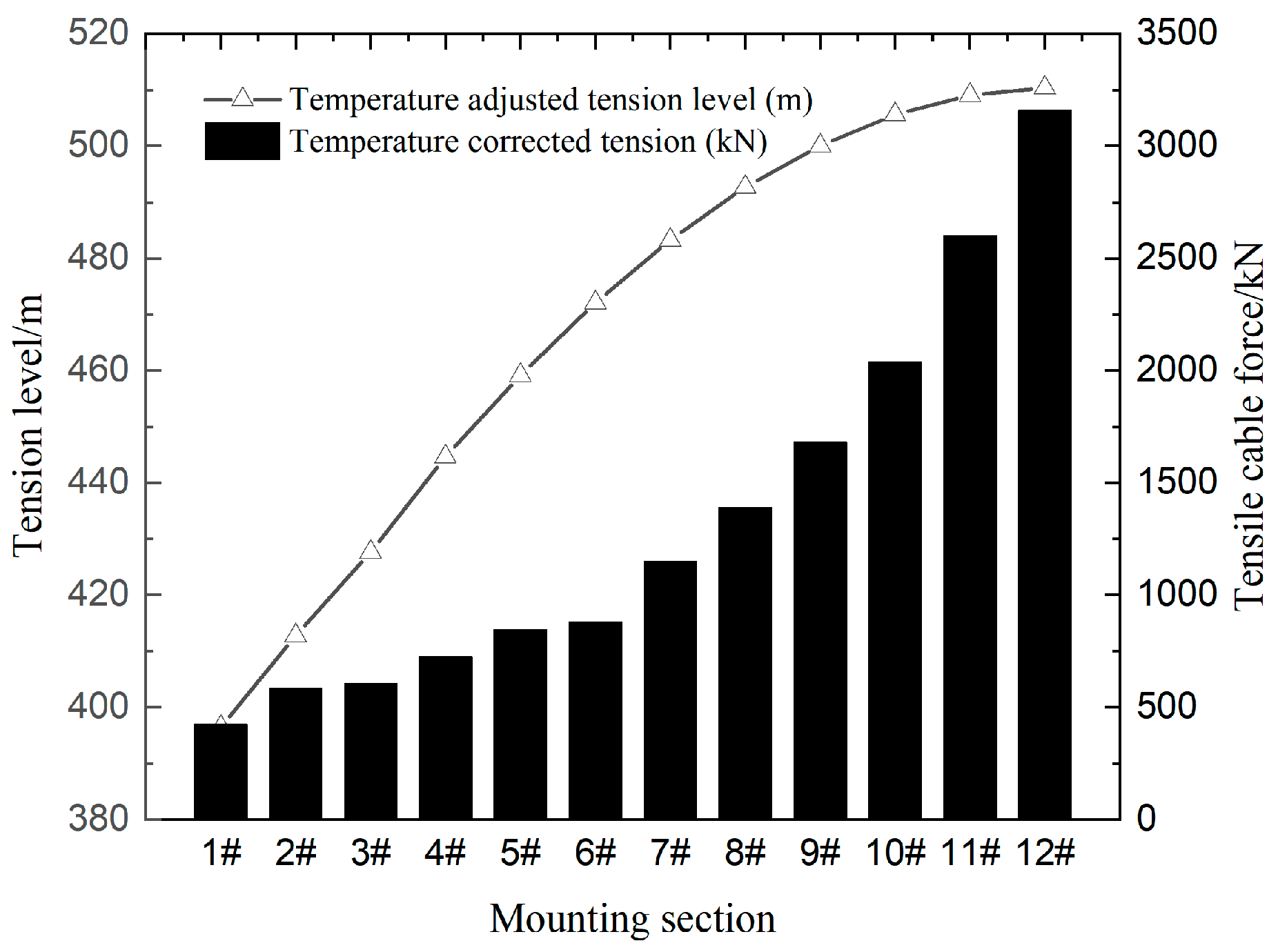

| Section | Manufacturing Elevation (m) | Tensile Elevation (m) | Initial Cable Force (kN) | Optimized Cable Force (kN) |
|---|---|---|---|---|
| 1# | 396.456 | 396.449 | 360 | 433 |
| 2# | 412.811 | 412.789 | 581 | 593 |
| 3# | 427.709 | 427.668 | 591 | 625 |
| 4# | 444.675 | 444.619 | 749 | 681 |
| 5# | 459.290 | 459.179 | 792 | 831 |
| 6# | 472.252 | 472.112 | 847 | 878 |
| 7# | 483.501 | 483.277 | 1132 | 1158 |
| 8# | 492.950 | 492.718 | 1410 | 1387 |
| 9# | 500.399 | 500.079 | 1722 | 1934 |
| 10# | 505.979 | 505.627 | 2134 | 1981 |
| 11# | 509.461 | 509.060 | 2848 | 2588 |
| 12# | 510.881 | 510.394 | 3418 | 3109 |
| No. | Time | Temperature | 1A/mm | 2A/mm | 3A/mm | 4A/mm | 5A/mm | Prediction 6A/mm | Post-Installation Measurement 6A/mm | Error Percentage/% |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3-28 9:21 AM | 15.7 | 0 | −2 | −4 | −6 | −12 | −19 | −20 | 5 |
| 3 | 3-28 10:31 AM | 17.9 | −2 | −1 | −2 | −7 | −18 | −34 | −31 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Li, C.; Wang, L.; Yu, M.; Zhuo, X.; Hao, T.; Wang, X. A Practical Approach to Alignment and Error Feedback Control for Long-Span Arch Bridges. Buildings 2024, 14, 1995. https://doi.org/10.3390/buildings14071995
Yao X, Li C, Wang L, Yu M, Zhuo X, Hao T, Wang X. A Practical Approach to Alignment and Error Feedback Control for Long-Span Arch Bridges. Buildings. 2024; 14(7):1995. https://doi.org/10.3390/buildings14071995
Chicago/Turabian StyleYao, Xinyu, Chuanxi Li, Longlin Wang, Mengsheng Yu, Xiaoli Zhuo, Tianzhi Hao, and Xirui Wang. 2024. "A Practical Approach to Alignment and Error Feedback Control for Long-Span Arch Bridges" Buildings 14, no. 7: 1995. https://doi.org/10.3390/buildings14071995
APA StyleYao, X., Li, C., Wang, L., Yu, M., Zhuo, X., Hao, T., & Wang, X. (2024). A Practical Approach to Alignment and Error Feedback Control for Long-Span Arch Bridges. Buildings, 14(7), 1995. https://doi.org/10.3390/buildings14071995






