Damage Evaluation of Fabricated Shear Wall Reinforced with Angle Steel Using Acoustic Emission Technology
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Specimens
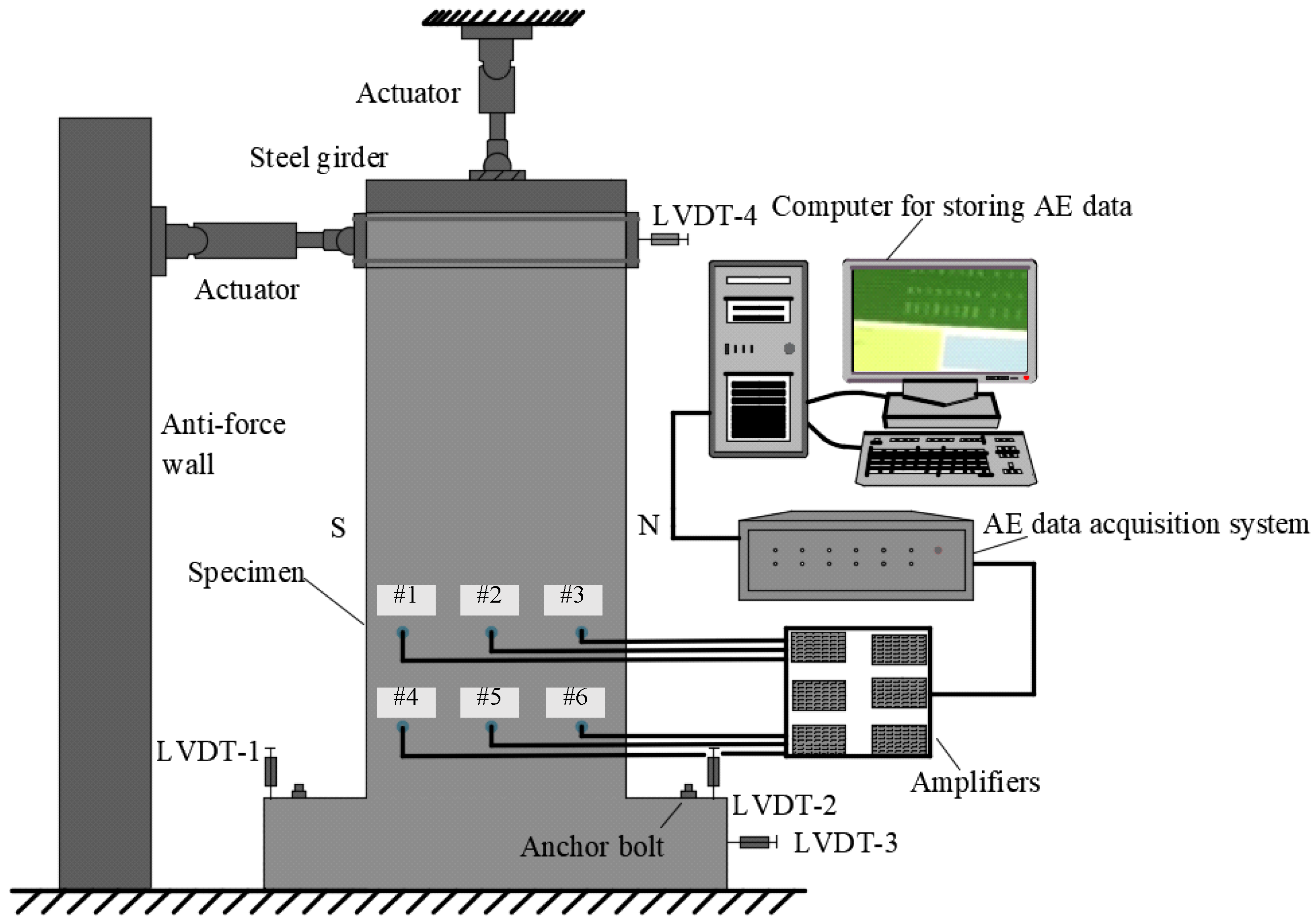
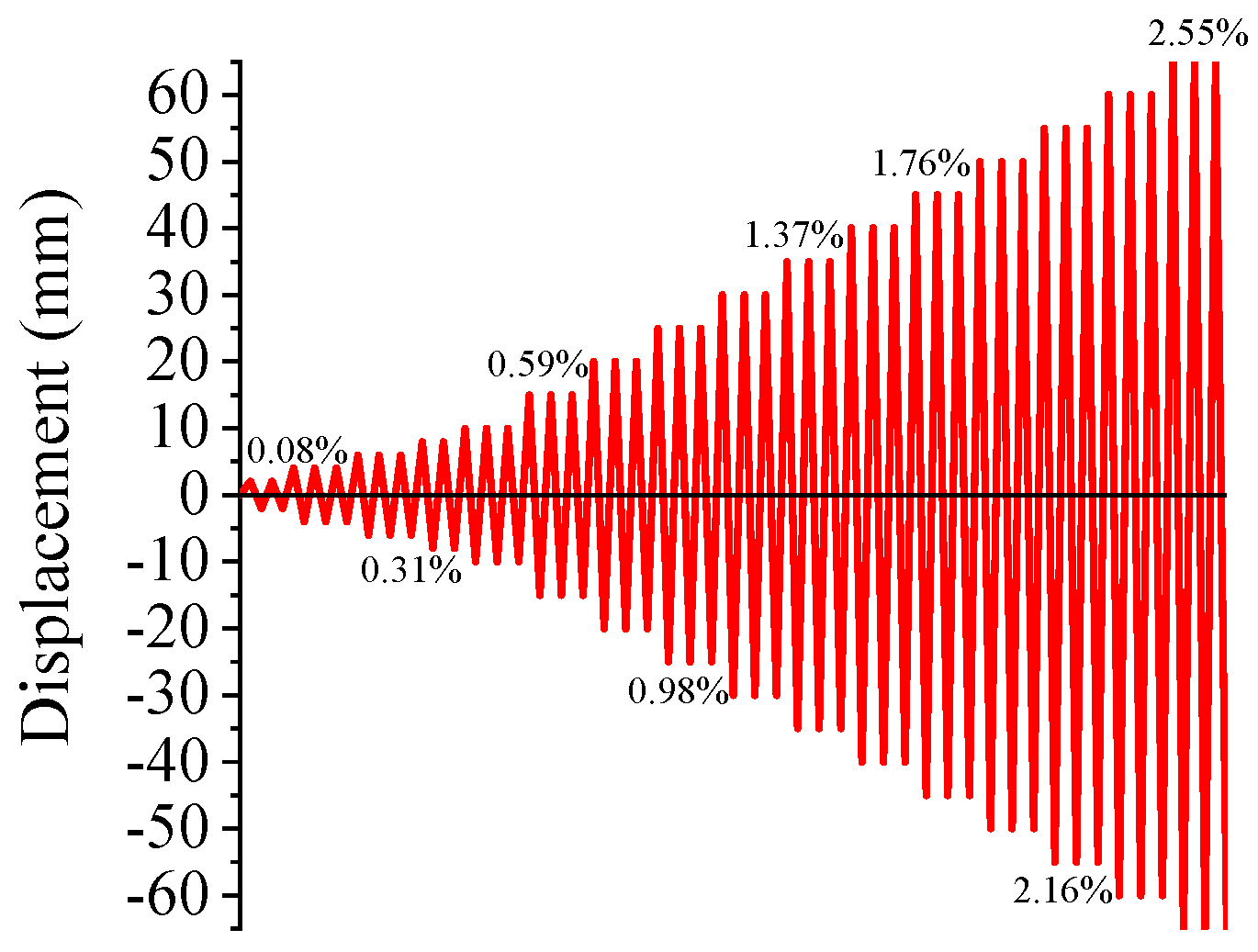
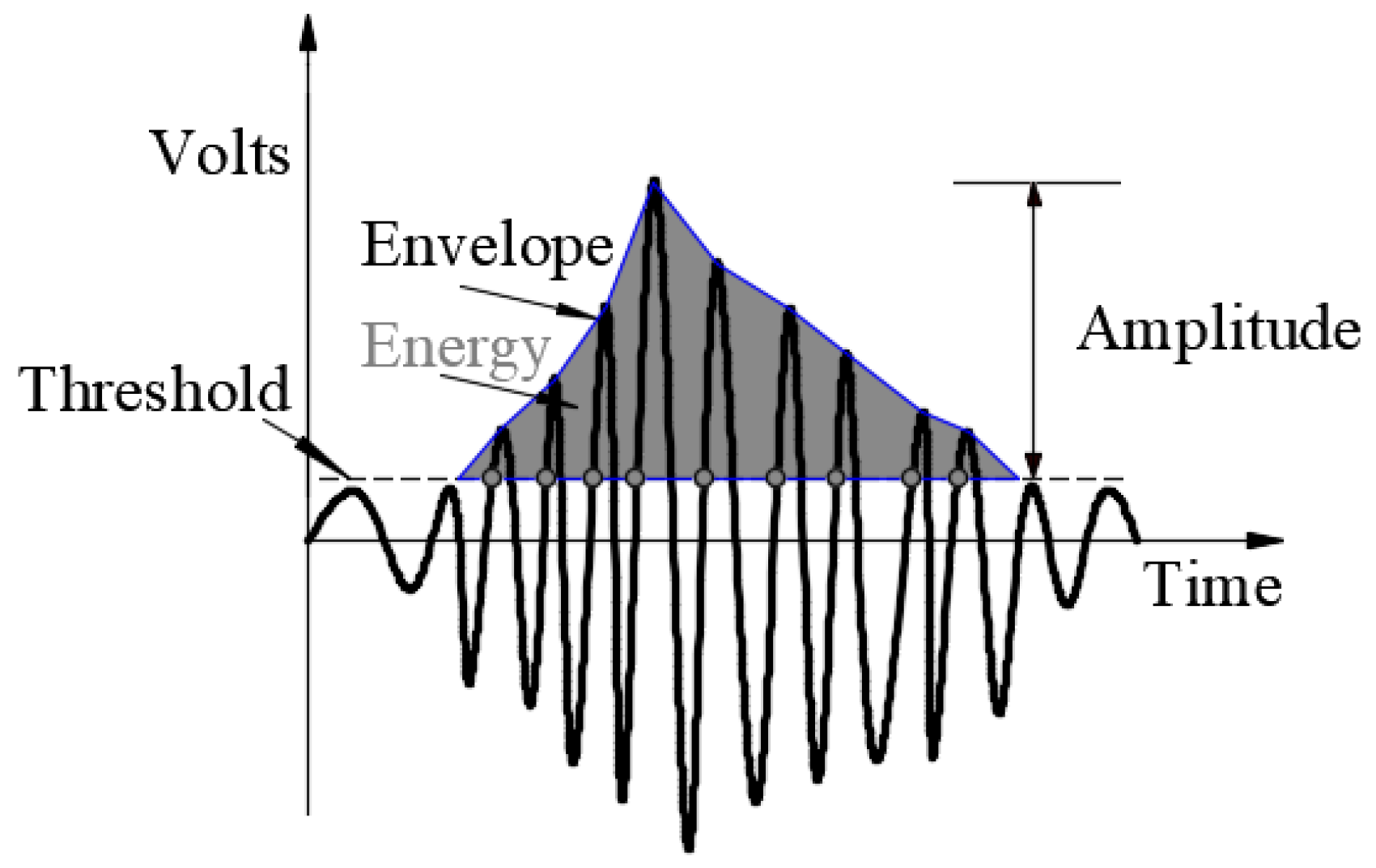
2.2. Loading Schedule and AE System
3. Results and Discussion
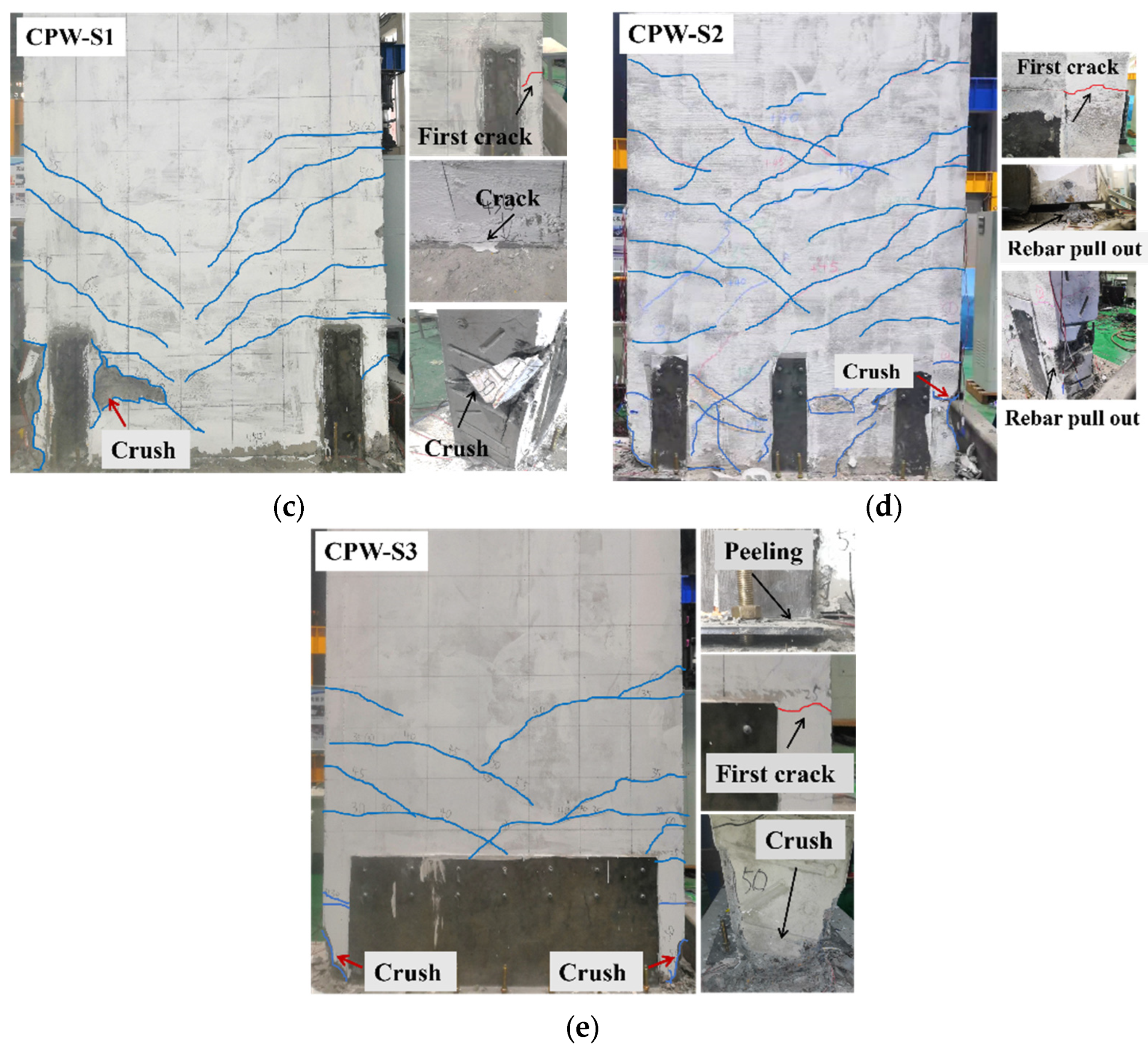
3.1. Destruction of Shear Wall
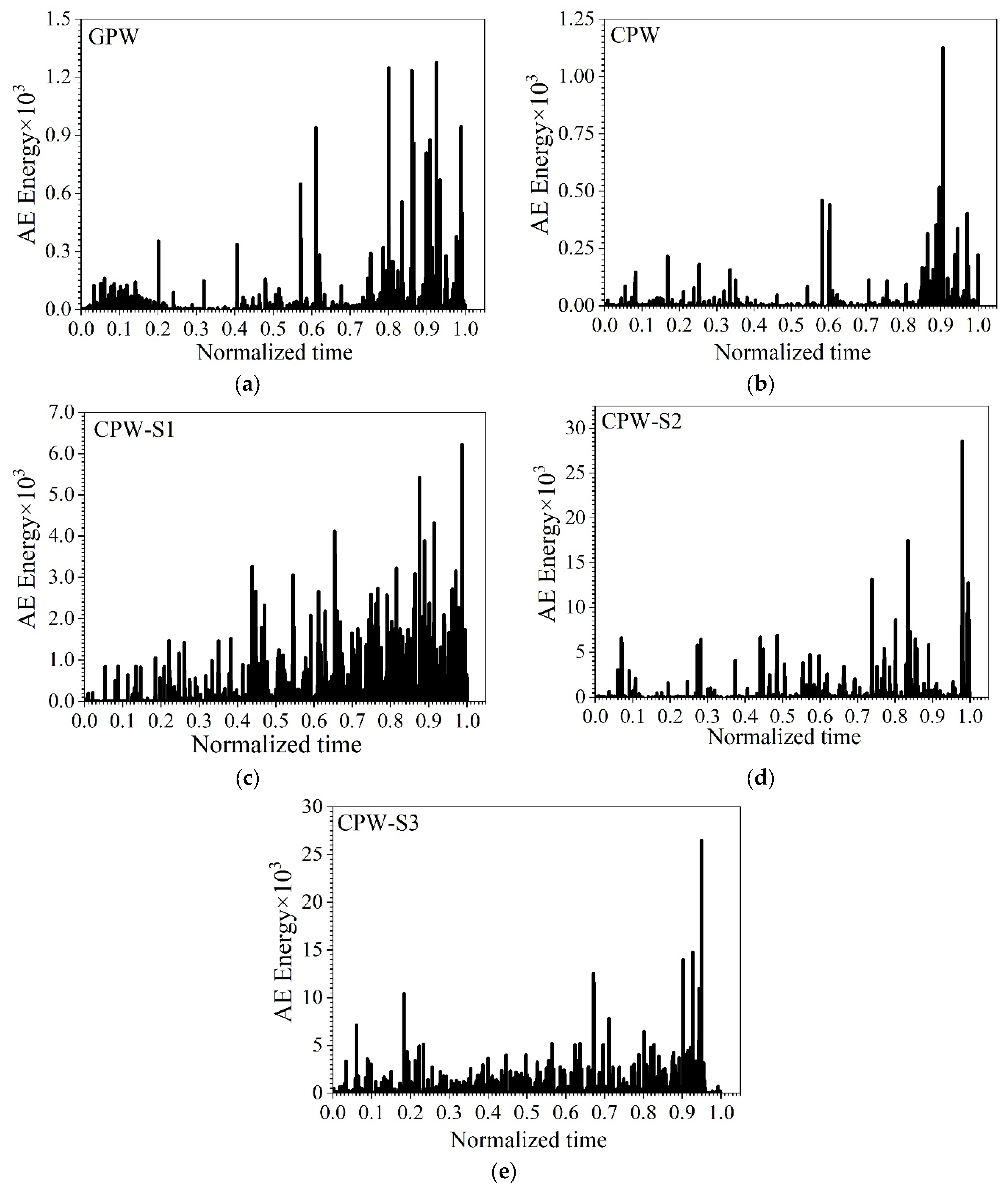
3.2. AE Energy
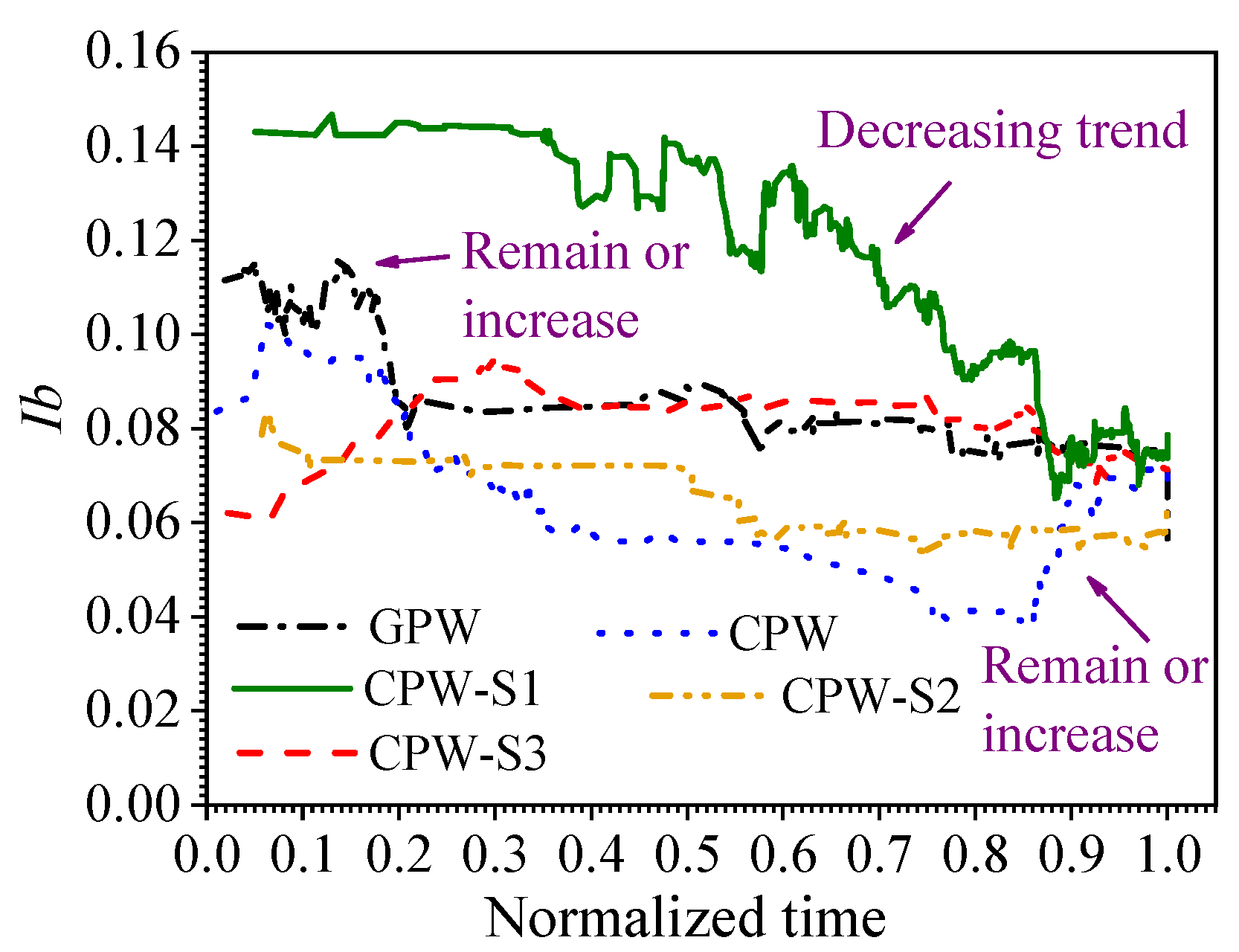
3.3. Ib Value Analysis
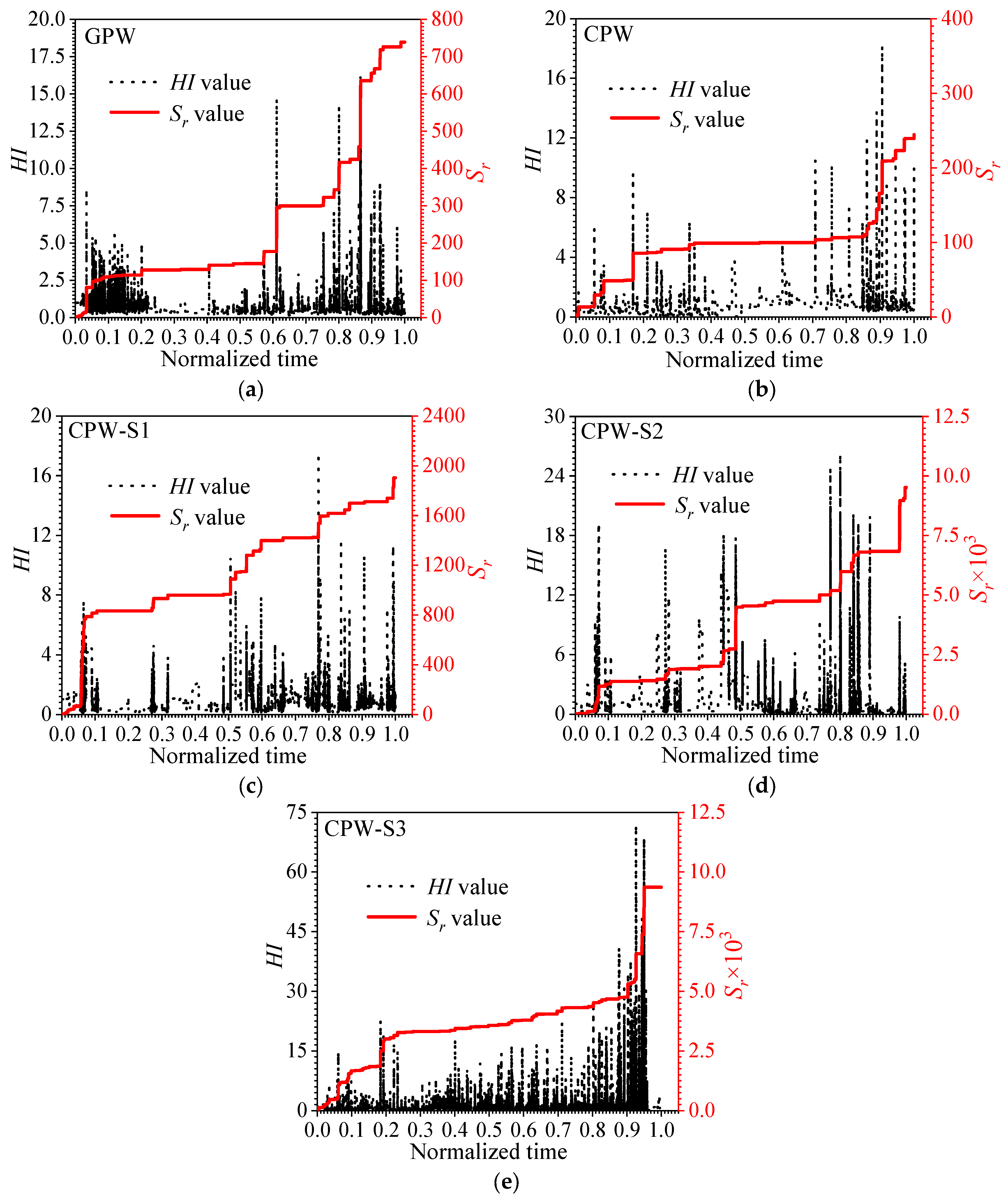
3.4. Intensity Analysis
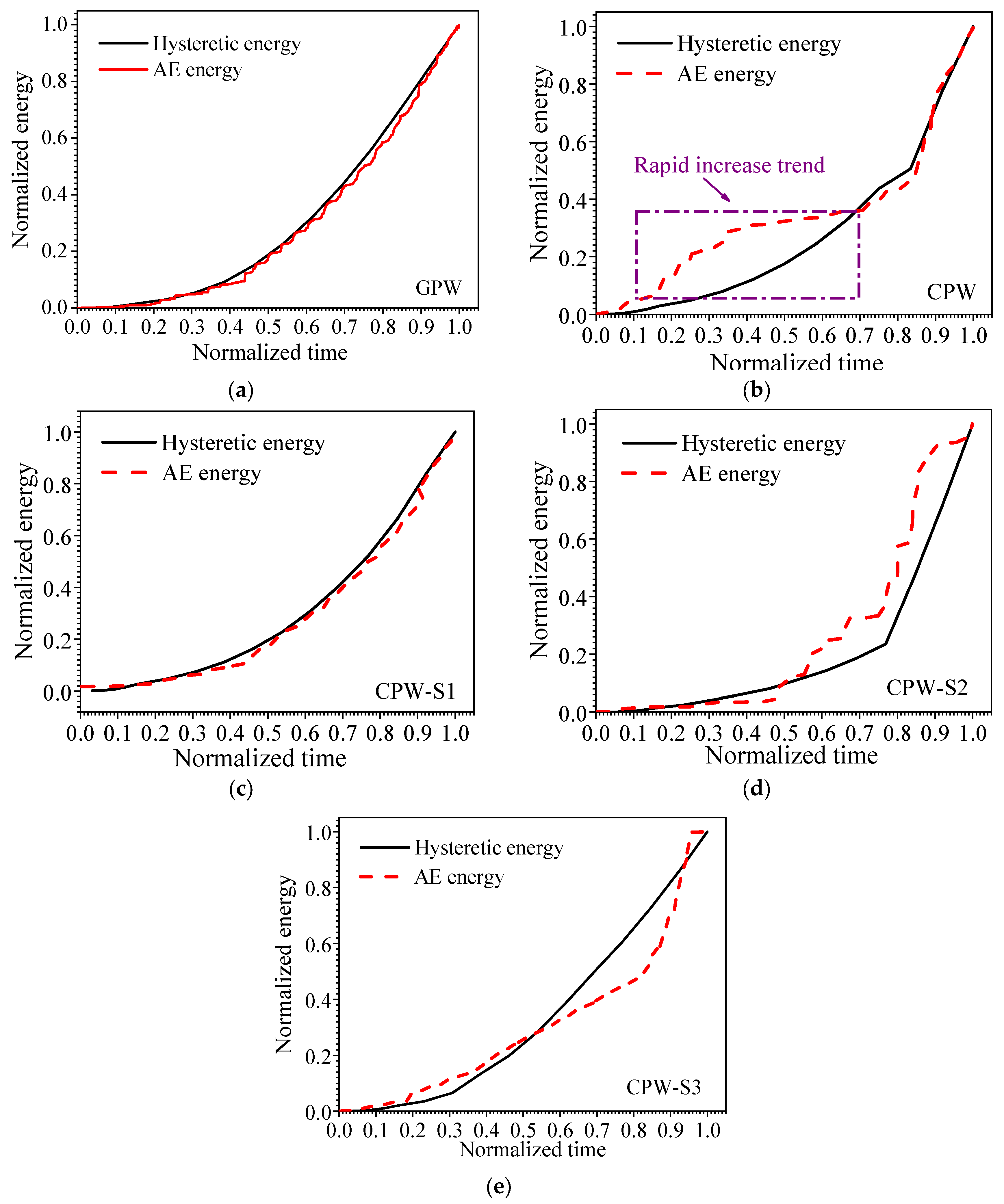
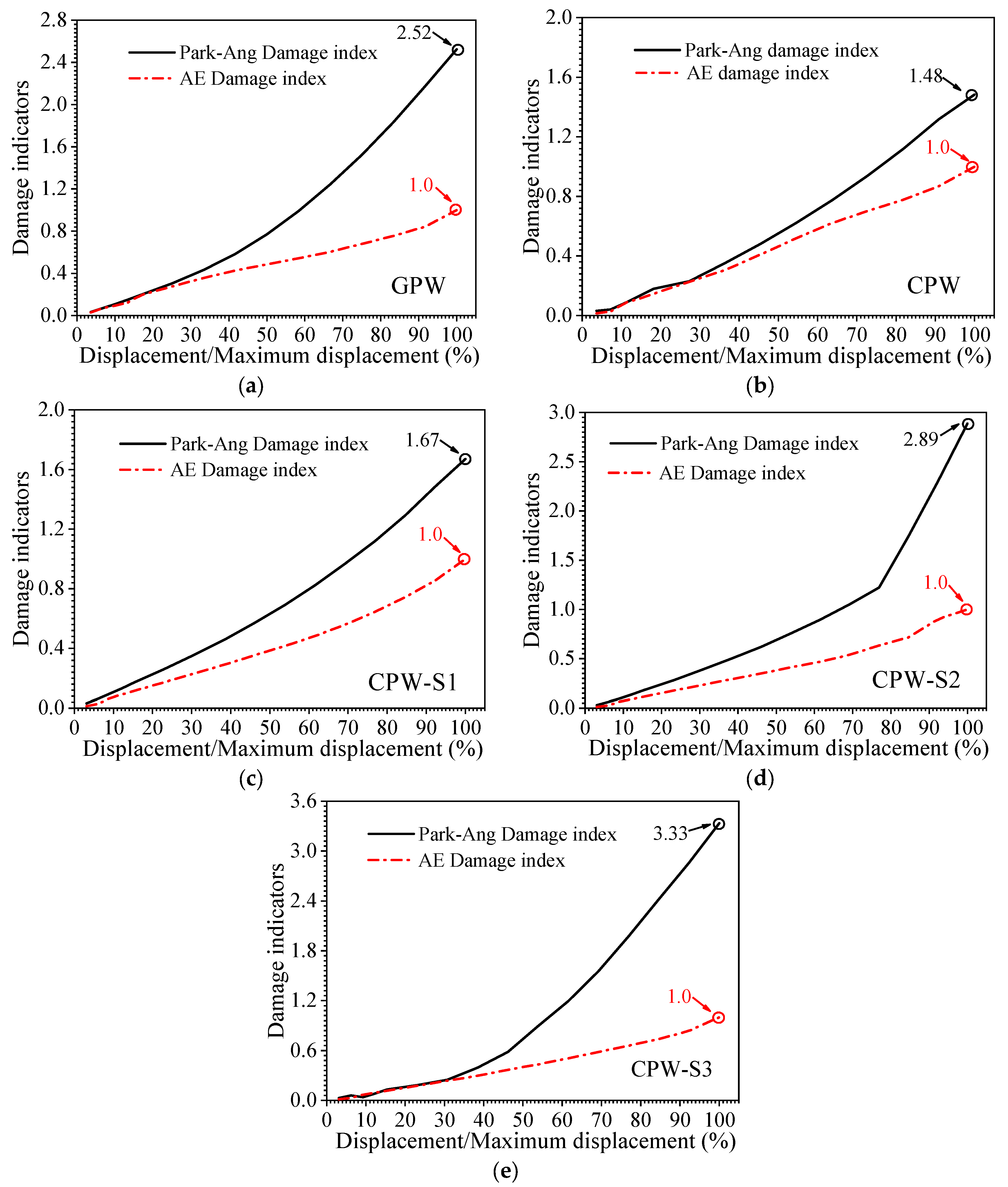
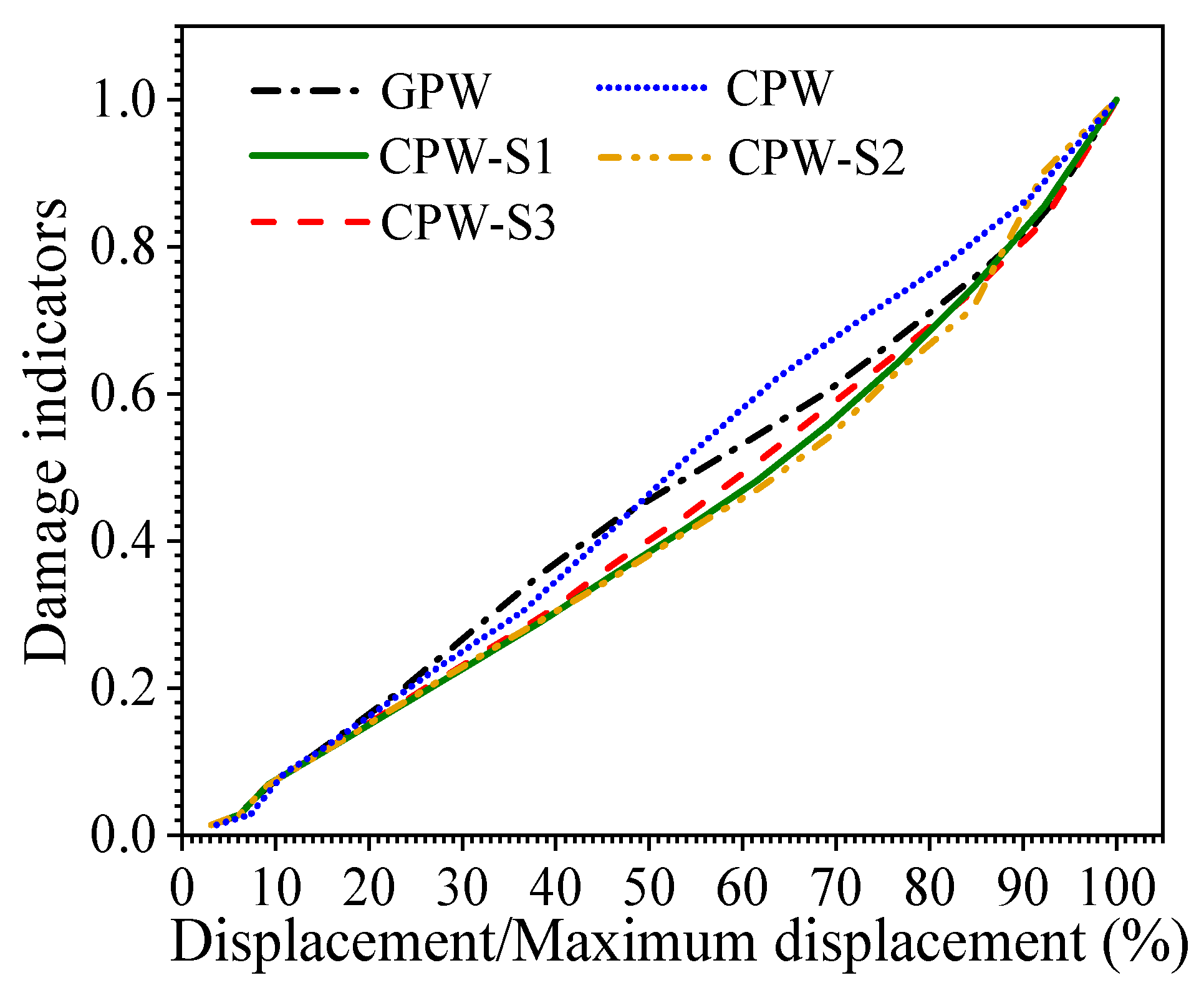
3.5. AE Damage Model
4. Conclusions
- (1)
- The crack propagation of the fabricated shear wall was better characterized by the trend of AE energy under low-cycle repeated loads; that is, the AE events of low energy corresponded to the appearance of micro-cracks, and the AE events of high energy corresponded to the appearance of macro-cracks in the shear wall.
- (2)
- The Ib value decreased with the increase in the damage degree of shear walls, and the Ib value results illustrated the damage to the shear wall CPW was more severe and more micro-cracks were generated at the end of loading.
- (3)
- The intensity analysis approach can better represent the damage evolution of shear walls with horizontal and low-cycle repeated loads, the Sr levels were increased with the increase in the damage of shear walls, and the increase in the HI levels at the peak of each fluctuation indicated that more macroscopic cracks were generated inside the shear walls.
- (4)
- The AE damage index was proposed based on the Park–Ang damage model incorporating AE fractal energy density, which could effectively evaluate the damage degree of shear walls under repeated loading. The trend of the damage model calculated by the AE damage index could represent the damage degree of shear walls. The AE damage model proposed in this study was effective for the damage evaluation of shear walls under repeated loads.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, T.; Zhang, G.; Chen, C. Experimental study on self-centering concrete wall with distributed friction devices. J. Earthq. Eng. 2014, 18, 214–230. [Google Scholar] [CrossRef]
- Gu, Q.; Dong, G.; Wang, X.; Jiang, H.; Peng, S. Research on pseudo-static cyclic tests of precast concrete shear walls with vertical rebar lapping in grout-filled constrained hole. Eng. Struct. 2019, 189, 396–410. [Google Scholar] [CrossRef]
- Han, R.; Li, S.; Sun, W. Effect of grouting material strength on bond strength of sleeve and acoustic emission characterization of bond failure damage process. Constr. Build. Mater. 2022, 324, 126503. [Google Scholar] [CrossRef]
- Dallyn, P.; El-Hamalawi, A.; Palmeri, A.; Knight, R. Experimental investigation on the development of wear in grouted connections for offshore wind turbine generators. Eng. Struct. 2016, 113, 89–102. [Google Scholar] [CrossRef]
- Tullini, N.; Minghini, F. Grouted sleeve connections used in precast reinforced concrete construction—Experimental investigation of a column-to-column joint. Eng. Struct. 2016, 127, 784–803. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Yan, T.; Zhang, A.-L.; Su, L.; Shen, C.-J. Experimental research on special steel frame with stiffened double steel plate shear wall. J. Constr. Steel Res. 2022, 189, 107067. [Google Scholar] [CrossRef]
- Khaloo, A.; Ghamari, A.; Foroutani, M. On the design of stiffened steel plate shear wall with diagonal stiffeners considering the crack effect. Structures 2021, 31, 828–841. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, C.; Ding, F.-X.; Duan, Q.; Cao, Z.; Xu, F.; Yang, C.-Q.; Lu, D.; Xiang, P. Mechanical performance of the grouted lapped double reinforcements anchored in embedded corrugated sleeves. Structures 2020, 28, 1354–1365. [Google Scholar] [CrossRef]
- Sayadi, A.A.; Rahman, A.B.A.; Bahmani, M.; Shahryari, L. Effective of elastic and inelastic zone on behavior of glass fiber reinforced polymer splice sleeve. Constr. Build. Mater. 2015, 80, 38–47. [Google Scholar] [CrossRef]
- Henin, E.; Morcous, G. Non-proprietary bar splice sleeve for precast concrete construction. Eng. Struct. 2015, 83, 154–162. [Google Scholar] [CrossRef]
- Ameli, M.J.; Pantelides, C.P. Seismic analysis of precast concrete bridge columns connected with grouted splice sleeve connectors. J. Struct. Eng. 2017, 143, 04016176. [Google Scholar] [CrossRef]
- Wu, G.; Han, R.; Li, S.; Guo, P. Quantitative damage analysis of brick masonry under uniaxial compression and shear using acoustic emission technology. Struct. Control. Health Monit. 2022, 29, e3130. [Google Scholar] [CrossRef]
- Li, S.; Wu, Y.; Shi, H. A novel acoustic emission monitoring method of cross-section precise localization of defects and wire breaking of parallel wire bundle. Struct. Control. Health Monit. 2019, 26, e2334. [Google Scholar] [CrossRef]
- Han, R.; Guo, P.; Li, S.; Zhang, P. Damage evaluation of UHPC-GFRP hybrid beams based on acoustic emission technology under bending experiment. Structures 2023, 56, 104890. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Guo, P.; Zhang, P.; Wang, C.; Sun, W.; Han, S. Characteristic analysis of acoustic emission monitoring parameters for crack propagation in UHPC-NC composite beam under bending test. Constr. Build. Mater. 2021, 278, 122401. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Castro, E.; Gallego, A. AE monitoring for damage assessment of RC exterior beam-column subassemblages subjected to cyclic loading. Struct. Health Monit. 2009, 8, 175–189. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, W.; Zhang, Z.; Li, B. AE monitoring of reinforced concrete squat wall subjected to cyclic loading with information entropy-based analysis. Eng. Struct. 2018, 165, 359–367. [Google Scholar] [CrossRef]
- Guzmán, C.; Torres, D.; Hucailuk, C.; Filipussi, D. Analysis of the acoustic emission in a reinforced concrete beam using a four points bending test. Procedia Mater. Sci. 2015, 8, 148–154. [Google Scholar] [CrossRef]
- Ma, G.; Li, H. Acoustic emission monitoring and damage assessment of FRP-strengthened reinforced concrete columns under cyclic loading. Constr. Build. Mater. 2017, 144, 86–98. [Google Scholar] [CrossRef]
- Ma, G.; Wu, C.; Hwang, H.-J.; Li, B. Crack monitoring and damage assessment of BFRP-jacketed concrete cylinders under compression load based on acoustic emission techniques. Constr. Build. Mater. 2021, 272, 121936. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Wang, D.; Zhao, G. Damage monitoring of masonry structure under in-situ uniaxial compression test using acoustic emission parameters. Constr. Build. Mater. 2019, 215, 812–822. [Google Scholar] [CrossRef]
- Shiotani, T.; Fujii, K.; Aoki, T.; Amou, K. Evaluation of progressive failure using AE sources and improved b-value on slope model tests. Prog. Acoust. Emiss. 1994, 7, 529–534. [Google Scholar]
- Zhang, X.; Li, B. Damage characteristics and assessment of corroded RC beam-column joint under cyclic loading based on acoustic emission monitoring. Eng. Struct. 2020, 205, 110090. [Google Scholar] [CrossRef]
- Golaski, L.; Pawel, G.; Kanji, O. Diagnostic of reinforced concrete bridge by acoustic emission. J. Acoust. Emiss. 2002, 20, 83–98. [Google Scholar]
- Shahidan, S.; Pulin, R.; Bunnori, N.M.; Holford, K.M. Damage classification in reinforced concrete beam by acoustic emission signal analysis. Constr. Build. Mater. 2013, 45, 78–86. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, H.S. Seismic damage analysis of reinforced concrete buildings. J. Struct. Eng. 1985, 114, 740–757. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, H.S. Mechanistic Seismic damage model for reinforced concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. Ministry of construction and General Administration of Quality Supervision: Beijing, China, 2003.
- JG/T 398-2019; The Grouting Coupler for Rebars Splicing. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2019.
- JG/T 408-2019; Cementitious Grout for Sleeve of Rebar Splicing. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2019.
- JGJ/T 101-2015; Specification of Seismic Test of Building. China Architecture & Building Press: Beijing, China, 2015.
- Jafari, A.; Beheshti, M.; Shahmansouri, A.A.; Bengar, H.A. Cyclic response and damage status of coupled and hybrid-coupled shear walls. Structures 2024, 61, 106010. [Google Scholar] [CrossRef]
- Lu, S.; Jiang, M.; Sui, Q.; Dong, H.; Sai, Y.; Jia, L. Acoustic emission location on aluminum alloy structure by using FBG sensors and PSO method. J. Mod. Opt. 2016, 63, 742–749. [Google Scholar] [CrossRef]
- Yin, S.; Cui, Z.; Kundu, T. Acoustic source localization in anisotropic plates with “Z” shaped sensor clusters. Ultrasonics 2018, 84, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Rivière, J.; Lv, Z.; Johnson, P.; Marone, C. Evolution of b-value during the seismic cycle: Insights from laboratory experiments on simulated faults. Earth Planet. Sci. Lett. 2018, 482, 407–413. [Google Scholar] [CrossRef]
- Li, S.; Wu, Y.; Li, W.; Li, P. Shear test on damage evolution of brick masonry based on acoustic emission technique. Constr. Build. Mater. 2021, 273, 121782. [Google Scholar] [CrossRef]
- Han, Q.; Yang, G.; Xu, J.; Fu, Z.; Lacidogna, G.; Carpinteri, A. Acoustic emission data analyses based on crumb rubber concrete beam bending tests. Eng. Fract. Mech. 2019, 210, 189–202. [Google Scholar] [CrossRef]
- Li, S.; Wu, G.; Shi, H. Acoustic emission characteristics of semi-rigid bases with three moisture conditions during bending tests. Road Mater. Pavement Des. 2019, 20, 187–198. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Wang, D. Characteristic analysis of acoustic emission signals of masonry specimens under uniaxial compression test. Constr. Build. Mater. 2019, 196, 637–648. [Google Scholar] [CrossRef]
- Wu, Y.; Gu, S.; Zhao, G.; Li, S. Damage assessment of the in-service brick masonry structure using acoustic emission technique. Mater. Struct. 2020, 53, 41. [Google Scholar] [CrossRef]
- Shiotani, T.; Ohtsu, M.; Ikeda, K. Detection and evaluation of AE waves due to rock deformation. Constr. Build. Mater. 2001, 15, 235–246. [Google Scholar] [CrossRef]
- Li, D.; Hai, C.; Jinping, O. Fracture behavior and damage evaluation of polyvinyl alcohol fiber concrete using acoustic emission technique. Mater. Des. 2012, 40, 205–211. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Pugno, N. Structural damage diagnosis and life-time assessment by acoustic emission monitoring. Eng. Fract. Mech. 2007, 74, 273–289. [Google Scholar] [CrossRef]
- Paulay, T.; Priestley, M.N. Seismic Design of Reinforced Concrete and Masonry Buildings; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Promis, G.; Ferrier, E.; Hamelin, P. Effect of external FRP retrofitting on reinforced concrete short columns for seismic strengthening. Compos. Struct. 2009, 88, 367–379. [Google Scholar] [CrossRef]
- Samiullah, Q.; Laurent, M.; Emmanuel, F. Seismic behavior of RC short shear wall strengthened with externally bonded CFRP strips. Compos. Struct. 2019, 211, 390–400. [Google Scholar]
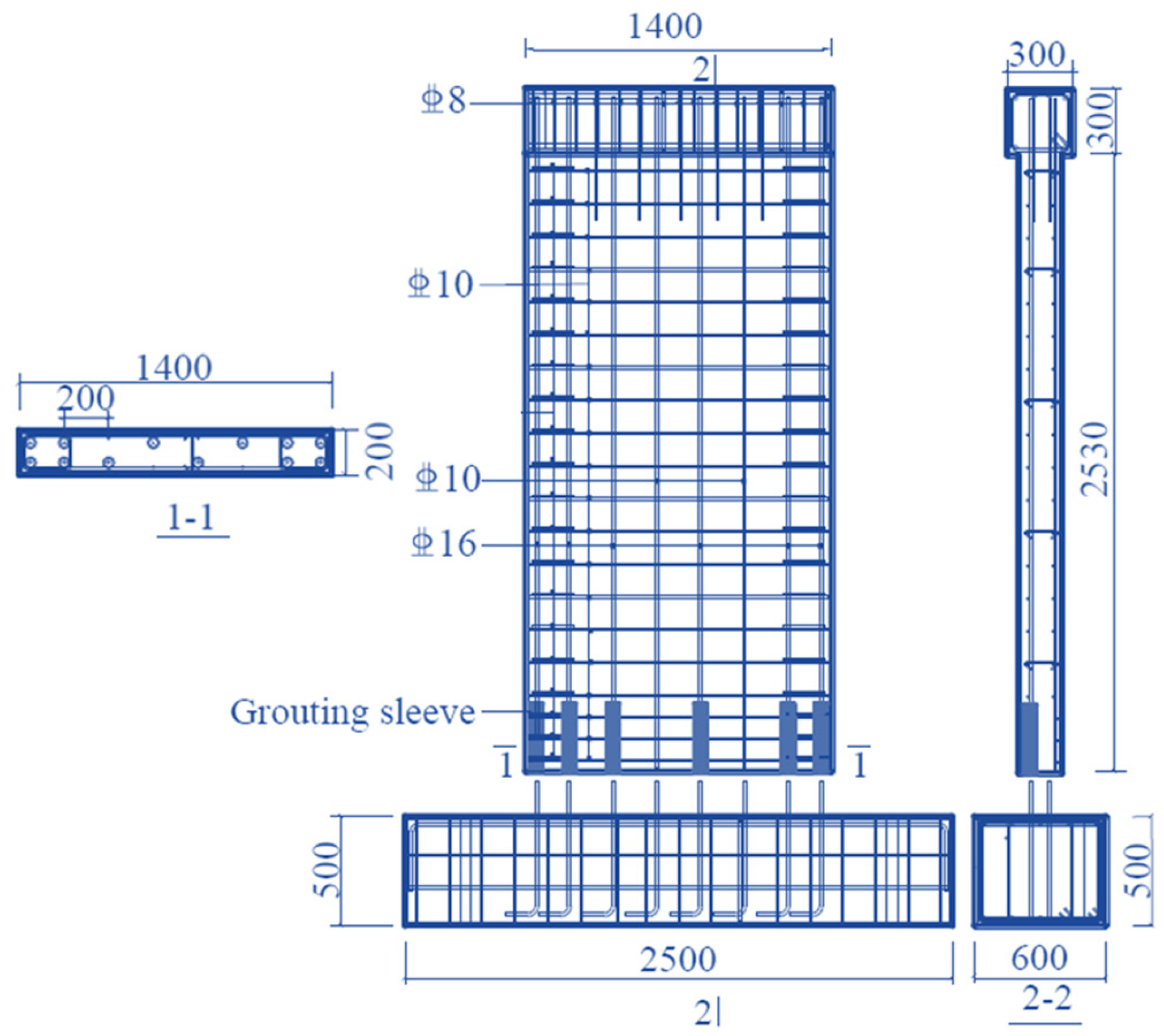
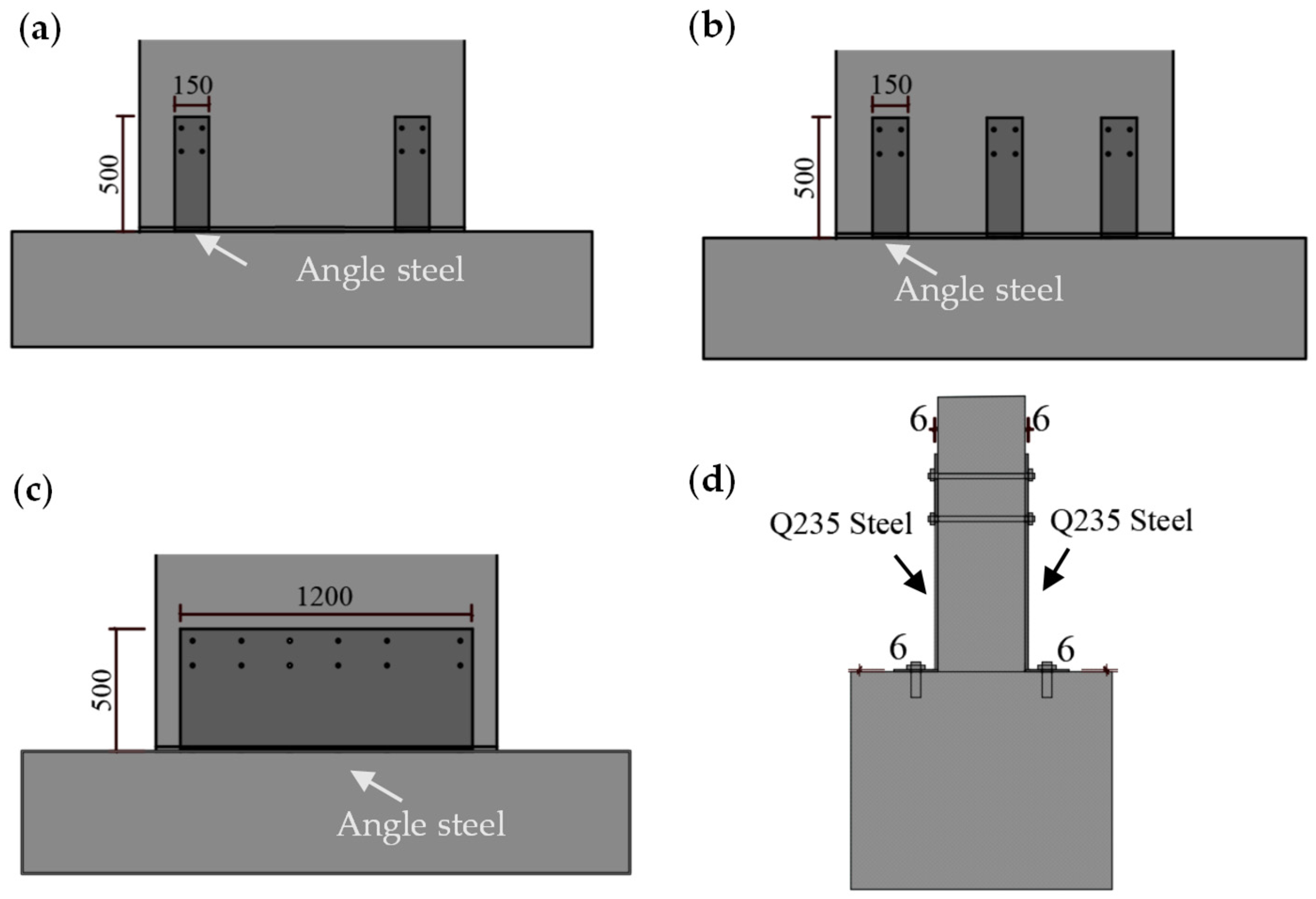

| Diameter do (mm) | 8 | 10 | 16 |
| Yield strength fy (MPa) | 460 | 445 | 460 |
| Elongation rate (%) | 24.0 | 24.1 | 15.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, R.; Li, S.; Wu, G. Damage Evaluation of Fabricated Shear Wall Reinforced with Angle Steel Using Acoustic Emission Technology. Buildings 2024, 14, 2038. https://doi.org/10.3390/buildings14072038
Han R, Li S, Wu G. Damage Evaluation of Fabricated Shear Wall Reinforced with Angle Steel Using Acoustic Emission Technology. Buildings. 2024; 14(7):2038. https://doi.org/10.3390/buildings14072038
Chicago/Turabian StyleHan, Ruiqing, Shengli Li, and Guangming Wu. 2024. "Damage Evaluation of Fabricated Shear Wall Reinforced with Angle Steel Using Acoustic Emission Technology" Buildings 14, no. 7: 2038. https://doi.org/10.3390/buildings14072038
APA StyleHan, R., Li, S., & Wu, G. (2024). Damage Evaluation of Fabricated Shear Wall Reinforced with Angle Steel Using Acoustic Emission Technology. Buildings, 14(7), 2038. https://doi.org/10.3390/buildings14072038





