Numerical Modeling of Four-Pile Caps Using the Concrete Damaged Plasticity Model
Abstract
:1. Introduction
2. Methodology
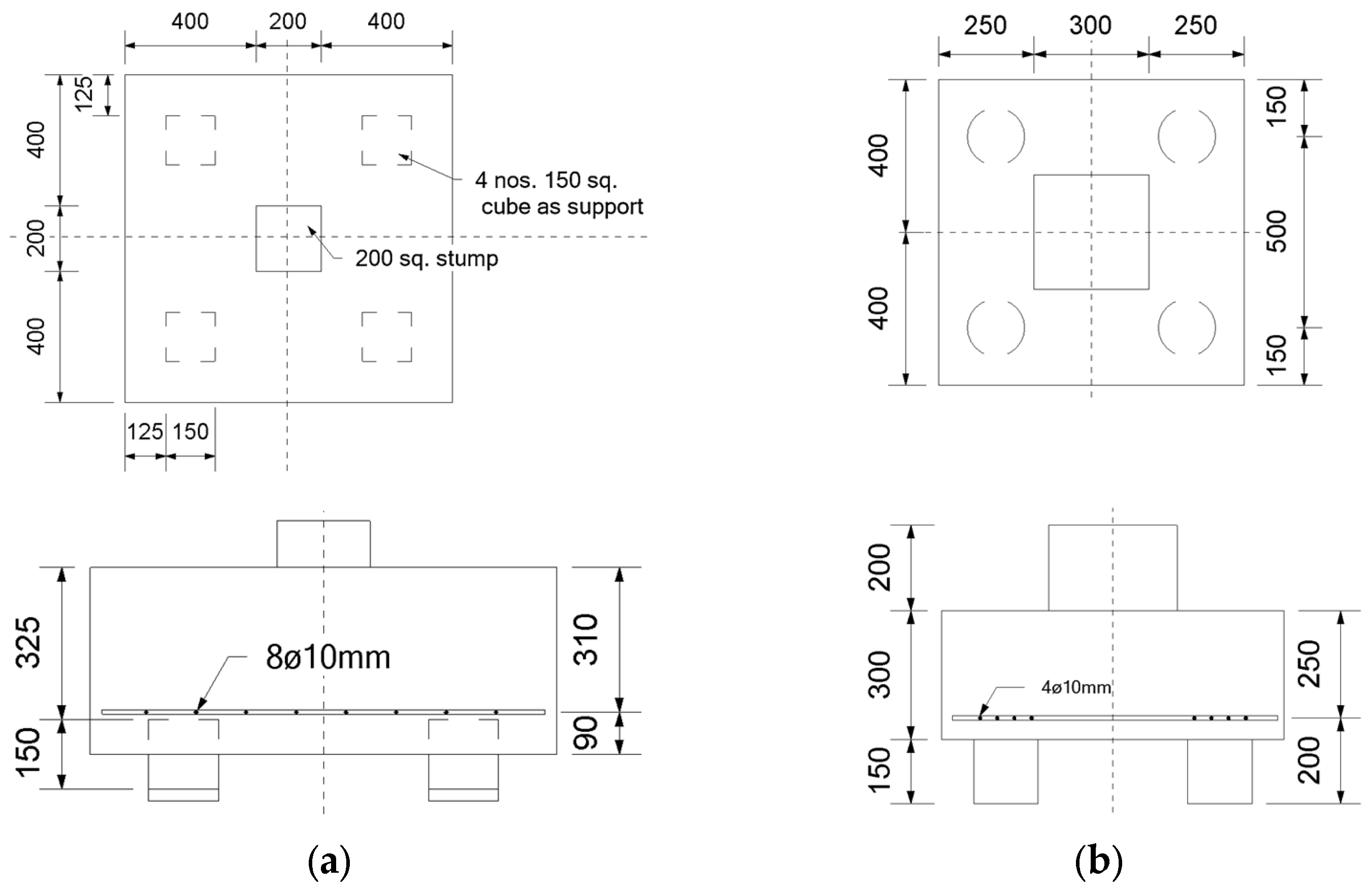
2.1. Experiments and Material Properties
2.2. Analisys Methods
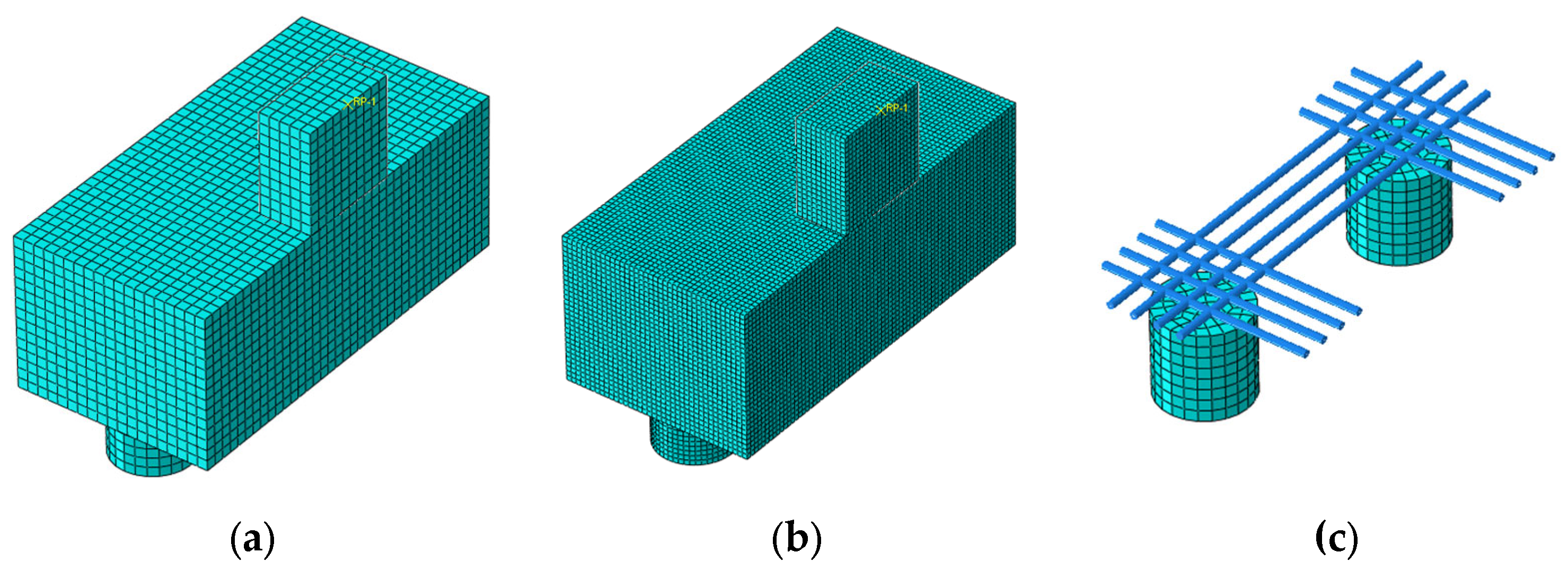
2.3. Numerical Modeling
2.4. Calibration and Analysis of the Influence of Parameters
2.5. Analysis of Feasibility of Extrapolated Models
3. Results and Discussion
3.1. Specimen of Chan and Poh [5]
3.1.1. Mesh Sensitivity
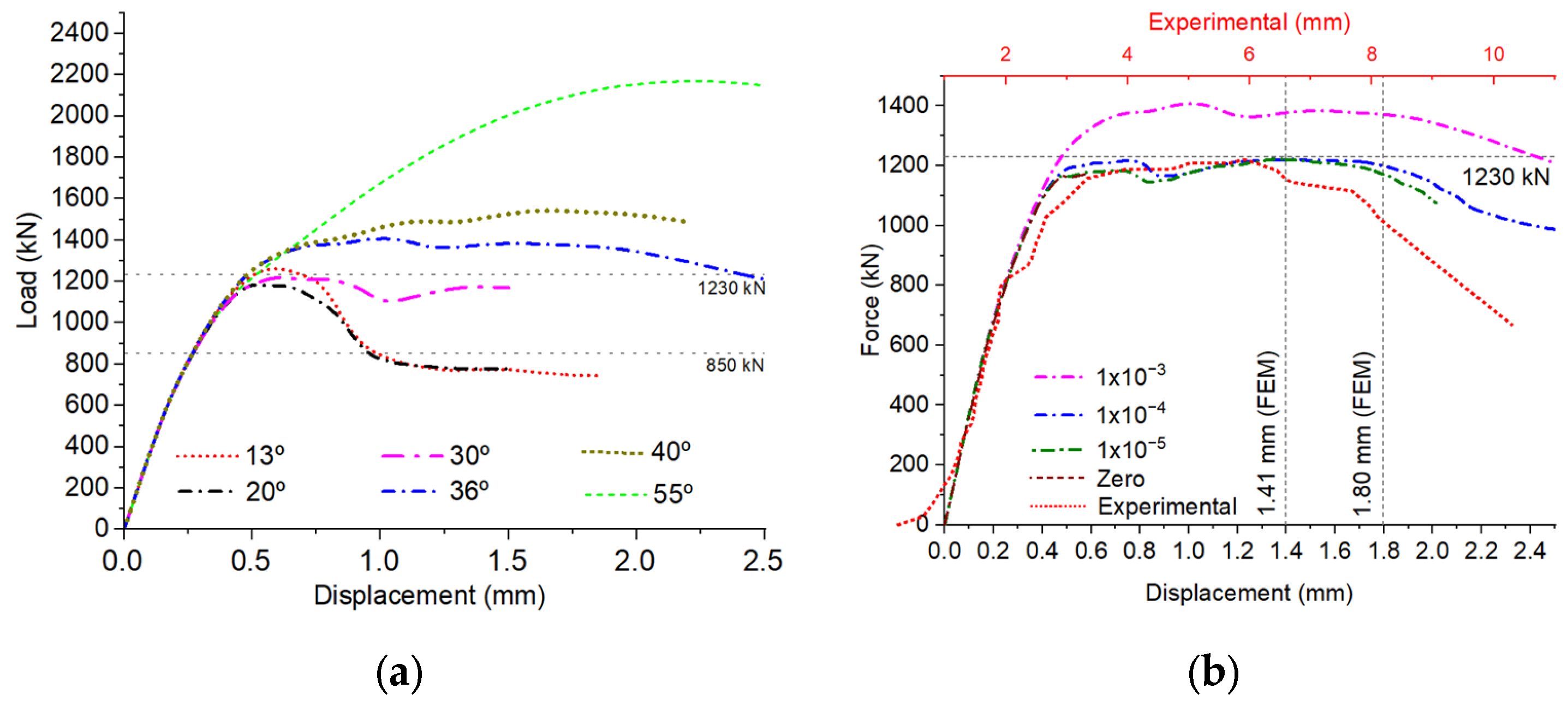
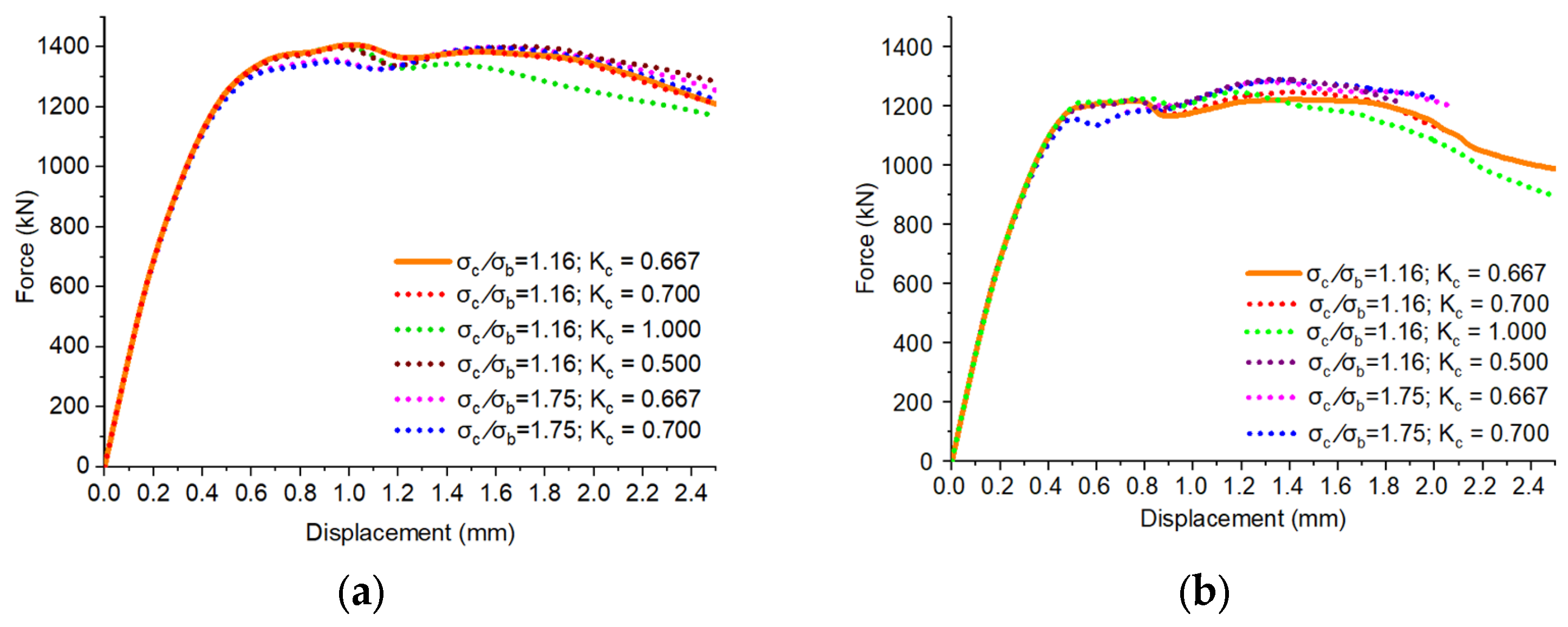
3.1.2. Influence of CDP Parameters on Force × Displacement Curves
Static Analysis
Quasi-Static Analysis
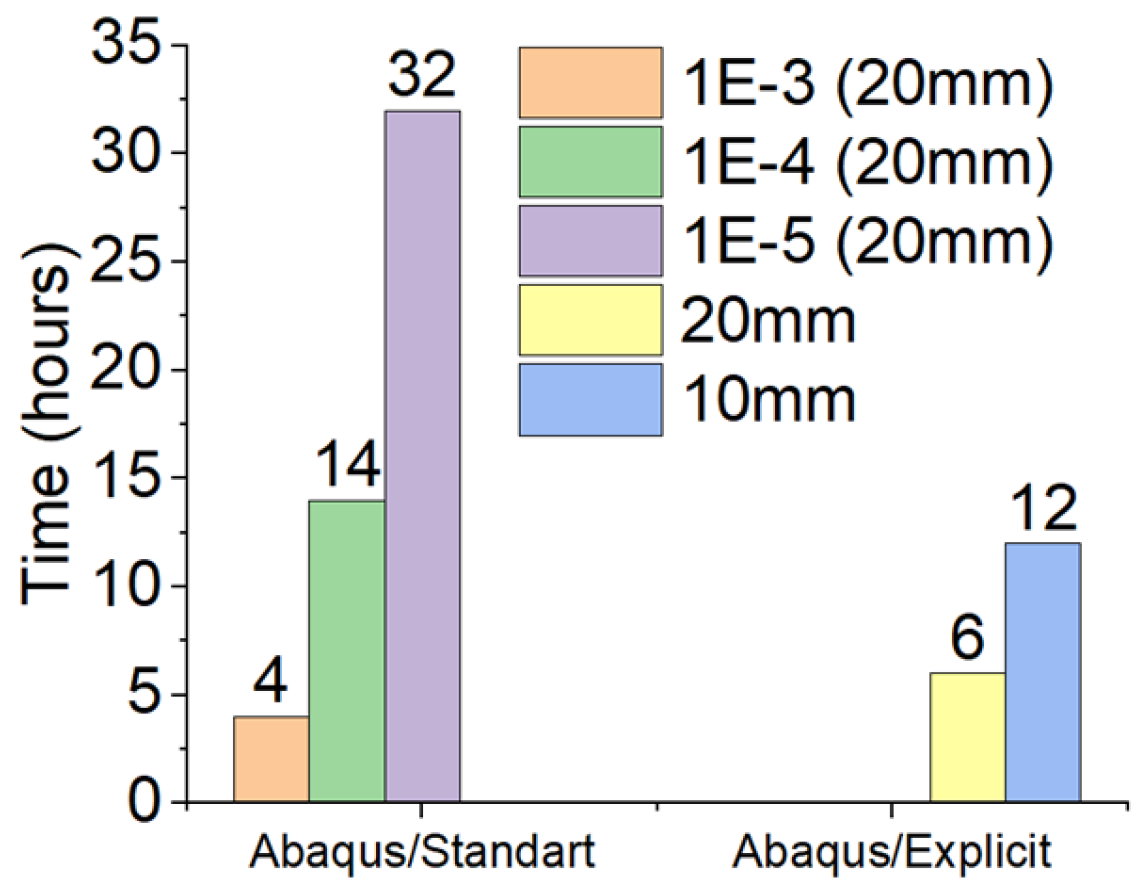
Computational Cost
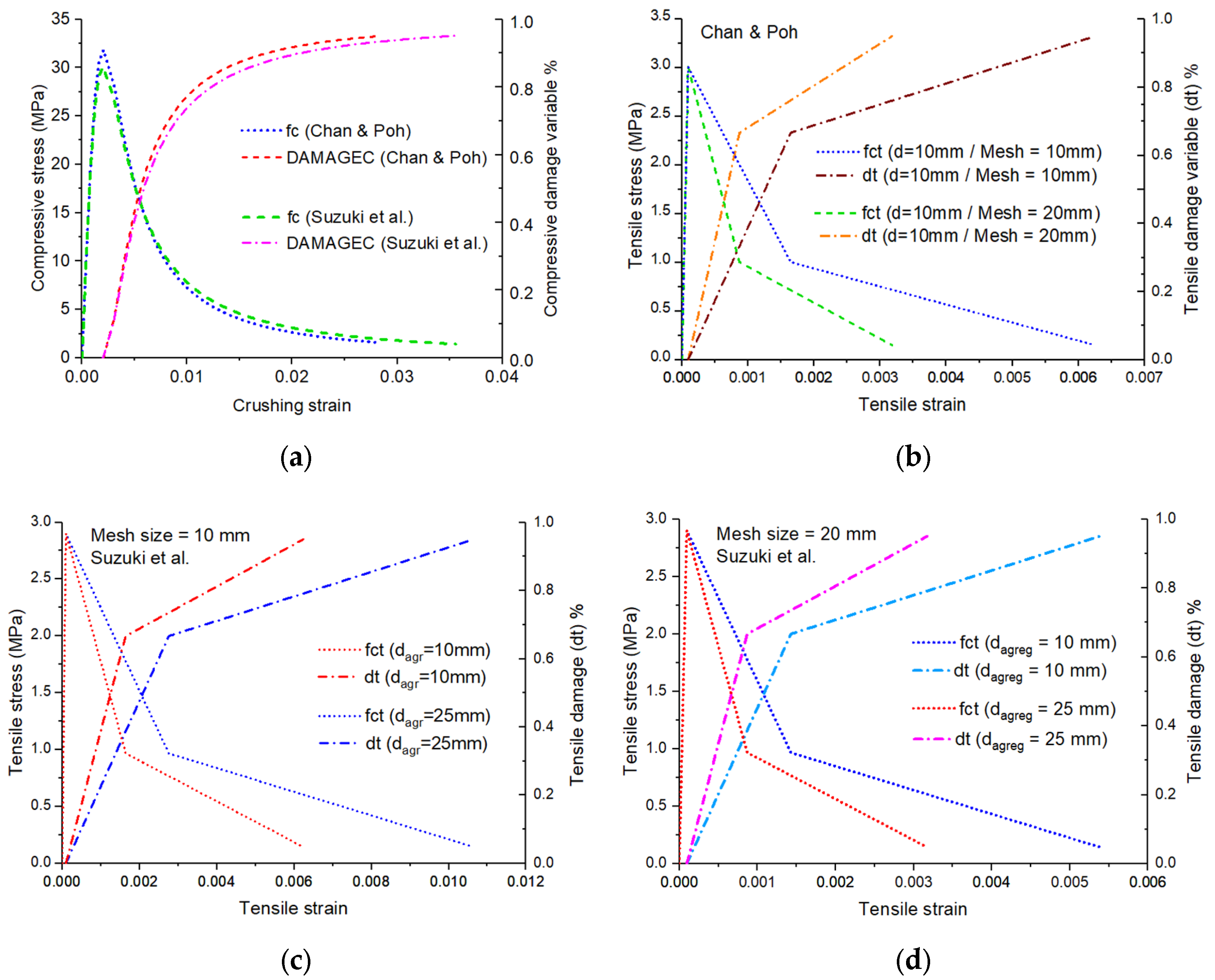
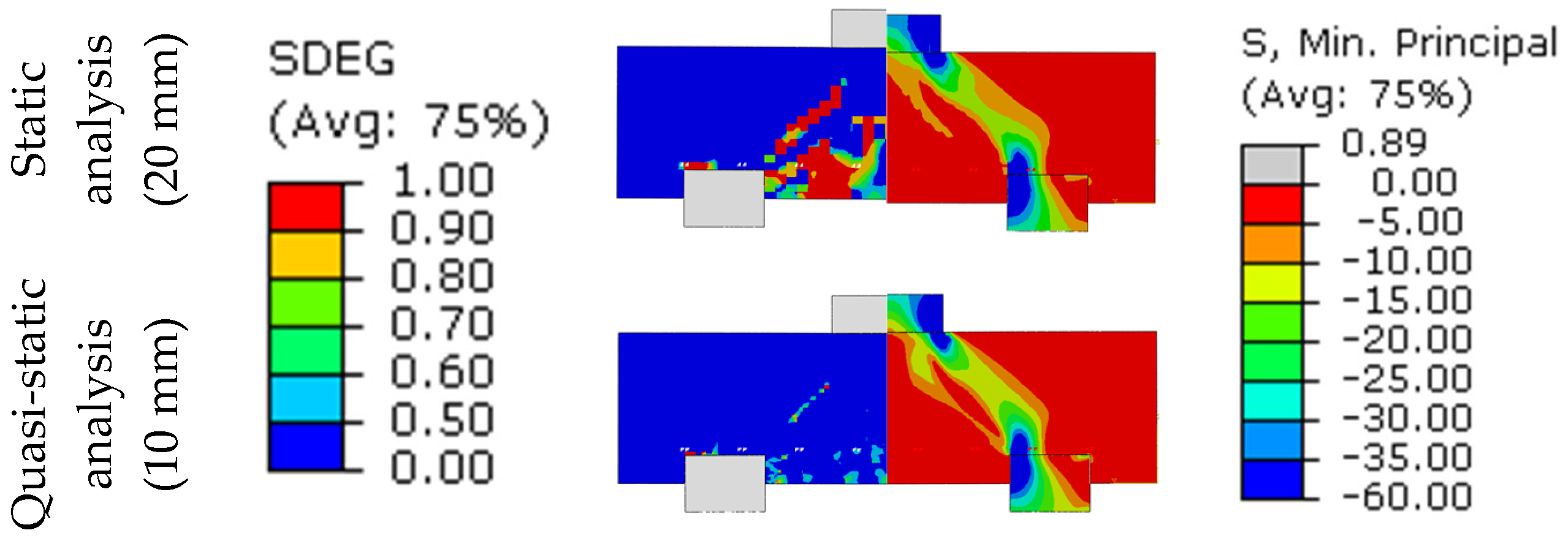
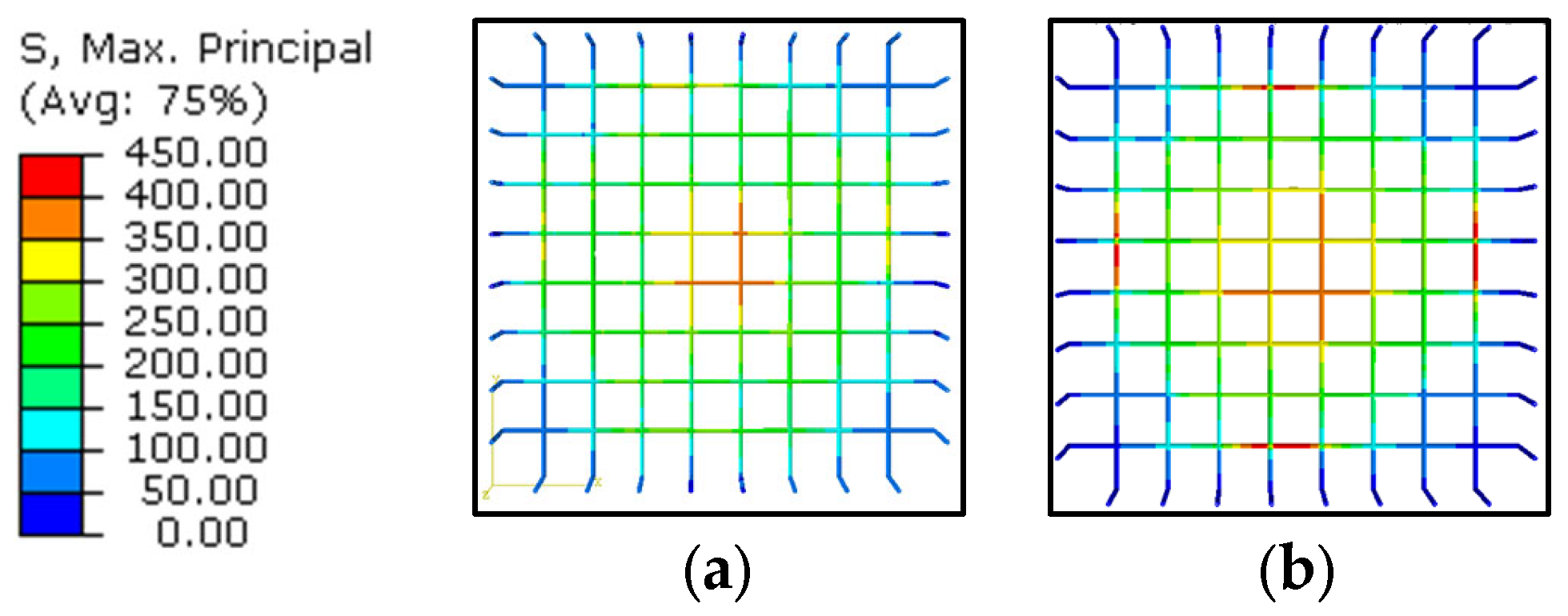
3.1.3. Compressive Stresses and Concrete Damage
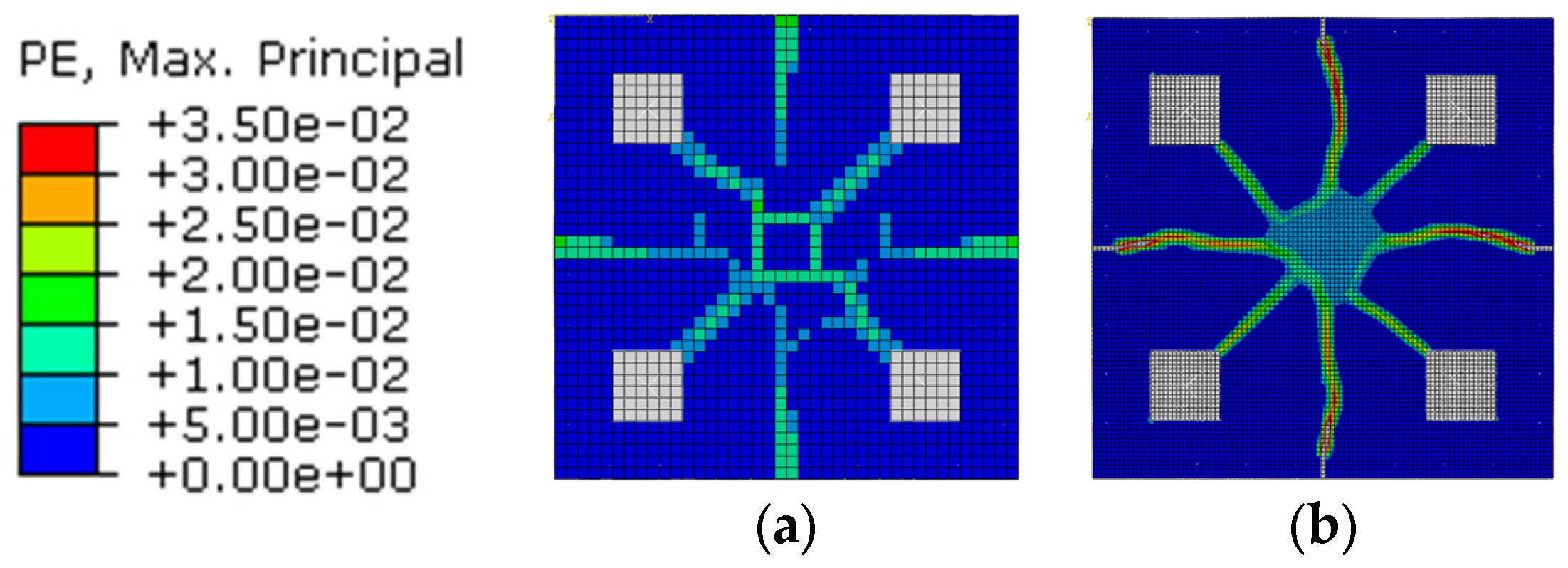
3.1.4. Reinforcement Stress and Cracking Pattern
3.2. Specimen of Suzuki, Otsuki, and Tsubata (1998)
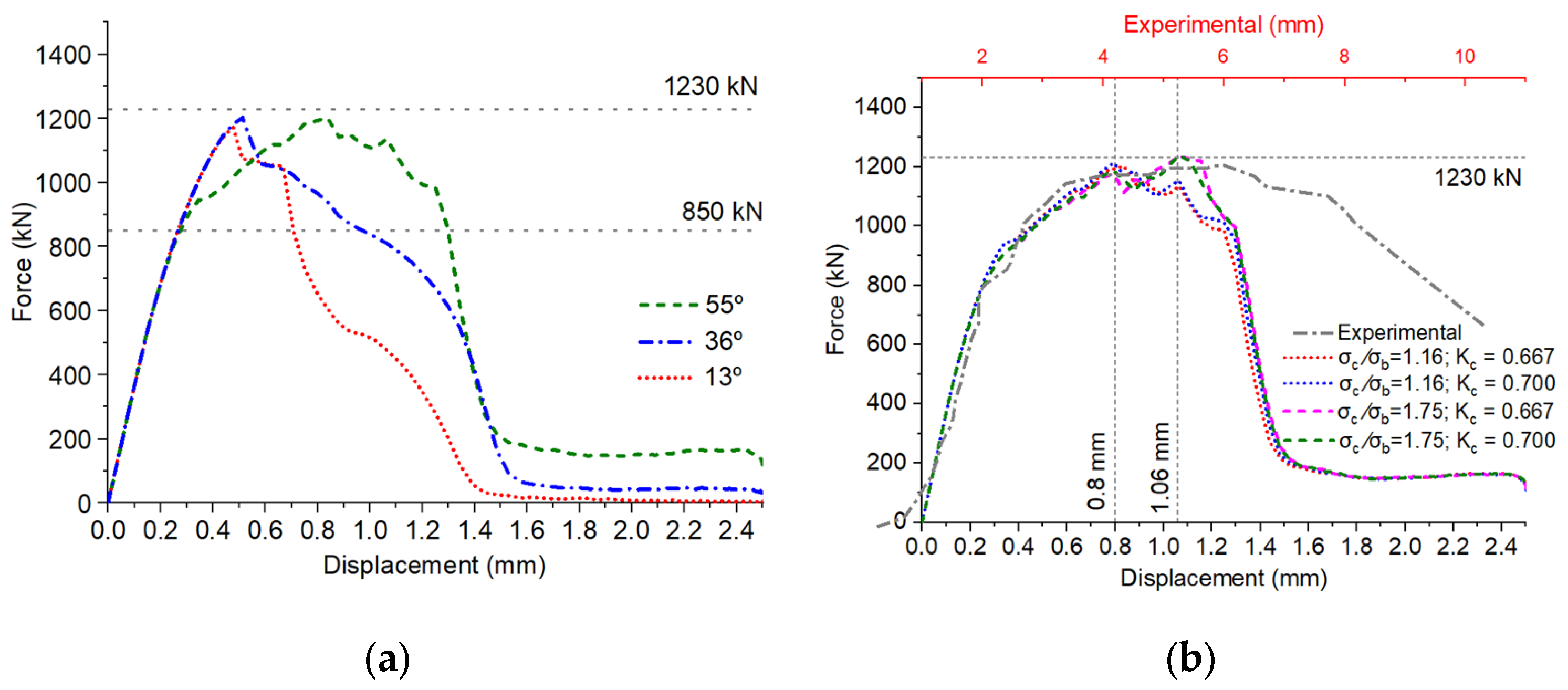
3.2.1. Calibration of Force × Displacement Curve
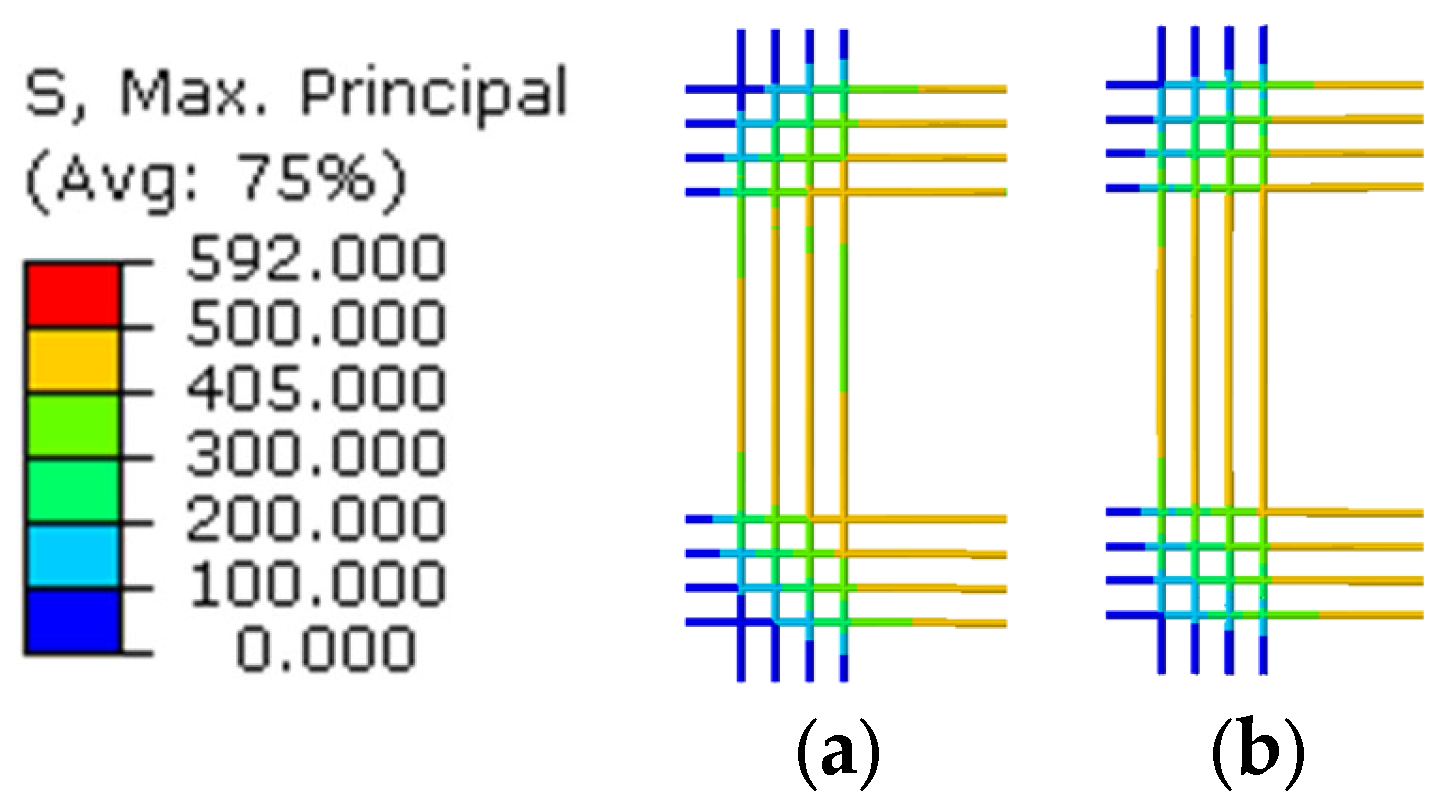
3.2.2. Compressive Stresses and Concrete Degradation
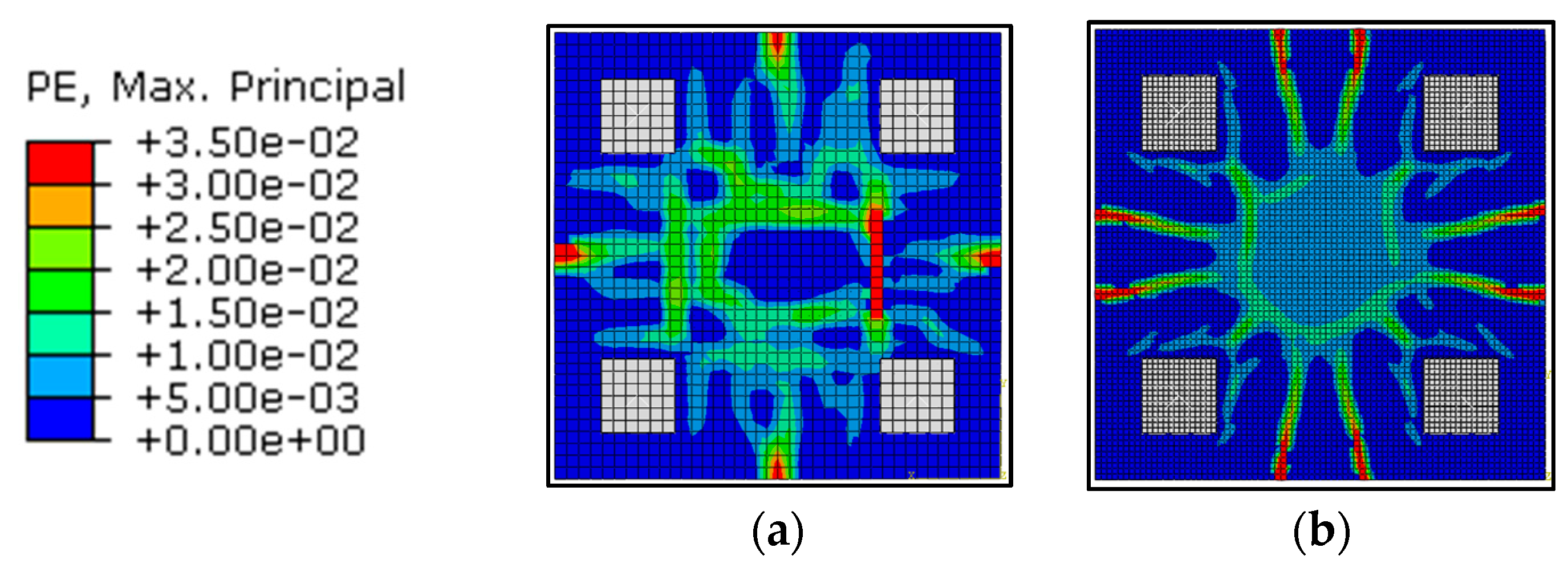
3.2.3. Reinforcement Stress and Cracking Pattern
3.3. Feasibility of Solvers for Extrapolated Numerical Models
4. Conclusions
- The CDP model presented favorable conditions for the numerical simulation of volumetric elements based on the case of the four-pile caps investigated.
- Regarding the modes or methods of analysis, it was found that the results of both solvers were equally sensitive to and parameters. This makes it possible to adopt the values recommended in the literature, that is, equal to 1.16 and 0.667, respectively. In the case of the parameter , for the “quasi-static” analysis mode, the results were greater and different in the calibrated models (45° and 50°). This result suggests that a calibration has to be carried out for its definition. For the “static” analysis mode, values of ψ and μ equal to 36° and 1 × 10−4, respectively, are recommended.
- The values of CDP parameters did not influence the initial branch of the force × displacement curve. However, the tensile stress × strain relation of concrete showed a greater influence on the calibration of the curve. In this case, it is important to highlight the need for the correct specification of materials for the definition of the uniaxial concrete tensile curve. It is also important due to the proper definition of 95% tensile damage which influences the ultimate load of the models.
- Regarding the computational cost of the analyzed models, the “quasi-static” analysis mode did not present benefits compared to the “static” analysis when was equal to 1 × 10−4. This occurred due to the need for a refined mesh in the “quasi-static” method.
- Both analysis modes using CDP produced models that presented fine agreement with the experimental force × displacement curves. However, the “static” analysis simulates more precisely the stress contour diagrams for specimens with shear failure (concrete splitting), which can be seen as a strut with intensified damage.
- In the calibration of force × displacement curves, problems were identified, and the reason for these can be associated with the absence of data from experimental tests. In this case, the boundary condition description showed to be crucial. Furthermore, the stress concentration over piles was similar in both solvers; however, the stress accuracy differs between the types of specimens investigated, which can be attributed to boundary condition considerations. This result highlights the necessity of standardizing the experimental setup.
- In the parametric study of geometrical parameters, the “quasi-static” analysis did not present a good correlation in the estimated values, indicating the need for studies for the identification of factors that led to this behavior. The coefficients of variation, obtained with results from the proposal by Melendez et al. [57], were 3.29% and 19.18% for the “static” and “quasi-static” analysis modes, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Blévot, J.; Frémy, R. Annales de l’Institut Technique du Batiment et des Travaux Publics; Institut Technique du Bâtiment et des Travaux Publics: Paris, France, 1967; Volume 20, pp. 223–295. [Google Scholar]
- ABNT NBR 6118. NBR 6118; Design of Concrete Structures—Procedure. Associação Brasileira de Normas Técnicas (ABNT): Rio de Janeiro, Brazil, 2023; Volume 238. (In Portuguese)
- Suzuki, K.; Otsuki, K.; Tsubata, T. Influence of Bar Arrangement on Ultimate Strength of Four-Pile Caps. Trans. Japan Concr. Inst. 1998, 20, 195–202. [Google Scholar]
- Clarke, J.L. Behaviour and Design of Pile Caps with Four Piles; Technical; Cement and Concrete Association: London, UK, 1973; p. 489. [Google Scholar]
- Chan, T.K.; Poh, C.K. Behaviour of precast reinforced concrete pile caps. Constr. Build. Mater. 2000, 14, 73–78. [Google Scholar] [CrossRef]
- Miguel-Tortola, L.; Miguel, P.F.; Pallarés, L. Strength of pile caps under eccentric loads: Experimental study and review of code provisions. Eng. Struct. 2019, 182, 251–267. [Google Scholar] [CrossRef]
- Meléndez, C.; Miguel, P.F. Modelling Boundary Conditions Imposed by Loads and Supports in 3D D-Regions. Computational Modelling of Concrete Structures; CRC Press: Boca Raton, FL, USA, 2018; pp. 679–688. [Google Scholar] [CrossRef]
- Sam, C.; Iyer, P.K. Nonlinear finite element analysis of reinforced concrete four-pile caps. Comput. Struct. 1995, 57, 605–622. [Google Scholar] [CrossRef]
- Nogueira, T.B.; Souza, R.A. de Análise, dimensionamento e verificaçao de elementos espaciais em concreto armado utilizando o método dos elementos finitos e o método das bielas. Rev. Int. Metod. Numer. Para Calc. Disen. Ing. 2006, 22, 31–44. [Google Scholar]
- Delalibera, R.G.; Sousa, G.F. Numerical analyses of two-pile caps considering lateral friction between the piles and soil. Rev. IBRACON Estrut. e Mater. 2021, 14, e14604. [Google Scholar] [CrossRef]
- Gonçalves, V.F.; Delalibera, R.G.; de Oliveira Filho, M.A. Analysis of the pile-to-cap connection of pile caps on two steel piles—An experimental and numerical study. Eng. Struct. 2022, 252, 113629. [Google Scholar] [CrossRef]
- Buttignol, T.E.T.; Almeida, L.C. Concrete compressive characteristic strength analysis of pile caps with three piles. Rev. IBRACON Estrut. Mater. 2013, 6, 158–177. [Google Scholar] [CrossRef]
- Oliveira, D.S.; Barros, R.; Giongo, J.S. Blocos de concreto armado sobre seis estacas: Simulação numérica e dimensionamento pelo método de bielas e tirantes. Rev. IBRACON Estrut. Mater. 2014, 7, 1–23. [Google Scholar] [CrossRef]
- Bloodworth, A.G.; Cao, J.; Xu, M. Numerical Modeling of Shear Behavior of Reinforced Concrete Pile Caps. J. Struct. Eng. 2012, 138, 708–717. [Google Scholar] [CrossRef]
- Randi, R.P.; Almeida, L.C.; Trautwein, L.M.; Munhoz, F.S. Análise da influência do comprimento de ancoragem da armadura do pilar no bloco sobre duas estacas. Rev. IBRACON Estrut. e Mater. 2018, 11, 1122–1150. [Google Scholar] [CrossRef]
- Munhoz, F.S. Análise Experimental e Numérica de Blocos Rígidos Sobre duas Estacas com Pilares de Seções Quadradas e Retangulares e Diferentes Taxas de Armadura; Digital Library of Intellectual Production of Universidade de São Paulo: São Paulo, Brazil, 2014; p. 358. [Google Scholar]
- Luchesi, G.L.; Randi, R.d.P.; Trautwein, L.M.; Almeida, L.C.D. Important aspects in experimental versus numerical comparative analysis in pile caps. Rev. IBRACON Estrut. Mater. 2022, 15, e15502. [Google Scholar] [CrossRef]
- Meléndez, C.; Miguel, P.F.; Pallarés, L. A simplified approach for the ultimate limit state analysis of three-dimensional reinforced concrete elements. Eng. Struct. 2016, 123, 330–340. [Google Scholar] [CrossRef]
- Basha, A.; Tayeh, B.A.; Maglad, A.M.; Mansour, W. Feasibility of improving shear performance of RC pile caps using various internal reinforcement configurations: Tests and finite element modelling. Eng. Struct. 2023, 289, 116340. [Google Scholar] [CrossRef]
- Earij, A.; Alfano, G.; Cashell, K.; Zhou, X. Nonlinear three–dimensional finite–element modelling of reinforced–concrete beams: Computational challenges and experimental validation. Eng. Fail. Anal. 2017, 82, 92–115. [Google Scholar] [CrossRef]
- Hafezolghorani, M.; Hejazi, F.; Vaghei, R.; Jaafar, M.S.B.; Karimzade, K. Simplified damage plasticity model for concrete. Struct. Eng. Int. 2017, 27, 68–78. [Google Scholar] [CrossRef]
- Sümer, Y.; Aktaş, M. Defining parameters for concrete damage plasticity model. Chall. J. Struct. Mech. 2015, 1, 149–155. [Google Scholar] [CrossRef]
- Silva, L.M.E.; Christoforo, A.L.; Carvalho, R.C. Calibration of concrete damaged plasticity model parameters for shear walls. Rev. Mater. 2021, 26, e12944. [Google Scholar] [CrossRef]
- Rainone, L.S.; Tateo, V.; Casolo, S.; Uva, G. About the Use of Concrete Damage Plasticity for Modeling Masonry Post-Elastic Behavior. Buildings 2023, 13, 1915. [Google Scholar] [CrossRef]
- Simulia Abaqus 6.11 Theory Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2017; Volume IV, p. 1172.
- Ali, A.; Kim, D.; Cho, S.G. Modeling of nonlinear cyclic load behavior of I-shaped composite steel-concrete shear walls of nuclear power plants. Nucl. Eng. Technol. 2013, 45, 89–98. [Google Scholar] [CrossRef]
- Dawood, H.; ElGawady, M.; Hewes, J. Behavior of Segmental Precast Posttensioned Bridge Piers under Lateral Loads. J. Bridg. Eng. 2012, 17, 735–746. [Google Scholar] [CrossRef]
- Dong, Y.R.; Xu, Z.D.; Zeng, K.; Cheng, Y.; Xu, C. Seismic behavior and cross-scale refinement model of damage evolution for RC shear walls. Eng. Struct. 2018, 167, 13–25. [Google Scholar] [CrossRef]
- Genikomsou, A.S.; Polak, M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- Milligan, G.J.; Polak, M.A.; Zurell, C. Finite element analysis of punching shear behaviour of concrete slabs supported on rectangular columns. Eng. Struct. 2020, 224, 111189. [Google Scholar] [CrossRef]
- Husain, M.; Eisa, A.S.; Hegazy, M.M. Strengthening of reinforced concrete shear walls with openings using carbon fiber-reinforced polymers. Int. J. Adv. Struct. Eng. 2019, 11, 129–150. [Google Scholar] [CrossRef]
- Jha, S.; Roshan, A.D.; Bishnoi, L.R. Floor response spectra for beyond design basis seismic demand. Nucl. Eng. Des. 2017, 323, 259–268. [Google Scholar] [CrossRef]
- Kaushik, S.; Dasgupta, K. Seismic behavior of slab-structural wall junction of RC building. Earthq. Eng. Eng. Vib. 2019, 18, 331–349. [Google Scholar] [CrossRef]
- Li, C.; Hao, H.; Bi, K. Numerical Study on the Seismic Performance of Precast Segmental Concrete Columns under Cyclic Loading. Eng. Struct. 2017, 148, 373–386. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Liu, J.; Zhou, X. Experimental investigation of special-shaped concrete-filled steel tubular column to steel beam connections under cyclic loading. Eng. Struct. 2017, 151, 68–84. [Google Scholar] [CrossRef]
- Michał, S.; Andrzej, W. Analysis of “d” regions of RC structures based on example of frame corners. AIP Conf. Proc. 2018, 1922, 130002. [Google Scholar] [CrossRef]
- Najafgholipour, M.A.; Dehghan, S.M.; Dooshabi, A.; Niroomandi, A. Finite element analysis of reinforced concrete beam-column connections with governing joint shear failure mode. Lat. Am. J. Solids Struct. 2017, 14, 1200–1225. [Google Scholar] [CrossRef]
- Pavlović, M.; Marković, Z.; Veljković, M.; Bucrossed, D.; Signevac, D. Bolted shear connectors vs. headed studs behaviour in push-out tests. J. Constr. Steel Res. 2013, 88, 134–149. [Google Scholar] [CrossRef]
- Pelletier, K.; Léger, P. Nonlinear seismic modeling of reinforced concrete cores including torsion. Eng. Struct. 2017, 136, 380–392. [Google Scholar] [CrossRef]
- Ren, W.; Sneed, L.H.; Yang, Y.; He, R. Numerical Simulation of Prestressed Precast Concrete Bridge Deck Panels Using Damage Plasticity Model. Int. J. Concr. Struct. Mater. 2015, 9, 45–54. [Google Scholar] [CrossRef]
- Surumi, R.S.; Jaya, K.P.; Greeshma, S. Modelling and Assessment of Shear Wall–Flat Slab Joint Region in Tall Structures. Arab. J. Sci. Eng. 2015, 40, 2201–2217. [Google Scholar] [CrossRef]
- Vojdan, B.M.; Aghayari, R. Investigating the seismic behavior of RC shear walls with openings strengthened with FRP sheets using different schemes. Sci. Iran. 2017, 24, 1855–1865. [Google Scholar] [CrossRef]
- Wang, M.Z.; Guo, Y.L.; Zhu, J.S.; Yang, X.; Tong, J.Z. Sectional strength design of concrete-infilled double steel corrugated-plate walls with T-section. J. Constr. Steel Res. 2019, 160, 23–44. [Google Scholar] [CrossRef]
- Wei, M.W.; Richard Liew, J.Y.; Fu, X.Y. Nonlinear Finite Element Modeling of Novel Partially Connected Buckling-Restrained Steel Plate Shear Walls. Int. J. Steel Struct. 2019, 19, 28–43. [Google Scholar] [CrossRef]
- Szczecina, M.; Winnicki, A. Relaxation Time in CDP Model Used for Analyses of RC Structures. Procedia Eng. 2017, 193, 369–376. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Minh, H.L.; Sang-To, T. A nonlinear concrete damaged plasticity model for simulation reinforced concrete structures using ABAQUS. Frat. Ed Integrita Strutt. 2021, 16, 232–242. [Google Scholar] [CrossRef]
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef]
- Neuberger, Y.M.; Andrade, M.V.; de Sousa, A.M.D.; Bandieira, M.; da Silva Júnior, E.P.; dos Santos, H.F.; Catoia, B.; Bolandim, E.A.; de Moura Aquino, V.B.; Christoforo, A.L.; et al. Numerical Analysis of Reinforced Concrete Corbels Using Concrete Damage Plasticity: Sensitivity to Material Parameters and Comparison with Analytical Models. Buildings 2023, 13, 2781. [Google Scholar] [CrossRef]
- Reginato, L.; de Sousa, A.M.D.; Santos, J.V.C.; El Debs, M.K. NLFEA of Reinforced Concrete Corbels: Proposed Framework, Sensibility Study, and Precision Level. Buildings 2023, 13, 1874. [Google Scholar] [CrossRef]
- de Azevedo Palhares, R.; Weitzel Rossignoli, F.; Sales de Melo, G.; Jorge Nery de Lima, H. A numerical model capable of accurately simulating the punching shear behavior of a reinforced concrete slab. Struct. Concr. 2022, 23, 1134–1150. [Google Scholar] [CrossRef]
- Arthi, S.; Jaya, K. Seismic performance of precast shear wall-slab connection under cyclic loading: Experimental test vs. numerical analysis. Earthq. Eng. Eng. Vib. 2020, 19, 739–757. [Google Scholar] [CrossRef]
- Hu, R.; Fang, Z.; Benmokrane, B. Nonlinear finite-element analysis for predicting the cyclic behavior of UHPC shear walls reinforced with FRP and steel bars. Structures 2023, 53, 265–278. [Google Scholar] [CrossRef]
- Scamardo, M.; Zucca, M.; Crespi, P.; Longarini, N.; Cattaneo, S. Seismic Vulnerability Evaluation of a Historical Masonry Tower: Comparison between Different Approaches. Appl. Sci. 2022, 12, 11254. [Google Scholar] [CrossRef]
- Nguyen, T.N.H.; Tan, K.H.; Kanda, T. Investigations on web-shear behavior of deep precast, prestressed concrete hollow core slabs. Eng. Struct. 2019, 183, 579–593. [Google Scholar] [CrossRef]
- Madkour, H.; Maher, M.; Ali, O. Finite element analysis for interior slab-column connections reinforced with GFRP bars using damage plasticity model. J. Build. Eng. 2022, 48, 104013. [Google Scholar] [CrossRef]
- Najafgholipour, M.A.; Sarhadi, F. A finite element study on the ultimate lateral drift capacity of interior reinforced concrete flat slab-column connections. Structures 2022, 46, 913–926. [Google Scholar] [CrossRef]
- Meléndez, C.; Sagaseta, J.; Miguel, P.F.; Rubio, L.P. Refined three-dimensional strut-and-tie model for analysis and design of four-pile caps. ACI Struct. J. 2019, 116, 15–29. [Google Scholar] [CrossRef]
- Comité Européen de Normalisation. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; British Standard Institution: London, UK, 2004; p. 1. [Google Scholar]
- Kmiecik, P.; Kamiński, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Dudziak, S.; Jackiewicz-Rek, W.; Kozyra, Z. On the calibration of a numerical model for concrete-to-concrete interface. Materials 2021, 14, 7204. [Google Scholar] [CrossRef] [PubMed]
- Nana, W.S.A.; Bui, T.T.; Limam, A.; Abouri, S. Experimental and Numerical Modelling of Shear Behaviour of Full-scale RC Slabs under Concentrated Loads. Structures 2017, 10, 96–116. [Google Scholar] [CrossRef]
- Panahi, H.; Genikomsou, A.S. Comparative evaluation of concrete constitutive models in non-linear finite element simulations of slabs with different flexural reinforcement ratios. Eng. Struct. 2022, 252, 113617. [Google Scholar] [CrossRef]
- Comité Euro-International du Béton. CEB-FIB-Model Code 1990: Design Code; Thomas Telford: London, UK, 1993. [Google Scholar]
- Comité Euro-International du Béton. CEB-FIP-Model Code; Precast Prestressed Concrete Institute: Lausanne, Switzerland, 2010; Volume 2010. [Google Scholar]
- Adebar, P.; Kuchma, D.; Collins, M.P. Strut-and-tie models for the design of pile caps: An experimental study. ACI Strucutural J. 1990, 87, 191–199. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]






| References | Structural Element | Analysis | (°) | ||||
|---|---|---|---|---|---|---|---|
| [25] | Standard values | - | 36 | 0.1 | 1.16 | 0.667 | - |
| Ali, Kim, and Cho [26] | Shear wall | NE | 30 | - | - | - | - |
| Dawood, Elgawady, and Hewes [27] | Precast post-tensioned bridge piers | Static | 1 | 0.1 | 1.16 | 0.66 | 0 |
| Dong et al. [28] | Shear walls | Static | 30 | 0.1 | 1.16 | 0.6667 | 0.0001 |
| Genikomsou and Polak [29] | Slab | Quasi-static | 40 | 0.1 | 1.16 | 0.667 | 0.00001 |
| Milligan, Polak, and Zurell [30] | Slab | Static/ quasi-static * | 45 | 0.1 | 1.16 | 0.667 | - |
| Husain, Eisa, and Hegazy [31] | Shear walls | Quasi-static | 37 | 0.1 | 1.16 | 0.67 | 0.001 |
| Jha, Roshan, and Bishnoi [32] | Specimen CAMUS: a 1/3-scale model of a representative 5-story reinforced concrete building | NE | 55 | 1.25 | 1.16 | 0.667 | 0.0005 |
| Kaushik and Dasgupta [33] | Slab structural wall junction of RC building | Static | 55 | 0.1 | 1.16 | 0.667 | 0.01 |
| Li, Hao, and Bi [34] | Columns | Static | 30 | 0.1 | 1.16 | 0.666 | 0.0001 |
| Liu et al. [35] | Concrete-filled steel tubular column for steel beam connections | NE | 30 | 0.1 | 1.16 | 0.667 | 0.005 |
| Michal and Andrzej [36] | “d” regions of RC structures | Static | 15 | - | - | - | 0.0001 |
| Najafgholipour et al. [37] | Beam–column connections | Static | 35 | 0.1 | 1.16 | 0.7 | - |
| Pavlović [38] | Shear connectors | Quasi-static | 36 | 0.1 | 1.16 | - | - |
| Pelletier and Léger [39] | Reinforced concrete cores | NE | 13 | 90 | 1.16 | 0.667 | - |
| Ren et al. [40] | Prestressed precast concrete Bridge deck panels | Static | 38 | 0.1 | 1.76 | 0.667 | 0.0005 |
| Surumi, Jaya, and Greeshma [41] | Shear walls | NE | 38 | 0.1 | 1.16 | 0.67 | 0 |
| Vojdan and Aghayari [42] | Shear walls | NE | 36/40 | 0.1 | 1.16 | 0.667 | - |
| Wang et al. [43] | Concrete-infilled double steel corrugated-plate walls | NE | 30 | 0.1 | 1.16 | 0.6667 | - |
| Wei, Richard Liew, and Fu [44] | Novel partially connected buckling-restrained steel plate shear walls | Quasi-static | 36 | 0.1 | 1.16 | - | - |
| Szczecina and Winnicki [45] | Frame corner | Static | 5 | 0.1 | 1.16 | 0.667 | 0.0001 |
| Cuong-Le, Minh, and Sang-To [46] | Beams/slab | NE | 30/40 | 0.1 | 1.16 | 0.7 | - |
| Alfarah, López-Almansa, and Oller [47] | Frame | NE | 13 | 0.1 | 1.16 | 0.7 | |
| Bash et al. [19] | Two-pile cap | NE | 26 | 0.1 | 1.16 | 0.667 | 0 |
| Silva, Christoforo, and Carvalho [23] | Shear walls | Static | 46.4 | 0.1 | 1.16 | 0.58 | 0.00001 |
| Neuberger et al. [48] | Corbels | Static | 48 | 0.1 | 1.16 | 0.667 | 0.0005 |
| Reginato et al. [49] | Corbels | Static | 42 | 0.1 | 1.16 | 0.667 | 0.0001 |
| Azevedo Palhares et al. [50] | Slab | Static | 25 | 0.1 | 1.16 | 0.667 | 0.0001 |
| Arthi and Jaya [51] | Precast shear wall–slab connection | NE | 38 | 0.1 | 1.12 | 0.67 | 0.666 |
| Hu, Fang, and Benmokrane [52] | UHPC shear walls reinforced | NE | 54 | 0.1 | 1.07 | 0.666 | - |
| Scamardo et al. [53] | Masonry | Static | 10 | 0.1 | 1.16 | 0.667 | 0.002 |
| Nguyen, Tan, and Kanda [54] | Precast prestressed concrete hollow core | Quasi-static | 28 ** | 0.1 | 1.16 | 0.667 | |
| Madkour, Maher, and Ali [55] | Slab | Static | 40 | 0.1 | 1.16 | 0.667 | 0.00001 |
| Model | Concrete | Steel Reinforcement | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Pile Cap | Column and Piles | ||||||||
(kN) | (MPa) | (MPa) | (MPa) | (MPa) | (cm2) | (MPa) | (MPa) | (GPa) | |
| Pile Cap A [5] | 1230 | 31.76 | 3.00 | 31,116.22 | 37,277.87 | 6.28 | 480 | 552 | 200 |
| BPC 30-30 [3] | 1034 | 30.09 | 2.90 | 30,606.90 | 5.70 | 405 | 592 | 200 | |
| Model | (mm) | (mm) | (mm) | (cm2) |
|---|---|---|---|---|
| MCalibrate | 250.00 | 500.00 | 300 | 5 |
| MShear | 250.00 | 500.00 | 300 | 10 |
| M25D50E | 250.00 | 500.00 | 200 | 10 |
| M25D45E | 250.00 | 450.00 | 200 | 10 |
| M25D37E | 250.00 | 375.00 | 200 | 10 |
| M28D50E | 287.50 | 500.00 | 200 | 10 |
| M28D45E | 287.50 | 450.00 | 200 | 10 |
| M28D38E | 287.50 | 375.00 | 200 | 10 |
| M32D50E | 325.00 | 500.00 | 200 | 10 |
| M32D45E | 325.00 | 450.00 | 200 | 10 |
| M32D37E | 325.00 | 375.00 | 200 | 10 |
| Kc | μ | (kN) | (mm) | |||
|---|---|---|---|---|---|---|
| 1.16 | 0.667 | 1 × 10−5 | 1220.61 | - | 1.39 | 0.992 |
| 1 × 10−4 | 1221.84 | 0.10 | 1.43 | 0.993 | ||
| 1 × 10−3 | 1406.81 | 15.25 | 1.02 | 1.143 | ||
| 0.700 | 1 × 10−5 | 1241.27 | - | 1.34 | 1.009 | |
| 1 × 10−4 | 1245.59 | 1.40 | 1.41 | 1.012 | ||
| 1 × 10−3 | 1405.07 | 13.56 | 1.02 | 1.142 | ||
| 1.75 | 0.667 | 1 × 10−5 | 1279.80 | - | 1.38 | 1.040 |
| 1 × 10−4 | 1281.00 | 0.09 | 1.29 | 1.041 | ||
| 1 × 10−3 | 1397.88 | 9.23 | 1.57 | 1.136 | ||
| 0.700 | 1 × 10−5 | 1283.58 | - | 1.31 | 1.043 | |
| 1 × 10−4 | 1286.27 | 0.02 | 1.37 | 1.045 | ||
| 1 × 10−3 | 1399.35 | 9.01 | 1.57 | 1.137 | ||
| Obs.: For all models, = 36° and = 0.1. | ||||||
| Kc | (kN) | (mm) | ||||
|---|---|---|---|---|---|---|
| Mesh size 20 mm | ||||||
| 55 | 1.16 | 0.667 | 1202.79 | - | 0.84 | 0.977 |
| 0.700 | 1213.29 | 0.87 | 0.79 | 0.986 | ||
| 1.75 | 0.667 | 1235.55 | - | 1.06 | 1.004 | |
| 0.700 | 1237.81 | 0.18 | 1.06 | 1.006 | ||
| Mesh size 10 mm | ||||||
| 55 | 1.16 | 0.667 | 1788.65 | - | 1.49 | 1.450 |
| 45 | 1.16 | 0.500 | 1371.20 | - | 0.66 | 1.114 |
| 0.667 | 1342.40 | - | 0.66 | 1.091 | ||
| 1.000 | 1372.78 | - | 0.66 | 1.116 | ||
| 1.75 | 0.500 | 1323.60 | - | 1.34 | 1.073 | |
| 0.667 | 1320.55 | - | 1.34 | 1.073 | ||
| 1.000 | 1319.40 | - | 1.34 | 1.072 | ||
| Mesh Size (mm) | (kN) | (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| - | - | - | - | - | - | Experimental | 1034.00 | ~2.00 | 1.000 |
| Static analysis | |||||||||
| 36 | 1.16 | 0.667 | 1 × 10−5 | 10 | 95 | 20 | 1024.82 | 1.70 | 0.991 |
| 36 | 1.16 | 0.667 | 1 × 10−5 | 10 | 80 | 20 | 1178.93 | 1.58 | 1.140 |
| 36 | 1.16 | 0.667 | 1 × 10−5 | 25 | 95 | 20 | 1106.62 | 1.56 | 1.070 |
| 36 | 1.16 | 0.667 | 1 × 10−4 | 25 | 95 | 20 | 1050.36 | 1.34 | 1.016 |
| 36 | 1.75 | 0.667 | 1 × 10−5 | 10 | 95 | 20 | 1048.64 | 1.87 | 1.014 |
| 36 | 1.75 | 0.667 | 1 × 10−5 | 25 | 95 | 20 | 1116.02 | 1.71 | 1.079 |
| 36 | 1.75 | 1.000 | 1 × 10−5 | 10 | 95 | 20 | 1069.18 | 1.96 | 1.034 |
| 30 | 1.75 | 0.667 | 1 × 10−4 | 25 | 95 | 20 | 1021.80 | 1.51 | 0.988 |
| Quasi static analysis | |||||||||
| 36 | 1.16 | 0.667 | - | 10 | 95 | 20 | 768.80 | 0.79 | 0.743 |
| 50 | 1.16 | 0.667 | - | 10 | 95 | 10 | 1071.61 | 1.60 | 1.036 |
| 50 | 1.16 | 0.667 | - | 10 | 80 | 10 | 1492.81 | 1.77 | 1.445 |
| 50 | 1.16 | 0.667 | - | 25 | 95 | 10 | 1206.33 | 0.88 | 1.165 |
| 50 | 1.75 | 0.667 | - | 25 | 95 | 10 | 1190.58 | 1.00 | 1.150 |
| 50 | 1.75 | 0.667 | - | 10 | 95 | 10 | 1080.55 | 1.52 | 1.045 |
| Model | (kN) | (kN) | (kN) | ||
|---|---|---|---|---|---|
| MCalibrate | 942 | 1024 | 1071 | 1.08 | 1.13 |
| MShear | 1105 | 1139 | 1362 | 1.03 | 1.23 |
| M25D50E | 880 | 862 | 852 | 0.98 | 0.96 |
| M25D45E | 983 | 1059 | 1149 | 0.98 | 1.16 |
| M25D37E | 1170 | 1236 | 1325 | 1.05 | 1.13 |
| M28D50E | 1004 | 1028 | 1081 | 1.02 | 1.07 |
| M28D45E | 1107 | 1123 | 793 | 1.01 | 0.71 |
| M28D38E | 1284 | 1351 | 1068 | 1.05 | 0.83 |
| M32D50E | 1108 | 1151 | 919 * | 1.04 | 0.79 |
| M32D45E | 1212 | 1306 | 986 * | 1.08 | 0.81 |
| M32D37E | 1375 | 1406 | 1085 * | 1.02 | 0.79 |
| AVG | 1.03 | 0.96 | |||
| SD | 0.03 | 0.19 | |||
| CV(%) | 3.29 | 19.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spozito, R.S.; Rodrigues, E.F.C.; Santos, H.F.d.; Oliveira, I.A.d.; Christoforo, A.L.; de Almeida Filho, F.M.; Delalibera, R.G. Numerical Modeling of Four-Pile Caps Using the Concrete Damaged Plasticity Model. Buildings 2024, 14, 2066. https://doi.org/10.3390/buildings14072066
Spozito RS, Rodrigues EFC, Santos HFd, Oliveira IAd, Christoforo AL, de Almeida Filho FM, Delalibera RG. Numerical Modeling of Four-Pile Caps Using the Concrete Damaged Plasticity Model. Buildings. 2024; 14(7):2066. https://doi.org/10.3390/buildings14072066
Chicago/Turabian StyleSpozito, Raphael Saverio, Edson Fernando Castanheira Rodrigues, Herisson Ferreira dos Santos, Ivanildo Amorim de Oliveira, André Luís Christoforo, Fernando Menezes de Almeida Filho, and Rodrigo Gustavo Delalibera. 2024. "Numerical Modeling of Four-Pile Caps Using the Concrete Damaged Plasticity Model" Buildings 14, no. 7: 2066. https://doi.org/10.3390/buildings14072066






