Study on Interprovincial Equity and the Decoupling of Carbon Emissions in the Construction Industry—A Case Study in China
Abstract
:1. Introduction
2. Methods and Data
2.1. Moran’s I
2.2. Dagum’s Gini Coefficient
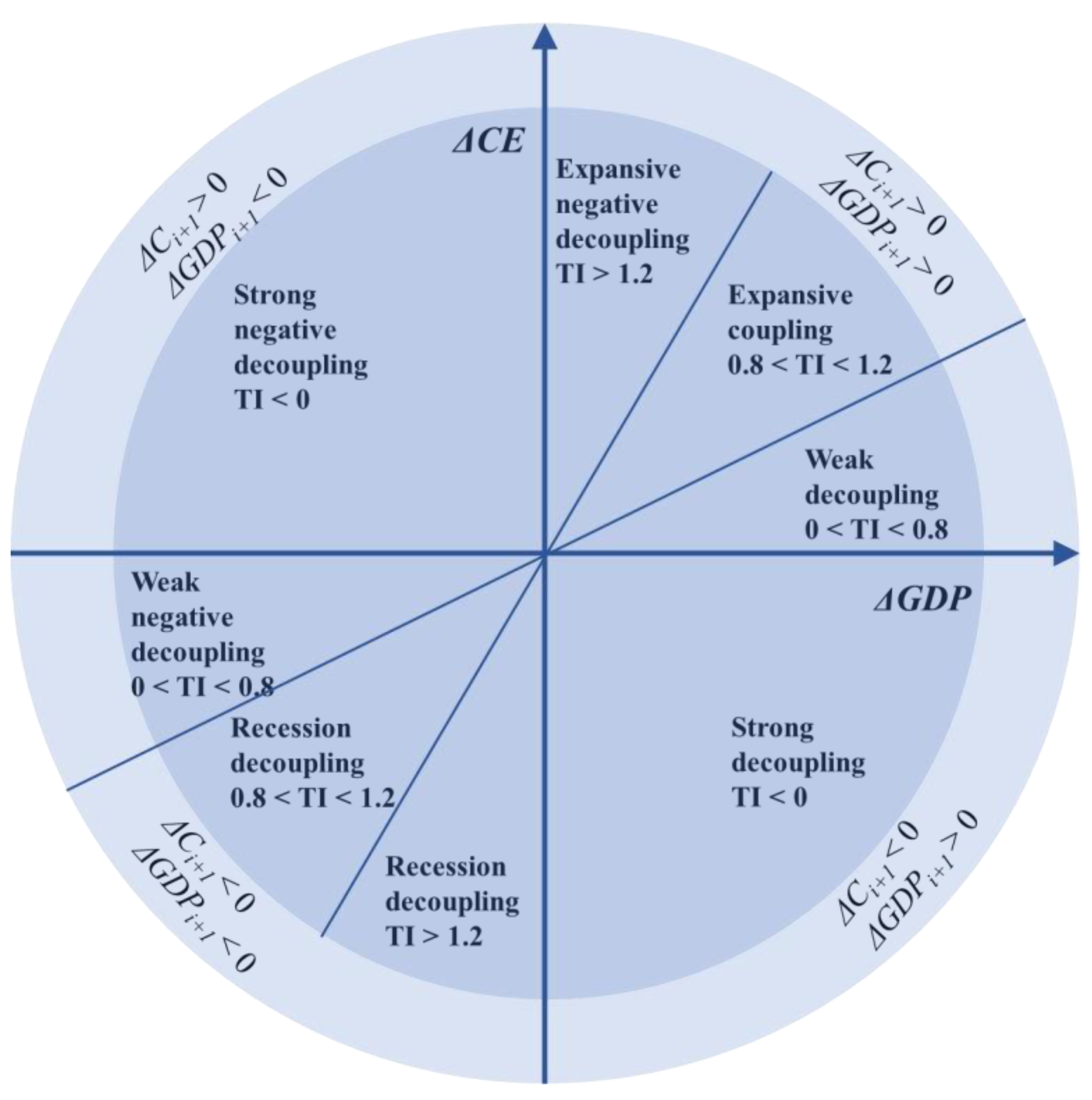
2.3. Tapio’s Decoupling Model
2.4. Variables and Data Sources
3. Analysis of Results
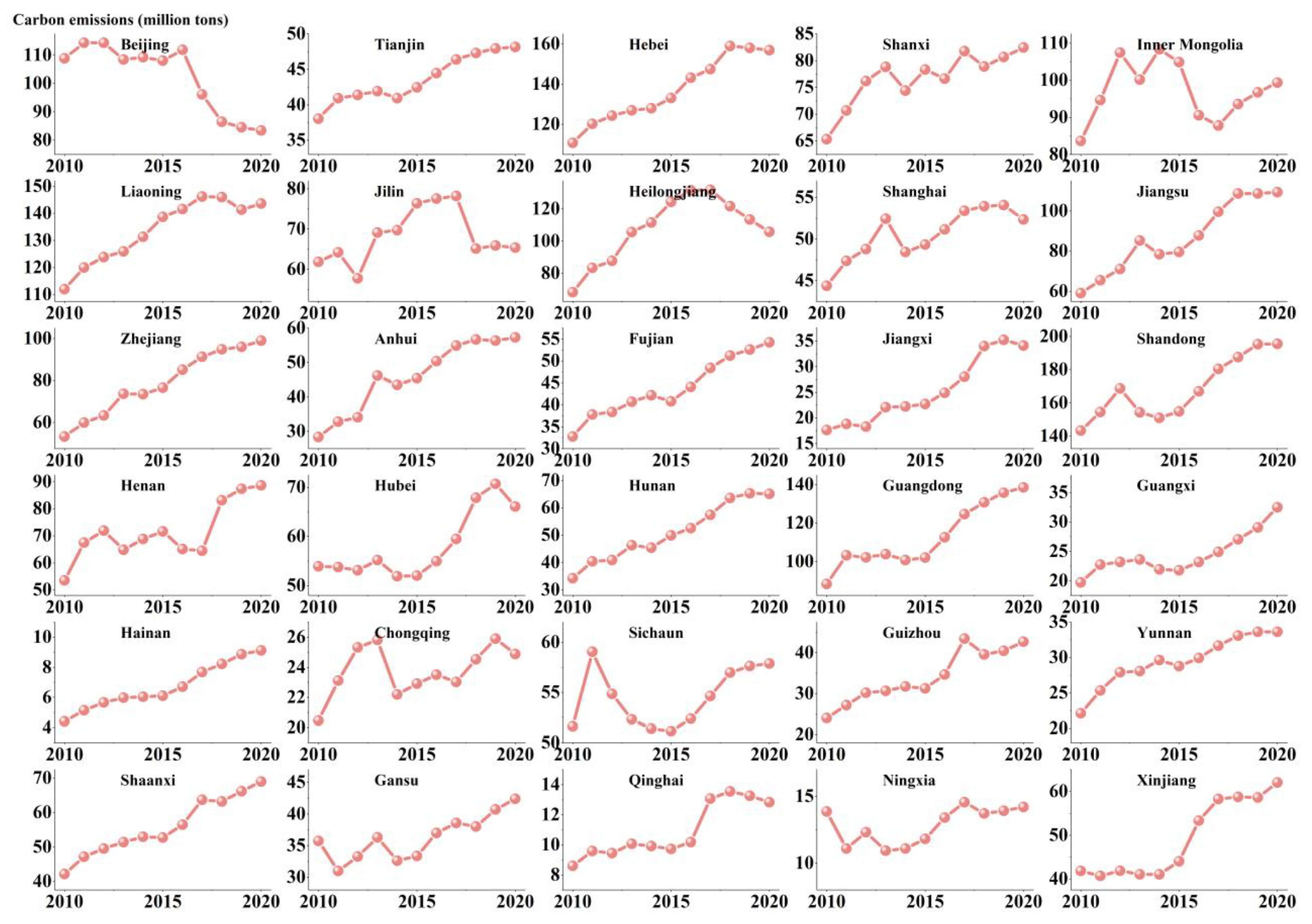
3.1. Analysis of the Spatial and Temporal Evolution of Carbon Emissions between Provinces
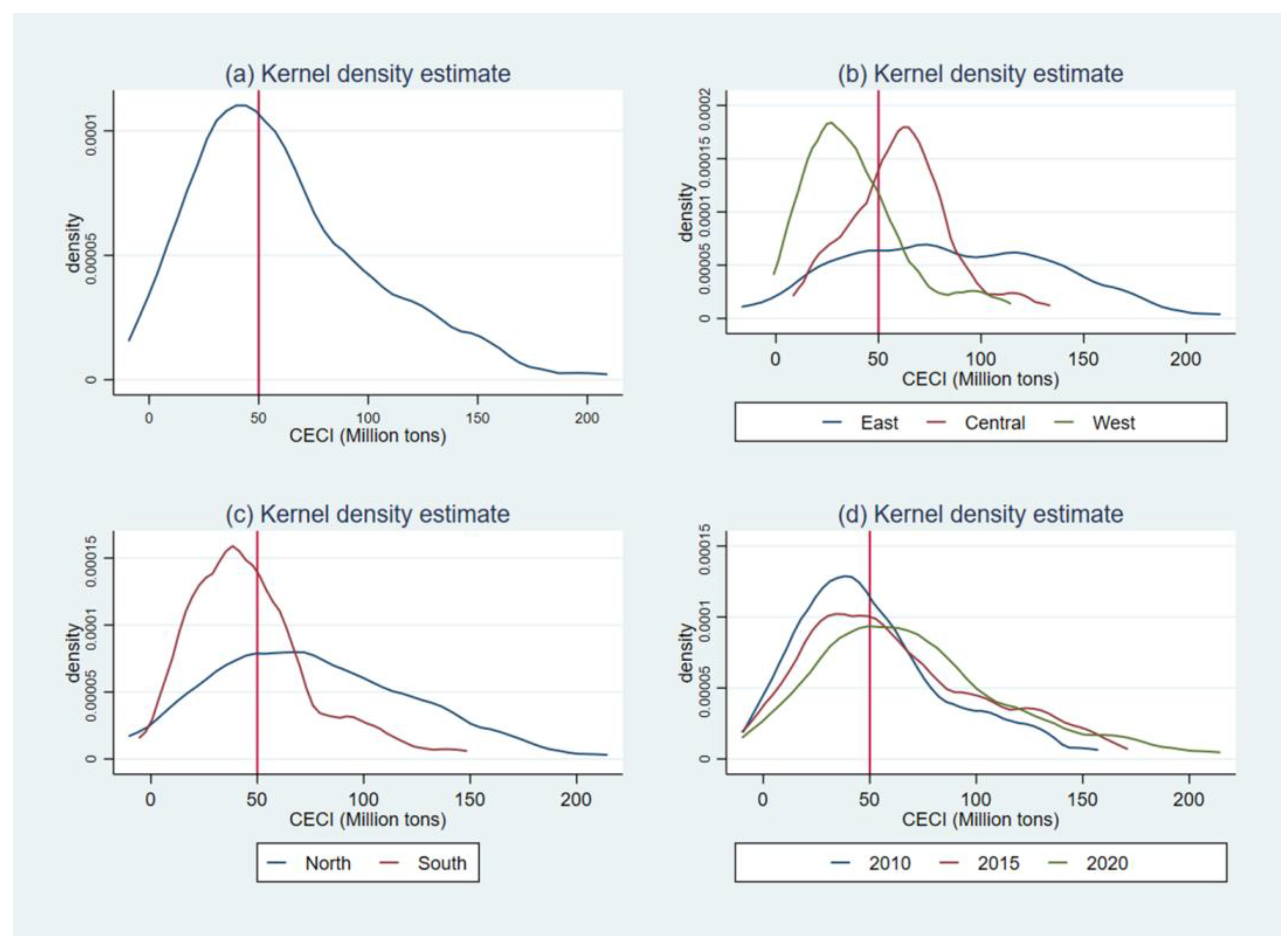
3.2. Kernel Density Analysis
3.3. Spatial Autocorrelation Analysis
3.4. Dagum Gini Coefficient Analysis
3.5. CECI Decoupling Analysis
4. Discussion
5. Conclusions and Shortcomings
- (1)
- The CECI values of the 30 provinces as a whole showed a growing trend, with the main growth areas in CECI being the eastern Bohai Rim region and the Pearl River Delta region, with average annual growth rates of 1.50% and 2.27%, respectively. Heilongjiang has realized a CECI carbon peak, and the per capita CECI of Inner Mongolia, Jilin, and Liaoning has been in the middle–high carbon emission region for a long time.
- (2)
- The CECI differences among the 30 provinces are gradually increasing. The CECI differences between the central and the western regions were greater than those in the eastern regions. However, the degree of inequality within them was lower, and the degree of inequality within the western provinces was the greatest. In terms of inter-group differences, inequality was greatest between the eastern and western regions and the least between the central and western regions. CECI inequality in the northern and southern regions has been decreasing yearly, with greater inequality within the northern provinces than in the southern provinces. CECI was predominantly high with high aggregation in the northeastern provinces and predominantly low with low aggregation in the western provinces.
- (3)
- CECI decoupling was better in Sichuan, Yunnan, and Beijing, followed by Shanghai, Fujian, and Guangdong, while the provinces with worse decoupling were mainly Tianjin, Liaoning, Inner Mongolia, Jilin, and Heilongjiang. The decoupling situation in Shandong, Guangxi, Guizhou, Hainan, Chongqing, Gansu, and Qinghai was mainly characterized by a good decoupling situation in the early stages and a gradual deterioration in the later stages.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guy, J.; Shears, E.; Meckling, J. National models of climate governance among major emitters. Nat. Clim. Chang. 2023, 13, 189–195. [Google Scholar] [CrossRef]
- Mallapaty, S. How China could be carbon neutral by mid-century. Nature 2020, 586, 482–483. [Google Scholar] [CrossRef]
- Chen, J.; Shen, L.; Song, X.; Shi, Q.; Li, S. An empirical study on the CO2 emissions in the Chinese construction industry. J. Clean. Prod. 2017, 168, 645–654. [Google Scholar] [CrossRef]
- Huo, T.; Du, Q.; Yuan, T.; Cai, W.; Zhang, W. Has the provincial-level residential building sector reached the carbon peak? An integrated assessment model. Environ. Impact Assess. Rev. 2024, 105, 107374. [Google Scholar] [CrossRef]
- Shi, Q.; Chen, J.; Shen, L. Driving factors of the changes in the carbon emissions in the Chinese construction industry. J. Clean. Prod. 2017, 166, 615–627. [Google Scholar] [CrossRef]
- Chen, X.; Liu, W.; Zhang, J.; Li, Z. The change pattern and driving factors of embodied SO2 emissions in China’s inter-provincial trade. J. Clean. Prod. 2020, 276, 123324. [Google Scholar] [CrossRef]
- Ahmed Ali, K.; Ahmad, M.I.; Yusup, Y. Issues, impacts, and mitigations of carbon dioxide emissions in the building sector. Sustainability 2020, 12, 7427. [Google Scholar] [CrossRef]
- Hossain, M.U.; Ng, S.T.; Antwi-Afari, P.; Amor, B. Circular economy and the construction industry: Existing trends, challenges and prospective framework for sustainable construction. Renew. Sustain. Energy Rev. 2020, 130, 109948. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, J.; Cai, W.; Huo, T.; Li, R. A novel allocation method of regional carbon allowance in building sector: Perspective from coupling equity and efficiency. Environ. Impact Assess. Rev. 2023, 102, 107192. [Google Scholar] [CrossRef]
- Li, B.; Han, S.; Wang, Y.; Wang, Y.; Li, J.; Wang, Y. Feasibility assessment of the carbon emissions peak in China’s construction industry: Factor decomposition and peak forecast. Sci. Total Environ. 2020, 706, 135716. [Google Scholar] [CrossRef]
- Xiao, Y.; Huang, H.; Qian, X.-M.; Zhang, L.-Y.; An, B.-W. Can new-type urbanization reduce urban building carbon emissions? New evidence from China. Sustain. Cities Soc. 2023, 90, 104410. [Google Scholar] [CrossRef]
- Hou, L.; Wang, Y.; Hu, L.; Wang, Y.; Li, Y.; Zheng, Y. Economic growth and carbon emissions analysis based on tapio-ekc coupled integration and scenario simulation: A case study of china’s transportation industry. Environ. Dev. Sustain. 2023, 26, 18855–18881. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, X.; Bai, Y.; Chen, J.; Zheng, W. Land use structure and emission intensity at regional scale: A case study at the middle reach of the Heihe River basin. Appl. Energy 2016, 183, 1581–1593. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, X.; Cui, Q. Effectiveness and equity implications of carbon policies in the United States construction industry. Build. Environ. 2012, 49, 259–269. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Du, Z. CO2 Emission Allocation for Urban Public Buildings Considering Efficiency and Equity: An Application at the Provincial Level in China. Buildings 2023, 13, 1570. [Google Scholar] [CrossRef]
- Fang, Y.; Ng, S.T.; Ma, Z.; Li, H. Quota-based carbon tracing model for construction processes in China. J. Clean. Prod. 2018, 200, 657–666. [Google Scholar] [CrossRef]
- Shi, Q.; Cai, R.; Huo, T.; You, K.; Cai, W. A fairly and effectively analysis for the sharing of CO2 emissions reduction responsibility in China’s provincial building sectors. Environ. Impact Assess. Rev. 2023, 99, 106984. [Google Scholar] [CrossRef]
- Xu, X.; Xu, P.; Zhu, J.; Liu, J.; Xue, Q. How to minimize the embodied environmental impact of green building envelope? An automatic optimization method. Environ. Impact Assess. Rev. 2022, 93, 106732. [Google Scholar] [CrossRef]
- Wu, Y.; Chau, K.; Lu, W.; Shen, L.; Shuai, C.; Chen, J. Decoupling relationship between economic output and carbon emission in the Chinese construction industry. Environ. Impact Assess. Rev. 2018, 71, 60–69. [Google Scholar] [CrossRef]
- Chen, L.; Liu, S.; Cai, W.; Chen, R.; Zhang, J.; Yu, Y. Carbon inequality in residential buildings: Evidence from 321 Chinese cities. Environ. Impact Assess. Rev. 2024, 105, 107402. [Google Scholar] [CrossRef]
- Gan, L.; Liu, Y.; Shi, Q.; Cai, W.; Ren, H. Regional inequality in the carbon emission intensity of public buildings in China. Build. Environ. 2022, 225, 109657. [Google Scholar] [CrossRef]
- Adger, W.N. Climate Change, Human Well-Being and Insecurity. New Political Econ. 2010, 15, 275–292. [Google Scholar] [CrossRef]
- Ikeme, J. Equity, environmental justice and sustainability: Incomplete approaches in climate change politics. Glob. Environ. Chang. 2003, 13, 195–206. [Google Scholar] [CrossRef]
- Wood, N.; Roelich, K. Tensions, capabilities, and justice in climate change mitigation of fossil fuels. Energy Res. Soc. Sci. 2019, 52, 114–122. [Google Scholar] [CrossRef]
- Oliveira, G.d.L.T.; McKay, B.; Plank, C. How biofuel policies backfire: Misguided goals, inefficient mechanisms, and political-ecological blind spots. Energy Policy 2017, 108, 765–775. [Google Scholar] [CrossRef]
- Lin, J. Comparison of Moran’s I and Geary’s c in Multivariate Spatial Pattern Analysis. Geogr. Anal. 2023, 55, 685–702. [Google Scholar] [CrossRef]
- Song, M.; Wu, J.; Song, M.; Zhang, L.; Zhu, Y. Spatiotemporal regularity and spillover effects of carbon emission intensity in China’s Bohai Economic Rim. Sci. Total Environ. 2020, 740, 140184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.-y.; Zhao, L.; Zhang, H.; Chen, M.-n.; Fang, R.-y.; Yao, Y.; Zhang, Q.-p.; Wang, Q. Spatial-temporal characteristics of carbon emissions from land use change in Yellow River Delta region, China. Ecol. Indic. 2022, 136, 108623. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, T.; Wang, J.; Guo, F.; Kan, X.; Yuan, R. Spatial analysis on carbon emission abatement capacity at provincial level in China from 1997 to 2014: An empirical study based on SDM model. Atmos. Pollut. Res. 2019, 10, 97–104. [Google Scholar] [CrossRef]
- Gini, C. Measurement of inequality of incomes. Econ. J. 1921, 31, 124–125. [Google Scholar] [CrossRef]
- Wu, S.; Zheng, X.; Wei, C. Measurement of inequality using household energy consumption data in rural China. Nat. Energy 2017, 2, 795–803. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, F. China’s carbon inequality of households: Perspectives of the aging society and urban-rural gaps. Resour. Conserv. Recycl. 2022, 185, 106449. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, L.; Hu, L.; Cai, W.; Xiao, D.; Chen, J.; Wang, C. Do areas with a higher proportion of single-person households save more on electricity consumption? Evidence from the difference-in-differences model. Energy Sustain. Dev. 2023, 77, 101350. [Google Scholar] [CrossRef]
- Gao, K.; Yuan, Y. Spatiotemporal pattern assessment of China’s industrial green productivity and its spatial drivers: Evidence from city-level data over 2000–2017. Appl. Energy 2022, 307, 118248. [Google Scholar] [CrossRef]
- Ke, N.; Lu, X.; Kuang, B.; Zhang, X. Regional disparities and evolution trend of city-level carbon emission intensity in China. Sustain. Cities Soc. 2023, 88, 104288. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, Z.; Kou, J.; Du, J. Regional differences and convergence of green innovation efficiency in China. J. Environ. Manag. 2023, 325, 116618. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Lin, B. Impacts of urbanization and industrialization on energy consumption/CO2 emissions: Does the level of development matter? Renew. Sustain. Energy Rev. 2015, 52, 1107–1122. [Google Scholar] [CrossRef]
- Ruffing, K. Indicators to measure decoupling of environmental pressure from economic growth. Sustain. Indic. Sci. Assess. 2007, 67, 211. [Google Scholar]
- Dong, F.; Li, J.; Huang, J.; Lu, Y.; Qin, C.; Zhang, X.; Lu, B.; Liu, Y.; Hua, Y. A reverse distribution between synergistic effect and economic development: An analysis from industrial SO2 decoupling and CO2 decoupling. Environ. Impact Assess. Rev. 2023, 99, 107037. [Google Scholar] [CrossRef]
- Shan, Y.; Fang, S.; Cai, B.; Zhou, Y.; Li, D.; Feng, K.; Hubacek, K. Chinese cities exhibit varying degrees of decoupling of economic growth and CO2 emissions between 2005 and 2015. One Earth 2021, 4, 124–134. [Google Scholar] [CrossRef]
- Hou, L.; Wang, Y.; Zheng, Y.; Zhang, A. The Impact of Vehicle Ownership on Carbon Emissions in the Transportation Sector. Sustainability 2022, 14, 12657. [Google Scholar] [CrossRef]
- Cai, B.; Wang, J.; Yang, S.; Mao, X.; Cao, L. Carbon dioxide emissions from cities in China based on high resolution emission gridded data. Chin. J. Popul. Resour. Environ. 2017, 15, 58–70. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, L.; Hu, L.; Cai, W.; Wang, L.; Dai, C.; Chen, J. How family structure type affects household energy consumption: A heterogeneous study based on Chinese household evidence. Energy 2023, 284, 129313. [Google Scholar] [CrossRef]
- Ni, G.; Fang, Y.; Niu, M.; Lv, L.; Song, C.; Wang, W. Spatial differences, dynamic evolution and influencing factors of China’s construction industry carbon emission efficiency. J. Clean. Prod. 2024, 448, 141593. [Google Scholar] [CrossRef]
- Chen, C.; Bi, L. Study on spatio-temporal changes and driving factors of carbon emissions at the building operation stage- A case study of China. Build. Environ. 2022, 219, 109147. [Google Scholar] [CrossRef]
- Li, W.; Sun, W.; Li, G.; Cui, P.; Wu, W.; Jin, B. Temporal and spatial heterogeneity of carbon intensity in China’s construction industry. Resour. Conserv. Recycl. 2017, 126, 162–173. [Google Scholar] [CrossRef]
- Lu, W.; Tam, V.W.Y.; Du, L.; Chen, H. Impact of industrial agglomeration on haze pollution: New evidence from Bohai Sea Economic Region in China. J. Clean. Prod. 2021, 280, 124414. [Google Scholar] [CrossRef]
- Gao, C.; Tao, S.; He, Y.; Su, B.; Sun, M.; Mensah, I.A. Effect of population migration on spatial carbon emission transfers in China. Energy Policy 2021, 156, 112450. [Google Scholar] [CrossRef]
- Long, H.; Li, J.; Liu, H. Internal migration and associated carbon emission changes: Evidence from cities in China. Energy Econ. 2022, 110, 106010. [Google Scholar] [CrossRef]
- Li, S.; Wu, Q.; Zheng, Y.; Sun, Q. Study on the spatial association and influencing factors of carbon emissions from the Chinese construction industry. Sustainability 2021, 13, 1728. [Google Scholar] [CrossRef]
- Yu, Y.; You, K.; Cai, W.; Feng, W.; Li, R.; Liu, Q.; Chen, L.; Liu, Y. City-level building operation and end-use carbon emissions dataset from China for 2015–2020. Sci. Data 2024, 11, 138. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Hu, J.; Zhao, K.; Chen, H.; Zhao, S.; Li, W. Dynamics and decoupling analysis of carbon emissions from construction industry in China. Buildings 2022, 12, 257. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, D.; Wang, T.; Tian, H.; Gan, L. Decoupling effect and spatial-temporal characteristics of carbon emissions from construction industry in China. J. Clean. Prod. 2023, 419, 138243. [Google Scholar] [CrossRef]
- Liu, Y.; Gan, L.; Cai, W.G.; Li, R. Decomposition and decoupling analysis of carbon emissions in China’s construction industry using the generalized Divisia index method. Environ. Impact Assess. Rev. 2024, 104. [Google Scholar] [CrossRef]

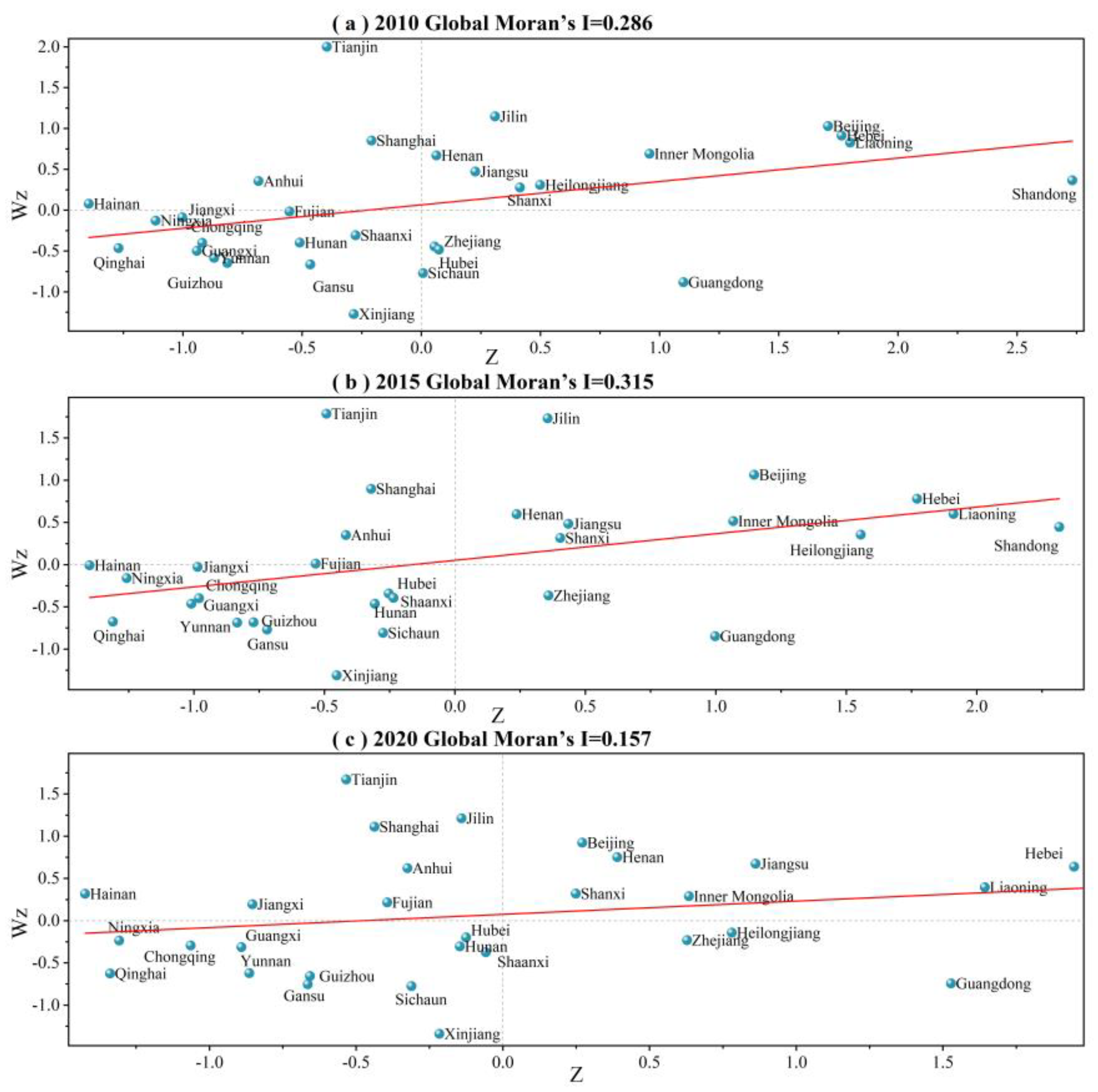


| Position | Abbreviation | Meaning | Moran’s I |
|---|---|---|---|
| First quadrant | High-observed–high-lag clusters (HH) | This type of area is a ‘high-level’ area in relation to its surroundings | Moran’s I > 0 |
| Second quadrant | Low-observed–high-lag clusters (LH) | ‘Low-level’ in this category, but ‘high-level’ in its immediate vicinity | Moran’s I < 0 |
| Third quadrant | Low-observed–low-lag clusters (LL) | This type of area is ‘low-level’ in relation to its surroundings | Moran’s I > 0 |
| Fourth quadrant | High-observed–low-lag clusters (HL) | Areas in this category are ‘high-level’, but their surroundings are ‘low-level’ | Moran’s I < 0 |
| Year | Moran I | Z-Value | p-Value |
|---|---|---|---|
| 2010 | 0.286 | 2.645 | 0.004 |
| 2011 | 0.274 | 2.54 | 0.006 |
| 2012 | 0.272 | 2.53 | 0.006 |
| 2013 | 0.296 | 2.726 | 0.003 |
| 2014 | 0.303 | 2.783 | 0.003 |
| 2015 | 0.315 | 2.882 | 0.002 |
| 2016 | 0.267 | 2.485 | 0.006 |
| 2017 | 0.207 | 1.993 | 0.023 |
| 2018 | 0.181 | 1.779 | 0.038 |
| 2019 | 0.173 | 1.708 | 0.044 |
| 2020 | 0.157 | 1.577 | 0.057 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, C.; Tan, Y.; Cao, S.; Liao, H.; Pu, J.; Cai, W. Study on Interprovincial Equity and the Decoupling of Carbon Emissions in the Construction Industry—A Case Study in China. Buildings 2024, 14, 2200. https://doi.org/10.3390/buildings14072200
Dai C, Tan Y, Cao S, Liao H, Pu J, Cai W. Study on Interprovincial Equity and the Decoupling of Carbon Emissions in the Construction Industry—A Case Study in China. Buildings. 2024; 14(7):2200. https://doi.org/10.3390/buildings14072200
Chicago/Turabian StyleDai, Chao, Yuan Tan, Shuangping Cao, Hong Liao, Jie Pu, and Weiguang Cai. 2024. "Study on Interprovincial Equity and the Decoupling of Carbon Emissions in the Construction Industry—A Case Study in China" Buildings 14, no. 7: 2200. https://doi.org/10.3390/buildings14072200
APA StyleDai, C., Tan, Y., Cao, S., Liao, H., Pu, J., & Cai, W. (2024). Study on Interprovincial Equity and the Decoupling of Carbon Emissions in the Construction Industry—A Case Study in China. Buildings, 14(7), 2200. https://doi.org/10.3390/buildings14072200






