Stochastic Optimal Bounded Parametric Control of Periodic Viscoelastomer Sandwich Plate with Supported Mass Based on Dynamical Programming Principle
Abstract
1. Introduction
2. Differential Equations for Controlled Periodic SP and Supported Mass
3. Multi-Dimensional System Equations with Parameters Dependent Nonlinearly on Control
4. OBPC Law and Controlled Responses of SP
5. Results and Discussions
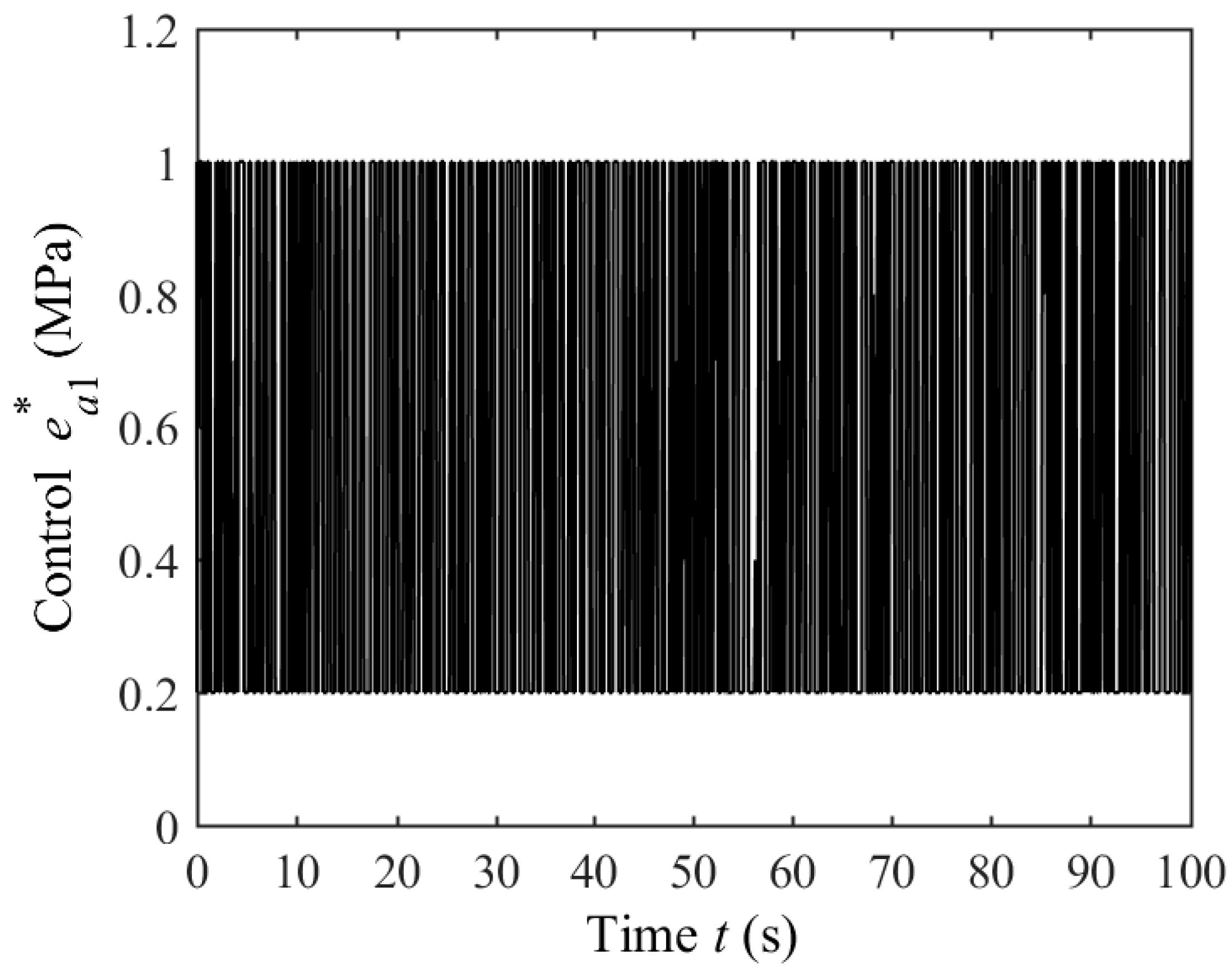
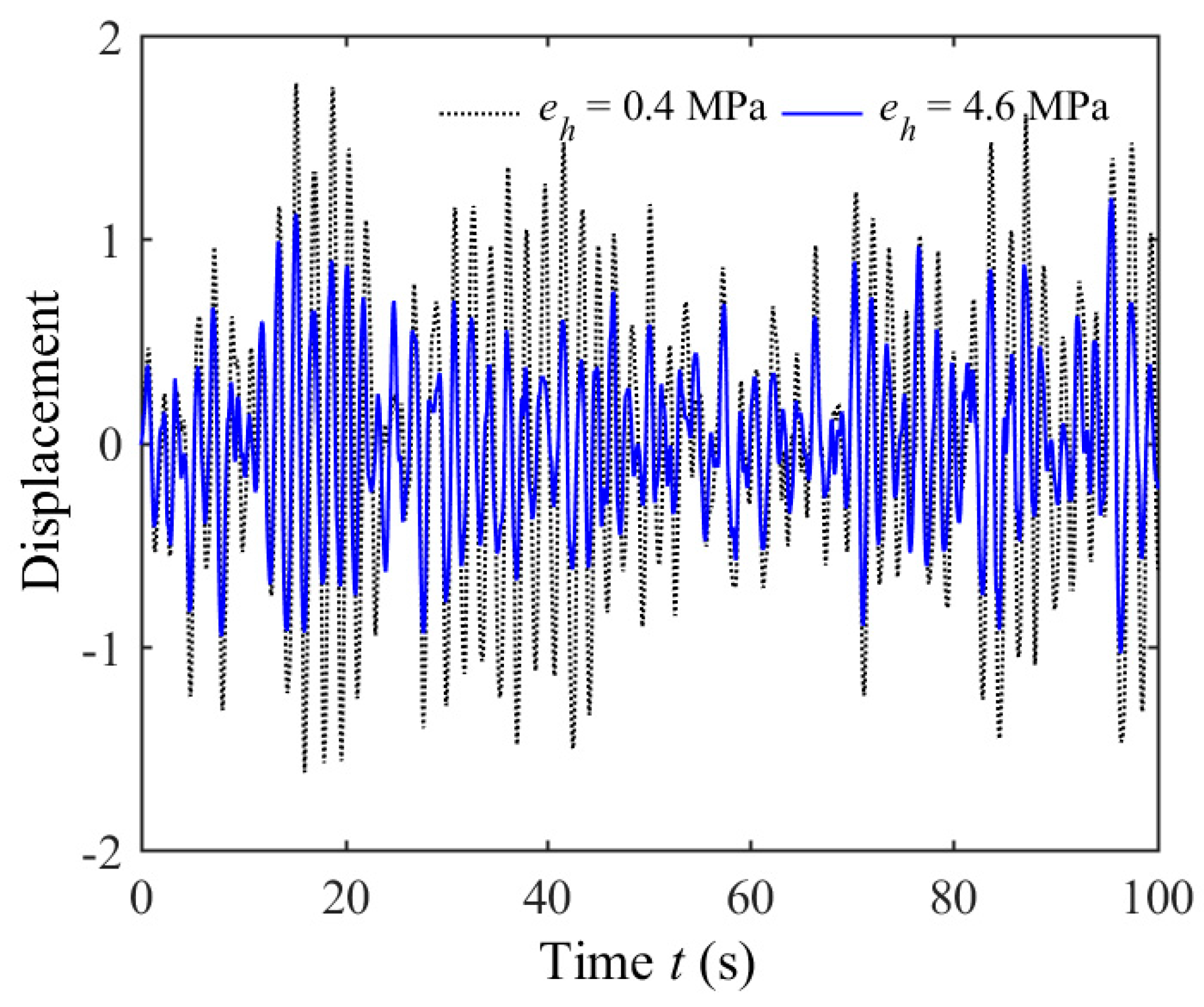
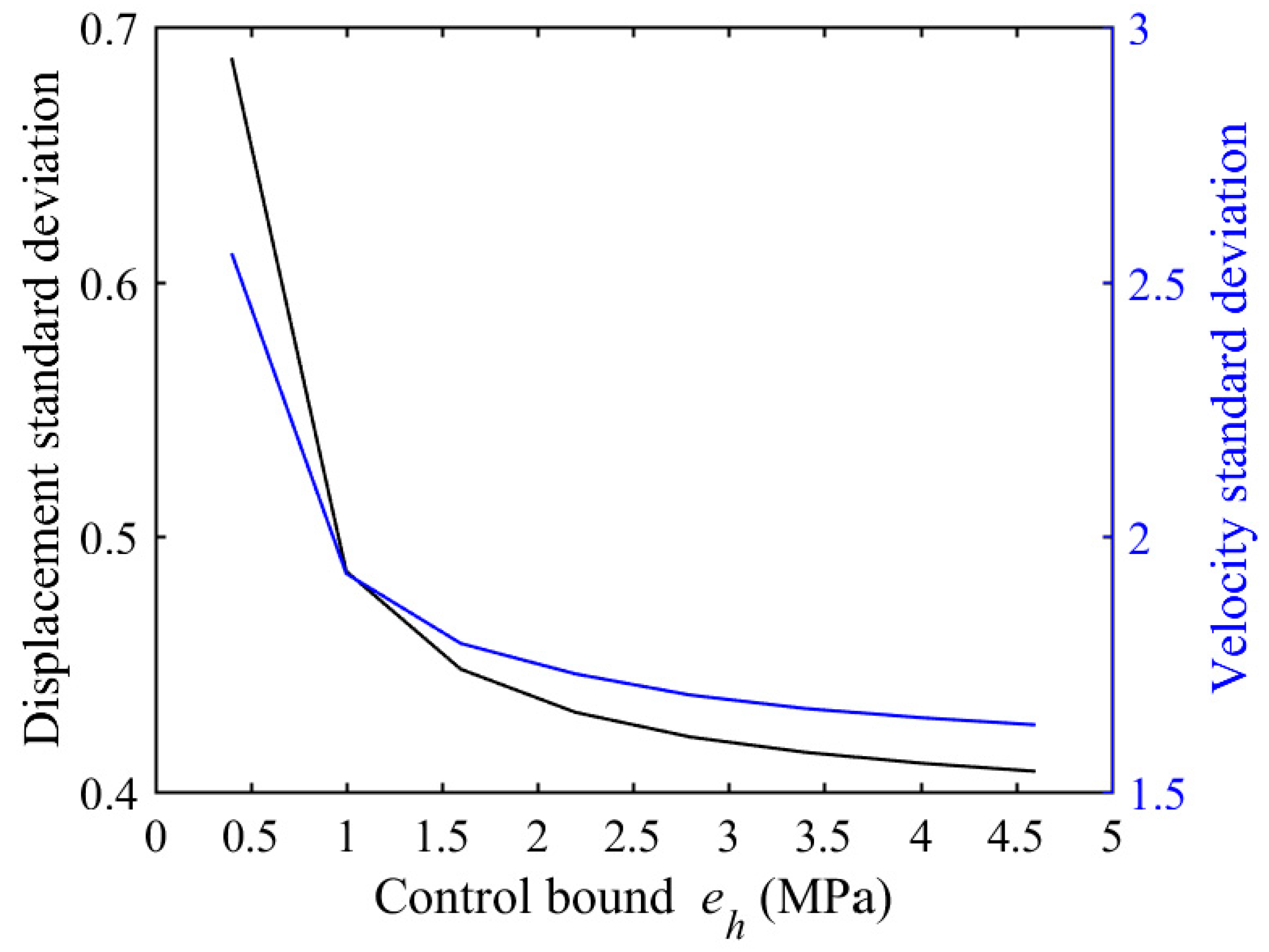
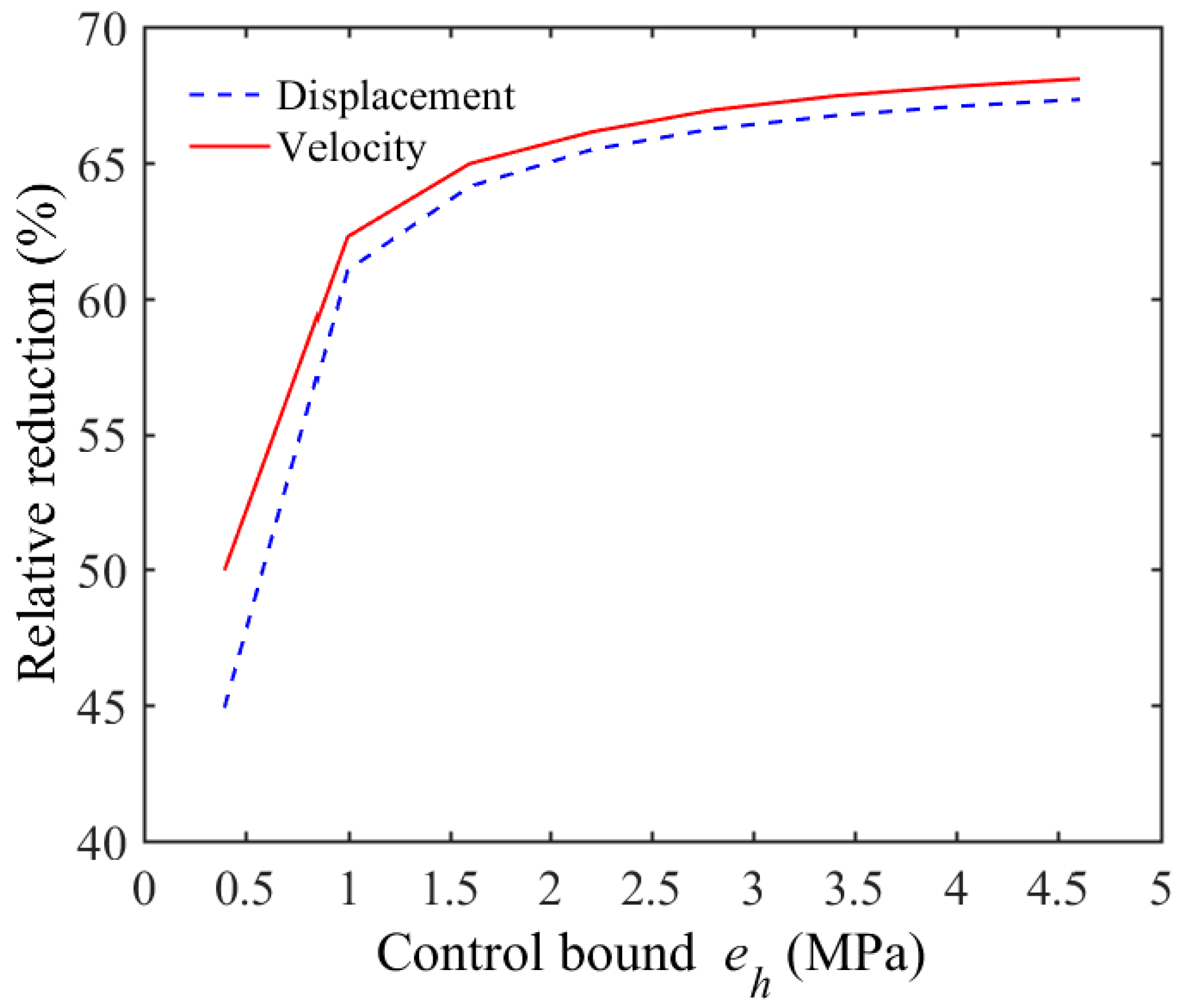
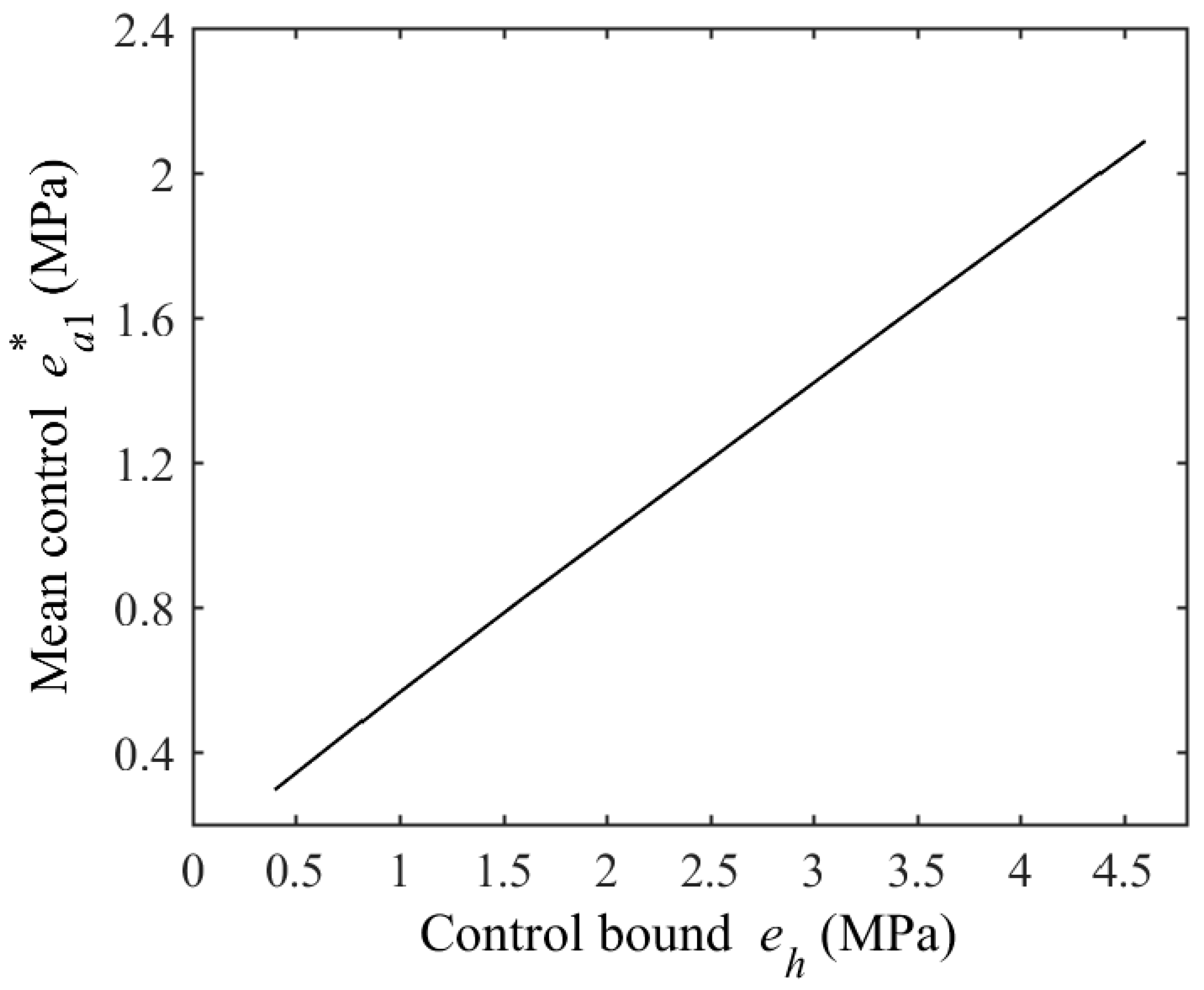
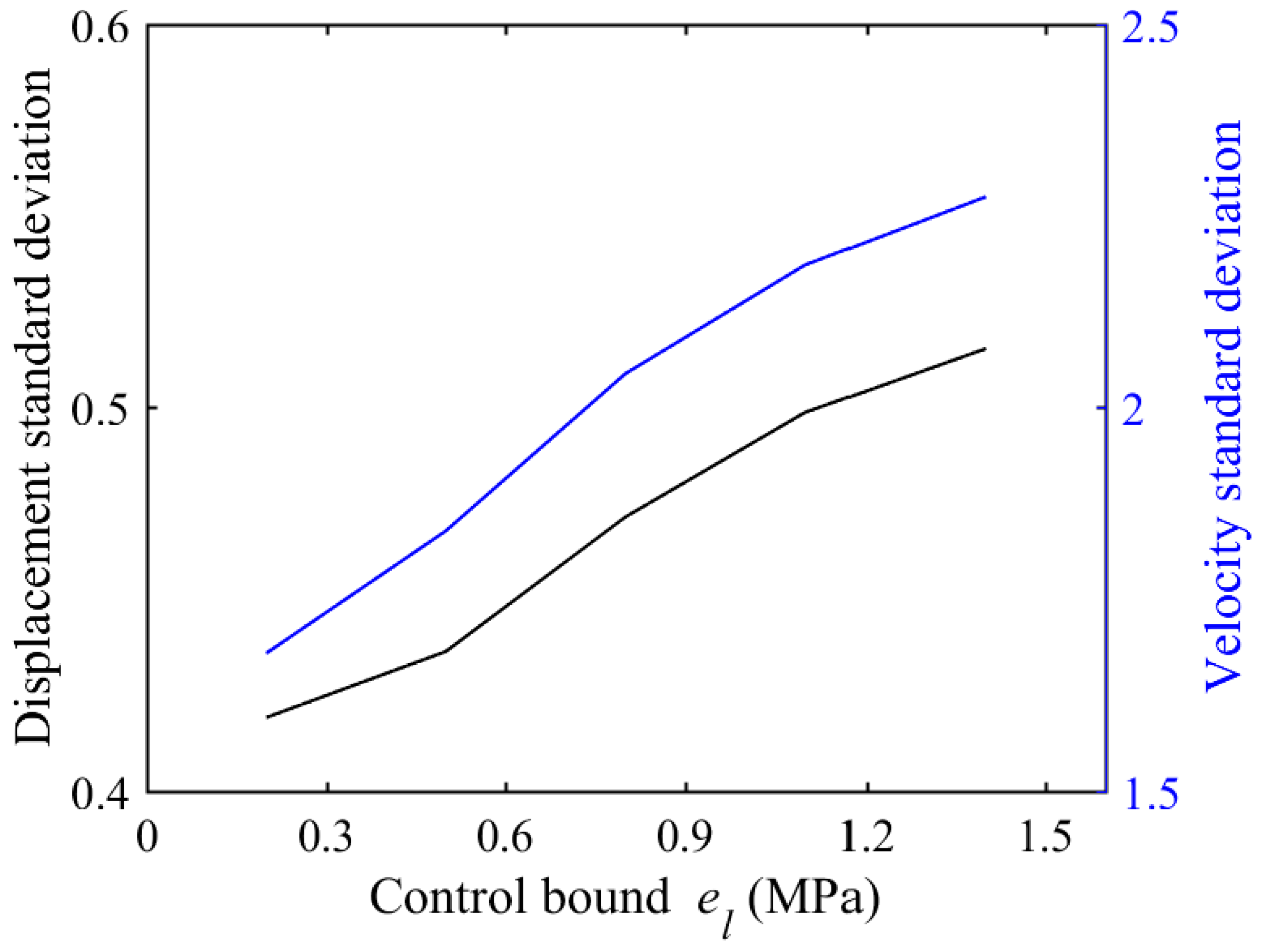
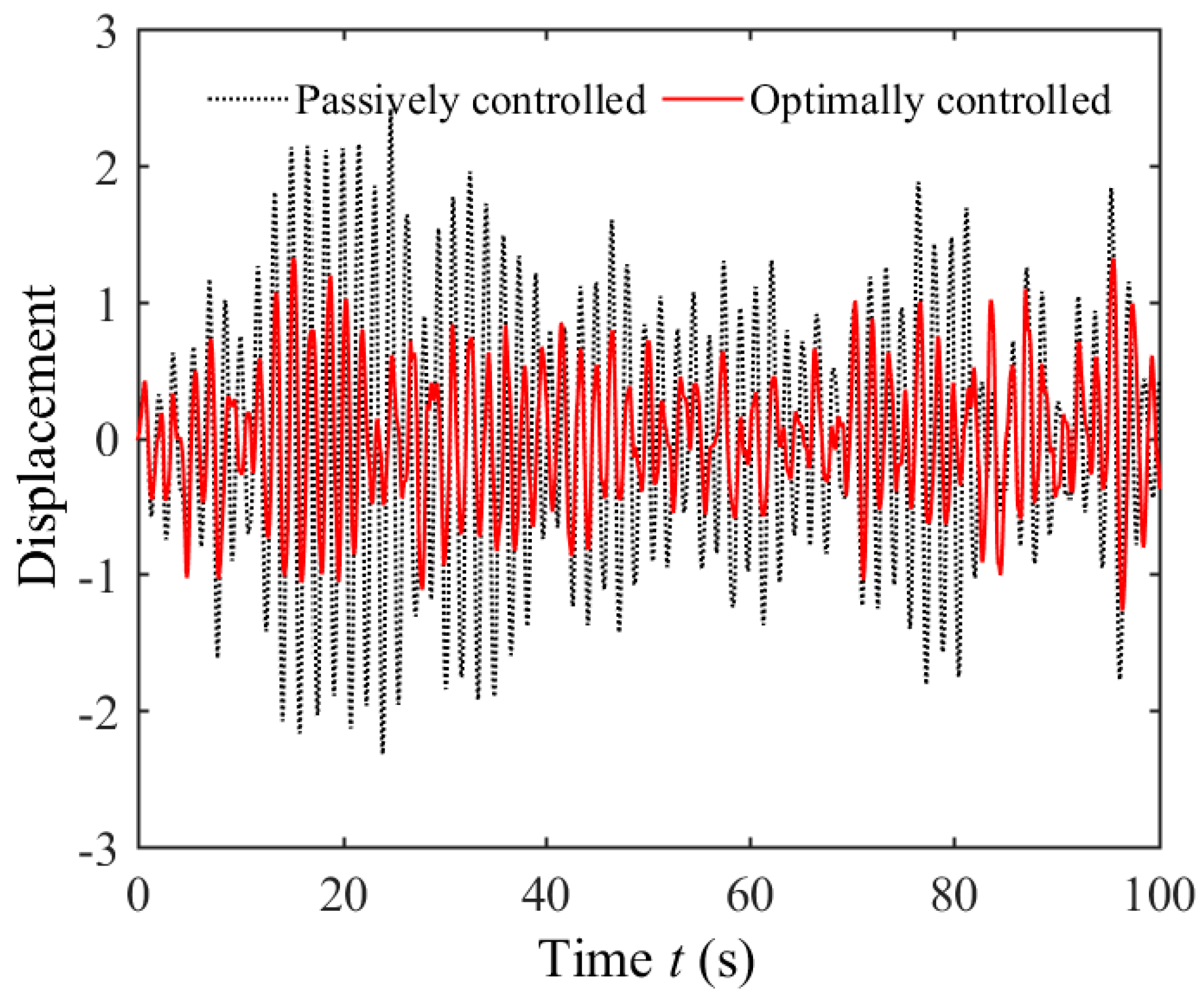
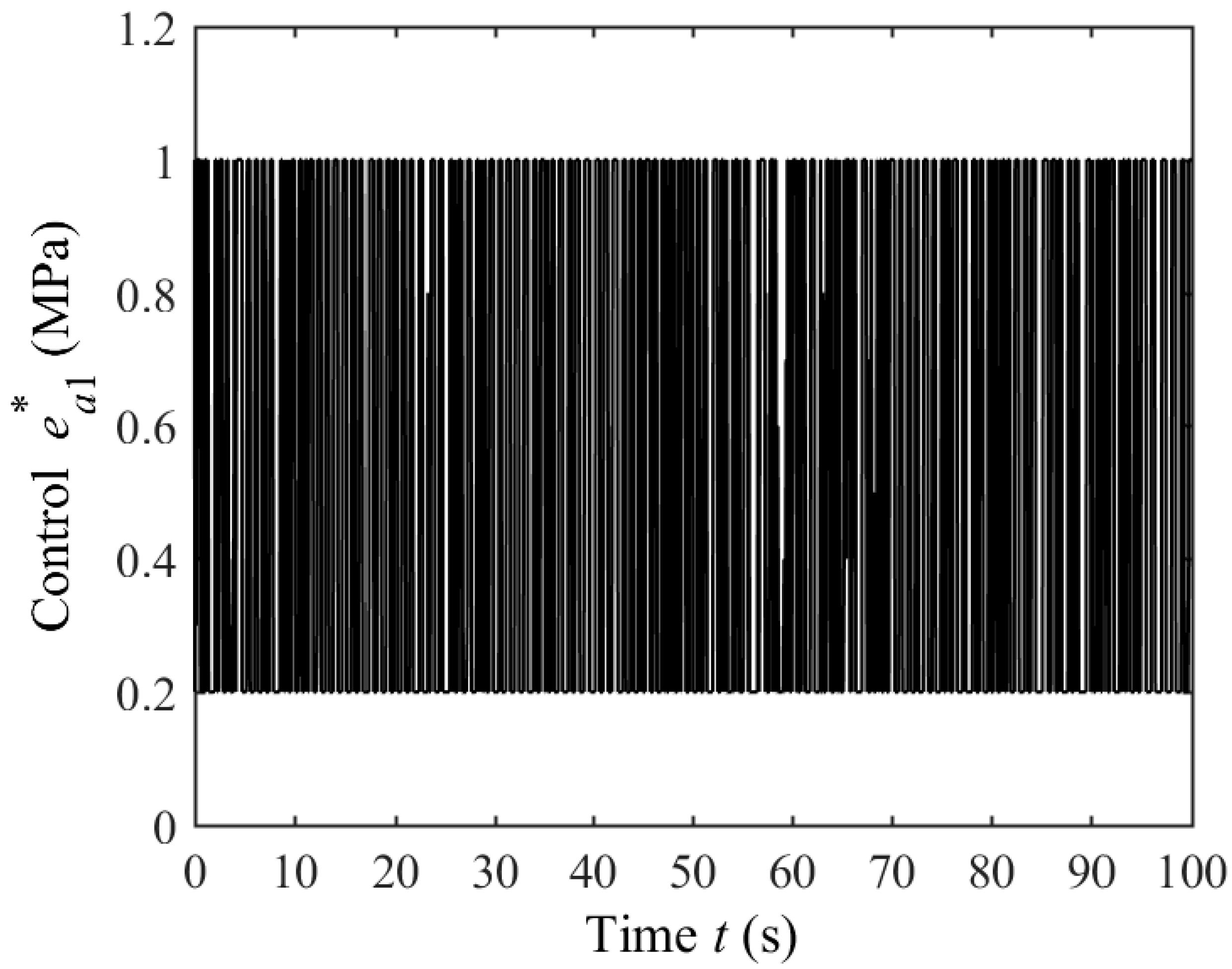
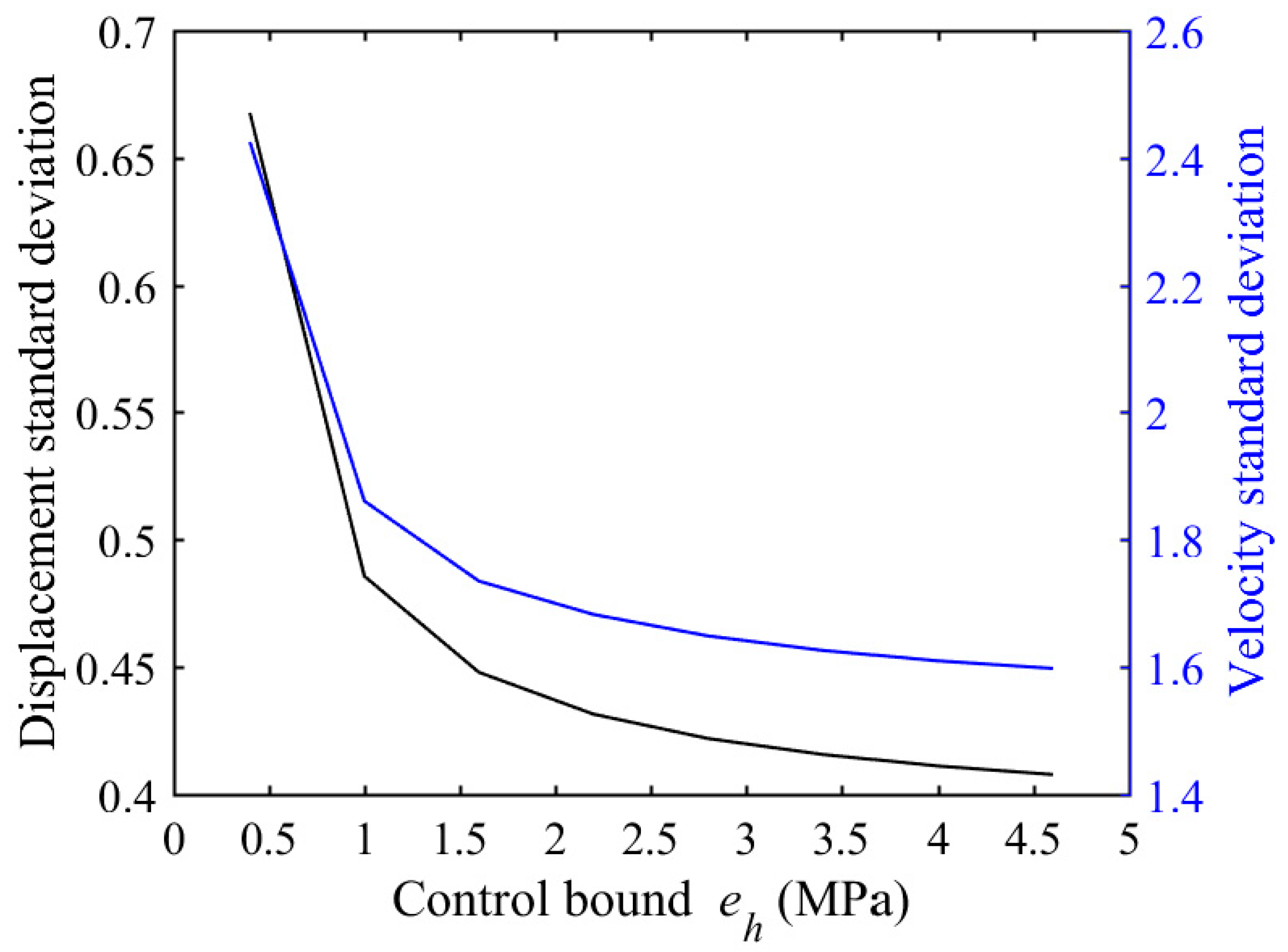
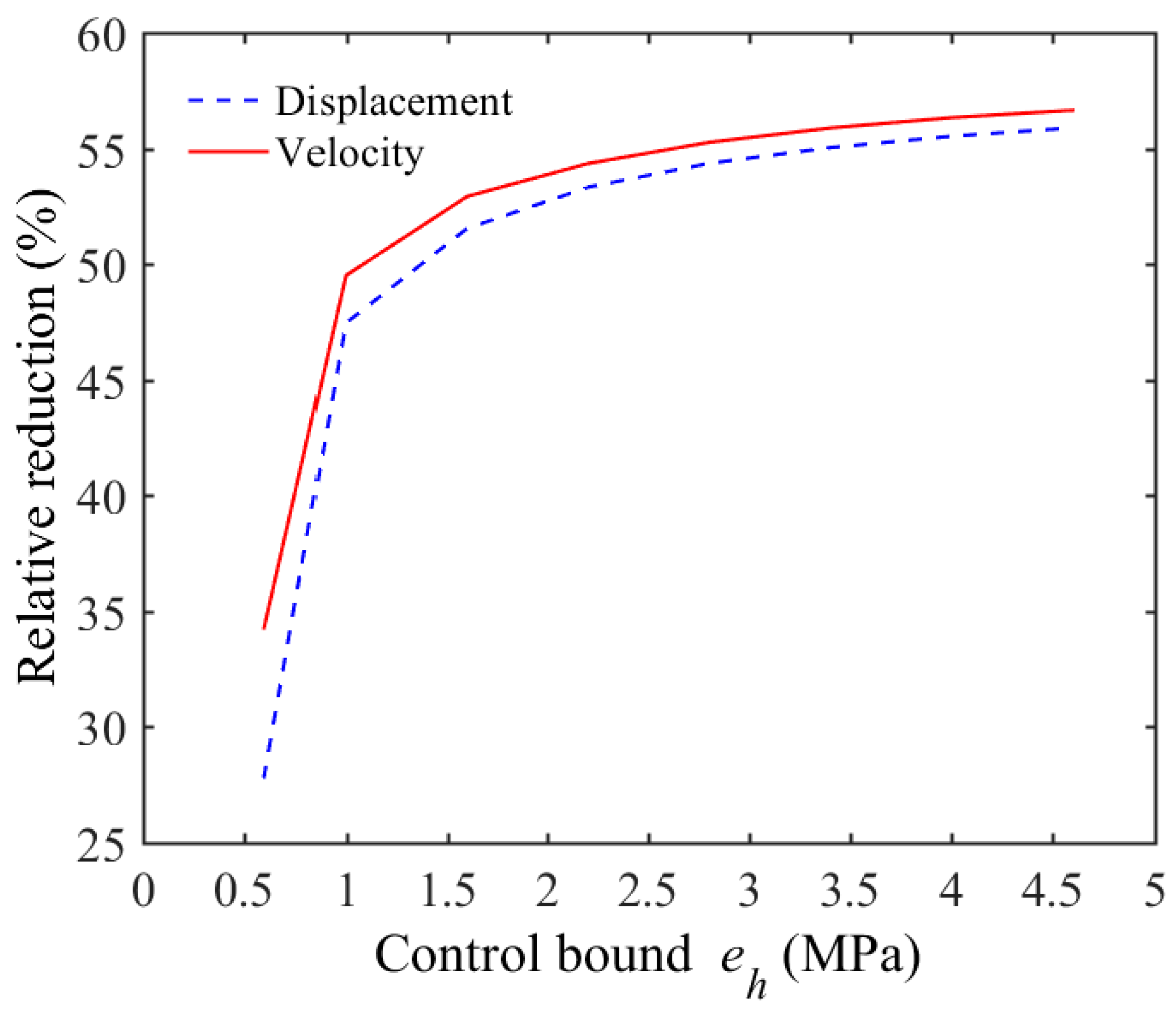
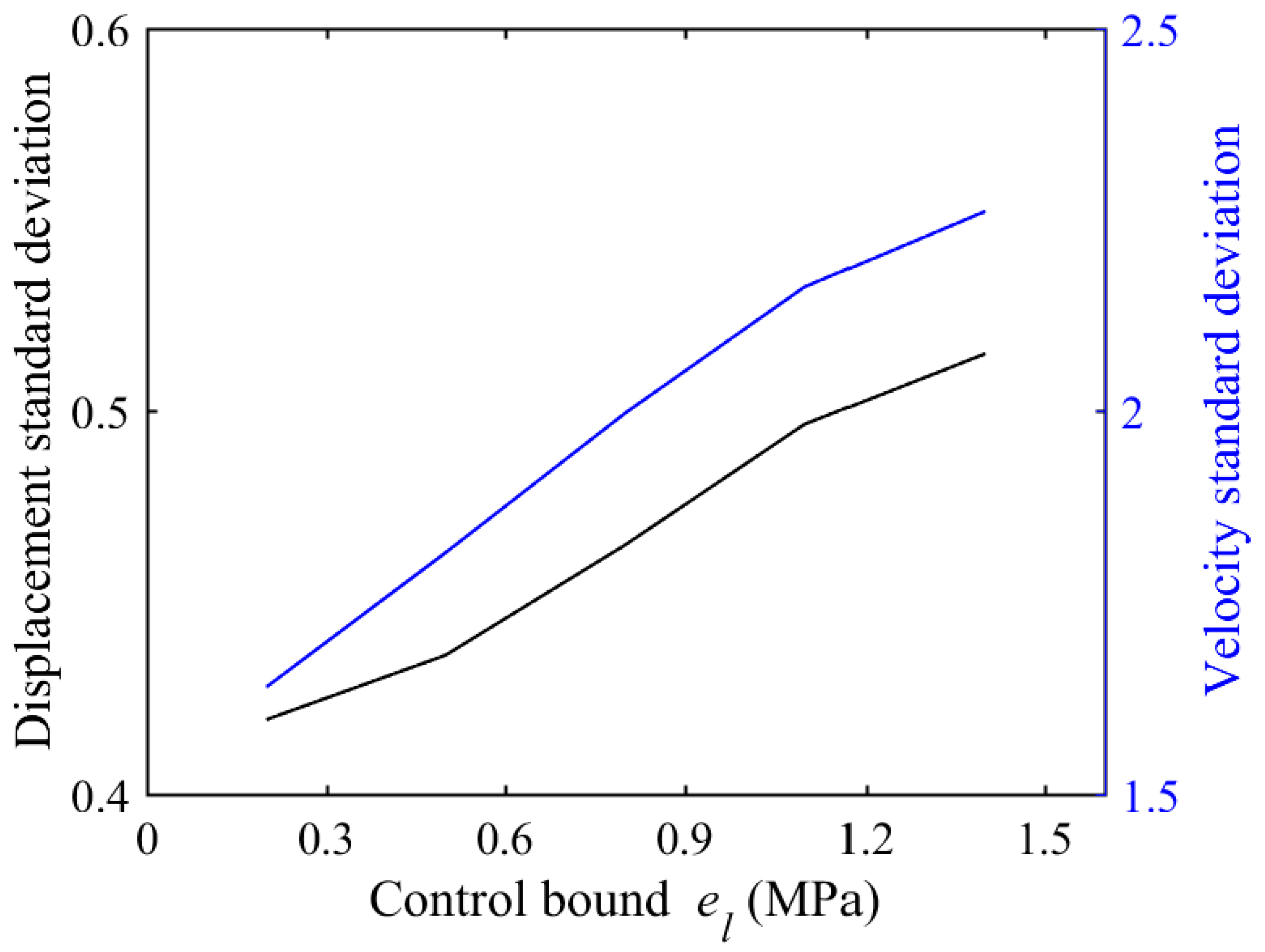
5.1. Optimal Control of SP with Uniform Parameters
5.2. Optimal Control of SP with Periodic Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Soong, T.T.; Spencer, B.F. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Spencer, B.F.; Nagarajaiah, S. State of the art of structural control. J. Struct. Eng. 2003, 129, 845–856. [Google Scholar] [CrossRef]
- Casciati, F.; Rodellar, J.; Yildirim, U. Active and semi-active control of structures -theory and application: A review of recent advances. J. Intell. Mater. Syst. Struct. 2012, 23, 1181–1195. [Google Scholar] [CrossRef]
- Datta, T.K. A brief review of stochastic control of structures. In Proceedings of International Symposium on Engineering under Uncertainty; Springer: Kolkata, India, 2013; pp. 119–139. [Google Scholar]
- Ni, Y.Q.; Ying, Z.G.; Chen, Z.H. Micro-vibration suppression of equipment supported on a floor incorporating magneto-rheological elastomer core. J. Sound Vib. 2011, 330, 4369–4383. [Google Scholar] [CrossRef]
- Eshaghi, M.; Sedaghati, R.; Rakheja, S. Dynamic characteristics and control of magnetorheological/electrorheological sandwich structures: A state-of-the-art review. J. Intell. Mater. Syst. Struct. 2016, 27, 2003–2037. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Wang, Q. Magnetorheological elastomer-based smart sandwich beams with nonconductive skins. Smart Mater. Struct. 2005, 14, 1001–1009. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Wang, Q. Study on the adjustable rigidity of magnetorheological-elastomer-based sandwich beams. Smart Mater. Struct. 2006, 15, 59–74. [Google Scholar] [CrossRef]
- Choi, W.J.; Xiong, Y.P.; Shenoi, R.A. Vibration characteristics of sandwich beam with steel skins and magnetorheological elastomer cores. Adv. Struct. Eng. 2010, 13, 837–847. [Google Scholar] [CrossRef]
- Bornassi, S.; Navazi, H.M. Torsional vibration analysis of a rotating tapered sandwich beam with magnetorheological elastomer core. J. Intell. Mater. Syst. Struct. 2018, 29, 2406–2423. [Google Scholar] [CrossRef]
- Dwivedy, S.K.; Mahendra, N.; Sahu, K.C. Parametric instability regions of a soft and magnetorheological elastomer cored sandwich beam. J. Sound Vib. 2009, 325, 686–704. [Google Scholar] [CrossRef]
- Nayak, B.; Dwivedy, S.K.; Murthy, K.S.R.K. Dynamic analysis of magnetorheological elastomer-based sandwich beam with conductive skins under various boundary conditions. J. Sound Vib. 2011, 330, 1837–1859. [Google Scholar] [CrossRef]
- Yeh, J.Y. Vibration analysis of sandwich rectangular plates with magnetorheological elastomer damping treatment. Smart Mater. Struct. 2013, 22, 035010. [Google Scholar] [CrossRef]
- Aguib, S.; Nour, A.; Zahloul, H.; Bossis, G.; Chevalier, P.; Lancon, P. Dynamic behavior analysis of a magnetorheological elastomer sandwich plate. Int. J. Mech. Sci. 2014, 87, 118–136. [Google Scholar] [CrossRef]
- Babu, V.R.; Vasudevan, R. Dynamic analysis of tapered laminated composite magnetorheological elastomer (MRE) sandwich plates. Smart Mater. Struct. 2016, 25, 035006. [Google Scholar] [CrossRef]
- Mikhasev, G.I.; Eremeyev, V.A.; Wilde, K.; Maevskaya, S.S. Assessment of dynamic characteristics of thin cylindrical sandwich panels with magnetorheological core. J. Intell. Mater. Syst. Struct. 2019, 30, 2748–2769. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Shabanimotlagh, M. Magnetic-field-dependent sound transmission properties of magnetorheological elastomer-based adaptive panels. Smart Mater. Struct. 2010, 19, 035006. [Google Scholar] [CrossRef]
- Ying, Z.G.; Ni, Y.Q.; Ye, S.Q. Stochastic micro-vibration suppression of a sandwich plate using a magneto-rheological visco-elastomer core. Smart Mater. Struct. 2014, 23, 025019. [Google Scholar] [CrossRef]
- Vemuluri, R.B.; Rajamohan, V.; Arumugam, A.B. Dynamic characterization of tapered laminated composite sandwich plates partially treated with magnetorheological elastomer. J. Sandw. Struct. Mater. 2018, 20, 308–350. [Google Scholar] [CrossRef]
- Vemuluri, R.B.; Rajamohan, V.; Sudhager, P.E. Structural optimization of tapered composite sandwich plates partially treated with magnetorheological elastomers. Compos. Struct. 2018, 200, 258–276. [Google Scholar] [CrossRef]
- Soleymani, T.; Arani, A.G. On aeroelastic stability of a piezo-MRE sandwich plate in supersonic airflow. Compos. Struct. 2019, 230, 111532. [Google Scholar] [CrossRef]
- Hoseinzadeh, M.; Rezaeepazhand, J. Dynamic stability enhancement of laminated composite sandwich plates using smart elastomer layer. J. Sandw. Struct. Mater. 2020, 22, 2796–2817. [Google Scholar] [CrossRef]
- Mead, D.J. Wave propagation in continuous periodic structures: Research contributions from Southampton. J. Sound Vib. 1996, 190, 495–524. [Google Scholar] [CrossRef]
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress and future outlook. Appl. Mech. Rev. 2014, 66, 040802. [Google Scholar] [CrossRef]
- Ruan, Z.G.; Ying, Z.G.; Ni, Y.Q. Response adjustable performance of a visco-elastomer sandwich plate with harmonic parameters and distributed supported masses under random loading. Meas. Control 2022, 55, 631–645. [Google Scholar] [CrossRef]
- Ying, Z.G.; Ruan, Z.G.; Ni, Y.Q. Response adjustability analysis of partial and ordinary differential coupling system for visco-elastomer sandwich plate coupled with distributed masses under random excitation via spatial periodicity strategy. Symmetry 2022, 14, 1794. [Google Scholar] [CrossRef]
- Bisegna, P.; Caruso, G. Dynamical behavior of disordered rotationally periodic structures: A homogenization approach. J. Sound Vib. 2011, 330, 2608–2627. [Google Scholar] [CrossRef]
- Pourasghar, A.; Chen, Z. Nonlinear vibration and modal analysis of FG nanocomposite sandwich beams reinforced by aggregated CNTs. Polym. Eng. Sci. 2019, 59, 1362–1370. [Google Scholar] [CrossRef]
- Pourasghar, A.; Chen, Z. Effect of hyperbolic heat conduction on the linear and nonlinear vibration of CNT reinforced size-dependent functionally graded microbeams. Int. J. Eng. Sci. 2019, 137, 57–72. [Google Scholar] [CrossRef]
- Domagalski, L.; Swiatek, M.; Jedrysiak, J. An analytical-numerical approach to vibration analysis of periodic Timoshenko beams. Compos. Struct. 2019, 211, 490–501. [Google Scholar] [CrossRef]
- Demir, O. Differential transform method for axisymmetric vibration analysis of circular sandwich plates with viscoelastic core. Symmetry 2022, 14, 852. [Google Scholar] [CrossRef]
- Ying, Z.G.; Ni, Y.Q.; Duan, Y.F. Stochastic vibration suppression analysis of an optimal bounded controlled sandwich beam with MR visco-elastomer cores. Smart Struct. Syst. 2017, 19, 21–31. [Google Scholar] [CrossRef]
- Stengel, R.F. Optimal Control and Estimation; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Yong, J.M.; Zhou, X.Y. Stochastic Controls, Hamiltonian Systems and HJB Equations; Springer: New York, NY, USA, 1999. [Google Scholar]
- Dimentberg, M.F.; Iourtchenko, A.S.; Brautus, A.S. Optimal bounded control of steady-state random vibrations. Probabilistic Eng. Mech. 2000, 15, 381–386. [Google Scholar] [CrossRef]
- Socha, L.A. Application of true linearization in stochastic quasi-optimal control problems. Struct. Control Health Monit. 2000, 7, 219–230. [Google Scholar] [CrossRef]
- Ying, Z.G.; Zhu, W.Q. Optimal bounded control for nonlinear stochastic smart structure systems based on extended Kalman filter. Nonlinear Dyn. 2017, 90, 105–114. [Google Scholar] [CrossRef]
- Zhou, S.; Huang, J.; Yuan, Q.; Ma, D.; Peng, S.; Chesne, S. Optimal design of tuned mass-damper-inerter for structure with uncertain-but-bounded parameter. Buildings 2022, 12, 781. [Google Scholar] [CrossRef]
- Ostrowski, M.; Jedlinska, A.; Poplawski, B.; Blachowski, B.; Mikulowski, G.; Pisarski, D.; Jankowski, L. Sliding mode control for semi-active damping of vibrations using on/off viscous structural nodes. Buildings 2023, 13, 348. [Google Scholar] [CrossRef]
- Soong, T.T. Active Structural Control: Theory and Practice; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Yan, M.J.; Dowell, E.H. Governing equations for vibrating constrained-layer damping sandwich plates and beams. J. Appl. Mech. 1972, 39, 1041–1046. [Google Scholar] [CrossRef]
- Mead, D.J. The damping properties of elastically supported sandwich plates. J. Sound Vib. 1972, 24, 275–295. [Google Scholar] [CrossRef]
- Flugge, W. Viscoelasticity; Springer: New York, NY, USA, 1975. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, Z.-G.; Ying, Z.-G.; Ying, Z.-Z.; Lei, H.; Wang, W.; Xia, L. Stochastic Optimal Bounded Parametric Control of Periodic Viscoelastomer Sandwich Plate with Supported Mass Based on Dynamical Programming Principle. Buildings 2024, 14, 2309. https://doi.org/10.3390/buildings14082309
Ruan Z-G, Ying Z-G, Ying Z-Z, Lei H, Wang W, Xia L. Stochastic Optimal Bounded Parametric Control of Periodic Viscoelastomer Sandwich Plate with Supported Mass Based on Dynamical Programming Principle. Buildings. 2024; 14(8):2309. https://doi.org/10.3390/buildings14082309
Chicago/Turabian StyleRuan, Zhi-Gang, Zu-Guang Ying, Zhao-Zhong Ying, Hua Lei, Wen Wang, and Lei Xia. 2024. "Stochastic Optimal Bounded Parametric Control of Periodic Viscoelastomer Sandwich Plate with Supported Mass Based on Dynamical Programming Principle" Buildings 14, no. 8: 2309. https://doi.org/10.3390/buildings14082309
APA StyleRuan, Z.-G., Ying, Z.-G., Ying, Z.-Z., Lei, H., Wang, W., & Xia, L. (2024). Stochastic Optimal Bounded Parametric Control of Periodic Viscoelastomer Sandwich Plate with Supported Mass Based on Dynamical Programming Principle. Buildings, 14(8), 2309. https://doi.org/10.3390/buildings14082309






