Horizontal Hysteretic Behavior of Circular Concrete-Filled Steel Tubular Columns with Ultra-Large Diameter-to-Thickness Ratios
Abstract
:1. Introduction
2. Test Survey
2.1. Specimen Design and Production
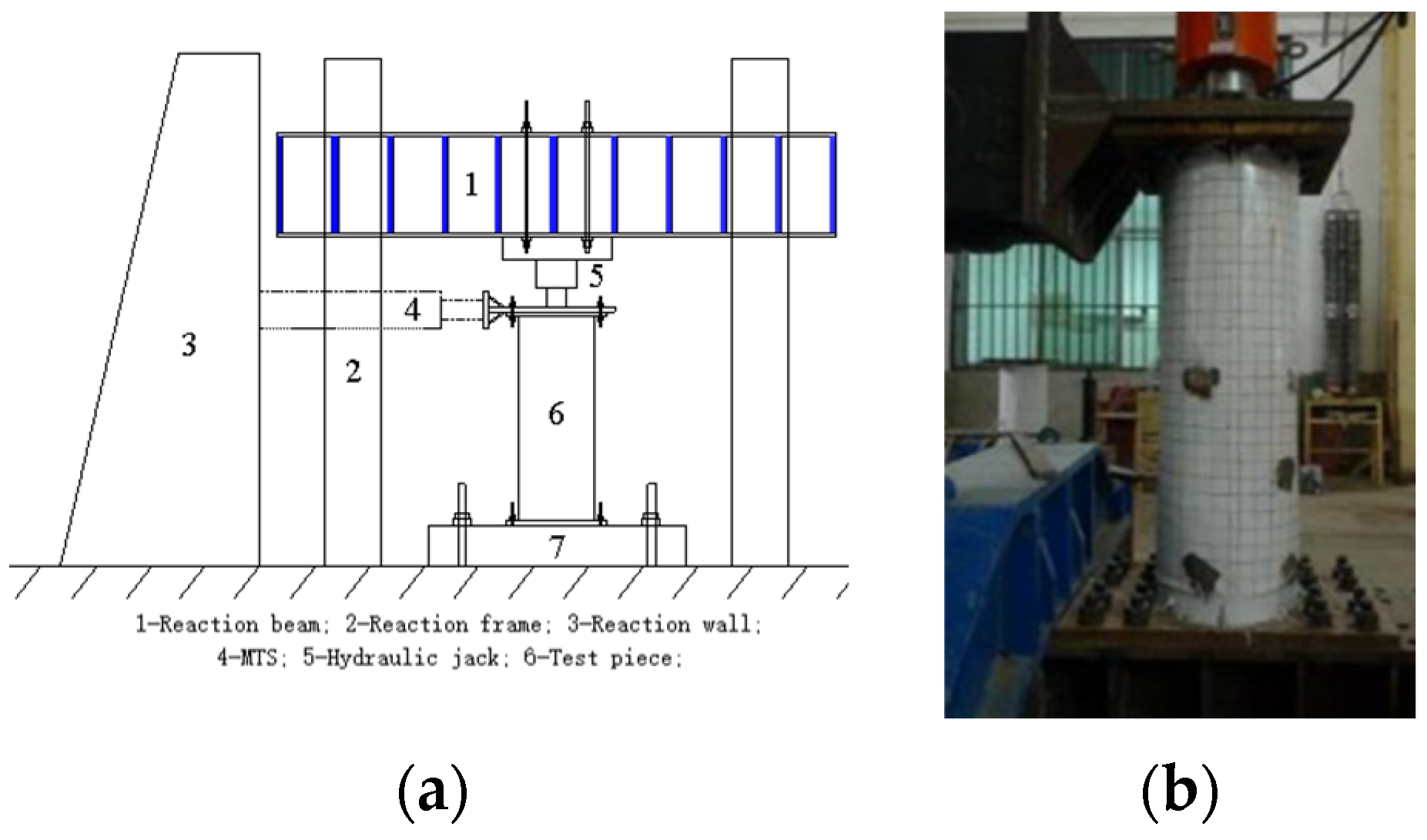
2.2. Test and Loading Scheme
3. Analysis of Test Process and Failure Mode
4. Test Results and Discussion
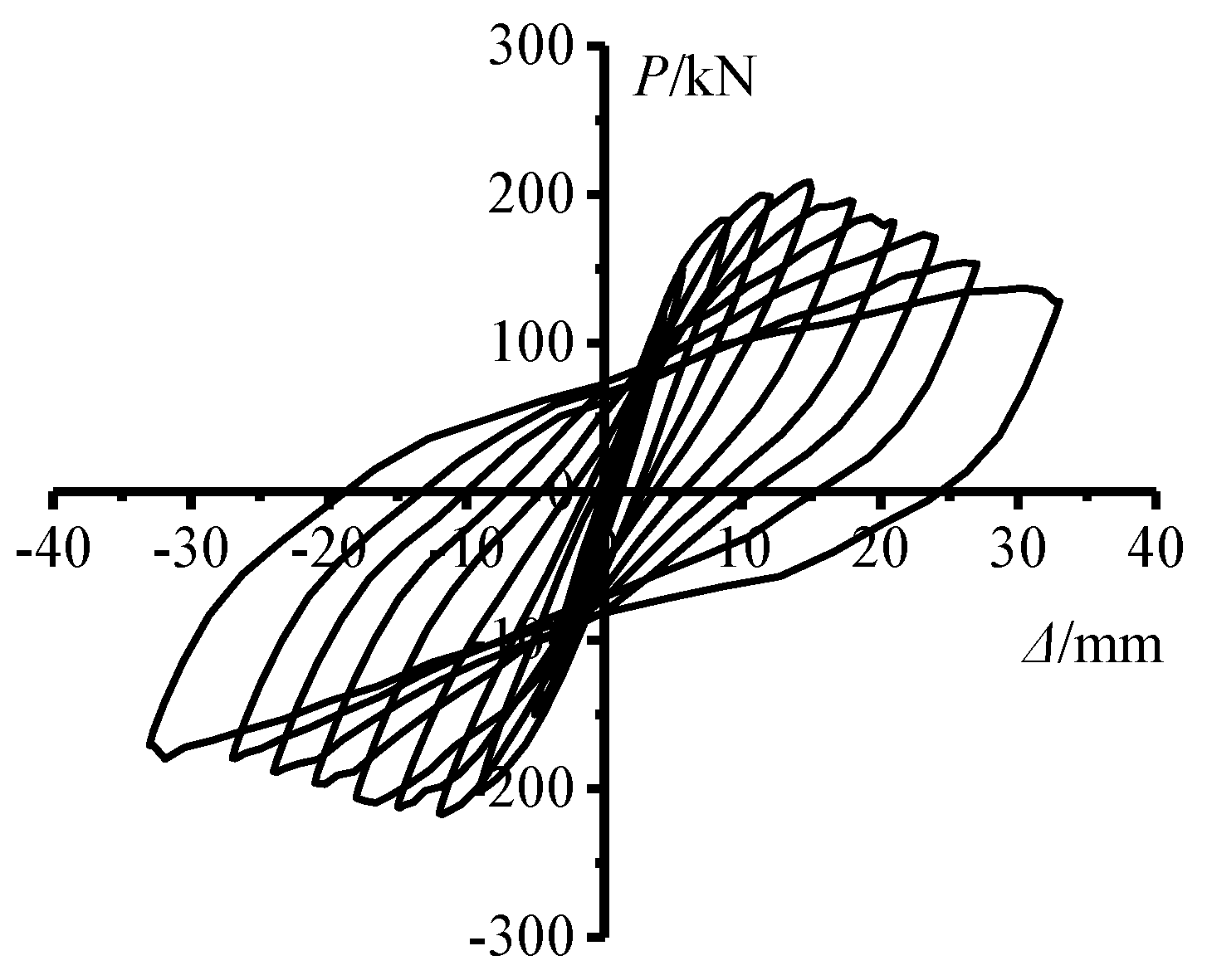
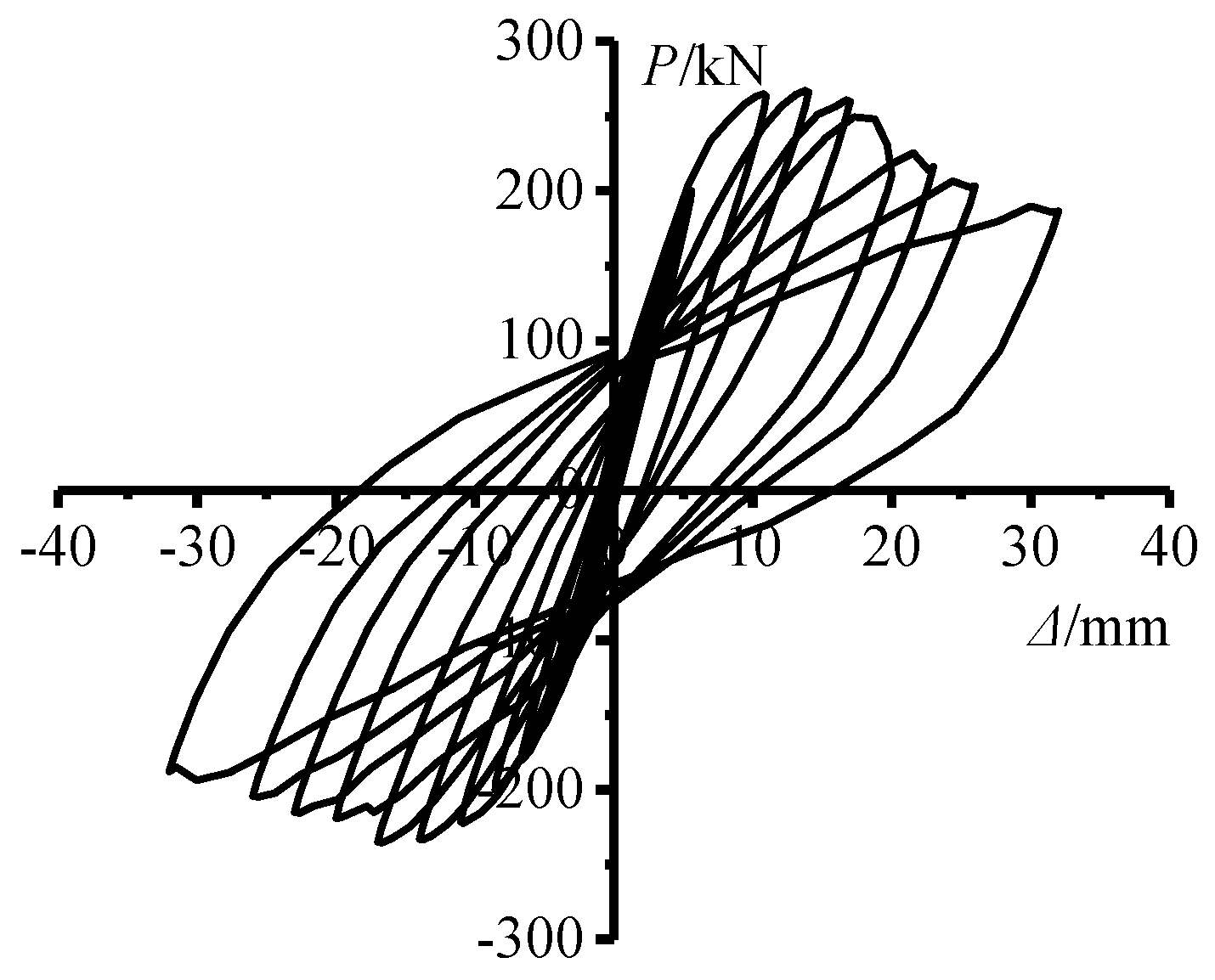
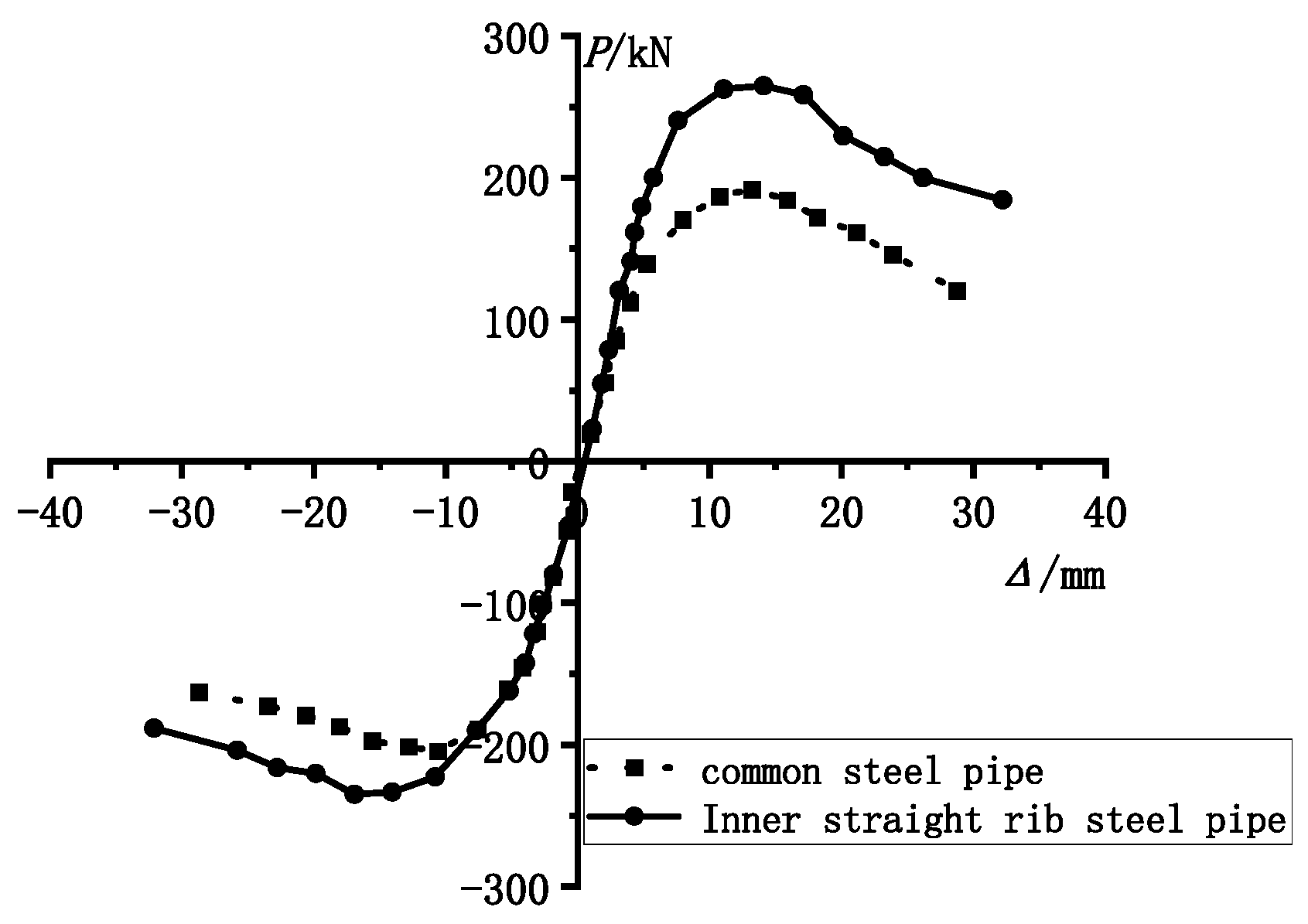
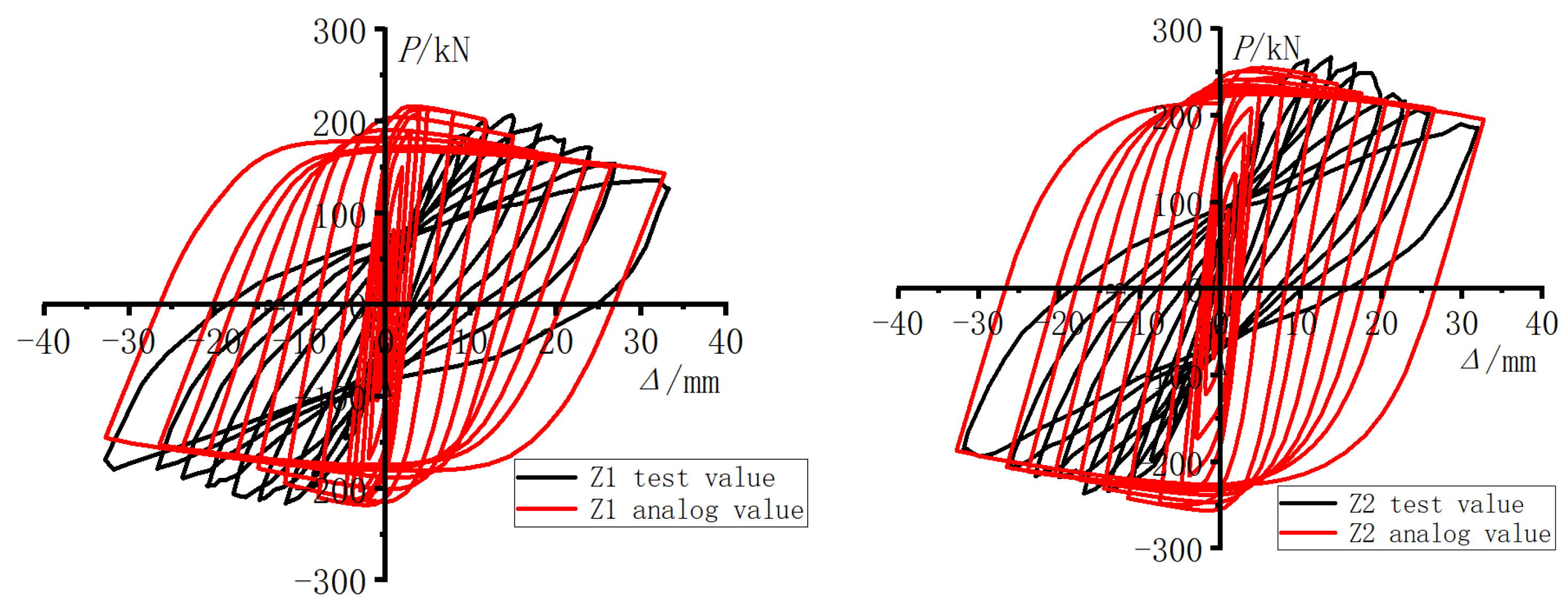
4.1. Load-Displacement Hysteresis Curves
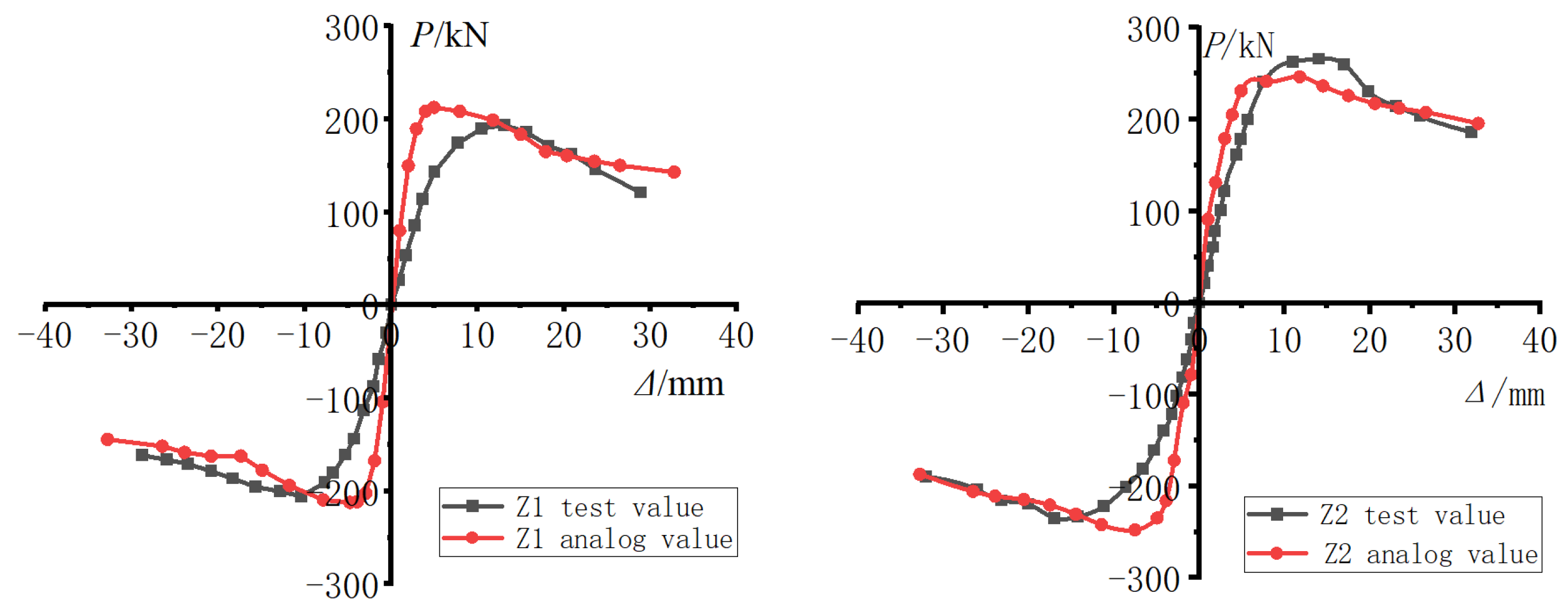
4.2. Skeleton Curves
4.3. Ductility Analysis
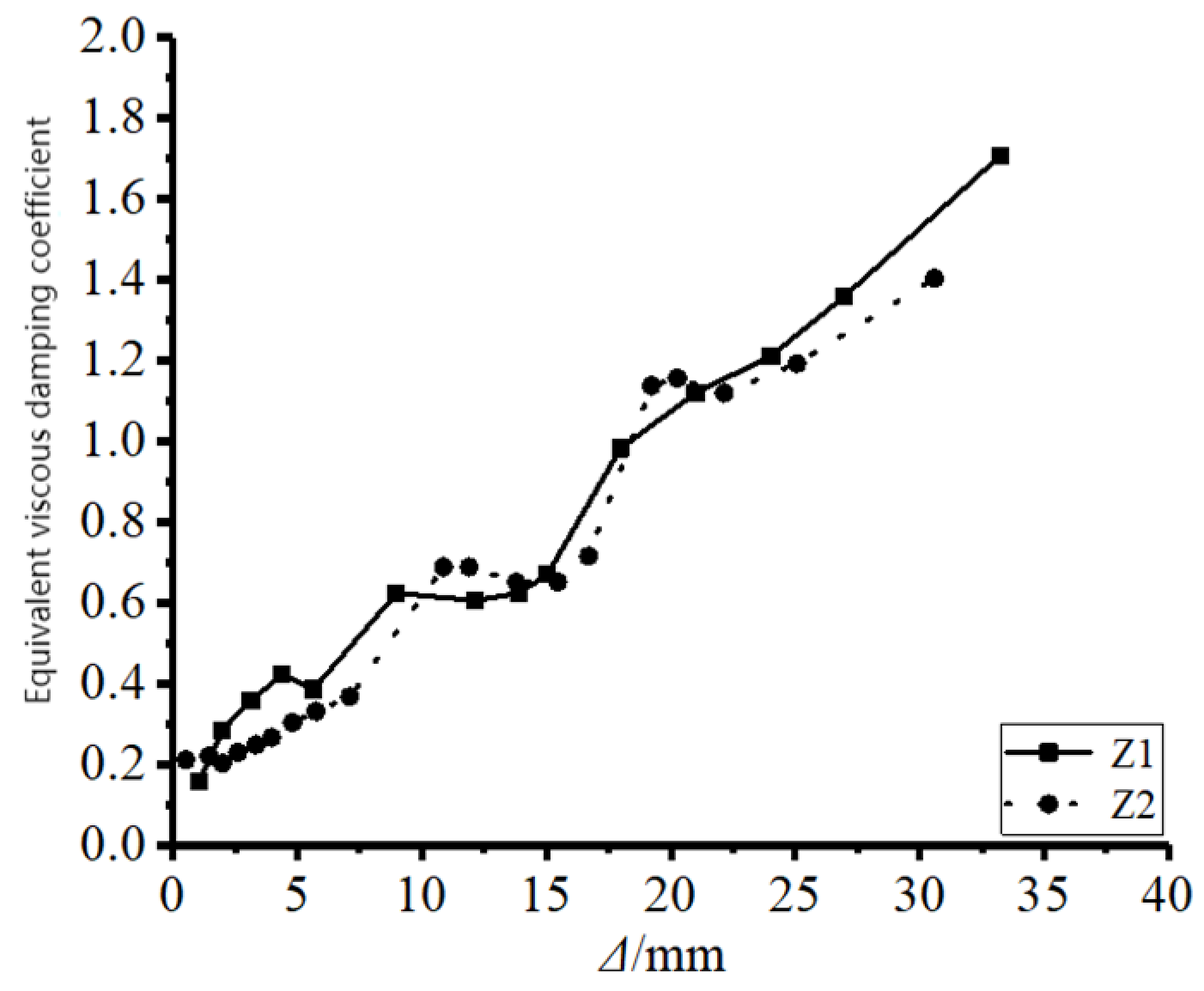
4.4. Energy Consumption Analysis
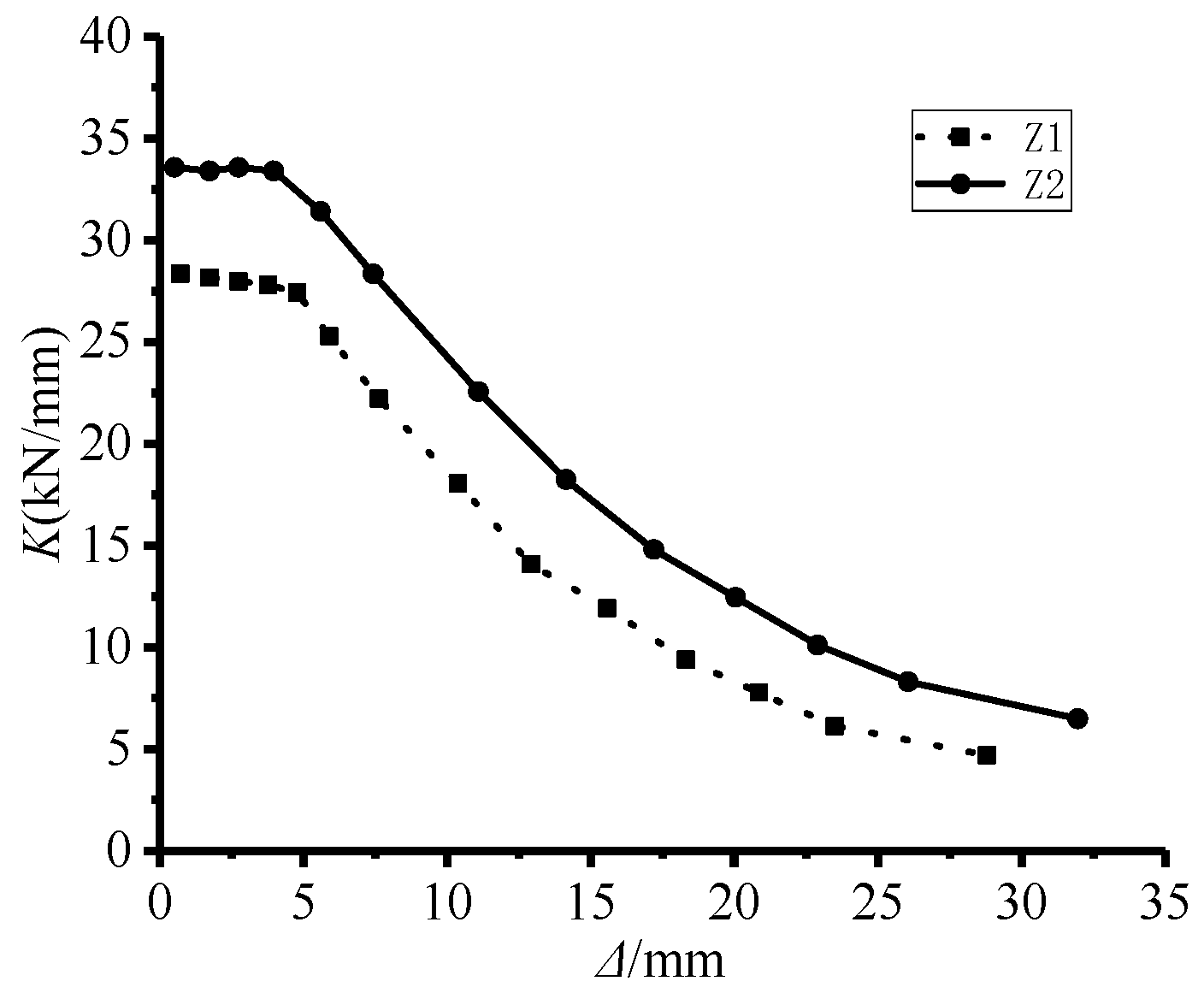
4.5. Rigidity Deterioration
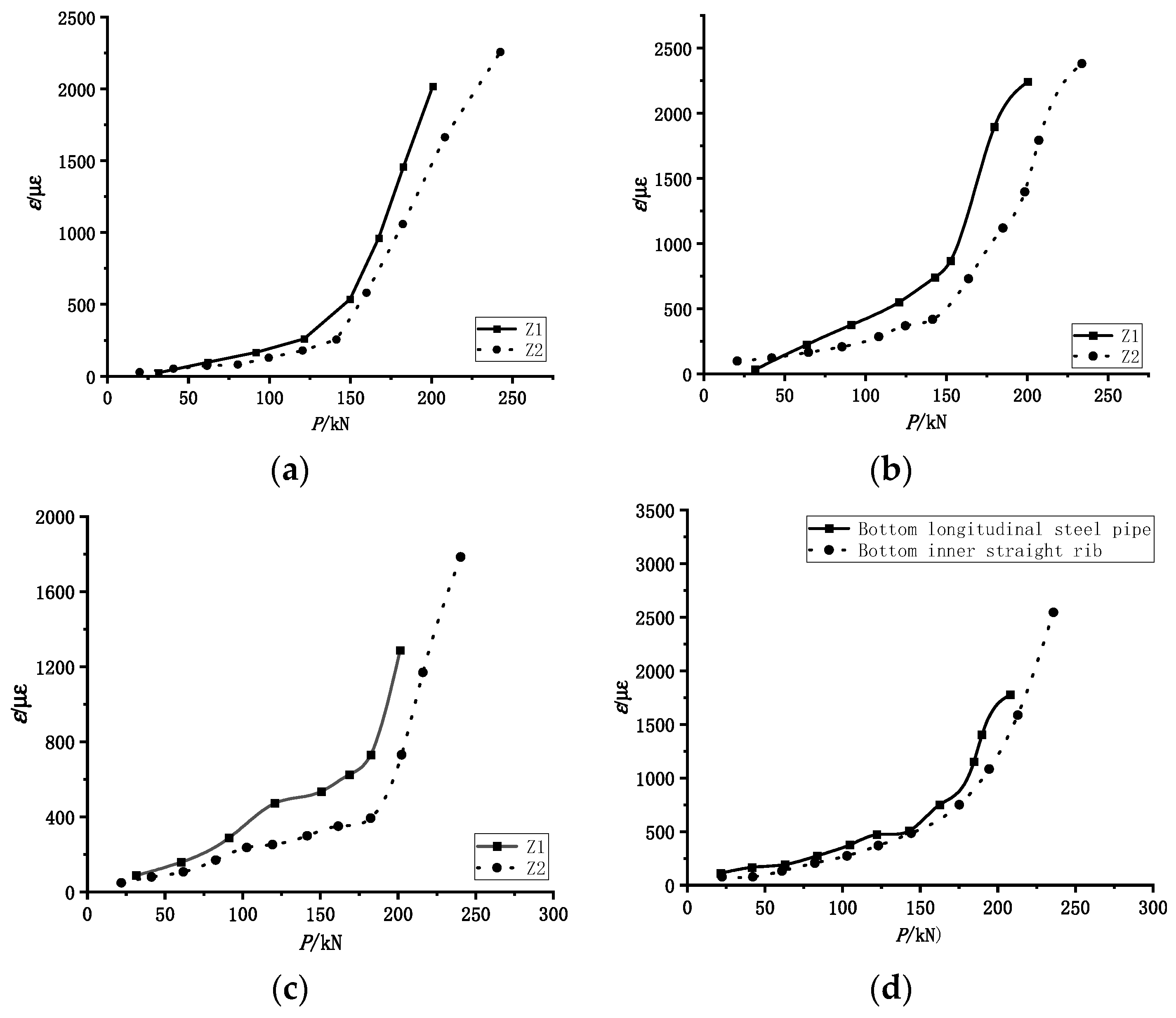
4.6. Strain Analysis
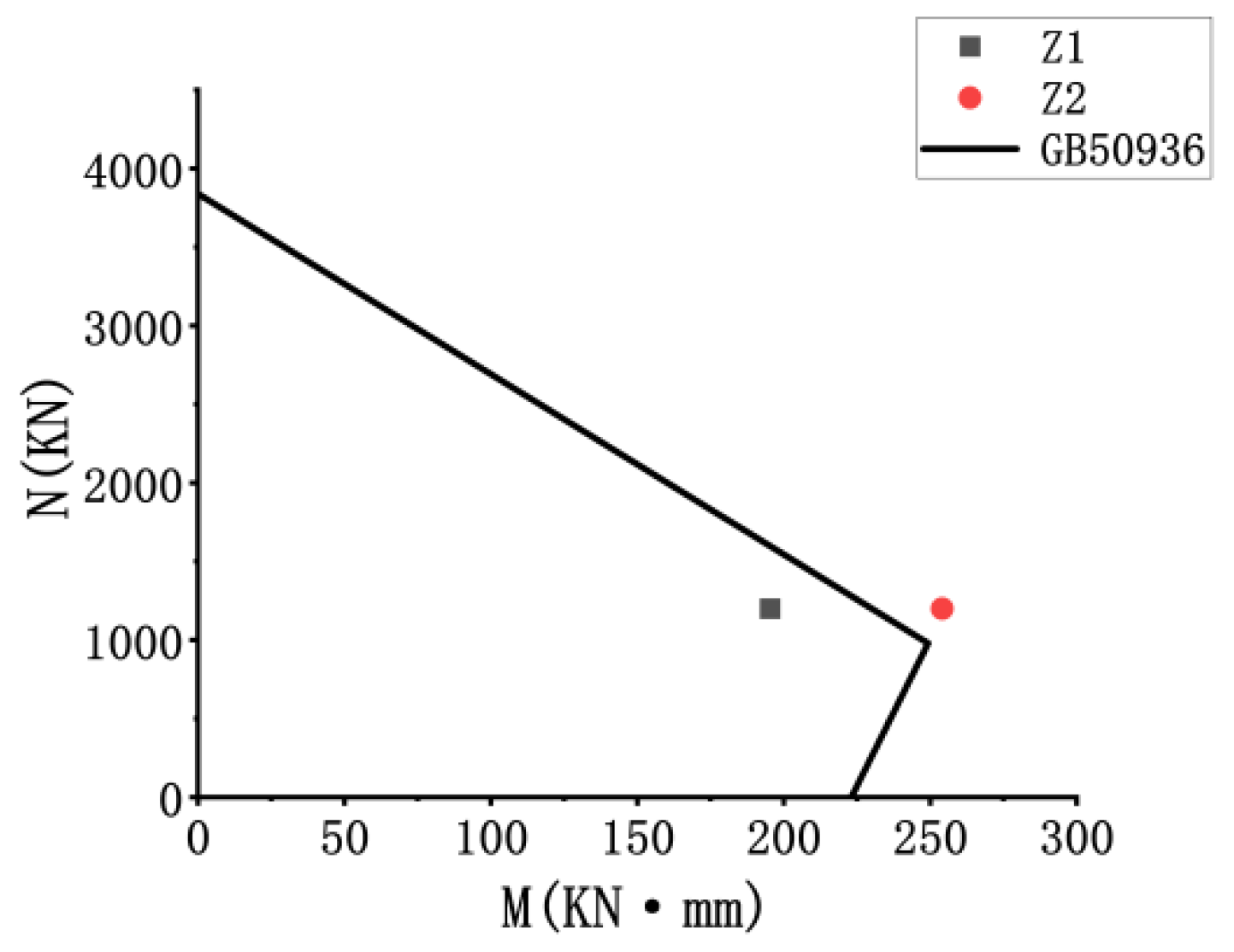
4.7. Analysis of Seismic Bearing Capacity and Performance
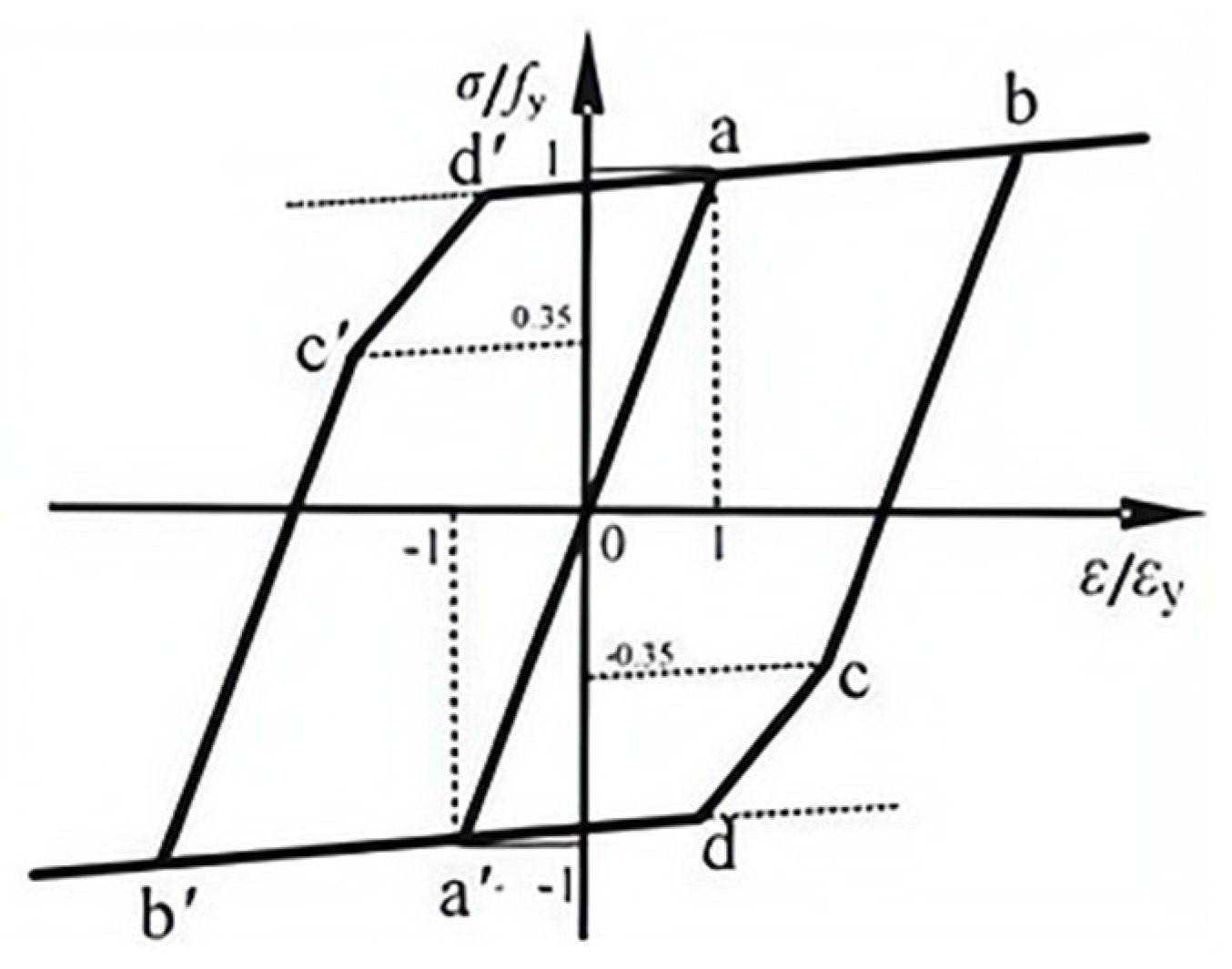
4.8. Establishment of Restoring Force Model
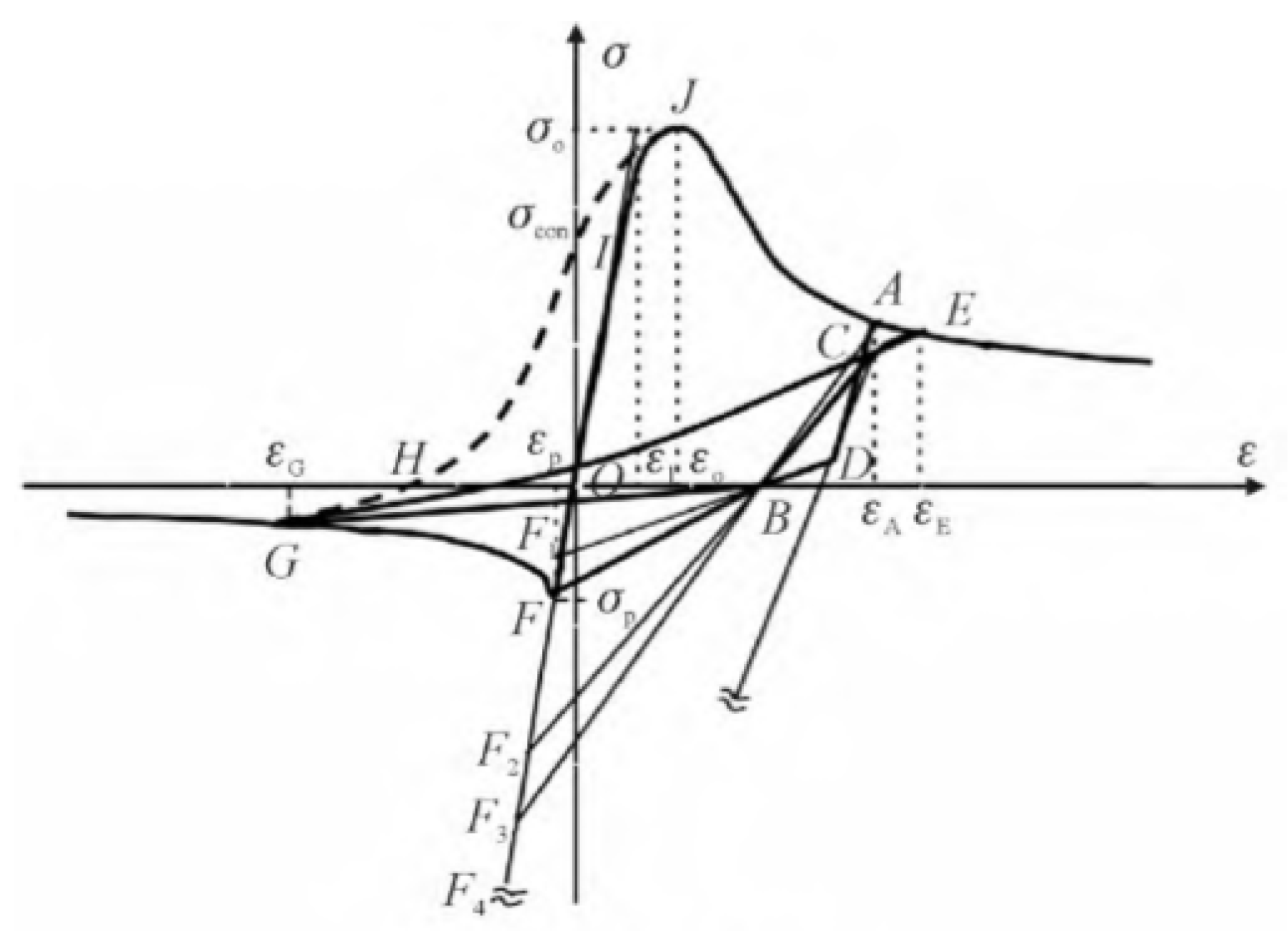
4.8.1. Skeleton Curve
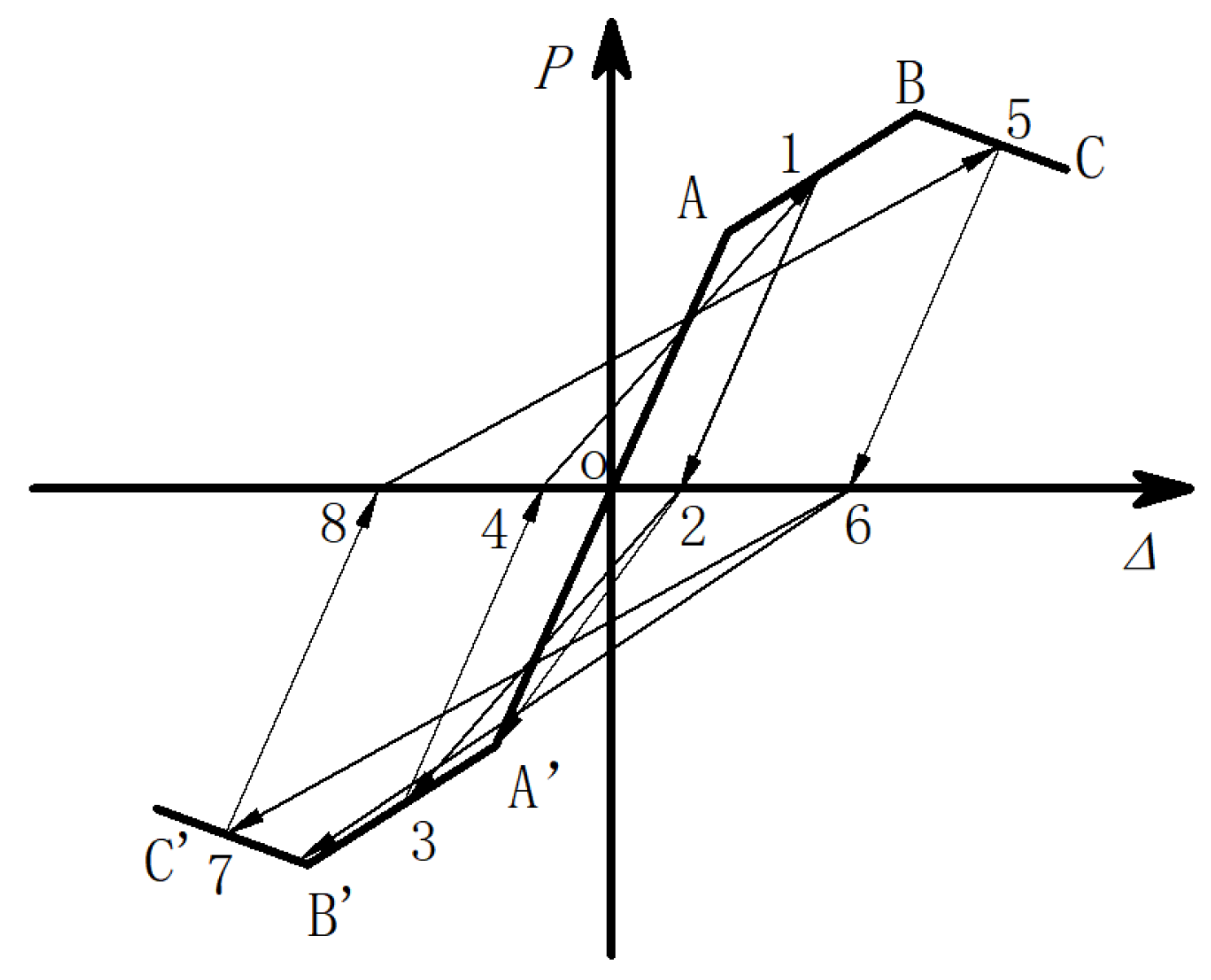
4.8.2. Hysteresis Rules
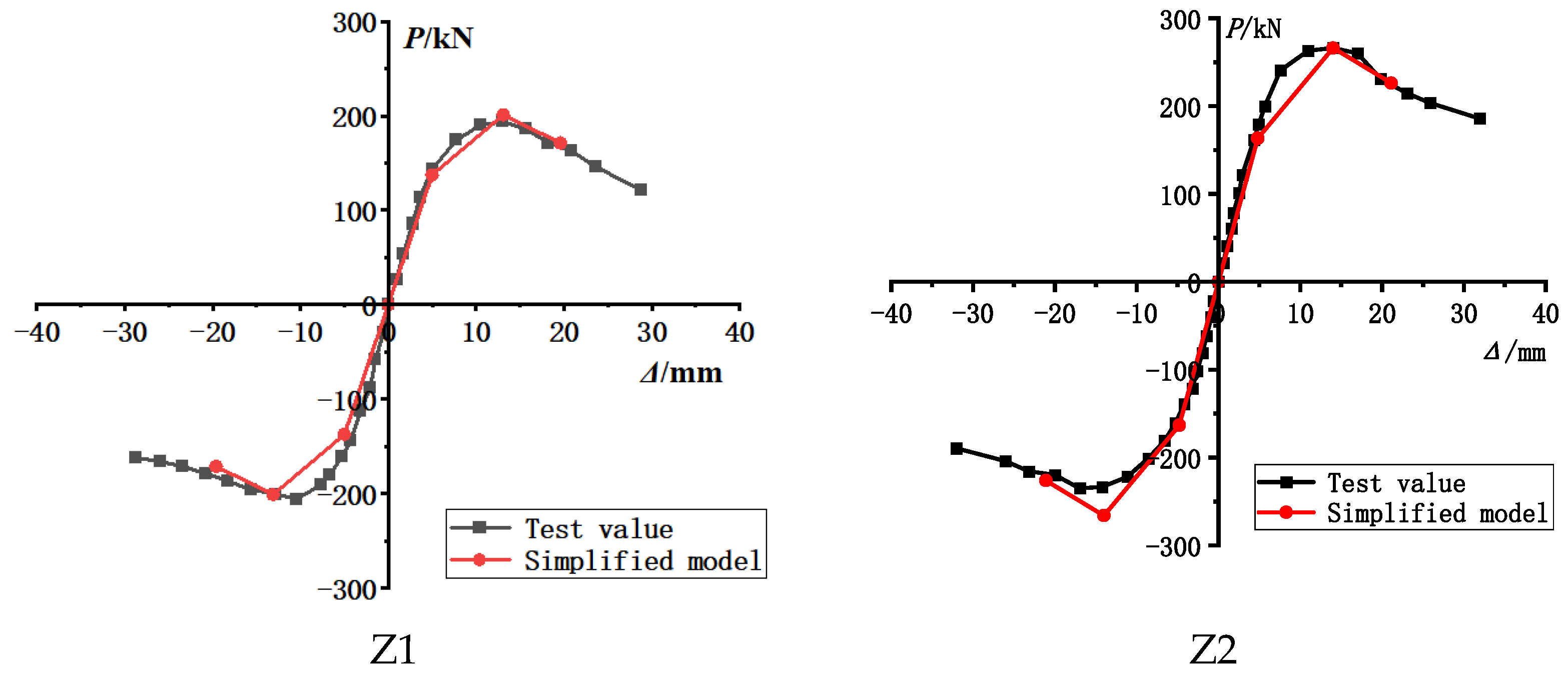
4.8.3. Comparison of Calculation Results with Test Results
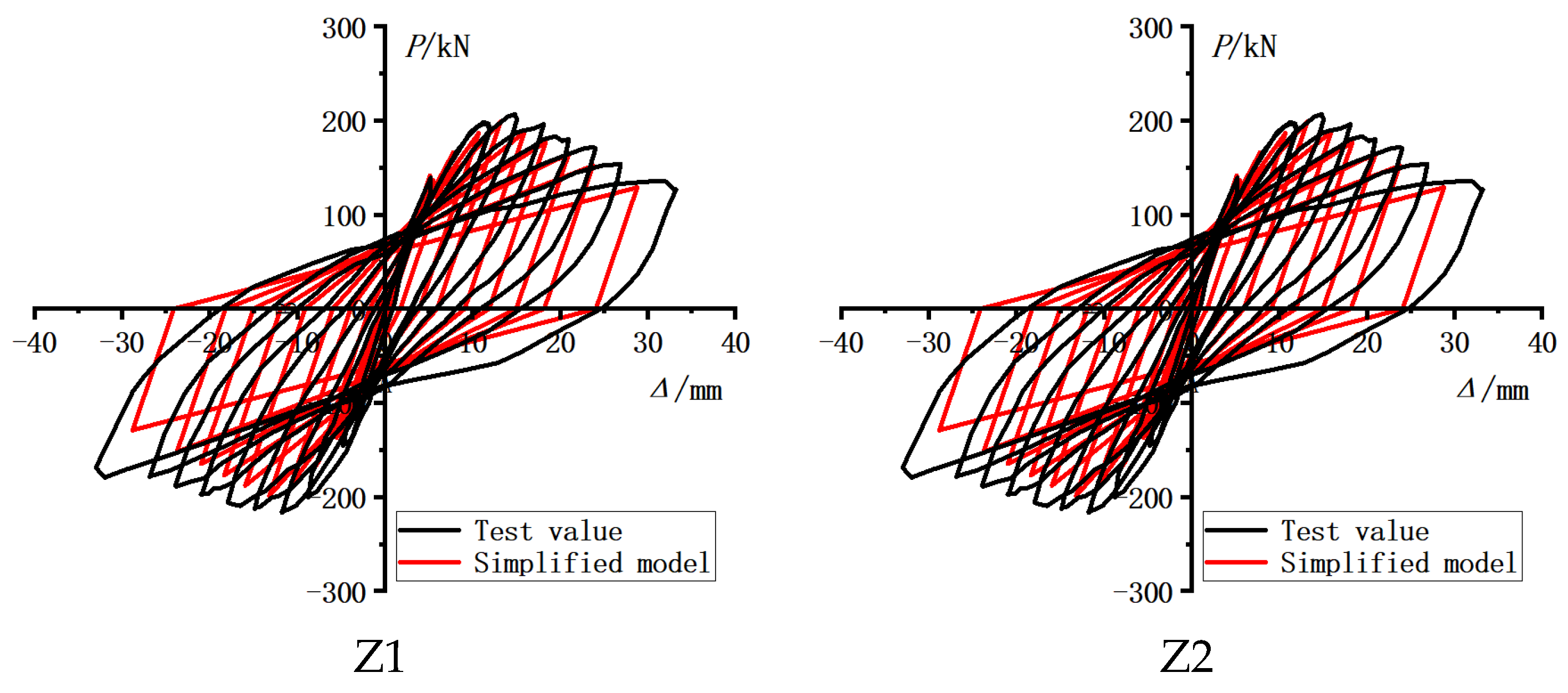
4.9. Finite Element Simulation Analysis
5. Conclusions
- (1)
- Destruction mode: When subjected to horizontal loads, ordinary and straight-ribbed thin-walled concrete-filled steel-tube columns exhibit similar failure modes, characterized by annular bulging along the bottom of the column. However, the stiffening ribs interrupt the bulging in the latter case. The main failure mode for both is bending failure.
- (2)
- Bearing capacity: The yield load of ordinary circular concrete-filled steel tubular columns with ultra-large diameter-to-thickness ratios is 140 kN, and the ultimate bearing capacity is 201 kN. After adding stiffening ribs, the yield load of thin-walled concrete-filled steel tube concrete columns increases to 160 kN, showing an increase of 14%. The ultimate bearing capacity is 266 kN, showing an increase of 31.7%, and this effect is notably significant.
- (3)
- Seismic performance: The ductility coefficient of circular concrete-filled steel tubular columns with ultra-large diameter-to-thickness ratios is 3.9. After adding stiffening ribs, the ductility coefficient of steel tube concrete columns reaches 4.4, showing an increase of 12.8%. In addition, the initial stiffness of the components increases by 20%. The bearing capacity safety margin and safety reserve of both components are roughly the same. However, the energy consumption capacity of the ribbed components exhibits a slight reduction. Overall, the addition of stiffening ribs helps to improve the seismic performance of these specimens.
- (4)
- Research recommendations: In the elastic–plastic stage, local buckling of the steel pipe occurs earlier. Therefore, seismic design should account for local buckling as the limit state for the bearing capacity, as at this point the pipe no longer meets its performance requirements. This approach aligns with the design concept of prioritizing resistance as the primary factor to be considered and energy dissipation as the secondary factor.
- (5)
- Resilience model: Through experimentation, relational expressions for each stage of the dimensionless three-fold line model were calculated. Consequently, a restoring force model suitable for circular steel-tube concrete columns with an ultra-large diameter-to-thickness ratio was established. The calculated results demonstrated good agreement with experimental values. In addition, for straight-ribbed circular steel tube concrete columns with a large diameter-to-thickness ratio, the thin-wall effect of such components needs to be considered. Applying a reduction factor of 0.8 to the calculated results is recommended when using theoretical specifications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, H.; Tang, Y.; Wu, Q. Quasi-static test research on seismic performance of steel bridge piers with thin-wall ribbed square cross section. J. Fuzhou Univ. Nat. Sci. Ed. 2016, 44, 459–464. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Zhang, S. Experimental research on seismic behavior of T-shaped concrete-filled steel tube columns with reinforcement stiffeners. J. Build. Struct. 2012, 33, 104–112. [Google Scholar]
- Gao, J.; Wu, Y.; Huo, J. Experimental study on the hysteretic behaviors of thin-walled corrugated concrete-filled steel tube column. World Earthq. Eng. 2012, 28, 34–42. [Google Scholar] [CrossRef]
- Ji, X.; Kang, H.; Chen, X.; Qian, J. Seismic behavior and strength capacity of steel tube-reinforced concrete composite columns. Earthq. Eng. Struct. Dyn. 2014, 43, 487–505. [Google Scholar] [CrossRef]
- Brown, N.K.; Kowalsky, M.J.; Nau, J.M. Impact of D/t on seismic behavior of reinforced concrete filled steel tubes. J. Constr. Steel Res. 2015, 107, 111–123. [Google Scholar] [CrossRef]
- Liao, X. Research on Seismic Behavior of Square CFST Columns with Binding Bars. Master’s Thesis, South China University of Technology, Guangzhou, China, 2015. [Google Scholar]
- Long, Y.; Cai, J.; Wang, Y.; Yang, C.; Chen, Q.; Zuo, Z. Experimental study on seismic behavior of rectangular concrete-filled steel tubular stub columns with binding bars. J. Build. Struct. 2016, 37, 133–141. [Google Scholar] [CrossRef]
- Luo, M. Study on the Buckling of Thin-walled Corrugated Concrete-Filled Tube Column. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2013. [Google Scholar]
- Denavit, M.D.; Hajjar, J.F. Nonlinear seismic analysis of circular concrete-filled steel tube members and frames. J. Struct. Eng. 2012, 138, 1089–1098. [Google Scholar] [CrossRef]
- Goto, Y.; Mizuno, K.; Prosenjit Kumar, G. Nonlinear finite element analysis for cyclic behavior of thin-walled stiffened rectangular steel columns with in-filled concrete. J. Struct. Eng. 2012, 138, 571–584. [Google Scholar] [CrossRef]
- Patel, V.I.; Uy, B.; Prajwal, K.A.; Aslani, F. Confined concrete model of circular, elliptical and octagonal CFST short columns. Steel Compos. Struct. 2016, 22, 497–520. [Google Scholar] [CrossRef]
- Bai, Y.; Lin, X.; Mou, B. Numerical modeling on post-local buckling behavior of circular and square concrete-filled steel tubular beam columns. Int. J. Steel Struct. 2016, 16, 531–546. [Google Scholar] [CrossRef]
- Wei, J.; Ying, H.; Yang, Y.; Zhang, W.; Yuan, H.; Zhou, J. Seismic performance of concrete-filled steel tubular composite columns with ultra high performance concrete plates. J. Eng. Struct. 2023, 278, 115500. [Google Scholar] [CrossRef]
- Huang, H.; Yuan, Y.; Zhang, W.; Li, M. Seismic behavior of a replaceable artificial controllable plastic hinge for precast concrete beam-column joint. J. Eng. Struct. 2021, 245, 112848. [Google Scholar] [CrossRef]
- GB50936-2014; Technical Code for Concrete Filled Steel Tubular Structures. Ministry of Housing and Urban-Rural Development: Beijing, China, 2014.
- DBJ/T 13-51-2010; Technical Specifications for Concrete-Filled Steel Tube Structures. The Department of Housing and Urban-Rural Development of Fujian Province: Fuzhou, China, 2010.
- Liu, W. Research on Mechanism of Concrete-Filled Steel Tubes Subjected to Local Compression. Ph.D. Thesis, Fuzhou University, Fuzhou, China, 2006. [Google Scholar]
- Han, L. Concrete-Filled Steel Tubular Structures—Theory and Practice; Science Press: Beijing, China, 2007. [Google Scholar]





| Test no | Stiffening Form | Size H × D (mm) | Stiffening B × t/(mm) | Pipe Diameter t/(mm) | Wall Thickness | D/t Ratio |
|---|---|---|---|---|---|---|
| Z1 | None | 1050 × 340 | None | 340 | 1.5 | 227 |
| Z2 | straight rib | 1050 × 340 | 50 × 3 | 340 | 1.5 | 227 |
| Water-Cement Ratio | Cement | Fly Ash | |
|---|---|---|---|
| C30 | 0.38 | 391.2 | 123.9 |
| Sand | Stone | Water | Water reducer |
| 767 | 987 | 180 | 5.03 |
| Strength Grade | fcu,k/MPa | fck/MPa | fc/MPa | Ec (×104)/MPa |
|---|---|---|---|---|
| C30 | 36.2 | 24.2 | 17.29 | 2.54 |
| Type | fy/MPa | fu/MPa | E (×106)/MPa | Elongation |
|---|---|---|---|---|
| 1.5 mm | 241.94 | 361.85 | 2.01 | 34.06 |
| 3.0 mm | 266.43 | 404.35 | 2.06 | 26.54 |
| Specimen | Yield Load Py/kN | Yield Displacement Δy/mm | Ultimate Load Pmax/kN | Ultimate Displacement Δmax/mm | Failure Load Pu/kN | Failure Displacement Δu/mm | Carrying Capacity Margin Pmax/Py | Safety Reserve Δu/Δmax |
|---|---|---|---|---|---|---|---|---|
| Z1 | 140 | 5.0 | 201 | 13.1 | 171 | 19.6 | 1.44 | 1.50 |
| Z2 | 160 | 4.8 | 266 | 14.0 | 226 | 21.1 | 1.66 | 1.51 |
| Specimen | Diameter D/mm | Experimental Value P/kN | Calculated Value P/kN | Ratio |
|---|---|---|---|---|
| Z1 | 340 | 201 | 204 | 0.958 |
| Z2 | 340 | 266 | 204 | 1.304 |
| Specimen | Diameter D/mm | Experimental Value P/kN | Calculated Value P/kN | Ratio |
|---|---|---|---|---|
| Z1 | 340 | 201 | 163.2 | 1.232 |
| Z2 | 340 | 266 | 163.2 | 1.630 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Hu, B.; Wang, Z.; Meng, H. Horizontal Hysteretic Behavior of Circular Concrete-Filled Steel Tubular Columns with Ultra-Large Diameter-to-Thickness Ratios. Buildings 2024, 14, 2313. https://doi.org/10.3390/buildings14082313
Wei J, Hu B, Wang Z, Meng H. Horizontal Hysteretic Behavior of Circular Concrete-Filled Steel Tubular Columns with Ultra-Large Diameter-to-Thickness Ratios. Buildings. 2024; 14(8):2313. https://doi.org/10.3390/buildings14082313
Chicago/Turabian StyleWei, Jun, Bo Hu, Zhenshan Wang, and Hao Meng. 2024. "Horizontal Hysteretic Behavior of Circular Concrete-Filled Steel Tubular Columns with Ultra-Large Diameter-to-Thickness Ratios" Buildings 14, no. 8: 2313. https://doi.org/10.3390/buildings14082313
APA StyleWei, J., Hu, B., Wang, Z., & Meng, H. (2024). Horizontal Hysteretic Behavior of Circular Concrete-Filled Steel Tubular Columns with Ultra-Large Diameter-to-Thickness Ratios. Buildings, 14(8), 2313. https://doi.org/10.3390/buildings14082313





