Influence of Ground Motion Non-Gaussianity on Seismic Performance of Buildings
Abstract
:1. Introduction
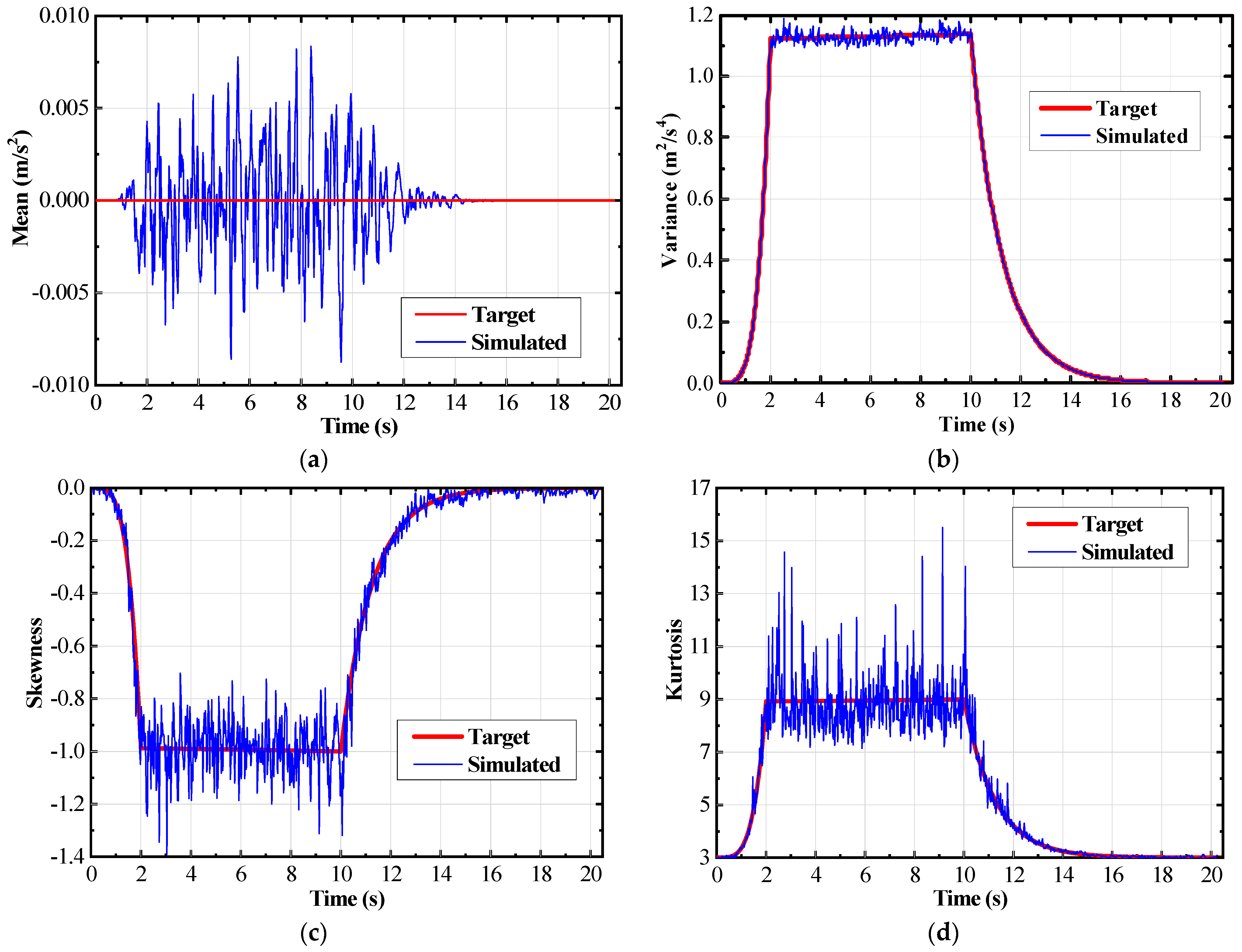
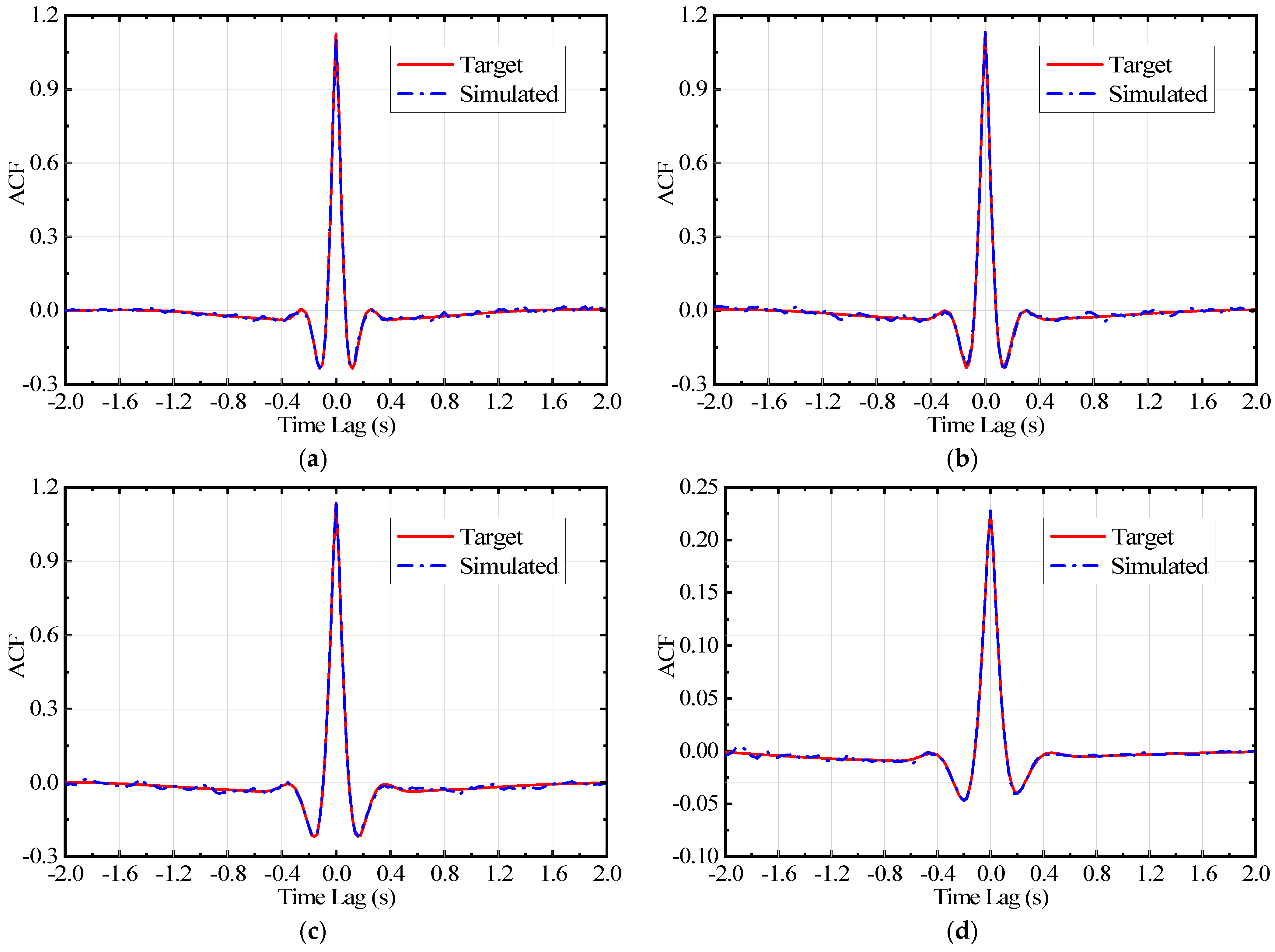
2. Simulation of Non-Gaussian Non-Stationary Ground Motions
2.1. Brief Review of the Simulation Algorithm
2.2. Generation of Non-Gaussian Non-Stationary Ground Motions
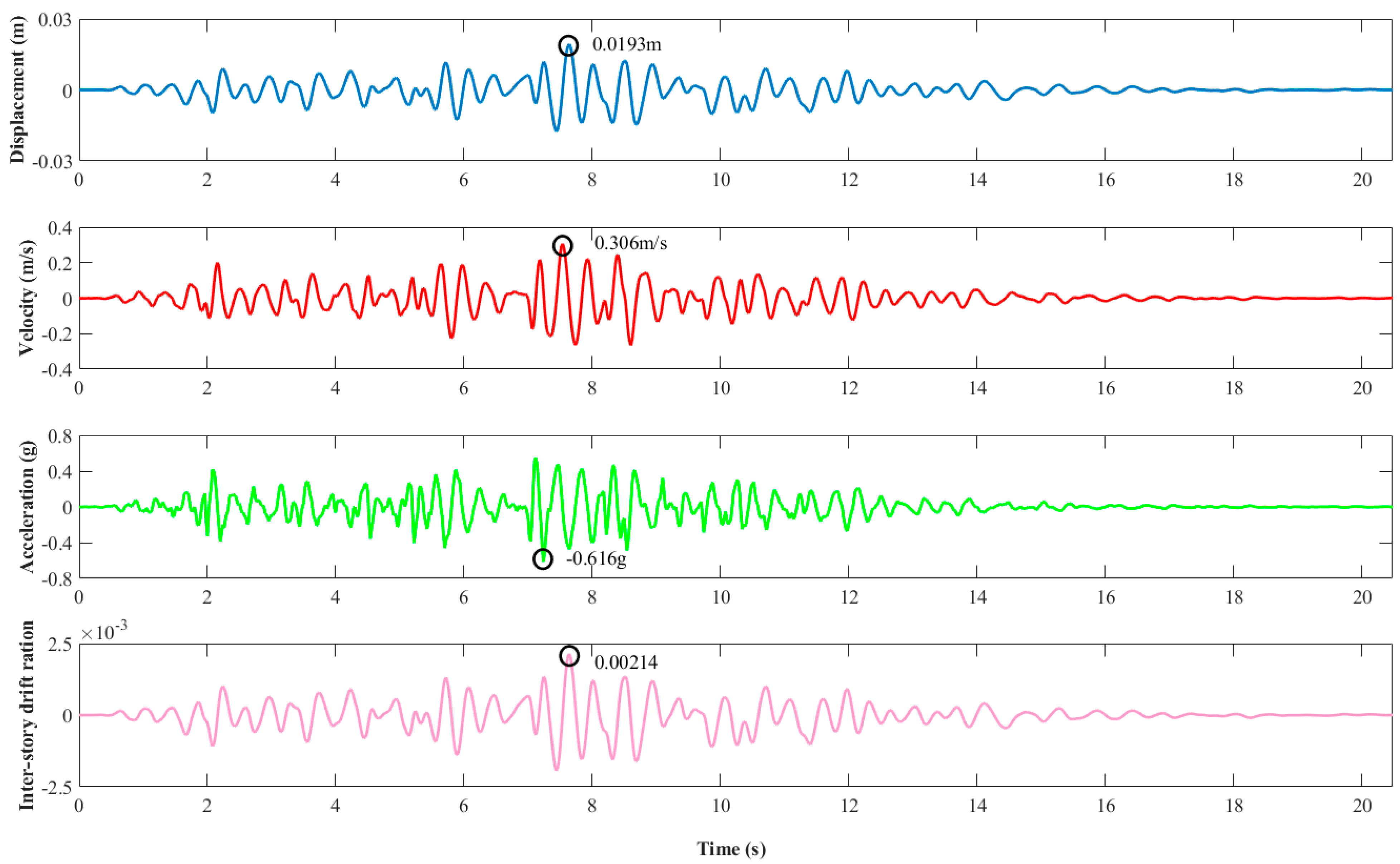
3. Numerical Examples
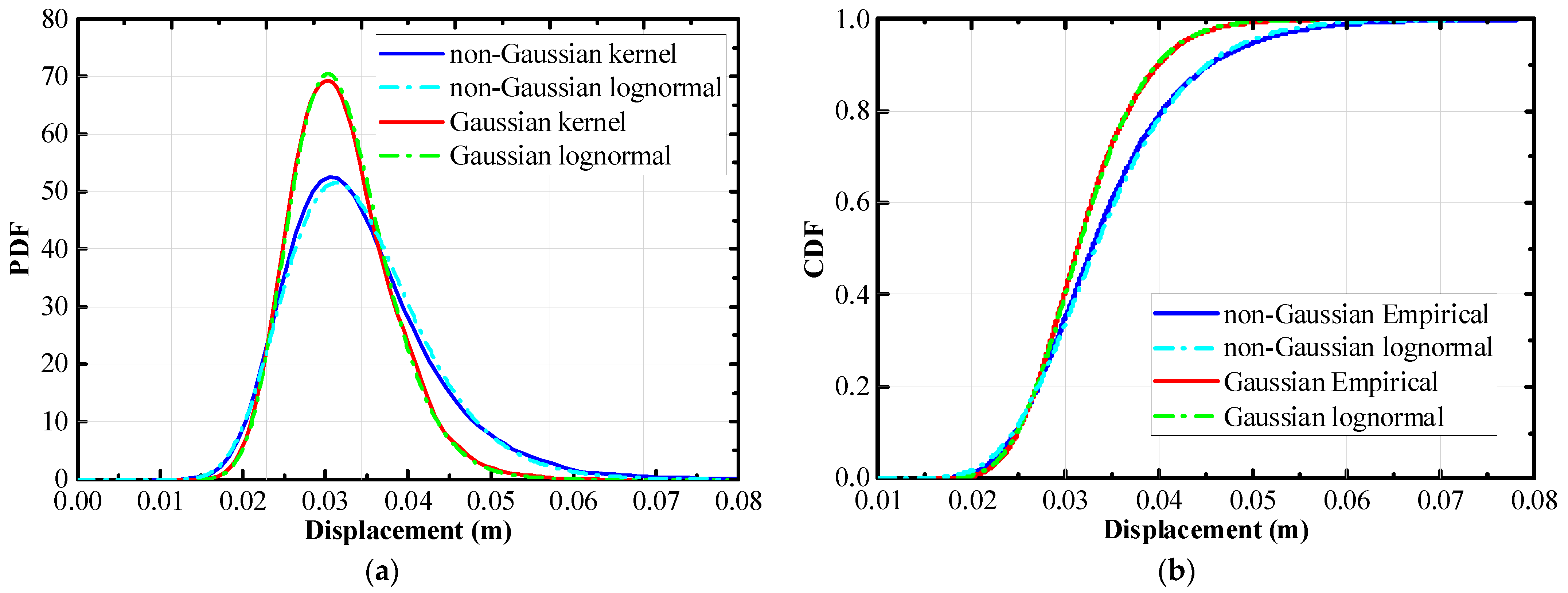
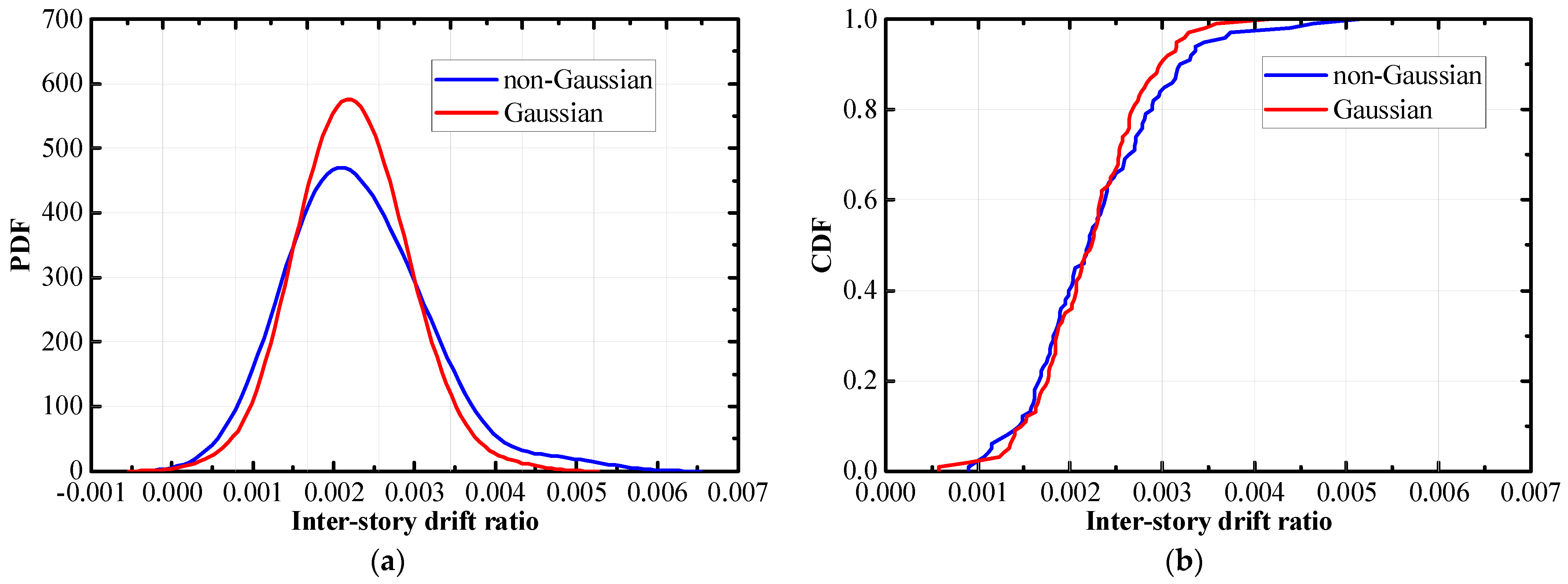
3.1. Multi-Story Frame Structure
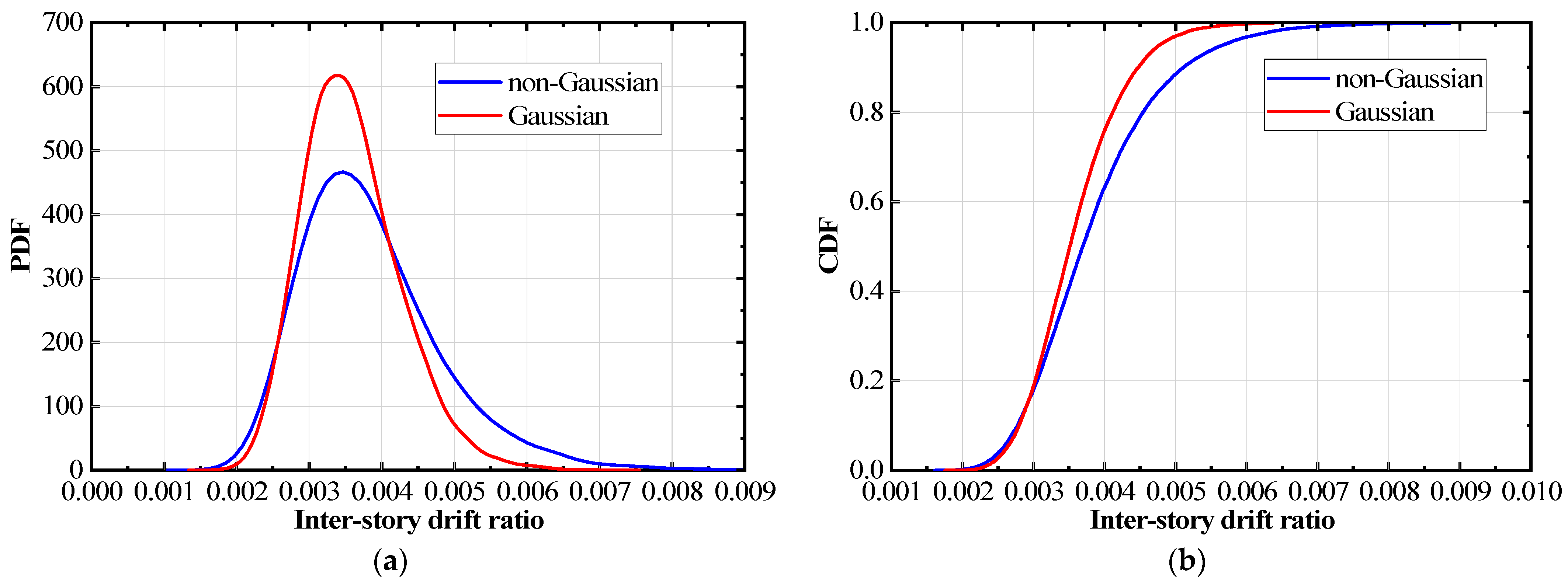
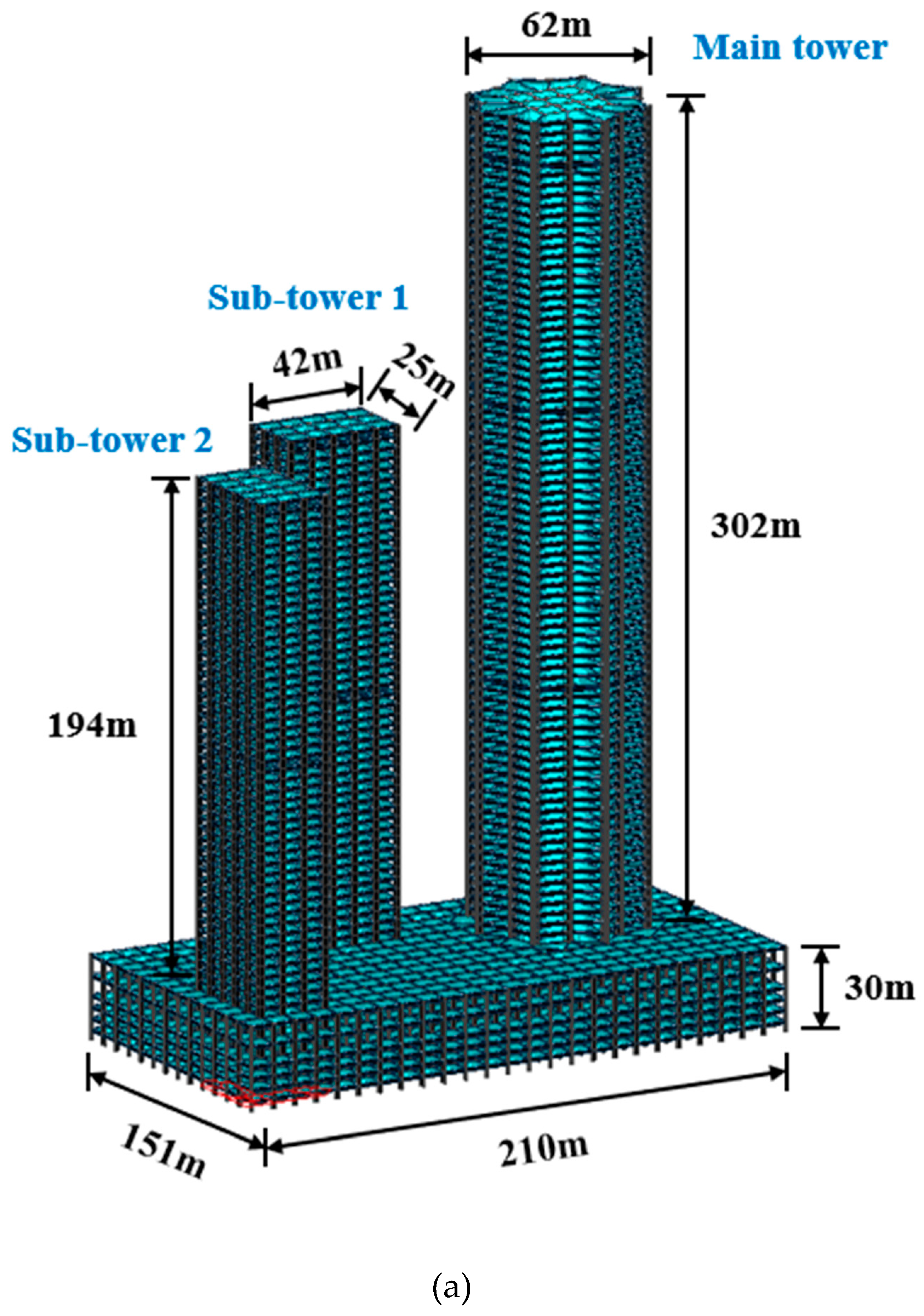
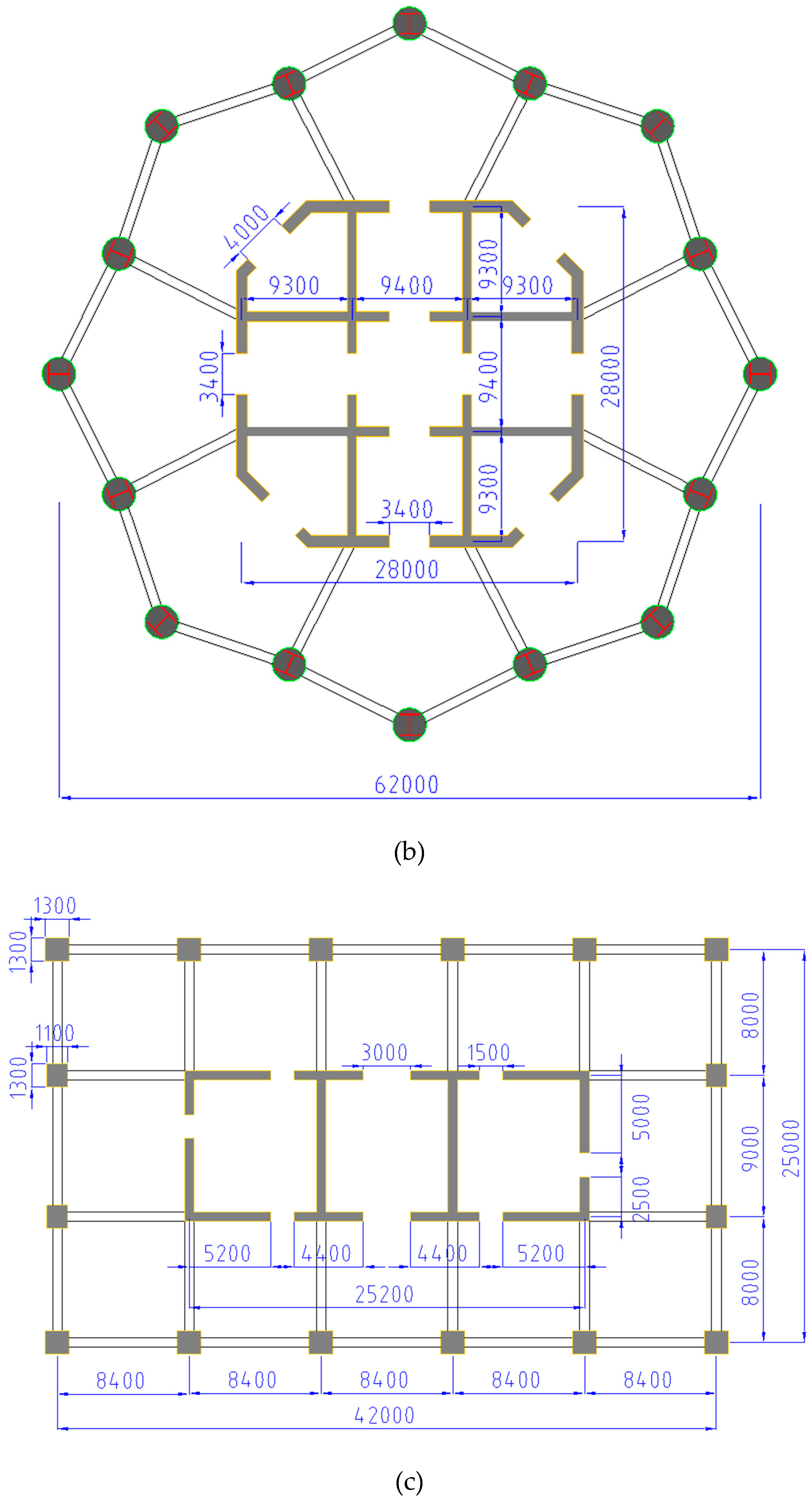
3.2. Multi-Tower High-Rise Building
4. Conclusions
- (a)
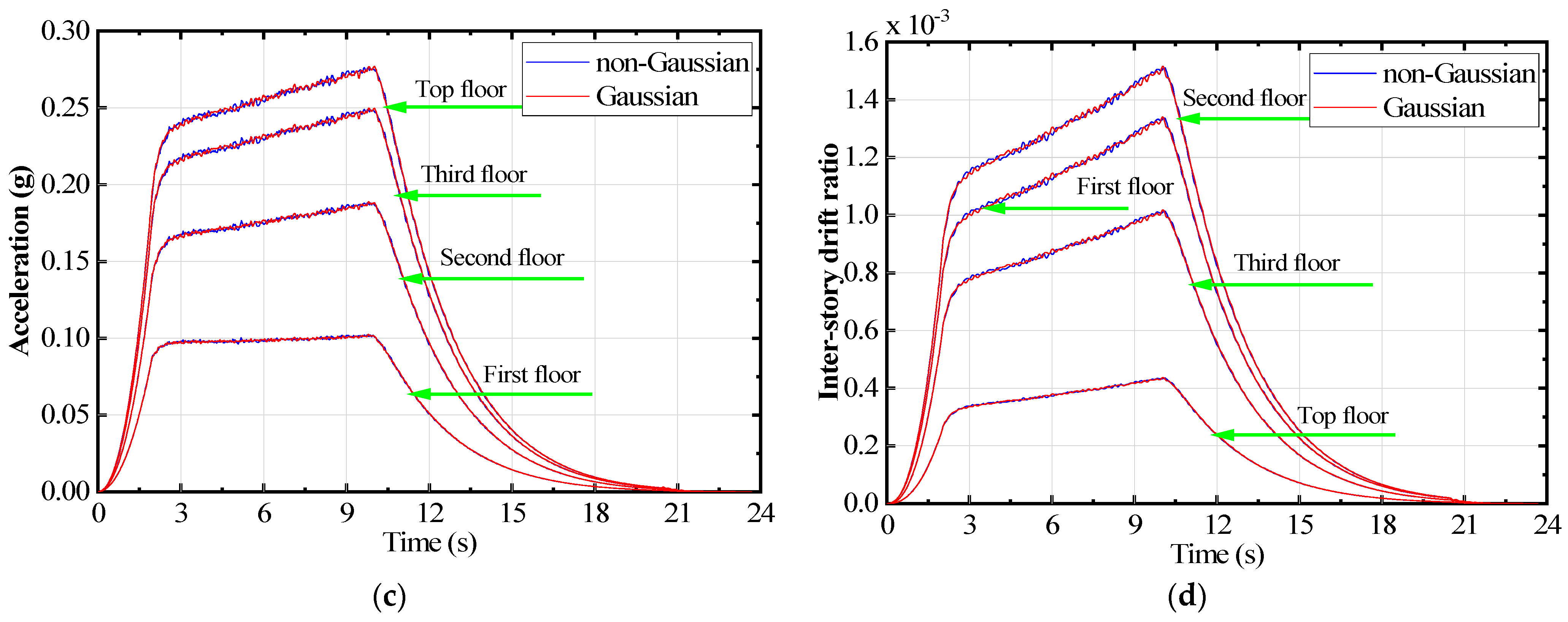
- The structural responses induced by both Gaussian and non-Gaussian earthquake groups, such as displacement, velocity, acceleration, and inter-story drift ratio, have identical first- and second-order moments, namely mean and standard deviation.
- (b)
- The higher-order moments of the structural responses caused by the two earthquake groups differ evidently. The responses of Gaussian earthquakes remain Gaussian; the responses of non-Gaussian earthquakes exhibit prominent non-Gaussian features, although the non-Gaussian strength is relatively weakened compared to the external excitation.
- (c)
- Due to the influence of non-Gaussianity, the probability density functions of the two groups of structural responses at any given time show significant differences.
- (d)
- The analysis of extreme values reveals that the tail of non-Gaussian structural response distribution is longer than that of the Gaussian counterpart. This results in a significantly larger value of non-Gaussian responses under high crossing probabilities, with an amplification that can exceed 18%.
- (e)
- Non-Gaussianity exhibits a significant amplifying effect on the seismic response of structures, which should be taken into account in seismic design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Gao, Y.; Zhang, N.; Zhang, F. Simulation of spatially varying non-Gaussian and nonstationary seismic ground motions by the spectral representation method. ASCE J. Eng. Mech. 2018, 144, 04017143. [Google Scholar] [CrossRef]
- Xu, F.; Ma, X. An efficient simulation algorithm for non-gaussian nonstationary processes. Probabilistic Eng. Mech. 2021, 63, 103105. [Google Scholar] [CrossRef]
- Gusev, A.A. Peak factors of Mexican accelerograms: Evidence of a non-gaussian amplitude distribution. J. Geophys. Res. Solid Earth 1996, 101, 20083–20090. [Google Scholar] [CrossRef]
- Kafali, G.; Grigoriu, M. Non-Gaussian model for spatially coherent seismic ground motions. In Application of Statistics and Probability in Civil Engineering; Der Kiureghian, A., Madanat, P., Eds.; Millpress: Rotterdam, The Netherlands, 2003. [Google Scholar]
- Zentner, I.; Poirion, F. Enrichment of seismic ground motion databases using Karhunen–Loéve expansion. Earthq. Eng. Struct. Dyn. 2012, 41, 1945–1957. [Google Scholar] [CrossRef]
- Romao, X.; Delgado, R.; Costa, A. Assessment of the statistical distributions of structural demand under earthquake loading. J. Earthq. Eng. 2011, 15, 724–753. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Zhang, Z. Quantitative identification of near-fault ground motions based on ensemble empirical mode decomposition. KSCE J. Civ. Eng. 2020, 24, 922–930. [Google Scholar] [CrossRef]
- Cheng, Y.; Dong, Y.R.; Bai, G.L.; Wang, Y.Y. IDA-based seismic fragility of high-rise frame-core tube structure subjected to multi-dimensional long-period ground motions. J. Build. Eng. 2021, 43, 102917. [Google Scholar] [CrossRef]
- Ansari, M.; Nazari, M.; Panah, A.K. Influence of foundation flexibility on seismic fragility of reinforced concrete high-rise building. Soil Dyn. Earthq. Eng. 2021, 142, 106521. [Google Scholar] [CrossRef]
- Guo, W.; Guo, L.; Zhai, Z.; Li, S. Seismic performance assessment of a super high-rise twin-tower structure connected with rotational friction negative stiffness damper and lead rubber bearing. Soil Dyn. Earthq. Eng. 2022, 152, 107039. [Google Scholar] [CrossRef]
- He, X.; Xu, C.; Xu, X.; Yang, Y. Advances on the avoidance zone and buffer zone of active faults. Nat. Hazards Res. 2022, 2, 62–74. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, W.; Bhatt, M.W.; Kumar, A. Seismic nonlinear vibration control algorithm for high-rise buildings. Nonlinear Eng. 2022, 10, 574–582. [Google Scholar] [CrossRef]
- Kandemir, E.C.; Mortazavi, A. Optimizing base isolation system parameters using a fuzzy reinforced butterfly optimization: A case study of the 2023 Kahramanmaras earthquake sequence. J. Vib. Control 2024, 30, 502–515. [Google Scholar] [CrossRef]
- Kandemir, E.C.; Mortazavi, A. Optimization of seismic base isolation system using a fuzzy reinforced swarm intelligence. Adv. Eng. Softw. 2022, 174, 103323. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon. Earthq. Eng. Struct. Dyn. 2005, 34, 1193–1217. [Google Scholar] [CrossRef]
- Hancock, J.; Watson-Lamprey, J.; Abrahamson, N.A.; Bommer, J.J.; Markatis, A.; McCoy, E.; Mendis, R. An improved method of matching response spectra of recorded earthquake ground motion using wavelets. J. Earthq. Eng. 2006, 10, 67–89. [Google Scholar] [CrossRef]
- Samanta, A.; Pandey, P. Effects of ground motion modification methods and ground motion duration on seismic performance of a 15-storied building. J. Build. Eng. 2018, 15, 14–25. [Google Scholar] [CrossRef]
- Taheri, S.; Mohammadi, R.K. An enhanced sequential ground motion selection for risk assessment using a Bayesian updating approach. J. Build. Eng. 2022, 46, 103745. [Google Scholar] [CrossRef]
- Zhu, X.; Broccardo, M.; Sudret, B. Seismic fragility analysis using stochastic polynomial chaos expansions. Probabilistic Eng. Mech. 2023, 72, 103413. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Chakraborty, S. Reliability of linear structures with parameter uncertainty under non-stationary earthquake. Struct. Saf. 2006, 28, 231–246. [Google Scholar] [CrossRef]
- Gupta, S.; Manohar, C.S. Reliability analysis of randomly vibrating structures with parameter uncertainties. J. Sound Vib. 2006, 297, 1000–1024. [Google Scholar] [CrossRef]
- Muscolino, G.; Santoro, R.; Sofi, A. Reliability assessment of structural systems with interval uncertainties under spectrum-compatible seismic excitations. Probabilistic Eng. Mech. 2016, 44, 138–149. [Google Scholar] [CrossRef]
- Deodatis, G.; Shinozuka, M. Auto-regressive model for nonstationary stochastic processes. ASCE J. Eng. Mech. 1988, 114, 1995–2012. [Google Scholar] [CrossRef]
- Deodatis, G. Non-stationary stochastic vector processes: Seismic ground motion applications. Probabilistic Eng. Mech. 1996, 11, 149–167. [Google Scholar] [CrossRef]
- Huang, G.; Liao, H.; Li, M. New formulation of Cholesky decomposition and applications in stochastic simulation. Probabilistic Eng. Mech. 2013, 34, 40–47. [Google Scholar] [CrossRef]
- Shields, M.D. Simulation of spatially correlated nonstationary response spectrum-compatible ground motion time histories. J. Eng. Mech. 2015, 141, 04014161. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, Y.; Zhang, L.; Li, D. Simulation of spatially varying ground motions in V-shaped symmetric canyons. J. Earthq. Eng. 2016, 20, 992–1010. [Google Scholar] [CrossRef]
- Stuart, B.; Ord, J. Kendall’s Advanced Theory of Statistics: Distribution Theory, 6th ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Sakamoto, S.; Ghanem, R. Simulation of multi-dimensional non-Gaussian non-stationary random fields. Probabilistic Eng. Mech. 2002, 17, 167–176. [Google Scholar] [CrossRef]
- Sakamoto, S.; Ghanem, R. Polynomial chaos decomposition for the simulation of non-Gaussian nonstationary stochastic processes. ASCE J. Eng. Mech. 2002, 128, 190–201. [Google Scholar] [CrossRef]
- Kim, H.; Shields, M. Simulation of Strongly Non-Gaussian Non-Stationary Stochastic Processes Utilizing Karhunen–Loeve Expansion; University of British Columbia: Vancouver, BC, Canada, 2015. [Google Scholar]
- Shields, M.; Deodatis, G. Estimation of evolutionary spectra for simulation of non-stationary and non-Gaussian stochastic processes. Comput. Struct. 2013, 126, 149–163. [Google Scholar] [CrossRef]
- Priestley, M. Evolutionary spectra and non-stationary processes. J. R. Stat. Soc. Ser. B 1965, 27, 204–237. [Google Scholar] [CrossRef]
- Gersch, W.; Kitagawa, G. Time varying AR coefficient model for modelling and simulating earthquake ground motion. Earthq. Eng. Struct. Dyn. 1985, 13, 243–254. [Google Scholar] [CrossRef]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley: New York, NY, USA, 1995; Volume 1. [Google Scholar]
- Winterstein, S. Non-normal responses and fatigue damage. J. Eng. Mech. 1985, 10, 1291–1295. [Google Scholar] [CrossRef]
- Ma, X.; Xu, F.; Liu, Z. A method for evaluation of the probability density function of white noise filtered non-Gaussian stochastic process. Mech. Syst. Signal Process. 2024, 211, 111242. [Google Scholar] [CrossRef]
- Ma, X.; Xu, F. Investigation on the sampling distributions of non-Gaussian wind pressure skewness and kurtosis. Mech. Syst. Signal Process. 2024, 220, 111610. [Google Scholar] [CrossRef]
- Benowitz, B.; Shields, M.; Deodatis, G. Determining evolutionary spectra from non-stationary auto-correlation functions. Probabilistic Eng. Mech. 2015, 41, 73–88. [Google Scholar] [CrossRef]
- GB 50011-2010; Ministry of Construction of the People’s Republic of China, Code for Seismic Design of Buildings. China Architecture and Building Press: Beijing, China, 2010.








| Structural Parameters | Floor Number | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Interlayer mass (×105) (kg) | m1 = 6 | m2 = 5 | m3 = 5 | m4 = 5 |
| Structural interlayer stiffness (×108) (N/m) | k1 = 6 | k2 = 5 | k3 = 5 | k4 = 4 |
| Layer height (m) | h1 = 3.5 | h2 = 3 | h3 = 3 | h4 = 3 |
| Damper stiffness (×108) (N/m) | kd1 = 0.7 | kd2 = 0.7 | kd3 = 0.7 | kd4 = 0.7 |
| Damping of dampers (×106) (N·s/m) | cd1 = 6.8 | cd2 = 6.8 | cd3 = 6.8 | cd4 = 6.8 |
| Displacement (cm) | Inter-Story Drift Ratio (×10−3) | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean | 75% | 85% | 95% | Mean | 75% | 85% | 95% | |
| Gaussian | 3.23 | 3.54 | 3.81 | 4.25 | 3.63 | 3.98 | 4.27 | 4.77 |
| Non-Gaussian | 3.42 | 3.86 | 4.24 | 5.02 | 3.86 | 4.35 | 4.78 | 5.66 |
| Increase ratio | 6.99% | 9.04% | 11.29% | 18.12% | 7.32% | 9.30% | 11.94% | 18.66% |
| Mode Order | Frequency (Hz) | Period (s) | Main Tower | Sub-Tower 1 | Sub-Tower 2 |
|---|---|---|---|---|---|
| 1 | 0.14 | 7.03 | First-order translation | / | / |
| 2 | 0.19 | 5.38 | / | Translation in Y-direction | Translation in X-direction |
| 3 | 0.29 | 3.41 | / | Translation in X-direction | Translation in Y-direction |
| 4 | 0.54 | 1.86 | / | First-order torsion | First-order torsion |
| 5 | 0.56 | 1.79 | First-order torsion | / | / |
| 6 | 0.72 | 1.39 | Second-order translation | / | / |
| Displacement (cm) | Inter-Story Drift Ratio (×10−3) | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean | 75% | 85% | 95% | Mean | 75% | 85% | 95% | |
| Gaussian | 45.1 | 54.3 | 60.3 | 72.1 | 2.33 | 2.76 | 3.01 | 3.51 |
| Non-Gaussian | 46.1 | 56.3 | 64.5 | 79.9 | 2.40 | 2.85 | 3.22 | 3.95 |
| Increase ratio | 2.17% | 3.64% | 6.87% | 11.01% | 3.16% | 3.55% | 6.74% | 12.51% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Liu, Z. Influence of Ground Motion Non-Gaussianity on Seismic Performance of Buildings. Buildings 2024, 14, 2364. https://doi.org/10.3390/buildings14082364
Ma X, Liu Z. Influence of Ground Motion Non-Gaussianity on Seismic Performance of Buildings. Buildings. 2024; 14(8):2364. https://doi.org/10.3390/buildings14082364
Chicago/Turabian StyleMa, Xingliang, and Zhen Liu. 2024. "Influence of Ground Motion Non-Gaussianity on Seismic Performance of Buildings" Buildings 14, no. 8: 2364. https://doi.org/10.3390/buildings14082364





