A Reliability-Based Design Approach for the Flexural Resistance of Compression Yielded Fibre-Reinforced Polymer (FRP)-Reinforced Concrete Beams
Abstract
:1. Introduction
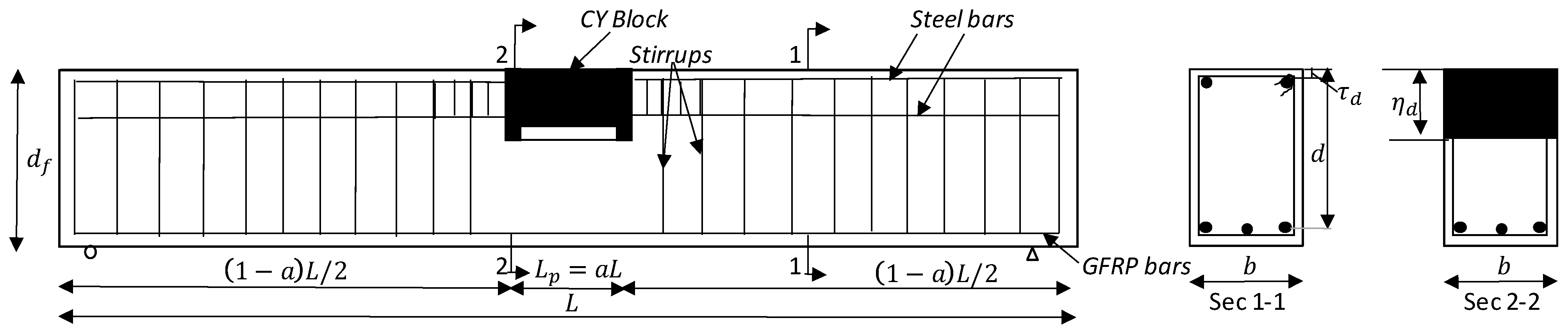
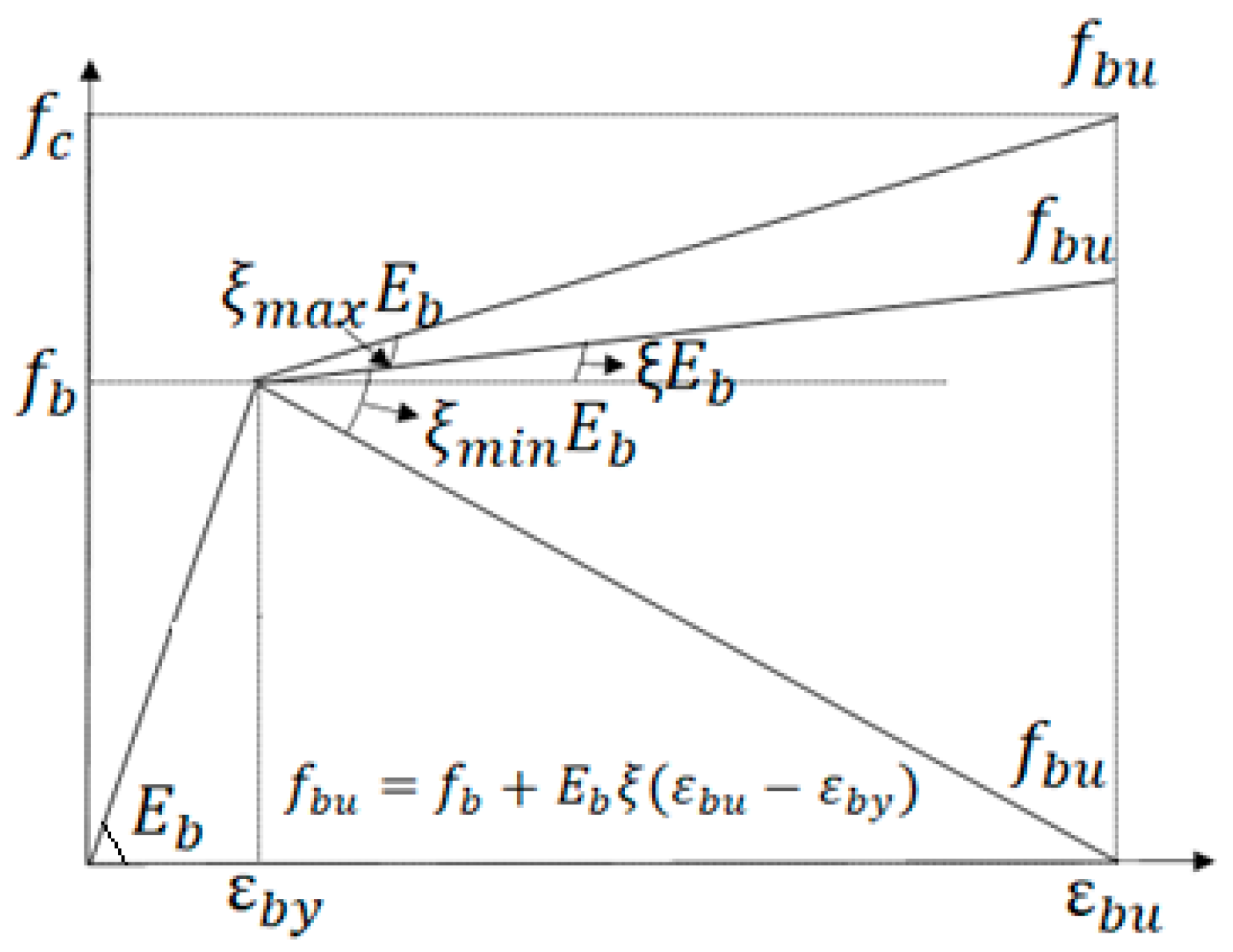
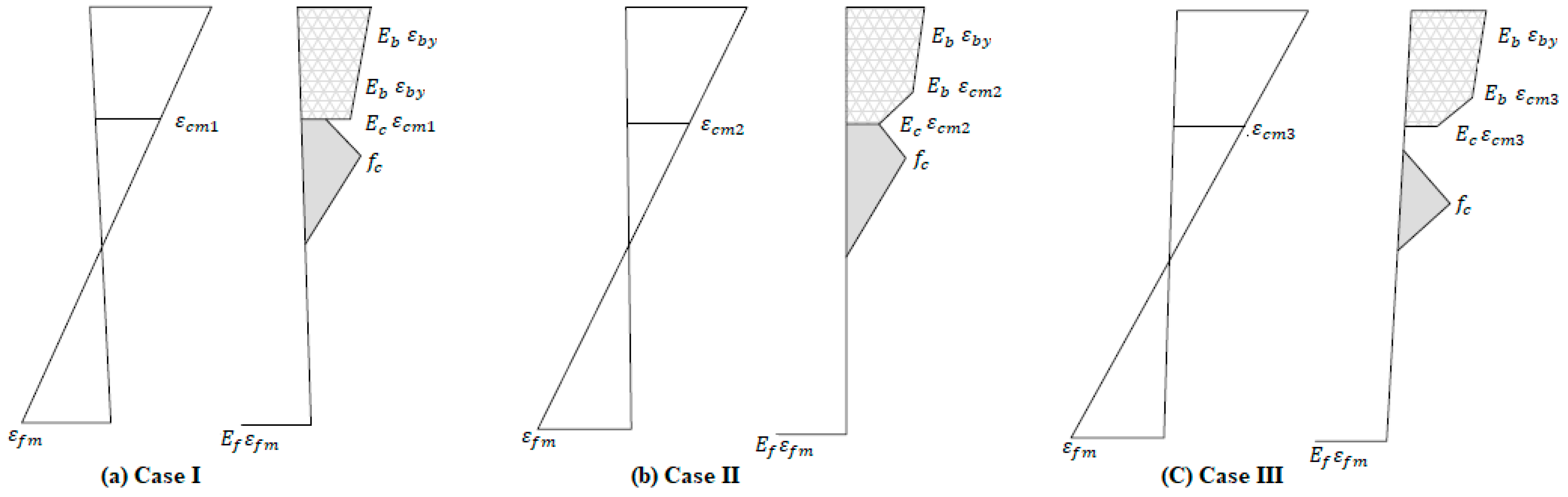
2. Compression-Yielded FRP-Reinforced Concrete Beam—Flexural Resistance
- A perfect bond is assumed between the concrete and reinforcing bars (i.e., FRP and steel bars) in order to ensure proper load transfer from the reinforcement to the concrete.
- A good contact is assumed between the CY block and concrete to eliminate the slipperiness between the CY block and concrete.
- Any section of the beam is plane before deflection and will remain plane after deflection.
- The tensile strength of concrete is ignored as the compression zone is the main zone of importance in the study.
3. Reliability Analysis
3.1. Load and Resistance Factor Design
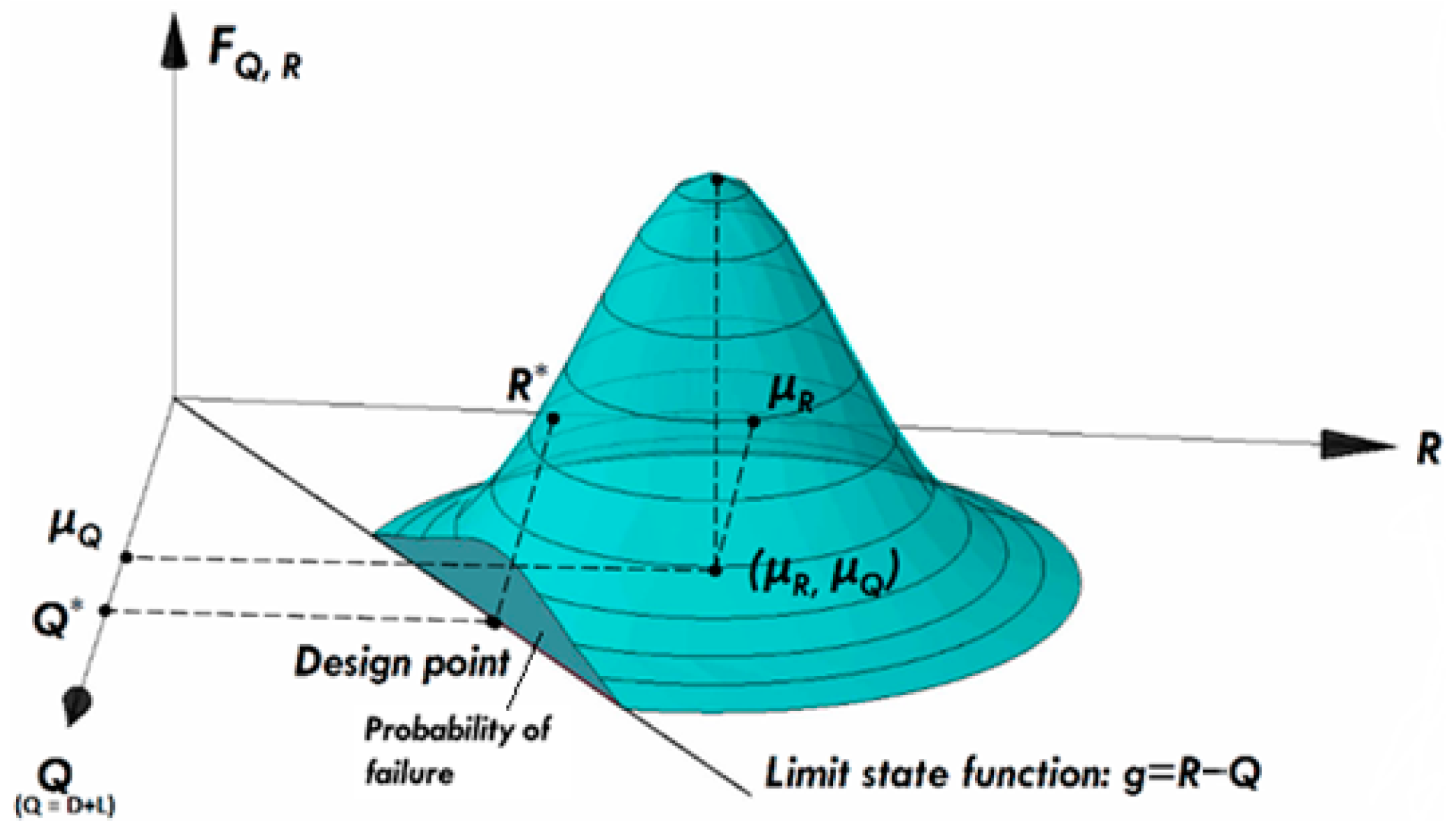
3.2. First-Order Reliability Method
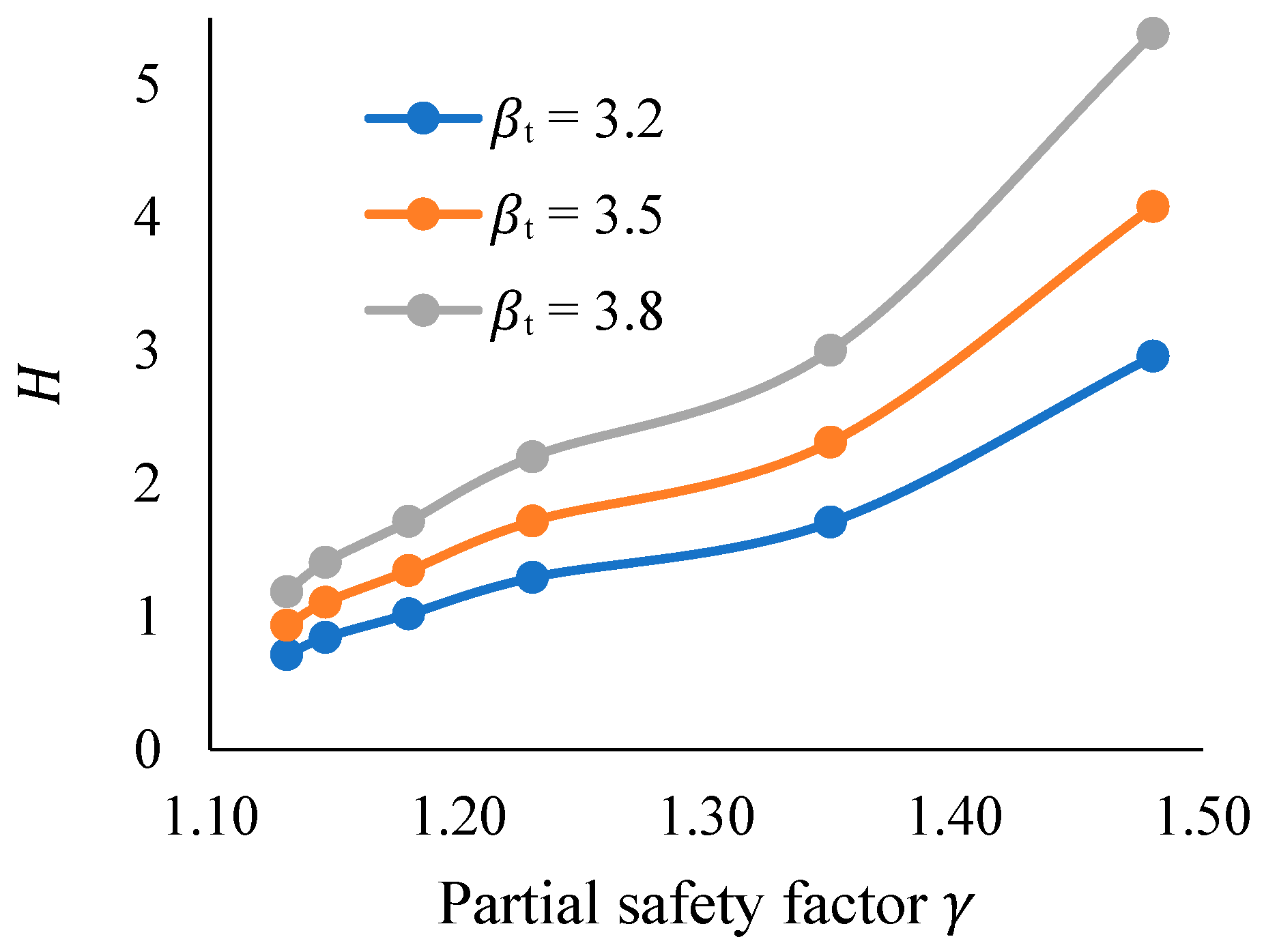
3.3. Target Reliability Index
3.4. Uncertainties Involved in Reliability Analysis
3.4.1. Model Uncertainties
3.4.2. Load Uncertainties
3.4.3. Uncertainties of Design Variables
4. CY Beam Reliability Analysis
4.1. Design Case
4.2. Reliability Analysis Procedure for the CY Beam
4.2.1. Hasofer–Lind Method
4.2.2. Monte Carlo Simulation
5. Results and Discussion
5.1. Matrix Procedure to Find Influence of Material Strength
5.2. Monte Carlo Simulation to Find Reliability Index
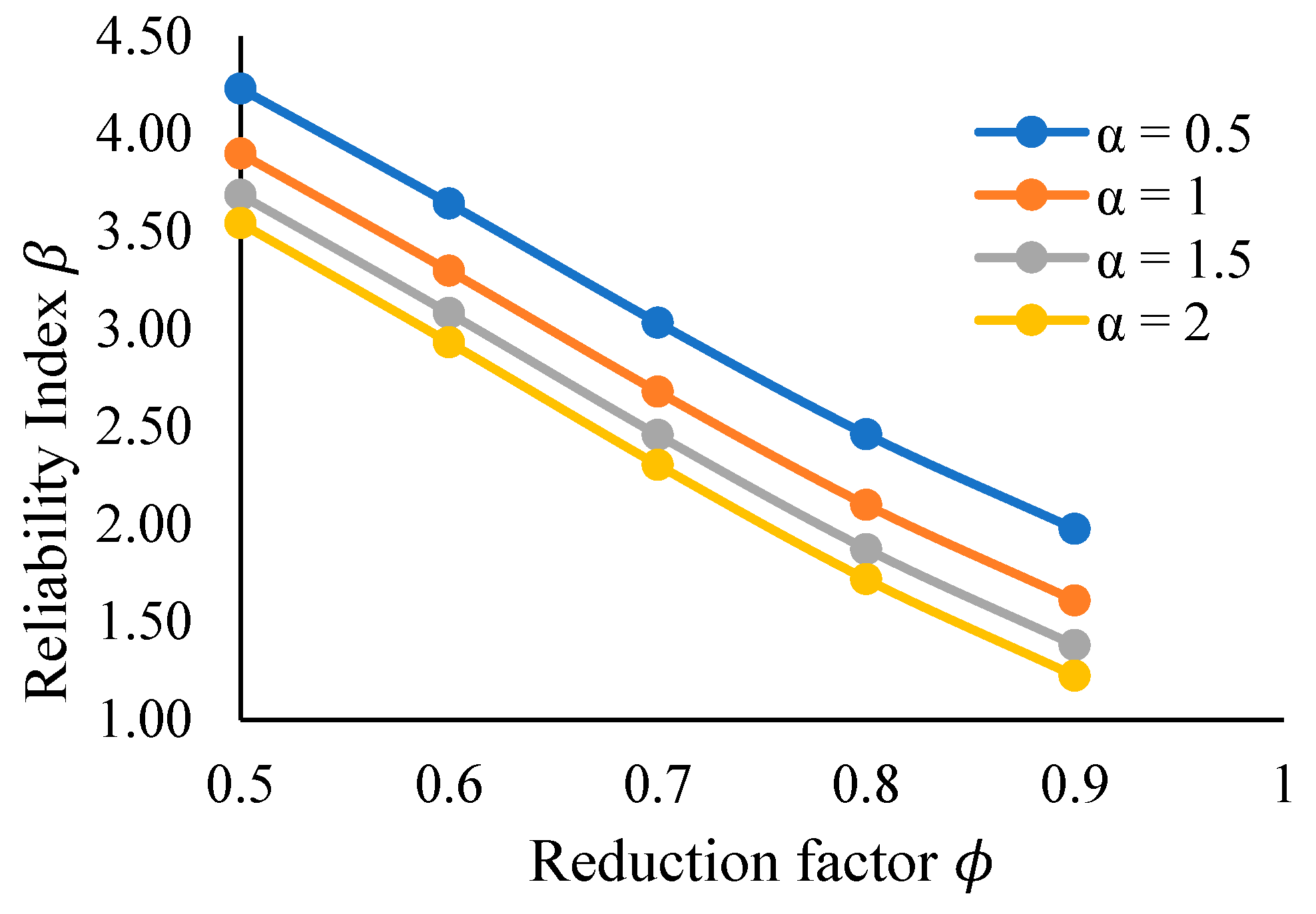
5.3. Reliability Index vs. Resistance Reduction Factor
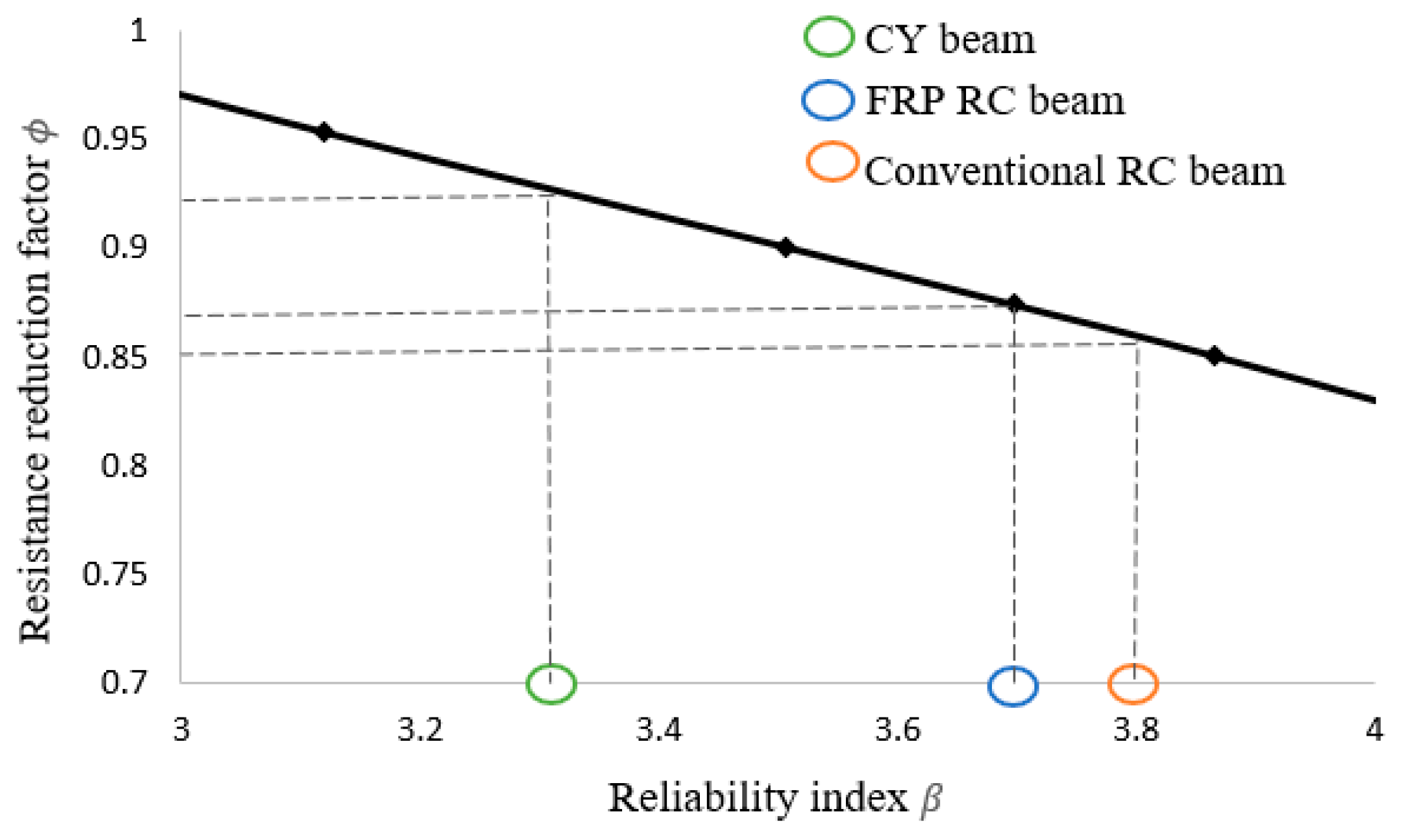
5.4. Optimal Value Factor
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldston, M.; Remennikov, A.; Sheikh, M.N. Experimental investigation of the behaviour of concrete beams reinforced with GFRP bars under static and impact loading. Eng. Struct. 2016, 113, 220–232. [Google Scholar] [CrossRef]
- Baena, M.; Torres, L.; Turon, A.; Barris, C. Experimental study of bond behaviour between concrete and FRP bars using a pull-out test. Compos. Part B Eng. 2009, 40, 784–797. [Google Scholar] [CrossRef]
- Robert, M.; Benmokrane, B. Effect of aging on bond of GFRP bars embedded in concrete. Cem. Concr. Compos. 2010, 32, 461–467. [Google Scholar] [CrossRef]
- Teng, X.; Zhang, Y.; Lin, X. Two new composite plate elements with bond–slip effect for nonlinear finite element analyses of FRP-strengthened concrete slabs. Comput. Struct. 2015, 148, 35–44. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y. Evaluation of bond stress-slip models for FRP reinforcing bars in concrete. Compos. Struct. 2014, 107, 131–141. [Google Scholar] [CrossRef]
- Pang, B.; Jin, Z.; Zhang, Y.; Xu, L.; Li, M.; Wang, C.; Zhang, Y.; Yang, Y.; Zhao, P.; Bi, J. Ultraductile waterborne epoxy-concrete composite repair material: Epoxy-fiber synergistic effect on flexural and tensile performance. Cem. Concr. Compos. 2022, 129, 104463. [Google Scholar] [CrossRef]
- Sun, L.; Wang, C.; Zhang, C.; Yang, Z.; Li, C.; Qiao, P. Experimental investigation on the bond performance of sea sand coral concrete with FRP bar reinforcement for marine environments. Adv. Struct. Eng. 2023, 26, 533–546. [Google Scholar] [CrossRef]
- Huang, H.; Yuan, Y.; Zhang, W.; Zhu, L. Property Assessment of High-Performance Concrete Containing Three Types of Fibers. Int. J. Concr. Struct. Mater. 2021, 15, 39. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y. Nonlinear finite element analyses of steel/FRP-reinforced concrete beams in fire conditions. Compos. Struct. 2013, 97, 277–285. [Google Scholar] [CrossRef]
- Balendran, R.; Rana, T.; Nadeem, A. Strengthening of concrete structures with FRP sheets and plates. Struct. Surv. 2001, 19, 185–192. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y. Novel composite beam element with bond-slip for nonlinear finite-element analyses of steel/FRP-reinforced concrete beams. J. Struct. Eng. 2013, 139, 06013003. [Google Scholar] [CrossRef]
- Neocleous, K.; Pilakoutas, K.; Guadagnini, M. Failure-mode-hierarchy-based design for reinforced concrete structures. Struct. Concr. 2005, 6, 23–32. [Google Scholar] [CrossRef]
- Pilakoutas, K.; Neocleous, K.; Guadagnini, M. Design philosophy issues of fiber reinfored polymer reinforced concrete structures. J. Compos. Constr. 2002, 6, 154–161. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y. Bond–slip behaviour of FRP-reinforced concrete beams. Constr. Build. Mater. 2013, 44, 110–117. [Google Scholar] [CrossRef]
- ACI PRC-440.2-17; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures. American Concrete Institute: Indianapolis, IN, USA, 2017; p. 112.
- Realfonzo, R.; Napoli, A. Concrete confined by FRP systems: Confinement efficiency and design strength models. Compos. Part B Eng. 2011, 42, 736–755. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Karabinis, A.I.; Kiousis, P.D. FRP-confined concrete members: Axial compression experiments and plasticity modelling. Eng. Struct. 2007, 29, 1343–1353. [Google Scholar] [CrossRef]
- Bank, L.C. Progressive failure and ductility of FRP composites for construction. J. Compos. Constr. 2013, 17, 406–419. [Google Scholar] [CrossRef]
- Kotynia, R. Debonding Phenomena in FRP–Strengthened Concrete Members. In Brittle Matrix Composites 8; Elsevier: Amsterdam, The Netherlands, 2006; pp. 109–122. [Google Scholar]
- Naaman, A. FRP reinforcements in structural concrete: Assessment, progress and prospects. Fibre Reinf. Polym. Reinf. Concr. Struct. 2003, 2, 3–24. [Google Scholar]
- Wu, Y.-F. Ductility demand of compression yielding fiber-reinforced polymer-reinforced concrete beams. ACI Struct. J. 2008, 105, 104. [Google Scholar]
- Wu, Y.-F.; Zhou, Y.-W.; Hu, B.; Huang, X.; Smith, S. Fused structures for safer and more economical constructions. Front. Struct. Civ. Eng. 2020, 14, 1–9. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Jiang, J.-F.; Liu, K. Perforated SIFCON blocks–An extraordinarily ductile material ideal for use in compression yielding structural systems. Constr. Build. Mater. 2010, 24, 2454–2465. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Leung, A.; Hou, J. Mechanical behavior of mild steel compressive yielding blocks. In Proceedings of the First Asia-Pacific Conference on FRP in Structures, Hong Kong, China, 12–14 December 2007; pp. 12–14. [Google Scholar]
- Zhou, Y.; Wu, Y.; Teng, J.; Leung, A. Parametric space for the optimal design of compression-yielding FRP-reinforced concrete beams. Mater. Struct. 2010, 43, 81–97. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Zhou, Y.-W.; He, X.-Q. Performance-based optimal design of compression-yielding FRP-reinforced concrete beams. Compos. Struct. 2010, 93, 113–123. [Google Scholar] [CrossRef]
- Guo, B.; Lin, X.; Wu, Y.; Zhang, L. Evaluation of flexural resistance of compression yielded concrete beams reinforced with fibre reinforced polymers. Eng. Struct. 2022, 250, 113416. [Google Scholar] [CrossRef]
- Feng, L.; Wu, Y.-F.; Guo, B.-C.; Huang, X.-X. Reducing target reliability index of concrete bridge beams through compression yielding. Eng. Struct. 2024, 316, 118506. [Google Scholar] [CrossRef]
- AS 3600; Concrete Structures. Standards Australia: Sydney, Australia, 2018.
- Nowak, A.S.; Collins, K.R. Reliability of Structures; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Kim, J.H.; Lee, H.S. Reliability assessment of reinforced concrete rectangular columns subjected to biaxial bending using the load contour method. Eng. Struct. 2017, 150, 636–645. [Google Scholar] [CrossRef]
- Pham, H.B.; Al-Mahaidi, R. Reliablity analysis of bridge beams retrofitted with fibre reinforced polymers. Compos. Struct. 2008, 82, 177–184. [Google Scholar] [CrossRef]
- Gu, X.; Guo, H.; Zhou, B.; Zhang, W.; Jiang, C. Corrosion non-uniformity of steel bars and reliability of corroded RC beams. Eng. Struct. 2018, 167, 188–202. [Google Scholar] [CrossRef]
- Ghasemi, S.H.; Nowak, A.S. Target reliability for bridges with consideration of ultimate limit state. Eng. Struct. 2017, 152, 226–237. [Google Scholar] [CrossRef]
- Standards Australia. Reinforced Concrete Design: In Accordance with AS 3600-2009; Cement & Concrete Aggregates Australia; Standards Australia: Sydney, Australia, 2011. [Google Scholar]
- Ellingwood, B. Development of a Probability Based Load Criterion for American National Standard A58: Building Code Requirements for Minimum Design Loads in Buildings and Other Structures; US Department of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1980; Volume 13.
- Huang, X.; Zhou, Y.; Xing, F.; Wu, Y.; Sui, L.; Han, N. Reliability-based design of FRP flexural strengthened reinforced concrete beams: Guidelines assessment and calibration. Eng. Struct. 2020, 209, 109953. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Assakkaf, I.A. Reliability-based structural design of ships using load and resistance factor design approach. Ship Struct. Comm. Rep. 2000, 1–21. [Google Scholar]
- Cornell, C.A. Bounds on the reliability of structural systems. J. Struct. Div. 1967, 93, 171–200. [Google Scholar] [CrossRef]
- Holicky, M. Reliability Analysis for Structural Design; SUN MeDIA Stellenbosch, 52 Ryneveld St, Stellenbosch Central: Stellenbosch, South Africa, 2009. [Google Scholar]
- Vrouwenvelder, A. Developments towards full probabilistic design codes. Struct. Saf. 2002, 24, 417–432. [Google Scholar] [CrossRef]
- Jonkman, S.; Steenbergen, R.; Morales-Nápoles, O.; Vrouwenvelder, A.; Vrijling, J. Probabilistic design: Risk and reliability analysis in civil engineering. Coll. CIE4130 2015. [Google Scholar]
- Foster, S.J.; Stewart, M.G.; Sirivivatnanon, V.; Mindy, K.Y.; Loo, M.A.; Ng, T.S.; Valipour, H. Reinforced Concrete Structures Designed to AS3600; The University of Newcastle: Newcastle, Australia, 2015; ISSN 0077-880X. [Google Scholar]
- AS 5104; General Principles on Reliability for Structures. Defines the reliability principles for design of structures. Standards Australia: Sydney, Australia, 2005; p. 75.
- Sykora, M.; Holicky, M.; Lenner, R.; Maňas, P. Target reliability levels for existing bridges considering emergency and crisis situations. Adv. Mil. Technol. 2014, 9, 45–57. [Google Scholar]
- Feng, L.; Li, P.-D.; Huang, X.-X.; Wu, Y.-F. Reliability-Based Design Analysis for FRP Reinforced Compression Yield Beams. Polymers 2022, 14, 4846. [Google Scholar] [CrossRef] [PubMed]
- ACI 440; Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars. American Concrete Institute: Indianapolis, IN, USA, 2006.
- GB50068; Unified Standard for Reliability Design of building Structures. China Architecture & Building Press: Beijing, China, 2001.
- ISO 2394:1998; I. General Principles on Reliability for Structures. International Organization for Standardization: Geneva, Switzerland, 1998.
- Stewart, M.; Lawrence, S. Model error, structural reliability and partial safety factors for structural masonry in compression. Mason. Int. 2007, 20, 107–116. [Google Scholar]
- Galambos, T.V.; Ellingwood, B.; MacGregor, J.G.; Cornell, C.A. Probability based load criteria: Assessment of current design practice. J. Struct. Div. 1982, 108, 959–977. [Google Scholar] [CrossRef]
- Huang, X.; Sui, L.; Xing, F.; Zhou, Y.; Wu, Y. Reliability assessment for flexural FRP-Strengthened reinforced concrete beams based on Importance Sampling. Compos. Part B Eng. 2019, 156, 378–398. [Google Scholar] [CrossRef]
- Lu, R.; Luo, Y.; Conte, J.P. Reliability evaluation of reinforced concrete beams. Struct. Saf. 1994, 14, 277–298. [Google Scholar] [CrossRef]
- Yongxin, Y. Reliability analysis of RC concrete beams strengthened with CFRP sheets. J. Build. Struct. 2008, 29, 88–91. [Google Scholar]
- Okeil, A.M.; El-Tawil, S.; Shahawy, M. Flexural reliability of reinforced concrete bridge girders strengthened with carbon fiber-reinforced polymer laminates. J. Bridge Eng. 2002, 7, 290–299. [Google Scholar] [CrossRef]
- Desayi, P.; Rao, K.B. Reliability of reinforced concrete beams in limit state of cracking—Failure rate analysis approach. Mater. Struct. 1989, 22, 269–279. [Google Scholar] [CrossRef]
- Atadero, R.A.; Karbhari, V.M. Calibration of resistance factors for reliability based design of externally-bonded FRP composites. Compos. Part B Eng. 2008, 39, 665–679. [Google Scholar] [CrossRef]
- Wu, Y.-F. New avenue of achieving ductility for reinforced concrete members. J. Struct. Eng. 2006, 132, 1502–1506. [Google Scholar] [CrossRef]
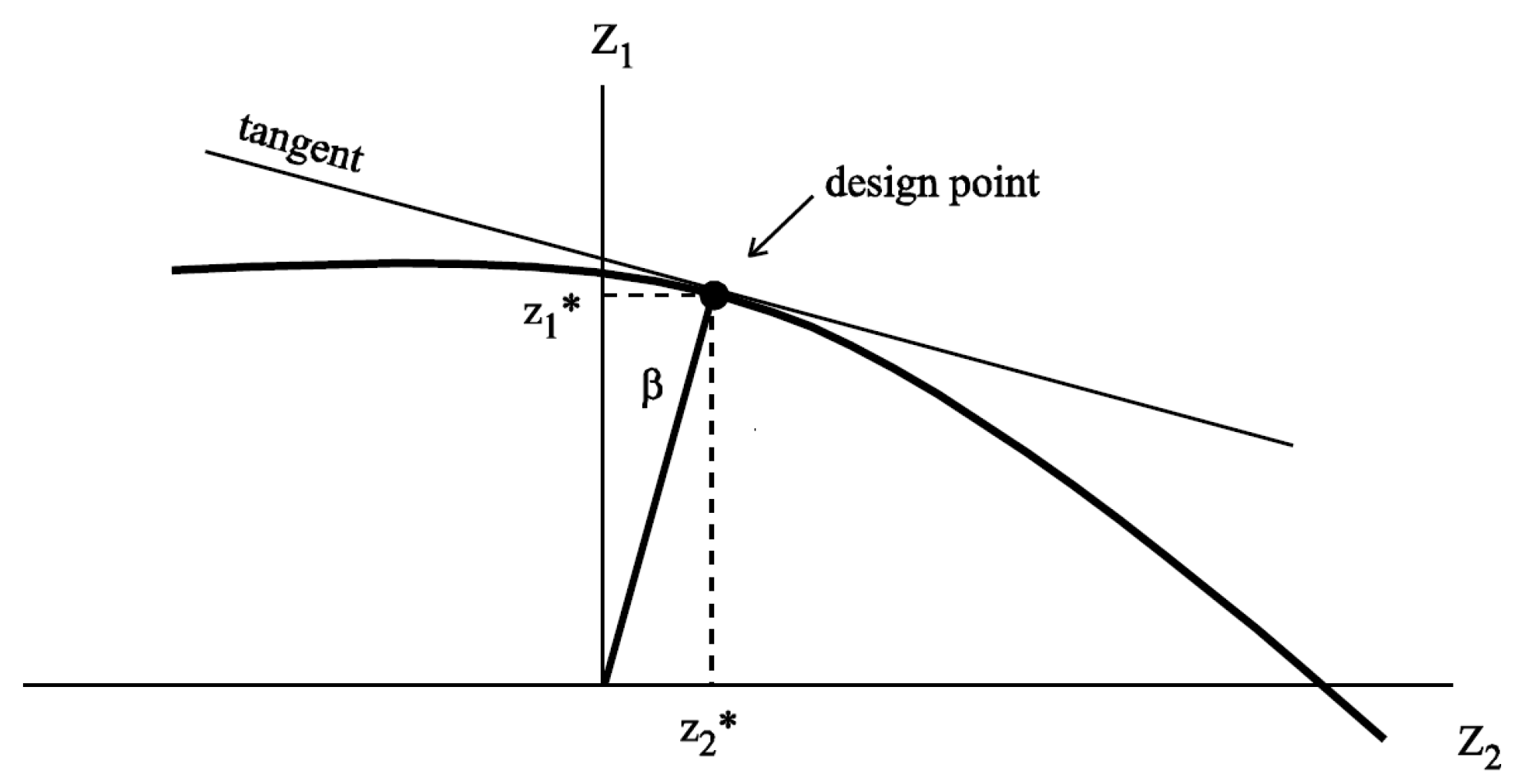

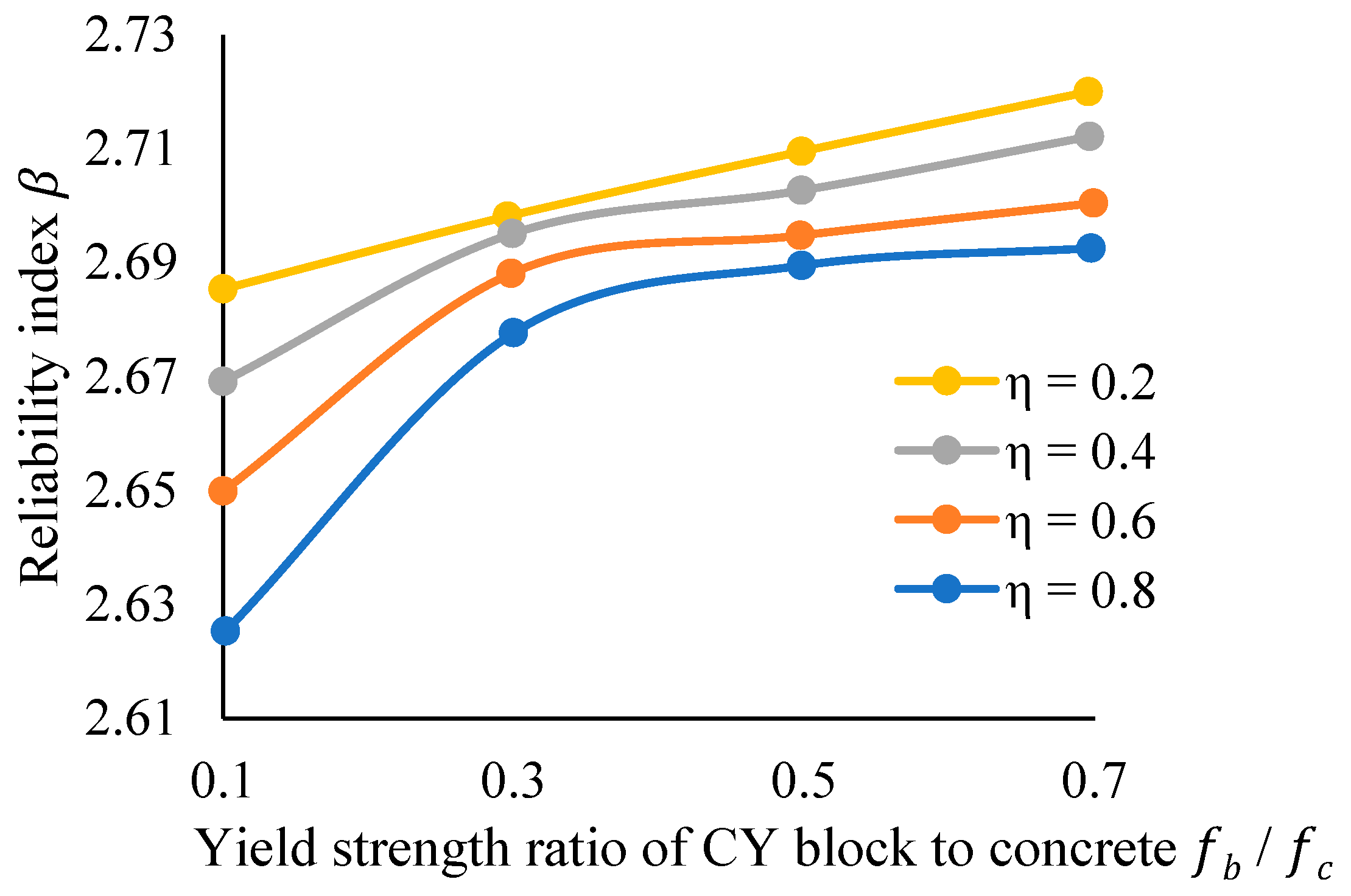
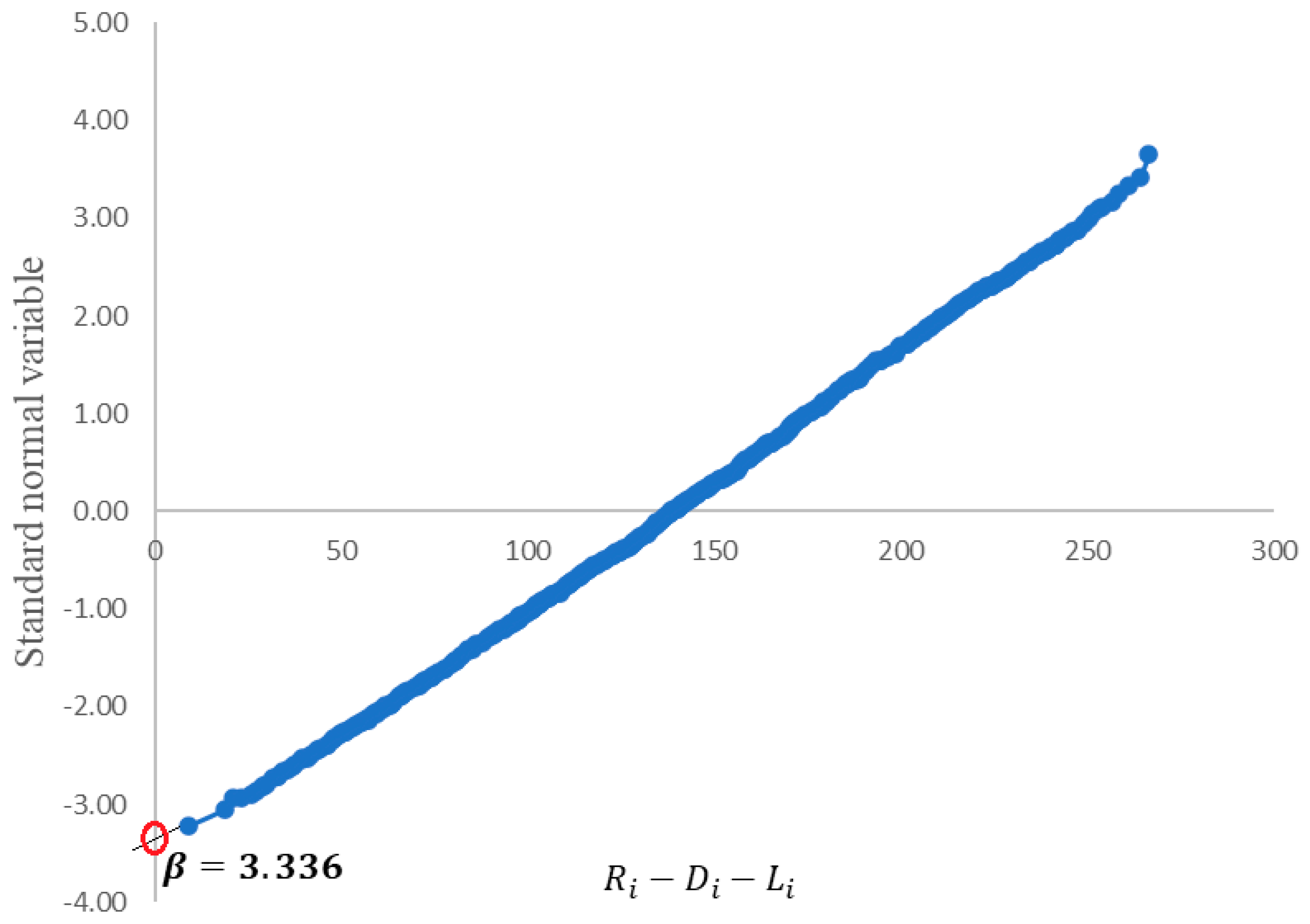
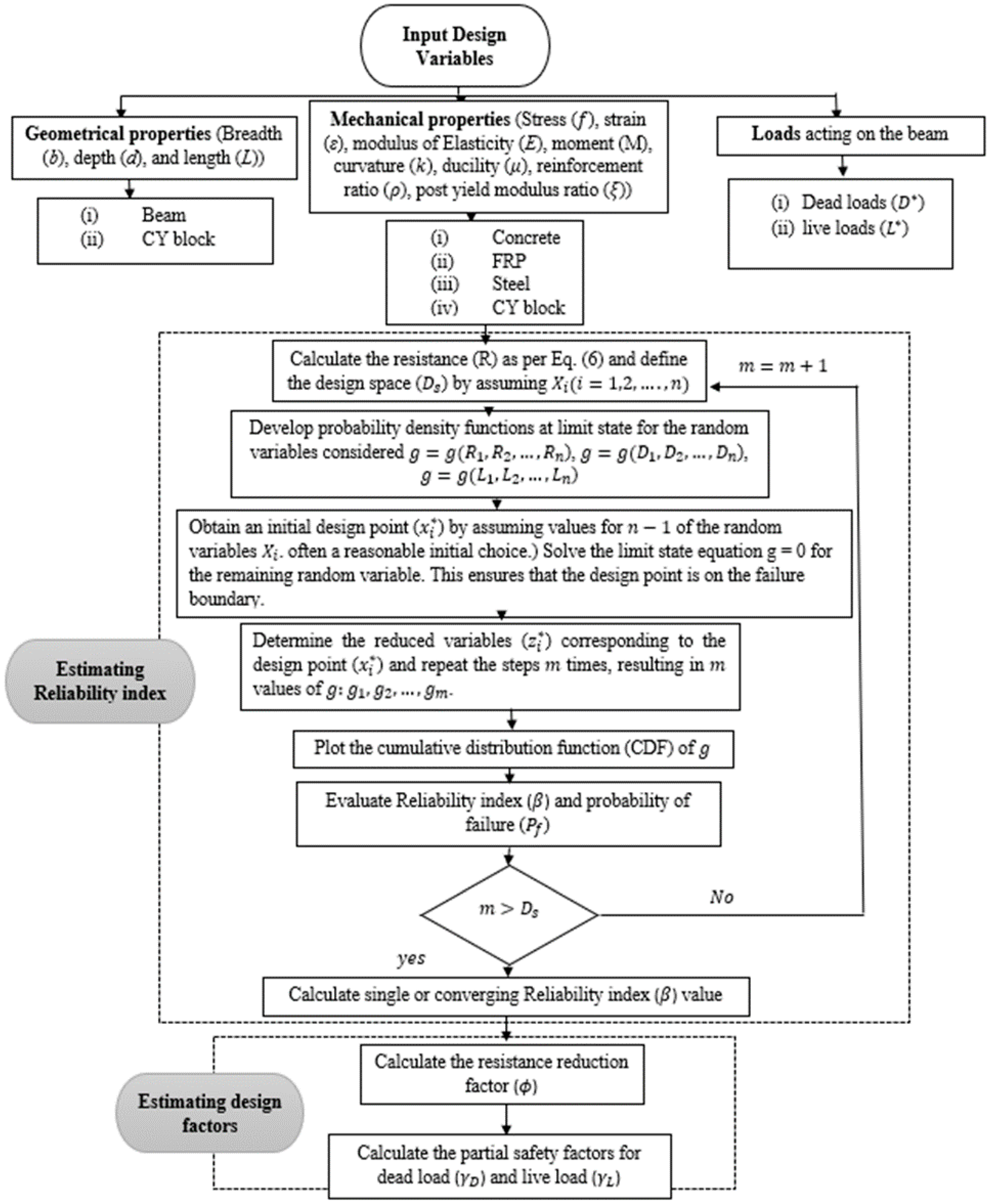
| Distribution | p Value | Mean | COV | Error % |
|---|---|---|---|---|
| Normal | 0.886 | 0.961 | 0.155 | 7.15 |
| Lognormal | 0.982 | 0.974 | 0.158 | 2.96 |
| Weibull | 0.341 | 0.953 | 0.161 | 17.03 |
| Extreme type I | 0.091 | 0.946 | 0.181 | 26.04 |
| Loads | Bias | COV | Distribution |
|---|---|---|---|
| Dead load | 1.05 | 0.12 | Normal |
| 0.95 | 0.25 | Extreme type I |
| Category | Variable | Bias | COV | Distribution | Reference |
|---|---|---|---|---|---|
| Geometry | (mm) | 1 | 0.02 | Normal | [53] |
| (mm) | 1 | 0.02 | Normal | [54] | |
| (mm) | 1 | 0.03 | Normal | [55] | |
| (mm) | 1 | 0.03 | Normal | [52] | |
| Concrete | (MPa) | 1.25 | 0.15 | Normal | [52] |
| Steel | (mm2) | 1 | 0.03 | Normal | [54] |
| (MPa) | 1 | 0.024 | Normal | [32] | |
| (MPa) | 1.1 | 0.075 | Normal | [56] | |
| FRP | (mm) | 1 | 0.05 | Lognormal | [57] |
| (MPa) | 1 | 0.04 | Normal | [52] | |
| (Mpa) | 1.15 | 0.1 | Weibull | [52] | |
| CY block | 1 | 0.02 | Normal | [25] | |
| (MPa) | 1 | 0.30 | Normal | [58] | |
| (Mpa) | 1 | 0.30 | Normal | [23] | |
| Loads | Dead load | 1.05 | 0.12 | Normal | [37] |
| Live load | 0.95 | 0.25 | Extreme Type I | [37] |
| Categories | Parameters | Values |
|---|---|---|
| Geometry | (mm) | 180 |
| (mm) | 350 | |
| (mm) | 300 | |
| (mm) | 2500 | |
| Concrete | (MPa) | 30 |
| 0.002 | ||
| 0.006 | ||
| Steel | (GPa) | 200 |
| 0.0015 | ||
| (%) | 0.5 | |
| FRP | (GPa) | 124 |
| 0.017 | ||
| (%) | 0.05 | |
| CY block [25,58] | (MPa) | 40.4 |
| 0.001 | ||
| 0.2 |
| Random Variables | Nominal Values | ) | Mean ) | COV ) | ) | Distribution |
|---|---|---|---|---|---|---|
| ) | 0.982 | 0.158 | Lognormal | |||
| ) | 1.05 | 0.12 | Normal | |||
| ) | 0.95 | 0.25 | Extreme type I |
| S. No | Random Nos | Random Nos | Random Nos | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.876 | 2.436 | 4.741 | 0.765 | 6.610 | 10.480 | 0.980 | 17.667 | 24.197 | 8.621 | 0.004 | −3.298 |
| 2 | 0.251 | 3.012 | 8.228 | 0.262 | 7.321 | 11.865 | 0.795 | 28.723 | 42.810 | 18.391 | 0.006 | −3.046 |
| 3 | 0.018 | 3.308 | 10.022 | 0.552 | 5.476 | 8.270 | 0.693 | 29.474 | 44.074 | 20.690 | 0.008 | −2.936 |
| 4 | 0.443 | 4.728 | 18.632 | 0.784 | 7.374 | 11.969 | 0.944 | 35.091 | 53.530 | 22.989 | 0.010 | −2.936 |
| 5 | 0.800 | 2.782 | 6.839 | 0.038 | 7.556 | 12.323 | 0.394 | 36.200 | 55.398 | 25.862 | 0.012 | −2.900 |
| 6 | 0.719 | 2.303 | 3.936 | 0.409 | 7.772 | 12.745 | 0.120 | 37.279 | 57.214 | 27.203 | 0.014 | −2.863 |
| 7 | 0.825 | 4.688 | 18.390 | 0.447 | 5.297 | 7.920 | 0.445 | 38.721 | 59.641 | 28.736 | 0.016 | −2.812 |
| 8 | 0.190 | 4.230 | 15.609 | 0.757 | 7.863 | 12.921 | 0.149 | 40.828 | 63.188 | 28.736 | 0.018 | −2.812 |
| 9 | 0.464 | 4.259 | 15.786 | 0.029 | 7.531 | 12.276 | 0.256 | 43.399 | 67.517 | 31.609 | 0.020 | −2.725 |
| 10 | 0.891 | 3.672 | 12.228 | 0.673 | 6.345 | 9.962 | 0.816 | 39.518 | 60.984 | 29.502 | 0.022 | −2.791 |
| 11 | 0.152 | 4.943 | 19.935 | 0.572 | 5.238 | 7.805 | 0.459 | 42.748 | 66.421 | 32.567 | 0.024 | −2.710 |
| 12 | 0.239 | 4.177 | 15.293 | 0.791 | 6.960 | 11.162 | 0.029 | 43.704 | 68.031 | 32.567 | 0.026 | −2.710 |
| 13 | 0.691 | 2.591 | 5.677 | 0.194 | 7.850 | 12.896 | 0.868 | 44.348 | 69.115 | 33.908 | 0.028 | −2.667 |
| 14 | 0.396 | 4.809 | 19.123 | 0.005 | 5.707 | 8.720 | 0.951 | 45.766 | 71.501 | 35.249 | 0.030 | −2.645 |
| 15 | 0.140 | 2.288 | 3.842 | 0.625 | 7.851 | 12.898 | 0.740 | 46.920 | 73.445 | 36.782 | 0.032 | −2.608 |
| 16 | 0.560 | 1.958 | 1.840 | 0.260 | 5.661 | 8.629 | 0.795 | 44.975 | 70.169 | 37.356 | 0.034 | −2.594 |
| 17 | 0.162 | 3.539 | 11.423 | 0.711 | 5.125 | 7.584 | 0.645 | 47.553 | 74.509 | 38.889 | 0.036 | −2.543 |
| 18 | 0.189 | 2.027 | 2.259 | 0.994 | 6.472 | 10.210 | 0.254 | 47.962 | 75.199 | 39.464 | 0.038 | −2.528 |
| 19 | 0.397 | 2.006 | 2.133 | 0.549 | 5.982 | 9.256 | 0.602 | 47.452 | 74.340 | 39.464 | 0.042 | −2.528 |
| 20 | 0.988 | 3.597 | 11.775 | 0.986 | 7.604 | 12.417 | 0.116 | 51.814 | 81.683 | 40.613 | 0.047 | −2.521 |
| 21 | 0.612 | 3.438 | 10.812 | 0.426 | 7.873 | 12.941 | 0.554 | 53.073 | 83.804 | 41.762 | 0.051 | −2.485 |
| 22 | 0.331 | 3.823 | 13.147 | 0.809 | 5.938 | 9.169 | 0.255 | 53.248 | 84.097 | 43.487 | 0.055 | −2.441 |
| 23 | 0.890 | 2.475 | 4.974 | 0.703 | 6.409 | 10.088 | 0.038 | 52.370 | 82.620 | 43.487 | 0.058 | −2.441 |
| 24 | 0.448 | 4.471 | 17.072 | 0.209 | 6.755 | 10.761 | 0.935 | 55.670 | 88.175 | 44.444 | 0.060 | −2.419 |
| 25 | 0.865 | 2.605 | 5.765 | 0.292 | 6.334 | 9.941 | 0.841 | 55.108 | 87.228 | 46.169 | 0.064 | −2.390 |
| 26 | 0.080 | 3.336 | 10.196 | 0.112 | 6.218 | 9.715 | 0.679 | 55.723 | 88.264 | 46.169 | 0.067 | −2.390 |
| 27 | 0.024 | 2.670 | 6.159 | 0.814 | 7.175 | 11.581 | 0.090 | 57.163 | 90.689 | 47.318 | 0.070 | −2.339 |
| 28 | 0.582 | 3.274 | 9.817 | 0.567 | 6.395 | 10.061 | 0.942 | 57.562 | 91.360 | 47.893 | 0.074 | −2.324 |
| 29 | 0.381 | 2.342 | 4.169 | 0.798 | 6.879 | 11.004 | 0.530 | 57.114 | 90.606 | 47.893 | 0.077 | −2.324 |
| 30 | 0.067 | 4.041 | 14.464 | 0.093 | 7.030 | 11.298 | 0.498 | 60.304 | 95.977 | 49.234 | 0.079 | −2.288 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramamoorthy, D.; Guo, B.; Kazmi, S.M.S.; Wu, Y. A Reliability-Based Design Approach for the Flexural Resistance of Compression Yielded Fibre-Reinforced Polymer (FRP)-Reinforced Concrete Beams. Buildings 2024, 14, 2415. https://doi.org/10.3390/buildings14082415
Ramamoorthy D, Guo B, Kazmi SMS, Wu Y. A Reliability-Based Design Approach for the Flexural Resistance of Compression Yielded Fibre-Reinforced Polymer (FRP)-Reinforced Concrete Beams. Buildings. 2024; 14(8):2415. https://doi.org/10.3390/buildings14082415
Chicago/Turabian StyleRamamoorthy, Dharinee, Bingcheng Guo, Syed Minhaj Saleem Kazmi, and Yufei Wu. 2024. "A Reliability-Based Design Approach for the Flexural Resistance of Compression Yielded Fibre-Reinforced Polymer (FRP)-Reinforced Concrete Beams" Buildings 14, no. 8: 2415. https://doi.org/10.3390/buildings14082415
APA StyleRamamoorthy, D., Guo, B., Kazmi, S. M. S., & Wu, Y. (2024). A Reliability-Based Design Approach for the Flexural Resistance of Compression Yielded Fibre-Reinforced Polymer (FRP)-Reinforced Concrete Beams. Buildings, 14(8), 2415. https://doi.org/10.3390/buildings14082415








