Application of an Improved Method Combining Machine Learning–Principal Component Analysis for the Fragility Analysis of Cross-Fault Hydraulic Tunnels
Abstract
:1. Introduction
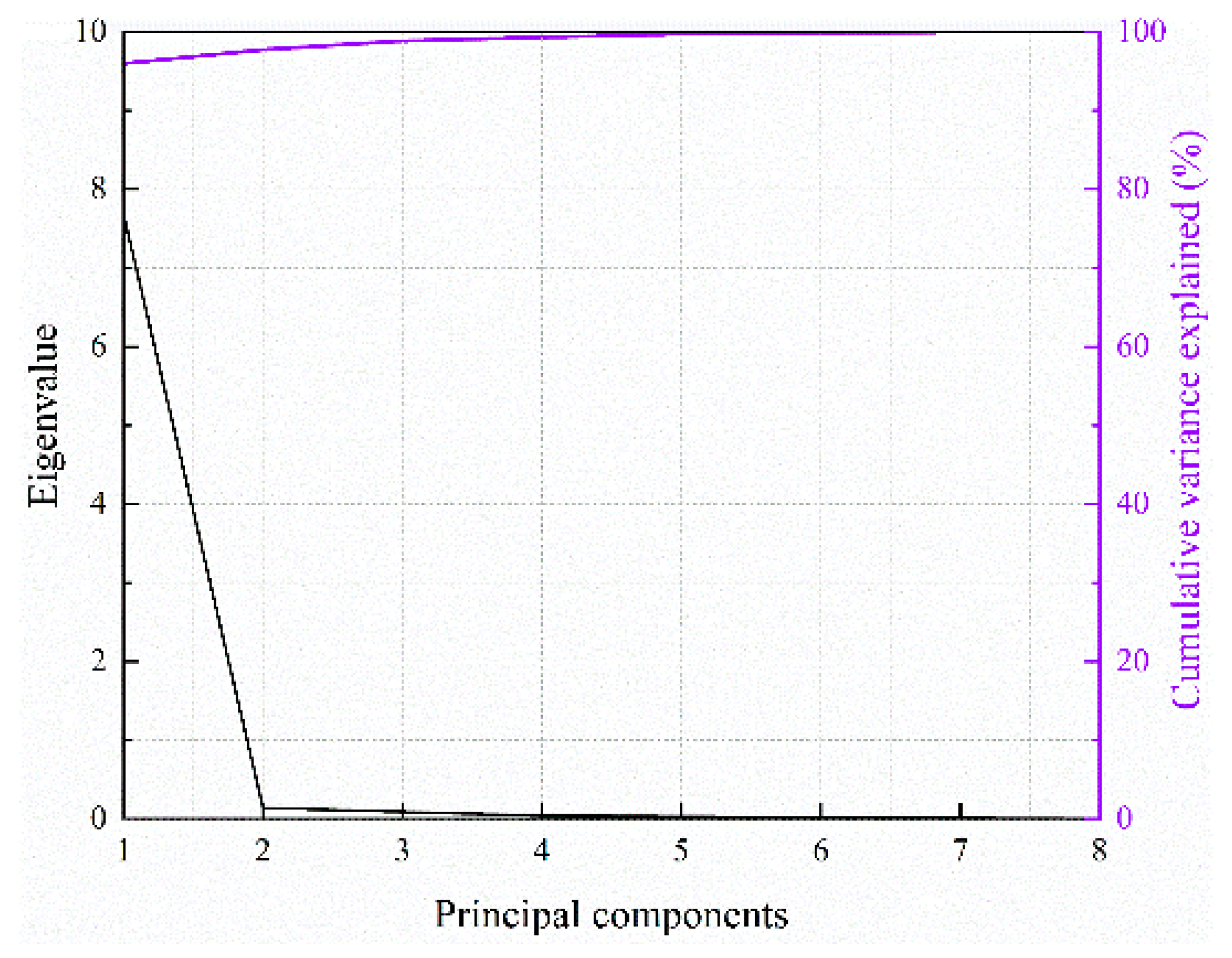
2. A Powerful Dimension-Reduction Method for PCA
3. Machine Learning
3.1. Stepwise Regression
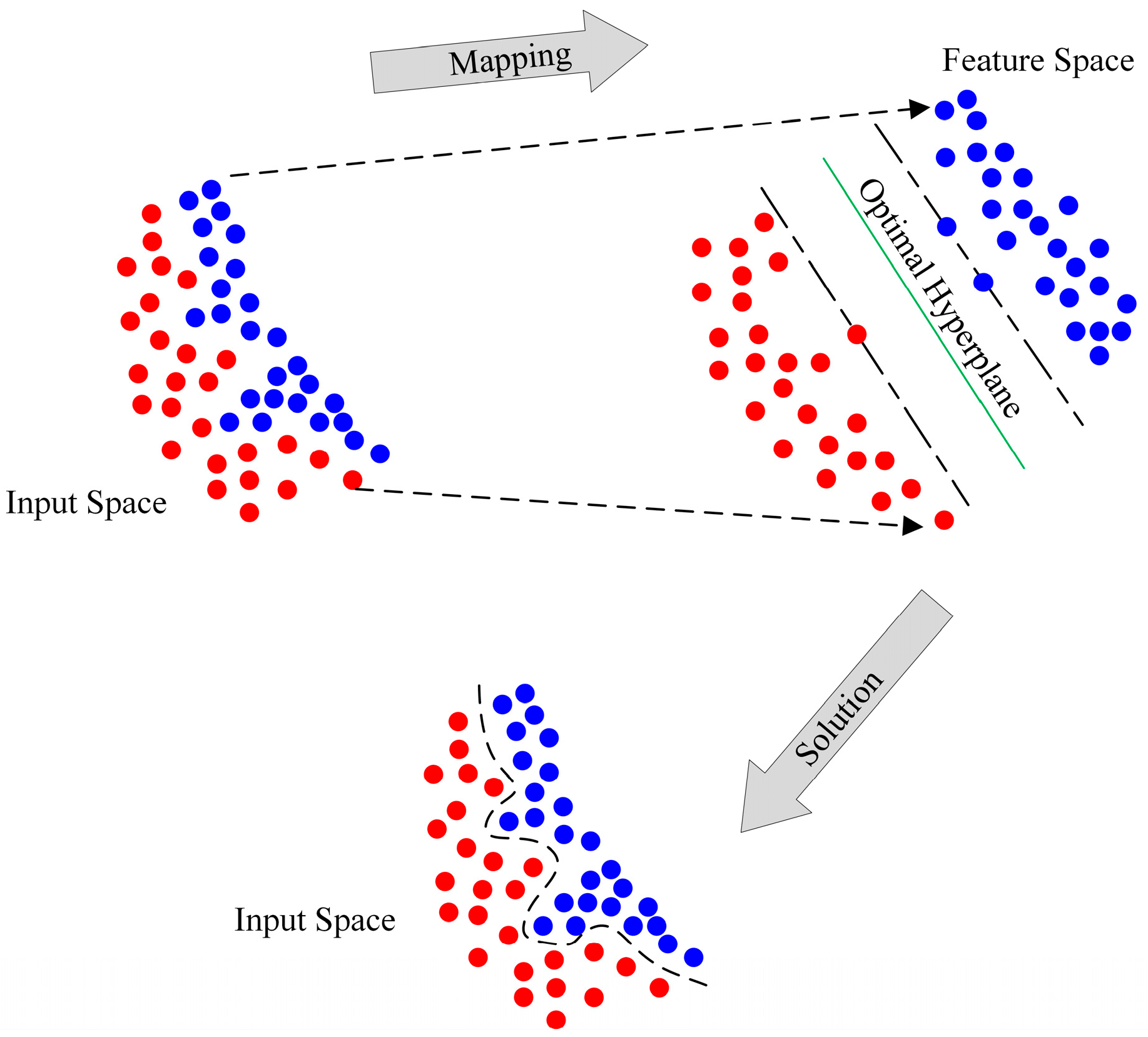
3.2. Support Vector Machine Regression
3.3. Decision Tree Regression
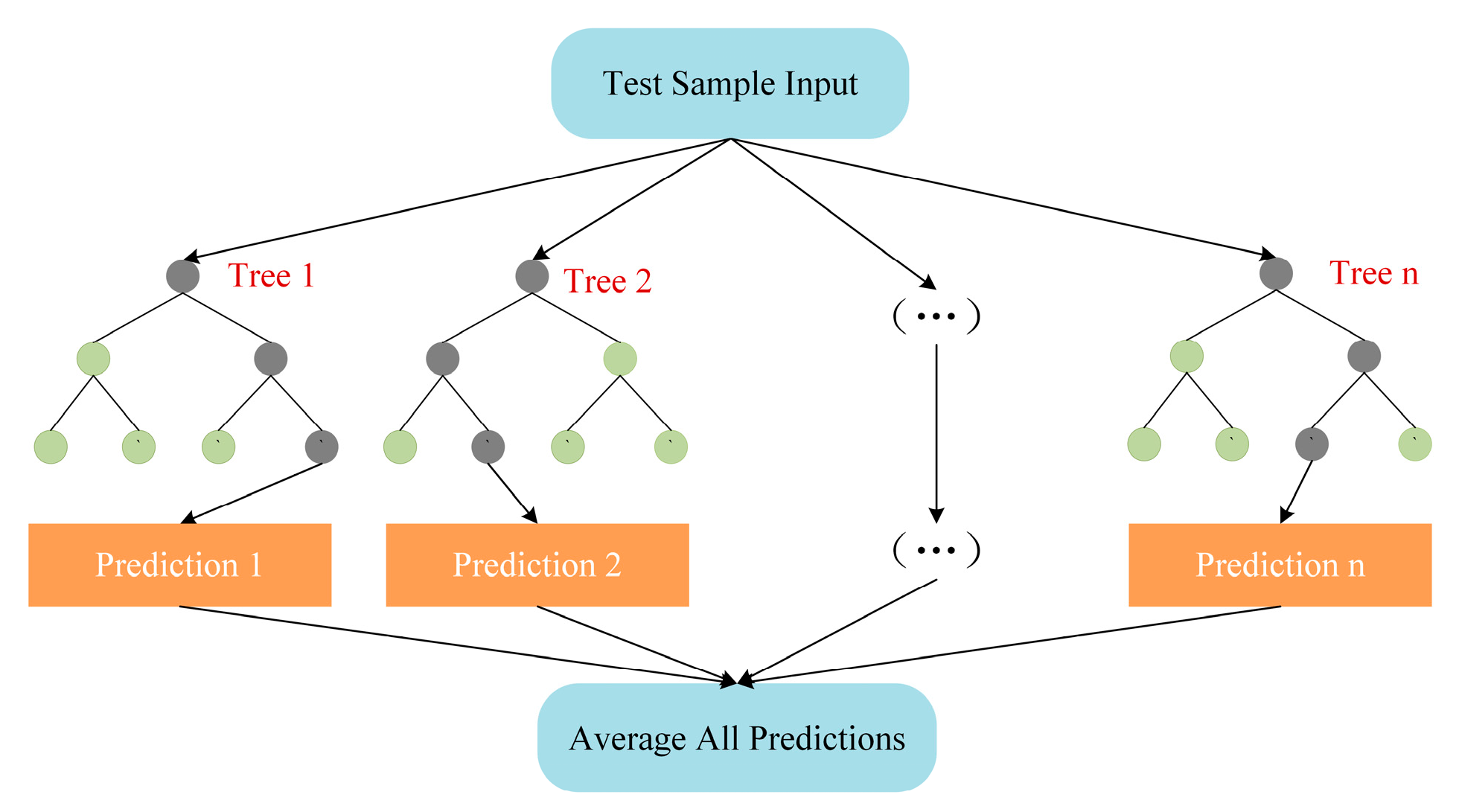
3.4. Random Forest Regression
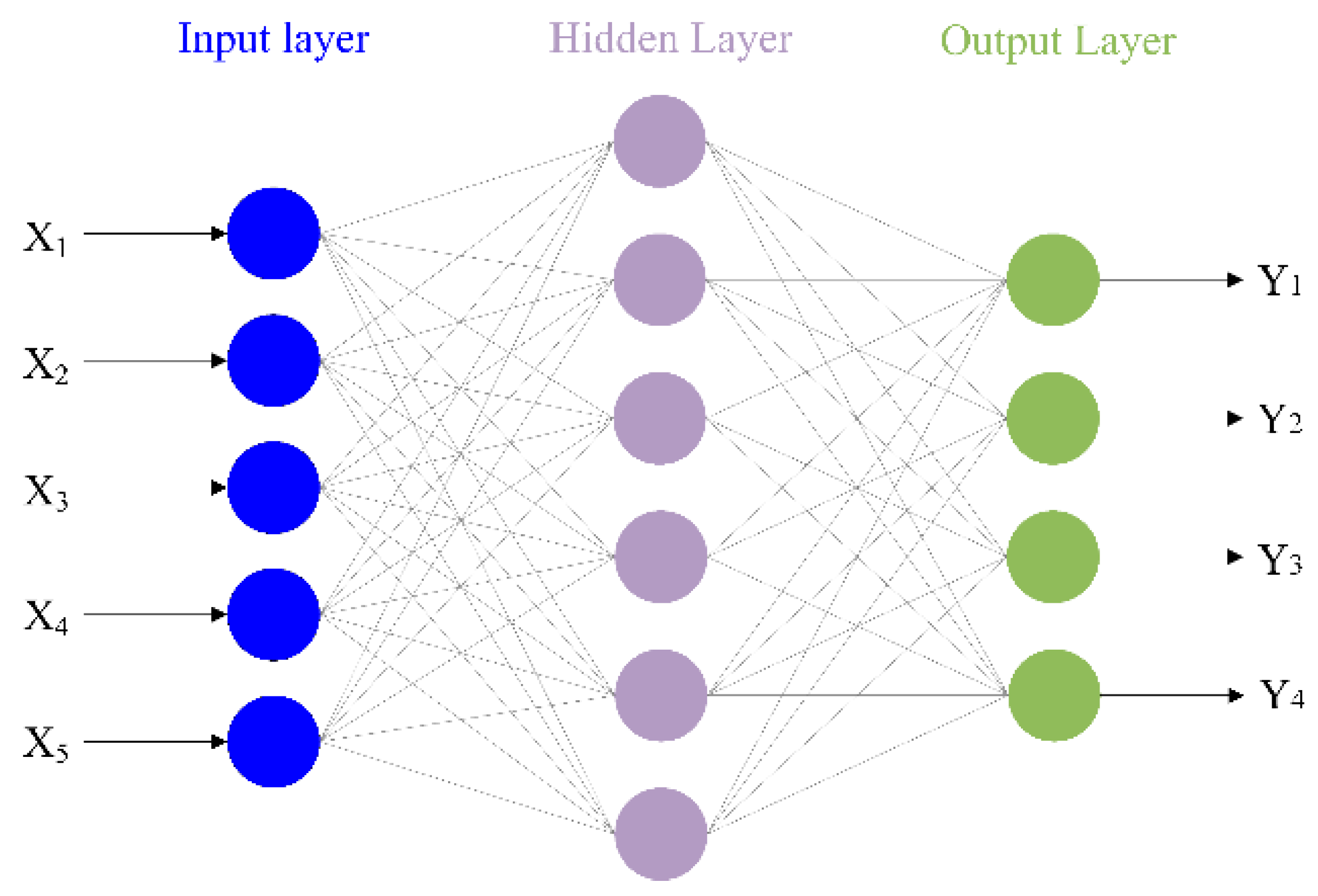
3.5. Neural Networks Regression
3.6. Gaussian Process Regression
4. Framework for the Fragility Curve Fitting Method Coupling the Predicting Data
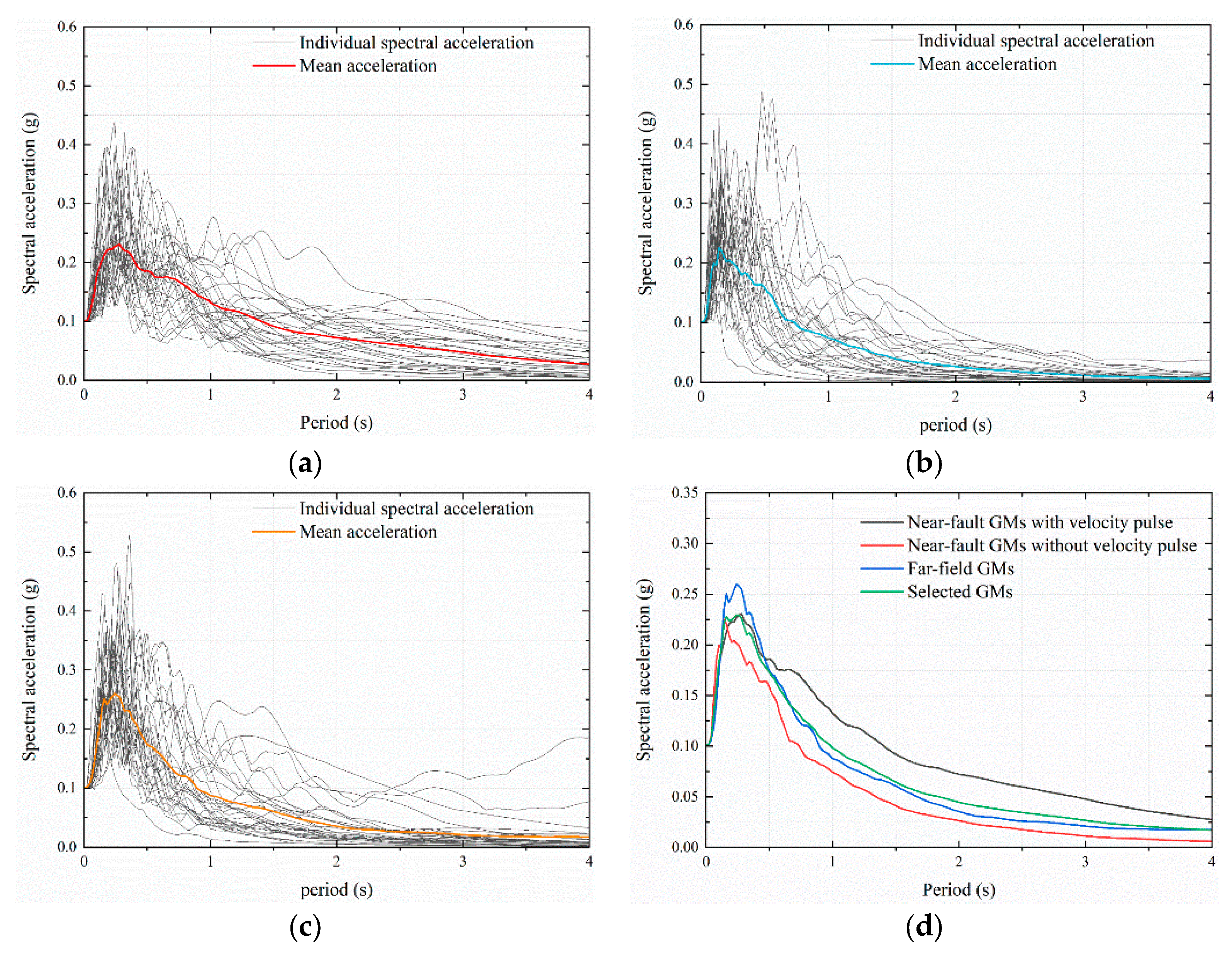
5. Pre-Processing of Ground Motions and Integrated IM
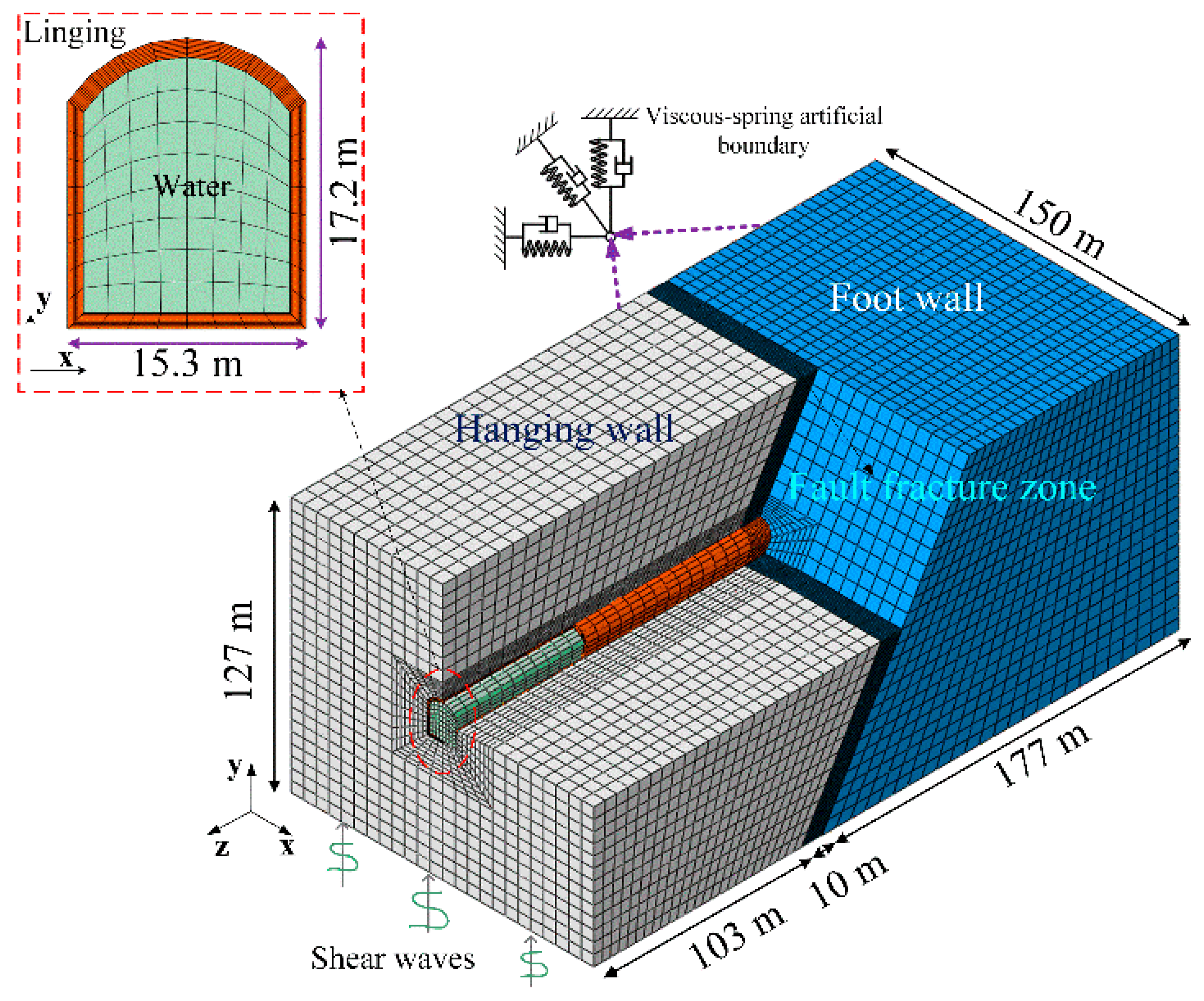
6. Numerical Method
7. Analysis Results and Discussion
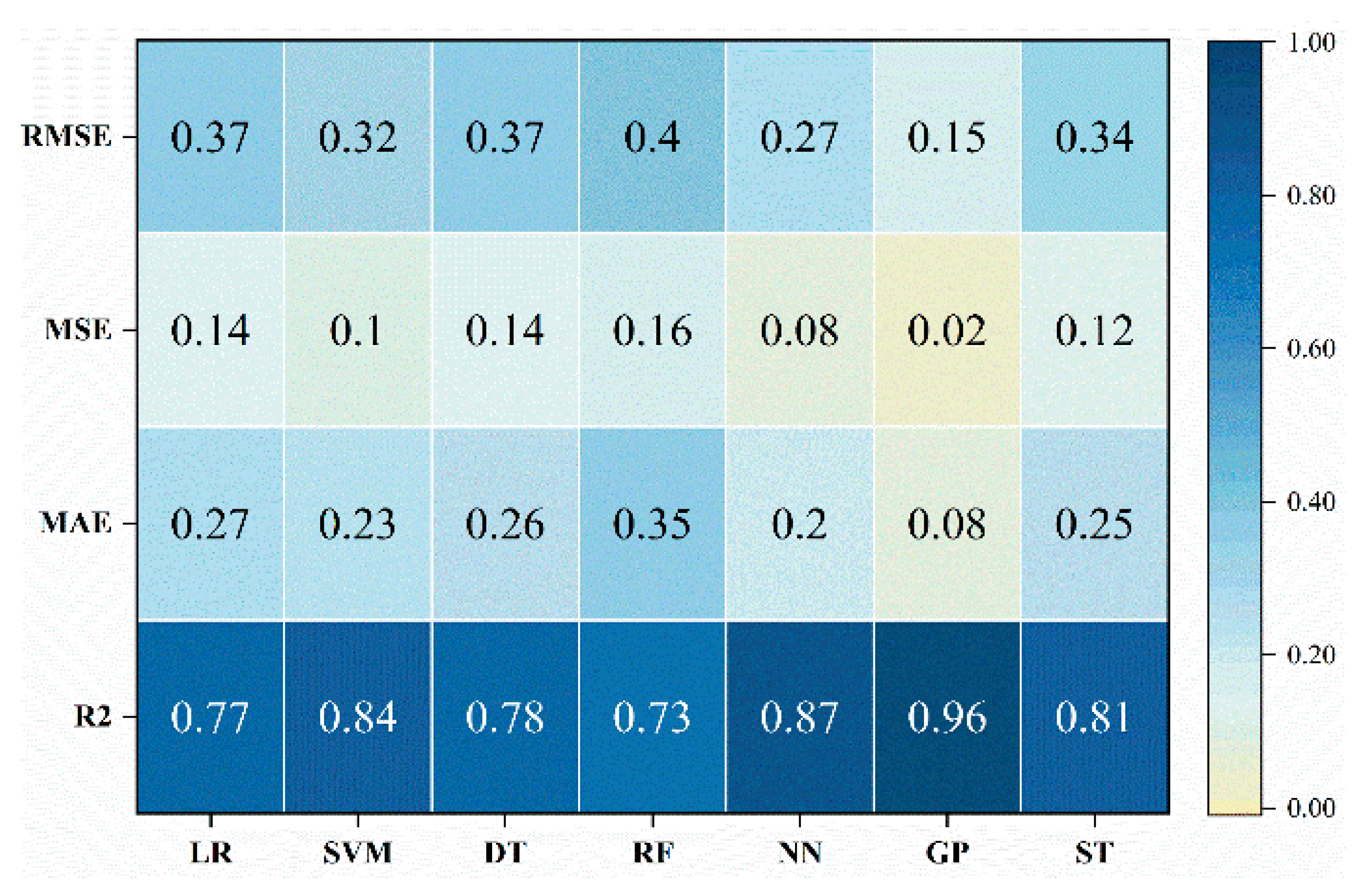
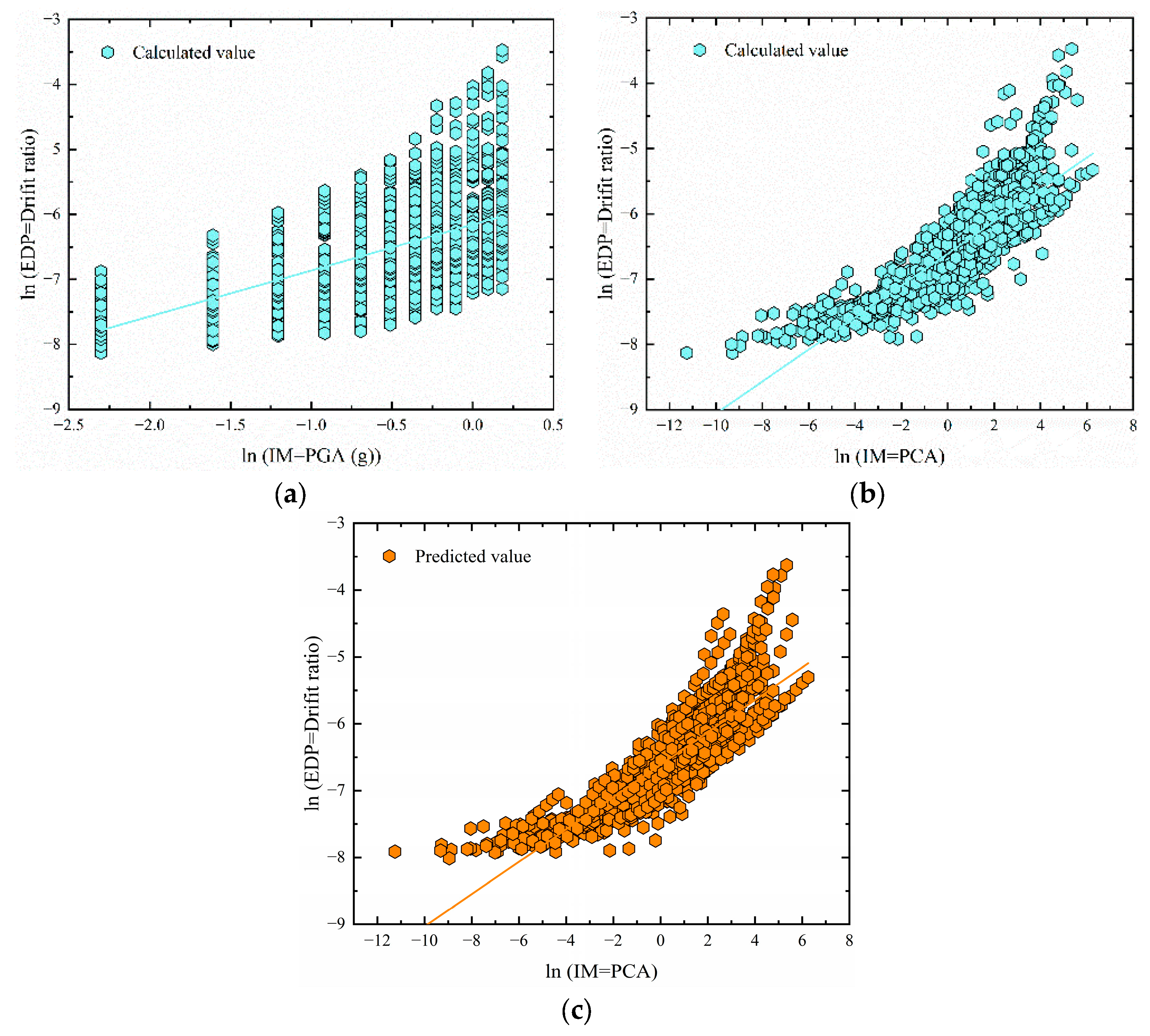
7.1. Predictive Capability Evaluation of Various ML-PCA Approaches
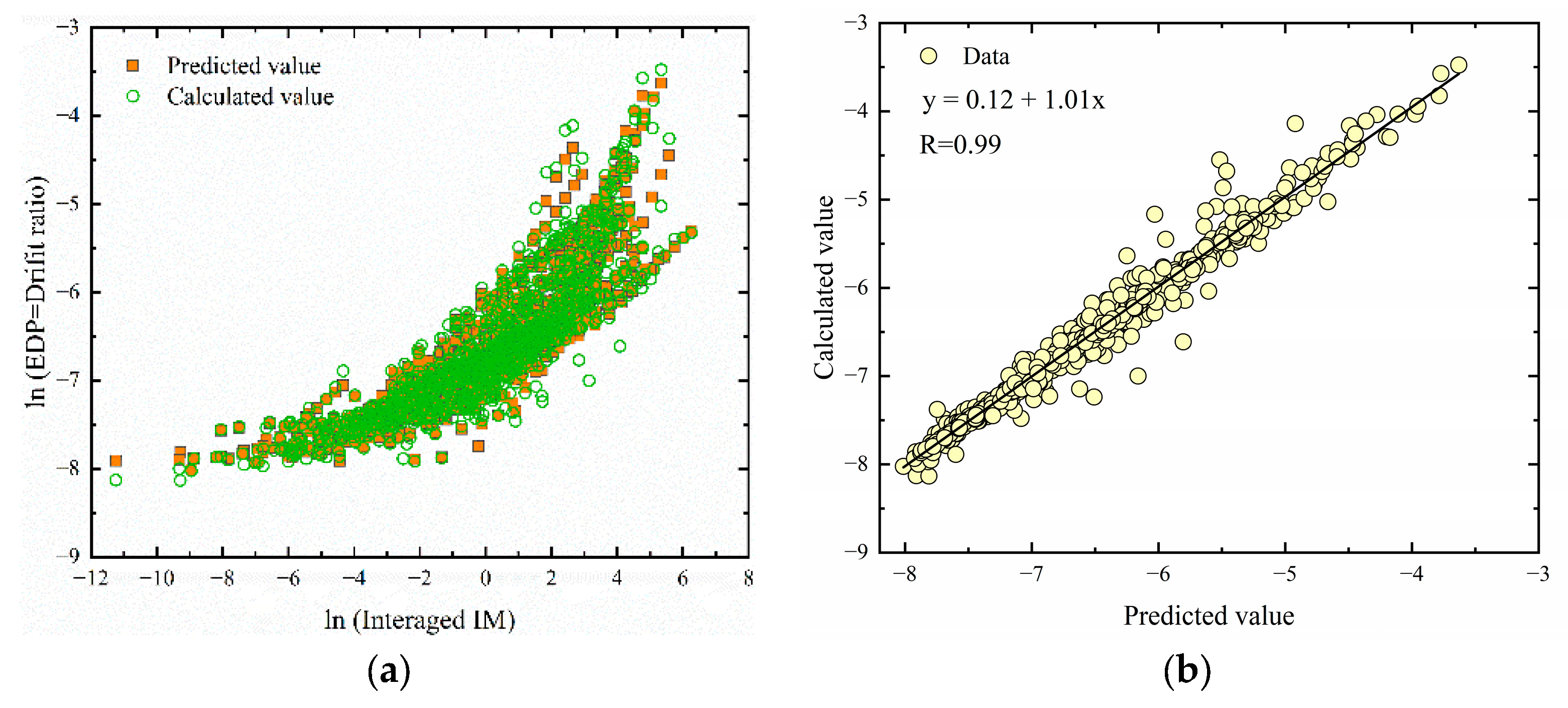
7.2. Traditional Trend Model and ML-PCA Predicted Model
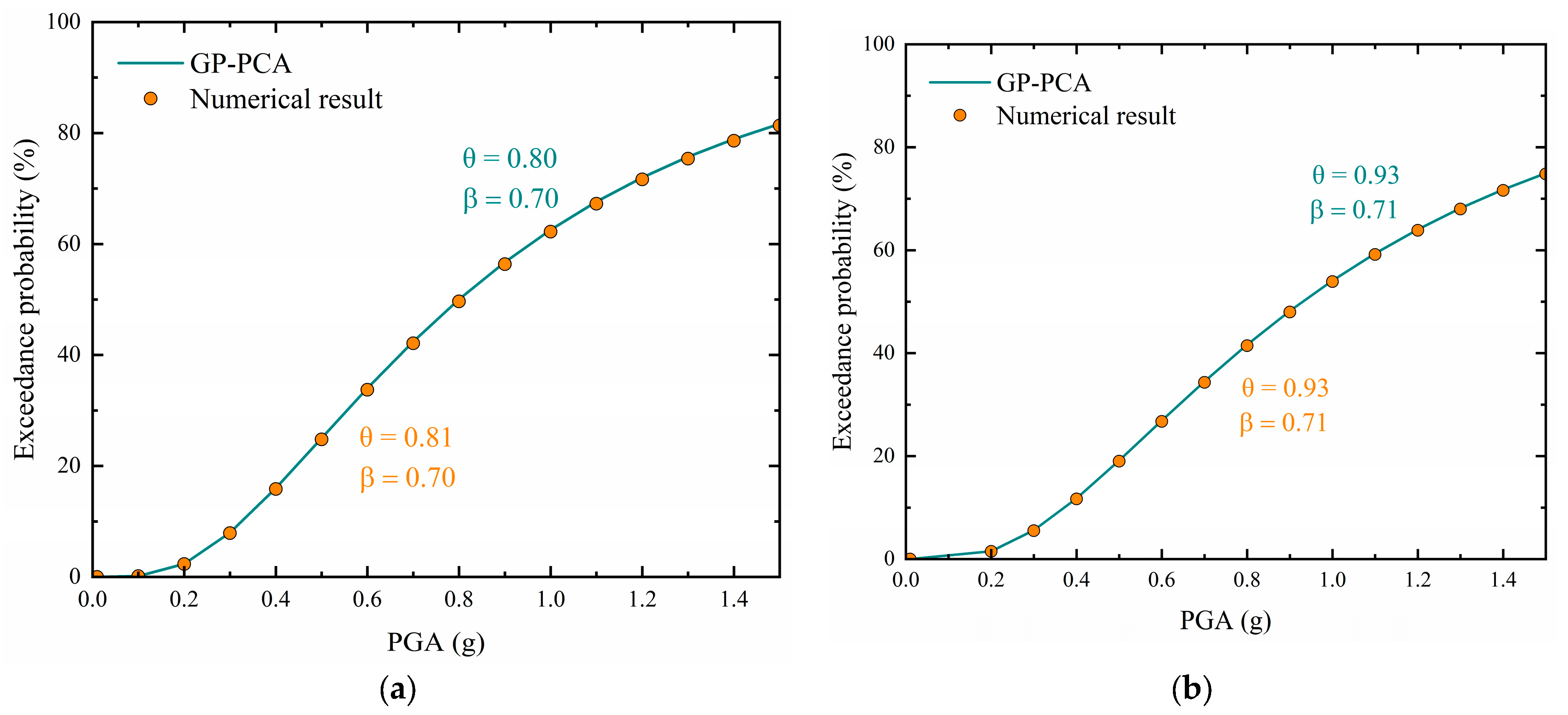
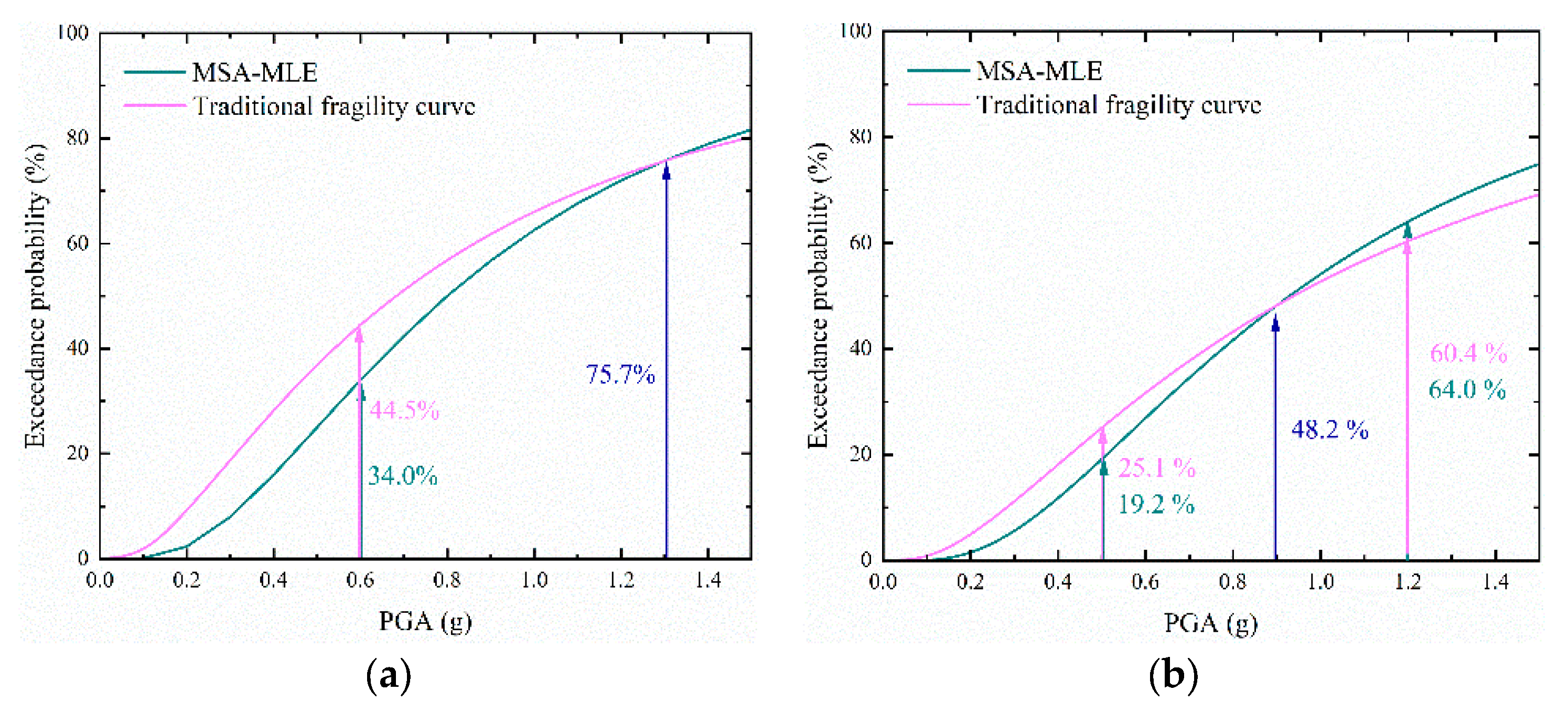
7.3. Fragility Analysis Utilizing the ML-PCA Model
8. Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hashash, Y.M.A.; Hook, J.J.; Schmidt, B.; Yao, J.I.C. Seismic design and analysis of underground structures. Tunn. Undergr. Sp. Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Li, T. Damage to mountain tunnels related to the Wenchuan earthquake and some suggestions for aseismic tunnel construction. Bull. Eng. Geol. Environ. 2012, 71, 297–308. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, B.; Yang, X.; Tao, S. Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after Wenchuan earthquake. Eng. Geol. 2014, 180, 85–98. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Xiao, M. Seismic damage assessment and mechanism analysis of underground powerhouse of the Yingxiuwan Hydropower Station under the Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2018, 113, 112–123. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Bobet, A.; Yuan, Y. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Sp. Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Baker, J.W. Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A.; Shome, N.; Carballo, J.E. Three proposals for characterizing MDOF nonlinear seismic response. J. Struct. Eng. 1998, 124, 1281–1289. [Google Scholar] [CrossRef]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Kim, T.; Song, J.; Kwon, O.-S. Probabilistic evaluation of seismic responses using deep learning method. Struct. Saf. 2020, 84, 101913. [Google Scholar] [CrossRef]
- Kiani, J.; Camp, C.; Pezeshk, S. On the application of machine learning techniques to derive seismic fragility curves. Comput. Struct. 2019, 218, 108–122. [Google Scholar] [CrossRef]
- Qin, S.; Cheng, Y.; Zhou, W.H. State-of-the-art review on pressure infiltration behavior of bentonite slurry into saturated sand for TBM tunneling. Smart Constr. Sustain. Cities 2023, 1, 14. [Google Scholar] [CrossRef]
- Huang, H.; Sun, Q.; Xu, T.; Zhou, W. Mechanism analysis of foam penetration in EPB shield tunnelling with a focus on FER and soil particle size. Undergr. Space 2024, 17, 170–187. [Google Scholar] [CrossRef]
- Sun, B.; Wang, P.X.; Deng, M.; Fang, H.; Xu, J.; Zhang, S.; Wang, C. Seismic performance assessment of hydraulic tunnels considering oblique incoming nonstationary stochastic SV waves based on the generalized PDEM. Tunn. Undergr. Space Technol. 2024, 143, 105481. [Google Scholar] [CrossRef]
- Sun, B.; Deng, M.; Zhang, S.; Liu, W.; Xu, J.; Wang, C.; Cui, W. Efficient Fragility Analysis of Cross-Fault Hydraulic Tunnels Combining Support Vector Machine and Improved Cloud Method. J. Earthq. Eng. 2024, 28, 2403–2421. [Google Scholar] [CrossRef]
- Jeddi, A.B.; Shafieezadeh, A.; Hur, J.; Ha, J.; Hahm, D.; Kim, M. Multi-hazard typhoon and earthquake collapse fragility models for transmission towers: An active learning reliability approach using gradient boosting classifiers. Earthq. Eng. Struct. Dyn. 2022, 51, 3552–3573. [Google Scholar] [CrossRef]
- Liu, C.; Macedo, J. Machine learning-based models for estimating seismically-induced slope displacements in subduction earthquake zones. Soil Dyn. Earthq. Eng. 2022, 160, 107323. [Google Scholar] [CrossRef]
- Huang, H.; Burton, H.V. Dynamic seismic damage assessment of distributed infrastructure systems using graph neural networks and semi-supervised machine learning. Adv. Eng. Softw. 2022, 168, 103113. [Google Scholar] [CrossRef]
- Kourehpaz, P.; Molina Hutt, C. Machine Learning for Enhanced Regional Seismic Risk Assessments. J. Struct. Eng. 2022, 148, 4022126. [Google Scholar] [CrossRef]
- Yu, X.; Wang, M.; Ning, C. A machine-learning-based two-step method for failure mode classification of reinforced concrete columns. J. Build. Struct. 2022, 43, 220. [Google Scholar]
- Morgenroth, J.; Khan, U.T.; Perras, M.A. An overview of opportunities for machine learning methods in underground rock engineering design. Geosciences 2019, 9, 504. [Google Scholar] [CrossRef]
- Chimunhu, P.; Topal, E.; Ajak, A.D.; Asad, W. A review of machine learning applications for underground mine planning and scheduling. Resour. Policy 2022, 77, 102693. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ibrahim, H.H.; Noori, K.M.G.; Abdulhamid, S.N.; Ali, H.F.H. Forecasting sidewall displacement of underground caverns using machine learning techniques. Autom. Constr. 2021, 123, 103530. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Hall, R. Using machine learning approach for microseismic events recognition in underground excavations: Comparison of ten frequently-used models. Eng. Geol. 2020, 268, 105519. [Google Scholar] [CrossRef]
- Hu, Z.; Wei, B.; Jiang, L.; Li, S.; Yu, Y.; Xiao, C. Assessment of optimal ground motion intensity measure for high-speed railway girder bridge (HRGB) based on spectral acceleration. Eng. Struct. 2022, 252, 113728. [Google Scholar] [CrossRef]
- Padgett, J.E.; Nielson, B.G.; DesRoches, R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–725. [Google Scholar] [CrossRef]
- Park, Y.-J.; Ang, A.H.-S.; Wen, Y.K. Seismic damage analysis of reinforced concrete buildings. J. Struct. Eng. 1985, 111, 740–757. [Google Scholar]
- Yan, Y.; Xia, Y.; Yang, J.; Sun, L. Optimal selection of scalar and vector-valued seismic intensity measures based on Gaussian Process Regression. Soil Dyn. Earthq. Eng. 2022, 152, 106961. [Google Scholar] [CrossRef]
- Sun, B.; Liu, W.; Deng, M.; Zhang, S.; Wang, C.; Guo, J.; Wang, J.; Wang, J. Compound intensity measures for improved seismic performance assessment in cross-fault hydraulic tunnels using partial least-squares methodology. Tunn. Undergr. Sp. Technol. 2023, 132, 104890. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar]
- Thompson, B. Stepwise regression and stepwise discriminant analysis need not apply here: A guidelines editorial. Educ. Psychol. Meas. 1995, 55, 525–534. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Myles, A.J.; Feudale, R.N.; Liu, Y.; Woody, N.A.; Brown, S.D. An introduction to decision tree modeling. J. Chemom. A J. Chemom. Soc. 2004, 18, 275–285. [Google Scholar] [CrossRef]
- Ellingwood, B. Validation studies of seismic PRAs. Nucl. Eng. Des. 1990, 123, 189–196. [Google Scholar] [CrossRef]
- Baker, J.W. Probabilistic structural response assessment using vector-valued intensity measures. Earthq. Eng. Struct. Dyn. 2007, 36, 1861–1883. [Google Scholar] [CrossRef]
- Sun, B.; Deng, M.; Zhang, S.; Wang, C.; Cui, W.; Li, Q.; Xu, J.; Zhao, X.; Yan, H. Optimal selection of scalar and vector-valued intensity measures for improved fragility analysis in cross-fault hydraulic tunnels. Tunn. Undergr. Sp. Technol. 2023, 132, 104857. [Google Scholar] [CrossRef]
- Nuttli, O.W. The Relation of Sustained Maximum Ground Acceleration and Velocity to Earthquake Intensity and Magnitude; US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1979. [Google Scholar]
- Dobry, R.; Idriss, I.M.; Ng, E. Duration characteristics of horizontal components of strong-motion earthquake records. Bull. Seismol. Soc. Am. 1978, 68, 1487–1520. [Google Scholar]
- Kramer, S.L. Geotechnical earthquake engineering. Bull. Earthq. Eng. 2013, 12, 1049–1070. [Google Scholar] [CrossRef]
- Arias, A. Measure of Earthquake Intensity; Massachusetts Institute of Technology: Cambridge, MA, USA; University of Chile: Santiago, Chile, 1970. [Google Scholar]
- Bolt, B.A. Duration of strong ground motion. In Proceedings of the 5th World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1973; pp. 1304–1313. [Google Scholar]
- Reed, J.W.; Kassawara, R.P. A criterion for determining exceedance of the operating basis earthquake. Nucl. Eng. Des. 1990, 123, 387–396. [Google Scholar] [CrossRef]
- Von Thun, J.L. Earthquake ground motions for design and analysis of dams Earthq. Eng. soil Dyn. II-recent Adv. Ground-Motion Eval. 1988, 20, 463–481. Available online: https://api.semanticscholar.org/CorpusID:132807569 (accessed on 30 July 2024).
- Housner, G.W. Spectrum Intensities of Strong-Motion Earthquakes; Earthquake Engineering Research Institute: Oakland, CA, USA, 1952. [Google Scholar]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Liu, J.B.; Du, Y.X.; Du, X. 3D viscous-spring artificial boundary in time domain. Earthq. Eng. Eng. Vib. 2006, 5, 93–102. [Google Scholar] [CrossRef]
- Wang, Z.; Pedroni, N.; Zentner, I.; Zio, E. Seismic fragility analysis with artificial neural networks: Application to nuclear power plant equipment. Eng. Struct. 2018, 162, 213–225. [Google Scholar] [CrossRef]
- Huang, P.; Chen, Z. Fragility analysis for subway station using artificial neural network. J. Earthq. Eng. 2021, 26, 6724–6744. [Google Scholar] [CrossRef]


| Type | Description | Symbol | Definition | Unit | Reference |
|---|---|---|---|---|---|
| Amplitude | Peak ground acceleration | PGA | g | - | |
| Peak ground velocity | PGV | m/s | - | ||
| Peak ground displacement | PGD | m | - | ||
| Sustained maximum acceleration | SMA | The third-largest absolute peak in the acceleration time history | m/s2 | [38] | |
| Sustained maximum velocity | SMV | The third-largest absolute peak in the velocity time history | m/s | [38] | |
| Integral | Acceleration root-mean-Square | Arms | g | [39] | |
| Velocity RMS | Vrms | m | [40] | ||
| Displacement RMS | Drms | m | [40] | ||
| Arias intensity | IA | m/s | [41] | ||
| Characteristic intensity | IC | - | [28] | ||
| Specific energy density | SED | m2/s | [42] | ||
| Cumulative absolute velocity | CAV | m/s | [43] | ||
| Frequency content | Acceleration spectrum Intensity | ASI | m*s | [44] | |
| Velocity spectrum intensity | VSI | m | [44] | ||
| Housner intensity | HI | m | [45] |
| IMs | Probabilistic Seismic Demand Models | Correlation Index (R) | |
|---|---|---|---|
| Peak ground acceleration (PGA) | −6.16 + 0.71ln(PGA) | 0.61 | 0.64 |
| Principal component analysis (PCA) | −6.61 + 0.24ln(Arms) | 0.42 | 0.85 |
| Gaussian process–principal component analysis (GP-PCA) | −6.61 + 0.24ln(Vrms) | 0.39 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Sun, B.; Deng, M.; Xu, J.; Wang, P. Application of an Improved Method Combining Machine Learning–Principal Component Analysis for the Fragility Analysis of Cross-Fault Hydraulic Tunnels. Buildings 2024, 14, 2608. https://doi.org/10.3390/buildings14092608
Xu Y, Sun B, Deng M, Xu J, Wang P. Application of an Improved Method Combining Machine Learning–Principal Component Analysis for the Fragility Analysis of Cross-Fault Hydraulic Tunnels. Buildings. 2024; 14(9):2608. https://doi.org/10.3390/buildings14092608
Chicago/Turabian StyleXu, Yan, Benbo Sun, Mingjiang Deng, Jia Xu, and Pengxiao Wang. 2024. "Application of an Improved Method Combining Machine Learning–Principal Component Analysis for the Fragility Analysis of Cross-Fault Hydraulic Tunnels" Buildings 14, no. 9: 2608. https://doi.org/10.3390/buildings14092608




