Study on Strength Model of Wastewater Concrete with Different Specimen Sizes under Freeze–Thaw Environment
Abstract
1. Introduction and Research
2. Raw Materials and Methods
2.1. Raw Material
2.2. Proportioning of Concrete
2.3. Test Method
2.3.1. Freeze–Thaw Cycle
2.3.2. Test Methods of Cube CS and STS
3. Test Results and Discussion
3.1. Appearance Changes
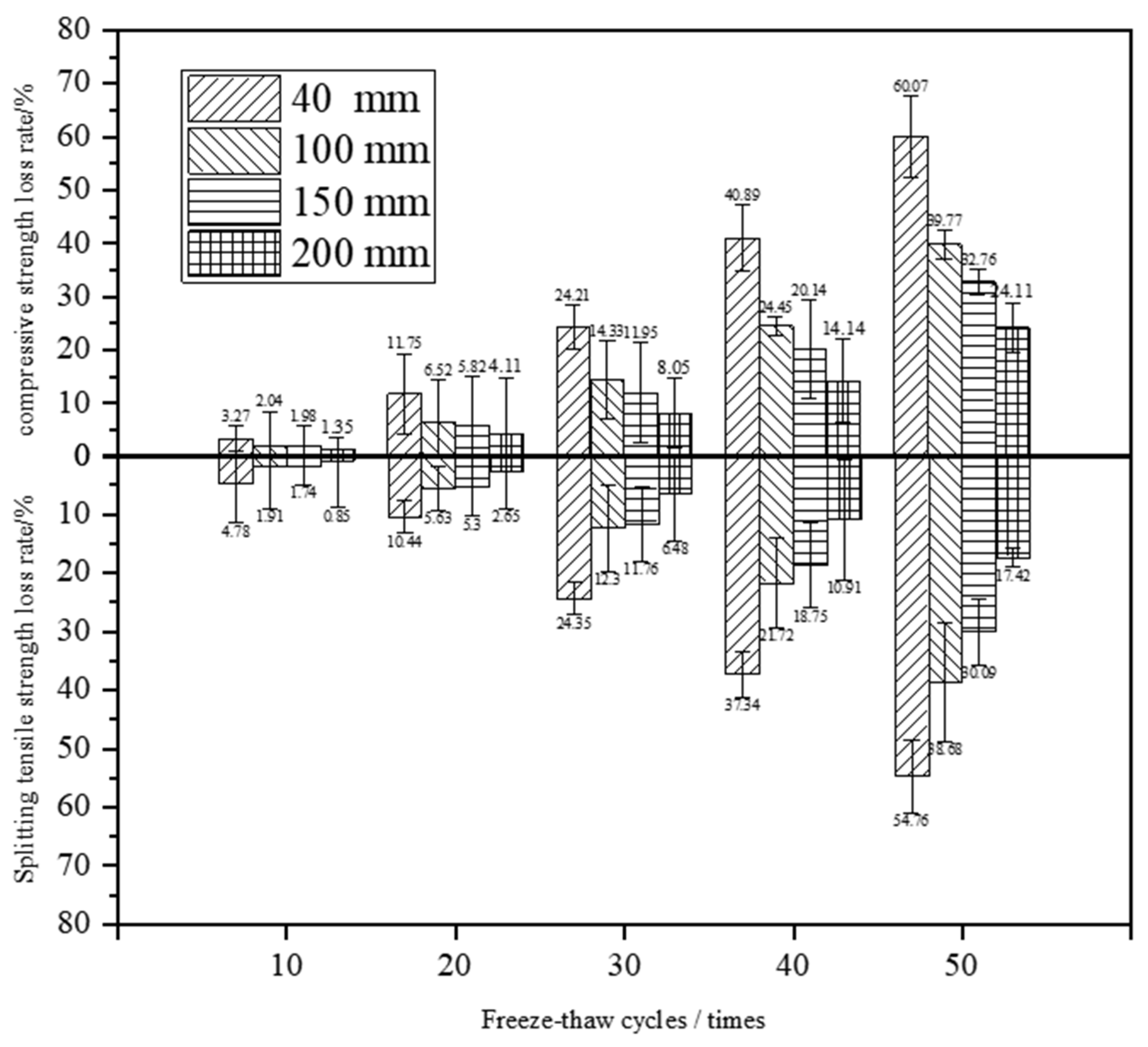
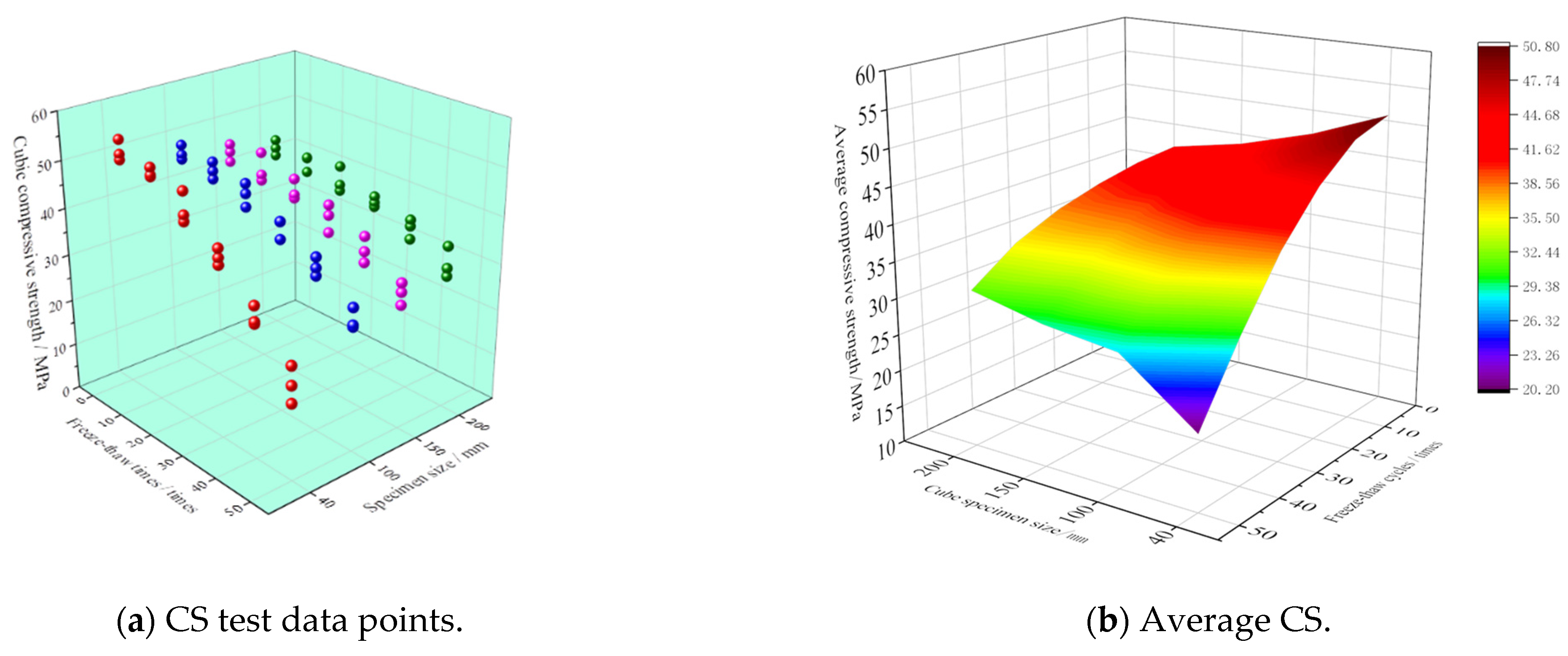
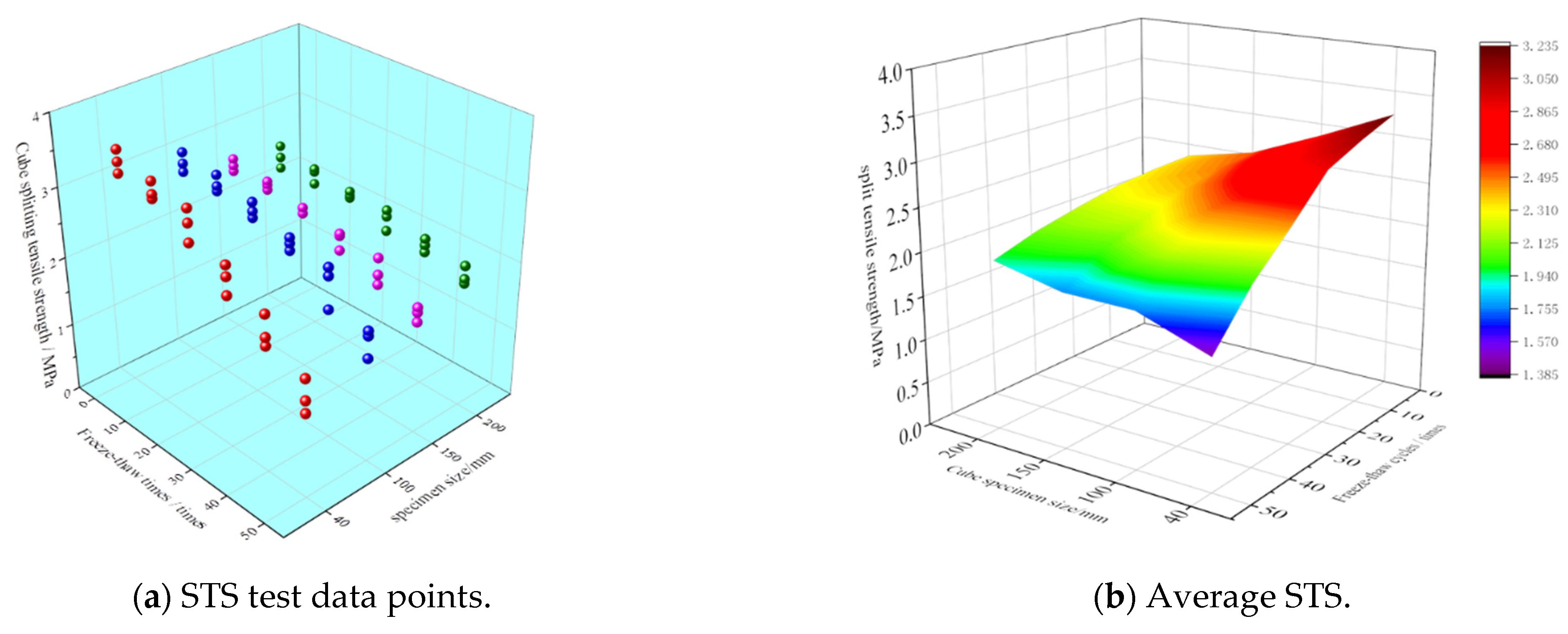
3.2. Cube CS and STS
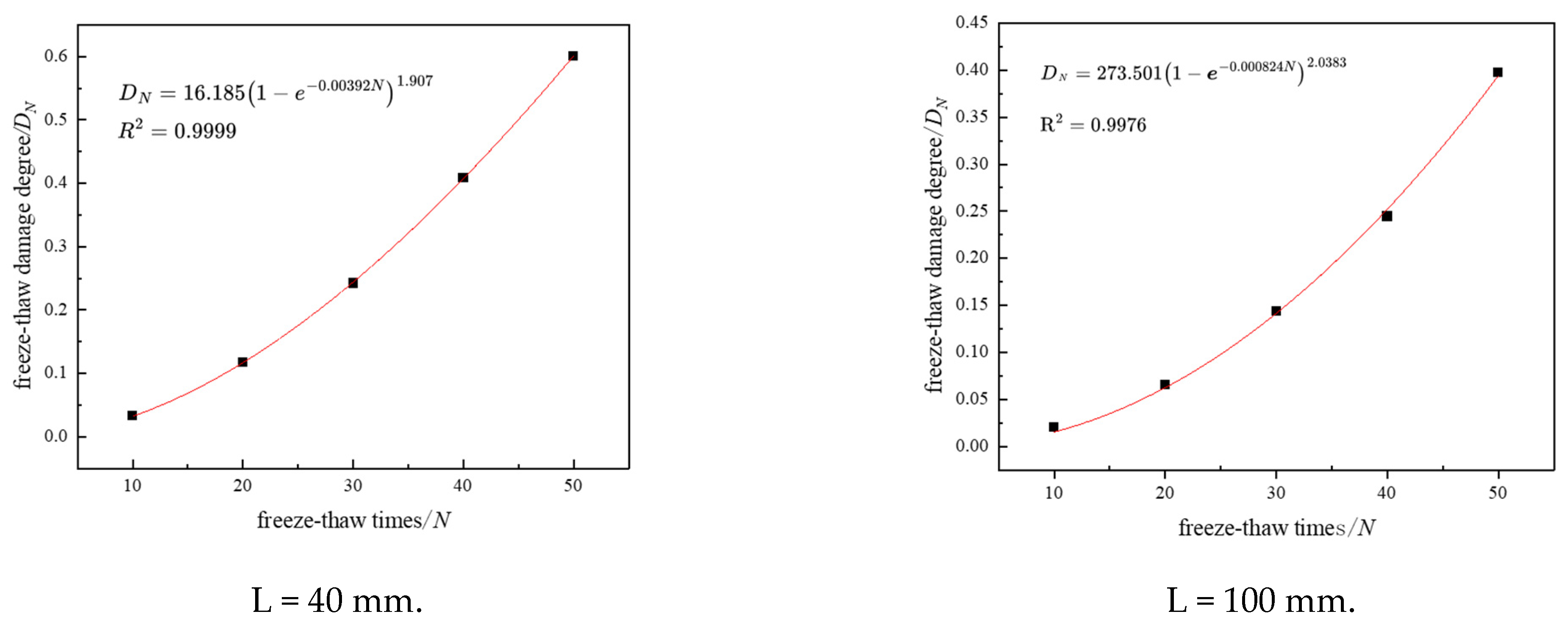
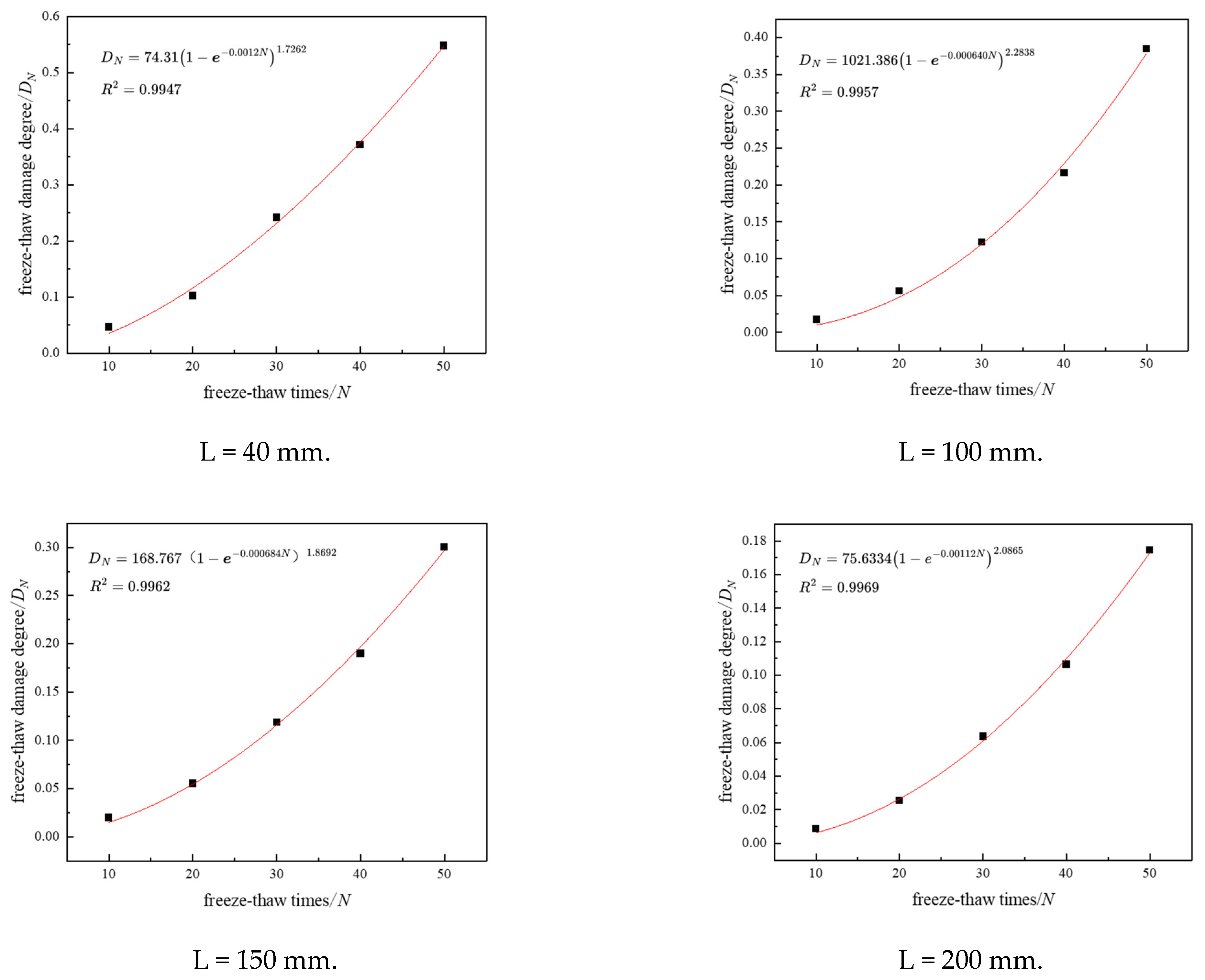
4. FTD Degree Model
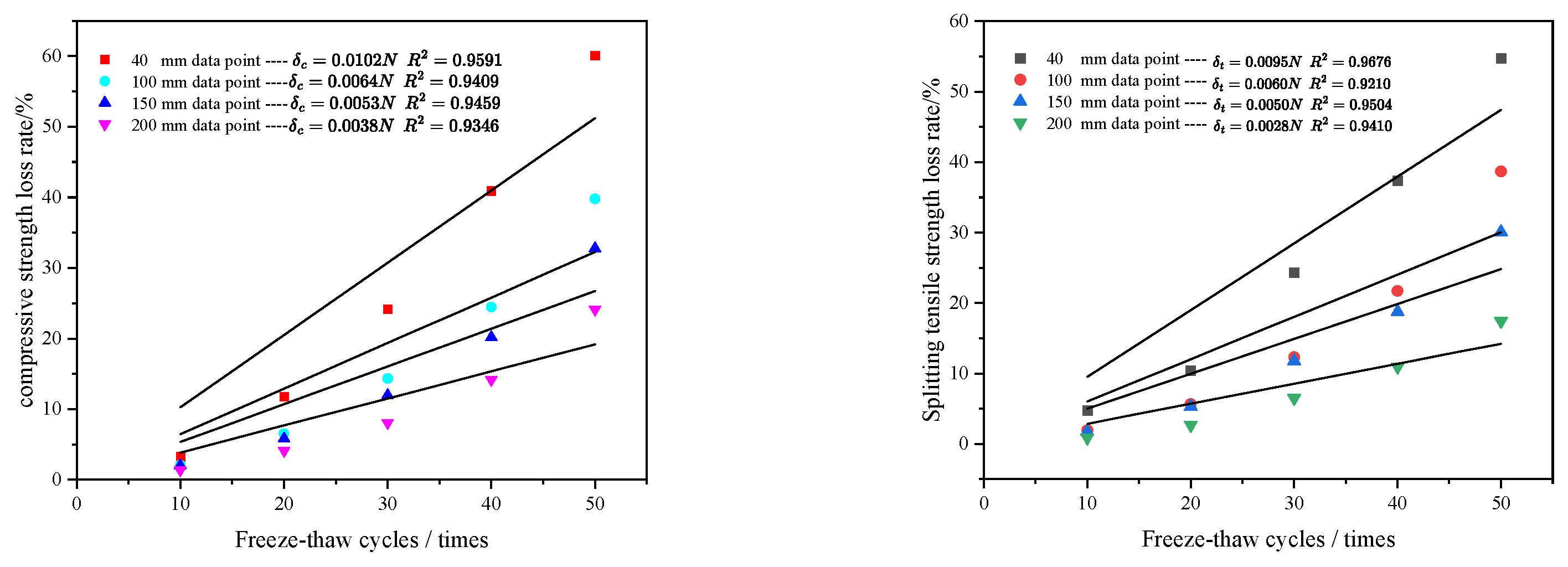
5. Strength Degeneracy Model
The Effect of FTCs and Specimen Size Coupling on CS
6. Conclusions and Prospect
- After 50 FTCs, the CS loss rates of cube specimens with side lengths of L = 40 mm, L = 100 mm, L = 150 mm, and L = 200 mm were 60.07%, 39.77%, 32.76%, and 24.11%, respectively. The loss rates of STS were 54.76%, 38.68%, 30.09%, and 17.42%, respectively.
- Based on the damage mechanics theory and the FTD model with CS and STS as damage variables, the FTD degree of concrete under the coupling effect of FTCs and specimen size can be accurately predicted.
- Based on the relationship between the CS and STS of concrete, the number of FTCs, and the size of the specimen, a concrete strength equation considering the coupling effect of the size change of the specimen and the number of FTCs was established.
- This model not only provides a scientific theoretical basis for evaluating the durability of WWC but also offers theoretical support for its application in practical engineering structures.
- In the study of mechanical properties and strength SEs of WWC in freeze–thaw environments, it is advisable to expand the range of specimen sizes to further validate and refine the results of this paper.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| FTCs | Freeze–thaw cycles |
| WWC | Wastewater concrete |
| SE | Size effect |
| CS | Compressive strength |
| STS | Splitting tensile strength |
| FTD | Freeze–thaw damage |
References
- Chen, Z.; Wu, C.; Luo, X.; Xu, W.; Liang, W.; Tang, Y. Spatio-temporal autogenous shrinkage and cracking behavior of core concrete in full-scale CFST: Insights from the world’s largest span arch bridge. Thin-Walled Struct. 2024, 200, 111899. [Google Scholar] [CrossRef]
- Huang, H.; Yan, S.; Wu, Z.; Zhou, Y.; Ni, K. Influence of wastewater of mixing station on concrete performance and recycling. Concrete 2020, 11, 157–160. (In Chinese) [Google Scholar] [CrossRef]
- He, T.; Li, X.; Wang, F.; Zhu, W.; Bai, F. Influence of Wastewater in Concrete Plant on Compressive Strength of C80 Concrete with Different Mineral Admixtures. Bull. Chin. Ceram. Soc. 2011, 30, 384–388. (In Chinese) [Google Scholar] [CrossRef]
- Chen, X.; Wu, J.; Ning, Y.; Zhang, W. Experimental study on the effect of wastewater and waste slurry of mixing plant on mechanical properties and microstructure of concrete. J. Build. Eng. 2022, 52, 104307. [Google Scholar] [CrossRef]
- Aruntaş, H.Y.; Nallı, E.; Kaplan, G. Usage of ready-mixed concrete plant wastewater in concrete with superplasticizer: Effect on physico-mechanical properties. Constr. Build. Mater. 2022, 348, 128641. [Google Scholar] [CrossRef]
- Yao, X.; Xu, Z.; Guan, J.; Liu, L.; Shangguan, L.; Xi, J. Influence of Wastewater Content on Mechanical Properties, Microstructure, and Durability of Concrete. Buildings 2022, 12, 1343. [Google Scholar] [CrossRef]
- Ye, J.; Yu, J.; Cui, C.; Wang, Y. Flexural size effect of ultra-high ductile concrete under different damage and ductility levels. Cem. Concr. Compos. 2021, 115, 103852. [Google Scholar] [CrossRef]
- Yang, H.T.; Tian, S.Z. Influence of size effect on the performance of recycled concrete. J. Cent. S. Univ. (Sci. Technol.) 2016, 47, 3818–3823. (In Chinese) [Google Scholar] [CrossRef]
- Zhu, C.; Liu, X.; Li, W.; Wu, Y.; Liu, Q. Study of freeze-thaw durability and damage model of hybrid fiber concrete. Ind. Constr. 2015, 45, 10–14. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.; Gu, X.; Xia, X.; Madenci, E.; Chen, A.; Zhang, Q. Peridynamic simulation of micro-internal damage and macro-mechanical properties of cement paste under freeze-thaw cycles. J. Build. Eng. 2024, 93, 109759. [Google Scholar] [CrossRef]
- Lu, J.; Liu, J.; Yang, H.; Wan, X.; Gao, J.; Zhang, J.; Li, P. Experimental investigation on the mechanical properties and pore structure deterioration of fiber-reinforced concrete in different freeze-thaw media. Constr. Build. Mater. 2022, 350, 128887. [Google Scholar] [CrossRef]
- Wan, X.; Hu, Q.; Liao, M. Salt crystallization in cold sulfate saline soil. Cold Reg. Sci. Technol. 2017, 137, 36–47. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Deng, X.; Sun, B.; Zhao, Y.; Fu, W. Coupled thermal model of wellbore and permafrost in Arctic regions. Appl. Therm. Eng. 2017, 123, 1291–1299. [Google Scholar] [CrossRef]
- Huang, K.L.; Song, Y.; Sheng, Y.M. Rainstorm Resistance of Recycled Pervious Concrete under the Coupling of Fatigue and Freeze–Thaw Cycles. Buildings 2024, 14, 294. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Q.; Teng, J.H.; Deng, P.; Sun, Y. Bond Performance of Anti-Corrosion Bar Embedded in Ceramsite Concrete in Freeze–Thaw Cycles and Corrosive Environments. Buildings 2023, 13, 884. [Google Scholar] [CrossRef]
- Chen, P.; Liu, C.; Wang, Y. Size effect on peak axial strain and stress-strain behavior of concrete subjected to axial compression. Constr. Build. Mater. 2018, 188, 645–655. [Google Scholar] [CrossRef]
- Guan, J.; Liu, L.; Yao, X.; Meng, J.; Han, L. Study on the strength size effect of wastewater concrete under freeze-thaw cycles. Constr. Build. Mater. 2024, 438, 137074. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, H.; Gong, X.; Wu, C.; Ma, H. Size effect on tensile strength of interface between coarse aggregate and mortar under freeze-thaw cycle. J. Build. Eng. 2023, 75, 106939. [Google Scholar] [CrossRef]
- GB175-2007; Common Portland Cement. Standardization Administration of the People’s Republic of China: Beijing, China, 2007.
- SL/T 352-2020; Test Code for Hydraulic Concrete. Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2020. (In Chinese)
- Xi, J.Y.; Li, X.; Yao, X.H.; Guan, J.F.; Shangguan, L.J.; Liu, L.J.; Xu, Z.W. Effect of Wastewater from Concrete Mixing Plant on Frost esistance of C60 Concrete. J. N. China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2023, 44, 69–75. (In Chinese) [Google Scholar] [CrossRef]



| Fineness Modulus | Soil Content | Bulk Density | Apparent Density |
|---|---|---|---|
| 2.6 | 0.8% | 1470 kg/m3 | 2650 kg/m3 |
| Grain Size | Apparent Density | Bulk Density | Soil Content | Crush Value |
|---|---|---|---|---|
| 5–20 mm | 2710 kg/m3 | 1630 kg/m3 | 0.47% | 10.1% |
| Chemical Composition | CaO | SiO2 | Al2O3 | MgO | Fe2O3 | SO3 | K2O | Na2O |
|---|---|---|---|---|---|---|---|---|
| Wt% | 41.95 | 32.64 | 13.24 | 3.7 | 3.63 | 1.74 | 1.24 | 0.524 |
| Strength Grade | Concrete Mix Ratio | ||||||
|---|---|---|---|---|---|---|---|
| Wastewater | Potable Water | Cement | Sand | Crushed Stone (5~20 mm) | Fly Ash | Water-Reducing Admixture | |
| C40 | 135 | 45 | 344 | 805 | 1095 | 84 | 15 |
| Specimen Number | CS Value of WWC under Different FTCs/MPa | |||||
|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | |
| 40—1 | 49.00 | 48.69 | 42.31 | 36.86 | 32.35 | 16.45 |
| 40—2 | 53.20 | 50.28 | 43.64 | 38.34 | 28.66 | 20.17 |
| 40—3 | 50.15 | 48.39 | 48.49 | 40.27 | 29.05 | 24.22 |
| Average value | 50.78 | 49.12 | 44.81 | 38.49 | 30.02 | 20.28 |
| 100—1 | 45.32 | 45.64 | 43.84 | 41.24 | 33.42 | 26.65 |
| 100—2 | 48.38 | 43.95 | 41.05 | 37.52 | 37.29 | 30.64 |
| 100—3 | 46.30 | 47.56 | 45.97 | 41.17 | 35.07 | 27.03 |
| Average value | 46.67 | 45.72 | 43.62 | 39.98 | 35.26 | 28.11 |
| 150—1 | 45.46 | 46.35 | 39.48 | 35.24 | 34.55 | 31.54 |
| 150—2 | 41.62 | 40.36 | 43.58 | 38.92 | 37.73 | 26.88 |
| 150—3 | 43.80 | 41.58 | 40.20 | 41.10 | 32.24 | 29.59 |
| Average value | 43.63 | 42.77 | 41.09 | 38.42 | 34.84 | 29.34 |
| 200—1 | 43.36 | 42.16 | 37.70 | 37.24 | 33.42 | 35.23 |
| 200—2 | 39.90 | 38.95 | 43.00 | 39.42 | 36.20 | 28.89 |
| 200—3 | 41.55 | 42.01 | 38.97 | 38.10 | 37.53 | 30.60 |
| Average value | 41.60 | 41.04 | 39.89 | 38.25 | 35.72 | 31.57 |
| Specimen Number | STS Value of WWC under Different FTCs/MPa | |||||
|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | |
| 40—1 | 3.40 | 2.98 | 3.12 | 2.64 | 2.28 | 1.73 |
| 40—2 | 3.23 | 3.22 | 2.92 | 2.48 | 1.96 | 1.24 |
| 40—3 | 3.07 | 3.04 | 2.65 | 2.22 | 1.84 | 1.42 |
| Average value | 3.23 | 3.08 | 2.90 | 2.45 | 2.03 | 1.46 |
| 100—1 | 3.01 | 2.71 | 2.82 | 2.42 | 2.48 | 1.52 |
| 100—2 | 2.85 | 2.94 | 2.60 | 2.52 | 2.36 | 1.84 |
| 100—3 | 2.73 | 2.78 | 2.69 | 2.60 | 1.89 | 1.91 |
| Average value | 2.86 | 2.81 | 2.70 | 2.51 | 2.24 | 1.76 |
| 150—1 | 2.52 | 2.42 | 2.42 | 2.08 | 2.26 | 1.65 |
| 150—2 | 2.44 | 2.49 | 2.42 | 2.32 | 1.88 | 1.86 |
| 150—3 | 2.62 | 2.54 | 2.34 | 2.29 | 2.02 | 1.79 |
| Average value | 2.53 | 2.48 | 2.39 | 2.23 | 2.05 | 1.77 |
| 200—1 | 2.52 | 2.42 | 2.28 | 2.33 | 2.00 | 2.09 |
| 200—2 | 2.35 | 2.20 | 2.34 | 2.03 | 2.10 | 1.90 |
| 200—3 | 2.19 | 2.38 | 2.25 | 2.24 | 2.19 | 1.84 |
| Average value | 2.35 | 2.33 | 2.29 | 2.20 | 2.10 | 1.94 |
| Type | Specimen Size/mm | Strength Loss Rate under Different FTCs/% | ||||
|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | ||
| CS | 40 | 3.27 | 11.75 | 24.21 | 40.89 | 60.07 |
| 100 | 2.04 | 6.52 | 14.33 | 24.45 | 39.77 | |
| 150 | 1.98 | 5.82 | 11.95 | 20.14 | 32.76 | |
| 200 | 1.35 | 4.11 | 8.05 | 14.14 | 24.11 | |
| STS | 40 | 4.78 | 10.44 | 24.35 | 37.34 | 54.76 |
| 100 | 1.91 | 5.63 | 12.30 | 21.72 | 38.68 | |
| 150 | 1.74 | 5.30 | 11.76 | 18.75 | 30.09 | |
| 200 | 0.85 | 2.65 | 6.48 | 10.91 | 17.42 | |
| Specimen Size | CS Loss Rate δc | STS Loss Rate δt | ||
|---|---|---|---|---|
| Relational Expression | R2 | Relational Expression | R2 | |
| 40 | δc = 0.0102 N | 0.9591 | δt = 0.0095 N | 0.9676 |
| 100 | δc = 0.0064 N | 0.9409 | δt = 0.0060 N | 0.9210 |
| 150 | δc = 0.0053 N | 0.9459 | δt = 0.0050 N | 0.9504 |
| 200 | δc = 0.0038 N | 0.9346 | δt = 0.0028 N | 0.9410 |
| Specimen Size/mm | Characteristic Parameter | ||
|---|---|---|---|
| a | b | R2 | |
| 40 | 16.185 | 1.907 | 0.9999 |
| 100 | 273.501 | 2.038 | 0.9976 |
| 150 | 334.218 | 1.978 | 0.9955 |
| 200 | 539.045 | 2.119 | 0.9914 |
| Specimen Size/mm | Characteristic Parameter | ||
|---|---|---|---|
| a | b | R2 | |
| 40 | 74.311 | 1.726 | 0.9947 |
| 100 | 1021.386 | 2.284 | 0.9957 |
| 150 | 168.767 | 1.869 | 0.9962 |
| 200 | 75.633 | 2.087 | 0.9969 |
| Specimen Size /mm | FTCs/Times | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | |||||||||||
| T | C | T/C | T | C | T/C | T | C | T/C | T | C | T/C | T | C | T/C | |
| 40 mm | 0.033 | 0.032 | 1.03 | 0.118 | 0.117 | 1.01 | 0.242 | 0.244 | 0.99 | 0.409 | 0.408 | 1.00 | 0.601 | 0.602 | 1.00 |
| 100 mm | 0.020 | 0.015 | 1.33 | 0.065 | 0.062 | 1.05 | 0.143 | 0.141 | 1.01 | 0.244 | 0.252 | 0.97 | 0.398 | 0.394 | 1.01 |
| 150 mm | 0.020 | 0.014 | 1.43 | 0.039 | 0.054 | 0.72 | 0.119 | 0.120 | 0.99 | 0.201 | 0.209 | 0.96 | 0.328 | 0.323 | 1.02 |
| 200 mm | 0.013 | 0.008 | 1.63 | 0.041 | 0.035 | 1.17 | 0.081 | 0.081 | 1.00 | 0.141 | 0.149 | 0.95 | 0.241 | 0.237 | 1.02 |
| Specimen Size /mm | FTCs/Times | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | |||||||||||
| T | C | T/C | T | C | T/C | T | C | T/C | T | C | T/C | T | C | T/C | |
| 40 mm | 0.046 | 0.036 | 1.28 | 0.102 | 0.116 | 0.88 | 0.241 | 0.232 | 1.04 | 0.372 | 0.377 | 0.99 | 0.548 | 0.549 | 1.00 |
| 100 mm | 0.017 | 0.010 | 1.70 | 0.056 | 0.048 | 1.17 | 0.122 | 0.120 | 1.02 | 0.217 | 0.230 | 0.94 | 0.385 | 0.380 | 1.01 |
| 150 mm | 0.020 | 0.015 | 1.33 | 0.055 | 0.055 | 1.00 | 0.119 | 0.116 | 1.03 | 0.190 | 0.197 | 0.96 | 0.300 | 0.297 | 1.01 |
| 200 mm | 0.009 | 0.006 | 1.50 | 0.026 | 0.027 | 0.96 | 0.064 | 0.061 | 1.05 | 0.106 | 0.111 | 0.95 | 0.174 | 0.174 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Liu, S.; Meng, J.; Shangguan, L.; Chen, S. Study on Strength Model of Wastewater Concrete with Different Specimen Sizes under Freeze–Thaw Environment. Buildings 2024, 14, 2922. https://doi.org/10.3390/buildings14092922
Yao X, Liu S, Meng J, Shangguan L, Chen S. Study on Strength Model of Wastewater Concrete with Different Specimen Sizes under Freeze–Thaw Environment. Buildings. 2024; 14(9):2922. https://doi.org/10.3390/buildings14092922
Chicago/Turabian StyleYao, Xianhua, Shiwen Liu, Jiangfeng Meng, Linjian Shangguan, and Shengqiang Chen. 2024. "Study on Strength Model of Wastewater Concrete with Different Specimen Sizes under Freeze–Thaw Environment" Buildings 14, no. 9: 2922. https://doi.org/10.3390/buildings14092922
APA StyleYao, X., Liu, S., Meng, J., Shangguan, L., & Chen, S. (2024). Study on Strength Model of Wastewater Concrete with Different Specimen Sizes under Freeze–Thaw Environment. Buildings, 14(9), 2922. https://doi.org/10.3390/buildings14092922







