Physically Guided Estimation of Vehicle Loading-Induced Low-Frequency Bridge Responses with BP-ANN
Abstract
:1. Introduction
2. Methodologies
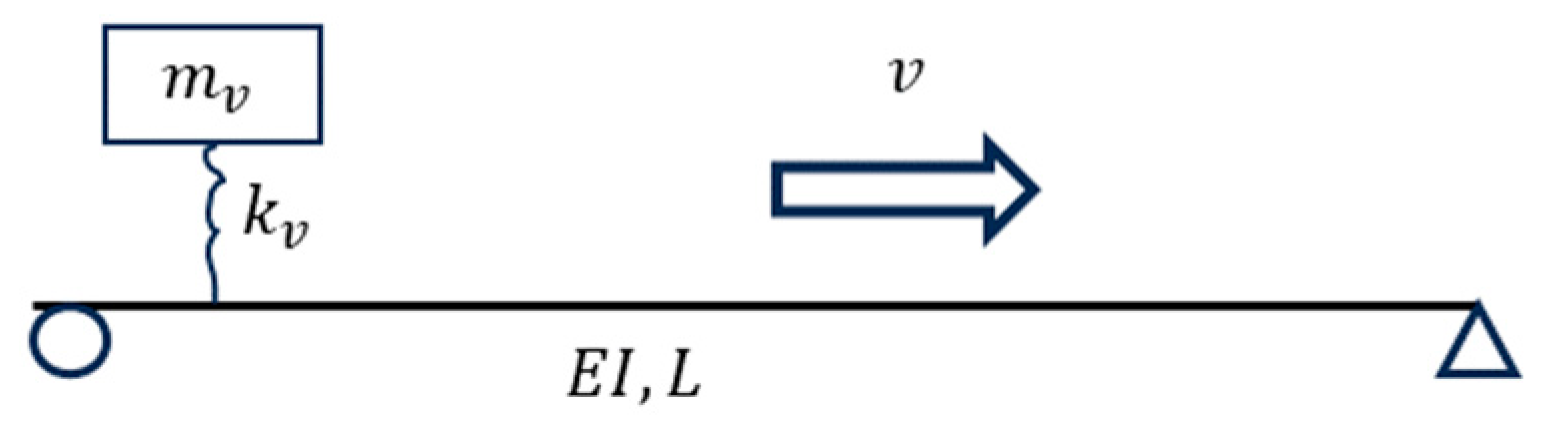
2.1. Dynamics of a Typical VBI System
2.1.1. Dynamic Equations and Modal Responses
2.1.2. Time Lag in Low-Frequency Bridge Displacement
2.1.3. Intersectional Relationship for the Simple VBI System
2.1.4. From a Simple Model to a General Bridge Structure
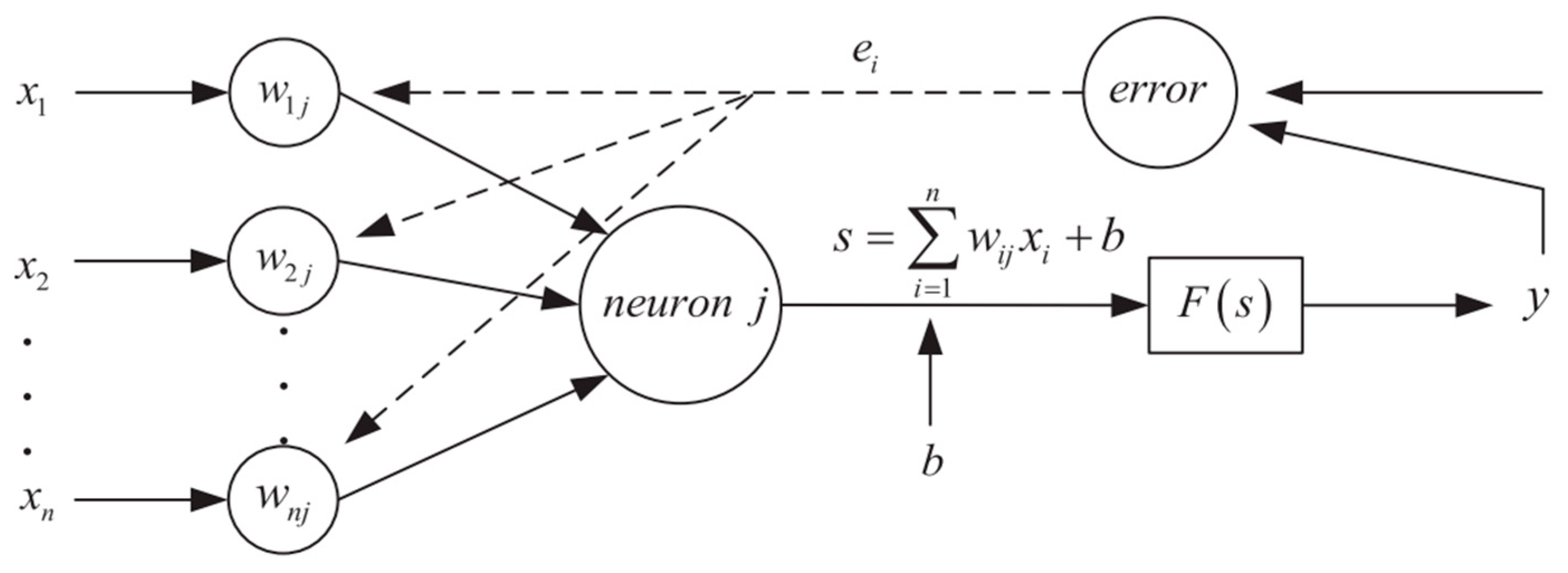
2.2. BP-ANN for Intersection Responses Prediction
3. Numerical Analysis
3.1. Numerical Models
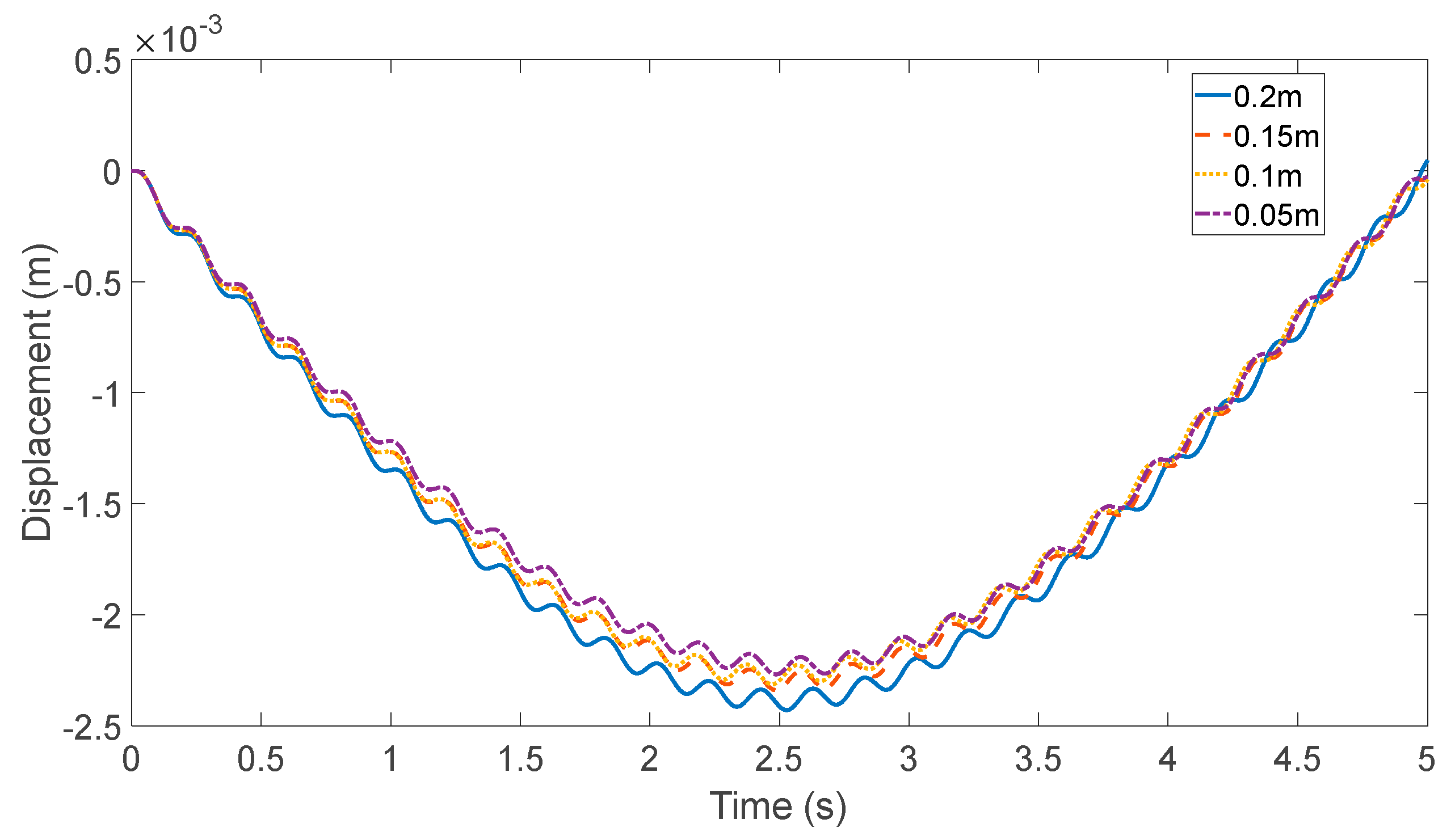
3.2. Cases’ Configuration
- (1)
- Reference case, where the moving speed was set to 5 m/s;
- (2)
- High-speed case, where the moving speed was set to 10 m/s;
- (3)
- Half-mass vehicle case, where the sprung mass was half that of the reference case;
- (4)
- Dual-vehicle case: The half-mass vehicle and the reference vehicle were running on the beam simultaneously. The high-frequency vehicle was moving at a speed of 3 m/s, while the reference vehicle was moving at a speed of 5 m/s.
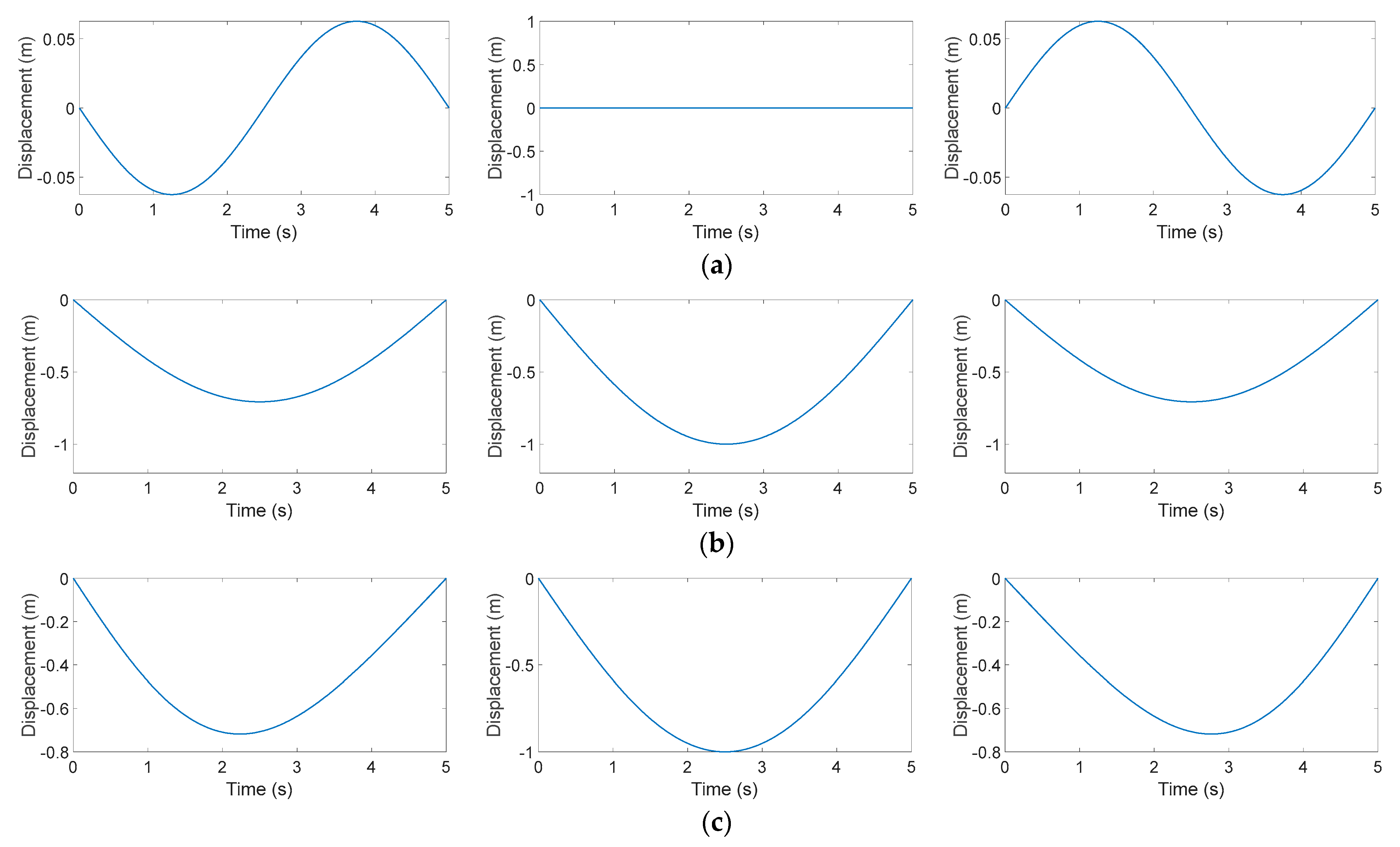
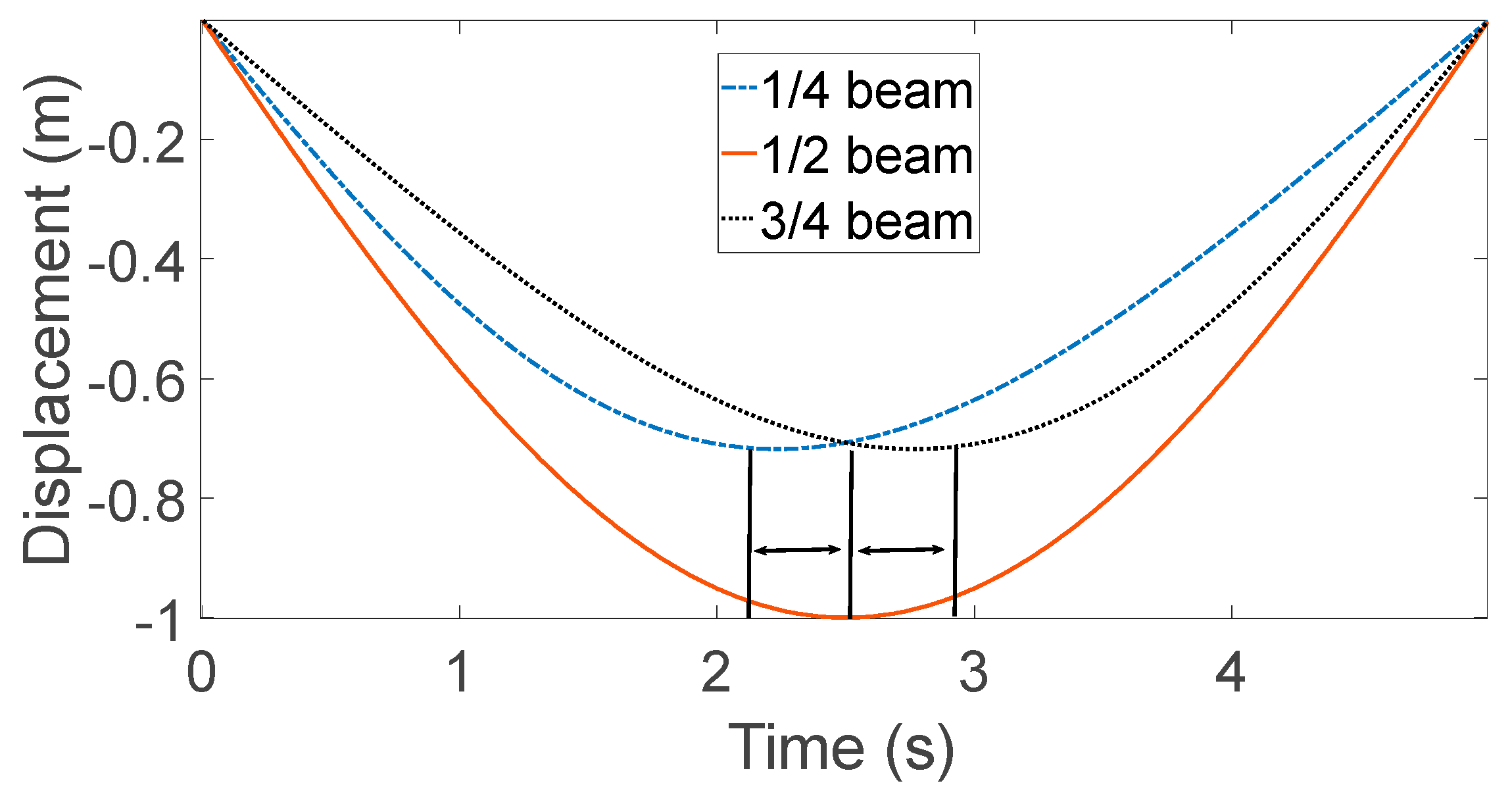
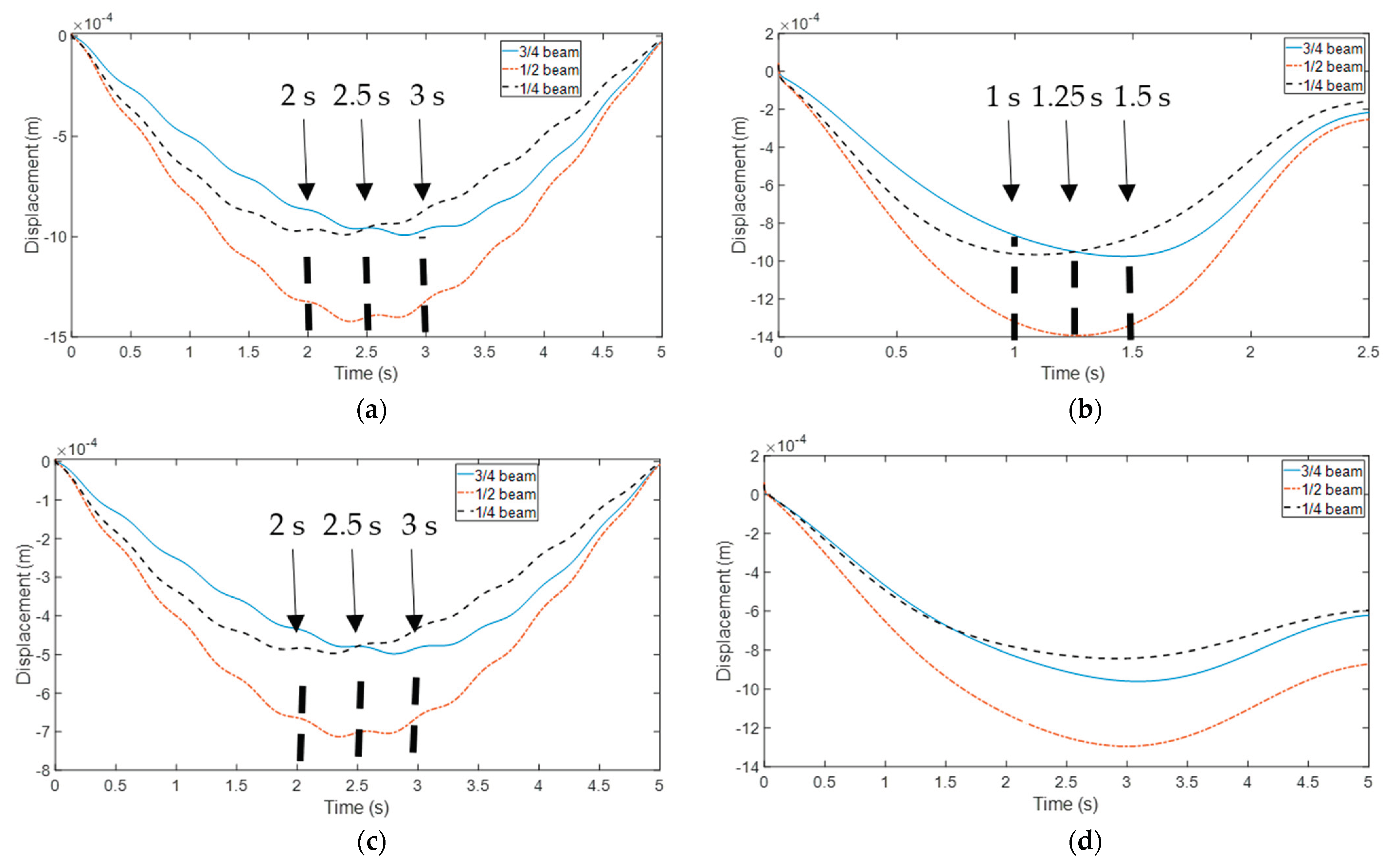
3.3. Simulation Result Analysis
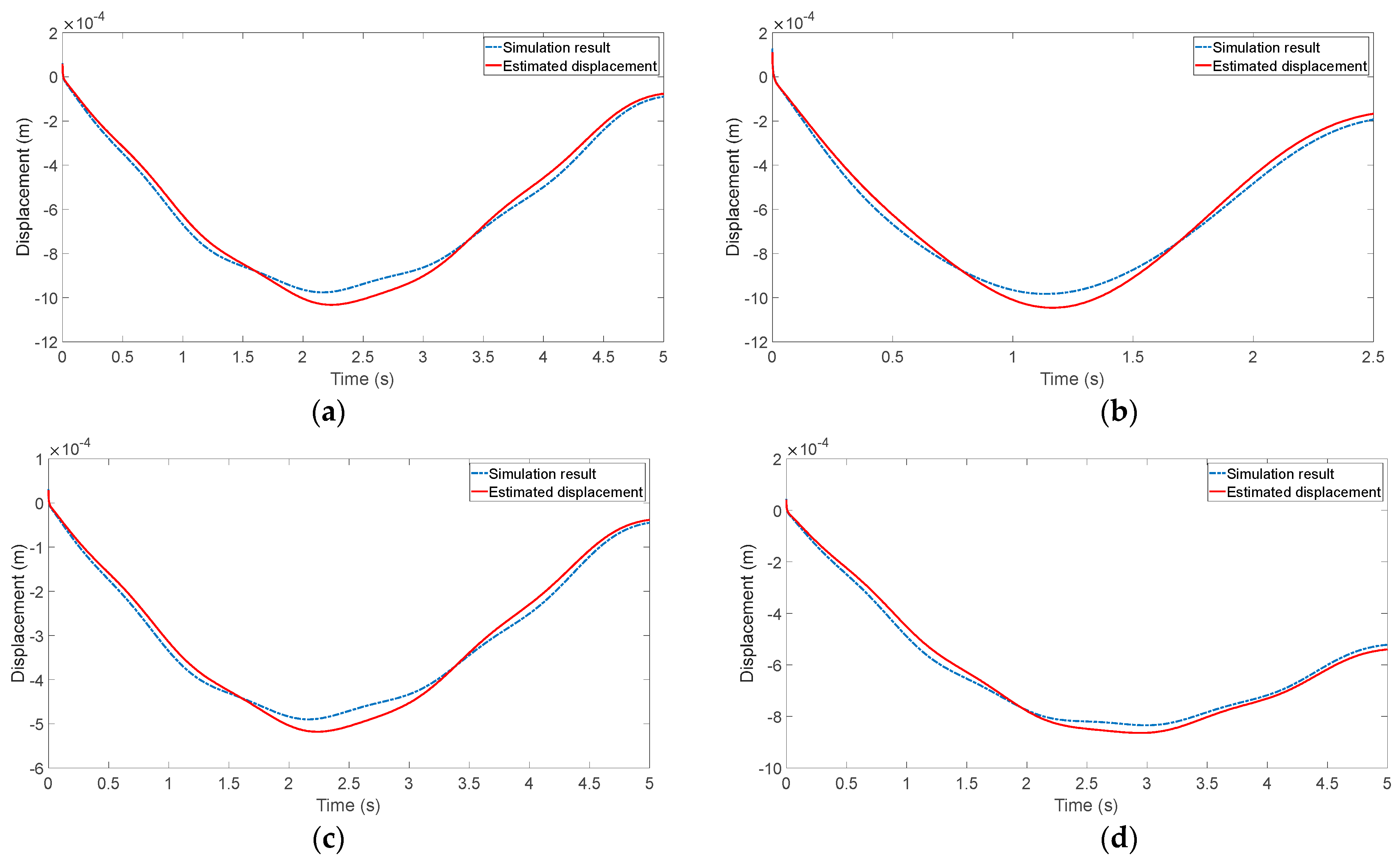
3.4. Validation of the BP-ANN with the Simulation Data
4. Validation with Field Test on a Continuous Bridge
4.1. Target Bridge and SHM System
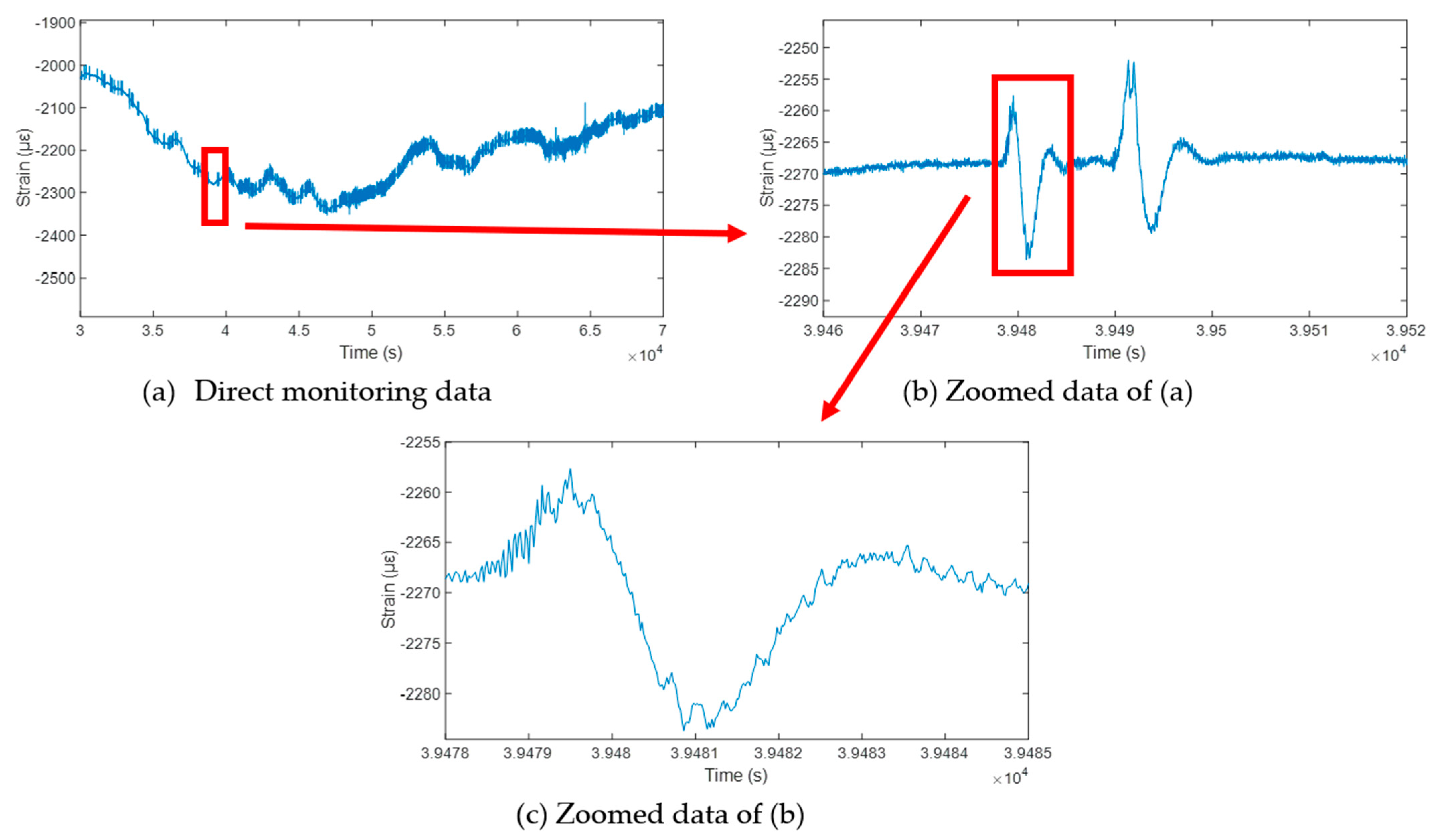
4.2. Monitoring Data
4.3. Scenarios and Data Configuration
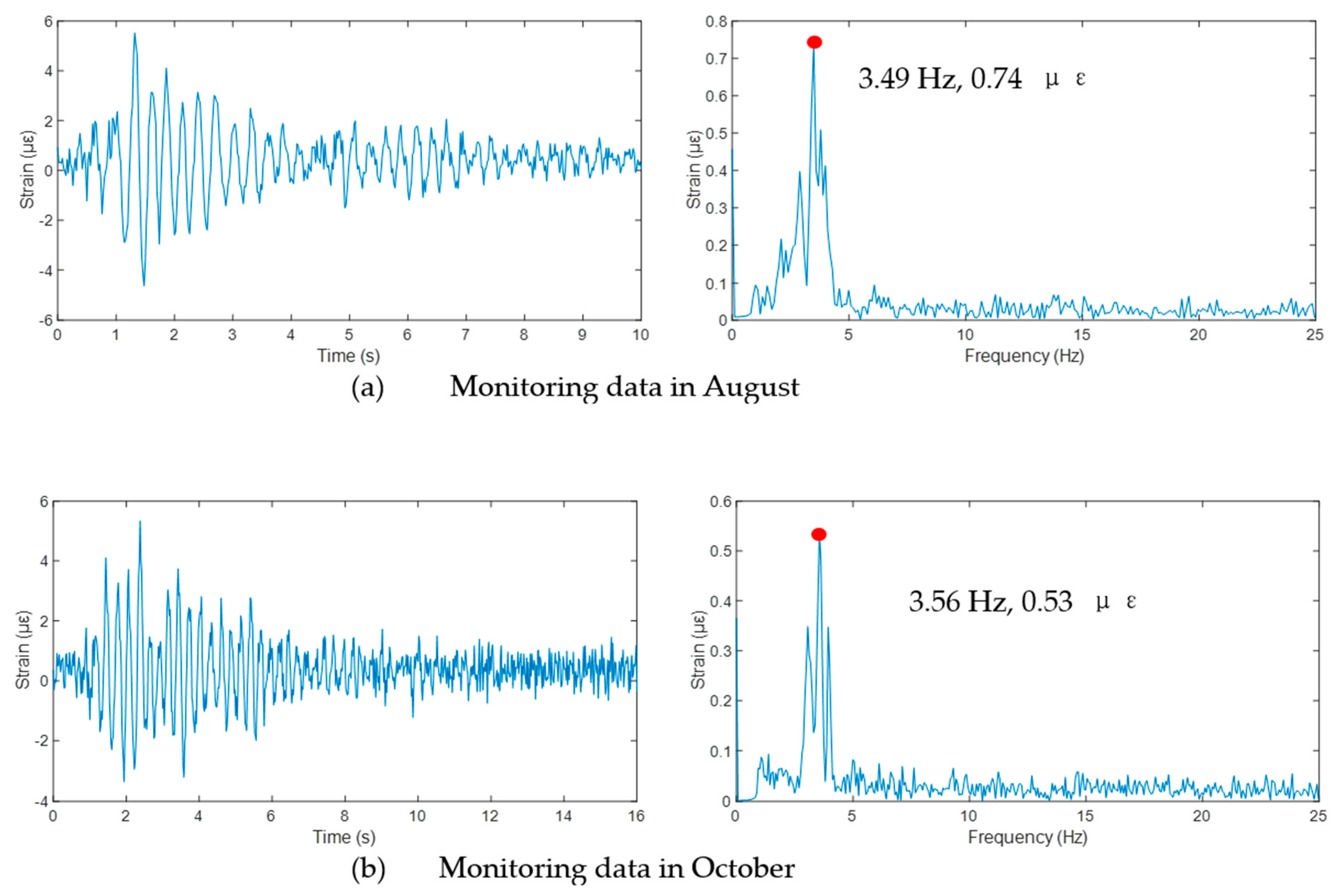
4.3.1. Confirmation of Time Lag, Random Traffic Condition, and Temperature Effect
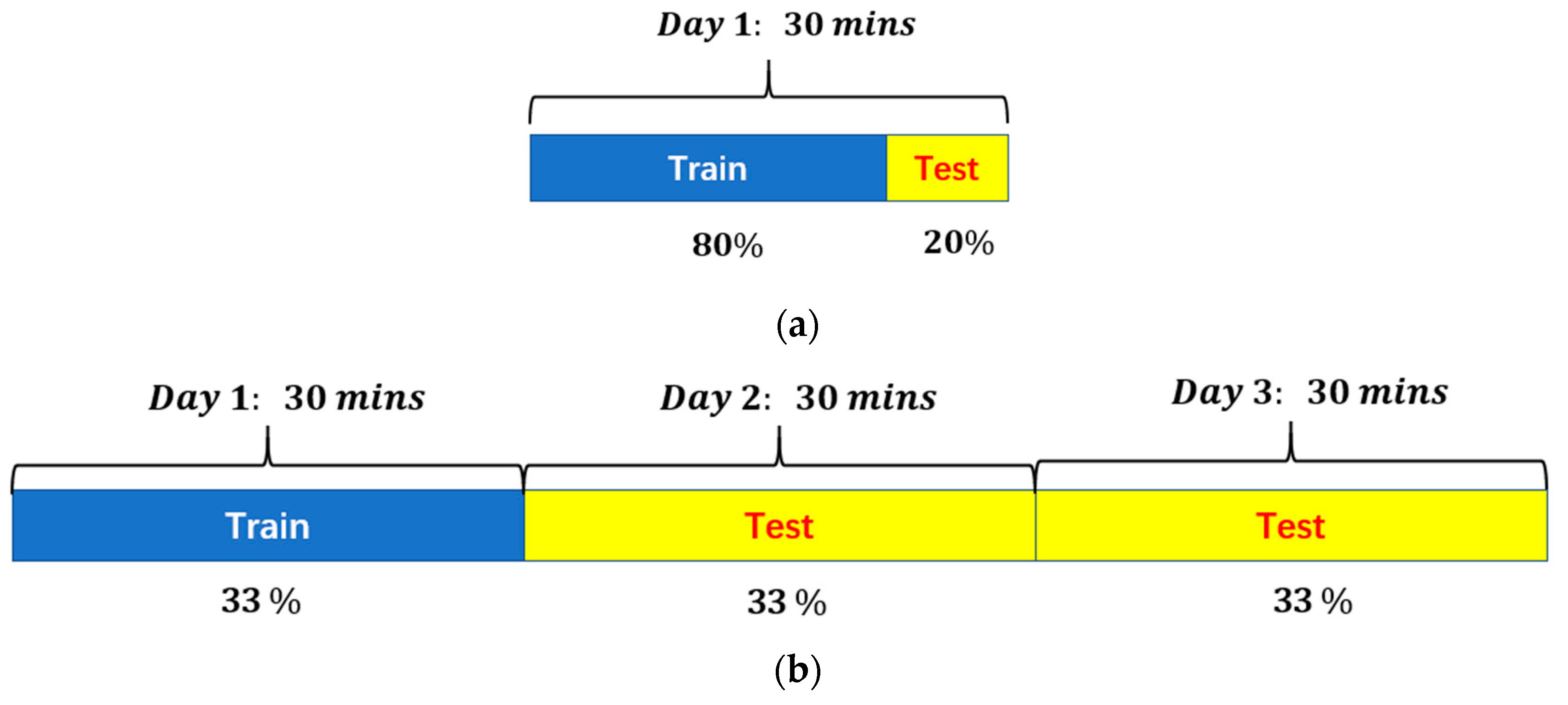
4.3.2. Case Configuration
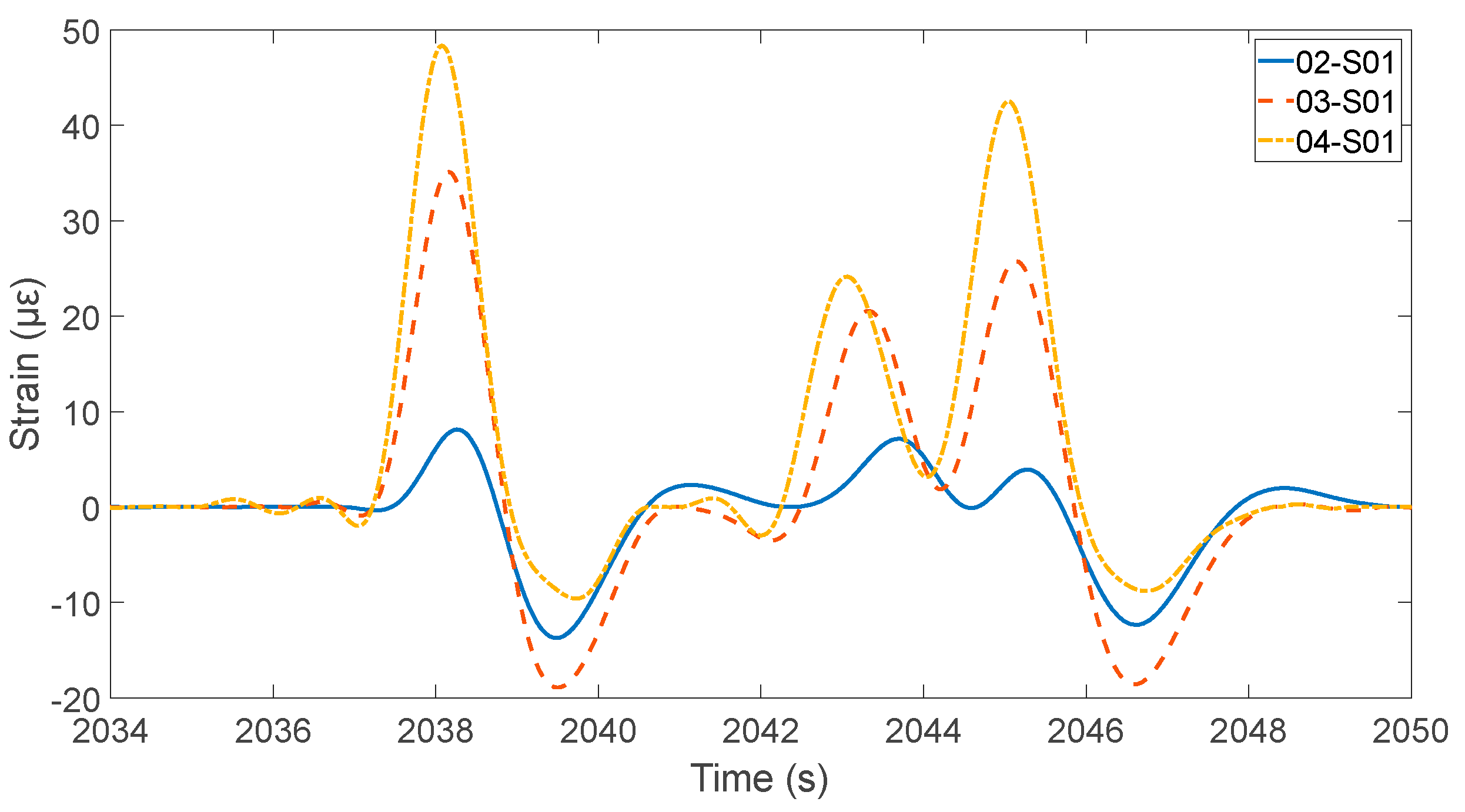
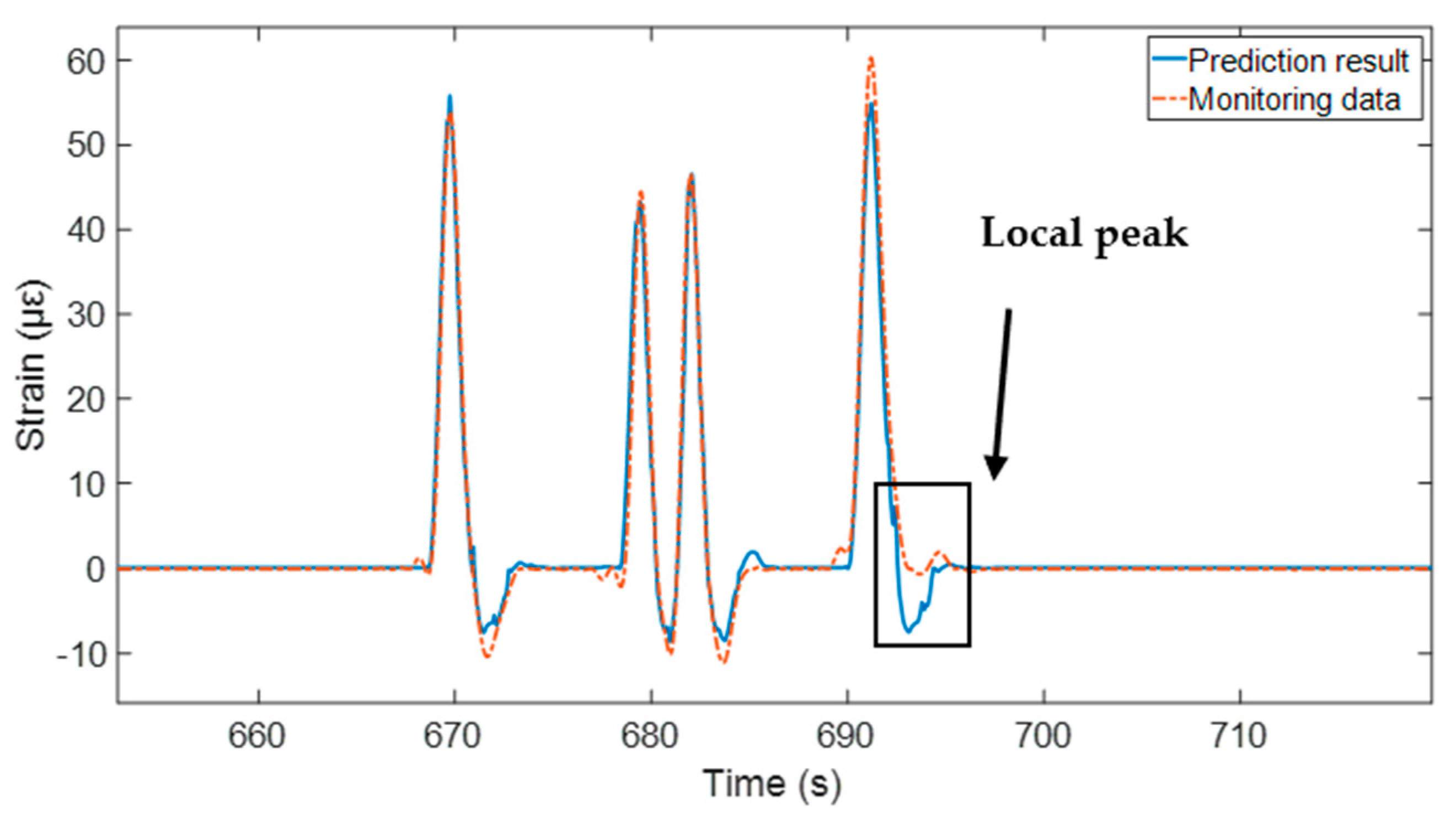
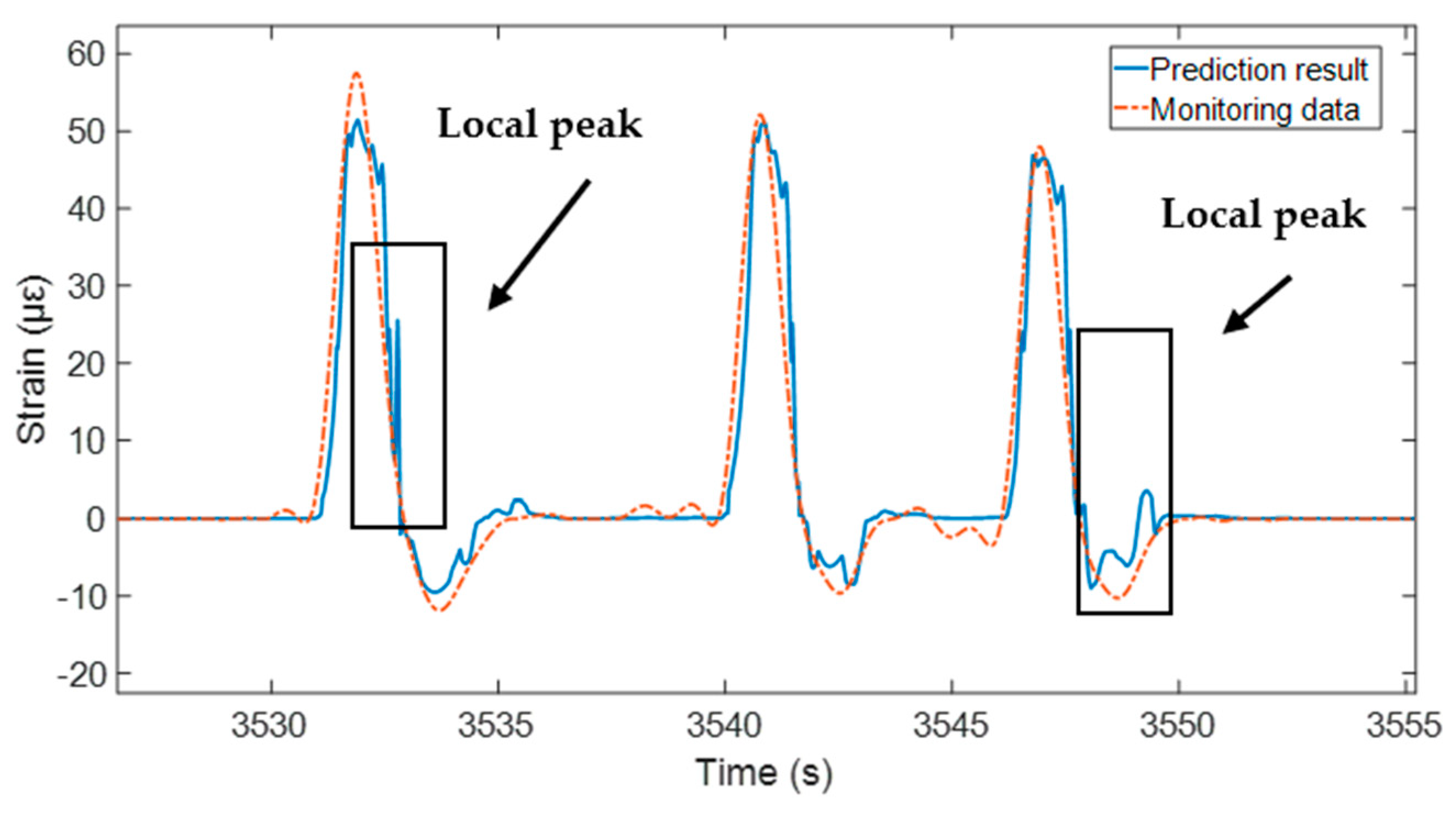
4.4. Result Discussion
5. Conclusions
- (1)
- A theoretical analysis established that, for typical highway VBI systems, the commonly employed “quasi-static” approach to bridge responses closely approximates low-frequency responses, which are primarily dictated by the driving force modes. More significantly, the target strain–vehicle interaction relationship is time-independent. Specifically, the transfer matrix is solely dependent on the bridge’s mode shapes, and it remains constant across varying temperature and traffic conditions.
- (2)
- Finite element simulations were initially conducted to validate the physical characteristics of the transfer matrix. It was confirmed that the transfer matrix remains stable under fluctuating traffic conditions, including variations in vehicle mass, quantity, and speed. Furthermore, the robustness of the proposed method was demonstrated through tests involving artificially introduced noise in the simulation data.
- (3)
- In the field tests, the proposed method was validated across two scenarios. Despite varying and unknown traffic conditions and temperatures, the method exhibited excellent performance. The estimated low-frequency responses were found to align well with the monitoring data. Additionally, it was demonstrated that the proposed method has the potential to construct an effective estimation model for long-term monitoring, utilizing a small data set collected over a short monitoring period.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Main Symbols and Abbreviations
| Vehicle mass. | |
| Spring stiffness. | |
| Vehicle vertical displacement. | |
| Vertical bridge displacement. | |
| Bridge unit mass. | |
| E | Material elastic modulus. |
| Moment of inertia of the beam cross-section. | |
| Interaction force. | |
| Modal shapes. | |
| Time-domain coordinate. | |
| Weight and bias of the (k + 1)-th iteration. | |
| Learning rate. | |
| The error between the true value and the simulated result. | |
| Bridge strain. |
References
- Tian, Y.; Xu, Y.; Zhang, D.; Li, H. Relationship Modeling between Vehicle-Induced Girder Vertical Deflection and Cable Tension by BiLSTM Using Field Monitoring Data of a Cable-Stayed Bridge. Struct. Control Health Monit. 2021, 28, e2667. [Google Scholar] [CrossRef]
- Oh, B.K.; Yoo, S.H.; Park, H.S. A Measured Data Correlation-Based Strain Estimation Technique for Building Structures Using Convolutional Neural Network. Integr. Comput. Aided Eng. 2023, 30, 395–412. [Google Scholar] [CrossRef]
- Lu, L.-J.; Zhou, H.-F.; Ni, Y.-Q.; Dai, F. Output-Only Modal Analysis for Non-Synchronous Data Using Stochastic Sub-Space Identification. Eng. Struct. 2021, 230, 111702. [Google Scholar] [CrossRef]
- Dosiek, L.; Zhou, N.; Pierre, J.W.; Huang, Z.; Trudnowski, D.J. Mode Shape Estimation Algorithms under Ambient Conditions: A Comparative Review. IEEE Trans. Power Syst. 2013, 28, 779–787. [Google Scholar] [CrossRef]
- Poncelet, F.; Kerschen, G.; Golinval, J.-C.; Verhelst, D. Output-Only Modal Analysis Using Blind Source Separation Techniques. Mech. Syst. Signal Process 2007, 21, 2335–2358. [Google Scholar] [CrossRef]
- Zhou, W.; Chelidze, D. Blind Source Separation Based Vibration Mode Identification. Mech. Syst. Signal Process 2007, 21, 3072–3087. [Google Scholar] [CrossRef]
- Xiao, F.; Sun, H.; Mao, Y.; Chen, G.S. Damage Identification of Large-Scale Space Truss Structures Based on Stiffness Separation Method. Structures 2023, 53, 109–118. [Google Scholar] [CrossRef]
- Xiao, F.; Yan, Y.; Meng, X.; Mao, Y.; Chen, G.S. Parameter Identification of Multispan Rigid Frames Using a Stiffness Separation Method. Sensors 2024, 24, 1884. [Google Scholar] [CrossRef]
- Gulgec, N.S.; Takáč, M.; Pakzad, S.N. Structural Sensing with Deep Learning: Strain Estimation from Acceleration Data for Fatigue Assessment. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 1349–1364. [Google Scholar] [CrossRef]
- Xu, W.; Shi, X. Machine-Learning-Based Predictive Models for Punching Shear Strength of FRP-Reinforced Concrete Slabs: A Comparative Study. Buildings 2024, 14, 2492. [Google Scholar] [CrossRef]
- Cheng, M.-C.; Bonopera, M.; Leu, L.-J. Applying Random Forest Algorithm for Highway Bridge-Type Prediction in Areas with a High Seismic Risk. J. Chin. Inst. Eng. 2024, 47, 597–610. [Google Scholar] [CrossRef]
- Li, S.; Liang, Z.; Guo, P. A FBG Pull-Wire Vertical Displacement Sensor for Health Monitoring of Medium-Small Span Bridges. Measurement 2023, 211, 112613. [Google Scholar] [CrossRef]
- Hidehiko, S.; Kosaku, K.; Chitoshi, M. Simplified Portable Bridge Weigh-in-Motion System Using Accelerometers. J. Bridge Eng. 2018, 23, 04017124. [Google Scholar] [CrossRef]
- Breccolotti, M.; Natalicchi, M. Bridge Damage Detection through Combined Quasi-Static Influence Lines and Weigh-in-Motion Devices. Int. J. Civ. Eng. 2022, 20, 487–500. [Google Scholar] [CrossRef]
- Zhao, H.; Uddin, N.; O’Brien, E.J.; Shao, X.; Zhu, P. Identification of Vehicular Axle Weights with a Bridge Weigh-in-Motion System Considering Transverse Distribution of Wheel Loads. J. Bridge Eng. 2014, 19, 04013008. [Google Scholar] [CrossRef]
- Yu, E.; Wei, H.; Han, Y.; Hu, P.; Xu, G. Application of Time Series Prediction Techniques for Coastal Bridge Engineering. Adv. Bridge Eng. 2021, 2, 6. [Google Scholar] [CrossRef]
- Hochreiter, S.; Jürgen, S. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Albawi, S.; Bayat, O.; Al-Azawi, S.; Ucan, O.N.; Lefevre, E. Social Touch Gesture Recognition Using Convolutional Neural Network. Intell. Neurosci. 2018, 2018, 6973103. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Zhao, H.; Ding, Y.; Li, A.; Sheng, W.; Geng, F. Digital Modeling on the Nonlinear Mapping between Multi-Source Monitoring Data of in-Service Bridges. Struct. Control Health Monit. 2020, 27, e2618. [Google Scholar] [CrossRef]
- Xin, J.; Zhou, C.; Jiang, Y.; Tang, Q.; Yang, X.; Zhou, J. A Signal Recovery Method for Bridge Monitoring System Using TVFEMD and Encoder-Decoder Aided LSTM. Measurement 2023, 214, 112797. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y. Bridge Weigh-in-motion Through Bidirectional Recurrent Neural Network with Long Short-term Memory and Attention Mechanism. Smart Struct. Syst. 2021, 27, 241–256. [Google Scholar]
- Li, Y.; Ni, P.; Sun, L.; Zhu, W. A Convolutional Neural Network-Based Full-Field Response Reconstruction Framework with Multitype Inputs and Outputs. Struct. Control Health Monit. 2022, 29, e2961. [Google Scholar] [CrossRef]
- Pamuncak, A.P.; Salami, M.R.; Adha, A.; Budiono, B.; Laory, I. Estimation of Structural Response Using Convolutional Neural Network: Application to the Suramadu Bridge. Eng. Comput. 2021, 38, 4047–4065. [Google Scholar] [CrossRef]
- Du, B.; Wu, L.; Sun, L.; Xu, F.; Li, L. Heterogeneous Structural Responses Recovery Based on Multi-Modal Deep Learning. Struct. Health Monit. 2023, 22, 799–813. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, C.; Jiang, J.; Shu, J.; Sun, L.; Zhang, Z. A Data-Driven Based Response Reconstruction Method of Plate Structure with Conditional Generative Adversarial Network. Sensors 2023, 23, 6750. [Google Scholar] [CrossRef]
- Zhuang, Y.; Qin, J.; Chen, B.; Dong, C.; Xue, C.; Easa, S.M. Data Loss Reconstruction Method for a Bridge Weigh-in-Motion System Using Generative Adversarial Networks. Sensors 2022, 22, 858. [Google Scholar] [CrossRef]
- Fan, G.; Li, J.; Hao, H.; Xin, Y. Data Driven Structural Dynamic Response Reconstruction Using Segment Based Generative Adversarial Networks. Eng. Struct. 2021, 234, 111970. [Google Scholar] [CrossRef]
- Yang, Y.B.; Li, Y.C.; Chang, K.C. Constructing the Mode Shapes of a Bridge from a Passing Vehicle: A Theoretical Study. Smart Struct. Syst. 2014, 13, 797–819. [Google Scholar] [CrossRef]
- Yang, Y.B.; Lin, C.W. Vehicle—Bridge Interaction Dynamics and Potential Applications. J. Sound Vib. 2005, 284, 205–226. [Google Scholar] [CrossRef]
- Biggs, J.M. Introduction to Structural Dynamics; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Frýba, L. Vibration of Solids and Structures under Moving Loads; ICE Publishing: London, UK, 1999. [Google Scholar]
- Huang, L.; Chen, J.; Tan, X. BP-ANN Based Bond Strength Prediction for FRP Reinforced Concrete at High Temperature. Eng. Struct. 2022, 257, 114026. [Google Scholar] [CrossRef]
- Nurunnahar, S.; Talukdar, D.B.; Rasel, R.I.; Sultana, N. A Short Term Wind Speed Forcasting Using SVR and BP-ANN: A Comparative Analysis. In Proceedings of the 2017 20th International Conference of Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 22–24 December 2017; pp. 1–6. [Google Scholar]
- Huang, X.; You, Y.; Zeng, X.; Liu, Q.; Dong, H.; Qian, M.; Xiao, S.; Yu, L.; Hu, X. Back Propagation Artificial Neural Network (BP-ANN) for Prediction of the Quality of Gamma-Irradiated Smoked Bacon. Food Chem. 2024, 437, 137806. [Google Scholar] [CrossRef] [PubMed]
- Al-Jarrah, R.; AL-Oqla, F.M. A Novel Integrated BPNN/SNN Artificial Neural Network for Predicting the Mechanical Performance of Green Fibers for Better Composite Manufacturing. Compos. Struct. 2022, 289, 115475. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Li, Y.C.; Chang, K.C. Effect of Road Surface Roughness on the Response of a Moving Vehicle for Identification of Bridge Frequencies. Interact. Multiscale Mech. 2012, 5, 347–368. [Google Scholar] [CrossRef]
- Paultre, P.; Chaallal, O.; Proulx, J. Bridge Dynamics and Dynamic Amplification Factors—A Review of Analytical and Experimental Findings. Can. J. Civ. Eng. 1992, 19, 260–278. [Google Scholar] [CrossRef]
- Dassault Systèmes. Abaqus 6.11 Analysis User’s Manual; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2011. [Google Scholar]
- Lu, X.; Kim, C.-W.; Chang, K.-C. Finite Element Analysis Framework for Dynamic Vehicle-Bridge Interaction System Based on ABAQUS. Int. J. Str. Stab. Dyn. 2020, 20, 2050034. [Google Scholar] [CrossRef]
- Lei, X.; Sun, L.; Xia, Y. Lost Data Reconstruction for Structural Health Monitoring Using Deep Convolutional Generative Adversarial Networks. Struct. Health Monit. 2021, 20, 2069–2087. [Google Scholar] [CrossRef]
- Xia, Y.; Lei, X.; Wang, P.; Liu, G.; Sun, L. Long-Term Performance Monitoring and Assessment of Concrete Beam Bridges Using Neutral Axis Indicator. Struct. Control Health Monit. 2020, 27, e2637. [Google Scholar] [CrossRef]
- MATLAB. Signal Processing Toolbox (Version R2022a). MathWorks. Available online: https://www.mathworks.com/help/signal/ref/highpass.html#mw_dcf4bbd2-1e29-4f0f-819f-39d872f77a14_seealso (accessed on 30 August 2024).

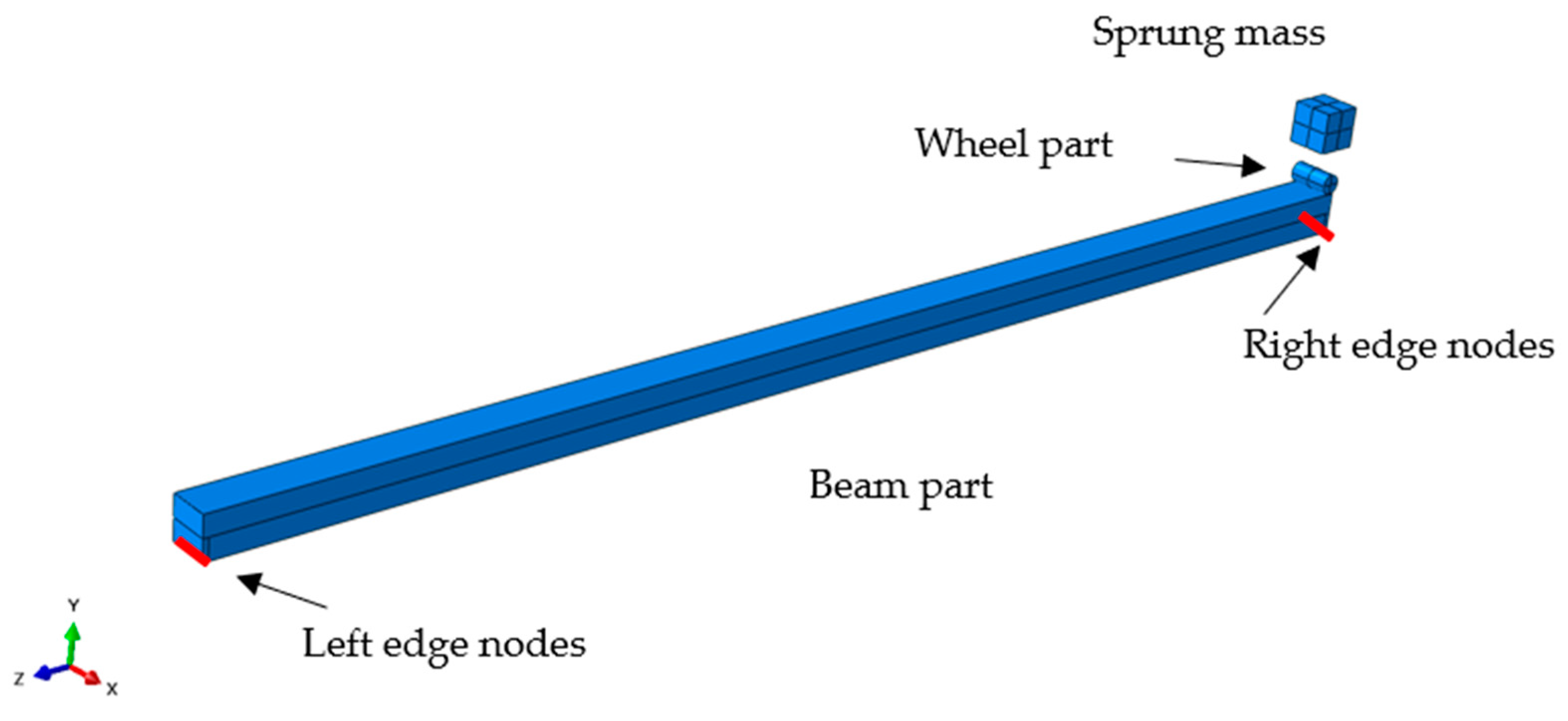



| Component | Type | Amount | Size (m × m × m) |
|---|---|---|---|
| Beam | C3D8R | 16,128 | 0.1 × 0.1 × 0.1 |
| Wheel | C3D8R | 320 | 0.08 × 0.08 × 0.08 |
| Sprung mass | C3D8R | 8000 | 0.04 × 0.04 × 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Qu, G.; Sun, L.; Xia, Y.; Sun, H.; Zhang, W. Physically Guided Estimation of Vehicle Loading-Induced Low-Frequency Bridge Responses with BP-ANN. Buildings 2024, 14, 2995. https://doi.org/10.3390/buildings14092995
Lu X, Qu G, Sun L, Xia Y, Sun H, Zhang W. Physically Guided Estimation of Vehicle Loading-Induced Low-Frequency Bridge Responses with BP-ANN. Buildings. 2024; 14(9):2995. https://doi.org/10.3390/buildings14092995
Chicago/Turabian StyleLu, Xuzhao, Guang Qu, Limin Sun, Ye Xia, Haibin Sun, and Wei Zhang. 2024. "Physically Guided Estimation of Vehicle Loading-Induced Low-Frequency Bridge Responses with BP-ANN" Buildings 14, no. 9: 2995. https://doi.org/10.3390/buildings14092995
APA StyleLu, X., Qu, G., Sun, L., Xia, Y., Sun, H., & Zhang, W. (2024). Physically Guided Estimation of Vehicle Loading-Induced Low-Frequency Bridge Responses with BP-ANN. Buildings, 14(9), 2995. https://doi.org/10.3390/buildings14092995







