Experimental Study of the Influence of Supplementary Reinforcement on Tensile Breakout Capacity of Headed Anchors in Nuclear Power Plant Equipment Foundations
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Specimens and Material Properties
2.2. Test Setup and Instrumentation
3. Experimental Results and Discussion
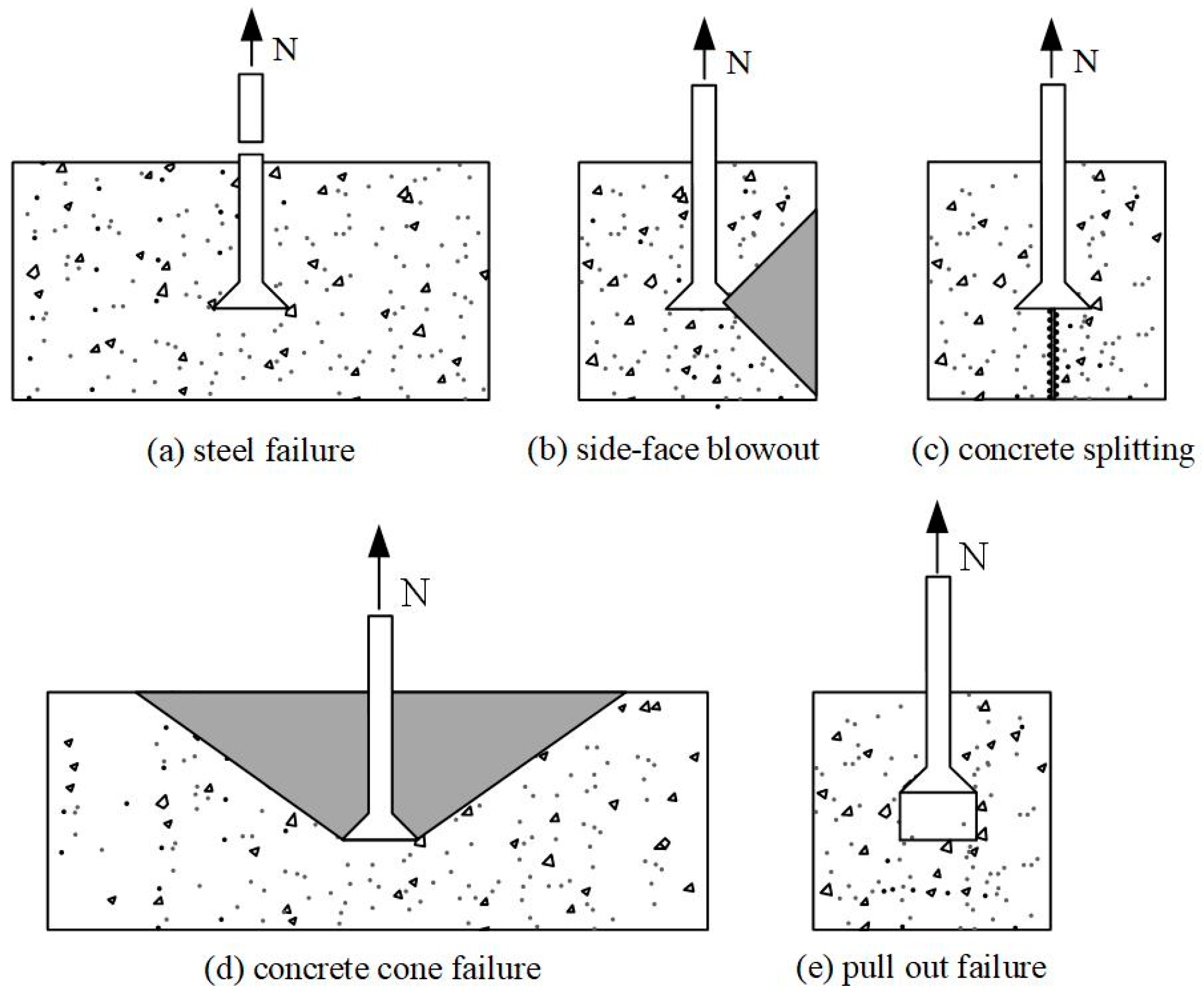
3.1. Test on Headed Anchors in Foundations without Supplementary Reinforcement
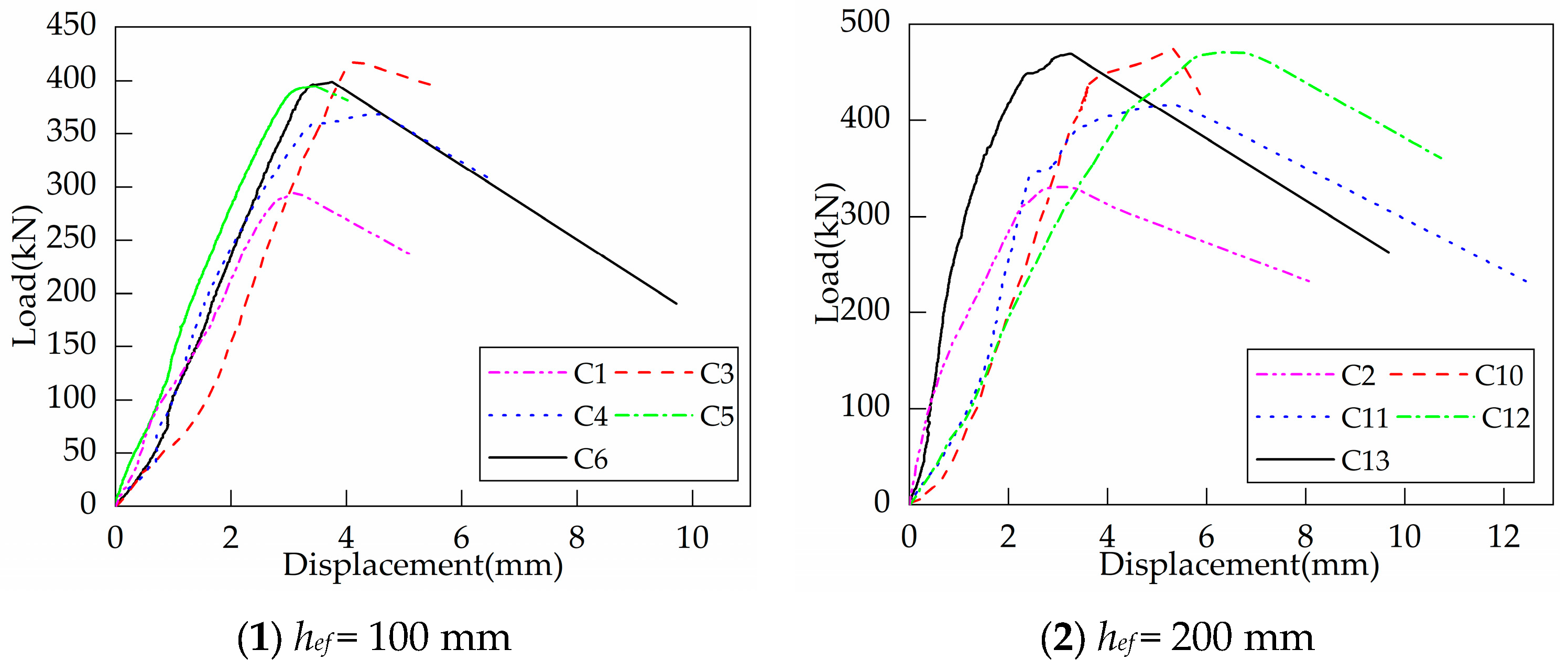
3.2. Test on Headed Anchors in Foundations with Supplemental Tie Bars
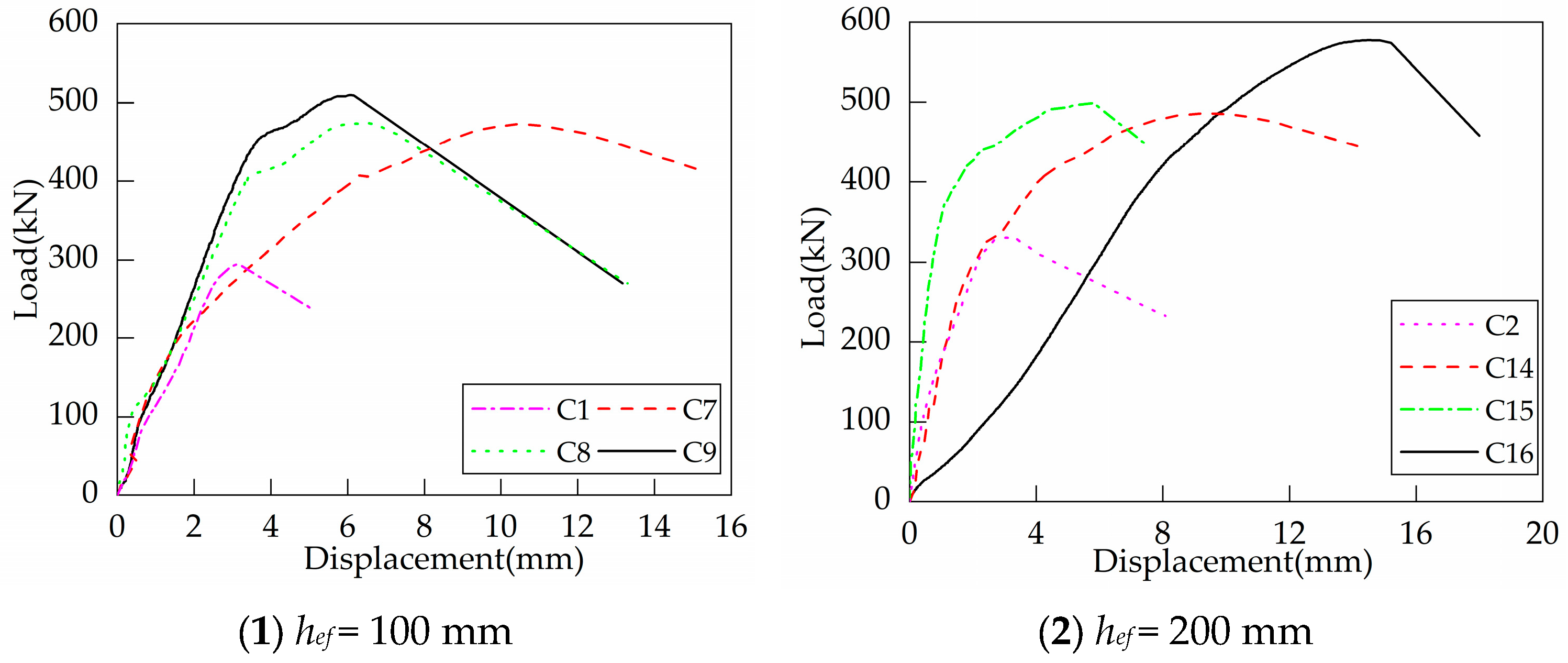
3.3. Test on Headed Anchors in Foundations with Supplemental U-Shaped Bars
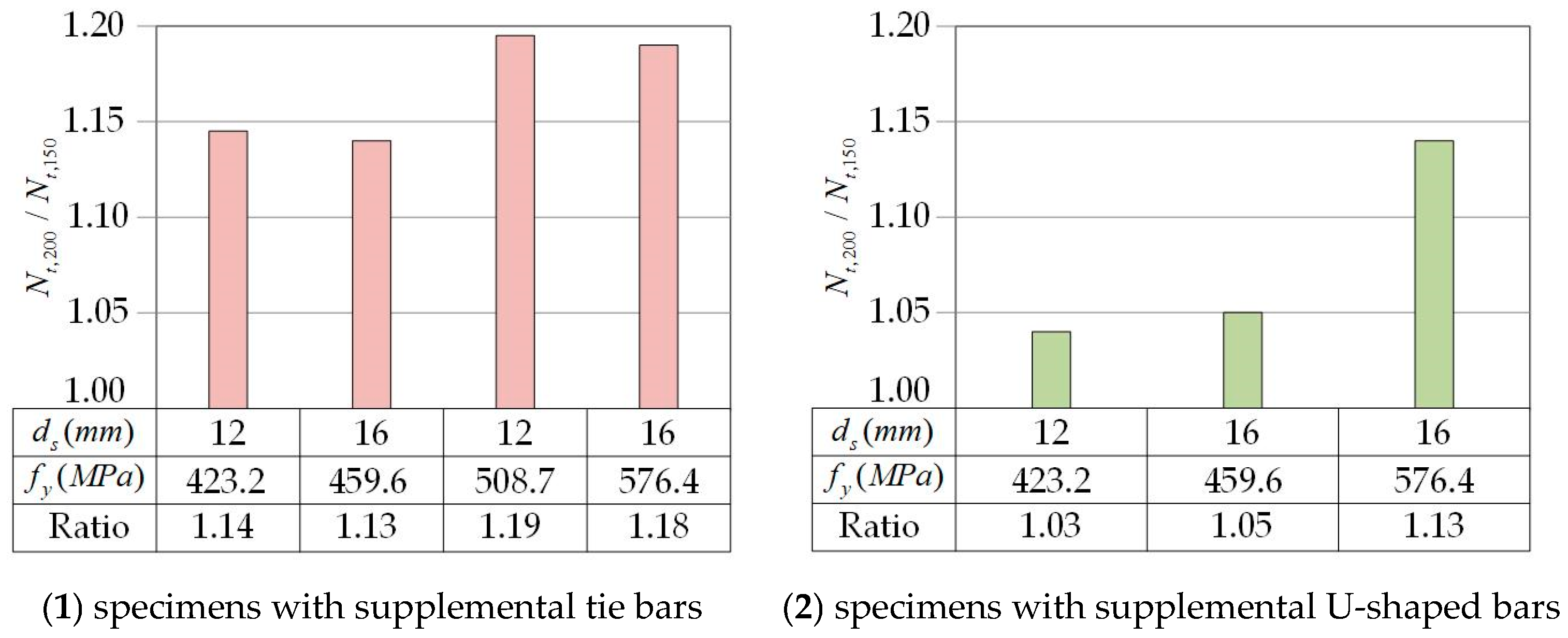
3.4. Influence of Supplementary Reinforcement
4. Presentation of the New Model
4.1. Model for Headed Anchors in Foundations with Supplemental Tie Bars
4.2. Model for Headed Anchors in Foundations with Supplemental U-Shaped Bars
4.3. Comparison with EN 1992-4:2018
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Area of supplementary reinforcement (mm2) | |
| Area of the i-th supplementary reinforcement (mm2) | |
| Reinforcement diameter (mm) | |
| Design bond strength according to EN 1992-1: 2004 | |
| Uniaxial compressive strength of concrete (cylinder) calculated by 0.8 (MPa) | |
| Concrete compressive strength measured on cubes with a side length of 150 mm at the time of the test (MPa) | |
| Yield strength of supplementary reinforcement (MPa) | |
| The anchorage length in the break-out body (mm) | |
| Embedment depth (mm) | |
| Number of supplemental reinforcement | |
| Capacity calculated by EN 1992-4: 2018 | |
| Ultimate load of reinforced foundation tensile breakout failure in tension (kN) | |
| Ultimate capacity of specimens with embedment depth of 150 mm (kN) | |
| Ultimate capacity of specimens with embedment depth of 200 mm (kN) | |
| Stress of reinforcement (MPa) | |
| Displacement at peak load (mm) | |
| Displacement at peak load of headed anchor with 150 mm embedment depth (mm) | |
| Displacement at peak load of headed anchor with 150 mm embedment depth (mm) |
References
- Li, X.; Gong, J. Probabilistic evaluation of the leak-tightness function of the nuclear containment structure subjected to internal pressure. Reliab. Eng. Syst. Saf. 2024, 241, 109684. [Google Scholar] [CrossRef]
- Li, X.; Wu, X.; Gong, J. Failure behavior and probabilistic safety assessment of containment structure under internal pressure considering time-varying prestress loss. Eng. Struct. 2024, 319, 118884. [Google Scholar] [CrossRef]
- ACI Committee 349; ACI 349-13: Code Requirements for Nuclear Safety-Related Concrete Structures and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2013.
- Karmokar, T.; Mohyeddin, A.; Lee, J.; Paraskeva, T. Concrete cone failure of single cast-in anchors under tensile loading–A literature review. Eng. Struct. 2021, 243, 112615. [Google Scholar] [CrossRef]
- Di Nunzio, G.; Muciaccia, G. Cast-in-place fasteners under tensile loading: A critical review. Structures 2022, 41, 1532–1545. [Google Scholar] [CrossRef]
- Eligehausen, R.; Mallée, R.; Silva, J.F. Design of Fastenings, Anchorage in Concrete Construction; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Fib Bulletin 58: Design of Anchorages in Concrete; Federation Internationale Dubeton: Lausanne, Switzerland, 2011.
- PCI Design Handbook: Precast and Prestressed Concrete, 2nd ed.; Prestressed Concrete Institute: Chicago, IL, USA, 1978.
- ACI Committee 349; ACI 349-76: Code Requirements for Nuclear Safety Related Concrete Structures and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 1976.
- Klingner, R.E.; Mendonca, J.A. Tensile capacity of short anchor bolts and welded studs: A literature review. J. Proc. 1982, 79, 270–279. [Google Scholar]
- Ballarini, R.; Shah, S.P.; Keer, L.M. Failure characteristics of short anchor bolts embedded in a brittle material. Proc. R. Soc. Lond. A Math. Phys. Sci. 1986, 404, 35–54. [Google Scholar]
- ACI Committee 349; ACI 349-85: Code Requirements for Nuclear Safety-Related Concrete Structures and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 1985.
- Eligehausen, R.; Sawade, G. A fracture mechanics based description of the pull-out behavior of headed studs embedded in concrete. In Fracture Mechanics of Concrete Structures (From Theory to Applications); University of Stuttgart: Stuttgart, Germany, 1989; pp. 281–298. [Google Scholar]
- Bažant, Z.P. Size effect in blunt fracture: Concrete, rock, metal. J. Eng. Mech. 1984, 110, 518–535. [Google Scholar] [CrossRef]
- Fuchs, W.; Eligehausen, R.; Breen, J.E. Concrete capacity design (CCD) approach for fastening to concrete. Struct. J. 1995, 92, 73–94. [Google Scholar]
- ACI Committee 318; ACI 318-19: Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- EN 1992-4; Eurocode 2. Design of Concrete Structures. Design of Fastenings for Use in Concrete. European Commission: Brussels, Belgium, 2018.
- Solomos, G.; Berra, M. Testing of anchorages in concrete under dynamic tensile loading. Mater. Struct. 2006, 39, 695–706. [Google Scholar] [CrossRef]
- ACI Committee 349; ACI 349-01: Code Requirements for Nuclear Safety-Related Concrete Structures and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2001.
- Lee, N.H.; Kim, K.S.; Chang, J.B.; Park, K.R. Tensile-headed anchors with large diameter and deep embedment in concrete. ACI Struct. J. 2007, 104, 479. [Google Scholar]
- ACI Committee 318; ACI 318-05: Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2005.
- ACI Committee 349; ACI 349-97: Code Requirements for Nuclear Safety-Related Concrete Structures and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 1997.
- Ferreira, M.; Pereira, F.M.; Lima, N.; Oliveira, M. Influence of the flexural and shear reinforcement in the concrete cone resistance of headed bars. Eng. Struct. 2021, 248, 113212. [Google Scholar] [CrossRef]
- Di Nunzio, G.; Muciaccia, G. Behavior and design of screwed-head fasteners in reinforced concrete in tension. Struct. Concr. 2021, 22, 894–910. [Google Scholar] [CrossRef]
- Petersen, D.; Lin, Z.; Zhao, J. Design of anchor reinforcement for seismic tension loads. Eng. Struct. 2018, 164, 109–118. [Google Scholar] [CrossRef]
- Nilforoush, R.; Nilsson, M.; Elfgren, L. Experimental evaluation of influence of member thickness, anchor-head size, and orthogonal surface reinforcement on the tensile capacity of headed anchors in uncracked concrete. J. Struct. Eng. 2018, 144, 04018012. [Google Scholar] [CrossRef]
- Rabi, M.; Cashell, K.A.; Shamass, R.; Desnerck, P. Bond behaviour of austenitic stainless steel reinforced concrete. Eng. Struct. 2020, 221, 111027. [Google Scholar] [CrossRef]
- Tóth, M.; Bokor, B.; Sharma, A. Anchorage in steel fiber reinforced concrete–concept, experimental evidence and design recommendations for concrete cone and concrete edge breakout failure modes. Eng. Struct. 2019, 181, 60–75. [Google Scholar] [CrossRef]
- Karmokar, T.; Mohyeddin, A.; Lee, J. Tensile behaviour of cast-in headed anchors in ambient-temperature cured geopolymer concrete. Eng. Struct. 2022, 266, 114643. [Google Scholar] [CrossRef]
- Li, F.; Gao, H.; Jiang, Y.; Wen, T.; Zhan, Y.; Chen, Z.; Shen, D. Tensile behavior of stud connectors in high strength concrete. Adv. Struct. Eng. 2021, 24, 3677–3690. [Google Scholar] [CrossRef]
- Shin, J.; Kim, J.H.; Chang, H.J. Anchor plate effect on the breakout capacity in tension for thin-walled concrete panels. Eng. Struct. 2016, 106, 147–153. [Google Scholar] [CrossRef]
- EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures–Part 1-1. General Rules and Rules for Buildings. European Commission: Brussels, Belgium, 2004.








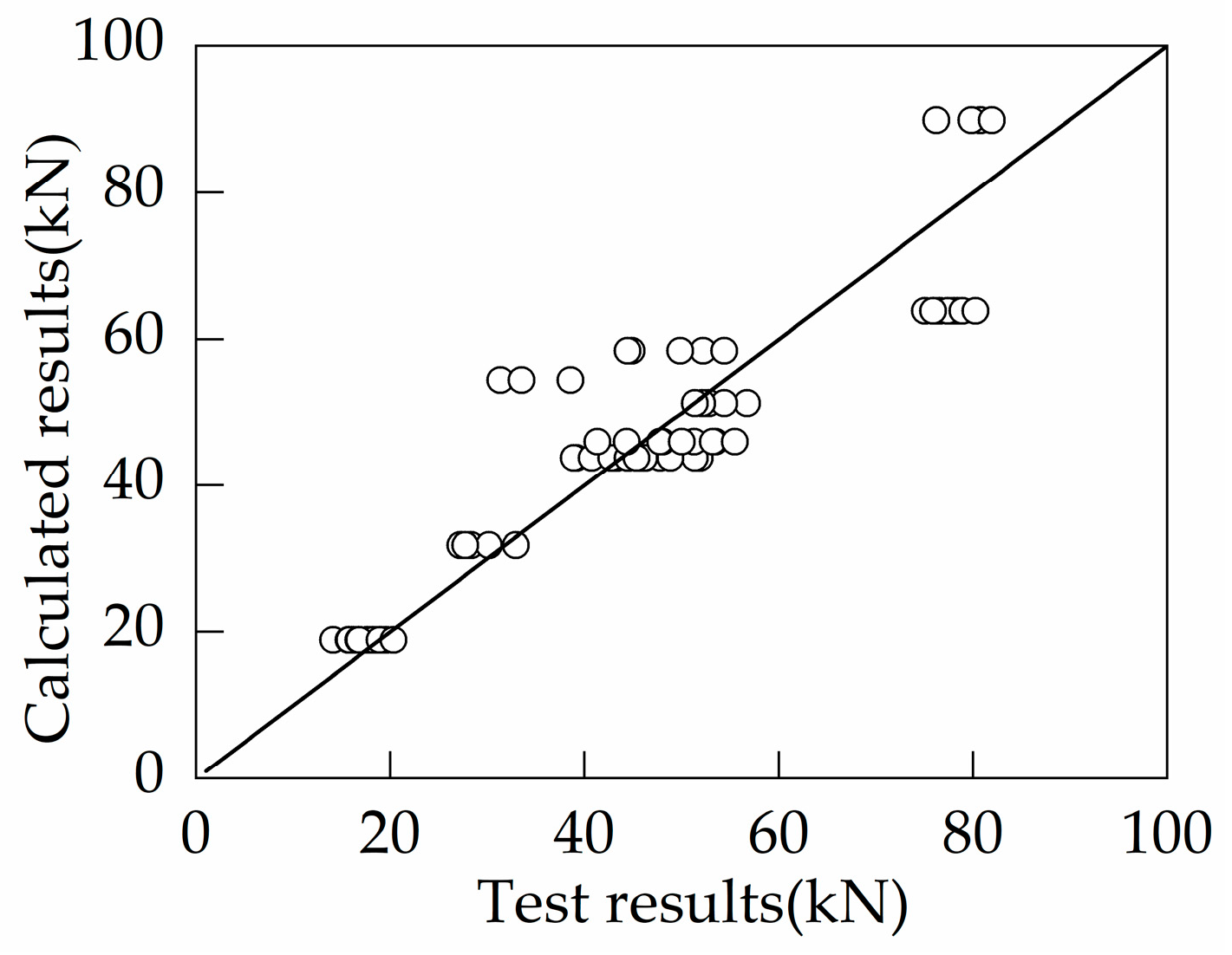

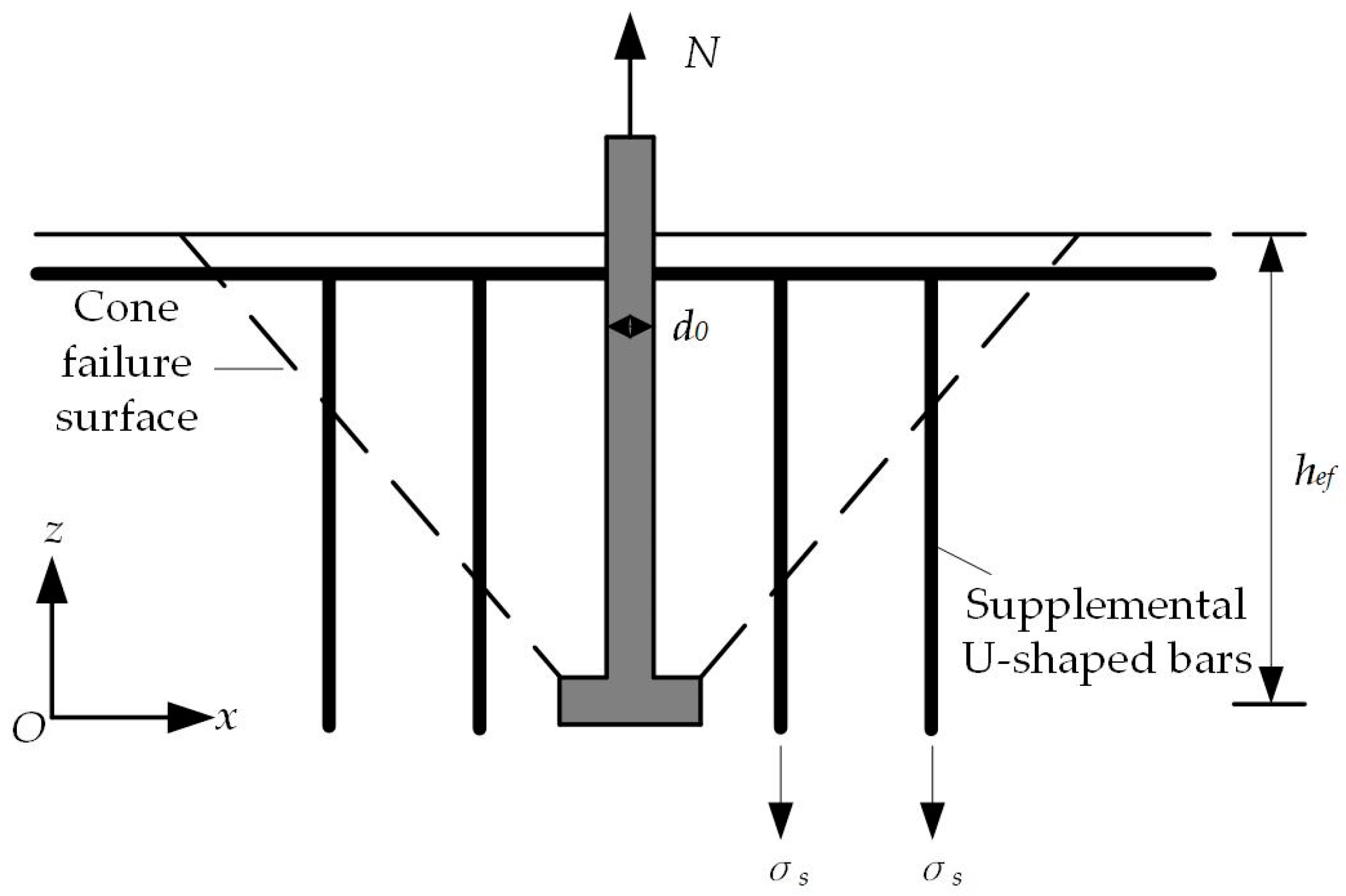

| Test No. | hef (mm) | ds (mm) | n | Reinforcement Form | fy (MPa) |
|---|---|---|---|---|---|
| C1 | 150 | - | - | - | - |
| C2 | 200 | - | - | - | - |
| C3 | 150 | 12 | 8 | tie bars | 423.2 |
| C4 | 150 | 16 | 8 | tie bars | 459.6 |
| C5 | 150 | 12 | 8 | tie bars | 508.7 |
| C6 | 150 | 16 | 8 | tie bars | 576.4 |
| C7 | 150 | 12 | 4 | U-shaped bars | 423.2 |
| C8 | 150 | 12 | 4 | U-shaped bars | 508.7 |
| C9 | 150 | 16 | 4 | U-shaped bars | 576.4 |
| C10 | 200 | 12 | 8 | tie bars | 423.2 |
| C11 | 200 | 16 | 8 | tie bars | 459.6 |
| C12 | 200 | 12 | 8 | tie bars | 508.7 |
| C13 | 200 | 16 | 8 | tie bars | 576.4 |
| C14 | 200 | 12 | 4 | U-shaped bars | 423.2 |
| C15 | 200 | 12 | 4 | U-shaped bars | 508.7 |
| C16 | 200 | 16 | 4 | U-shaped bars | 576.4 |
| Test | (MPa) | (MPa) | Df (mm) | (mm) | (kN) | Failure Mode | ||
|---|---|---|---|---|---|---|---|---|
| C1 | 53.64 | 42.91 | 980 (6.53 hef) | 3.09 | 294.53 | 1.00 | 1.00 | C |
| C2 | 53.64 | 42.91 | 1070 (5.35 hef) | 3.14 | 330.34 | 1.00 | 1.00 | C |
| C3 | 50.71 | 40.57 | 490 (3.27 hef) | 4.15 | 417.68 | 1.42 | 1.34 | C |
| C4 | 50.71 | 40.57 | 381 (2.54 hef) | 4.55 | 368.19 | 1.25 | 1.47 | C |
| C5 | 54.30 | 43.44 | 479 (3.19 hef) | 3.46 | 394.49 | 1.34 | 1.12 | C |
| C6 | 54.30 | 43.44 | 493 (3.29 hef) | 3.75 | 399.02 | 1.35 | 1.21 | C |
| C7 | 50.71 | 40.57 | 353 (1.77 hef) | 10.45 | 472.42 | 1.60 | 3.38 | C |
| C8 | 54.95 | 43.96 | 446 (2.23 hef) | 6.52 | 473.79 | 1.61 | 2.11 | C |
| C9 | 54.95 | 43.96 | 410 (2.05 hef) | 6.07 | 509.55 | 1.73 | 1.96 | S |
| C10 | 46.36 | 37.09 | 336 (1.68 hef) | 5.34 | 474.76 | 1.44 | 1.70 | C |
| C11 | 46.36 | 37.09 | 266 (1.77 hef) | 5.23 | 415.80 | 1.26 | 1.67 | C |
| C12 | 54.30 | 43.44 | 492 (3.28 hef) | 6.45 | 470.84 | 1.43 | 2.05 | C |
| C13 | 54.30 | 43.44 | 425 (2.83 hef) | 3.59 | 469.11 | 1.42 | 1.14 | C |
| C14 | 46.36 | 37.09 | 423 (2.12 hef) | 9.54 | 485.80 | 1.47 | 3.04 | C |
| C15 | 54.95 | 43.96 | 529 (2.65 hef) | 5.82 | 499.10 | 1.51 | 1.85 | C |
| C16 | 54.95 | 43.96 | 397 (1.99 hef) | 14.51 | 577.51 | 1.75 | 4.62 | S |
| Test | hef (mm) | fc (MPa) | As (mm2) | fy (MPa) | Asfy (kN) | Nco (kN) | (kN) | Nt (kN) | Ncl (kN) | |
|---|---|---|---|---|---|---|---|---|---|---|
| C3 | 150 | 40.57 | 904.8 | 423.2 | 382.91 | 156.68 | 533.55 | 417.68 | 381.41 | 0.91 |
| C4 | 150 | 40.57 | 1608.8 | 459.6 | 739.40 | 156.68 | 890.04 | 368.19 | 411.61 | 1.12 |
| C5 | 150 | 43.44 | 904.8 | 508.7 | 460.27 | 162.13 | 615.50 | 394.49 | 391.62 | 0.99 |
| C6 | 150 | 43.44 | 1608.8 | 576.4 | 927.31 | 162.13 | 1082.54 | 399.02 | 414.41 | 1.04 |
| C10 | 200 | 37.09 | 904.8 | 423.2 | 382.91 | 230.65 | 606.97 | 474.76 | 459.65 | 0.97 |
| C11 | 200 | 37.09 | 1608.8 | 459.6 | 739.40 | 230.65 | 963.46 | 415.80 | 410.63 | 0.99 |
| C12 | 200 | 43.44 | 904.8 | 508.7 | 460.27 | 249.61 | 699.26 | 470.84 | 459.73 | 0.98 |
| C13 | 200 | 43.44 | 1608.8 | 576.4 | 927.31 | 249.61 | 1166.30 | 469.11 | 471.01 | 1.00 |
| Test | hef (mm) | fc (MPa) | As (mm2) | fy (MPa) | Asfy (kN) | Nco (kN) | (kN) | Nt (kN) | Ncl (kN) | |
|---|---|---|---|---|---|---|---|---|---|---|
| C7 | 150 | 40.57 | 452.4 | 423.2 | 191.46 | 156.68 | 348.14 | 472.42 | 460.00 | 0.97 |
| C8 | 150 | 43.96 | 452.4 | 508.7 | 230.14 | 163.10 | 393.23 | 473.79 | 482.02 | 1.02 |
| C9 | 150 | 43.96 | 804.4 | 576.4 | 463.66 | 163.10 | 626.75 | 509.55 | - | - |
| C14 | 200 | 37.09 | 452.4 | 423.2 | 191.46 | 230.65 | 422.11 | 485.80 | 494.92 | 1.02 |
| C15 | 200 | 43.96 | 452.4 | 508.7 | 230.14 | 251.10 | 481.24 | 499.10 | 493.75 | 0.99 |
| C16 | 200 | 43.96 | 804.4 | 576.4 | 463.66 | 251.10 | 714.76 | 577.51 | - | - |
| Supplementary Reinforcement | Test | (kN) | (kN) | (kN) | ||
|---|---|---|---|---|---|---|
| Supplemental tie bars | C3 | 417.68 | 381.41 | 196.79 | 0.47 | 0.91 |
| C4 | 368.19 | 411.61 | 262.39 | 0.71 | 1.12 | |
| C5 | 394.49 | 391.62 | 196.79 | 0.50 | 0.99 | |
| C6 | 399.02 | 414.41 | 262.39 | 0.66 | 1.04 | |
| C10 | 474.76 | 459.65 | 295.18 | 0.62 | 0.97 | |
| C11 | 415.80 | 410.63 | 393.58 | 0.95 | 0.99 | |
| C12 | 470.84 | 459.73 | 295.18 | 0.63 | 0.98 | |
| C13 | 469.11 | 471.01 | 393.58 | 0.84 | 1.00 | |
| Average | 0.67 | 1.00 | ||||
| COV | 0.24 | 0.06 | ||||
| Supplemental U-shaped bars | C7 | 472.42 | 460.00 | 191.46 | 0.41 | 0.97 |
| C8 | 473.79 | 482.02 | 230.14 | 0.49 | 1.02 | |
| C9 | 509.55 | - | 463.66 | 0.91 | - | |
| C14 | 485.80 | 494.92 | 191.46 | 0.39 | 1.02 | |
| C15 | 499.10 | 493.75 | 230.14 | 0.46 | 0.99 | |
| C16 | 577.51 | - | 463.66 | 0.80 | - | |
| Average | 0.335 | 1.00 | ||||
| COV | 0.15 | 0.03 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Chen, C.; Xie, M.; Gong, J. Experimental Study of the Influence of Supplementary Reinforcement on Tensile Breakout Capacity of Headed Anchors in Nuclear Power Plant Equipment Foundations. Buildings 2024, 14, 3027. https://doi.org/10.3390/buildings14093027
Xu Y, Chen C, Xie M, Gong J. Experimental Study of the Influence of Supplementary Reinforcement on Tensile Breakout Capacity of Headed Anchors in Nuclear Power Plant Equipment Foundations. Buildings. 2024; 14(9):3027. https://doi.org/10.3390/buildings14093027
Chicago/Turabian StyleXu, Yang, Chaoqun Chen, Minglei Xie, and Jinxin Gong. 2024. "Experimental Study of the Influence of Supplementary Reinforcement on Tensile Breakout Capacity of Headed Anchors in Nuclear Power Plant Equipment Foundations" Buildings 14, no. 9: 3027. https://doi.org/10.3390/buildings14093027
APA StyleXu, Y., Chen, C., Xie, M., & Gong, J. (2024). Experimental Study of the Influence of Supplementary Reinforcement on Tensile Breakout Capacity of Headed Anchors in Nuclear Power Plant Equipment Foundations. Buildings, 14(9), 3027. https://doi.org/10.3390/buildings14093027





