Review of Prediction Models for Chloride Ion Concentration in Concrete Structures

Abstract

Chloride ion concentration significantly impacts the durability of reinforced concrete, particularly regarding corrosion. Accurately assessing how this concentration varies with the age of structures is crucial for ensuring their safety and longevity. Recently, several predictive models have emerged to analyze chloride ion concentration over time, classified into empirical models and machine learning models based on their data processing techniques. Empirical models directly relate chloride ion concentration to the age of concrete through specific functions. Their primary advantage lies in their low data requirements, making them convenient for engineering use. However, these models often fail to account for multiple influencing factors, which can limit their accuracy. Conversely, machine learning models can handle various factors simultaneously, providing a more detailed understanding of how chloride concentration evolves. When adequately trained with sufficient experimental data, these models generally offer superior prediction accuracy compared to mathematical models. The downside is that they necessitate a larger dataset for training, which can complicate their practical application. Future research could focus on combining machine learning and empirical models, leveraging their respective strengths to achieve a more precise evaluation of chloride ion concentration in relation to structural age.

1. Introduction

Concrete structures are extensively utilized in civil engineering projects, including but not limited to housing construction, factory structures, and bridges due to their excellent performance. The surface and interior of this material often contain numerous pores and cracks that are too fine to be detected by the naked eye. On the other hand, during the mixing process of concrete, if the chloride ion ($C{l}^{-}$) content is too high, it will combine with calcium ions ($C{a}^{2+}$) in the concrete to form calcium chloride ($CaC{l}_2$), a powder-like compound with no strength. This process can lead to localized loosening within the concrete, significantly reducing its strength and durability. Additionally, chloride ions act as catalysts for electrochemical corrosion, accelerating the damage to concrete structures. This effect may render the concrete unable to meet the strength standards and service life expectations outlined in the design [1]. For example, Equations (1)–(6) present some of the main chemical reaction processes occurring in concrete, which may all be accelerated by the presence of chloride ions. In marine environments, chloride ion penetration and erosion are major factors causing severe damage to concrete structures. Prolonged penetration, combined with physical effects such as continuous erosion by seawater and chemical corrosion from acidic substances within it, exacerbates the damage process caused by chloride ions, thereby accelerating the deterioration of concrete structures [2]. Studying models of chloride ion concentration changes over the structural age is of great significance for understanding the overall safety and durability of concrete structures and adopting necessary protective measures to cope with various situations.

The concentration of chloride ions is influenced by numerous factors, with the primary ones being the climate conditions (such as variations in temperature and humidity) in the environment where the concrete is situated, as well as the salt concentration or pollution level of the water it comes into contact with [3]. On the surface of steel reinforcement, electrochemical corrosion occurs due to the presence of potential differences (anode and cathode), combined with the availability of water and oxygen. Chloride ions serve to decrease the corrosion potential, thereby making corrosion more likely to occur, as demonstrated by the chemical reactions represented in equations [4]. Through comprehensive research, it has been established that the lifespan of reinforced concrete structures can be drastically reduced due to the accumulation of chloride ions after 20 to 30 years of usage [5]. If left unaddressed, the infiltration of chloride ions can severely compromise the overall structure of the concrete, posing a considerable and immediate threat to personal safety and property integrity [6,7,8]. Therefore, accurately assessing the changes in chloride ion concentration over the structural age is pivotal for precisely estimating the structure’s expected lifespan, accurately identifying potential risks of structural damage, and planning suitable maintenance and repair measures. This assessment enables a more refined understanding of the concrete’s structural performance [9]. By doing so, it not only significantly extends the lifespan of the structure but also effectively ensures the safety of users [10,11,12,13].

$$Fe\to F{e}^{2+}+2e^{-}$$

(1)

$$O_2+2H_{2}O+4e^{-}\to 4O{H}^{-}$$

(2)

$$F{e}^{2+}+2O{H}^{-}\to Fe{(OH)}_2$$

(3)

$$4Fe{\left(OH\right)}_2+O_2+2H_{2}O\to 4Fe{\left(OH\right)}_3$$

(4)

$$2Fe{(OH)}_3\to F{e}_2{O}_3+3H_{2}O$$

(5)

$$6Fe{(OH)}_2+O_2\to F{e}_3{O}_4+6H_{2}O$$

(6)

Over the past century, scientists from various countries have conducted extensive and in-depth research and analysis on the changes in chloride ion concentration in concrete, which has significantly enhanced the durability of concrete structures. Over the years, a thorough understanding of the internal processes and factors affecting the variation of chloride ion concentration with the aging of concrete structures has emerged globally. This deep knowledge has prompted the creation of various predictive models that account for diverse variables and dimensions. Such models enhance the scientific basis for evaluating the quality of reinforced concrete structures and offer robust theoretical and empirical support for accurately assessing their performance and reasonably estimating their service life [14,15]. In recent years, extensive research has been conducted on models that predict how chloride ion concentration changes with the age of concrete structures. To gain deeper insights into the durability of concrete and develop efficient and reliable corrosion prevention technologies, these chloride ion concentration prediction models developed by scientists have demonstrated immense practical value in the construction industry. They not only provide a scientific basis for accurately assessing the expected service life of concrete structures but also facilitate the optimization of structural design and the formulation of maintenance strategies, laying a solid foundation for the sustainable development of the construction industry. Recently, through extensive and in-depth comprehensive literature analysis, it is clear that the classification of prediction methods for chloride ion concentration changes with the age of concrete structures mainly depends on the types of data used and the algorithms employed to process these data.

Currently, cross-sea bridge projects, as a crucial part of transportation infrastructure, face enormous challenges in extreme marine environments. Their piers and piles are directly exposed to seawater, not only needing to withstand the fierce impact of strong winds, huge waves, and currents but also enduring continuous erosion from seawater and the accumulation of fatigue damage [16,17]. The high salinity, high humidity, and drastic temperature changes in seawater jointly act on bridge structures, causing severe corrosion issues. In particular, high concentrations of chloride ions can penetrate and destroy the passivation protective layer on the surface of steel reinforcement, leading to rapid rusting and expansion of the steel, which then triggers a series of problems such as aging, cracking, spalling, and a significant reduction in concrete strength. These all pose significant threats to the service life and safety of bridges [18,19]. Steel reinforcement corrosion has become one of the main reasons for the deterioration and failure of concrete structures [20]. Data show that in 2014, the cost of corrosion in China reached CNY 2.1 trillion, equivalent to 3.34% of the gross domestic product (GDP) for that year. Among these, corrosion losses in infrastructure and transportation accounted for a significant proportion, reaching 31%, with a specific value of CNY 350.177 billion [21,22]. A report released by the American Society of Civil Engineers (ASCE) in 2017 indicated that the estimated cost to strengthen and reinforce existing bridges across the United States would exceed USD 120 billion. Japan conducted a detailed survey of 103 seaport terminals and found that all terminals with more than 20 years of service had suffered severe corrosion, manifested by rusting of steel reinforcement in concrete structures and obvious spalling of concrete surfaces. The corrosion situation of marine engineering in China cannot be ignored as well. According to survey results from relevant units of the Ministry of Transport, among 18 concrete terminals in the southern coastal areas with service lives ranging from 7 to 25 years, 16 showed signs of corrosion, and 9 had severe corrosion. In the southeastern coastal areas, of the 22 terminals surveyed with service lives between 8 and 32 years, 55.6% faced severe spalling of the concrete protective layer. Additionally, almost all 14 terminals in the northern coastal areas, with service lives ranging from 2 to 57 years, showed varying degrees of concrete corrosion [23]. These survey data clearly indicate that the erosion of concrete by chloride ions is an increasingly significant problem. Given these severe conditions, in-depth exploration of the variation law of chloride ion concentration with the age of concrete structures undoubtedly has important practical significance. Therefore, this paper aims to comprehensively summarize recent research findings on the variation of chloride ion concentration with structural age and provide useful suggestions for the future development of more complete and reliable prediction models of chloride ion concentration changes over time by deeply analyzing the advantages and disadvantages of various prediction models. These models have important practical significance for preventing concrete structure corrosion, guiding timely protective measures, and enhancing the safety and durability of marine engineering structures such as cross-sea bridges.

This review is anchored in an extensive corpus of 101 scholarly articles retrieved from the Scopus database, adhering strictly to the PRISMA guidelines and registration protocols. An illustrative procedural outline is depicted in Figure 1. The influencing factors under consideration have been meticulously classified, with a thorough examination and comprehensive discussion of the foundational principles governing each category. Additionally, the study integrates numerous case studies, aiming to fortify the evidence base concerning the impact of these factors by comparing research findings across diverse researchers. It strives to delineate the quantitative interrelationships among these factors, fostering a deeper insight into their interplay. This research provides valuable insights for evaluating the corrosion status of concrete structures, taking timely maintenance measures, and estimating the lifespan of concrete structures.

2. Mathematical Curve Model for the Variation of Chloride Ion Concentration with Structural Age

2.1. Fick’s Law Model

Chloride ingress is a critical factor in the performance degradation of reinforced concrete structures in marine environments. Given its importance and ubiquity, the development of a technology that can accurately simulate the chloride penetration process and predict its concentration distribution is crucial. This technology not only effectively assesses the health of reinforced concrete structures but also provides a scientific basis for maintenance, repair, and design optimization of structures, ensuring their safety and durability. Over the past few decades, researchers have dedicated themselves to studying the process of chloride intrusion into concrete through the construction of physical models and computer simulations. In the early stages of this exploration, Fick’s Second Law was widely adopted as the foundation for modeling due to its accurate description of diffusion phenomena, providing powerful theoretical support for understanding and predicting the distribution of chloride in concrete [24,25,26,27,28,29,30]. The equation is as follows:

$$C\left(x,t\right)=C_0+\left(C_S-C_0\right)\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{t{D}_{\mathrm{cl}}}}}\right)\right]$$

(7)

In Equation (7), $C(x,t)$ represents the concentration of $C{l}^{-}$ at the erosion depth $x$ at the erosion age $t$, $C_0$ is the initial concentration of $C{l}^{-}$, $C_s$ is the surface concentration of $C{l}^{-}$, $D$ is the diffusion coefficient of $C{l}^{-}$, and $erf(x)$ is the Gaussian error function. In the literature [31], Equation (7) has been tested in both laboratory and field environments. The model demonstrates good applicability in laboratory settings, particularly under uniform diffusion conditions, with low fitting errors and computational complexity. However, its applicability is limited in field applications, where it struggles to adapt to nonlinear diffusion scenarios.

Fick’s Second Law is a classic model that describes the variation of solute concentration with time and position during one-dimensional diffusion processes. It is commonly used to characterize changes in concentration over time, particularly in conventional diffusion processes. The applicability of this law is based on the following key assumptions: firstly, the diffusion coefficient (D) is considered constant, implying that the diffusion rate does not change with time or space during the diffusion process; secondly, the initial concentration distribution is assumed to be uniform, meaning that the solute is evenly distributed in the medium at the start of diffusion; and finally, the diffusion medium is considered uniform, lacking heterogeneity or uneven structures, thereby ensuring that the diffusion process of the solute within it is not affected by the medium’s non-uniformity. The advantage of the Fick’s Second Law model lies in its ingenious design, where its core parameters (such as chloride ion concentration, diffusion coefficient, and diffusion time) all possess clear physical meanings. This makes the law not only easy to understand but also convenient for direct application in practical engineering problems. It establishes a direct link between chloride ion concentration and age and, through the key parameter of the diffusion coefficient, effectively reveals the diffusion pattern of chloride ions in concrete. This approach serves as an intuitive and effective tool for evaluating the durability of concrete structures. However, in practical applications, the diffusion coefficient often varies due to the influence of time, temperature, or spatial location, especially in environments with changing conditions, varying physicochemical properties of the solute, or complex media (such as concrete and soil). Furthermore, concrete often exhibits pores, microcracks, or other structural heterogeneities of varying sizes and shapes, which significantly impact diffusion behavior. Simultaneously, the surface binding effect of chloride ion concentration in concrete notably affects the accuracy of long-term predictions. This effect manifests as chloride ions binding to cement hydration products at the concrete surface, reducing the free diffusion rate of chloride ions. Consequently, the migration of surface chloride ions lags behind the actual diffusion process. Traditional chloride ion migration models typically overlook this effect, potentially leading to underestimations of chloride ion concentrations within concrete in short-term predictions and deviations in long-term predictions. In such circumstances, Fick’s Second Law fails to accurately describe the actual diffusion process. Therefore, when making long-term predictions of chloride ion concentrations, it is imperative to consider the lag and release effects of surface binding on chloride ion migration to enhance prediction accuracy and optimize durability assessments of concrete [32]. These factors often interact in real-world engineering contexts and significantly influence chloride ion diffusion behavior. Consequently, under complex operational conditions, relying solely on Fick’s Second Law may not adequately represent the true diffusion process of chloride ions in concrete [30,31,32,33].

When applying Fick’s Law to study chloride ion diffusion in concrete, different scholars have adopted various simplifying assumptions. Funahashi et al.’s research considered more basic factors, and their model may not have fully captured the diffusion characteristics in the complex environment of concrete [34]. In contrast, Prezzi et al. took a step forward by specifically considering the binding capacity of concrete for chloride ions, which is an important factor affecting the distribution and accumulation of chloride ions in concrete [35]. However, Mangat et al. focused on the time dependency of the chloride diffusion coefficient, a property that reflects the impact of concrete material aging and environmental condition changes on diffusion behavior over time [36]. Despite these studies having different focuses, they all failed to comprehensively consider the complex effects of structural defects such as internal microcracks and pore structure changes that may occur in concrete materials during long-term use on chloride ion diffusion. These structural defects can significantly alter the permeation pathways and rates of chloride ions in concrete, thereby affecting their diffusion behavior and the accuracy of durability assessments.

Based on Fick’s Second Law, and taking into account the chloride binding capacity of concrete, the time-dependency of the chloride diffusion coefficient, as well as the impact of internal microdefects within concrete structures on the diffusion process, Reference [37] derives a new chloride diffusion equation.

$${\displaystyle \frac{\partial c_f}{\partial c_t}}={\displaystyle \frac{K{D}_0{t}_0^m}{1+R}}·t^{-m}·{\displaystyle \frac{{\partial }^2{c}_f}{\partial x^2}}$$

(8)

In Equation (8), $c_f$ represents the concentration of free chloride ions, $c_t$ represents the total chloride ion concentration at a distance x from the surface of the concrete, $K$ is the coefficient of deterioration in the chloride diffusion performance of the concrete, $t_0$ denotes the hydration age of the concrete, $D_0$ is the chloride diffusion coefficient of the concrete measured at the hydration age, and $m$ is an experimental constant, with a value of 0.64 as given in Reference [38].

The initial condition for the aforementioned equation is when $t=0$ and $x>0$, $c_f=c_0$. The boundary condition is when $x=0$ and $t>0$, denoted as $c_f=c_s$. Based on these initial and boundary conditions, the theoretical model for chloride ion diffusion in concrete is obtained as follows:

$$c_f=c_0+\left(c_s-c_0\right)\left[1-erf{\displaystyle \frac{x}{2\sqrt{\frac{K{D}_0{t}_0^m}{\left(1+R\right)\left(1-m\right)}}·t^{1-m}}}\right]$$

(9)

In Equation (9), $c_0$ denotes the initial chloride ion concentration within the concrete, $c_s$ represents the chloride ion concentration at the exposed surface of the concrete, and $erf$ refers to the error function [37]. Equation (9) has also been tested in both laboratory and field environments, as documented in Reference [31]. This model demonstrates applicability to complex diffusion conditions in laboratory settings, despite having a moderate level of fitting error, and its computational complexity remains relatively low. However, in field applications, the model’s advantage becomes more apparent as it is better able to accurately explain the actual occurrence of nonlinear diffusion phenomena.

2.2. Considering the Time-Dependent Diffusion Coefficient Model

To enhance the simulation of chloride ion diffusion in concrete, many studies have proposed time-dependent diffusion coefficient models. These models recognize that the diffusion coefficient is not static but changes over time, primarily due to ongoing hydration reactions within the concrete, the evolving microstructure, and the effects of various physicochemical processes. By incorporating the time-varying nature of the diffusion coefficient, these models provide a more accurate representation of the actual diffusion behavior of chloride ions in concrete. Through a series of rapid diffusion tests, Luping et al. conducted in-depth investigations and found that the diffusion coefficient of chloride ions in concrete is not a fixed value but exhibits a significant correlation with time [39]. This relationship can be explicitly expressed as a mathematical function, which can be formulated as follows:

$$D\left(t\right)=D_0{(t/t_0)}^{-n}$$

(10)

In Equation (10), $D_0$ represents the effective diffusion coefficient of chloride ions in concrete during the initial exposure period or a specific time interval of the structure; $t_0$ refers to the time point corresponding to $D_0$; and $n$ is the time decay coefficient.

Therefore, in recognition of the time-varying nature of the chloride ion diffusion coefficient in concrete, various models have been proposed in the academic community to predict the diffusion behavior of chloride ion concentration within concrete as it ages.

Model I: Mangat et al. [40] simplified the process by combining the curing time $t_{ex}$ of the concrete before exposure to the environment with the subsequent total exposure time (i.e., the actual exposure time $t$ plus the curing time $t_{ex}$) and simplifying it into a time interval from 0 to $t$. Based on this, they constructed a computational model for describing the diffusion process of chloride ions in concrete.

$$C\left(x,t\right)=C_s\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{\frac{D_0}{1-n}{\left(\frac{t_0}{t}\right)}^{n}t}}}\right)\right]$$

(11)

In the literature [41], Equation (11) has been tested in both laboratory and field environments. This model typically exhibits a large and stable diffusion coefficient in laboratory settings, with a time exponent that tends to approach ideal values (such as n = 0.5). The boundary conditions are constant, resulting in high-fit results with a certain level of fitting error, albeit with relatively low computational complexity. However, in field applications, the model’s diffusion coefficient is significantly influenced by environmental factors, leading to large fluctuations. The time exponent may deviate from ideal values and requires field calibration. The boundary conditions are uncertain and require additional modeling. The fit may be lower and requires consideration of multiple influencing factors. Although this increases its computational complexity to some extent, the model can more accurately explain the actual nonlinear diffusion phenomena, demonstrating its significant advantages in field applications.

Model II: Luping et al. [42] conducted in-depth research on the combined influence of concrete curing time and soaking time on the calculation results, particularly highlighting the significant impact of curing time on the final calculation results. Based on this finding, they constructed a computational model.

$$C=C_s\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{D_{a}t}}}\right)\right]=C_s\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{\frac{D_0}{1-n}\left[{\left(1+\frac{t_{ex}}{t}\right)}^{1-n}-{\left(\frac{t_{ex}}{t}\right)}^{1-n}\right]}{\left(\frac{t_0}{t}\right)}^{n}t}}\right)\right]$$

(12)

Equation (12) has also been tested in both laboratory and field environments, as documented in Reference [41]. The model exhibits a diffusion coefficient that is easy to control and measure, with uniform medium characteristics and fixed boundary conditions. These conditions result in a shorter time scale for the model, with experiments typically completed within a few hours to a few days, yielding high-fit results despite a certain level of fitting error. The computational complexity is relatively low. However, in field applications, the diffusion coefficient of the model is affected by non-uniform and variable media, exhibiting dynamic changes and being difficult to measure directly. The boundary conditions also become dynamic, increasing the uncertainty of the model. Additional modeling is required to improve the fit, and the time scale extends to several months to several years. Therefore, field calibration of the model is necessary to adapt to different environmental conditions.

When concrete specimens are only briefly cured (denoted as $t_{ex}$) after molding or pouring and then directly exposed to an environment containing chloride salts, or when specimens are tested in a chloride salt solution in a simplified manner (as shown in Equation (11)), it is noteworthy that in laboratory immersion tests designed to study chloride ion diffusion behavior, the exposure time in the environment (denoted as $t$) is often much greater than the curing time $t_{ex}$. In such cases, the originally complex calculation model (as shown in Equation (12)) can be simplified. However, due to limitations in experimental conditions, it is often difficult to accurately simulate the aforementioned idealized relationship between curing and exposure times [43].

3. Considering the Time-Varying Model of Surface Chloride Ion Concentration

Currently, service life models used to predict the initiation time of chloride-induced corrosion of steel in concrete structures primarily rely on a simplified assumption, which treats the surface chloride concentration (Cs) as a critical boundary condition. When dealing with Cs, these models often adopt two strategies: one is to consider it as a constant, disregarding its dynamic changes in practical situations; the other is to acknowledge that Cs varies over time but simplifies it to a single function of time, neglecting numerous other complex factors that may affect Cs [44]. For example, the classic Fickian model adopts the assumption of a constant Cs, while some existing time-varying models, although improved, are still limited to treating Cs as a direct function of time, failing to fully capture the combined effects of the environment, material properties, and various physicochemical processes on Cs [45]. Therefore, these models have certain limitations in prediction accuracy and applicability.

Based on the above research status, various mathematical models have been proposed for the chloride ion concentration on concrete surfaces both domestically and internationally, including linear models [46,47], square root models [48,49], power function models [50,51,52], logarithmic models [40], and exponential models [52]. However, these models exhibit significant differences when describing actual data. Notably, recent related research has shown that exponential models demonstrate greater rationality and accuracy in describing the time-varying nature of chloride ion concentration on concrete surfaces [53].

Wang Zhanfei and Yang Dingyi [54], along with their colleagues, systematically studied the durability of reinforced concrete under sulfate and chloride salt erosion using the natural diffusion method. By measuring the chloride ion concentration on the concrete surface, they clarified the quantitative influence of water–cement ratio and sulfate ion concentration on this concentration. Considering the time-varying nature of chloride ion concentration, they accurately fitted the experimental data using an exponential model, which can be expressed as:

$$C_s\left(t\right)=D_{\max }\left(1-e^{-rt}\right)$$

(13)

In Equation (13), $C_s\left(t\right)$ represents the chloride ion concentration on the concrete surface at time $t$; $D_{\max }$ represents the chloride ion concentration on the concrete surface after it has stabilized; $r$ is the fitting coefficient for the accumulation factor; and $t$ represents the erosion time.

Given the abundance of sulfate ions in the marine environment, which inevitably affects the chloride ion concentration on the concrete surface, they constructed a time-varying model for the chloride ion concentration on the concrete surface based on a comprehensive consideration of both the water–cement ratio and sulfate ion concentration. The mathematical expression for this model [54] is:

$$C_{S{A}_1{K}_1}\left(t\right)=A_1{D}_{\max }{k}_1\left(1-e^{-rt}\right)$$

(14)

In Equation (14), $t$ represents the erosion time, $C_{S{A}_1{K}_1}\left(t\right)$ stands for the surface chloride ion concentration at erosion time $t$, considering the influence of sulfate and water–cement ratio; $K_1$ is the coefficient representing the influence of water–cement ratio on the stabilized surface chloride ion concentration ($D_{\max }$); and $A_1$ reflects the impact of sulfate ions on the chloride ion concentration ($C_s$) on the concrete surface.

When constructing a predictive model for chloride ion diffusion within concrete, considering the comprehensive effects of time-varying chloride ion concentration on the concrete surface, chloride binding capacity, chloride diffusion coefficient, and microdefects in the concrete structure, the expression is usually based on Fick’s second law or its modified form, incorporating quantitative parameters for these influencing factors. The formula is as follows:

$$C\left(x,t\right)=A_1{D}_{\max }{k}_1\{1-erf({\displaystyle \frac{x}{4K{D}_{0}t}})-e^{-{\displaystyle \frac{x^2}{4K{D}_{0}t}}}\mathrm{Re}\left[e^{-g^2}erfc(-ig)\right]\}$$

(15)

In Equation (15), $g={(rt)}^{1/2}+i{\displaystyle \frac{x}{4K{D}_{0}t}},i={(-1)}^{1/2}$ $\mathrm{Re}$ denotes taking the real part, $x$ represents the distance from the surface within the concrete, $C\left(x,t\right)$ is the chloride ion concentration at position $x$ and time $t$, $t$ is the age of the structure, $D_0$ is the chloride ion diffusion coefficient, $D_{\max }$ is the stabilized surface chloride ion concentration, $K_1$ is the coefficient representing the influence of water–cement ratio on the stabilized surface chloride ion concentration, and $A_1$ reflects the impact of sulfate ions on the chloride ion concentration on the concrete surface. In the Reference [55], Equation (15) has been tested in laboratory settings. The model demonstrates a diffusion coefficient that is easy to control and measure, with uniform medium characteristics, fixed boundary conditions, and a short time scale. It is capable of obtaining a precisely measured and uniformly distributed concentration, with a high degree of fitting for experimental results. However, in field applications, the diffusion coefficient of the model dynamically changes due to the influence of non-uniform and variable media, and the boundary conditions are uncertain. The concentration distribution becomes complex as it fluctuates with environmental conditions. These characteristics of field data lead to difficulties in optimizing complex parameter terms, increasing the challenge of field application.

Zheng Shansuo and his colleagues, in accordance with the relevant provisions of the “Technical Standard for Testing of Building Structures” (GB/T 50344-2019) [56], accurately determined the chloride ion content in core samples drilled from concrete structures using the silver nitrate titration method. From this, they estimated the chloride ion concentration near the surface of the steel reinforcement (denoted as $C_s$) to assess the corrosion risk of the steel in the concrete. Furthermore, they found that the chloride ion concentration on the steel surface ($C_s$) exhibits specific variation patterns as the age of the concrete structure increases. To more precisely capture the variation pattern of chloride ion concentration with the aging of the concrete structure, a quadratic polynomial model was utilized for fitting. The resulting mathematical expression is as follows:

$$C_s=-1.358\times {10}^{-4}{t}^2+1.536\times {10}^{-2}t-0.166$$

(16)

In Equation (16), $t$ represents the age of the structure, and $C_s$ denotes the chloride ion concentration.

The study found that the chloride ion concentration on the surface of steel reinforcement exhibits a gradual accumulation trend as the age of the concrete structure increases, but the rate of this accumulation significantly slows down. This phenomenon is mainly attributed to two aspects: firstly, as the service time of the structure extends, the hydration reaction inside the concrete continues to deepen, resulting in a denser structure that reduces the penetration pathways for chloride ions. Secondly, the accumulation of chloride ion concentration inside the concrete gradually reduces the chloride ion concentration gradient and potential difference between the surface and the interior of the concrete, thereby slowing down the migration rate of chloride ions towards the steel reinforcement surface. This manifests as a gradual decrease in the surface chloride ion concentration as the service age of the structure increases [44].

Mahmoud Shakouri and David Trejo proposed an enhanced S-shaped time-varying $C_{\mathrm{s}}$ model that not only meticulously describes the dynamic changes of $C_s$ with exposure time but also innovatively incorporates the cumulative effect of exposure time and variations in chloride concentration in the exposure environment into consideration [45]. By utilizing optimal subset sampling analysis techniques, they carefully screened and evaluated the experimental data, aiming to accurately identify the independent and interactive effects of water–cement ratio, exposure duration, chloride concentration in the exposure environment, and time factors on $C_{\mathrm{s}}$.

The experimental results show that regardless of the specific settings of the water–cement ratio and exposure conditions, $C_{\mathrm{s}}$ exhibits a trend of increasing over time. This finding is consistent with the previous research conclusions of Moradllo et al. [57] and Annet et al. [58]. Moradllo et al. [57] confirmed the phenomenon of increasing $C_{\mathrm{s}}$ content over time but did not reveal a clear growth pattern or trend. Similarly, Annet et al. [58] reported that chloride accumulates gradually on the surface of concrete in marine environments over time. However, they also observed that the difference in this surface chloride accumulation gradually diminishes as time progresses.

A possible explanation for the aforementioned phenomenon is that when concrete samples are removed from the curing environment and rapidly exposed to a solution containing chloride ions, their surfaces quickly reach saturation. In contrast, if the concrete samples are exposed to such an environment at a later stage, due to the potentially drier surface and internal microstructure, chloride ions can penetrate more rapidly into the interior of the concrete. This rapid transport of chloride ions to deeper layers actually slows down the accumulation rate of chloride ions on the surface. However, as time passes, the concrete gradually becomes more saturated overall, at which point chloride ions are more inclined to accumulate on the surface, leading to an increase in surface chloride ion concentration. The improved model constructed demonstrates significantly enhanced capabilities in predicting the behavior of $C_s$ in concrete exposed to chloride environments. Specifically, the model can more accurately simulate and predict the dynamic changes of $C_s$ within the concrete. Furthermore, when using this model to predict the service life of concrete structures, the results obtained are more precise and reliable compared to traditional methods, providing a stronger basis for decision-making by owners and effectively reducing potential financial losses and engineering risks.

Table 1. Concrete mix proportion in some literature.

Model	Cement Content (kg/m3)	Water–Cement Ratio	Aggregate Content (kg/m3)	Fly Ash Content (%)	Slag Powder Content (%)
Reference [25]	350	0.5	1900	10	0
Reference [38]	380	0.45	1950	12	8
Reference [40]	400	0.4	2000	20	15
Reference [54]	370	0.48	1940	10	10

provides the mix proportions of concrete used in experiments reported in some literature.

Table 2. Comparison of some empirical models.

Model	Application Scope and Reliability
The model in reference [25]: $C\left(x,t\right)=C_0+\left(C_S-C_0\right)\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{t{D}_{\mathrm{cl}}}}}\right)\right]$ $C(x,t)$: the concentration of at the erosion depth $x$ at the erosion age $t$; $C_0$: the initial concentration of $C{l}^{-}$; $C_s$: the surface concentration of $C{l}^{-}$; $D_{cl}$: the diffusion coefficient of $C{l}^{-}$ $erf(x)$: the Gaussian error function.	This model is mainly applicable to classic diffusion, with constant diffusion coefficients and semi-infinite media. This model is simple and easy to use, suitable for basic diffusion problems but unable to describe nonlinear diffusion, with significant spatial limitations. Compared to actual measurements in marine environments, its applicability in field applications is limited, making it difficult to adapt to nonlinear diffusion scenarios.
The model in reference [38]: $c_f=c_0+\left(c_s-c_0\right)\left[1-erf{\displaystyle \frac{x}{2\sqrt{\frac{K{D}_0{t}_0^m}{\left(1+R\right)\left(1-m\right)}}·t^{1-m}}}\right]$ $c_0$: the initial chloride ion concentration within the concrete; $c_s$: the chloride ion concentration at the exposed surface of the concrete; $erf$: error function; $K$: the coefficient of deterioration in the chloride diffusion performance of the concrete $D_0$: the chloride diffusion coefficient of the concrete measured at the hydration age; $m$: experimental constant $t_0$: the hydration age of the concrete	This model is primarily applicable to nonlinear diffusion where the diffusion coefficient varies over time. This model is more aligned with actual complex situations, featuring flexible parameters but complex calculations, and relies on experimental data for parameter fitting. Compared to actual measurements in marine environments, the advantages of this model become even more evident, as it is better able to accurately explain the actual occurrence of nonlinear diffusion phenomena.
The model in reference [40]: $C\left(x,t\right)=C_s\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{\frac{D_0}{1-n}{\left(\frac{t_0}{t}\right)}^{n}t}}}\right)\right]$ $C(x,t)$: the concentration of at the erosion depth $x$ at the erosion age $t$ $C_s$: the surface concentration of $C{l}^{-}$ $erf$: error function; $D_0$: the chloride diffusion coefficient of the concrete measured at the hydration age; $t_0$: the hydration age of the concrete	This model is suitable for systems that can be described using time-dependent diffusion, offering high accuracy in its predictions. The computational cost of this model is relatively low, requiring precise measurements of diffusion-related parameters and concentration distribution data. The difficulty in obtaining these data depends on the complexity of the system. Compared to actual measurements in marine environments, the diffusion coefficient of this model is susceptible to significant influence from environmental factors, resulting in larger fluctuations. However, the model’s ability to more accurately explain actual nonlinear diffusion phenomena demonstrates its significant advantages in field applications.
The model in reference [43]: $C=C_s\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{D_{a}t}}}\right)\right]=C_s\left[1-erf\left({\displaystyle \frac{x}{2\sqrt{\frac{D_0}{1-n}\left[{\left(1+\frac{t_{ex}}{t}\right)}^{1-n}-{\left(\frac{t_{ex}}{t}\right)}^{1-n}\right]}{\left(\frac{t_0}{t}\right)}^{n}t}}\right)\right]$ $C_s$:the surface concentration of $C{l}^{-}$ $erf$: error function; $x$: Depth; $t$: Time	This model exhibits strong descriptive capability and high accuracy for complex diffusion processes. The formula of this model is relatively complex, and numerical simulations and parameter fitting may increase computational costs, especially when dealing with large-scale grids or multi-parameter optimization. It necessitates precise measurements of multiple parameters and experimental data, making it suitable for research and applications where sufficient data are available. Compared to actual measurements in marine environments, the diffusion coefficient of this model is influenced by inhomogeneous and variable media, exhibiting dynamic changes that are difficult to measure directly.
The model in reference [54]: $C\left(x,t\right)=A_1{D}_{\max }{k}_1\{1-erf({\displaystyle \frac{x}{4K{D}_{0}t}})-e^{-{\displaystyle \frac{x^2}{4K{D}_{0}t}}}\mathrm{Re}\left[e^{-g^2}erfc(-ig)\right]\}$ $C\left(x,t\right)$: the chloride ion concentration at position $x$ and time $t$ $D_{\max }$: the stabilized surface chloride ion concentration $K_1$: the coefficient representing the influence of water–cement ratio on the stabilized surface chloride ion concentration $A_1$: the impact of sulfate ions on the chloride ion concentration on the concrete surface $erf$: error function; $D_0$: the chloride diffusion coefficient of the concrete measured at the hydration age; $g={(rt)}^{1/2}+i{\displaystyle \frac{x}{4K{D}_{0}t}},i={(-1)}^{1/2}$	This model is suitable for describing diffusion processes under specific conditions, especially those involving dynamic changes in both time and space variables. This model can be applied to diffusion processes under complex boundary conditions, taking into deep consideration the changes of substances over different times. However, it features complex mathematical expressions, large computational demands, and sensitivity to input parameters, requiring precise measurements. Compared to actual measurements in marine environments, during field applications of this model, the diffusion coefficient undergoes dynamic changes due to the influence of inhomogeneous and variable media, and the boundary conditions are also uncertain. This adds challenges to its field application.

summarizes and compares the performance of the aforementioned empirical models when applied in laboratory or field environments.

4. Numerical Simulation Model

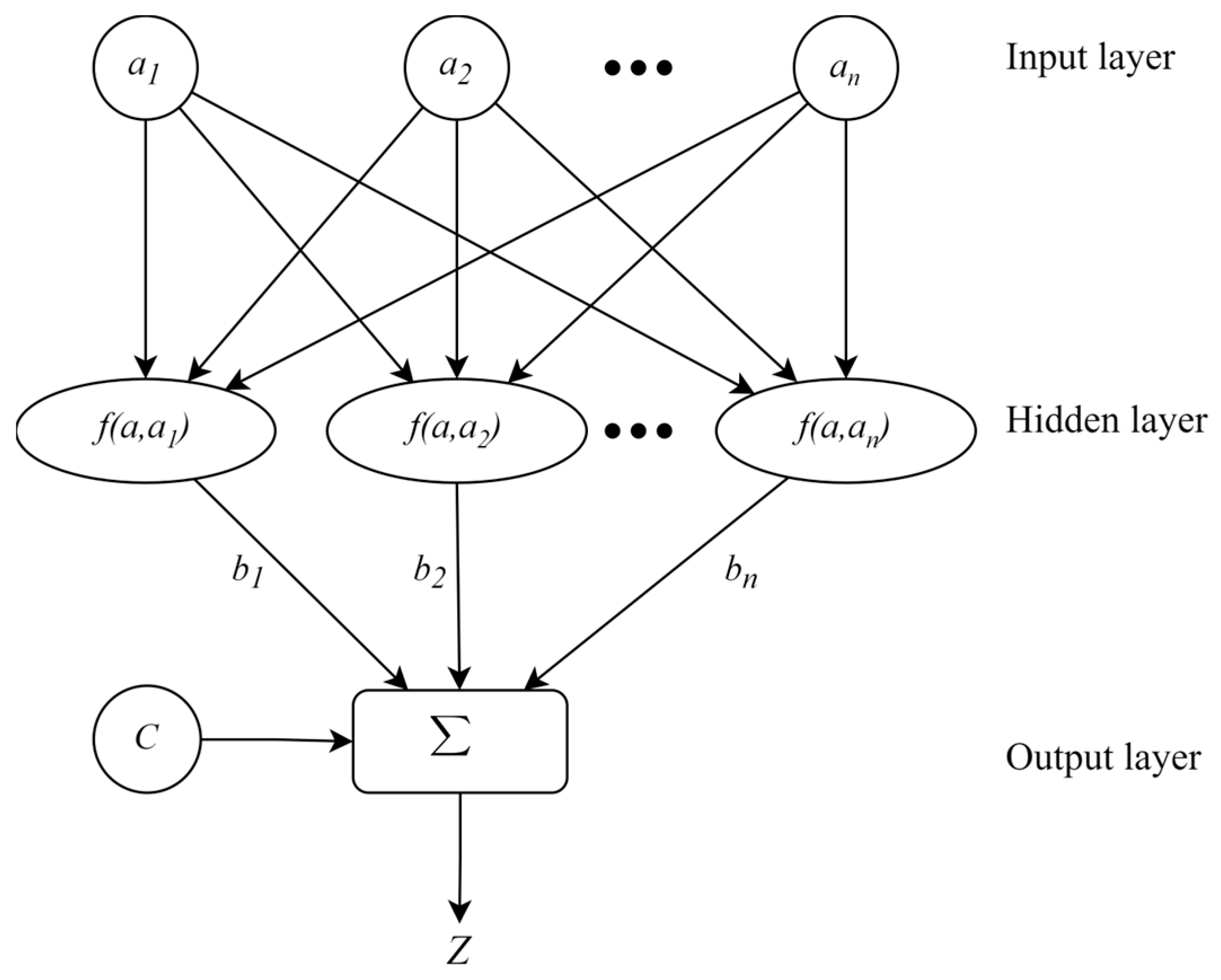
Artificial Neural Network Prediction Model

ANNs are inspired by early models of sensory processing in the brain and are considered a soft computing approach. Their architecture generally consists of input, hidden, and output layers. The hidden layer connects with other layers through weights, biases, and transfer functions. The discrepancy between the network’s output and the intended target establishes the error function, which is then propagated backward, leading to adjustments in weights and biases using optimization techniques [59]. This iterative process, known as training, allows the network to learn by simulating neural processes, refining its output accuracy over repeated cycles. Once trained, the network can validate unseen data using the optimized weights and biases. Over time, significant advancements have been made, leading to the development of numerous network models that improve machine learning efficiency. Examples include BP, CNN, and WNN models, among others [60]. Each model is tailored to solve specific problems; for instance, CNNs are often used in image recognition, while WNNs are employed in signal processing. As research progresses, these models evolve, becoming essential tools in various fields, including architecture. ANNs offer two primary benefits: they enable direct learning and data analysis while also handling complex modeling tasks, such as identifying outliers. This capacity to directly analyze large datasets and manage intricate modeling processes makes ANNs particularly valuable for addressing complicated data scenarios [61].

In recent years, the application of ANN methods has significantly increased in modeling studies of chloride ion content in concrete. The Parichatprecha team, Song team, and Hodhod team utilized datasets of 86, 120, and 300, respectively, combined with relevant input parameters of concrete mix proportions, to construct models for the variation of chloride ions in high-performance concrete (HPC) with structural age. Jin L, Dong T, Fan T [62], and others demonstrated the feasibility of ANNs in studies on chloride ions in recycled coarse aggregates (RAC). The results showed that ANNs are effective tools for analyzing chloride ion properties of RACs from different sources. Liu et al. [63] utilized the characteristics of ANN technology to establish a reasonable and effective prediction model for the chloride ion diffusion coefficient in concrete. The research results indicated that ANNs can be used as an effective tool with strong predictive potential. Shaban et al. [64] proposed a physics-informed deep neural network to simulate the diffusion mechanism of chloride ions in concrete and predict the distribution of chloride ion concentrations. The results showed that the model could effectively simulate the transport behavior of chloride ions and predict the diffusion coefficient of concrete with high accuracy. Asghshahr et al. [65] used accelerated chloride ion permeation tests under laboratory conditions simulating marine environments to develop classification and regression tree (CART) and ANN as subsets of artificial intelligence methods. The results showed that both ANN and CART had good ability and accuracy in predicting chloride ion concentrations in concrete under marine environmental conditions. In current research, ANN methods have demonstrated higher accuracy. Delgado et al. [66] used ANN modeling to map the relationship between the analyzed variables and ion penetration depth. The results showed that the ANN model could effectively estimate the penetration depth and diffusion coefficient of chloride ions in concrete. Mohamed et al. [67] utilized ANNs to predict chloride penetration levels, using 294 data points for training and validation. This trained ANN was used to validate 20 experimentally assessed specimens of self-consolidating concrete (SCC) with different compositions for chloride ion penetration levels. When the chloride ion concentration exceeds the chloride threshold (CT), active corrosion occurs in carbon steel in reinforced concrete. Zhu et al. [68] adopted a coupled method of Kohonen self-organized map (KSOM) and regression ANN to find missing values of independent variables in sparse databases and quantitatively assess the impact of these variables represented by [Cl]/[OH] on CT values. ANNs are widely used because they can effectively capture the nonlinear relationship between chloride ion concentrations in concrete and various input variables, while also making good predictions for unseen data, thus demonstrating strong generalization ability [69,70]. However, neural network models also have certain limitations. For instance, they have strict requirements for the quantity and quality of data. Compared to empirical models, neural network models exhibit greater complexity, longer training times, and poorer interpretability [60,61,62,63,64,65,66,67,68,69,70]. Specifically, if the network structure is too complex or the training data are insufficient, the model may overfit, performing well on the training set but poorly on the test set [71]. The training times of neural network models, when compared quantitatively with other methods, can typically be provided through timing functions in numerical simulation software. Therefore, further research is needed to optimize the use of ANNs in predicting chloride ion concentration models in concrete. Batch normalization is widely adopted to improve training speed and stability. Studies have shown that standardizing inputs helps reduce internal covariate shift and improve the convergence speed of neural networks [72]. Barret Zoph and Quoc V. Le [73] introduced a method using reinforcement learning for neural architecture search to automate the design of optimal network structures. The results showed that the networks obtained using this method performed better than manually designed networks on multiple tasks. Their research aims to establish relationship models between various influencing factors and chloride ion concentrations, and through regularization techniques and optimization algorithms, the risk of overfitting can be effectively reduced, enabling the model to have better generalization ability on unseen data. These optimizations make the data fitting for chloride ion concentration changes more accurate.

In the field of predictive modeling, there exist other neural network models as well. One such model is the BP (Back Propagation) neural network, which is a multi-layer feedforward network propagation algorithm trained through error backpropagation and possessing strong nonlinear mapping capabilities [74]. Numerous researchers have conducted in-depth explorations and optimizations of the BP neural network. Zheng and Cai employed the Extreme Gradient Boosting (XGBoost) algorithm, the Back Propagation (BP) algorithm, the Support Vector Regression (SVR) algorithm, and the BP algorithm optimized by the Bayesian formula to predict chloride ion diffusion coefficients (CIDC). The research results indicate that the Bayesian-BP model yields the best prediction performance [75].

Yao et al. employed a Particle Swarm Optimization (PSO) algorithm based on the BP neural network to predict chloride ion penetration in concrete. The PSO-BP neural network can improve upon the shortcomings of the BP neural network. By comparing the results of PSO-BP, BP, and experimental data, it was found that the accuracy of the PSO-BP neural network is superior to that of the BP neural network [76]. Li et al. combined the Black Widow Optimization (BWO) algorithm with the BP neural network, further enhancing the model’s performance and achieving high detection accuracy [77]. Feng et al. utilized the Bat Algorithm (BA), Ant Colony Optimization (ACO), and Particle Swarm Optimization (PSO) to optimize the model. Through comparison, it was discovered that the PSO-BPNN model exhibits the highest accuracy in predicting the correlation between concrete mix proportions, RC durability, and chloride ion concentration [78].

The decision tree prediction model has proven to be highly effective in forecasting changes in chloride ion concentration within concrete as it ages, showing substantial advancements in the last twenty years. This robust method facilitates the extraction of insights from intricate datasets, allowing for the creation of precise predictive models. The algorithm works by systematically partitioning a dataset into smaller subsets based on specific criteria, ultimately resulting in a tree-like structure. This organized framework can then be utilized for making reliable predictions and informed decisions [79,80,81]. A decision tree [82] is a machine learning technique that determines classification labels for samples by formulating a series of questions derived from the features of a training dataset. Serving as a core instrument in machine learning and decision theory, a decision tree comprises a root node, various internal nodes, and multiple leaf nodes. The leaf nodes indicate the final decision outcomes, whereas the internal nodes correspond to feature evaluations. The structure of a decision tree is depicted in Figure 2 [83].

In comparison to various other artificial intelligence prediction models, decision tree models are advantageous due to their simplicity and ease of visualization, as they do not require extensive data preprocessing. However, these models often struggle with complex datasets and a wide range of problems, making them susceptible to overfitting. Furthermore, when applied to large datasets, decision trees can exhibit significant instability in response to minor data changes, with even small variations potentially resulting in dramatically different predictions [84]. To overcome these limitations, it is recommended to adopt decision trees as the base model within ensemble algorithms and improve prediction accuracy by integrating a large number of decision trees within the ensemble [85]. Tran et al. proposed the application of the Enhanced Decision Tree Boosting (EDT Boost) model to predict the surface chloride concentration of marine concrete $C_s$, and established and validated the predictive capability of the EDT model [86]. Random Forest is an ensemble learning method based on the decision tree algorithm. Golafshani et al. introduced two new extensions of ensemble artificial intelligence algorithms: Genetic Programming Forest (GPF) and Linear Genetic Programming Forest (LGPF), which were used for modeling the chloride diffusion coefficient (DC) in concrete. Additionally, the Random Forest (RF) method was employed as a comparative control ensemble technique. The results showed that the optimal LGPF model performed better than the optimal GPF and RF models [87]. Cai et al. developed and applied an ensemble ML model to predict the chloride concentration on the surface of concrete. The results indicated that, by incorporating RF predictions, the ensemble ML model achieved higher prediction accuracy and performance compared to all standalone ML models tested in this study [88]. Breiman [89] introduced the Random Forest technique, which is frequently used for regression and classification problems due to its excellent accuracy and flexibility.

SVM is a widely used supervised learning technique in machine learning, applicable for both classification and regression tasks [90]. SVM is well-known for its robust generalization capability [91,92]. SVM can be applied to either classification or regression analysis of chloride concentration. For handling nonlinear problems, through the use of kernel functions, SVM is able to process nonlinear data, allowing it to perform well in complex chloride concentration models [93,94]. Additionally, SVM has built-in feature selection capabilities, which can identify the variables that have the greatest impact on chloride concentration, thereby simplifying the model [95]. However, there are also certain limitations. The performance of SVM highly depends on the choice of parameters, and cross-validation is required to determine the optimal parameters. In the modeling process of Support Vector Machines (SVM), the choice of kernel function is crucial. The linear kernel is suitable for linearly separable data and is computationally efficient. For nonlinearly separable data, the Radial Basis Function (RBF) kernel exhibits a relatively high computational complexity, especially on large-scale datasets. The polynomial kernel is also applicable to nonlinearly separable data. Furthermore, the regularization parameter C controls the model’s tolerance for error: a larger C value may lead to overfitting, where the model has a low tolerance for error and strives to avoid classification mistakes; conversely, a smaller C value may result in underfitting, where the model has a high tolerance for error. Therefore, in practical applications, it is necessary to select the appropriate kernel function and regularization parameter C based on the characteristics and specific requirements of the data to achieve optimal classification performance and model complexity. Figure 3 [83] illustrates the basic working structure of SVM.

SVMs have become highly valuable in the construction industry, where accurate predictions of concrete mechanical properties are essential to ensure structural safety and durability. Originally introduced by Vapnik in 1963, the SVM algorithm was later adapted into a nonlinear model by Vapnik and Kurt [96] in 1995. Since that time, researchers have made significant advancements in optimizing and enhancing SVM algorithms. This has led to extensive research showcasing the strong potential of SVMs in concrete studies. For instance, Cevik et al. [97] conducted a review and analysis of SVM applications in structural engineering, demonstrating its effectiveness in this domain. Chaabene et al. [98] developed a Support Vector Regression (SVR) model that utilizes SVM for regression tasks. Zhang et al. [99] proposed a hybrid prediction framework that integrates LSSVM with a metaheuristic algorithm. Zhen et al. concluded that the Particle Swarm Optimization–Support Vector Regression (PSO-SVR) model exhibits significant accuracy and generalization ability, being closer to actual values on both the training and test sets [100]. Li et al. proposed methods for predicting chloride diffusion coefficients in concrete using both SVMs and ANNs, and compared the accuracy of the two methods [64]. Zewdu et al. studied the application of SVMs in concrete with different water–cement ratios, demonstrating that SVMs perform excellently in predicting chloride diffusion coefficients under various parameter combinations [101].

In the context of predicting chloride ion concentration in concrete, SVM, Decision Tree, and ANN can all provide effective modeling approaches, but they have different advantages, disadvantages, and suitability for different applications. By considering the characteristics of chloride ion concentration models, we can further analyze the application strengths and limitations of these algorithms. The application advantages of SVM in chloride ion concentration models are as follows: ① Suitability for high-dimensional data: Chloride ion concentration models involve many influencing factors (such as temperature, humidity, concrete mix ratio, etc.), resulting in a high number of feature dimensions. SVM performs well in high-dimensional feature spaces. ② Effective handling of nonlinear relationships: Chloride ion diffusion may be influenced by complex and nonlinear relationships among multiple factors. SVM can effectively map these relationships through kernel functions, especially when the model involves nonlinear diffusion equations. The disadvantages include: ① High computational complexity: Concrete chloride ion concentration datasets may be large and contain many features, leading to long training times and high computational costs for SVM. ② Sensitivity to noisy data: If there is noise or outliers in the chloride ion concentration data, the performance of the SVM model may be affected. The advantages of Decision Trees are: ① Easy to interpret and visualize: The clear hierarchical structure of a Decision Tree helps in understanding the influence of various factors (such as temperature, humidity, etc.) on chloride ion concentration. ② Efficient computation: For chloride ion prediction scenarios with large datasets and high real-time requirements, Decision Trees have high computational efficiency and are suitable for rapid modeling. ③ Low data preprocessing requirements: Concrete chloride ion concentration model data may contain both numerical and categorical features, which Decision Trees can handle without additional processing. However, Decision Trees are prone to overfitting on training data, especially if the data sampling is limited or biased towards a specific distribution, which may reduce the accuracy of chloride ion concentration predictions. The application of ANNs in chloride ion concentration models allows for fitting complex nonlinear relationships, particularly suitable for large-scale and complex models with abundant data. Moreover, for chloride ion diffusion data involving multiple levels and multi-time scales, ANNs have good adaptability and can capture implicit relationships among data through deep networks. However, ANNs perform moderately under conditions of small sample data. For situations with limited chloride ion concentration data, they may not be applicable.

Table 3. Advantages and disadvantages of common machine learning models in predicting chloride ion concentration.

Model	SVM	DT	ANN
advantage	Suitable for high-dimensional and nonlinear relationships with strong generalization ability.	Highly interpretable, clear structure, and efficient computation.	Strong nonlinear modeling capability, good robustness, suitable for multi-level data.
Defect	High computational complexity and sensitive to noise.	Prone to overfitting and sensitive to distribution and noise.	Long training time, poor interpretability, and poor performance with small sample sizes.
Applicable scenarios	Prediction of chloride ion concentration for high-dimensional and complex relationships.	Prediction of chloride ion concentration with clear data and strong visualization requirements.	Prediction of chloride ion concentration with multiple factors, large data volumes, and complex nonlinear relationships.
Dataset Size	Small to medium-sized datasets (hundreds to thousands of samples)	Small to large datasets (hundreds to tens of thousands of samples)	Medium to large datasets (thousands to millions of samples)

presents the advantages and disadvantages of the three modeling methods in predicting chloride ion concentration in concrete.

5. Challenges and Suggested Improvements

Traditionally, predictions of chloride ion concentration have primarily relied on mathematical models based on diffusion theory, such as the Fick’s diffusion model, which describes the change in concentration over time and diffusion distance by assuming a constant diffusion coefficient. While these models are computationally simple, they have some obvious limitations. Since the diffusion coefficient is influenced by environmental factors such as temperature and humidity in practical situations, traditional models struggle to effectively account for these variations, leading to insufficient prediction accuracy. To improve effectiveness, it is recommended to experimentally correct the diffusion coefficient or add environmental correction factors to make the model closer to reality. With the increase in data availability and computational power, machine learning models (such as SVM, RF, ANN, etc.) have been widely applied to predict chloride ion concentration. These models can integrate multi-dimensional input data (including concrete properties and environmental factors) to establish complex nonlinear relationships. However, machine learning models depend on a large amount of high-quality data, which is not easily obtained and can be of varying quality in practice. Furthermore, complex models like deep neural networks are difficult to interpret and prone to overfitting when data are insufficient. It is recommended to enhance the prediction reliability of machine learning models in this direction through data augmentation, model optimization, and multi-model fusion. Future trends may focus on hybrid models combining physics and data-driven approaches, such as Physics-Guided Machine Learning, which integrates the theoretical foundation of mathematical models with the flexibility of machine learning. This approach enables more accurate predictions by leveraging real-time data while adhering to physical laws.

6. Conclusions

This article summarizes the existing prediction models for chloride ion concentration as it varies with the age of structures. The main conclusions are as follows:

• Empirical models provide a theoretical foundation for predicting chloride ion concentration. By utilizing formulas based on diffusion theory, such as the Fick’s diffusion model, these models describe the process of chloride ion diffusion in concrete over time. Such models are concise, easy to understand, and possess a certain degree of physical plausibility. However, in practical applications, they are susceptible to variations in environmental factors. Due to the difficulty in encompassing all influencing factors, the prediction accuracy of empirical models is relatively limited. The key to improving these models lies in experimental calibration and the introduction of correction factors to make them more adaptable to different operating conditions.
• ANN has received considerable attention in chloride ion concentration prediction due to its powerful nonlinear fitting capabilities. ANN is capable of processing a large number of complex input variables and learning the intricate relationships governing concentration changes through its deep network structure. However, neural network models have stringent requirements for the quantity and quality of data. In large sample sets, compared to empirical models, neural network models exhibit greater complexity, longer training times, and poorer interpretability. This is attributed to their intricate structures and numerous parameters, whereas empirical models boast simple structures, fewer parameters, and clear physical meanings, making them less demanding in terms of data requirements. In chloride ion prediction, ANN is suitable for scenarios with sufficient data support, and it requires precise regulation of the model’s training process and parameter adjustments to achieve good prediction results.
• Decision tree models possess high interpretability in chloride ion concentration prediction, as they can intuitively demonstrate the contribution of each feature to the prediction results through a tree structure. Decision trees are easy to understand and implement, making them suitable for processing small-scale data. However, their prediction accuracy may be limited by the depth of the tree structure and data fluctuations, and a single tree model may suffer from overfitting when the data contain significant noise. Ensemble methods based on decision trees (such as Random Forests) can enhance the stability and accuracy of predictions, making them suitable for short- to medium-term predictions of chloride ion concentration in concrete as it varies with age.
• SVM, with its ability to establish boundary classification in high-dimensional spaces, is suitable for predicting chloride ion concentration as it varies with age. SVM can effectively handle nonlinear relationships and maintains good generalization performance even with limited data. However, SVM is highly sensitive to parameters, and selecting appropriate kernel functions and regularization parameters based on the data characteristics is necessary to achieve good prediction results. SVM is suitable for scenarios with moderate data size and clear features, but the computational complexity is higher when dealing with large data volumes and numerous features.
• In the prediction of chloride ion concentration as it varies with age, machine learning methods perform well overall and can flexibly handle various complex relationships. By combining multiple models (such as decision trees, neural networks, support vector machines, etc.) with methods like feature selection and regularization, machine learning is able to capture the nonlinear dynamic characteristics of chloride ion diffusion. Although it has high requirements for data and computational resources, machine learning models can effectively improve prediction accuracy and stability through algorithm optimization and multi-model integration. With the increase in data volume and advancements in algorithms, machine learning will continue to play an important role in the prediction of chloride ion concentration in concrete.