Review of Condition Rating and Deterioration Modeling Approaches for Concrete Bridges
Abstract
1. Introduction
2. Materials and Methods
3. Scientometric Review
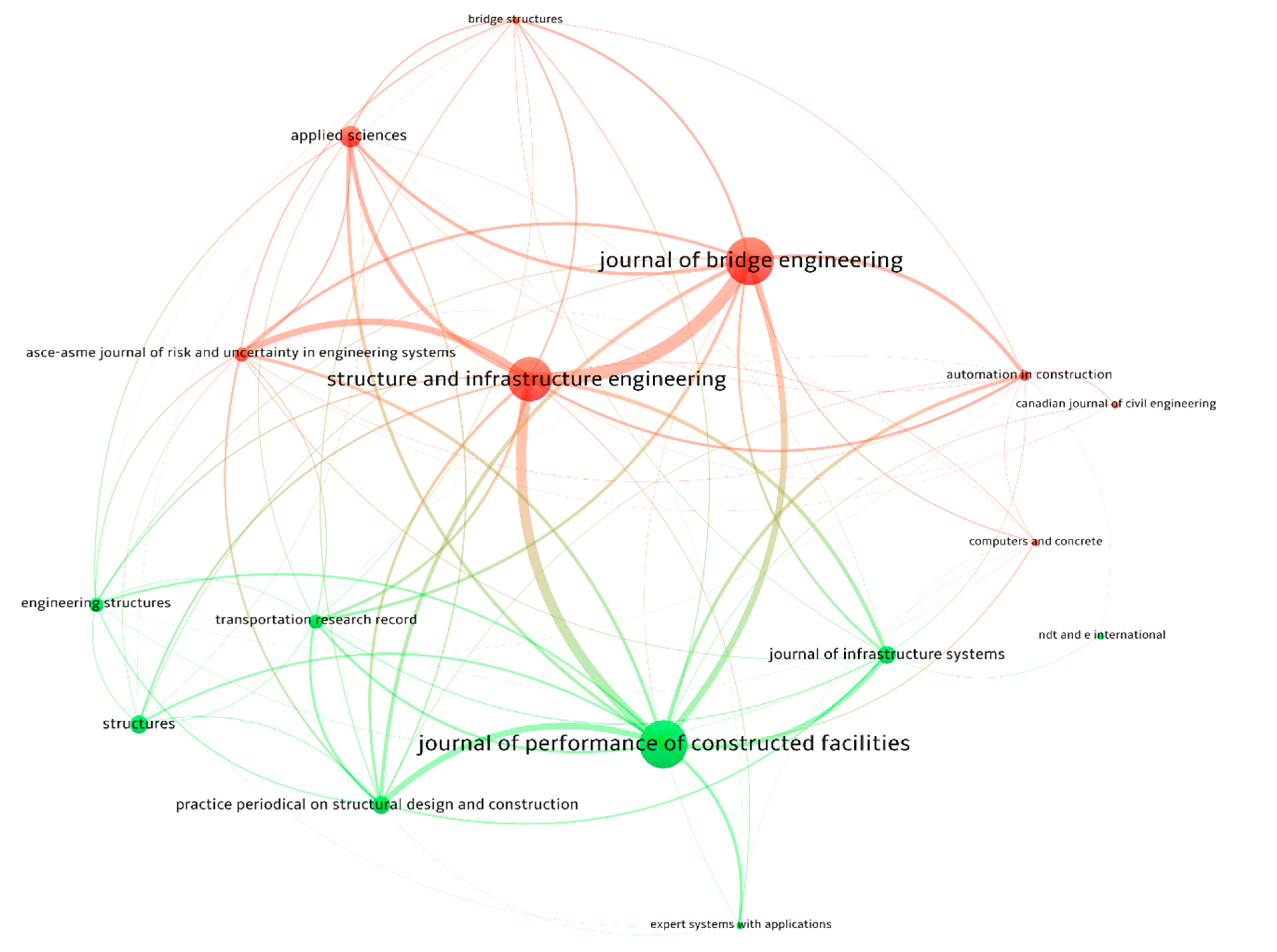
3.1. Journals Co-Citation Analysis
3.2. Leading Institutions and Authors
3.3. Keywords Analysis
3.3.1. Most Occurred Author Keywords
3.3.2. Keyword Co-Occurrence Map
3.3.3. Temporal Analysis
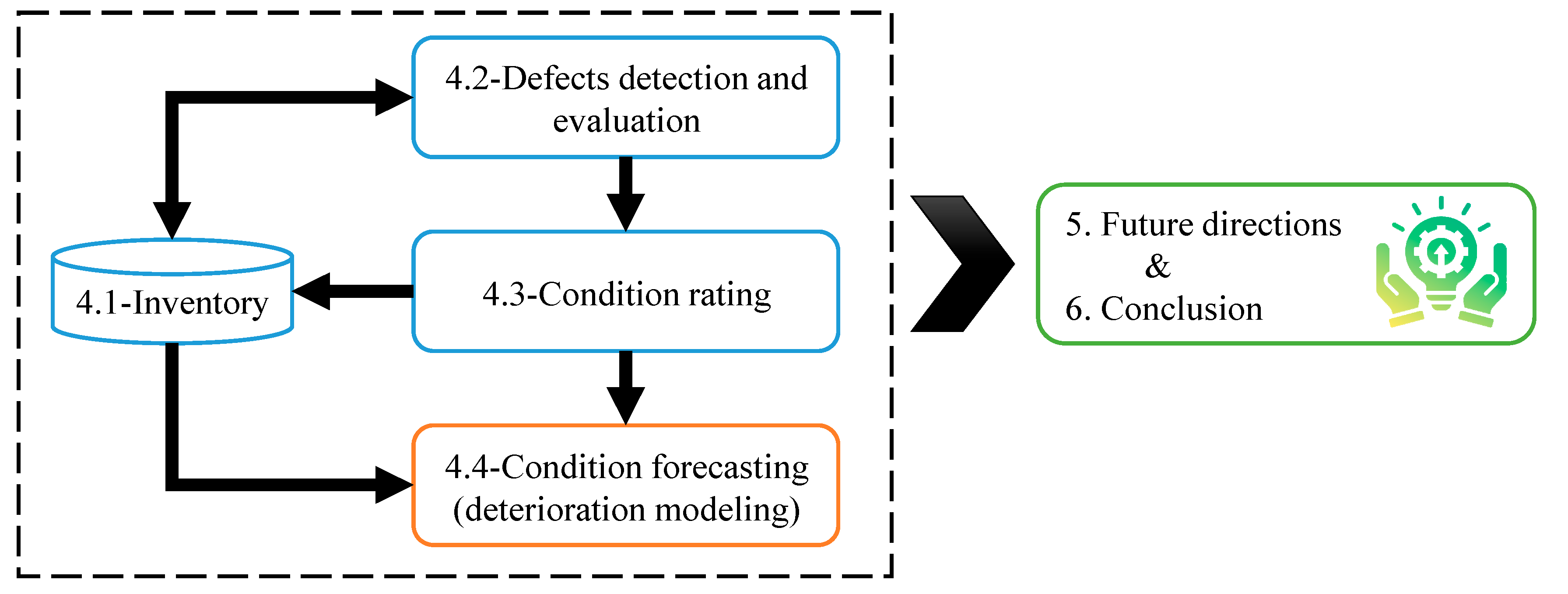
4. Systematic Review
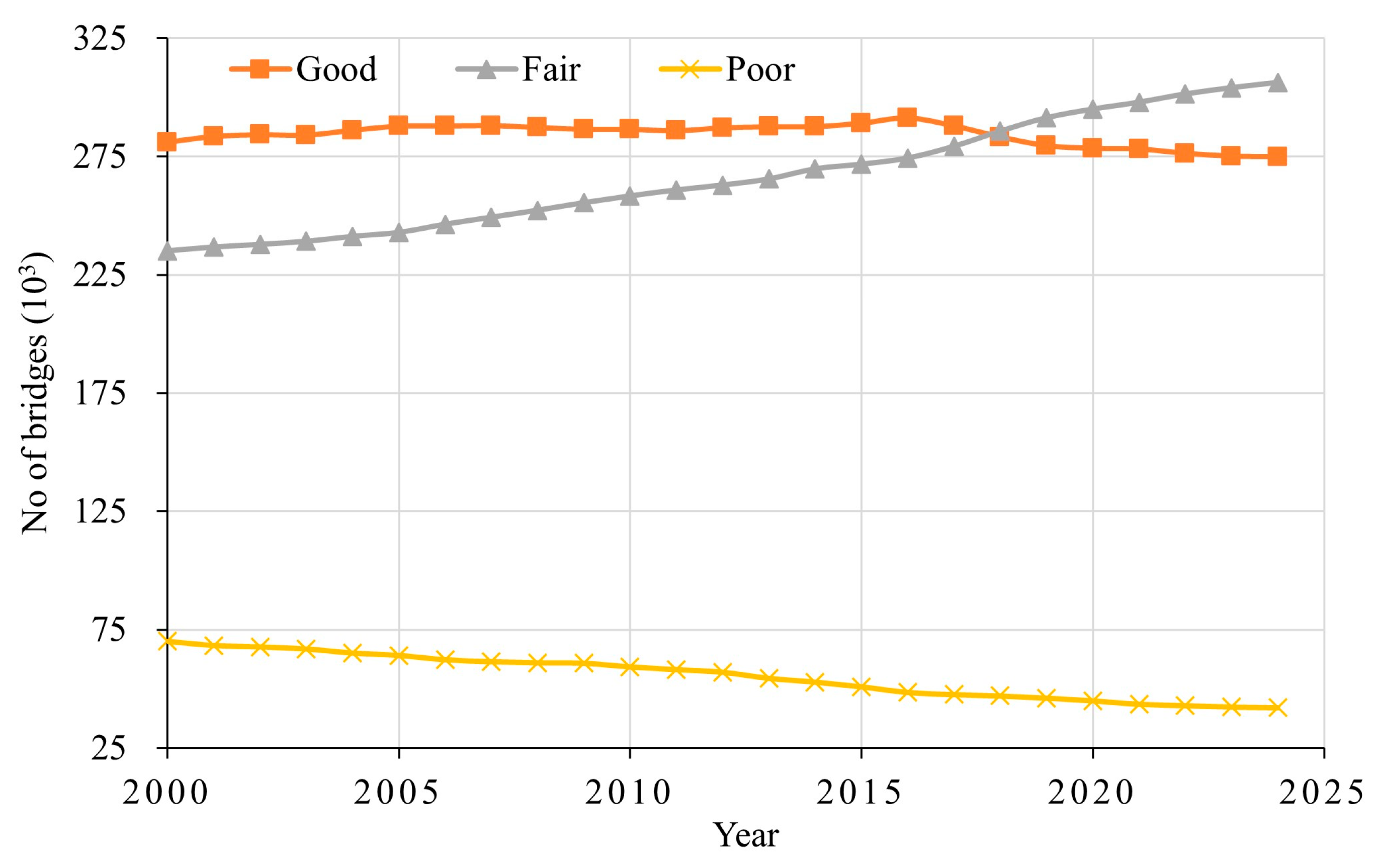
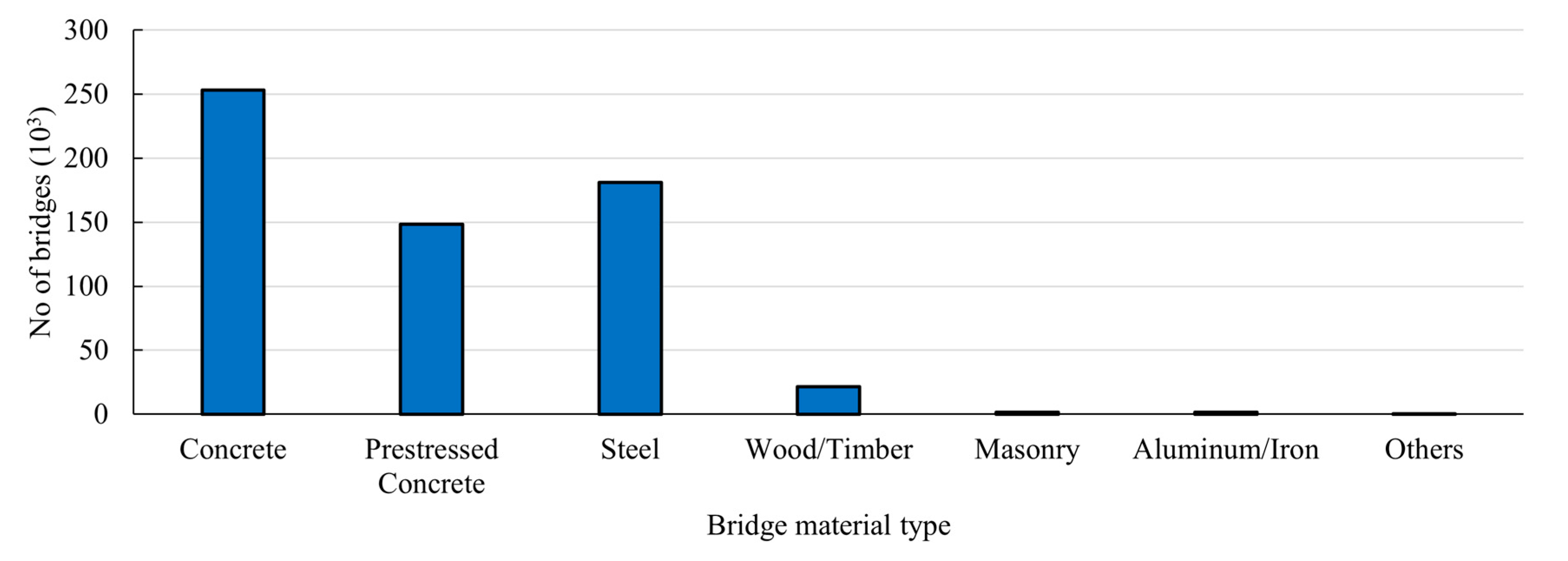
4.1. Inventory
4.2. Defects Detection and Evaluation
4.2.1. Visual Inspection-Based Defect Evaluation
4.2.2. DL-Based Surface Defects Inspection
4.2.3. Non-Destructive Defect Evaluation
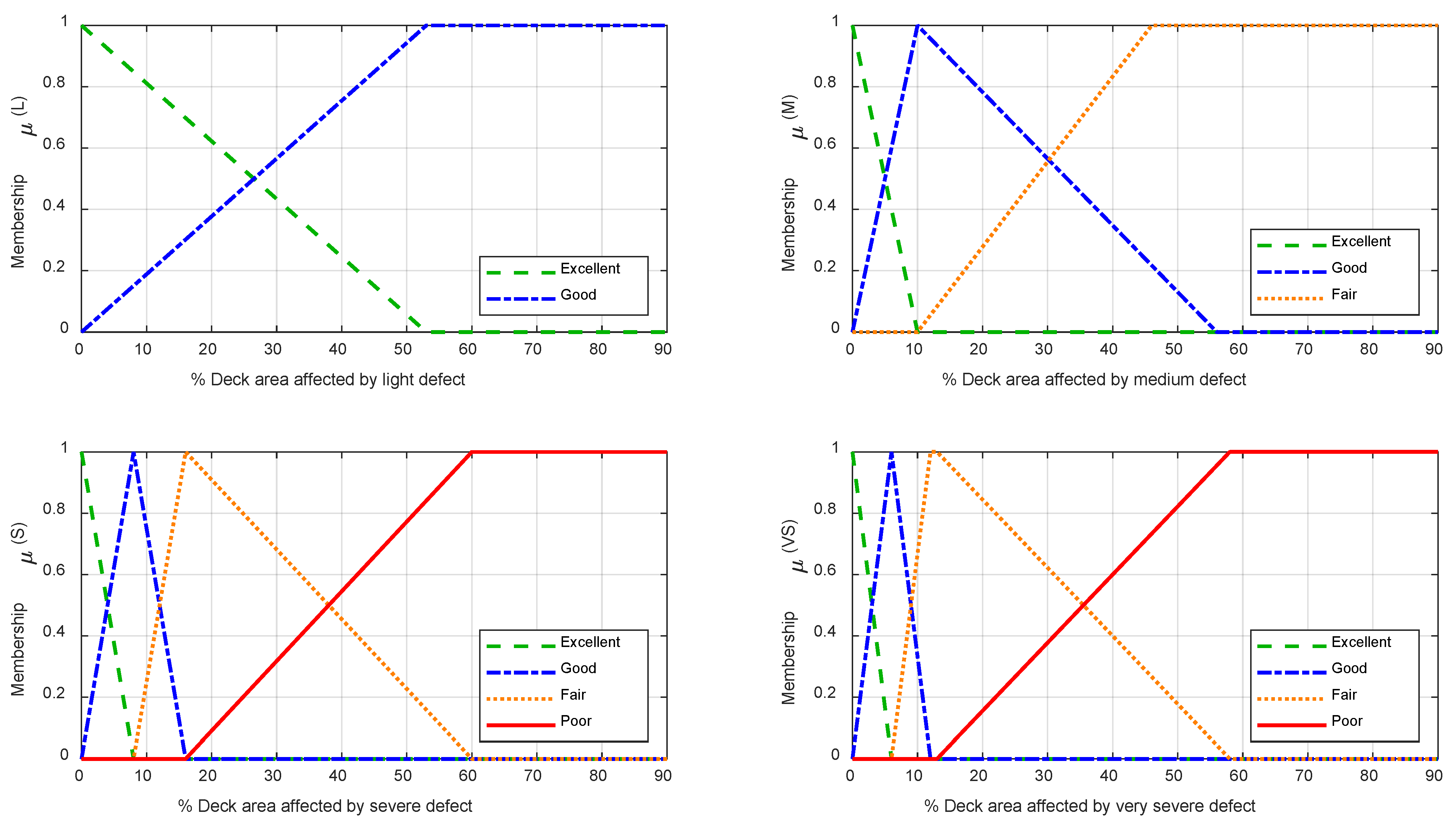
4.2.4. Fuzzified Defects Evaluation
4.3. Condition Rating
4.3.1. Ratio-Based Condition Rating
4.3.2. Categorial Weighted-Based Condition Rating
4.3.3. Worst-Conditioned Component-Based Condition Rating
4.3.4. Other Methods
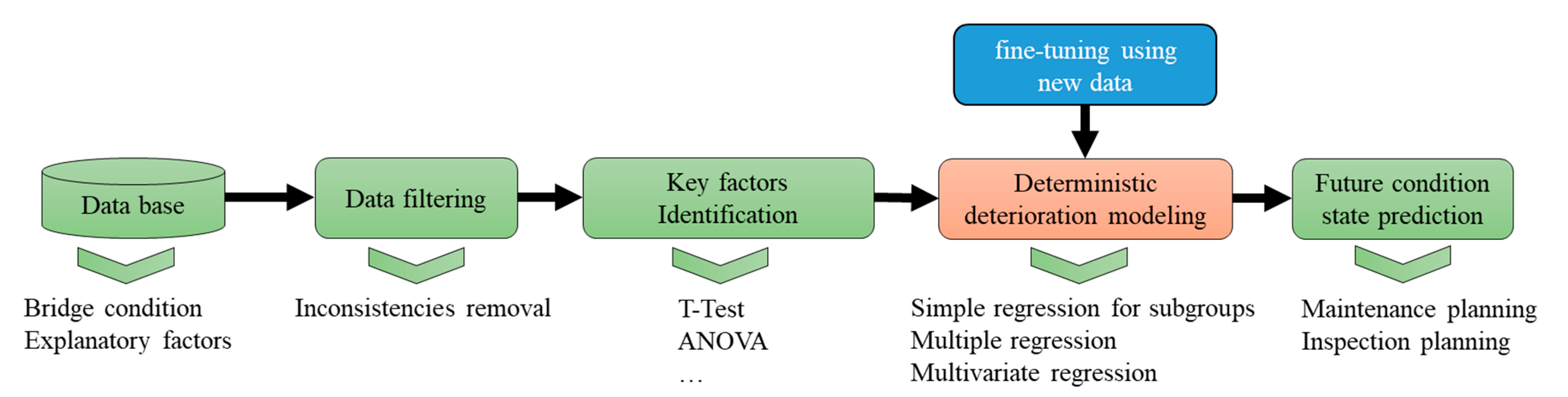
4.4. Condition Forecasting and Deterioration Models
4.4.1. Statistical Deterioration Models
Deterministic Regression
Descriptive Statistics
| Ref. | Component | Data | Category | Method | Factors |
|---|---|---|---|---|---|
| [64] | Deck, substructure, and superstructure. | Illinois DOT | Regression | 3rd-degree polynomial | Age, material, structure, location, and ADT |
| [65] | Bridge. | NBI | Regression | 3rd-degree polynomial | Age, material, structure, and ADT. |
| [70] | Deck | NBI | Regression | Logistic regression | ADT, environmental factors, structural characteristics, and maintenance activities. |
| [67] | Superstructure | NBI | Regression | Multiple regression | Age, ADT, percent of truck, structure length, deck width, roadway width, skewness, span length, and structure type. |
| [68] | Deck | NBI | Regression | Multiple regression | Skewness, span length, structure length, road width, deck width, inspection frequency, and ADTT. |
| [46] | Deck and superstructure | Australia DOTs | Descriptive | ANOVA and trend analysis. | Construction year, inspection year, inspector, and road class. |
| [72] | Bridge | NBI | Descriptive | Trend analysis | Decaying salt, coastal distance, year of construction, materials, and structural types. |
| [71] | Deck and superstructure. | NBI | Descriptive | ANOVA and trend analysis. | Design, ADT, and environment. |
| [40,42,66] | Deck | NDT | Regression | Sigmoid functions | Design, ADT, and environment, and age. |
| [73] | Deck | NBE rating | Descriptive | % of bridges in condition states 3 and 4. | Deck design, ADT, route type, skewness, and coating type. |
| [69] | Superstructure and substructure. | NBI | Regression | t-statistics and multivariate regression | Age, number of spans, ADT, waterways, route, interstate-state, and coastal distance. |
| [78] | Deck | NBI | Regression | 3rd degree polynomial. | Age and ADTT. |
| [79] | Bridge | Spain | Descriptive | Durability index | Age, design, and environment. |
| [74] | Bridge | NBI | Descriptive | ATICR and K-M | Age, ADT environment, wearing surface, classification, skewness, and design parameters. |
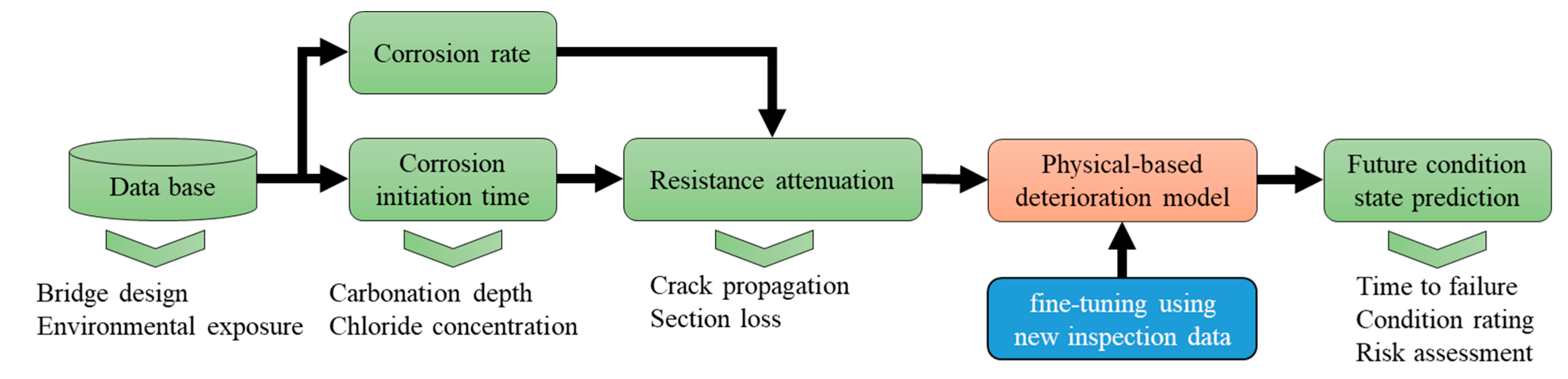
4.4.2. Mechanistic Deterioration Models
| Ref | Component | Location | Deterioration Indicator | Methodology | Objective | Factors |
|---|---|---|---|---|---|---|
| [62] | Deck | Korea | Chloride corrosion. | Corrosion modeling, stress-strain evaluation. | Time to failure. | Traffic loads, environmental effects, material, and structural evaluation. |
| [85] | Bridge | India | Carbonation corrosion | Time to corrosion-Carbonation rate. | Time to failure. | Material, environment, and cover depth. |
| [94] | Girders | Colombia | Chloride corrosion and fatigue. | Model corrosion–fatigue under various environments. | Time to failure | Fatigue loads, and environment. |
| [12] | Bridge | Iran | Chloride corrosion-crack. | ANN to model corrosion cracking. | Maintenance planning. | Environment, chloride, cover depth, and material. |
| [3] | Deck and superstructure | Canada | Chloride corrosion. | Finite element modeling. | Reliability analysis | Structure, loads, and environment |
| [95] | Bridge | UK | Chloride and carbonation-corrosion. | Corrosion modeling | condition-monitoring. | Overweight trucks. |
| [96] | Bridge | China | Chloride corrosion | Corrosion and resistance attenuation modeling. | Time to failure. | Loads and material. |
| [97] | Deck | Australia | GPR corrosivity. | Finite element model | Reliability index. | Design and age. |
| [98] | Bridge | Austria | Chloride corrosion | Chloride ingress model | Reliability analysis. | Age, material, environment, and cover depth. |
| [88] | Deck | NBI | Chloride corrosion. | Time to corrosion and cracking, Bayesian updating. | Inspection planning. | Age, material, and environment. |
| [90] | Girders and deck | Korea | Chloride corrosion | Corrosion rate and resistance attenuation | Reliability index. | Environment, Age, and ADT. |
| [91] | Bridge | China | Chloride and carbonation corrosion. | Gamma process, AHP, and fuzzy to model resistance deterioration. | Load rating, reliability assessment, and time to failure. | Age, environment, and load. |
| [99] | Girders | China | Chloride corrosion | Flexural capacity degradation | Reliability index | Age, environment, material, and load. |
| [89] | Column | New York DOT | Chloride corrosion | Corrosion-cracking propagation simulation | Condition prediction. | Age and environment. |
| [100] | Bridge | Australia | Chloride and carbonation corrosion. | Faraday’s law for corrosion modeling. | Reliability index. | Age. |
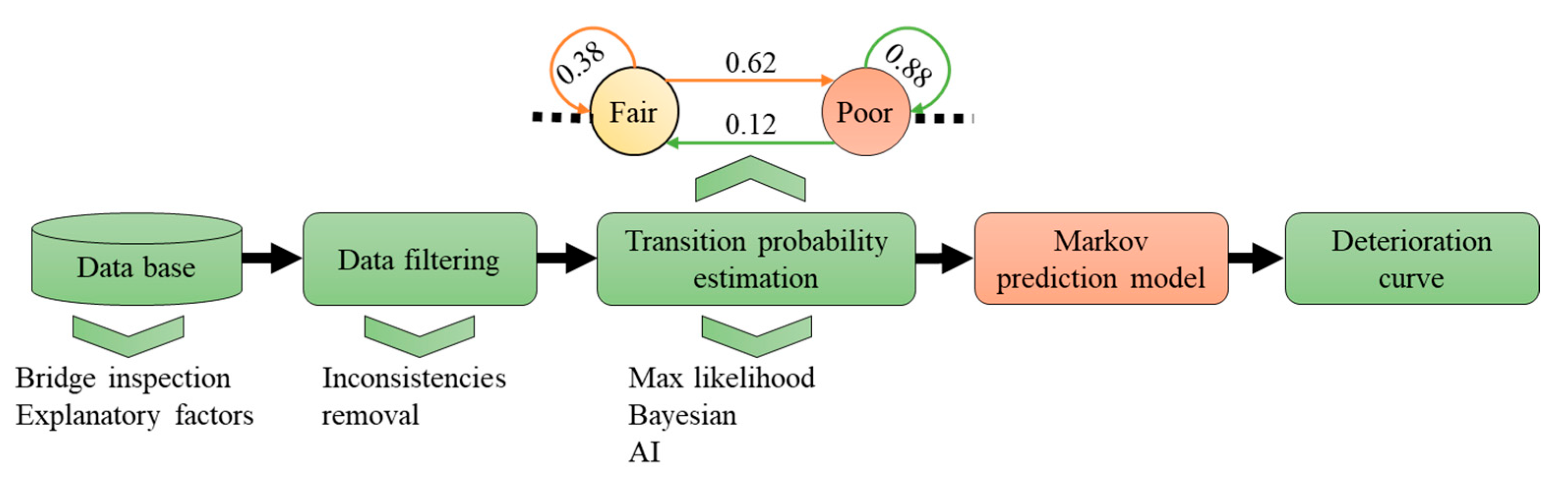
4.4.3. Stochastic Deterioration Models
State-Based Markov Models
State-Based Semi-Markov Model
Time-Based Stochastic Models
| Ref | Component | Data Source | Category | Methodology | Factors |
|---|---|---|---|---|---|
| [106] | Deck | Australia | State-based | Markov and Bayesian theory | Environmental exposure, structure type, and age. |
| [115] | Bridge | Florida DOT | State-based | Semi-Markovian | Age, type, and location. |
| [107] | Deck | Japan VI | State-based | Markov and Bayesian theory | Structural, amount of decaying salts, and age. |
| [108] | Bridge | Serbia DOTs | State-based | Markov chains and expectation maximization algorithm. | Age. |
| [121] | Bridge | New Zealand DOTs | State-based | Semi-Markovian | Material and age. |
| [102] | Deck | Ohio DOT | State-based | Markov and Bayesian theory | Age. |
| [103] | Deck | Quebec DOT | State-based | Markov and Bayesian theory | Bridge defects, and age. |
| [9] | Bridge | Austria | State-based | Analytical deterioration models and Semi-Markov | Age, material, and environment. |
| [110] | Bridge | Florida DOT | State-based | Corrosion-cracking simulation and Markov. | Age and environment |
| [112] | Bridge | Ontario DOT | State-based | GA-Markov | Age and material. |
| [116] | Bridge | Synthesized | State-based | Semi-Markovian | Chloride diffusion. |
| [117] | Bridge | Brazil DOTs | State-based | Semi-Markovian | Material, age, span number, length, bridge typology, traffic load, and environmental conditions. |
| [101] | Bridge | NBI | State-based | CNN-Markov | Age, ADT, ADTT, maintenance actions, inspection history, climate, and 19 design parameters. |
| [111] | Deck | Florida DOT | State-based | Corrosion-cracking simulation and Markov. | Age and environment. |
| [109,122] | Bridge pylons, and columns. | China | State-based | Thermal loads, finite elements and Markov | Temperature. |
| [123] | Box Girder Bridges | NBI | State-based | Semi-Markovian and Weibull distribution | Age and bridge length. |
| [77] | Bridge | NBI | State-based | ReliefF, ENN, and Markov | Age, ADTT, material, bridge type, and skew. |
| [92] | Bridge | New York DOT | Time-based | Compared time-based and state-based | Region, material types, and design types. |
| [118] | Bridge | Florida DOT | Time-based | Weibull distribution | Age, type, and location. |
| [119] | Superstructure | NBI | Time-based | Weibull distribution | Material, and age. |
| [113] | Deck | Portuguese DOTs | Time-based | Gamma distribution | Type, distance to the sea, material, and age. |
| [120] | Deck | Pennsylvania DOT | Time-based | Weibull distribution | Structural, average daily traffic (ADT), route type, and environmental conditions. |
| [124] | Deck | NBI | Time-based | Weibull and lognormal distributions. | Environmental factors. |
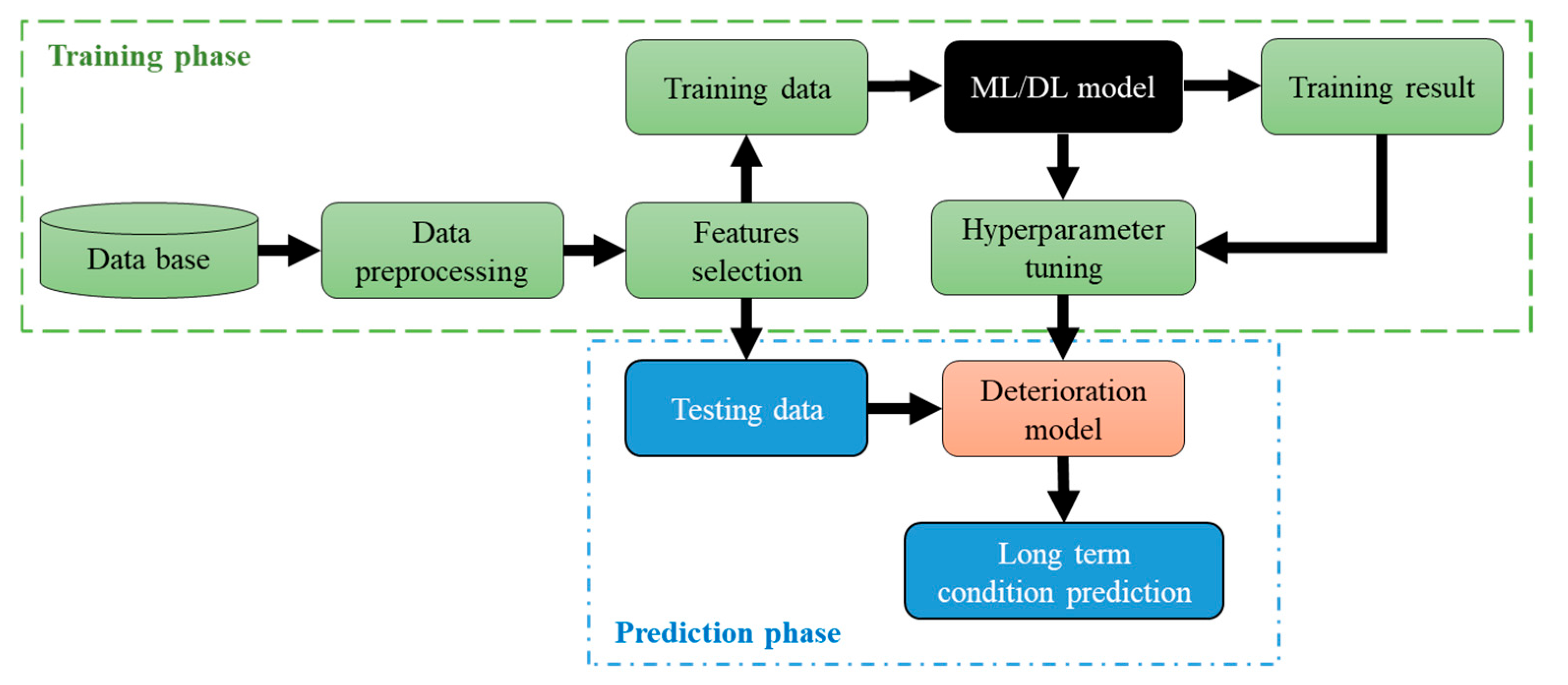
4.4.4. Artificial Intelligence Deterioration Models
ML and DL Deterioration Models
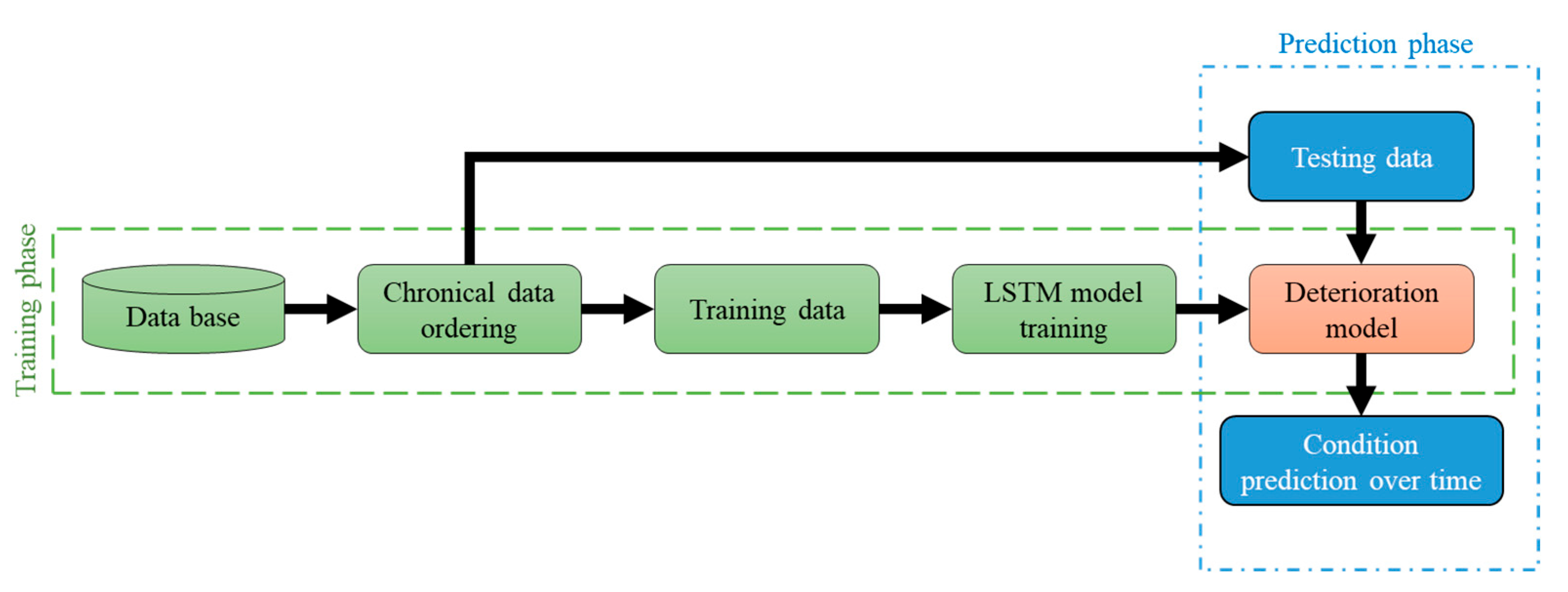
Sequential DL Deterioration Models
Knowledge-Informed ML Deterioration Models
| Ref | Component | Data | Method | Performance | Factors | |
|---|---|---|---|---|---|---|
| Metric | Result | |||||
| [135] | Deck | Wisconsin DOT | ANOVA, ANN | Accuracy | 75% | Age, maintenance history, inspection history, district, ADT, environment, and 5 design parameters. |
| [136] | Bridge | NBI | CNN | Accuracy | 85%. | Geographic location, ADT, ADTT, operation history, age, and 11 design parameters. |
| [127] | Abutment | NBI | ENNs | Accuracy | 86% | Age, temperature, ADT, surface type, structural type, and 3 design parameters. |
| [11] | Deck | NBI | ANNs | MAE | 0.31 | Age. |
| [137] | Bridge | China | U-Net | Accuracy | 92% | Age, ADT, ADTT, maintenance actions, inspection history, and 10 design parameters. |
| [128] | Bridge | Texas DOT | ReliefF, RNN, and CNN | Accuracy | 80–93% | Age, Geographic location, ADTT, inspection history, and 6 design parameters. |
| [138] | Deck | Michigan DOT | CatBoost | Accuracy | 96% | Age, ADT, inspection history, 4 design parameters |
| [139] | Bridge | Ontario | MGGP | RMSE | 2.85 | Age, Geographic location, climate, inspection history, material, geometry. |
| [75] | Deck | NBI | XGBoost | Accuracy | 70% | Age, freeze–thaw, ADTT, and rainfall. |
| [76] | Deck | Japan | RNN | Accuracy | 85% | Age, environment, ADT, ADTT, deck type, deck area. |
| [125] | Bridge | NBI | RF | Accuracy | 93% | Age, ADT, ADTT, maintenance actions, inspection history, climate, and 19 design parameters. |
| [126] | Bridge | NBI | AE-RF | Accuracy | 90% | Age, ADT, inspection history, and 3 design parameters. |
| [130] | Deck | Korea | LSTM | RMSE | 5.25 | Age and environment. |
| [131] | Bridge | Japan | LSTM | Accuracy | 80% | Age, elevation, ADT, ADTT, temperature, CO2, salt, weather, length, and width. |
| [140] | Deck | NBI | LSTM-CNN | Accuracy | 95% | Age, Geographic location, ADT, ADTT, inspection history, 2 design parameters. |
| [132] | Box girder | China | LSTM-RNN | RSME | 1.135 | Age, inspection history, ADT, length, and width. |
| [141] | Deck | NBI | CNN-LSTM | Accuracy | 90% | Age, inspection history, ADT, environment, and 10 design parameters. |
| [134] | Bridge | NBI | DT-KL-Onto | Precision/Recall | 75%/33% | Age, climate factors, loading, material, design. |
| [133] | Bridge | Greece | k-NN and finite element | - | - | Vertical deflection and concrete properties. |
5. Gaps and Future Directions
5.1. Condition Rating Methods
5.1.1. Current State in Condition Rating
- The ratio-based condition rating method offers an objective and comprehensive assessment of bridge conditions by evaluating the severity and extent of defects. This approach provides a detailed overview of defect quantities and severities, facilitating the planning of maintenance, repair, and rehabilitation activities, as well as enabling efficient resource allocation at the network level. However, its application may be limited for agencies lacking the element-level evaluation required to assign a health index. Moreover, incorporating the quantitative cost of defects involves multiple assumptions and uncertainties, which can affect the method’s reliability.
- The weighted categorical condition rating method offers a comprehensive perspective on bridge condition and aids in planning maintenance and rehabilitation activities by providing a consistent framework within the agency. However, accurately determining the weight or impact of individual element conditions on the overall structural integrity of the bridge remains a significant challenge.
- The worst-conditioned component method plays a crucial role in identifying high-risk bridges and evaluating their vulnerability during extreme events or disasters. This approach also aids in comparing bridge conditions and performance across different DOTs, allowing for the identification of trends in the deterioration or improvement of the nation’s bridge infrastructure. Despite its advantages, this method has limitations, as it does not offer a comprehensive view of how deterioration is distributed throughout the entire bridge structure.
- The condition rating approaches in the literature and industry heavily rely on qualitative VI, which depends significantly on the subjective judgment of inspectors. As a result, VI may underestimate or overestimate the severity of observed defects and may overlook underlying issues. Incorporating quantitative DL-based surface defect detection and NDE techniques can provide more objective evaluations. Additionally, the use of fuzzy logic offers a promising method to reduce uncertainty in condition ratings.
5.1.2. Condition Rating Research Needs and Future Directions
- The condition rating approaches in the literature and industry heavily rely on subjective assumptions. For instance, in the ratio-based condition rating method, more research is needed to provide more objective assumptions regarding defects’ quantitative cost. In addition, in the weighted categorical condition rating method, further research is still needed to objectively determine the weight or impact of elements’ conditions on overall bridge structural integrity, considering variations in bridge design and other influencing factors.
- DL surface defects evaluation promises to address the limitations of VI. However, the performance of these models is constrained by the availability and the quality of training datasets. In addition, quantifying damage dimensions and integrating spatial positional data into the detected defects remain underexplored, despite their importance for structural health assessment. These limitations underscore the need for future research to develop scalable, accurate, and multifunctional damage detection systems that incorporate advanced frameworks for defect detection, quantification, and spatial positioning.
- NDE and fuzzy logic have the potential to reduce the uncertainties associated with condition rating approaches. However, NDE methods currently lack standardized protocols to ensure consistent and reliable condition assessments. Furthermore, research on applying fuzzy logic in this area remains limited. Therefore, there is an urgent need to develop systematic methodologies for standardizing and integrating NDE and fuzzy logic into bridge condition rating systems, enabling bridge inspectors to readily implement these approaches and minimize uncertainty in condition assessments.
- Future research is also needed to propose multi-dimensional condition rating frameworks that integrate various rating methods, leveraging the strengths of each approach. This framework could include tools to translate ratings between methods for a more comprehensive assessment of bridge conditions.
5.2. Deterioration Modeling
5.2.1. Current State of Deterioration Modeling
- Statistical deterioration models are simple and provide valuable insights into deterioration trends and significant deterioration factors, especially at the network level. However, these models do not take into consideration the inherent uncertainty in infrastructure deterioration. In addition, these models cannot represent the interaction between bridge elements.
- Mechanistic models provide quantitative deterioration modeling to predict damages in bridge elements and are suitable for reliability analysis. However, these models are complex and computationally demanding, rendering them inappropriate for network-level modeling. Moreover, most available mechanistic deterioration models predict damage in straightforward scenarios and do not account for complex factors such as the presence of epoxy overlays, cathodic protection, maintenance interventions, and other complications. Thus, these models are considered more suitable for the project level or as supplementary to other deterioration modeling
- Markov models provide a simple stochastic method for predicting bridge conditions and generating survival-analysis curves at the network level. They are compatible with limited and discrete bridge condition data. However, these models assume uniform deterioration rates and stationary transition probabilities and rely solely on the current condition, which are unrealistic simplifications. In addition, the transition probabilities are often challenging to assess objectively. Thus, these models usually provide a qualitative prediction of future condition states, making them unsuitable for reliability assessment.
- The Semi-Markov model is a more comprehensive approach than the conventional Markov chain models as they take into consideration the current state and the time spent in that state. Thus, they enhance the accuracy of condition predictions. Moreover, the time dependency enables the model to handle irregularities in inspection intervals in cases where inspections are not uniformly spaced. However, Semi-Markov models require more complex and extensive data collection, making it infeasible for limited databases.
- DL-based deterioration models for concrete bridges hold significant potential for improving condition prediction accuracy by capturing the complex interactions among various deterioration factors. However, their effectiveness is heavily reliant on the availability of structured and comprehensive bridge condition databases, which are often lacking.
- Sequential deep learning models can capture the time-based patterns that reflect how the current condition behaves in the future. Models like LSTM can improve condition prediction accuracy by capturing the temporal dependencies in condition data and environmental exposure. Accordingly, this improves maintenance planning and prevents critical failure. However, these models demand high-quality data to capture the long-term dependencies.
- Knowledge-informed ML models demonstrated improved training and condition prediction performance. This method has the potential to improve deterioration modeling approaches and reduce the demand for historical data. However, they need more research to prove their validity in complex problems such as concrete bridge deterioration modeling.
5.2.2. Deterioration Modeling Research Needs and Future Directions
- In stochastic models, assessing transition probabilities objectively is often challenging. Thus, integrating AI and mechanistic models with stochastic approaches, such as Markovian deterioration models, can significantly improve their predictive accuracy while maintaining minimal computational costs. Consequently, further research is essential to effectively merge AI and mechanistic models with stochastic deterioration modeling, offering promising advancements in predicting concrete bridge deterioration.
- Physical-informed ML, can significantly enhance the efficiency and accuracy of condition prediction, reduce computational costs, and lessen the reliance on extensive historical data. However, there is a need to improve the representativeness of physics-informed machine learning by integrating new concepts from emerging mathematical physics models and extending its ability to capture the semantics of bridge data. In addition, future research should focus on developing frameworks that seamlessly integrate heterogeneous bridge data and scientific structural knowledge to develop efficient physics-informed ML methods.
- To unlock the full potential of deep learning models, additional research is necessary to enhance their performance, optimize their computational efficiency, and improve their adaptability to various data conditions, including cases with incomplete datasets.
- Many agencies do not have a comprehensive inventory of bridge conditions and inspection data necessary for modeling deterioration. There is a significant gap in effective methods for collecting data from the vast number of bridges across the country. Therefore, research is needed to develop and validate convenient, affordable, and scalable data collection methods using innovative technologies such as smartphones, drones, and cloud computing. Additionally, it is important to advance AI techniques to extract vital information from unstructured data sources, such as inspection images and monitoring reports. This will facilitate the use of diverse and non-standardized data formats in deterioration modeling.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- FHA Bridge Condition by Highway System. Available online: https://www.fhwa.dot.gov/bridge/nbi/condition.cfm (accessed on 14 November 2024).
- Ibrahim, A.; Abdelkhalek, S.; Zayed, T.; Qureshi, A.H.; Mohammed Abdelkader, E. A Comprehensive Review of the Key Deterioration Factors of Concrete Bridge Decks. Buildings 2024, 14, 3425. [Google Scholar] [CrossRef]
- Ghodoosi, F.; Bagchi, A.; Zayed, T. System-Level Deterioration Model for Reinforced Concrete Bridge Decks. J. Bridg. Eng. 2015, 20, 04014081. [Google Scholar] [CrossRef]
- FHA Bridges by Year Built, Year Reconstructed and Material Type. Available online: https://www.fhwa.dot.gov/bridge/nbi/no10/yrblt_yrreconst13.cfm#a (accessed on 14 November 2024).
- Minchin, R.E.; Zayed, T.; Boyd, A.J.; Mendoza, M. Best Practices of Bridge System Management—A Synthesis. J. Manag. Eng. 2006, 22, 186–195. [Google Scholar] [CrossRef]
- Alsharqawi, M.; Zayed, T.; Abu Dabous, S. Integrated Condition-Based Rating Model for Sustainable Bridge Management. J. Perform. Constr. Facil. 2020, 34, 04020091. [Google Scholar] [CrossRef]
- Sasmal, S.; Ramanjaneyulu, K. Condition Evaluation of Existing Reinforced Concrete Bridges Using Fuzzy Based Analytic Hierarchy Approach. Expert Syst. Appl. 2008, 35, 1430–1443. [Google Scholar] [CrossRef]
- Tarighat, A.; Miyamoto, A. Fuzzy Concrete Bridge Deck Condition Rating Method for Practical Bridge Management System. Expert Syst. Appl. 2009, 36, 12077–12085. [Google Scholar] [CrossRef]
- Zambon, I.; Vidović, A.; Strauss, A.; Matos, J. Condition Prediction of Existing Concrete Bridges as a Combination of Visual Inspection and Analytical Models of Deterioration. Appl. Sci. 2019, 9, 148. [Google Scholar] [CrossRef]
- Kim, S.; Ge, B.; Frangopol, D.M. Probabilistic Optimum Bridge System Maintenance Management Considering Correlations of Deteriorating Components and Service Life Extensions. ASCE-ASME J. Risk Uncertain. Eng. Syst. A Civ. Eng. 2022, 8, 04022023. [Google Scholar] [CrossRef]
- Santamaria Ariza, M.; Zambon, I.; Sousa, H.S.; Campos e Matos, J.A.; Strauss, A. Comparison of Forecasting Models to Predict Concrete Bridge Decks Performance. Struct. Concr. 2020, 21, 1240–1253. [Google Scholar] [CrossRef]
- Firouzi, A.; Rahai, A. Reliability Assessment of Concrete Bridges Subject to Corrosion-Induced Cracks during Life Cycle Using Artificial Neural Networks. Comput. Concr. 2013, 12, 91–107. [Google Scholar] [CrossRef]
- Di Mucci, V.M.; Cardellicchio, A.; Ruggieri, S.; Nettis, A.; Renò, V.; Uva, G. Artificial Intelligence in Structural Health Management of Existing Bridges. Autom. Constr. 2024, 167, 105719. [Google Scholar] [CrossRef]
- Srikanth, I.; Arockiasamy, M. Deterioration Models for Prediction of Remaining Useful Life of Timber and Concrete Bridges: A Review. J. Traffic Transp. Eng. 2020, 7, 152–173. [Google Scholar] [CrossRef]
- Kamioka, H. Preferred Reporting Items for Systematic Review and Meta-Analysis Protocols (Prisma-p) 2015 Statement. Jpn. Pharmacol. Ther. 2019, 47, 1177–1185. [Google Scholar]
- Echchakoui, S. Why and How to Merge Scopus and Web of Science during Bibliometric Analysis: The Case of Sales Force Literature from 1912 to 2019. J. Mark. Anal. 2020, 8, 165–184. [Google Scholar] [CrossRef]
- Scopus Content Coverage Guide; Elsevier: Amsterdam, The Netherlands, 2020.
- Centre for Science and Technology Studies, Leiden University. Vosviewer. Available online: https://www.vosviewer.com/ (accessed on 15 November 2024).
- K-Synth Srl Bibliometrix. Available online: https://www.bibliometrix.org/home/ (accessed on 15 November 2024).
- Watanabe, M.; Goso, T.; Ibayashi, K. Method for the Rapid Creation of Bridge Database Systems and Practices in Developing Countries. Pract. Period. Struct. Des. Constr. 2023, 28, 04022062. [Google Scholar] [CrossRef]
- The United States Department of Transportation. Specifications for the National Bridge Inventory; The United States Department of Transportation: Washington, DC, USA, 2022. [Google Scholar]
- Radovic, M.; Ghonima, O.; Schumacher, T. Data Mining of Bridge Concrete Deck Parameters in the National Bridge Inventory by Two-Step Cluster Analysis. ASCE-ASME J. Risk Uncertain. Eng. Syst. A Civ. Eng. 2017, 3, F4016004. [Google Scholar] [CrossRef]
- Chase, S.B.; Adu-Gyamfi, Y.; Aktan, A.E.; Minaie, E. Synthesis of National and International Methodologies Used for Bridge Health Indices; Technical Report for United States Department of Transportation; Department of Transportation: Springfield, VA, USA, 2016. [Google Scholar]
- New Jersey Department of Transportation. Bridge Element Inspection Manual; New Jersey Department of Transportation: Trenton, NJ, USA, 2014; Volume 2014. [Google Scholar]
- Stochino, F.; Fadda, M.L.; Mistretta, F. Low Cost Condition Assessment Method for Existing RC Bridges. Eng. Fail. Anal. 2018, 86, 56–71. [Google Scholar] [CrossRef]
- Abdelkhalek, S. Managing the Inspection Process of Concrete Bridge Decks. Ph.D. Thesis, The Hong Kong Polytechnic University, Kowloon, Hong Kong, 2022. [Google Scholar]
- Alsharqawi, M.; Zayed, T.; Abu Dabous, S. Integrated Condition Rating and Forecasting Method for Bridge Decks Using Visual Inspection and Ground Penetrating Radar. Autom. Constr. 2018, 89, 135–145. [Google Scholar] [CrossRef]
- Xiong, C.; Zayed, T.; Mohammed, E. A Novel YOLOv8-GAM-Wise-IoU Model for Automated Detection of Bridge Surface Cracks. Constr. Build. Mater. 2024, 414, 135025. [Google Scholar] [CrossRef]
- Bae, H.; Jang, K.; An, Y.K. Deep Super Resolution Crack Network (SrcNet) for Improving Computer Vision–Based Automated Crack Detectability in in Situ Bridges. Struct. Heal. Monit. 2021, 20, 1428–1442. [Google Scholar] [CrossRef]
- Wan, H.; Gao, L.; Yuan, Z.; Qu, H.; Sun, Q.; Cheng, H.; Wang, R. A Novel Transformer Model for Surface Damage Detection and Cognition of Concrete Bridges. Expert Syst. Appl. 2023, 213, 119019. [Google Scholar] [CrossRef]
- Zhang, C.; Chang, C.C.; Jamshidi, M. Concrete Bridge Surface Damage Detection Using a Single-Stage Detector. Comput. Civ. Infrastruct. Eng. 2020, 35, 389–409. [Google Scholar] [CrossRef]
- Rubio, J.J.; Kashiwa, T.; Laiteerapong, T.; Deng, W.; Nagai, K.; Escalera, S.; Nakayama, K.; Matsuo, Y.; Prendinger, H. Multi-Class Structural Damage Segmentation Using Fully Convolutional Networks. Comput. Ind. 2019, 112, 103121. [Google Scholar] [CrossRef]
- Ding, W.; Yang, H.; Yu, K.; Shu, J. Crack Detection and Quantification for Concrete Structures Using UAV and Transformer. Autom. Constr. 2023, 152, 104929. [Google Scholar] [CrossRef]
- Saleem, M.R.; Park, J.W.; Lee, J.H.; Jung, H.J.; Sarwar, M.Z. Instant Bridge Visual Inspection Using an Unmanned Aerial Vehicle by Image Capturing and Geo-Tagging System and Deep Convolutional Neural Network. Struct. Heal. Monit. 2021, 20, 1760–1777. [Google Scholar] [CrossRef]
- Lin, J.J.; Ibrahim, A.; Sarwade, S.; Golparvar-Fard, M. Bridge Inspection with Aerial Robots: Automating the Entire Pipeline of Visual Data Capture, 3D Mapping, Defect Detection, Analysis, and Reporting. J. Comput. Civ. Eng. 2021, 35, 04020064. [Google Scholar] [CrossRef]
- Abdelkader, E.M.; Zayed, T.; Faris, N. Synthesized Evaluation of Reinforced Concrete Bridge Defects, Their Non-Destructive Inspection and Analysis Methods: A Systematic Review and Bibliometric Analysis of the Past Three Decades. Buildings 2023, 13, 800. [Google Scholar] [CrossRef]
- Pailes, B.M.; Gucunski, N. Multimodal Nondestructive Testing Damage Quantification, Presentation, and Condition Rating of Bridge Decks. Transp. Res. Rec. 2015, 2481, 26–31. [Google Scholar] [CrossRef]
- Omar, T.; Nehdi, M.L.; Zayed, T. Integrated Condition Rating Model for Reinforced Concrete Bridge Decks. J. Perform. Constr. Facil. 2017, 31, 04017090. [Google Scholar] [CrossRef]
- Faris, N.; Zayed, T.; Abdelkader, E.M.; Fares, A. Corrosion Assessment Using Ground Penetrating Radar in Reinforced Concrete Structures: Influential Factors and Analysis Methods. Autom. Constr. 2023, 156, 105130. [Google Scholar] [CrossRef]
- Rashidi, M.; Azari, H.; Nehme, J. Assessment of the Overall Condition of Bridge Decks Using the Jensen-Shannon Divergence of NDE Data. NDT E Int. 2020, 110, 102204. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Jiao, Y.; He, X.; Wang, B. Condition Evaluation for Existing Reinforced Concrete Bridge Superstructure Using Fuzzy Clustering Improved by Particle Swarm Optimisation. Struct. Infrastruct. Eng. 2017, 13, 955–965. [Google Scholar] [CrossRef]
- Gucunski, N.; Pailes, B.; Kim, J.; Azari, H.; Dinh, K. Capture and Quantification of Deterioration Progression in Concrete Bridge Decks through Periodical NDE Surveys. J. Infrastruct. Syst. 2017, 23, B4016005. [Google Scholar] [CrossRef]
- Calò, M.; Ruggieri, S.; Nettis, A.; Uva, G. A MTInSAR-Based Early Warning System to Appraise Deformations in Simply Supported Concrete Girder Bridges. Struct. Control Heal. Monit. 2024, 2024, 8978782. [Google Scholar] [CrossRef]
- Gagarin, N.; Goulias, D.; Mekemson, J.; Cutts, R.; Andrews, J. Development of Novel Methodology for Assessing Bridge Deck Conditions Using Step Frequency Antenna Array Ground Penetrating Radar. J. Perform. Constr. Facil. 2020, 34, 04019113. [Google Scholar] [CrossRef]
- Sasmal, S.; Ramanjaneyulu, K.; Gopalakrishnan, S.; Lakshmanan, N. Fuzzy Logic Based Condition Rating of Existing Reinforced Concrete Bridges. J. Perform. Constr. Facil. 2006, 20, 261–273. [Google Scholar] [CrossRef]
- Ramezanianpout, A.A.; Shahhosseini, V.; Moodi, F. A Fuzzy Expert System for Diagnosis Assessment of Reinforced Concrete Bridge Decks. Comput. Concr. 2009, 6, 281–303. [Google Scholar] [CrossRef]
- Abu Dabous, S.; Alkass, S.; Zaki, A. A Probabilistic Methodology for Bridge Deck Condition Assessment. Bridg. Struct. 2008, 4, 49–56. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, X.; Gong, M. Comparative Analysis of Condition Assessment Standards for Roads and Bridges Based on Fuzzy Comprehensive Evaluation. Aust. J. Civ. Eng. 2023, 1–11. [Google Scholar] [CrossRef]
- Dinh, K.; Zayed, T. GPR-Based Fuzzy Model for Bridge Deck Corrosiveness Index. J. Perform. Constr. Facil. 2016, 30, 04015069. [Google Scholar] [CrossRef]
- Wang, X.; Foliente, G. Identifying Bridge Structural Condition Development Trends via Categorical Inspection Condition Rating with Case Studies. Struct. Infrastruct. Eng. 2008, 4, 449–466. [Google Scholar] [CrossRef]
- Stochino, F.; Fadda, M.L.; Mistretta, F. Assessment of RC Bridges Integrity by Means of Low-Cost Investigations. Frat. Ed Integrita Strutt. 2018, 12, 216–225. [Google Scholar] [CrossRef]
- Inkoom, S.; Sobanjo, J. Availability Function as Bridge Element’s Importance Weight in Computing Overall Bridge Health Index. Struct. Infrastruct. Eng. 2018, 14, 1598–1610. [Google Scholar] [CrossRef]
- Abu Dabous, S.; Yaghi, S.; Alkass, S.; Moselhi, O. Concrete Bridge Deck Condition Assessment Using IR Thermography and Ground Penetrating Radar Technologies. Autom. Constr. 2017, 81, 340–354. [Google Scholar] [CrossRef]
- Pushpakumara, B.H.J.; De Silva, S.; Subashi De Silva, G.H.M.J. Visual Inspection and Non-Destructive Tests-Based Rating Method for Concrete Bridges. Int. J. Struct. Eng. 2017, 8, 74–91. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, Y.; Cui, G.; Zhang, A.; Gao, Y.; Wang, X.; Ouyang, J.; Sun, H.; Liang, Y.; Liu, Z.; et al. Comprehensive Measurement Techniques and Multi-Index Correlative Evaluation Approach for Structural Health Monitoring of Highway Bridges. Meas. J. Int. Meas. Confed. 2020, 152, 107360. [Google Scholar] [CrossRef]
- Akgul, F. Inspection and Evaluation of a Network of Concrete Bridges Based on Multiple NDT Techniques. Struct. Infrastruct. Eng. 2020, 17, 1076–1095. [Google Scholar] [CrossRef]
- Abdelkhalek, S.; Zayed, T. Performance Assessment Model of Non-Destructive Technologies in Inspecting Concrete Bridge Decks. Struct. Infrastruct. Eng. 2023, 19, 216–237. [Google Scholar] [CrossRef]
- Rens, K.L.; Nogueira, C.L.; Transue, D.J. Bridge Management and Nondestructive Evaluation. J. Perform. Constr. Facil. 2005, 19, 3–16. [Google Scholar] [CrossRef]
- Johnson, M.B.; Kerr, R.I.; Thompson, T.S.; Ailaney, R.K. Bridge Management Experiences of California, Florida, and South Dakota; The United States Department of Transportation: Washington, DC, USA, 2005; p. 28. [Google Scholar]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Arong; Murakami, S.; Ichikawa, H.; Zadeh, L.A.; Yiliguoqi. Utilization of SVM in the Soundness Evaluation of Reinforced Concrete Slab Bridge. J. Japan Soc. Civ. Eng. 2020, 8, 59–70. [Google Scholar] [CrossRef]
- Oh, B.H.; Lew, Y.; Choi, Y.C. Realistic Assessment for Safety and Service Life of Reinforced Concrete Decks in Girder Bridges. J. Bridg. Eng. 2007, 12, 410–418. [Google Scholar] [CrossRef]
- FHWA LTBP Tools and Products. Available online: https://highways.dot.gov/research/long-term-infrastructure-performance/ltbp/products (accessed on 25 December 2024).
- Bolukbasi, M.; Mohammadi, J.; Arditi, D. Estimating the Future Condition of Highway Bridge Components Using National Bridge Inventory Data. Pract. Period. Struct. Des. Constr. 2004, 9, 16–25. [Google Scholar] [CrossRef]
- Tolliver, D.; Lu, P. Analysis of Bridge Deterioration Rates: A Case Study of the Northern Plains Region. J. Transp. Res. Forum 2012, 50, 87–100. [Google Scholar] [CrossRef]
- Kim, J.; Gucunski, N.; Dinh, K. Deterioration and Predictive Condition Modeling of Concrete Bridge Decks Based on Data from Periodic NDE Surveys. J. Infrastruct. Syst. 2019, 25, 04019010. [Google Scholar] [CrossRef]
- Hasan, S.; Elwakil, E. Stochastic Regression Deterioration Models for Superstructure of Prestressed Concrete Bridges in California. J. Struct. Integr. Maint. 2019, 4, 97–108. [Google Scholar] [CrossRef]
- Hasan, S.; Elwakil, E. National Bridge Inventory Data-Based Stochastic Modeling for Deck Condition Rating of Prestressed Concrete Bridges. Pract. Period. Struct. Des. Constr. 2020, 25, 04020022. [Google Scholar] [CrossRef]
- Srikanth, I.; Arockiasamy, M. Remaining Service Life Prediction of Aging Concrete Bridges Based on Multiple Relevant Explanatory Variables. Pract. Period. Struct. Des. Constr. 2021, 26, 04021036. [Google Scholar] [CrossRef]
- Ghonima, O.; Anderson, J.C.; Schumacher, T.; Unnikrishnan, A. Performance of US Concrete Highway Bridge Decks Characterized by Random Parameters Binary Logistic Regression. ASCE-ASME J. Risk Uncertain. Eng. Syst. A Civ. Eng. 2020, 6, 04019025. [Google Scholar] [CrossRef]
- Kim, Y.J.; Queiroz, L.B. Big Data for Condition Evaluation of Constructed Bridges. Eng. Struct. 2017, 141, 217–227. [Google Scholar] [CrossRef]
- Alogdianakis, F.; Charmpis, D.C.; Balafas, I. Macroscopic Effect of Distance from Seacoast on Bridge Deterioration—Statistical Data Assessment of Structural Condition Recordings. Structures 2020, 27, 319–329. [Google Scholar] [CrossRef]
- Treat, C.; Dymond, B.Z. Deterioration of Concrete Bridge Decks Containing Epoxy-Coated and Uncoated Reinforcement. J. Bridg. Eng. 2021, 26, 2–5. [Google Scholar] [CrossRef]
- Srikanth, I.; Arockiasamy, M. Development of Non-Parametric Deterioration Models for Risk and Reliability Assessments of Concrete and Timber Bridges. J. Perform. Constr. Facil. 2022, 36, 04021114. [Google Scholar] [CrossRef]
- Yang, C.; Wang, X.; Nassif, H. Impact of Environmental Conditions on Predicting Condition Rating of Concrete Bridge Decks. Transp. Res. Rec. 2024. [Google Scholar] [CrossRef]
- Miao, P.; Yokota, H. Comparison of Markov Chain and Recurrent Neural Network in Predicting Bridge Deterioration Considering Various Factors. Struct. Infrastruct. Eng. 2024, 20, 250–262. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, H.; Cui, X.; Li, P.; Zou, Y. Condition Rating Prediction for Highway Bridge Based on Elman Neural Networks and Markov Chains. Appl. Sci. 2024, 14, 1444. [Google Scholar] [CrossRef]
- Lou, P.; Nassif, H.; Su, D.; Truban, P. Effect of Overweight Trucks on Bridge Deck Deterioration Based on Weigh-in-Motion Data. Transp. Res. Rec. 2016, 2592, 86–97. [Google Scholar] [CrossRef]
- Alonso Medina, P.; León González, F.J.; Todisco, L. Data-Driven Prediction of Long-Term Deterioration of RC Bridges. Constr. Build. Mater. 2022, 317, 125790. [Google Scholar] [CrossRef]
- Fu, P.; Li, X.; Xu, L.; Xin, L. Life-Cycle Seismic Damage Identification and Components Damage Sequences Prediction for Cable-Stayed Bridge Based on Fragility Analyses. Bull. Earthq. Eng. 2021, 19, 6669–6692. [Google Scholar] [CrossRef]
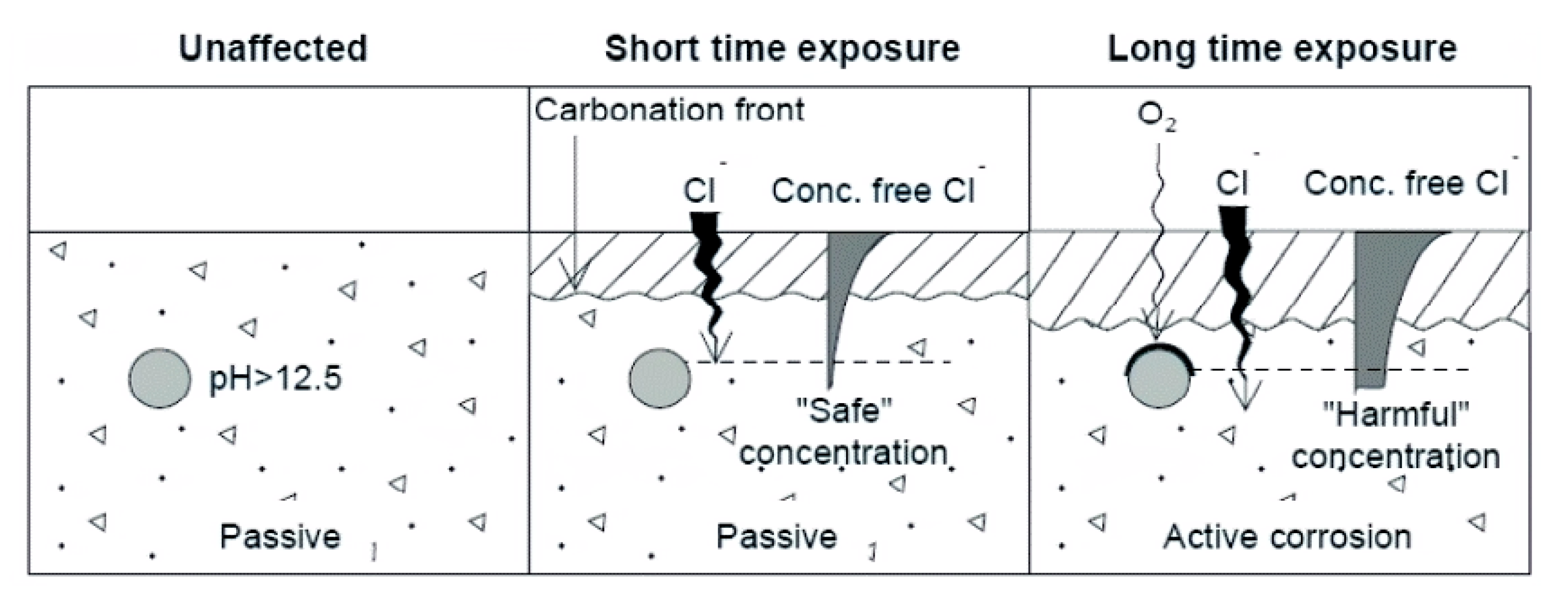
- Isgor, O.B.; Razaqpur, A.G. Modelling Steel Corrosion in Concrete Structures. Mater. Struct. Constr. 2006, 39, 291–302. [Google Scholar] [CrossRef]
- Quraishi, M.; Nayak, D.; Kumar, R.; Kumar, V. Corrosion of Reinforced Steel in Concrete and Its Control: An Overview. J. Steel Struct. Constr. 2017, 3, 1–6. [Google Scholar] [CrossRef]
- Faris, N.; Zayed, T.; Fares, A.; Abdelkhalek, S.; Abdelkader, E.M. Automated Rebar Recognition and Corrosion Assessment of Concrete Bridge Decks Using Ground Penetrating Radar. Autom. Constr. 2024, 166, 105631. [Google Scholar] [CrossRef]
- Liu, Y.; Weyers, R. Modeling the Time-to-Corrosion Cracking in Chloride Contaminated Reinforced Concrete Structures. ACI Mater. J. 1998, 95, 675–680. [Google Scholar] [CrossRef]
- Parameswaran, L.; Kumar, R.; Sahu, G.K. Effect of Carbonation on Concrete Bridge Service Life. J. Bridg. Eng. 2008, 13, 75–82. [Google Scholar] [CrossRef]
- Balafas, I.; Burgoyne, C.J. Modeling the Structural Effects of Rust in Concrete Cover. J. Eng. Mech. 2011, 137, 175–185. [Google Scholar] [CrossRef]
- Hu, N.; Haider, S.W.; Burgueno, R. Development and Validation of Deterioration Moels Fo Concree Bridge Decks—Phase 2: Mechanics-Based Degradation Models; Technical Report for United States Department of Transportation: Lansing, MI, USA, 2013. [Google Scholar]
- Atadero, R.A.; Jia, G.; Abdallah, A.; Ozbek, M.E. An Integrated Uncertainty-Based Bridge Inspection Decision Framework with Application to Concrete Bridge Decks. Infrastructures 2019, 4, 50. [Google Scholar] [CrossRef]
- Wang, H.; Ranade, R.; Okumus, P. Calibrating a Physics-Based Corrosion Model with Field-Based Bridge Condition Data. J. Bridg. Eng. 2023, 28, 04023020. [Google Scholar] [CrossRef]
- Heo, W.H. Performance-Based Reliability Estimates for Highway Bridges Considering Previous Inspection Data. Appl. Sci. 2020, 10, 1873. [Google Scholar] [CrossRef]
- Yuan, Y.; Han, W.; Guo, T.; Chen, X.; Xie, Q. Establishment and Updating of Nonstationary Resistance Deterioration Model of Existing Concrete Bridge Component. J. Perform. Constr. Facil. 2020, 34, 04020104. [Google Scholar] [CrossRef]
- Agrawal, A.K.; Kawaguchi, A.; Chen, Z. Deterioration Rates of Typical Bridge Elements in New York. J. Bridg. Eng. 2010, 15, 419–429. [Google Scholar] [CrossRef]
- Nickless, K.; Atadero, R.A. Mechanistic Deterioration Modeling for Bridge Design and Management. J. Bridg. Eng. 2018, 23, 04018018. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Bressolette, P.; Chateauneuf, A.; Sánchez-Silva, M. Probabilistic Lifetime Assessment of RC Structures under Coupled Corrosion-Fatigue Deterioration Processes. Struct. Saf. 2009, 31, 84–96. [Google Scholar] [CrossRef]
- Jones, G.; Lambert, P. Predicting Service Life from Site-Accessed Corrosion Rate Data. Proc. Inst. Civ. Eng. Forensic Eng. 2016, 169, 53–60. [Google Scholar] [CrossRef]
- Jiang, H.; Li, S.; Jiang, R. Residual Service Life Prediction for Bridges Based on Critical Life Curves. J. Perform. Constr. Facil. 2017, 31, 04017053. [Google Scholar] [CrossRef]
- Ghodoosi, F.; Bagchi, A.; Zayed, T.; Hosseini, M.R. Method for Developing and Updating Deterioration Models for Concrete Bridge Decks Using GPR Data. Autom. Constr. 2018, 91, 133–141. [Google Scholar] [CrossRef]
- Zambon, I.; Vidović, A.; Strauss, A.; Matos, J. Use of Chloride Ingress Model for Condition Assessment in Bridge Management. Gradjevinar 2019, 71, 359–373. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Su, H.; Du, J. Time-Dependent Robustness-Based Condition Assessment of RC Bridges Subjected to Corrosion. Structures 2021, 34, 4500–4510. [Google Scholar] [CrossRef]
- Alam, J.; Zhang, H.; Neves, L.A.C.; Dias-da-Costa, D. Sequential Bayesian Updating for Time-Variant Reliability Analysis of Ageing Structures. Mech. Syst. Signal Process. 2023, 204, 110774. [Google Scholar] [CrossRef]
- Liu, H.; Nehme, J.; Lu, P. An Application of Convolutional Neural Network for Deterioration Modeling of Highway Bridge Components in the United States. Struct. Infrastruct. Eng. 2023, 19, 731–744. [Google Scholar] [CrossRef]
- Mishalani, R.G.; Shafieezadeh, A.; Li, Z. Updating Bridge Deck Condition Transition Probabilities as New Inspection Data Are Collected: Methodology and Empirical Evaluation. Transp. Res. Rec. 2018, 2672, 93–102. [Google Scholar] [CrossRef]
- Mohammed Abdelkader, E.; Zayed, T.; Marzouk, M. A Computerized Hybrid Bayesian-Based Approach for Modelling the Deterioration of Concrete Bridge Decks. Struct. Infrastruct. Eng. 2019, 15, 1178–1199. [Google Scholar] [CrossRef]
- Madanat, S.; Mishalani, R.; Wan Ibrahim, W.H. Estimation of Infrastructure Transition Probabilities from Condition Rating Data. J. Infrastruct. Syst. 1995, 1, 120–125. [Google Scholar] [CrossRef]
- Jiang, Y.; Sinha, K.C. Bridge Service Life Prediction Model Using the Markov Chain. Transp. Res. Rec. 1989, 1223, 24–30. [Google Scholar]
- Wang, X.; Nguyen, M.; Foliente, G.; Ye, L. An Approach to Modelling Concrete Bridge Condition Deterioration Using a Statistical Causal Relationship Based on Inspection Data. Struct. Infrastruct. Eng. 2007, 3, 3–15. [Google Scholar] [CrossRef]
- Mizutani, D.; Matsuoka, K.; Kaito, K. Statistical Deterioration Prediction Model Considering the Heterogeneity in Deterioration Rates by Hierarchical Bayesian Estimation. Struct. Eng. Int. J. Int. Assoc. Bridg. Struct. Eng. 2013, 23, 394–401. [Google Scholar] [CrossRef]
- Zhang, M.; Ruan, X.; Li, Y.; Fu, B. Probability-Based Surface Deterioration Assessment of Bridge Pylon and State Updating Using Inspected Crack Length Distribution. Struct. Infrastruct. Eng. 2023, 21, 1–19. [Google Scholar] [CrossRef]
- Khatami, D.; Shafei, B. Impact of Climate Conditions on Deteriorating Reinforced Concrete Bridges in the US Midwest Region. J. Perform. Constr. Facil. 2021, 35, 04020129. [Google Scholar] [CrossRef]
- Khatami, D.; Shafei, B.; Bektas, B. Data-Assisted Prediction of Deterioration of Reinforced Concrete Bridges Using Physics-Based Models. J. Infrastruct. Syst. 2023, 29, 05023003. [Google Scholar] [CrossRef]
- Yosri, A.; Elleathy, Y.; Hassini, S.; El-Dakhakhni, W. Genetic Algorithm-Markovian Model for Predictive Bridge Asset Management. J. Bridg. Eng. 2021, 26, 04021052. [Google Scholar] [CrossRef]
- Zambon, I.; Vidovic, A.; Strauss, A.; Matos, J.; Amado, J. Comparison of Stochastic Prediction Models Based on Visual Inspections of Bridge Decks. J. Civ. Eng. Manag. 2017, 23, 553–561. [Google Scholar] [CrossRef]
- Ibe, O.C. Controlled Markov Processes. In Markov Processes for Stochastic Modeling; Elsevier: Waltham, MA, USA, 2013; ISBN 9780124077959. [Google Scholar]
- Sobanjo, J.O. State Transition Probabilities in Bridge Deterioration Based on Weibull Sojourn Times. Struct. Infrastruct. Eng. 2011, 7, 747–764. [Google Scholar] [CrossRef]
- Guo, C.; Liang, Z. Semi-Markovian Maintenance Optimization for Reinforced Concrete Enabled by a Synthesized Deterioration Model. IEEE Trans. Reliab. 2022, 71, 1577–1589. [Google Scholar] [CrossRef]
- Furtado, F.; Ribeiro, D. Railway Bridge Management System Based on Visual Inspections with Semi-Markov Continuous Time Process. KSCE J. Civ. Eng. 2023, 27, 233–250. [Google Scholar] [CrossRef]
- Sobanjo, J.; Mtenga, P.; Rambo-Roddenberry, M. Reliability-Based Modeling of Bridge Deterioration Hazards. J. Bridg. Eng. 2010, 15, 671–683. [Google Scholar] [CrossRef]
- Nasrollahi, M.; Washer, G. Estimating Inspection Intervals for Bridges Based on Statistical Analysis of National Bridge Inventory Data. J. Bridg. Eng. 2015, 20, 04014104. [Google Scholar] [CrossRef]
- Manafpour, A.; Guler, I.; Radlińska, A.; Rajabipour, F.; Warn, G. Stochastic Analysis and Time-Based Modeling of Concrete Bridge Deck Deterioration. J. Bridg. Eng. 2018, 23, 04018066. [Google Scholar] [CrossRef]
- Mašović, S.; Hajdin, R. Modelling of Bridge Elements Deterioration for Serbian Bridge Inventory. Struct. Infrastruct. Eng. 2014, 10, 976–987. [Google Scholar] [CrossRef]
- Bush, S.J.W.; Henning, T.F.P.; Raith, A.; Ingham, J.M. Development of a Bridge Deterioration Model in a Data-Constrained Environment. J. Perform. Constr. Facil. 2017, 31, 04017080. [Google Scholar] [CrossRef]
- Zhang, K.; Lei, J.; Wang, Z.; Yuan, Q. A Numerical Algorithm for Damage Progression of Reinforced Concrete Bridge Piers during Air Temperature and Solar Radiation Cycles. Eng. Struct. 2024, 319, 118876. [Google Scholar] [CrossRef]
- Zhu, Z.; Ye, K.; Yu, X.; Lin, Z.; Xu, G.; Guo, Z.; Lu, S.; Nie, B.; Chen, H. State-Based Technical Condition Assessment and Prediction of Concrete Box Girder Bridges. Buildings 2024, 14, 543. [Google Scholar] [CrossRef]
- Chyad, A.M.; Abudayyeh, O. Impact of Environmental Factors on the Condition Rating of Concrete Bridge Decks Using Statistical-Distribution Methods. Pract. Period. Struct. Des. Constr. 2021, 26, 04021014. [Google Scholar] [CrossRef]
- Mia, M.M.; Kameshwar, S. Machine Learning Approach for Predicting Bridge Components’ Condition Ratings. Front. Built Environ. 2023, 9, 1254269. [Google Scholar] [CrossRef]
- Rajkumar, M.; Nagarajan, S.; Arockiasamy, M. Bridge Infrastructure Management System: Autoencoder Approach for Predicting Bridge Condition Ratings. J. Infrastruct. Syst. 2023, 29, 04022042. [Google Scholar] [CrossRef]
- Li, Z.; Burgueño, R. Using Soft Computing to Analyze Inspection Results for Bridge Evaluation and Management. J. Bridg. Eng. 2010, 15, 430–438. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y. Feature Selection and Deep Learning for Deterioration Prediction of the Bridges. J. Perform. Constr. Facil. 2021, 35, 04021078. [Google Scholar] [CrossRef]
- Feng, D.C.; Wang, W.J.; Mangalathu, S.; Sun, Z. Condition Assessment of Highway Bridges Using Textual Data and Natural Language Processing- (NLP-) Based Machine Learning Models. Struct. Control Heal. Monit. 2023, 2023, 761154. [Google Scholar] [CrossRef]
- Kwon, T.H.; Kim, J.; Park, K.T.; Jung, K.S. Long Short-Term Memory-Based Methodology for Predicting Carbonation Models of Reinforced Concrete Slab Bridges: Case Study in South Korea. Appl. Sci. 2022, 12, 12470. [Google Scholar] [CrossRef]
- Miao, P.; Yokota, H.; Zhang, Y. Deterioration Prediction of Existing Concrete Bridges Using a LSTM Recurrent Neural Network. Struct. Infrastruct. Eng. 2023, 19, 475–489. [Google Scholar] [CrossRef]
- Jing, G.; Ruiying, L.; Yao, Z. Comparison of Regression Model and LSTM-RNN Model in Predicting Deterioration of Prestressed Concrete Box Girder Bridges. Struct. Eng. Mech. 2024, 91, 39–47. [Google Scholar] [CrossRef]
- Kazantzi, A.K.; Moutsianos, S.; Bakalis, K.; Mitoulis, S.A. Cause-Agnostic Bridge Damage State Identification Utilising Machine Learning. Eng. Struct. 2024, 320, 118887. [Google Scholar] [CrossRef]
- Hu, X.; Liu, K. Structural Deterioration Knowledge Ontology towards Physics-Informed Machine Learning for Enhanced Bridge Deterioration Prediction. J. Comput. Civ. Eng. 2023, 37, 04022051. [Google Scholar] [CrossRef]
- Huang, Y.-H. Artificial Neural Network Model of Bridge Deterioration. J. Perform. Constr. Facil. 2010, 24, 597–602. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y. Bridge Condition Rating Data Modeling Using Deep Learning Algorithm. Struct. Infrastruct. Eng. 2020, 16, 1447–1460. [Google Scholar] [CrossRef]
- Lei, X.; Xia, Y.; Komarizadehasl, S.; Sun, L. Condition Level Deteriorations Modeling of RC Beam Bridges with U-Net Convolutional Neural Networks. Structures 2022, 42, 333–342. [Google Scholar] [CrossRef]
- Almarahlleh, N.; Liu, H.; Abudayyeh, O.; Almamlook, R. Predicting Concrete Bridge Deck Deterioration: A Hyperparameter Optimization Approach. J. Perform. Constr. Facil. 2024, 38, 04024009. [Google Scholar] [CrossRef]
- Elleathy, Y.; Ghaith, M.; Haggag, M.; Yosri, A.; El-Dakhakhni, W. Climate-Induced Deterioration Prediction for Bridges: An Evolutionary Computing-Based Framework. Innov. Infrastruct. Solut. 2024, 9, 114. [Google Scholar] [CrossRef]
- Saremi, S.G.; Goulias, D.; Zhao, Y. Alternative Sequence Classification of Neural Networks for Bridge Deck Condition Rating. J. Perform. Constr. Facil. 2023, 37, 04023025. [Google Scholar] [CrossRef]
- Abu Dabous, S.; Ibrahim, F.; Alzghoul, A. Modelling Bridge Deterioration Using Long Short-Term Memory Neural Networks: A Deep Learning-Based Approach. Smart Sustain. Built Environ. 2024; ahead of print. [Google Scholar] [CrossRef]



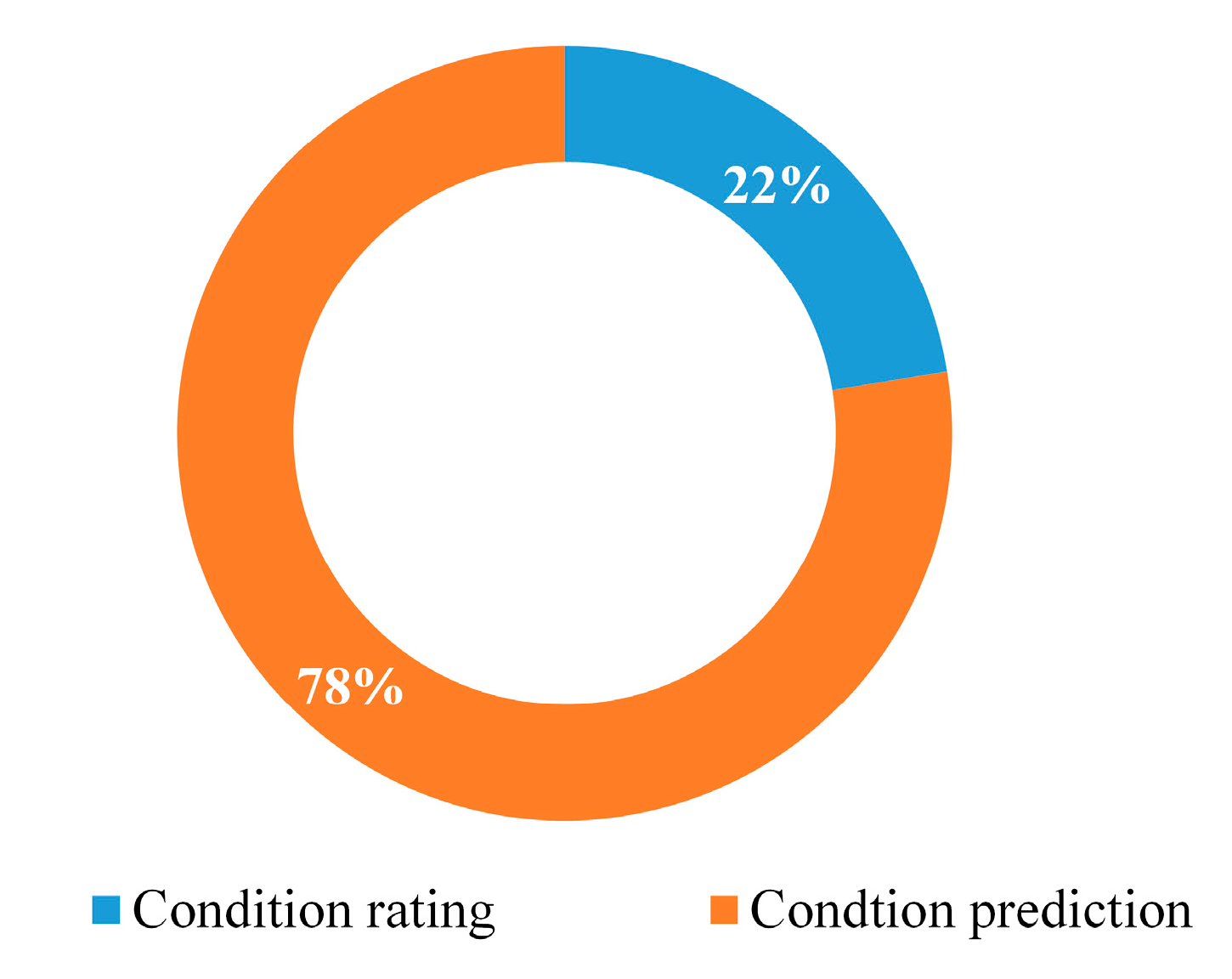






| Source | h_Index | Publications |
|---|---|---|
| Journal of Bridge Engineering | 9 | 13 |
| Journal of Performance of Constructed Facilities | 9 | 13 |
| Structure and Infrastructure Engineering | 8 | 12 |
| Applied Sciences (Switzerland) | 4 | 6 |
| Structures | 4 | 5 |
| Asce-Asme Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering | 3 | 4 |
| Automation in Construction | 3 | 3 |
| Journal of Infrastructure Systems | 3 | 5 |
| Practice Periodical on Structural Design and Construction | 3 | 5 |
| Transportation Research Record | 3 | 4 |
| Affiliation | Publications | Country | Publications | Author | Publications |
|---|---|---|---|---|---|
| Concordia University | 8 | USA | 78 | Zayed T | 8 |
| Tongji University | 5 | China | 49 | Abu Dabous | 4 |
| Turner–Fairbank Highway Research Center | 5 | Canada | 28 | Bagchi A | 4 |
| Amirkabir University of Technology | 4 | Japan | 18 | Dinh K | 4 |
| Florida Atlantic Univ. | 4 | India | 9 | Strauss A | 4 |
| Hokkaido University | 4 | Australia | 8 | Wang X | 4 |
| Southeast University | 4 | Portugal | 7 | Zambon I | 4 |
| University Of Sharjah | 4 | UAE | 7 | Arockiasamy M | 3 |
| Colorado State University | 3 | Iran | 6 | Ghodoosi F | 3 |
| Concordia Univ. | 3 | Republic of Korea | 6 | Gucunski N | 3 |
| Keyword | Occurrence | Total Link Strength |
|---|---|---|
| Deterioration | 75 | 514 |
| Concrete | 59 | 427 |
| Bridges | 48 | 355 |
| Concrete bridges | 45 | 326 |
| Bridge deck | 34 | 268 |
| Inspection | 33 | 256 |
| Deterioration modeling | 30 | 215 |
| Forecasting | 28 | 238 |
| Condition assessment | 26 | 207 |
| Bridge management system | 21 | 171 |
| Corrosion | 21 | 122 |
| Maintenance | 20 | 155 |
| Reliability | 18 | 110 |
| Condition rating | 17 | 143 |
| Decision making | 17 | 131 |
| Nondestructive evaluation | 15 | 131 |
| Visual inspection | 15 | 103 |
| Markov processes | 14 | 121 |
| Inventory Requirement | Details | |
|---|---|---|
| Descriptive data | Bridge identification | Identification (name, number, …) |
| Location (state, place, …) | ||
| Classification (owner, maintenance responsibility, …) | ||
| Bridge material and type | Span material and type (number of spans, span type, …) | |
| Substructure material and type (configuration, foundation type, …) | ||
| Roadside hardware (railing, transitions, …) | ||
| Bridge geometry | Geometries and dimensions (total length, span length, …) | |
| Bridge features | Feature identification (type, name, …) | |
| Routes (number, type, service type, …) | ||
| Highways (function classification, traffic load, …) | ||
| Railroads (service type, dimensions, …) | ||
| Navigable waterways (dimensions, substructure navigation protection, …) | ||
| Loads, load rating, and posting | Loads and load rating (design load, load rating factor, …) | |
| Load posting status (statues, change date, …) | ||
| Load evaluation and posting (legal load rating, configuration, …) | ||
| Condition data | Inspections | Inspection requirements (fatigue details, underwater inspection, …) |
| Inspection events (type, due date, interval, …) | ||
| Bridge condition | Component condition ratings (deck, superstructure, substructure, …) | |
| Element identification (number, quantity, …) | ||
| Element conditions (state 1, state 2 state 3 state 4) | ||
| Appraisal (scour vulnerability, seismic vulnerability, …) | ||
| Work events (year build, …) |
| Defects | Condition States | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Good | Fair | Poor | Sever | |
| Delamination/patched area/spall | None | Sound patch. Delamination/spall depth < 1 in or diameter < 6 in. | Non sound patch. Delamination/spall depth > 1in or diameter > 6 in. | The defects may impact the strength or serviceability of the element or bridge. |
| Exposed Rebar | None | No measurable losses in rebar. | With measurable losses but does not threaten the structural integrity. | |
| Rust/Efflorescence Staining | None | No heavy build-up. | Heavy build-up. | |
| Cracking | Width < 0.012 in or spacing > than 3 ft. | Width (0.012–0.05) in or spacing (1–3) ft. | Width > 0.05 in or spacing < than 1 ft. | |
| Damage | Not applicable. | State 2 material damage. | State 3 material damage. | State 4 material damage. |
| Reference | Cracks/Spall | Delamination | Corrosion | Concrete Health | Loading | Input Type |
|---|---|---|---|---|---|---|
| [45,46,47,48] | VI | Fuzzy | ||||
| [46,47,49] | VI | Crisp | ||||
| [8] | VI | Hammer | GPR, HCP, ER. | Fuzzy | ||
| [37] | VI | IE, CD | GPR, HCP, ER. | Crisp | ||
| [48] | GPR | Fuzzy | ||||
| [38] | VI | IR | GPR | Fuzzy | ||
| [6,27] | VI | GPR | Crisp | |||
| [50] | VI | IR | GPR | Crisp | ||
| [41] | VI | HCP | RH | Acceleration sensors | Crisp | |
| [42] | DP | IE | GPR, ER, HCP | UPV | Crisp | |
| [51] | VI | ER | RH, UPV | Crisp | ||
| [40] | IE | ER, HCP, GPR. | UPV | Crisp | ||
| [52] | HCP | Stress-strain gage | Crisp | |||
| [53] | VI | HCP | UPV, Penetration resistance. | Crisp |
| NDE | Cost | Speed | Complexity | Performance | Capability |
|---|---|---|---|---|---|
| GPR | poor | poor | poor | fair | very good |
| IE | very poor | very poor | very poor | poor | very good |
| UPV | very poor | very poor | very poor | poor | very good |
| HCP | poor | very poor | very poor | poor | fair |
| ER | poor | poor | very poor | poor | fair |
| IR | fair | poor | poor | very poor | very good |
| DP | good | good | moderate | poor | fair |
| Code | Condition | Description |
|---|---|---|
| 9 | Excellent | Isolated inherent defects. |
| 8 | Very good | Some inherent defects. |
| 7 | Good | Some minor defects. |
| 6 | Satisfactory | Widespread minor or isolated moderate defects. |
| 5 | Fair | Some moderate defects; strength and performance of the component are not affected. |
| 4 | Poor | Widespread moderate or isolated major defects; strength and/or performance of the component is affected. |
| 3 | Serious | Major defects; strength and/or performance of the component is seriously affected. Condition typically necessitates more frequent monitoring, load restrictions, and/or corrective actions. |
| 2 | Critical | Major defects; component is severely compromised. Condition typically necessitates frequent monitoring, significant load restrictions, and/or corrective actions in order to keep the bridge open. |
| 1 | Imminent failure | Bridge is closed to traffic due to component condition. Repair or rehabilitation may return the bridge to service. |
| 0 | Failed | Bridge is closed due to component condition, and is beyond corrective action. Replacement is required to restore service. |
| Ref. | Component | Defects | Tools | Input | Methodology |
|---|---|---|---|---|---|
| [60] | Deck | Crack, spalling, and delamination | VI | Fuzzy | Monto Carlo simulation to defuzzify the final CI. |
| [8] | Deck | Crack, spalling, delamination, and corrosion | VI, hammer tapping, HCP | Fuzzy | Fuzzy rules inference system to combine the condition from various defects. |
| [58] | Deck | Crack | VI | Fuzzy | Fuzzy rules inference system to combine fuzzified inputs for crack width and depth. Difuzzified using center of the area. |
| [37] | Deck | Severe delamination, incipient delamination, corrosion, and corrosiveness. | CD, IE, HCP, ER, and GPR. | Crisp | Assign a CI of 0 to 9 based on the area of severe delamination and area of other defects. |
| [48] | Deck | Corrosion | GPR | Fuzzy | Used weighted fuzzy union (WFU) and centroid defuzzification to yield an HI from 0 to 100. |
| [38] | Deck | Delamination, corrosion, scaling cracking, spalling, pop-out. | IR, GPR, VI | Fuzzy | The fuzzy condition of defects was integrated via weighted summation. WFU was used to defuzzify and yield a HI from 0 to 100. |
| [41] | Superstructure | Concrete strength, corrosion, crack, strain, and natural frequency. | VI, HCP, RH, and acceleration sensors. | Crisp | FCM-PSO to cluster the bridges into five condition categories based on five metrics for maintenance prioritization. |
| [50] | Deck | Surface defect, corrosion, and delamination. | VI, GPR, and IR. | Crisp | Remove overlap to calculate the defected area percentage, and use the Colorado DOT manual to assign a CI from 1 to 5 based on total defected area. |
| [42] | Deck | Corrosion, delamination, and material damage. | ER, HCP, GPR, IE, and UPV. | Crisp | Provide HI (0–100) for each NDE and use the average as the overall HI. |
| [27] | Deck | Delamination, scaling cracking, spalling, deposits, joints, pop-out, and corrosion. | VI and GPR | Crisp | Quality Function Deployment integrating VI and Ground Penetrating Radar (GPR) evaluation |
| [40] | Deck | Corrosion, material damage, and delamination. | ER, HCP, GPR, UPV, and IE. | Crisp | Time laps NDE inspection was used along with Jensen- Shannon divergence to provide a CI of (0–10). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faris, N.; Zayed, T.; Fares, A. Review of Condition Rating and Deterioration Modeling Approaches for Concrete Bridges. Buildings 2025, 15, 219. https://doi.org/10.3390/buildings15020219
Faris N, Zayed T, Fares A. Review of Condition Rating and Deterioration Modeling Approaches for Concrete Bridges. Buildings. 2025; 15(2):219. https://doi.org/10.3390/buildings15020219
Chicago/Turabian StyleFaris, Nour, Tarek Zayed, and Ali Fares. 2025. "Review of Condition Rating and Deterioration Modeling Approaches for Concrete Bridges" Buildings 15, no. 2: 219. https://doi.org/10.3390/buildings15020219
APA StyleFaris, N., Zayed, T., & Fares, A. (2025). Review of Condition Rating and Deterioration Modeling Approaches for Concrete Bridges. Buildings, 15(2), 219. https://doi.org/10.3390/buildings15020219








