Research on Concrete Beam Damage Detection Using Convolutional Neural Networks and Vibrations from ABAQUS Models and Computer Vision

Abstract

Researchers have already used vibration data and deep learning methods, such as Convolutional Neural Networks (CNNs), to detect structural damage. Moreover, some researchers have employed image-based displacement sensors (such as the template matching and edge detection methods) to obtain structural vibration information. It is necessary to verify whether deep learning methods can detect minor damage inside beams, for example, small hollowing in concrete. In addition, there is an urgent need to develop an effective image-based displacement sensor that can simultaneously detect a large number of reliable vibration data from different measurement points. In this study, the vibration data of two beam-ABAQUS models were used as the input data for a newly designed deep learning-based structural health monitoring method. There were 500 vibration samples for each case, and the peak of vibrations was several millimeters. The proposed CNN model can locate damage positions in beams with high accuracy (close to 100%), and the damage sizes are 3 cm and 6 cm. Laboratory experiments were carried out on four beams with different damage. The optimized displacement sensor developed based on the edge detection method was used to detect the displacement of the beams. Each beam had 200 vibration data, and there were 800 vibration data in total. These vibration data were used as input data to train the proposed deep learning architecture, and satisfactory accuracy was achieved in detecting the damage of the beams with an accuracy of 97%. The training process is satisfactory in that the training loss and validation loss dropped very quickly.

1. Introduction

Conventionally, contact-type displacement sensors, such as linear variable differential transformers (LVDTs) and laser-based displacement sensors [1], are employed for measuring structural displacements. Accelerometers, which do not need a stationary reference to be placed, can calculate displacement through double integration of the acceleration data. However, this method typically introduces large errors due to the double integration. Global positioning systems [2] have some strengths because of their non-contact features. However, their large cost hinders widespread application in monitoring civil engineering structures.

In recent years, vision-based displacement measurement techniques have gained significant attention as a promising alternative to traditional sensors. These non-contact methods utilize computer vision algorithms and image processing techniques to extract displacement information from video footage of structures. Vision-based approaches offer several advantages, including the ability to measure displacements at multiple points simultaneously, reduced installation complexity, and potential cost-effectiveness for large-scale monitoring projects. One popular vision-based technique is Digital Image Correlation (DIC), which tracks the movement of surface patterns or features in a series of images to calculate displacements. Another approach involves using artificial targets or markers attached to the structure, which can be tracked with high precision using specialized algorithms. These computer vision-based displacement methods have shown promising laboratory results and controlled experiments in the field, demonstrating their potential for practical applications in structural health monitoring.

However, vision-based displacement measurement techniques also face challenges that need to be addressed for widespread adoption. These include sensitivity to environmental factors such as lighting conditions and weather, the need for high-resolution cameras and stable camera positioning, and computational requirements for real-time processing of large amounts of image data. Ongoing research aims to overcome these limitations and improve the robustness and reliability of vision-based displacement measurements for various types of civil engineering structures. In the past 20 years, image-based displacement sensors have become increasingly attractive due to their low cost and efficiency. To adopt such computer vision methods in structural health monitoring, template matching is typically used to trace structural displacements. This technique calculates the coordinates of the template in images. The accuracy is always satisfying. Connections like a bolts group are often used as the template. Olaszek [3] pioneered the use of a template-matching-based method and used this method to obtain bridges’ dynamic characteristics. Wahbeh et al. [4] used a novel vision-based approach and detected the true displacement history at locations of civil infrastructure systems through a camera with high resolution and a laser-based displacement sensor for comparison. Lab experiments successfully verified this approach. Lee et al. [5] proposed an image-based displacement method to measure bridges’ vibrations, enabling on-site monitoring in real time.

Lei et al. [6] introduced a template-matching method using a fast Normalized Cross-Correlation (NCC) that significantly reduced computation time and increased efficiency. This method uses a search algorithm after being modified locally on detecting small and negligible motions. When multiple suitable templates exist in one image, template matching can simultaneously obtain vibrations at various points. Multiple templates within one region of interest (ROI) can obtain structural motions at multiple positions. Lin et al. [7] developed a displacement method using videogrammetry to obtain vibrations. Then, these vibrations are used to calculate structural dynamic behavior. Jurjo et al. [8] proposed a computer vision-based method to detect vibrations using a template-matching method.

However, when suitable natural targets are absent at measured points and attaching artificial targets is difficult or dangerous—such as on bridges spanning large rivers or canyons, then, a target-free computer vision-based vibration monitoring method becomes increasingly necessary. This advancement would significantly progress in the field.

Dynamic characteristics of structures, especially bridges—such as natural frequency, the damping ratio, and mode shape—can be used for structural health evaluation by identifying and locating damage [9]. This approach is based on the theory that structural damage could cause changes in mass and stiffness, leading to changes in dynamic characteristics [10,11,12]. The relationships between vibrations and damage information can be built using the dynamic theory [13]. However, dynamic characteristics like natural frequencies are sensitive to some small damages. Also, these dynamic characteristics can be easily affected by environmental effects [14,15]. Following a similar approach to image-based structural condition assessment, some researchers have investigated identifying damage through deep learning models using vibration data inputs. Lin et al. [16] developed a CNN-based model to be trained using the raw vibration of a beam and detected damage with 94.57% accuracy. Some other researchers have used CNN-based methods to find damage caused by loose bolts in steel trusses with high accuracy [17]. Tran et al. [18] proposed a one-dimensional CNN to detect damage using time series data without manual feature extraction. Mai et al. [19] used deep learning to predict permanent transverse displacement with high accuracy. Jiang et al. [20] performed experiments on an eight-level steel frame structure, using 1D-CNN to extract damage locations with over 99% accuracy. Additional research has explored using vibration data and deep learning to detect damage [21,22,23,24,25,26]. Recently, some researchers have used fused data from fault images and vibration data in damage diagnosis [27,28], though they did not use raw vibration data for civil structures or combine these approaches.

This study explores an edge detection-based method for structural condition assessment, verifying whether the vibrations obtained using an edge detection-based displacement sensor can train a CNN model with high accuracy. To enhance efficiency, a new approach is proposed to simultaneously obtain vibrations at multiple measured points. The proposed methods would reduce the cost of bridge damage detection in the field, because only the camera needs to be prepared and there is no need to attach any sensors to the bridge.

The first main goal of this study is verifying whether the proposed CNN model could detect accurately small damage to a beam using vibrations from simulation data or lab experiments accurately. The second main goal of this study is to activate an optimized image-based displacement sensor that could detect vibrations at all measured points in the meantime. Then, finally, this study aims to verify whether vibrations obtained by the developed computer vision-based sensor could train the CNN model. And, using this method, the findings obtained in this investigation show that beam damage was successfully, effectively, and accurately obtained for both damage location and damage magnitude.

2. Deep Learning Models Using Vibration Signals

2.1. Deep Learning-Based Damage Detection Using Vibration Data Obtained in ABAQUS

As shown in Figure 1, a CNN network typically uses three main sections to detect structural damage through vibration data at a structure’s measurement points: (1) dataset collection, (2) CNN model training, and (3) validation and prediction. The ABAQUS model provides vibrations at measurement points under dynamic loads. To expand the collected vibration database, Gaussian white noise with varying Signal-to-Noise Ratios (SNRs) was added to different cases using Equations (1) and (2) below [29]. The SNR represents the ratio of the power of the useful signal to the power of the background noise.

$$SNR={\displaystyle \frac{Signal Power}{Noise Power}}$$

(1)

$$SNR\left(dB\right)=10 {\mathit{log}}_{10}{\displaystyle \frac{Signal Power}{Noise Power}}$$

(2)

Here, the signal power and the noise power are defined as ${\int }_{-T/2}^{T/2}{x\left(t\right)}^{2}dt$, respectively, with x(t) as the original signal or noise. T is the time period of the original signal or noise.

The vibration data undergo a meticulous classification process, categorizing them into distinct patterns based on various damage cases. These classified data are then randomly partitioned into three essential groups: a substantial 70% dedicated to training, 15% allocated for validation purposes, and the remaining 15% reserved for testing. The training data, which form the largest portion, are carefully input into the proposed Convolutional Neural Network (CNN) model to initiate and refine the system’s learning process. Both the training and validation sections play pivotal roles in the development of the CNN model, working in tandem to enhance its feature learning sensitivity and bolster its classification performance. The validation data help to fine-tune the model’s parameters and prevent overfitting. Upon completion of the training and validation phases, the test data are systematically fed into the model. This final step serves two critical purposes: to predict outcomes based on the model’s learned features and to rigorously assess its accuracy in real-world scenarios.

The CNN model employed in this section is architected with three fundamental layers, each serving a unique purpose in the data processing pipeline. These layers are the convolution layer, responsible for feature extraction; the pooling layer, which reduces spatial dimensions and the computational load; and the fully connected layer, which integrates learned features for the final classification. These layers are meticulously composed of artificial neurons. They are arranged in three dimensions, which are the width, height, and depth. The input data consist of raw vibrations collected from measured points on the structure under investigation. These data forms a two-dimensional matrix, rich with temporal and spatial information. As this matrix progresses through each successive layer of the CNN model, it undergoes a series of transformations. These transformations gradually distill the raw vibration data into increasingly abstract and meaningful features. By the time the data reach the final layer, the CNN has effectively transformed the initial two-dimensional matrix into a one-dimensional vector. This vector corresponds directly to the damage category, providing a clear and interpretable output for structural health monitoring purposes.

2.2. CNN-Based Structural Damage Detection Through Raw Vibration Data Obtained in Experiments

Figure 2 shows the process of the intended CNN damage detection model for experiments. First, the vibrations of the beam are calculated using the proposed optimized computer vision-based displacement sensor. There are 200 vibrations for each beam and 800 vibrations in total. These 800 vibrations are divided into 70% training data, 20% validation data, and 10% test data. These data are sent to the designed CNN model to train it. Finally, the training results are obtained to detect beam damages using vibrations and the proposed CNN structure.

2.3. The Proposed CNN Model

CNNs are intricate architectures composed of multiple layers, each meticulously containing artificial neurons. These layers are posted in three parts: height, depth and width, which are the dimensions of the layers. This sophisticated arrangement allows for complex pattern recognition and feature extraction. In the context of this part, the input source consists of raw displacements measured at several different points on the structure under investigation. This input is represented as a two-dimensional matrix, capturing both spatial and temporal aspects of the structural response. For example, if the 10 measured points and 1000 displacements for each point are used, the size of the two-dimensional matrix is 10 × 1000. As the data progress through each layer of the CNN model, a remarkable transformation occurs. The initial two-dimensional matrix undergoes a series of operations and transformations, ultimately becoming a single-dimensional matrix. This vector corresponds to a specific classification, effectively translating the complex input data into a meaningful classification output. This process exemplifies the CNN’s ability to extract high-level features and make informed decisions based on the input data. Figure 3 provides a comprehensive visual representation of the entire process within the proposed CNN system. This illustration offers valuable insights into the data flow and transformations occurring at each stage of the network. The CNN architecture employed in this study comprises three main types of layers, each serving a crucial function in the overall process: the convolution layer, the pooling layer, and the fully connected layer. These layers work in concert to process the input data, learn relevant features, and ultimately make accurate predictions regarding structural damage detection. This proposed CNN system is newly designed in this study using vibrations as input.

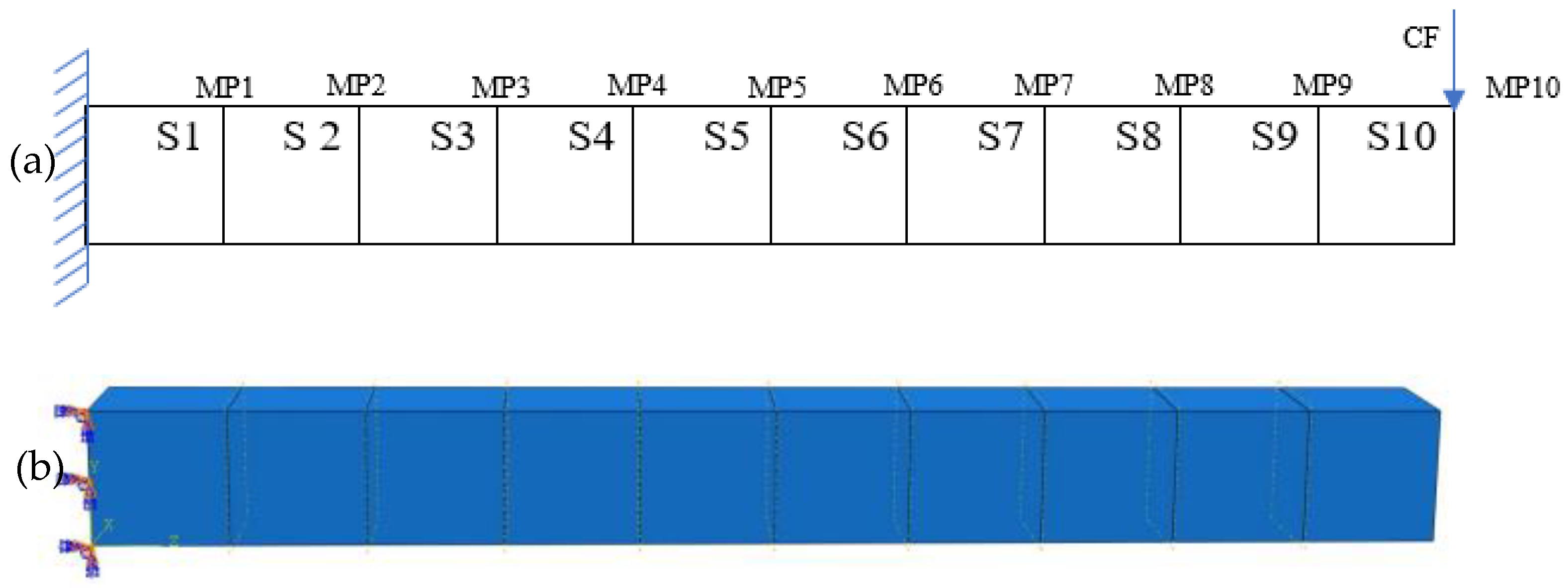
2.4. Data Collection Through ABAQUS Modeling

As shown in Figure 4a, a beam’s diagram was created using ABAQUS. The 10 parts and 10 monitored points are shown in this model. In each case, different segments were damaged by being replaced using plastic material whose modulus is 80% of the healthy part. The concentrated force was then placed at the beam’s end. Then, the concentrated force was released, and the beam performed vibrations with damping. This process enabled the measurement of vibrations at all measured points of the beam. Then, these vibrations were labeled and used to train the proposed deep learning model. Figure 4b depicts the beam that is modeled by ABAQUS. To expand the training dataset, Gaussian noise was applied, resulting in a total of 8000 samples. The 10 measured points and 1000 displacements for each point were used, and the size of the two-dimensional matrix was 10 × 1000.

Table 1. The damage locations of individual cases.

Case	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Damage	Healthy	1#	2#	3#	4#	5#	6#	7#	8#	9#	10#	1#,4#	3#,6#	1#,5#	4#,8#	5#,9#

displays various damage positions for all cases. The 10 cases with a single damage location (cases No. 2 to No. 11), one healthy beam (case No. 1), and five cases (No. 12 to No. 16) with two damage positions are shown. For instance, case No. 15 shows damages at both element #4 and element #8.

Figure 5 shows the model of the beam in ABAQUS. This beam model was separated into 90 elements. A total of 15 cases that have 15 different damage positions was performed. These cases included one healthy beam, six beams with only one damage position, five beams that have two damage positions, and three beams with three damage positions. Beam vibrations were initiated by releasing a concentrated force at the beam’s free end.

Figure 5a displays 10 measurement points. To expand the training dataset, Gaussian noise was applied, resulting in a total of 7500 samples. Element damage was simulated by replacing them using plastics material.

Table 2. All cases from (0) to (14) in the beam 2 experiment.

Case	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Damage	Healthy	S1 d	S1 c	S1 h	S2 b	S2 g	S3 e	S2 S9 b	S1 S4 b	S2 S4 f	S3 S4 f	S2 S8 d	S2 S7 S9 e	S3 S6 S9 c	S1 S4 S7 a

shows the 15 cases. For instance, case 9 has two damages at S2 and S4. And the damage is located at the f part of the cross section of the beam.

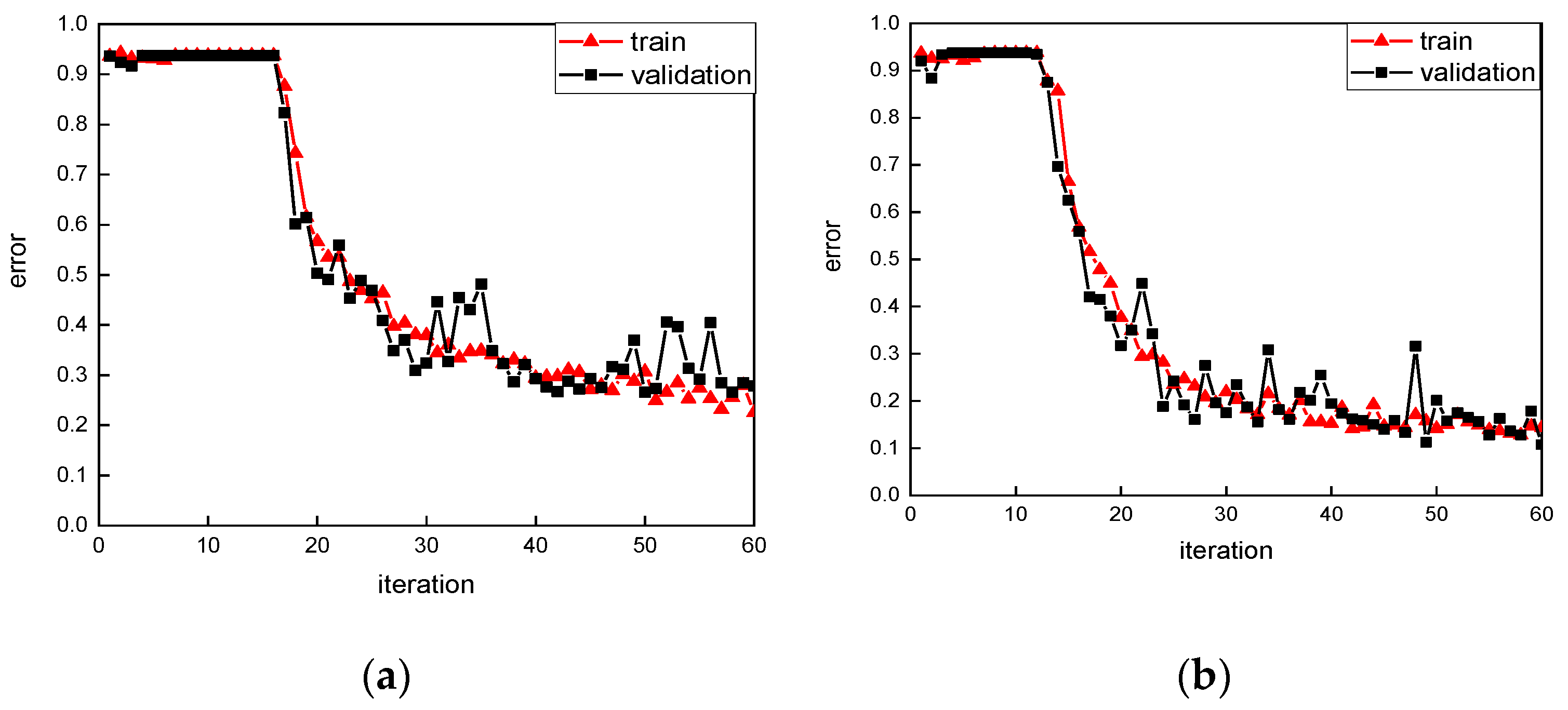
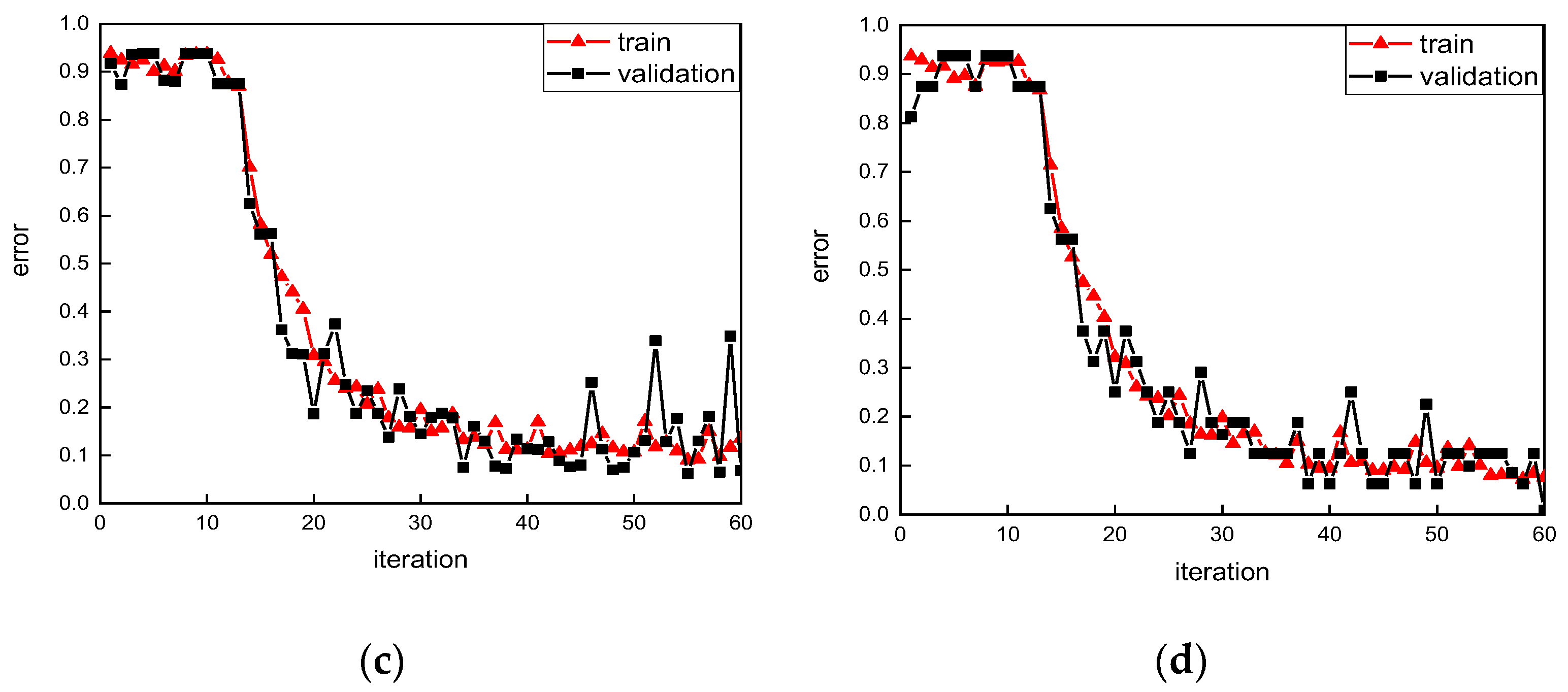
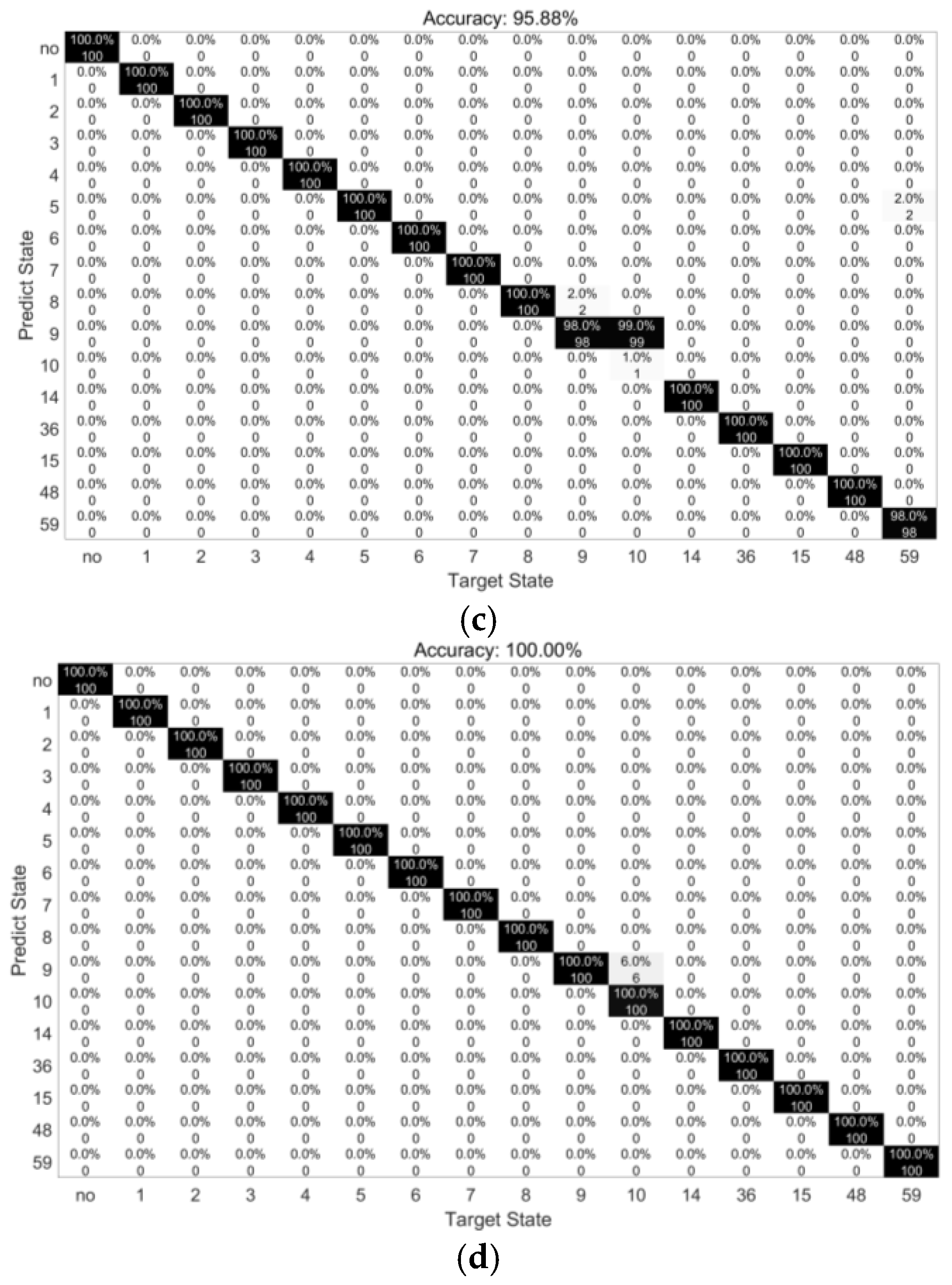
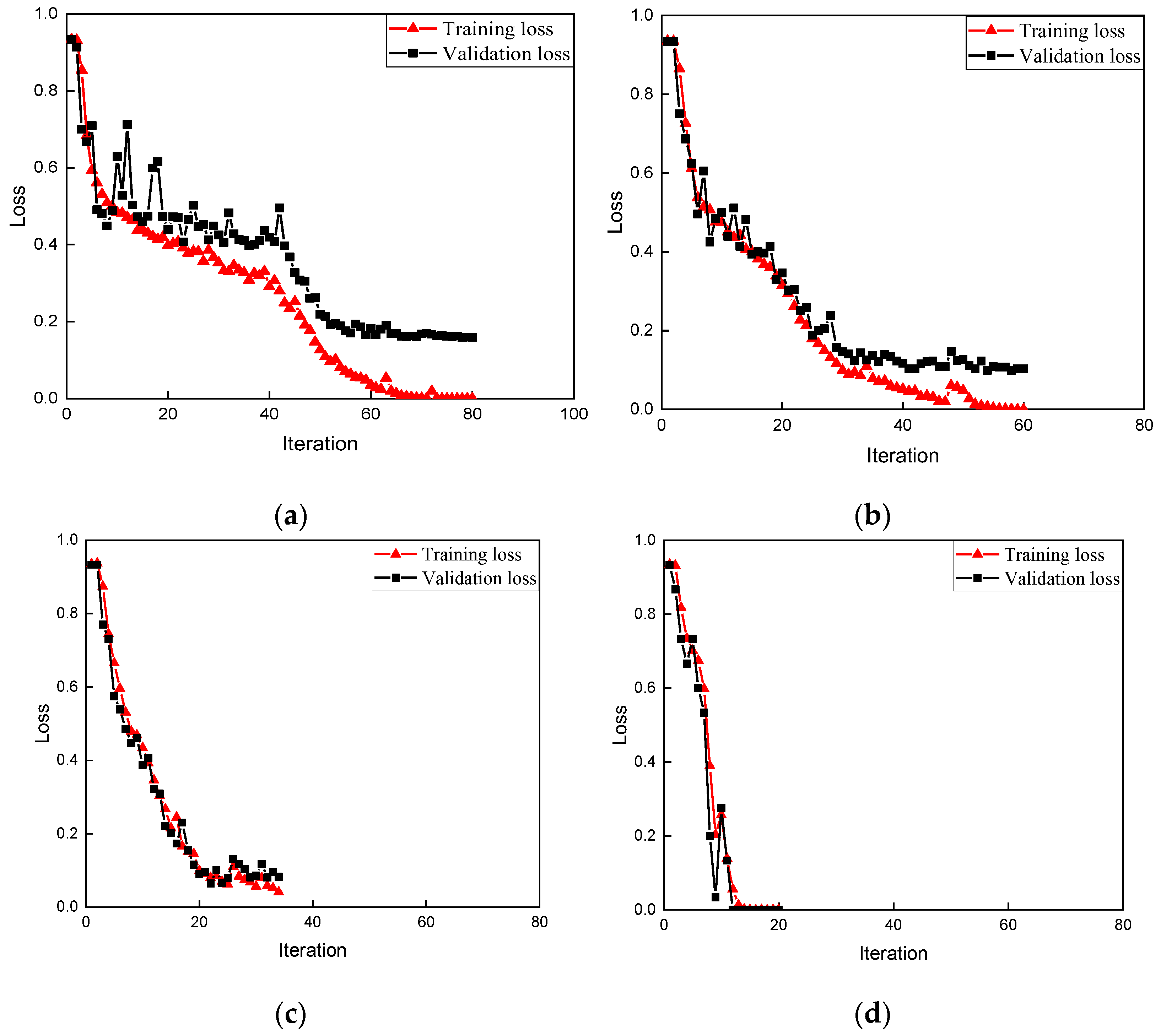
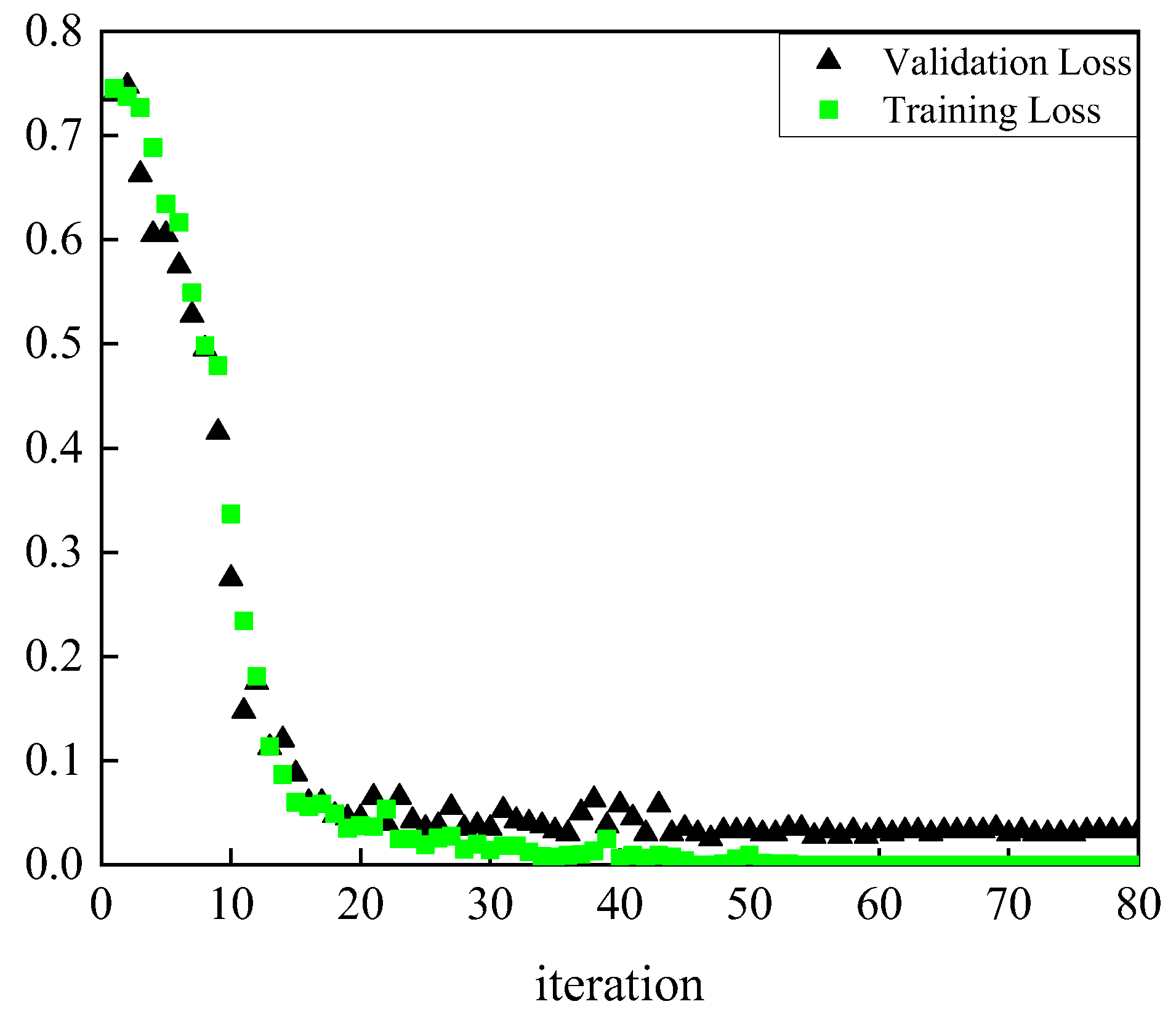
3. Results of Simulation Model for Training, Validation, and Prediction

The process described above yielded satisfactory results for both beams. For beam 1, the changes become evident after applying noise, which significantly expanded the dataset. Figure 6 illustrates this by comparing (a) the raw displacement data with (b) the displacement data including the noise.

Figure 7 shows an accuracy of 74.36% when the SNR is 90 dB. The x-axis is the iteration circle of the proposed CNN structure. The training processes that have different noise levels exhibit very similar overall shapes. As the noise decreases, the accuracy approaches 100%. The loss function is calculated by taking the difference between the predicted labels and the actual labels of the training data.

As shown in Figure 8, the minimum accuracy is 74.36%, which is satisfactory. The target state refers to the true damage type, and the predict state refers to the results from the CNN. The main errors occur at points 8, 9, and 10, partly because damage at locations close to the free end always has a smaller effect on the beam’s characteristics. The two damaged cases always are affected by cases that have at least one matching damage location, like cases 5 and 59.

The prediction accuracies are included in

Table 3. The accuracies of different cases with different SNRs.

Noise level	90	100	110	120
Accuracy	74.36%	87.88%	95.88%	100.00%

for comparison.

Figure 9 depicts the vibrations when the noises are 85 dB and in the absence of noise. The vibrations underwent significant alterations for the cases of 85 dB.

For beam 2, analogous outcomes can be witnessed in Figure 10. When the SNR is below 90 dB, the accuracy lies within the range of 80% to 90%. For SNR values spanning from 90 dB to 100 dB, the accuracy approximates 100%. Scenarios featuring a solitary damaged location exhibit more errors, whereas those with multiple damaged locations manifest higher accuracy.

Figure 11 illustrates the training processes at various SNR levels. A lower SNR requires more iterations to stabilize the training curves. As the SNR decreases, accuracy drops and the gap between the training and validation losses widens.

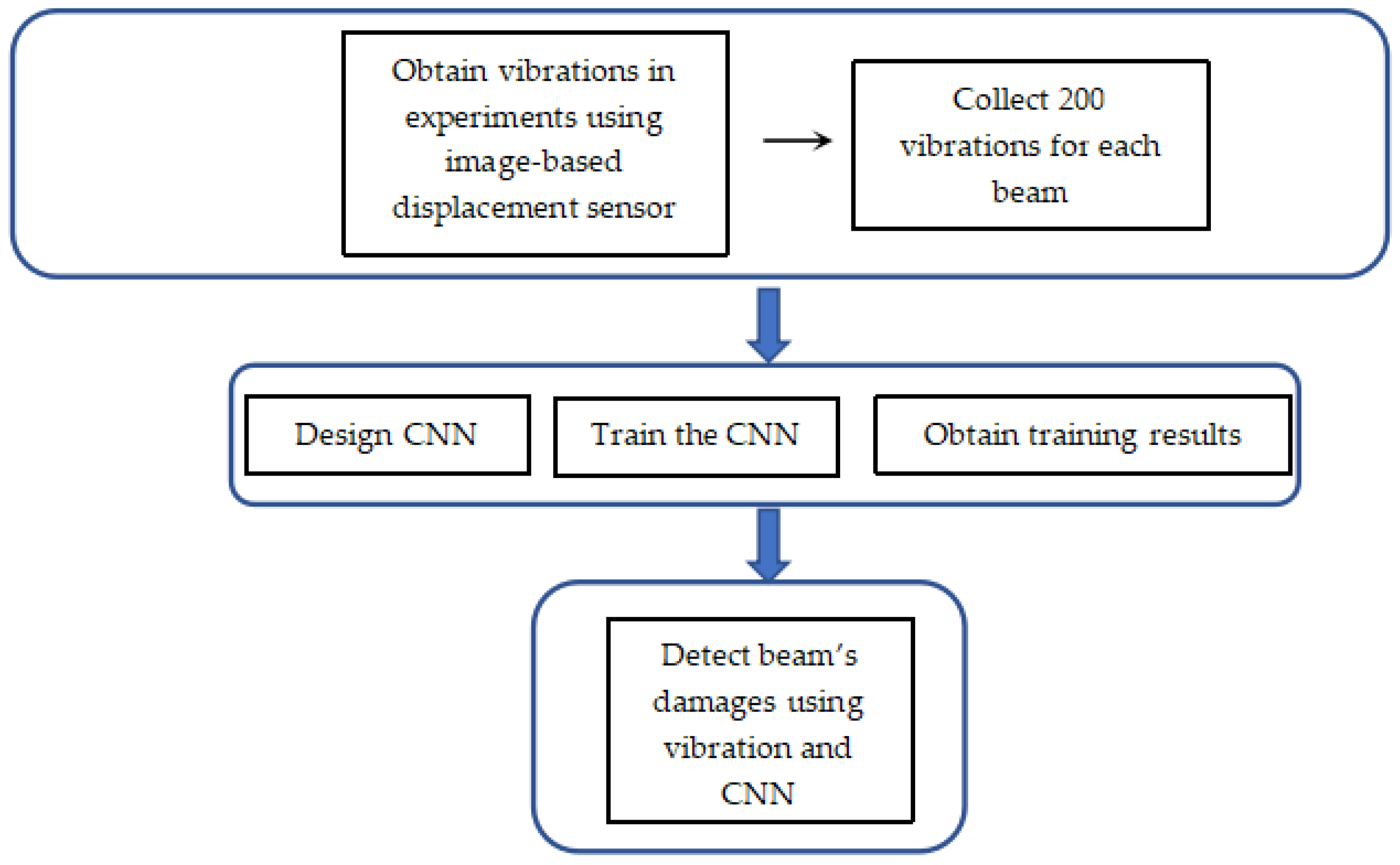
4. Experiment on Beams in Lab

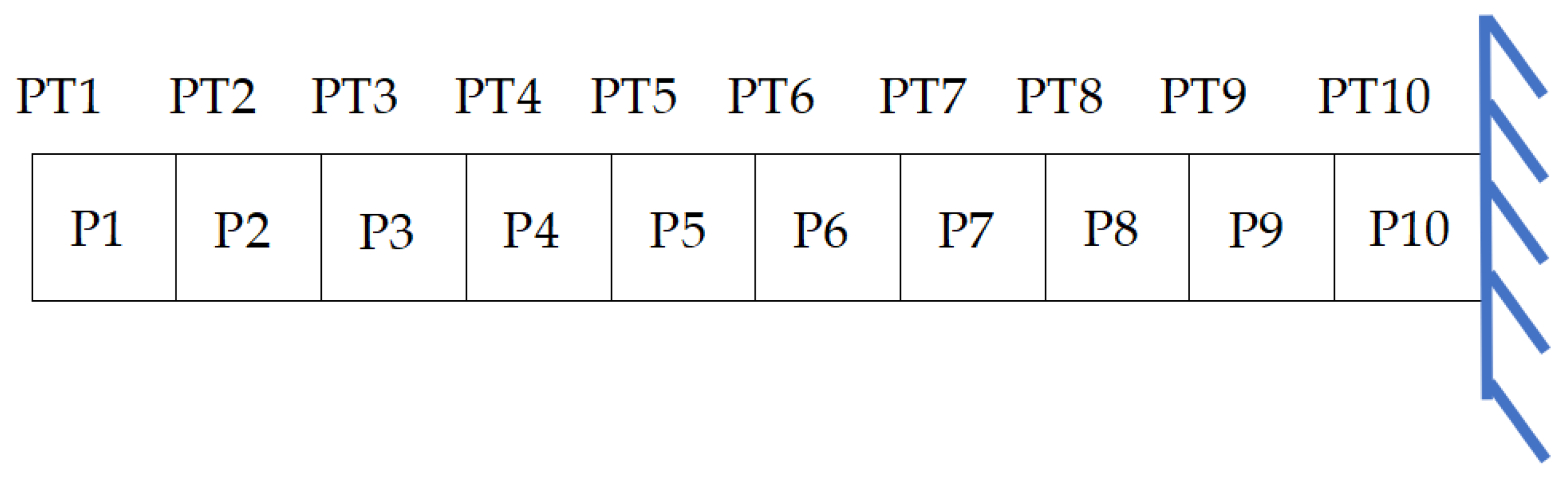
4.1. Methodologies of the Proposed Computer Vision-Based Displacement Sensor

The innovative computer vision-based displacement sensor proposed in this study functions analogously to an array of LVDT or laser displacement sensors. Its primary capability lies in focusing on the edges of beams and calculating their displacement within captured images. The camera, which must remain stationary throughout the process, serves as a fixed reference point for all measurements. As illustrated in Figure 12, the process begins with the acquisition of vibration videos, which are subsequently converted into individual image frames. These frames are then transformed into grayscale images to facilitate edge detection. An edge detection algorithm is applied to these grayscale images to identify the edges, with particular attention paid to the edges at predetermined measurement points. These specific edges are then traced using the proposed method, allowing for precise tracking of their movement over time. The final step in this process involves the application of appropriate scale factors to the tracked edge movements. This crucial step translates the pixel-based measurements from the image space into real-world displacement values. By doing so, the relative vibrations of the beams can be accurately determined and quantified, providing valuable data for structural analysis and monitoring applications. To achieve higher accuracy in displacement calculations, the researchers employed a sophisticated Zernike moment-based sub-pixel edge detection method, which enables precision at the sub-pixel level [30].

4.2. Optimized Computer Vision-Based Displacement Sensor

Figure 13 shows the different images in the camera view, including the original image, the grayscale original image, the edges in the whole image and a zoom-in to the edges in the whole image. The edges at the measured points can be traced and their coordinates can be obtained using the proposed method. Compared with existing computer vision-based displacement sensors, the proposed method can detect these 10 vibrations at 10 measured points in the meantime. And the running time is less with high accuracy.

Because the gradients at these 10 parts of the measured points in the whole image are different, these parts need different parameters to obtain the edges using an edge detector and to remove other fake edges from the background. In this study, a method called an adaptable parameters edge detector is proposed, which could set different parameters at different areas and remove the edges that are not from the beam structure. Figure 13e,f show the edges obtained without adaptable parameters and the edges obtained by applying adaptable parameters. After applying the proposed adaptable parameters of the edge detector, all fake edges that would cause huge errors are removed successfully.

4.3. Plan of the Experiment

Experiments were performed to obtain vibrations of the beam at different damage conditions using a computer vision-based displacement sensor. Figure 14 shows the experiment’s setup. An iPhone14 pro max with 60 frames per second and 1920 × 1080 pixel resolution was used. And the camera was fixed 1 m away from the beam to record the video of the beams’ displacement. There were four different beams with different damage inside the beams, as shown in

Table 4. The different damages of the four beams.

Beam	1	2	3	4
Damage position	Healthy	P7, P2	P3, P2	P7, P2
Damage type	\	6 cm cube	3 cm cube	3 cm cube

. Figure 14c shows the crushed stone that was put into the wooden box and reduced the cement to cause damage to the beam. The dimensions of the beams were 150 mm × 100 mm × 1000 mm. The beams would perform vibrations after percussion. And each beam would be triggered 200 times, and 200 vibrations of each beam would be collected to collect enough training data and enhance the robustness of this experiment. Each vibration had 45 displacement points and 10 measured points. The dataset was a two-dimensional matrix of 10 × 45.

Figure 15 shows a schematic diagram of the beams. The beam consisted of 10 parts (P1 to P10) and 10 points on the beam (PT1 to PT10).

Table 4 shows the different damage positions and sizes for the four beams. This damage is caused by reducing the cement at the damage positions. And there are two different damage types: a 6 cm cube and a 3 cm cube.

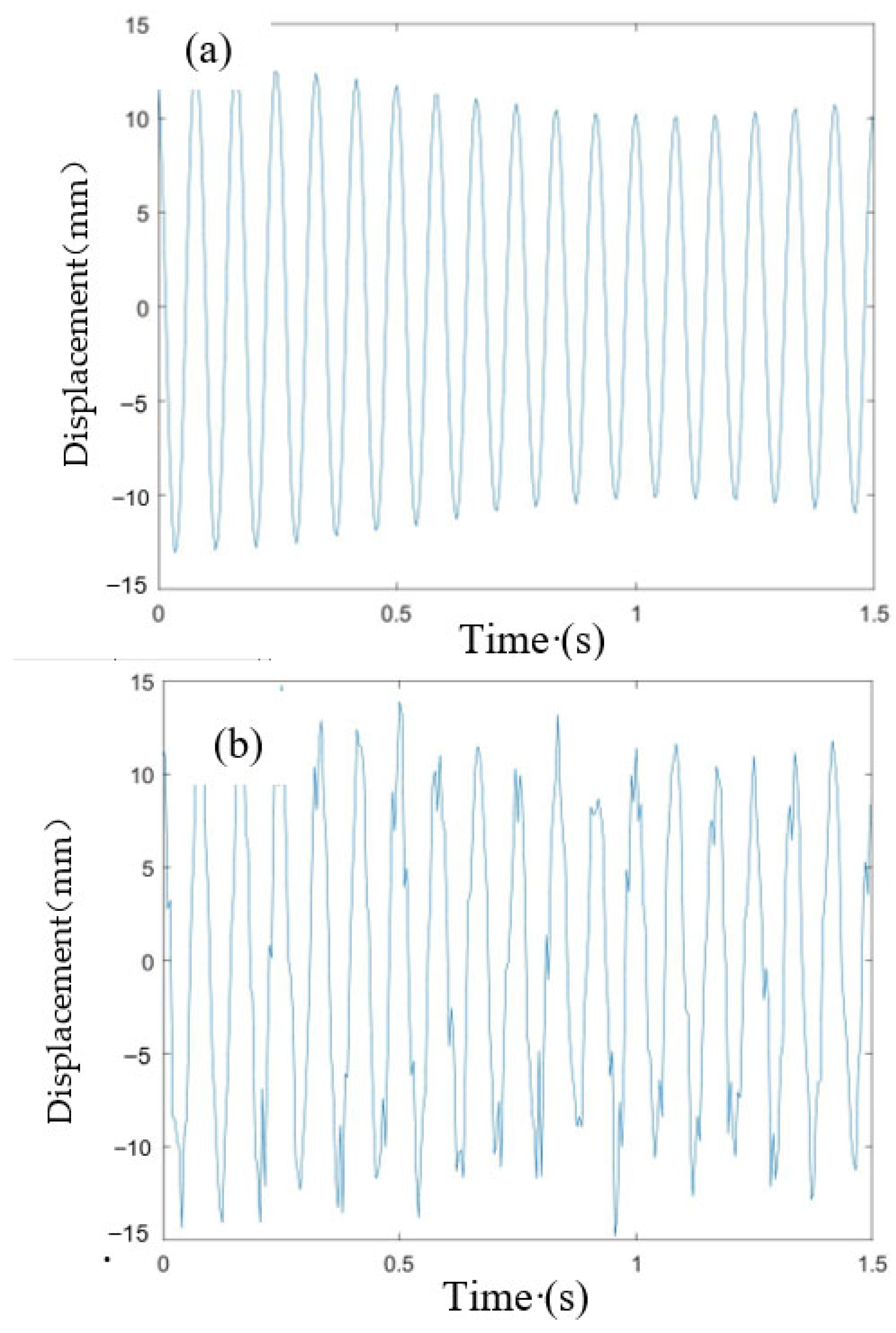
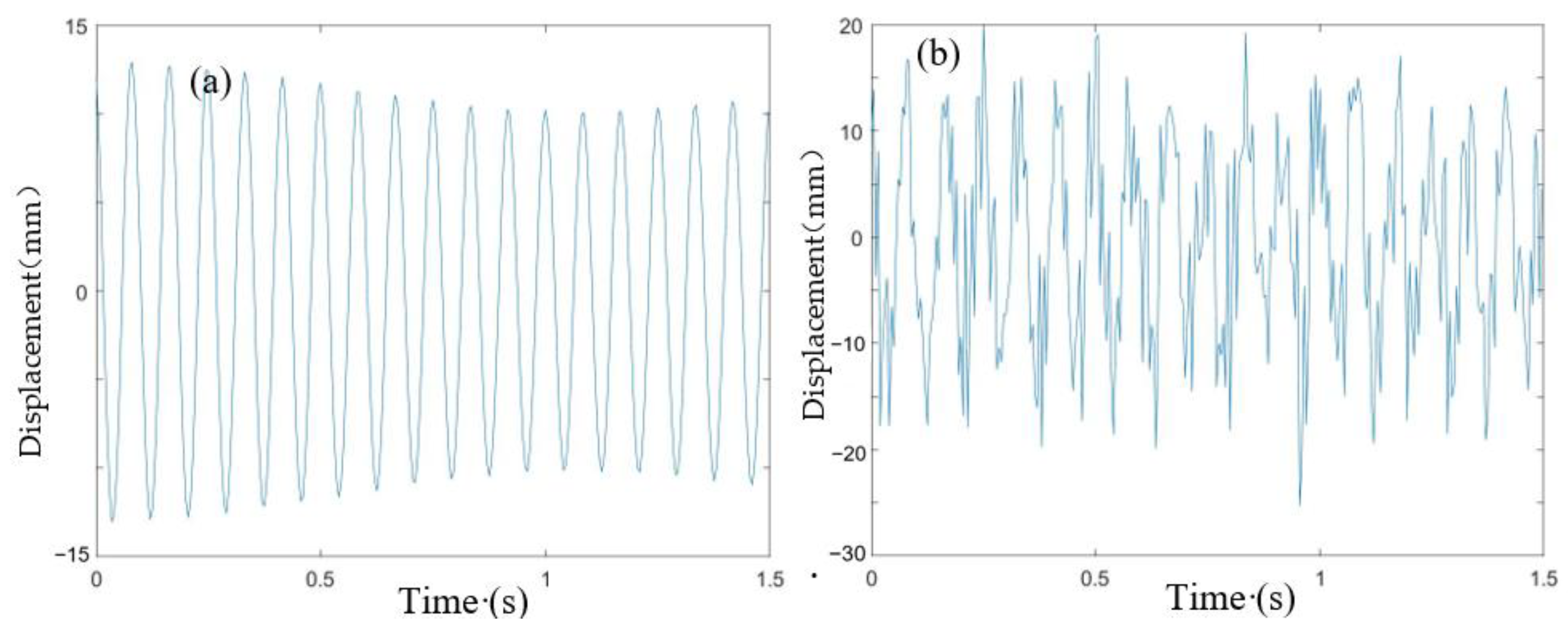
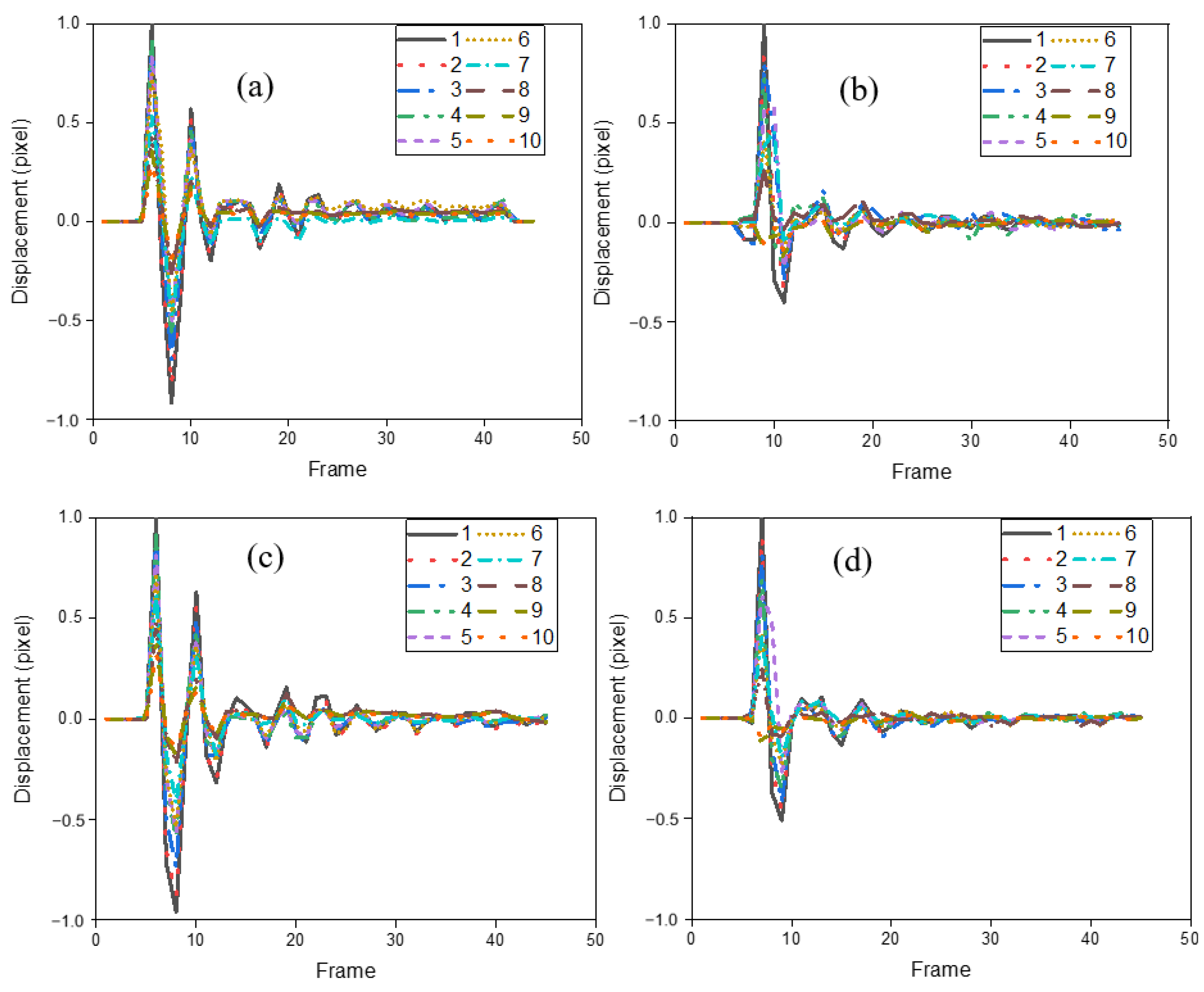
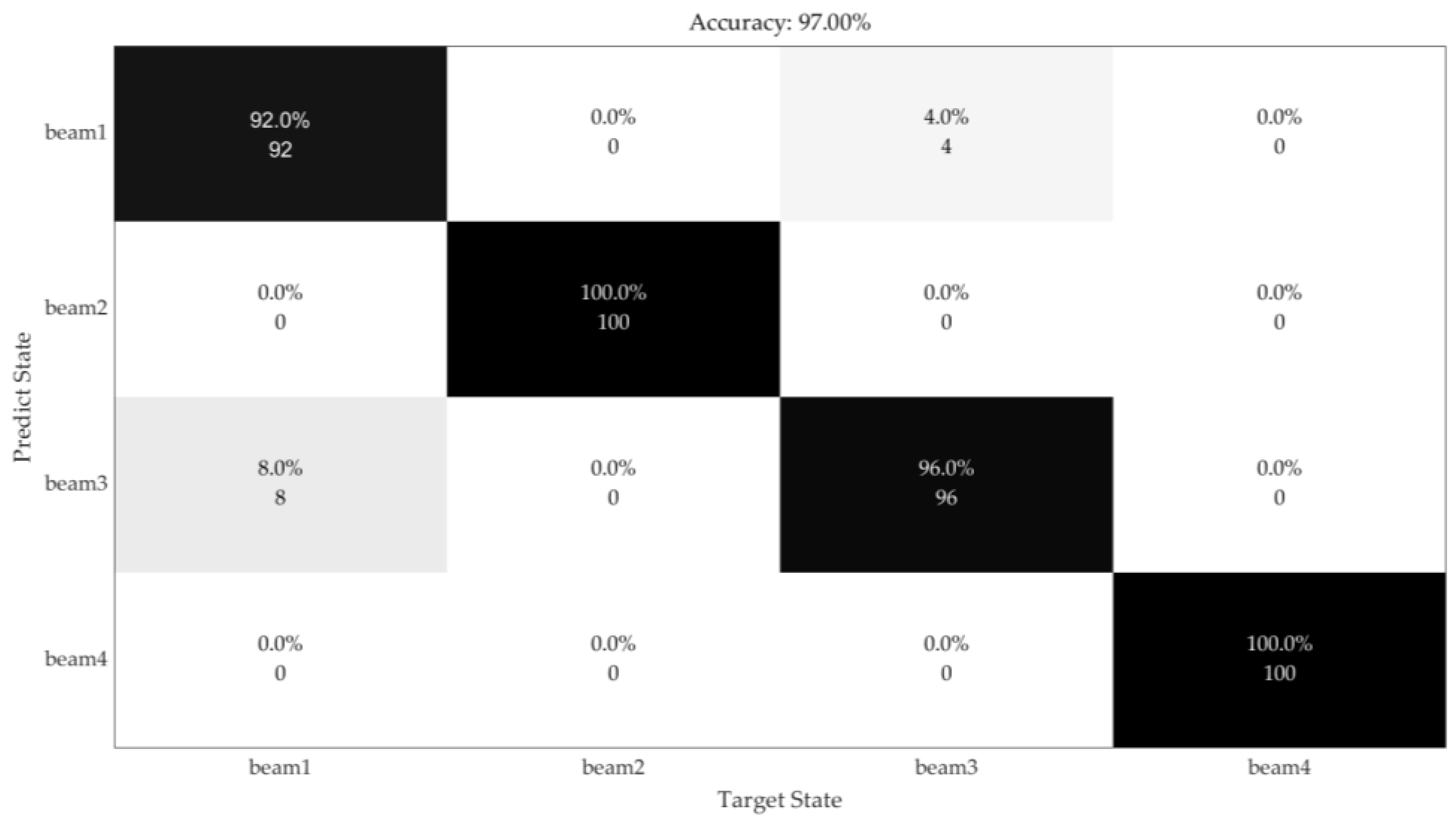
4.4. Results of Lab Experiments

Figure 16 shows examples of four groups of normalized vibrations obtained using the proposed image-based displacement sensor for beam 1, beam 2, beam 3, and beam 4. The proposed image-based displacement sensor detected vibrations of the beams successfully. These four vibrations had similar shapes and trends. There were 200 vibrations to each beam by applying different excitations, and there were 800 beam vibrations in total. These different excitations were made by each different force when the hammer was hit on the beam by the researcher.

Figure 17 shows the training process for the experimental results of the beams. The validation loss and training loss dropped at the beginning of the training process and were very stable at the end of the training process.

As shown in Figure 18, the overall accuracy of the test results of the training process was 97%. The target state refers to the true damage type and the predict state refers to the results from the CNN. And the main errors were found between beam 1 and beam 3, with the possible reason being that the damage of beam 3 was too small and very close to the free end of the beam, which could only generate a small change in the dynamic vibration curves.

5. Conclusions

In this study, a newly designed CNN and an image-based displacement sensor were developed. The proposed CNN can use raw vibration data to detect damage to beams. And the proposed image-based displacement sensor can detect vibrations at several measured points in the meantime with high precision. Two beams in an ABAQUS model provided inputs for the new CNN-based structural damage detection method proposed in this study. Also, four beams with different damage were investigated, and 200 vibrations under excitation were detected using the proposed image-based displacement sensor. The damages in the four beams were a 3 cm cube and a 6 cm cube. These vibrations were sent to the proposed deep learning net, and a nearly 97% accuracy was achieved. The effectiveness of the computer vision-based displacement sensor and deep learning models in vibration-based assessment is summarized as follows:

• The proposed deep learning-based system was trained on beams’ raw displacement collected from ABAQUS, with an accuracy of nearly 100%.
• The proposed computer vision-based displacement sensor detected the vibration of the beams successfully with high accuracy. And the developed computer vision-based displacement method detected the vibrations at 10 different points on the beam successfully. And this method only needs around 15 s to operate 700 images that contain 7000 coordinates in total.
• The proposed deep learning net detected beams’ damage with 97% accuracy using the vibrations obtained by the developed computer vision-based vibration system.
• The training processes of the beams in lab experiments decreased significantly at the beginning, which means the network worked very well and each group of vibrations obtained by the proposed image-based sensor contain unique characters.

In summary, computer vision-based displacement sensors are a convenient method to obtain structural vibrations and displacement. The proposed deep learning net could detect small damages to the beam and was verified through both simulations and lab experiments. In this study, the proposed computer vision-based displacement sensor was engaged to detect 10 vibrations using adaptable edge detector parameters in the meantime successfully.

Regarding the limitations of the proposed computer vision-based displacement sensor, the camera would limit the precision, and the distance between the camera and the bridge would limit the precision in the field. Regarding the limitations of the proposed CNN, the method of collecting reliable bridge information is important.

These two proposals could scale to more complex structures and larger datasets in the future, because the theory inside these methods is the same when they scale to other structures.

In the future, we will continue to create new methods, and experiments on the bridges in the field will be performed, and the proposed image-based displacement sensor will be used. Also, we will find a method to enhance the precision of the proposed computer vision-based displacement sensor further.