FS-DDPG: Optimal Control of a Fan Coil Unit System Based on Safe Reinforcement Learning
Abstract
:1. Introduction
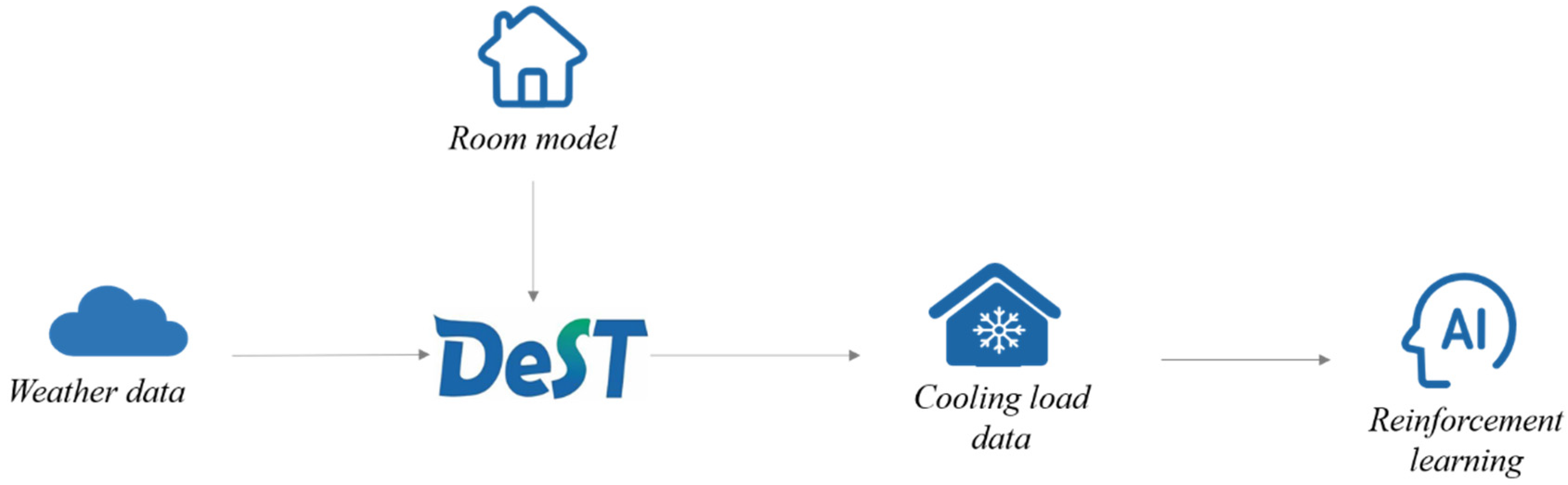
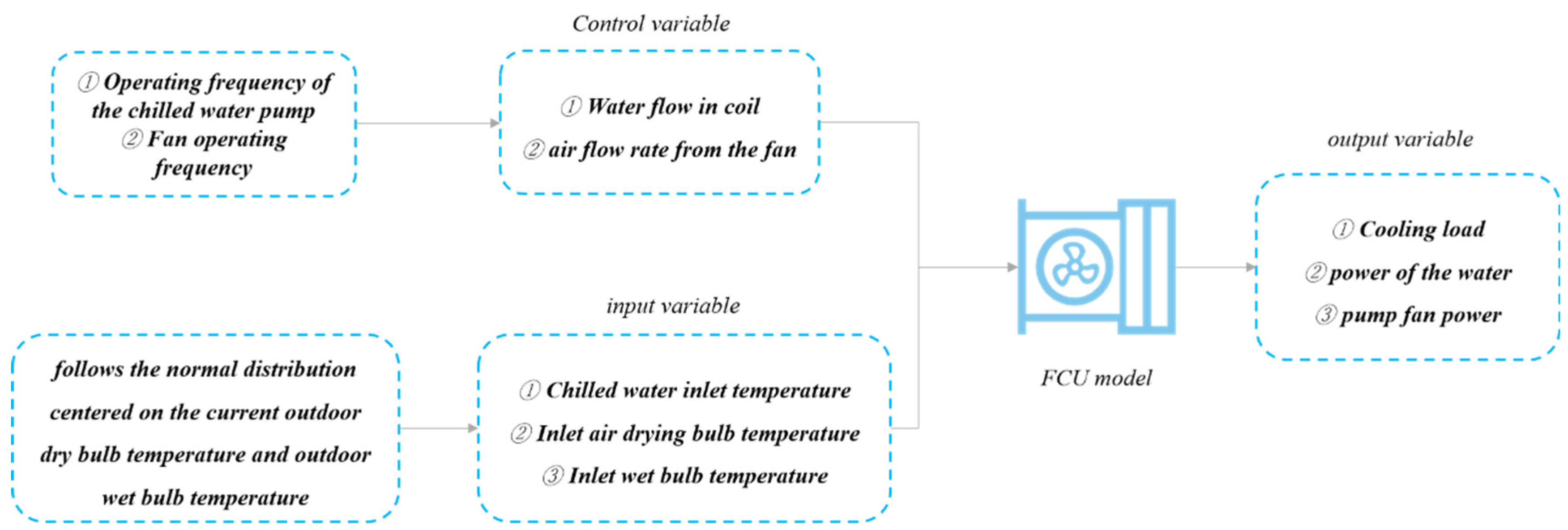
- Based on historical weather data, an office room model was established by using the DeST to calculate the required cooling load for the corresponding period. A heat and mass transfer model for an FCU (incorporating both the theory of thermal and moisture exchange as well as the calculation of parameters within the model) was constructed using Python, which was also validated for its feasibility.
- To address the issue of significant system fluctuations caused by the use of RL methods in controlling the FCU process, the FCU control process is modeled as a constrained Markov decision process. A penalty term regarding process constraints is added to the actual reward function, and constraint tightening is introduced to limit the action space perceived by the agent.
- We propose the FS-DDPG algorithm to optimize the control strategy of an FCU based on reinforcement learning. Compared with the traditional RL algorithm, FS-DDPG not only seeks the maximum reward but also restrains the violent action fluctuation in the control process and greatly reduces the risk of equipment damage caused by the large-scale regulation of the unit.
- The experimental results indicate that this method demonstrates high generalizability and stability, exhibiting significant adaptability in dynamic environments. It not only meets the cooling load requirements within a room while reducing system energy consumption but also ensures the long-term stable operation of the system to the greatest extent. The code and FCU model have been published for future research on the referenced website (available online: https://github.com/leecy123123/fcu_1.git (accessed on 10 January 2025)).
2. Related Work
3. Case Study
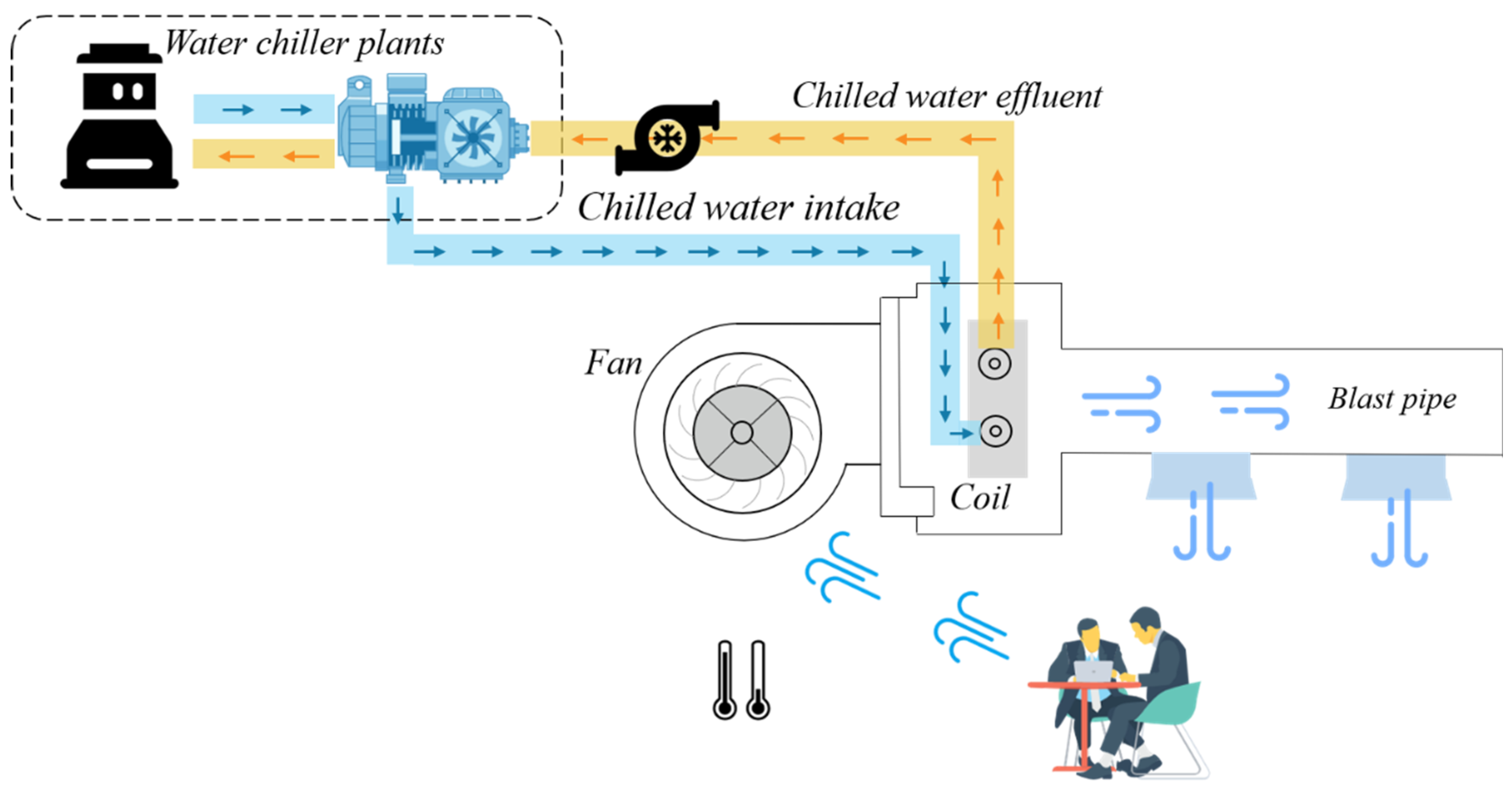
3.1. System Operation Overview
3.2. Building Room Model and Simulating Cooling Load
3.3. Modeling of Fan Coil
4. Methodology and Control Process
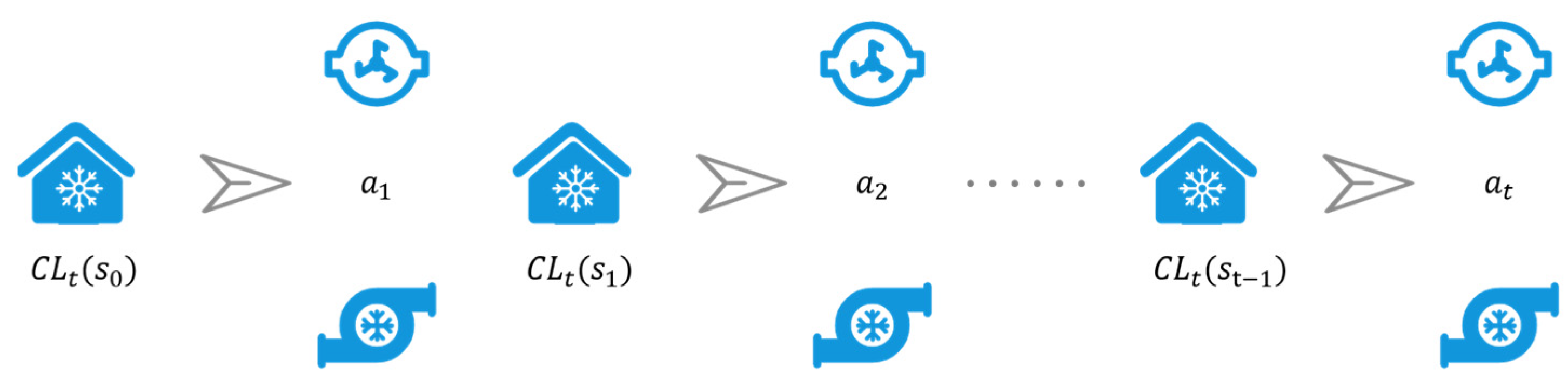
4.1. CMDP Modeling
- State
- 2.
- Action
- 3.
- Reward
- 4.
- Constraint
4.2. Action Constraint
4.2.1. Punishment Constraint Method
4.2.2. Action Restriction Method
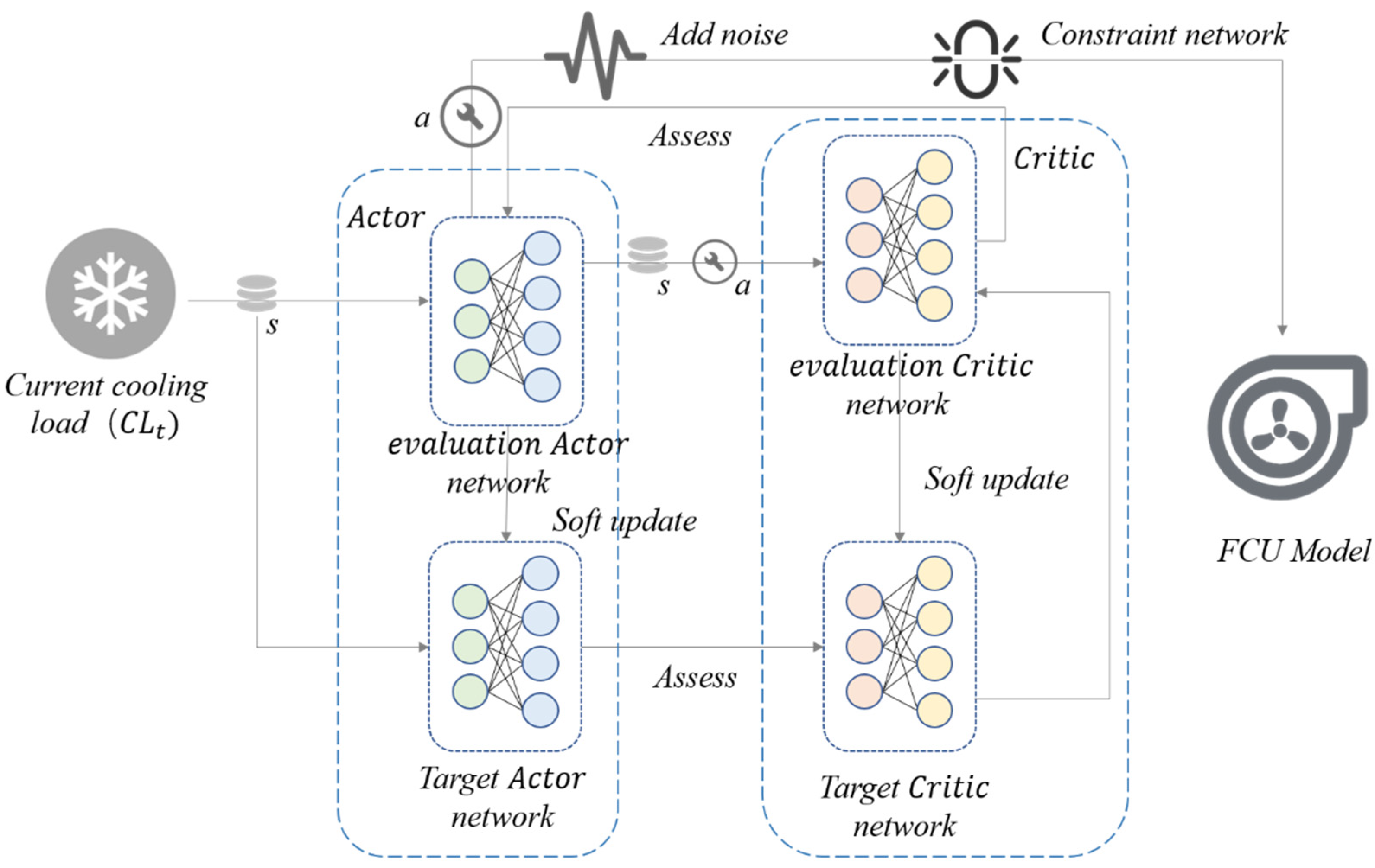
4.3. FCU Process Based on SRL FS-DDPG
- 1.
- At each time step , the agent needs to receive the state of the current environment (cooling load).
- 2.
- We select and . We take the currently required cooling load as input to the actor network, while adding a noise signal to obtain and in the actor network. The method involves using the action pair output by the actor network, incorporating the standard deviation parameter to form a normal distribution, and then randomly generating a new action pair from this distribution to replace the one generated by the original network. Finally, the network action pair is restricted within the safe range by Equation (10).
- 3.
- Model training. After interacting with the environment by the action pair in Step 2, the current reward and the next state can be obtained. The experience data samples generated by the interaction between the actor network and the environment are stored in the experience replay pool. After that, we take a batch of data samples for model training, where the correlation and dependence of samples are removed, which can prompt the convergence of the algorithm.
- 4.
- We end the current learning and go to Step 1. A dual neural network architecture (actor–critic network) is used in DDPG algorithm architecture, and a dual neural network model architecture (target-actor network and target-critic network) is used for both the policy function and the value function. Among them, the state () is the input of DDPG, and the output actions interact with the environment and are stored in the experience replay pool. Figure 8 shows the control method based on FS-DDPG.
4.4. FS-DDPG Algorithm Based on SRL
| Algorithm 1. The control method of an FCU based on FS-DDPG is presented. |
| . For episode = 1, M do N for action exploration For t = 1, to T do # The selected action cannot exceed the limit value and observe new # By calculating the relative error and constraining the actions Update critic network by minimizing the loss function: Update the actor network using the sampled deterministic policy gradient: Soft update the target networks: # Updating the target network by soft updating helps to stabilize the training process End for End for |
5. Experimental Results and Analysis
5.1. Experimental Parameter Setting
5.2. Experimental Comparison Method
- DDPG control method: DDPG is a widely used DRL algorithm in continuous action spaces. The advantage of DDPG lies in its ability to automatically adjust control strategies through training, without relying on manually designed rules. However, DDPG tends to exhibit significant action fluctuations in high-dynamic environments, which can compromise equipment safety, reduce energy efficiency and fail to meet practical application requirements. By comparing with DDPG, FS-DDPG can clearly demonstrate significant advantages in reducing flow fluctuations, improving energy efficiency and enhancing control performance. It also proves its effectiveness in addressing the safety issues present in real-world applications. Apart from the strategy constraint optimization, the network parameters in DDPG are the same as those in the FS-DDPG control method.
- MBC control method: In practice, it is usually difficult to obtain an accurate FCU model. Moreover, the MBC method here is obtained by exhaustively enumerating all control nodes of FCU. This method obtains the optimal solution from the global perspective, but it consumes a lot of computing resources and lacks dynamic adaptability. Adopting this method, the gap between the FS-DDPG method and the optimal method can be reflected. The objective function for this method is provided in Equation (15):where and are the independent variables. , and can be calculated through and . represents the relative error in the actions of the fan and pump before and after. By maximizing the function through a traversal method, the optimal water flow and air flow for each state are determined.
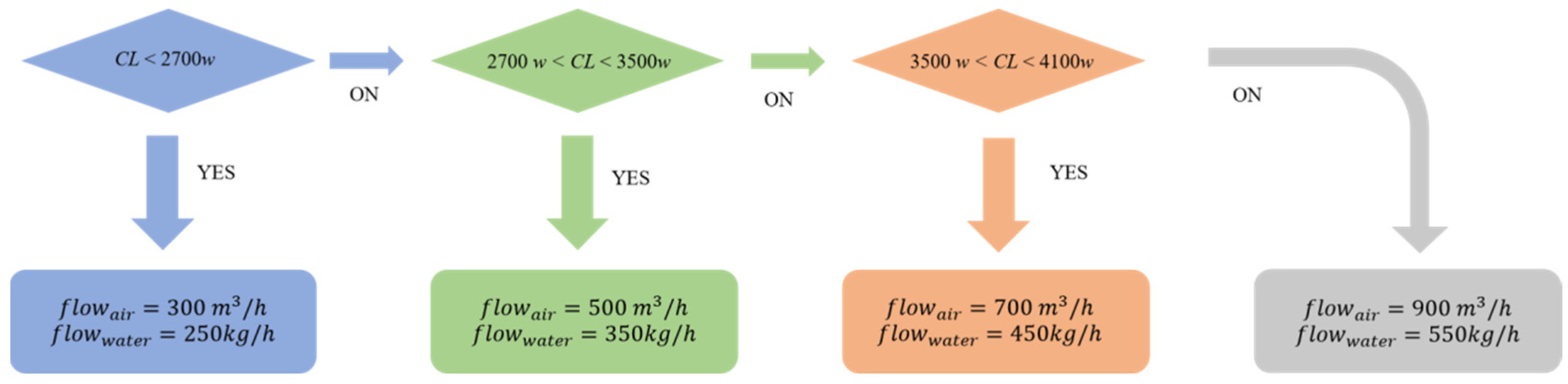
- RBC control method: RBC is a traditional control method that typically adjusts system control parameters based on experience and rules. The RBC method is simple and intuitive, performing well in static or relatively stable environments. However, when facing dynamic changes in the environment, RBC often requires frequent rule adjustments, which is not feasible in complex or uncertain systems. Additionally, RBC has a limited capability in optimizing system energy consumption. In contrast to RBC, FS-DDPG demonstrates its advantages in dynamic environments, particularly in significantly improving system energy efficiency and control accuracy. According to expert experience, the RBC control method is implemented through sequential decision-making, as shown in Figure 9.
- The control logic for this sequential decision is as follows: When , set and ; when CL , set and ; when , set and ; when , set and .
- DQN control method: In MDP modeling, the setting of state, action and reward is the same as that of DDPG. The value range of water flow for pump is 80–700 kg/h, and the step size is 5 . The value range of air flow for fan is 100–1200 m3/h, and the step size is 5 m3/h. The policy network and target network of the agent are composed of two hidden layers containing 32 neurons. The training batch is set to 32, and the discount factor is set to 0.01. The update step is set to 200; the learning rate is set to 0.01; and the experience pool capacity is set to 2000. Detailed parameter settings are shown in Table 5.
5.3. Experimental Results
5.3.1. Analysis of Algorithm Convergence
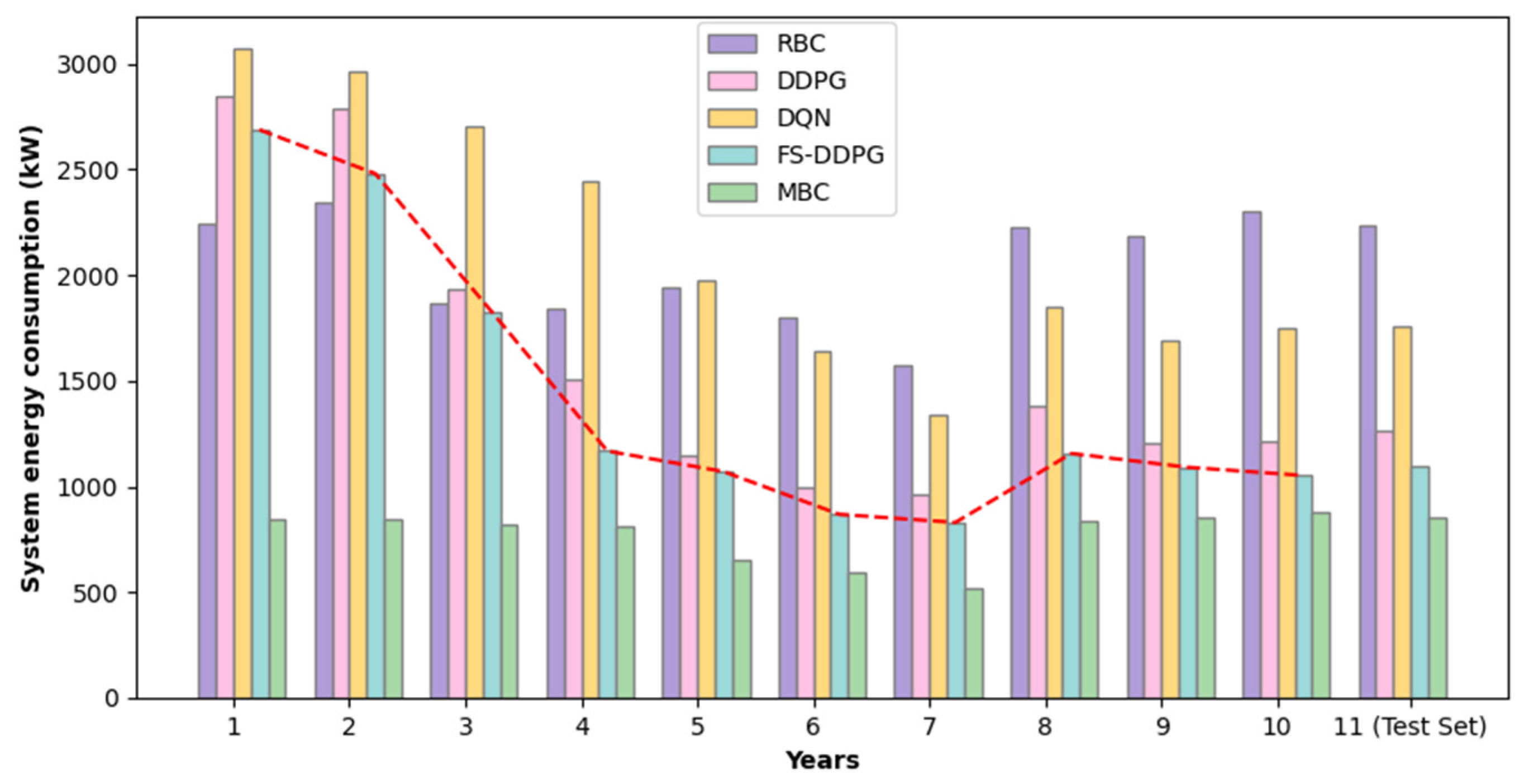
5.3.2. Energy Consumption Analysis
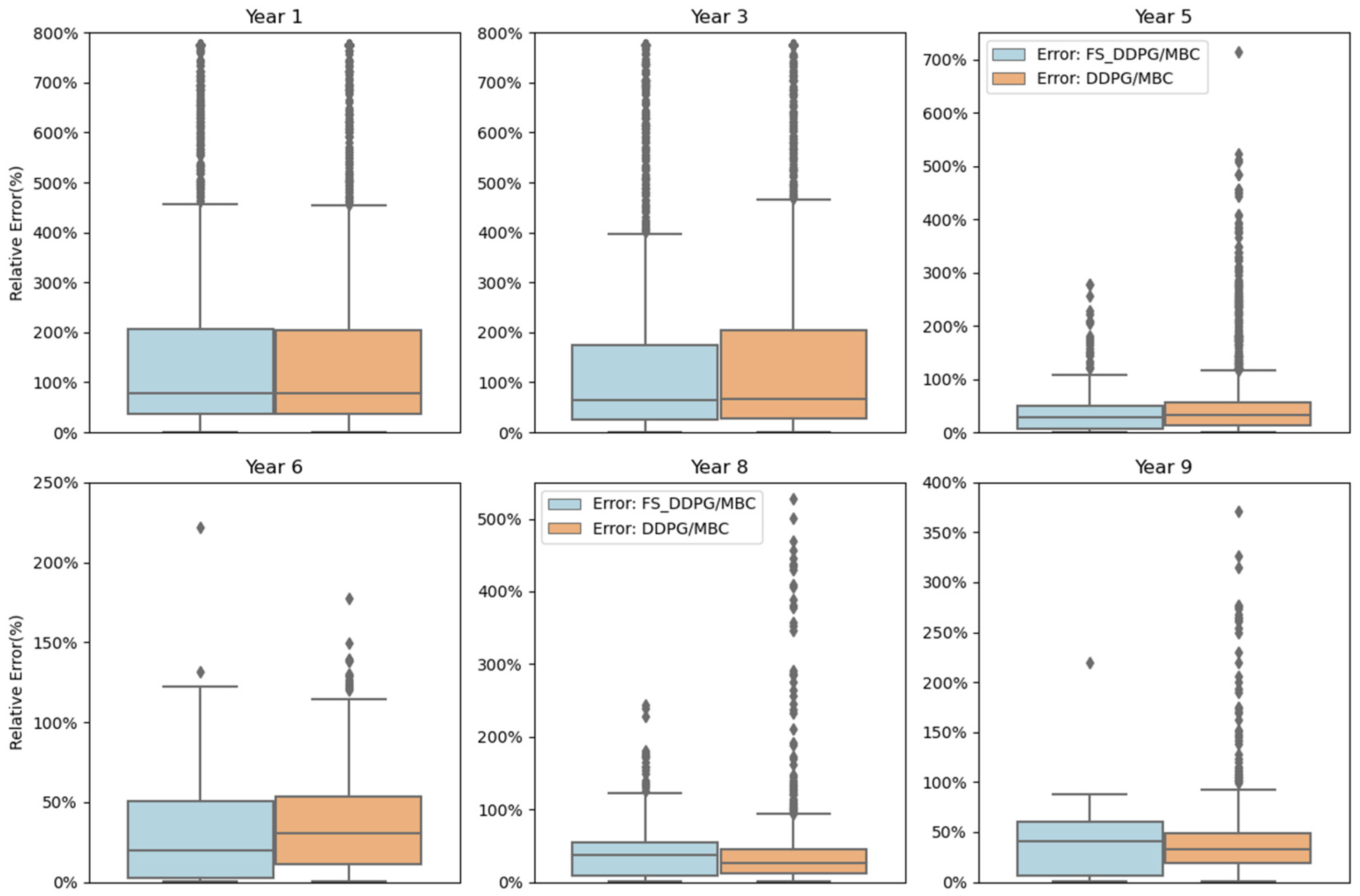
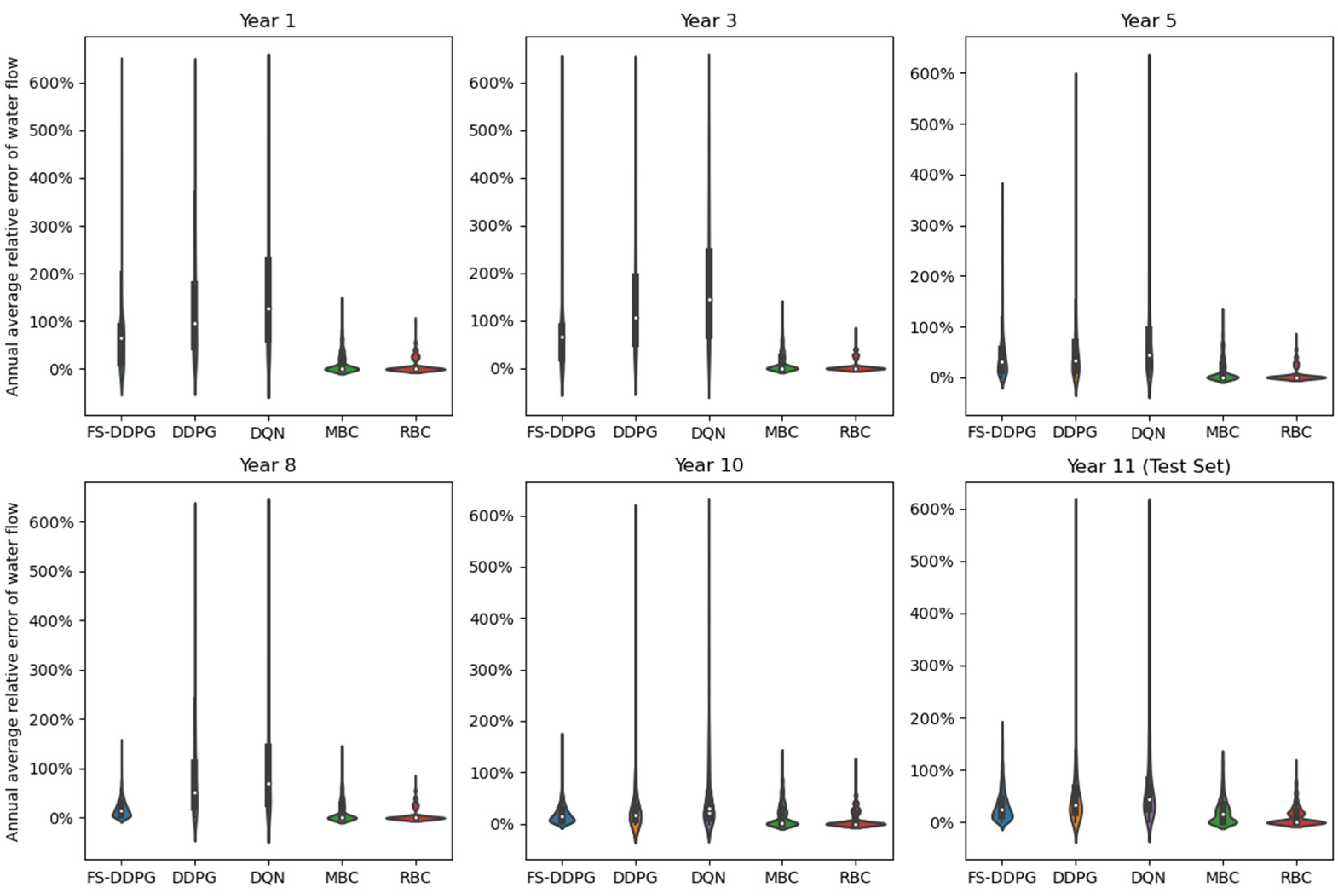
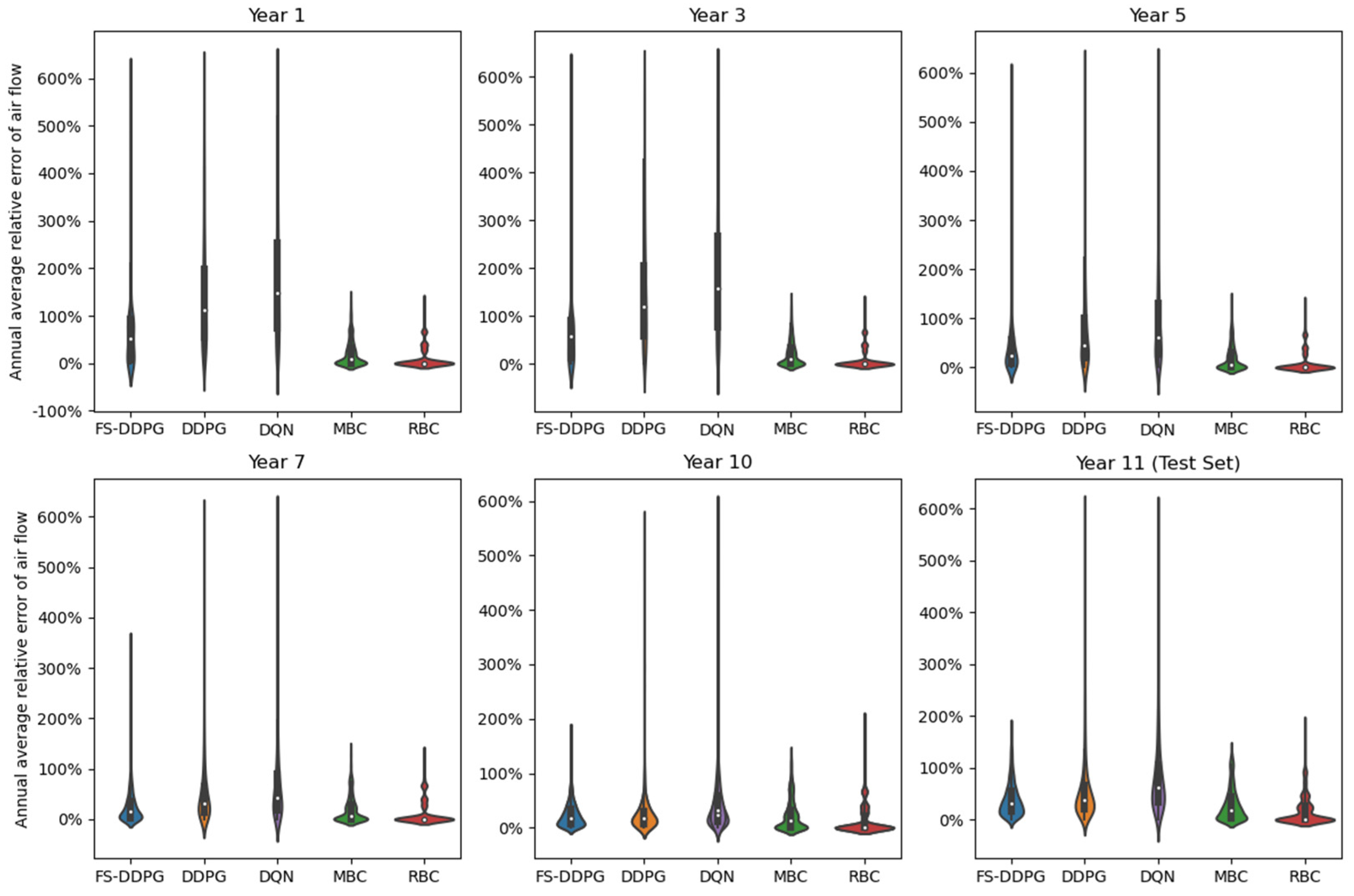
5.3.3. System Operation Performance Analysis
5.3.4. System Safety Analysis
5.3.5. Satisfaction Analysis
5.3.6. Sensitivity Analysis
6. Conclusions and Future Work
- Compared with DDPG, FS-DDPG can suppress 98.20% of pump flow fluctuations and 95.82% of fan airflow fluctuations. Additionally, compared with RBC and DDPG, FS-DDPG achieves energy savings of 11.9% and 51.76%, respectively.
- The proposed method shows performance and satisfaction levels very close to those of MBC, indicating that FS-DDPG is highly adaptable to dynamic environments, able to meet the indoor cooling load requirements, reduce system energy consumption and ensure long-term stable operation of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter Name | Value |
|---|---|
| Fin thickness | 0.2 mm |
| Tube wall thickness | 1 mm |
| Pipe outside diameter | 10 mm |
| Pipe spacing perpendicular to the airflow | 25 mm |
| Spacing of pipes parallel to the airflow | 20 mm |
| Number of rows of tubes parallel to the air flow | 2 |
| Number of rows of tubes perpendicular to the air flow | 8 |
| Number of waterways | 2 |
| Spacing of fins | 2.2 mm |
| Effective length of coil heat transfer | 1 m |
Appendix B
- 1.
- Calculate and .
- 2.
- Calculate and to determine dry or wet conditions.
- 3.
- Calculate the wind parameters.
- 4.
- Calculate and judge the correctness of the iterative hypothesis.
- 5.
- System power consumption.
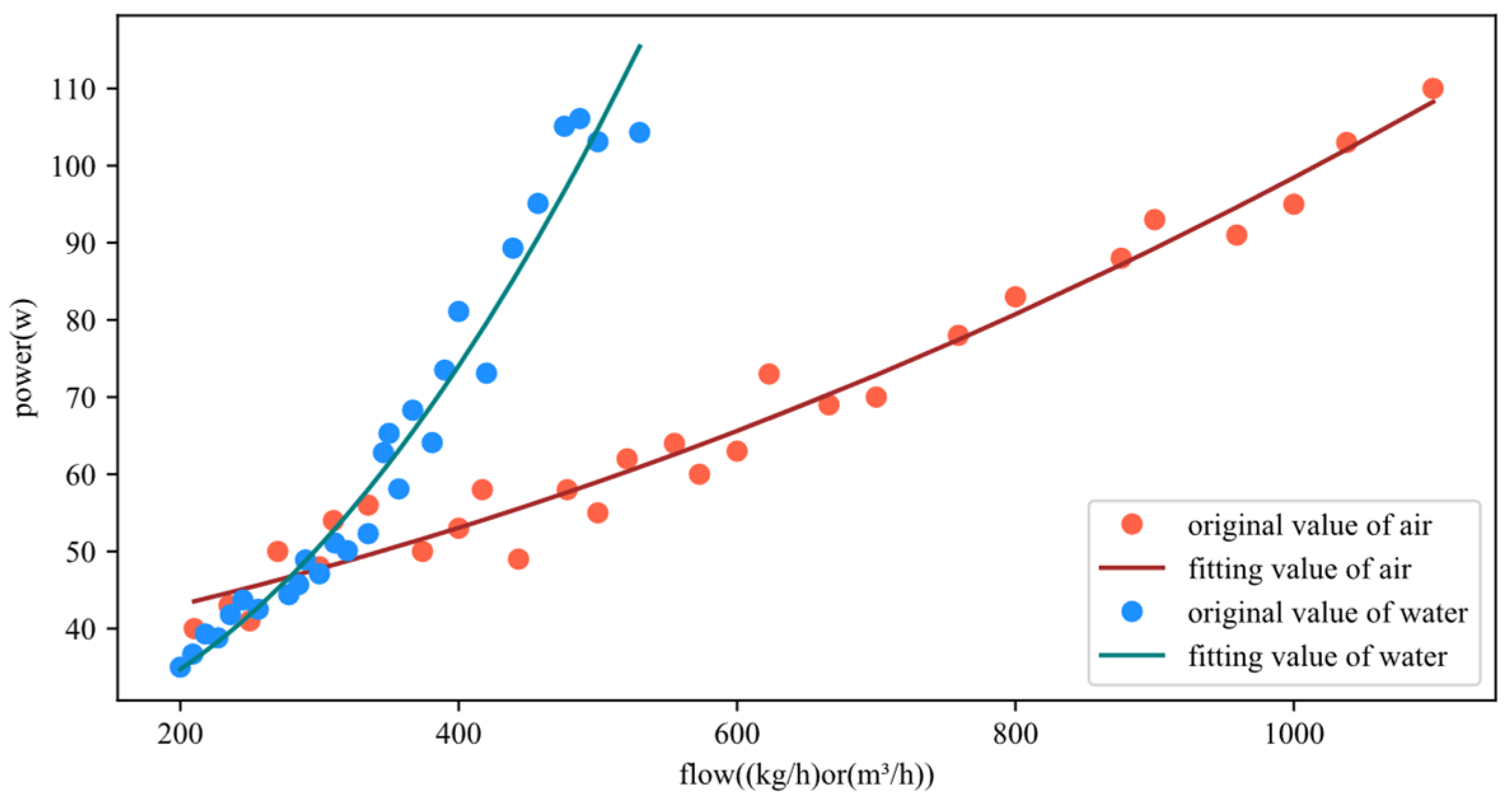
| Air Coefficient | Value | Water Coefficient | Value |
|---|---|---|---|
| 3.22086094 × 10−5 | 3.68380722 × 10−4 | ||
| 3.05481795 × 10−2 | −2.43551880 × 10−2 | ||
| 3.56900355e × 101 | 2.48530002 × 101 |
Appendix C
| Generated Quantity | Relative Error | |
|---|---|---|
| Dry Condition | Wet Condition | |
| Cooling capacity | 6.9045 | 13.8871 |
| Air-drying bulb temperature | 4.1135 | 6.6515 |
| Outgoing air humidity ball temperature | 4.0281 | 5.6513 |
| Effluent temperature | 0.4210 | 6.1226 |
References
- Ding, Z.K.; Fu, Q.M.; Chen, J.P.; Wu, H.J.; Lu, Y.; Hu, F.Y. Energy-efficient control of thermal comfort in multi-zone residential HVAC via reinforcement learning. Conn. Sci. 2022, 34, 2364–2394. [Google Scholar] [CrossRef]
- World Energy Outlook 2023. Available online: www.iea.org/terms (accessed on 8 January 2025).
- Fang, Z.; Tang, T.; Su, Q.; Zheng, Z.; Xu, X.; Ding, Y.; Liao, M. Investigation into optimal control of terminal unit of air conditioning system for reducing energy consumption. Appl. Therm. Eng. 2020, 177, 115499. [Google Scholar] [CrossRef]
- Dezfouli, M.M.S.; Dehghani-Sanij, A.R.; Kadir, K.; Suhairi, R.; Rostami, S.; Sopian, K. Is a fan coil unit (FCU) an efficient cooling system for net-zero energy buildings (NZEBs) in tropical regions? An experimental study on thermal comfort and energy performance of an FCU. Results Eng. 2023, 20, 101524. [Google Scholar] [CrossRef]
- Kou, X.; Du, Y.; Li, F.; Pulgar-Painemal, H.; Zandi, H.; Dong, J.; Olama, M.M. Model-based and data-driven HVAC control strategies for residential demand response. IEEE Open Access J. Power Energy 2021, 8, 186–197. [Google Scholar] [CrossRef]
- In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. Available online: https://ieeexplore.ieee.org/xpl/conhome/8789884/proceeding (accessed on 10 January 2025).
- Fu, Q.; Han, Z.; Chen, J.; Lu, Y.; Wu, H.; Wang, Y. Applications of reinforcement learning for building energy efficiency control: A review. J. Build. Eng. 2022, 50, 104165. [Google Scholar] [CrossRef]
- Lee, D.; Ooka, R.; Ikeda, S.; Choi, W.; Kwak, Y. Model predictive control of building energy systems with thermal energy storage in response to occupancy variations and time-variant electricity prices. Energy Build. 2020, 225, 110291. [Google Scholar] [CrossRef]
- Yang, S.; Wan, M.P. Machine-learning-based model predictive control with instantaneous linearization—A case study on an air-conditioning and mechanical ventilation system. Appl. Energy 2022, 306, 118041. [Google Scholar] [CrossRef]
- Ding, Z.; Huang, Y.; Yuan, H.; Dong, H. Introduction to reinforcement learning. In Deep Reinforcement Learning: Fundamentals, Research and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 47–123. [Google Scholar]
- Zhou, S.L.; Shah, A.A.; Leung, P.K.; Zhu, X.; Liao, Q. A comprehensive review of the applications of machine learning for HVAC. DeCarbon 2023, 2, 100023. [Google Scholar] [CrossRef]
- Esrafilian-Najafabadi, M.; Haghighat, F. Occupancy-based HVAC control systems in buildings: A state-of-the-art review. Build. Environ. 2021, 197, 107810. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Fu, Q.; Chen, J.; Wang, Y.; Lu, Y.; Liu, L. Priori knowledge-based deep reinforcement learning control for fan coil unit system. J. Build. Eng. 2023, 82, 108157. [Google Scholar] [CrossRef]
- Qiu, S.; Li, Z.; Li, Z.; Li, J.; Long, S.; Li, X. Model-free control method based on reinforcement learning for building cooling water systems: Validation by measured data-based simulation. Energy Build. 2020, 218, 110055. [Google Scholar] [CrossRef]
- Gao, C.; Wang, D. Comparative study of model-based and model-free reinforcement learning control performance in HVAC systems. J. Build. Eng. 2023, 74, 106852. [Google Scholar] [CrossRef]
- Han, Z.; Fu, Q.; Chen, J.; Wang, Y.; Lu, Y.; Wu, H.; Gui, H. Deep Forest-Based DQN for Cooling Water System Energy Saving Control in HVAC. Buildings 2022, 12, 1787. [Google Scholar] [CrossRef]
- Li, S.; Wei, M.; Wei, Y.; Wu, Z.; Han, X.; Yang, R. A fractional order PID controller using MACOA for indoor temperature in air-conditioning room. J. Build. Eng. 2021, 44, 103295. [Google Scholar] [CrossRef]
- Li, S.; Wang, D.; Han, X.; Cheng, K.; Zhao, C. Auto-tuning parameters of fractional PID controller design for air-conditioning fan coil unit. J. Shanghai Jiaotong Univ. (Sci.) 2021, 26, 186–192. [Google Scholar] [CrossRef]
- Verhelst, J.; Van Ham, G.; Saelens, D.; Helsen, L. Model selection for continuous commissioning of HVAC-systems in office buildings: A review. Renew. Sustain. Energy Rev. 2017, 76, 673–686. [Google Scholar] [CrossRef]
- Zhao, A.; Wei, Y.; Quan, W.; Xi, J.; Dong, F. Distributed model predictive control of fan coil system. J. Build. Eng. 2024, 94, 110028. [Google Scholar] [CrossRef]
- Sanama, C.; Xia, X.; Nguepnang, M. PID-MPC Implementation on a Chiller-Fan Coil Unit. J. Math. 2022, 2022, 8405361. [Google Scholar] [CrossRef]
- Martinčević, A.; Vašak, M.; Lešić, V. Identification of a control-oriented energy model for a system of fan coil units. Control Eng. Pract. 2019, 91, 104100. [Google Scholar] [CrossRef]
- Guillen, D.P.; Anderson, N.; Krome, C.; Boza, R.; Griffel, L.M.; Zouabe, J.; Al Rashdan, A.Y. A RELAP5-3D/LSTM model for the analysis of drywell cooling fan failure. Prog. Nucl. Energy 2020, 130, 103540. [Google Scholar] [CrossRef]
- Lin, C.M.; Liu, H.Y.; Tseng, K.Y.; Lin, S.-F. Heating, ventilation, and air conditioning system optimization control strategy involving fan coil unit temperature control. Appl. Sci. 2019, 9, 2391. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Asgarkhani, N.; Yoo, D.Y. Machine-learning methods for estimating compressive strength of high-performance alkali-activated concrete. Eng. Appl. Artif. Intell. 2024, 136, 109053. [Google Scholar] [CrossRef]
- Chen, C.; An, J.; Wang, C.; Duan, X.; Lu, S.; Che, H.; Qi, M.; Yan, D. Deep Reinforcement Learning-Based Joint Optimization Control of Indoor Temperature and Relative Humidity in Office Buildings. Buildings 2023, 13, 438. [Google Scholar] [CrossRef]
- NOAA. National Centers for Environmental Information. Available online: http://www.noaa.gov (accessed on 8 January 2025).

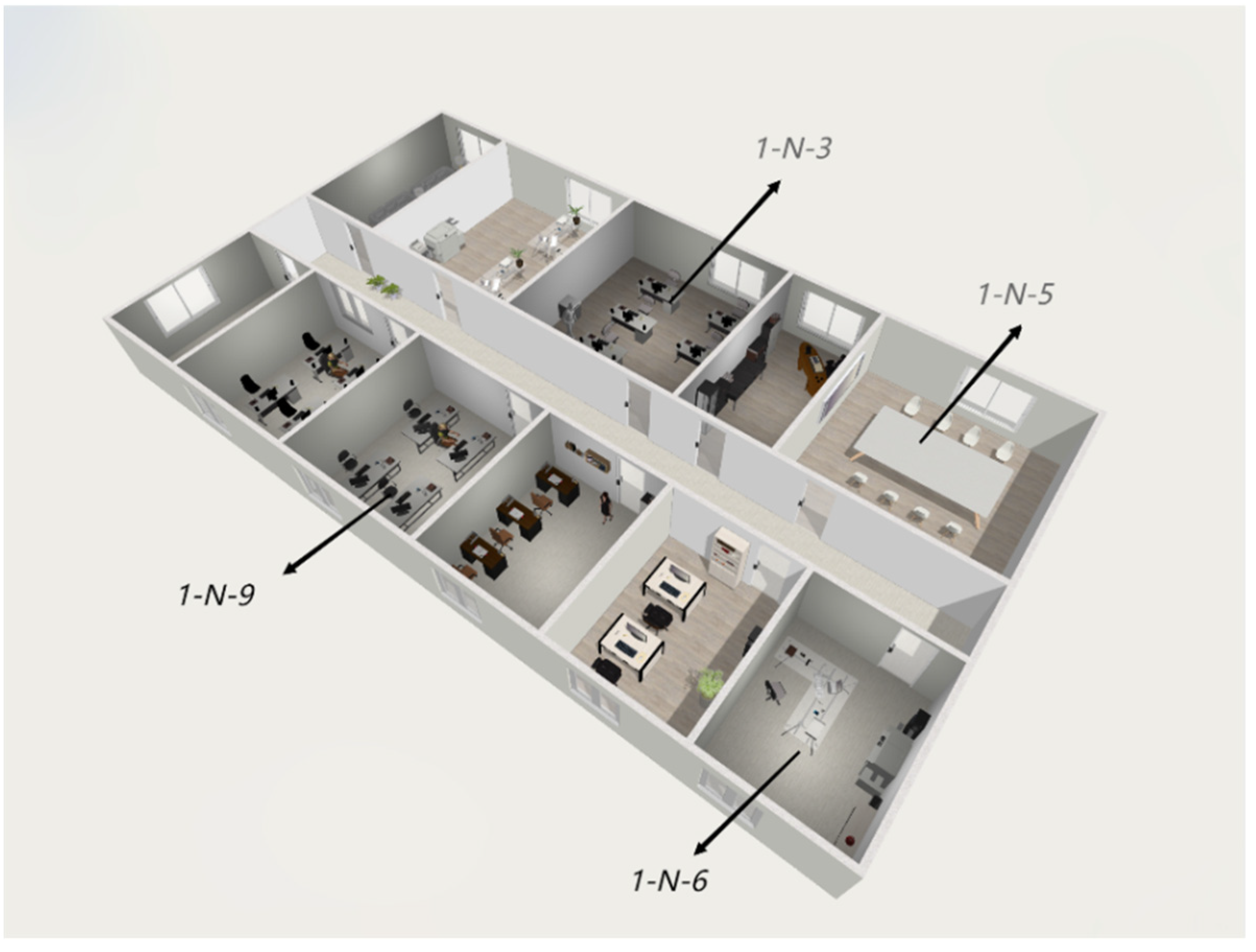




| Room Number | Room Function | Room Area | Interior Design Temperature |
|---|---|---|---|
| 1-N-1 | Lounge | 32 | 26 |
| 1-N-2 | Office | 96 | 25 |
| 1-N-3 | Office | 96 | 25 |
| 1-N-4 | Office | 32 | 25 |
| 1-N-5 | Conference Room | 96 | 26 |
| 1-N-6 | Office | 64 | 25 |
| 1-N-7 | Office | 64 | 25 |
| 1-N-8 | Office | 64 | 25 |
| 1-N-9 | Office | 64 | 25 |
| 1-N-10 | Office | 64 | 25 |
| 1-N-11 | Supply Room | 32 | No Set |
| 1-N-12 | Hallway | 176 | No Set |
| Metrics | Maximum Value | Minimum Value | Median | Mean Value | Unit |
|---|---|---|---|---|---|
| 2 m air temperature | 37.26 | −7.61 | 18.59 | 17.82 | °C |
| Surface pressure | 1041.42 | 981.76 | 1016.41 | 1015.94 | |
| Surface temperature | 38.38 | −8.08 | 17.98 | 17.17 | °C |
| Dew point temperature | 28.93 | 20.55 | 13.66 | 13.34 | °C |
| Relative humidity | 99.99 | 15.09 | 80.72 | 76.93 | % |
| East wind speed | 8.84 | 10.95 | −0.41 | 0.32 | |
| North wind speed | 8.38 | −13.50 | −1.03 | 0.75 | |
| Total solar irradiance | 3653.08 | 0 | 20.46 | 583.70 | |
| Net solar irradiance | 3096.26 | 0 | 17.71 | 499.52 | |
| Amount of precipitation | 14.24 | 0 | 0 | 0.18 | |
| Evaporation capacity | 0.04 | 0.76 | -0.04 | 0.11 | |
| Ultraviolet intensity | 410.87 | 0 | 2.74 | 65.62 |
| Network | Number of Neurons | Activation Function | Learning Rate | Optimizer |
|---|---|---|---|---|
| Actor | 1→64 | ReLU | 0.002 | Adam |
| 64→2 | Tanh | |||
| Critic | [1→64], [2→64] | ReLU | 0.001 | Adam |
| 64→1 | ReLU |
| Hyperparameter | Value |
|---|---|
| Soft renewal coefficient | 0.01 |
| Replay pool size | 2000 |
| Sample batch size | 64 |
| Discount factor | 0.01 |
| Standard deviation minimum | 0.15 |
| Standard deviation decay | 0.995 |
| Hyperparameter | Value |
| Neurons in hidden layers | 32, 32 |
| Sample batch size | 32 |
| Discount factor | 0.01 |
| Learning rate | 0.001 |
| Replay pool size | 2000 |
| Update step | 200 |
| Training round | 20 |
| Year | Energy Consumption Confidence Interval Analysis (kWh) | ||||
|---|---|---|---|---|---|
| RBC | DDPG | DQN | FS-DDPG | MBC | |
| 1 | (2030.85, 2450.54) | (2743.08, 2955.51) | (3062.25, 3274.68) | (2482.97, 2890.17) | (814.68, 872.57) |
| 2 | (2362.05, 2851.11) | (2457.47, 2691.95) | (2843.67, 3078.15) | (2258.52, 2699.19) | (812.85, 876.83) |
| 3 | (1692.23, 2046.08) | (1832.25, 2025.76) | (2594.17, 2807.03) | (1739.33, 1916.79) | (795.48, 852.10) |
| 4 | (1654.64, 2025.36) | (1399.21, 1618.03) | (2323.62, 2564.32) | (1113.18, 1221.68) | (778.72, 838.32) |
| 5 | (1641.67, 2241.42) | (1008.48, 1289.48) | (1841.49, 2122.49) | (1003.07, 1144.15) | (622.35, 690.82) |
| 6 | (1489.11, 2112.28) | (982.09, 1253.88) | (1495.38, 1794.35) | (864.03, 1024.02) | (561.55, 628.13) |
| 7 | (2407.06, 2845.89) | (880.16, 1036.82) | (1198.10, 1485.62) | (783.36, 909.26) | (496.16, 547.21) |
| 8 | (2015.07, 2442.22) | (1150.62, 1404.40) | (1706.29, 1985.44) | (1040.31, 1271.24) | (812.83, 865.38) |
| 9 | (2083.30, 2510.34) | (1117.06, 1295.12) | (1590.59, 1786.45) | (964.74, 1113.13) | (828.22, 884.86) |
| 10 | (2281.93, 2668.55) | (1104.88, 1315.05) | (1642.64, 1852.81) | (925.97, 1034.22) | (851.87, 902.40) |
| Year | AC | |||
|---|---|---|---|---|
| Water Flow | Air Flow | |||
| DDPG | FS-DDPG | DDPG | FS-DDPG | |
| 1 | 45.00% | 46.13% | 39.87% | 41.60% |
| 2 | 45.66% | 46.03% | 42.95% | 43.74% |
| 3 | 48.93% | 52.52% | 44.12% | 48.09% |
| 4 | 57.10% | 71.43% | 57.11% | 59.76% |
| 5 | 73.72% | 83.99% | 73.43% | 74.79% |
| 6 | 84.78% | 86.41% | 84.46% | 87.44% |
| 7 | 83.66% | 86.74% | 85.65% | 90.48% |
| 8 | 82.77% | 85.15% | 83.97% | 84.78% |
| 9 | 83.34% | 88.70% | 85.03% | 88.71% |
| 10 | 83.74% | 89.96% | 86.59% | 89.23% |
| Year | > 1) | |||||
|---|---|---|---|---|---|---|
| Water Flow | Air Flow | |||||
| DDPG | FS-DDPG | Reduced Proportion | DDPG | FS-DDPG | Reduced Proportion | |
| 1 | 1038 | 496 | 52.22% | 1092 | 525 | 52.04% |
| 2 | 1136 | 487 | 57.13% | 1095 | 571 | 47.89% |
| 3 | 1184 | 539 | 54.48% | 1135 | 551 | 51.47% |
| 4 | 735 | 447 | 39.18% | 882 | 483 | 45.29% |
| 5 | 472 | 172 | 63.56% | 530 | 237 | 55.66% |
| 6 | 359 | 61 | 83.01% | 464 | 133 | 71.32% |
| 7 | 366 | 57 | 84.43% | 363 | 79 | 78.25% |
| 8 | 640 | 9 | 98.59% | 712 | 28 | 96.07% |
| 9 | 595 | 4 | 99.33% | 677 | 18 | 97.34% |
| 10 | 430 | 11 | 97.44% | 538 | 26 | 95.17% |
| 11 (Test Set) | 557 | 10 | 98.20% | 645 | 27 | 95.82% |
| Year | SR | ||||
|---|---|---|---|---|---|
| DDPG | FS-DDPG | RBC | MBC | DQN | |
| DDPG | FS-DDPG | DDPG | FS-DDPG | ||
| 1 | 15.51% | 17.13% | 58.19% | 92.89% | 12.84% |
| 2 | 26.72% | 25.02% | 59.34% | 93.45% | 22.83% |
| 3 | 37.67% | 38.52% | 60.04% | 93.24% | 28.34% |
| 4 | 46.94% | 49.43% | 59.48% | 92.96% | 39.12% |
| 5 | 65.79% | 70.99% | 59.12% | 92.67% | 53.64% |
| 6 | 74.78% | 77.41% | 59.79% | 94.11% | 59.79% |
| 7 | 78.66% | 83.74% | 60.51% | 92.82% | 68.51% |
| 8 | 84.17% | 85.15% | 58.96% | 93.05% | 71.96% |
| 9 | 83.34% | 83.16% | 59.22% | 94.25% | 70.22% |
| 10 | 84.74% | 84.706% | 60.16% | 92.74% | 72.16% |
| 11 (Test Set) | 84.18% | 84.33% | 59.77% | 93.46% | 69.77% |
| Satisfaction Rate (SR) | Energy Consumption | Fluctuation Reduction Ratio (Compared to DDPG) | |||
|---|---|---|---|---|---|
| Water flow | Air flow | ||||
| 10.0 | 1.0 | 84.33% | 1080.75 kWh | 98.20% | 95.82% |
| 5.0 | 1.0 | 84.22% | 1157.91 kWh | 84.18% | 76.69% |
| 15.0 | 1.0 | 82.35% | 1201.93 kWh | 99.57% | 98.81% |
| 10.0 | 0.5 | 82.17% | 1278.47 kWh | 99.83% | 99.15% |
| 10.0 | 2.0 | 83.94% | 1137.62 kWh | 65.72% | 59.09% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Fu, Q.; Chen, J.; Lu, Y.; Wang, Y.; Wu, H. FS-DDPG: Optimal Control of a Fan Coil Unit System Based on Safe Reinforcement Learning. Buildings 2025, 15, 226. https://doi.org/10.3390/buildings15020226
Li C, Fu Q, Chen J, Lu Y, Wang Y, Wu H. FS-DDPG: Optimal Control of a Fan Coil Unit System Based on Safe Reinforcement Learning. Buildings. 2025; 15(2):226. https://doi.org/10.3390/buildings15020226
Chicago/Turabian StyleLi, Chenyang, Qiming Fu, Jianping Chen, You Lu, Yunzhe Wang, and Hongjie Wu. 2025. "FS-DDPG: Optimal Control of a Fan Coil Unit System Based on Safe Reinforcement Learning" Buildings 15, no. 2: 226. https://doi.org/10.3390/buildings15020226
APA StyleLi, C., Fu, Q., Chen, J., Lu, Y., Wang, Y., & Wu, H. (2025). FS-DDPG: Optimal Control of a Fan Coil Unit System Based on Safe Reinforcement Learning. Buildings, 15(2), 226. https://doi.org/10.3390/buildings15020226







