A New Method for Predicting Pile Accumulated Deformation and Stiffness of Evolution Under Long-Term Inclined Cyclic Loading
Abstract
1. Introduction
2. Model Overview
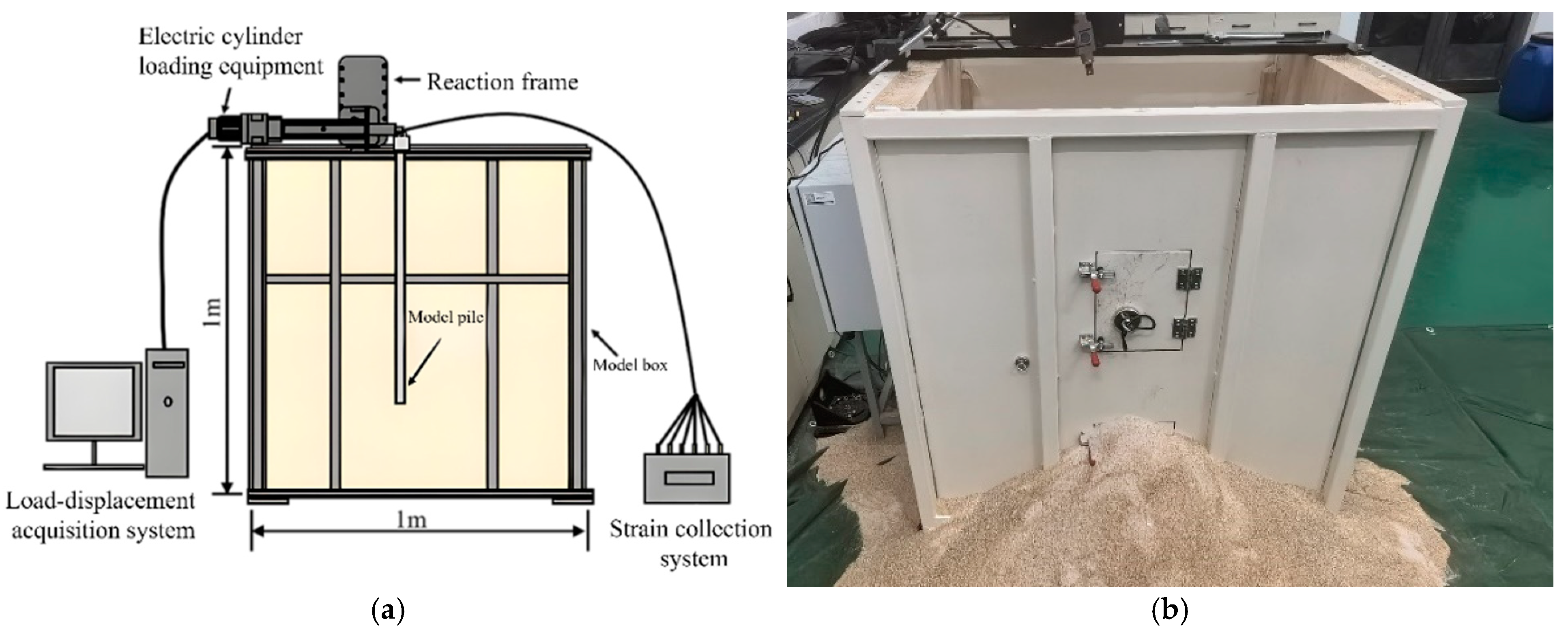
2.1. Cyclic Loading System
2.2. Test the Preparation of Soil Samples
2.3. Design and Manufacture of Pile Specimen
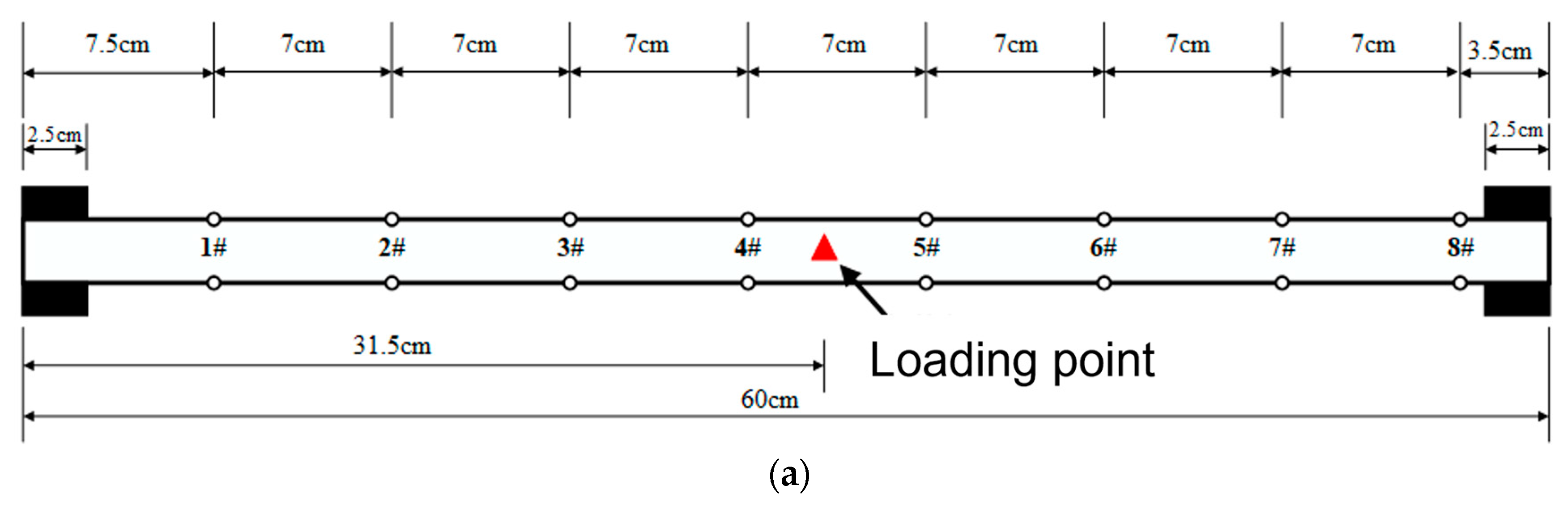
2.4. Test Scheme
3. Cumulative Deformation Test Results and Analysis
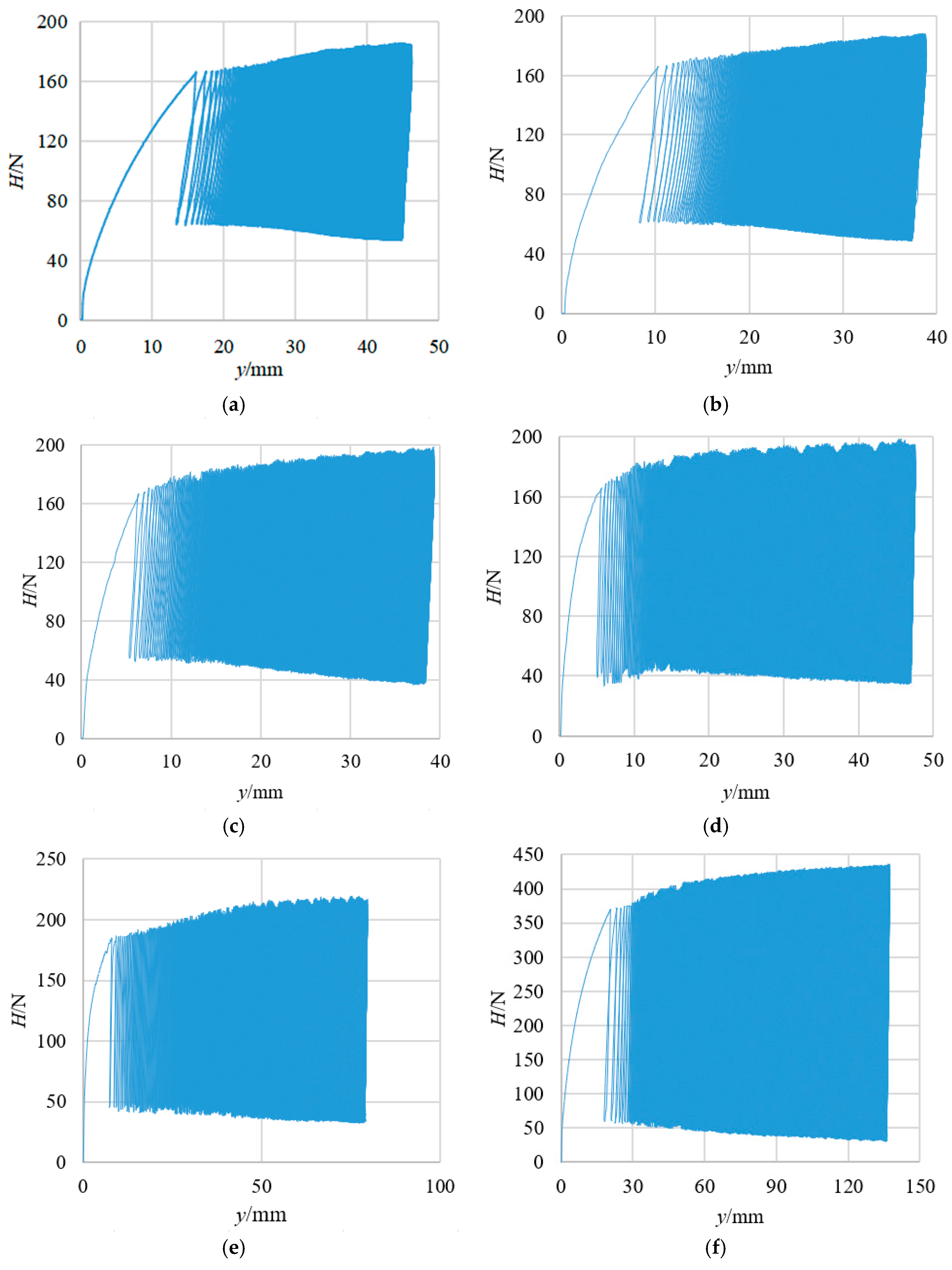
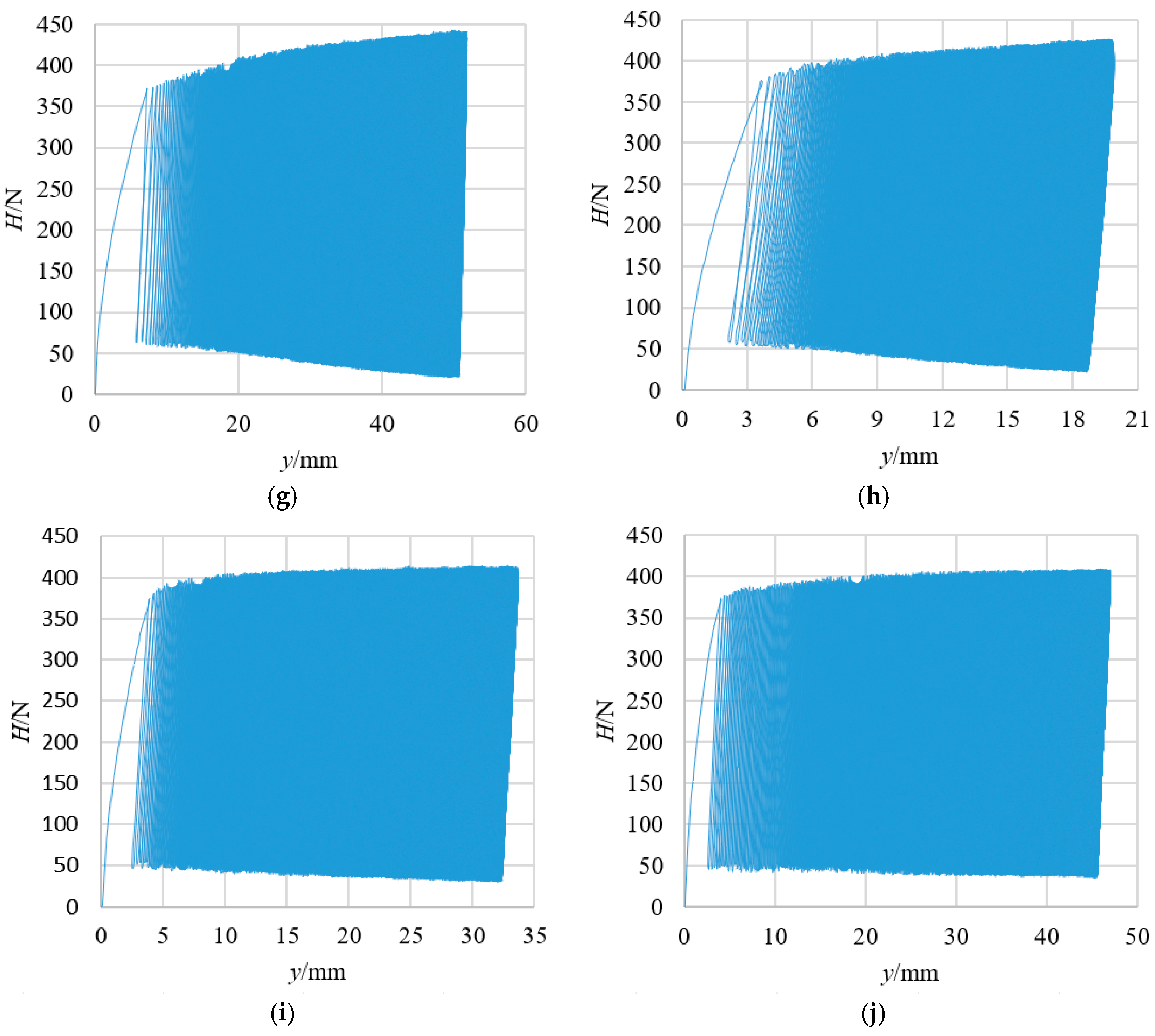
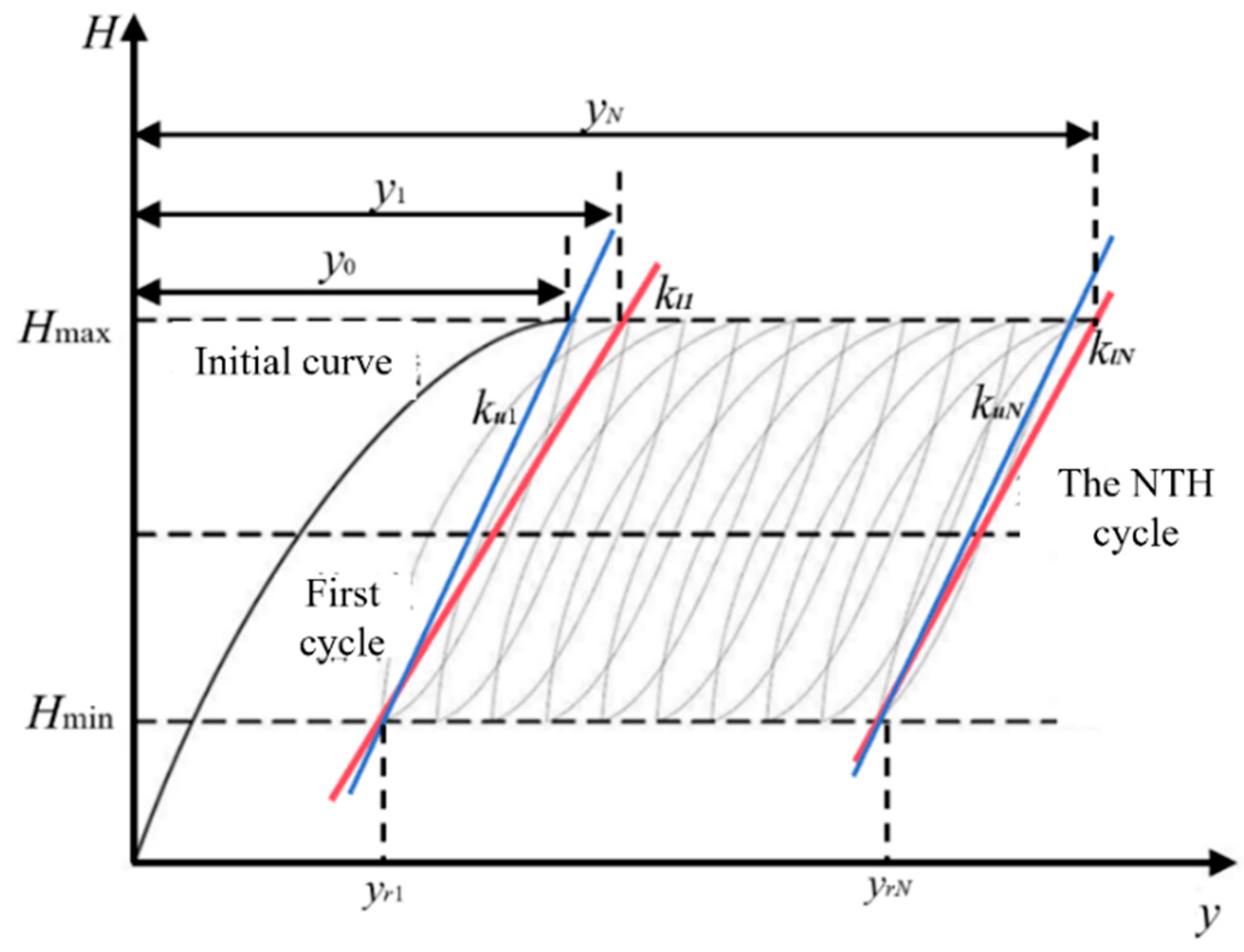
3.1. Load–Displacement Curve Under Inclined Cyclic Load
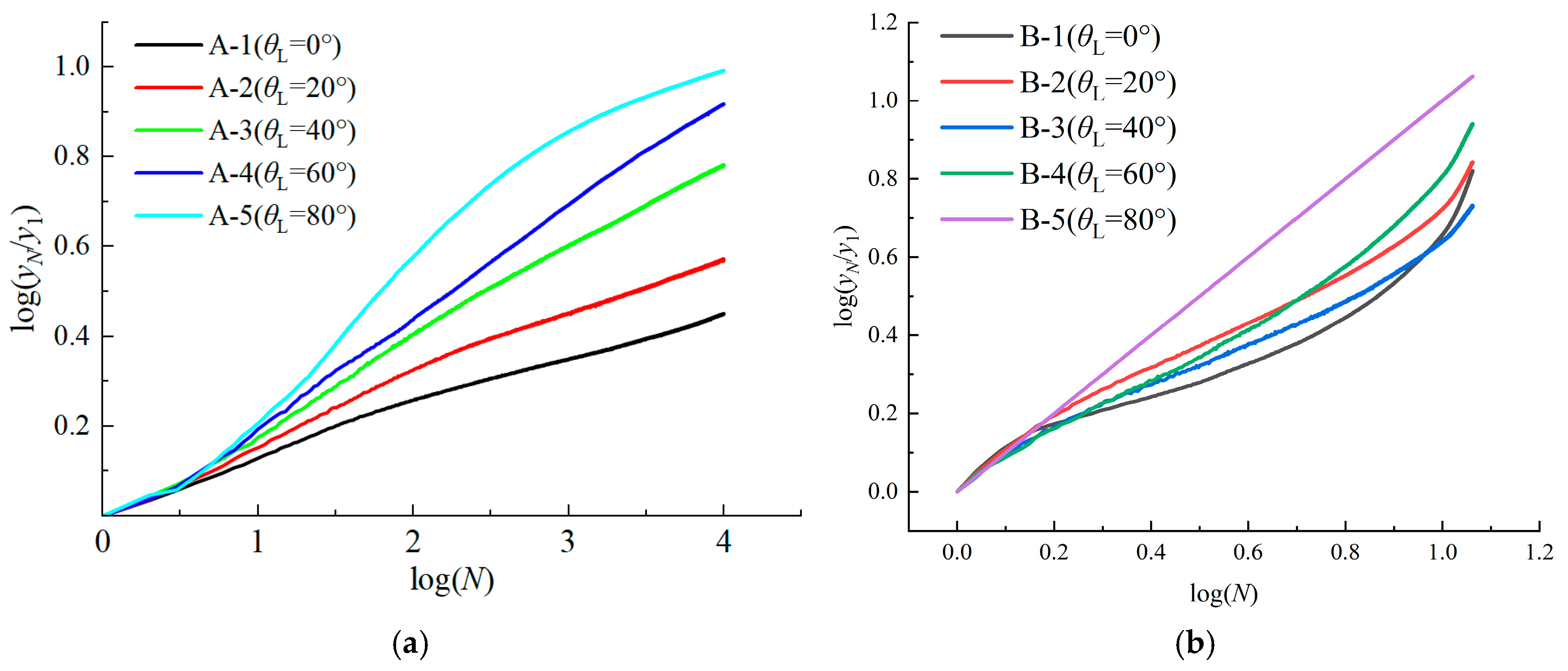
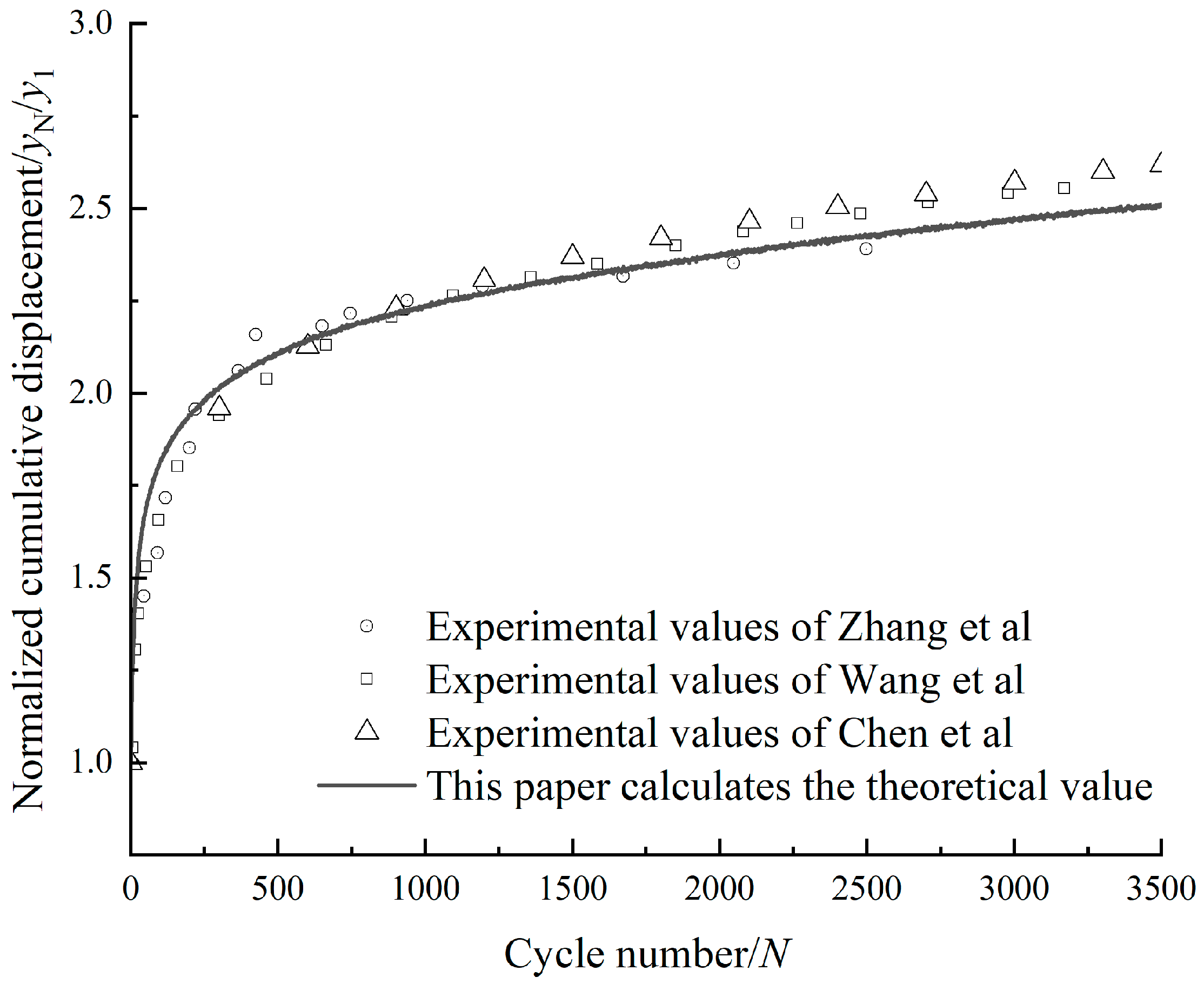
3.2. Development Law of Cumulative Displacement
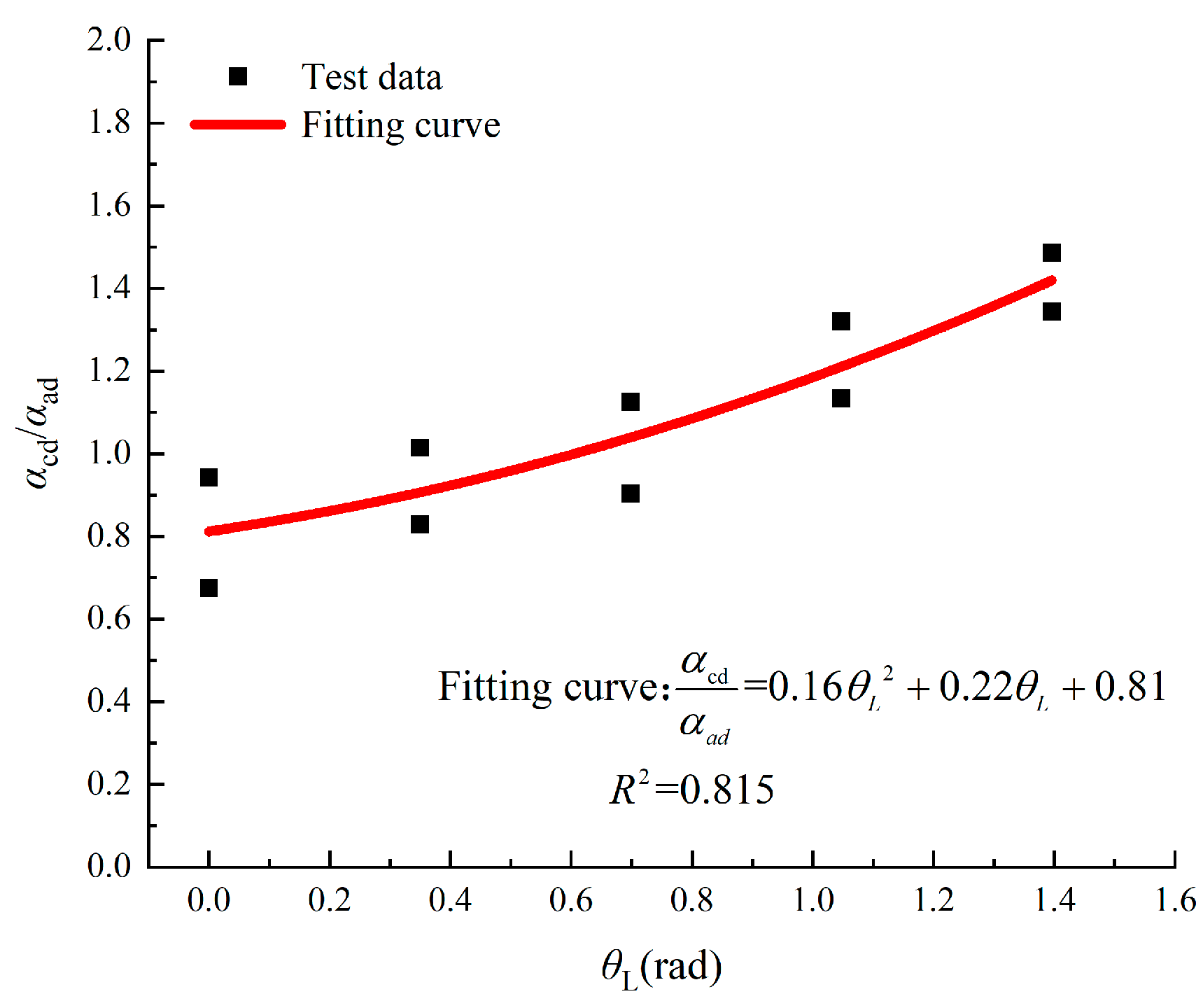
3.3. Prediction Formula of Cumulative Displacement
4. Loading and Unloading Stiffness Test Results and Analysis
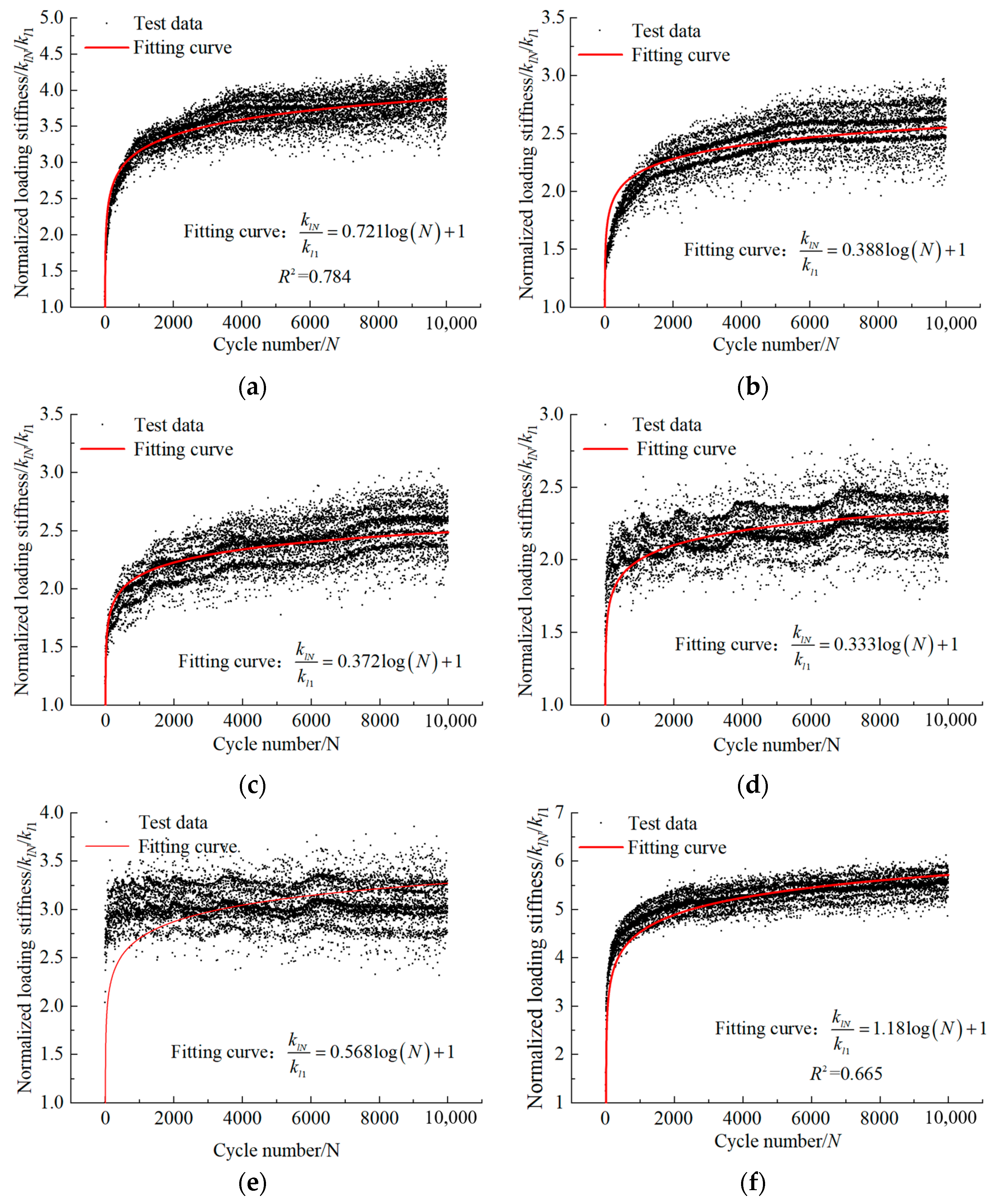
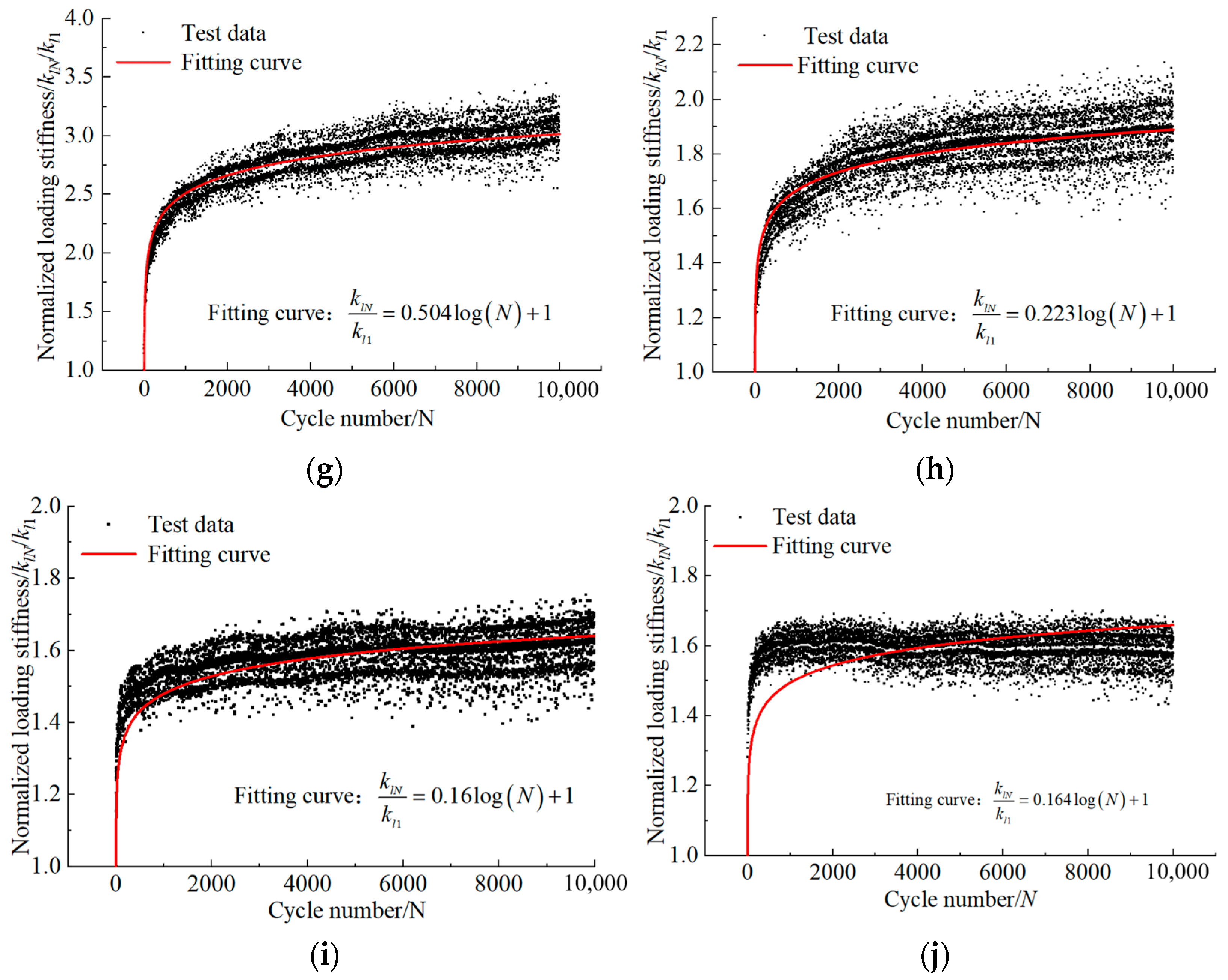
4.1. Development Law of Inclined Cyclic Loading Stiffness
4.2. Prediction Formula of Inclined Cyclic Loading Stiffness
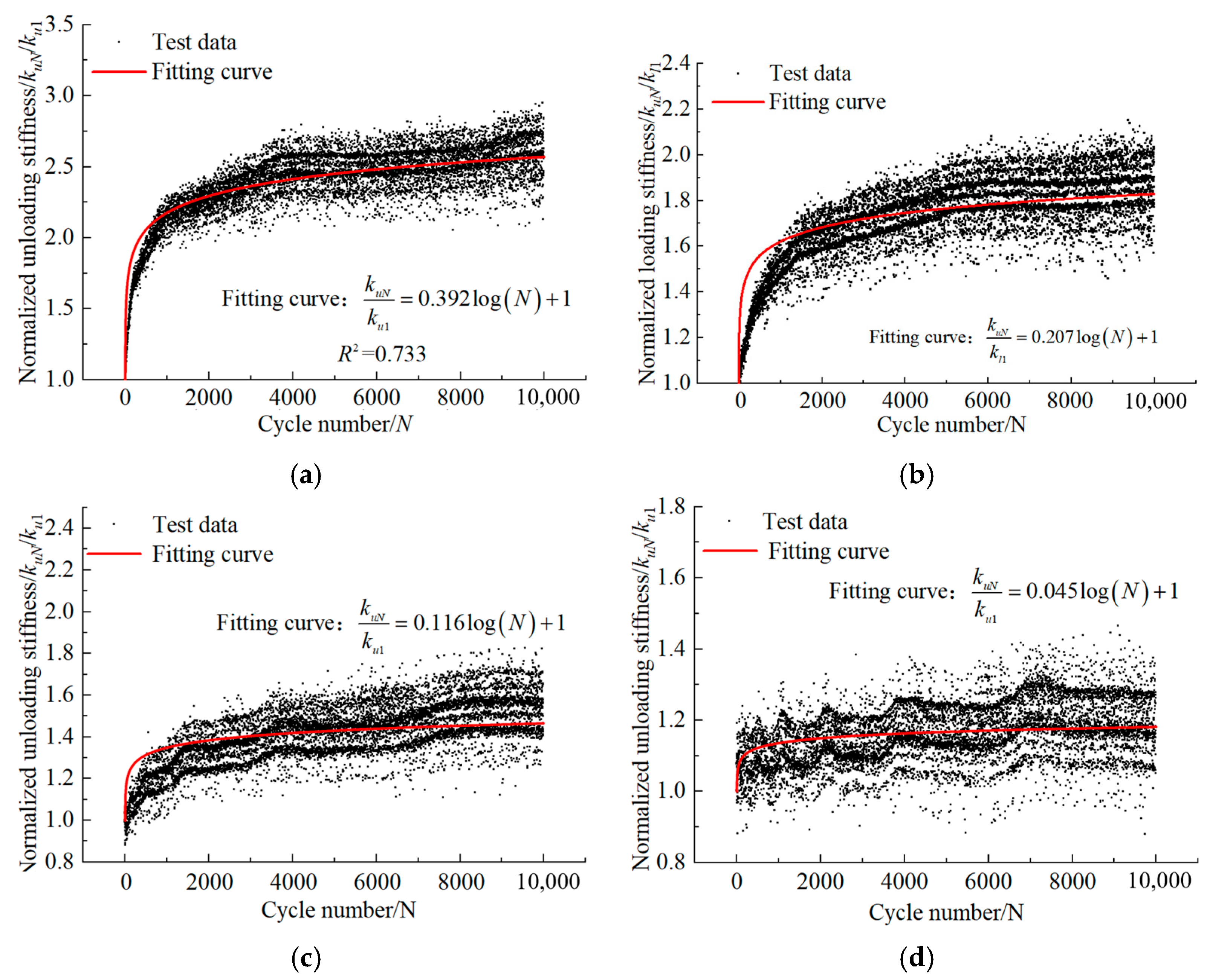
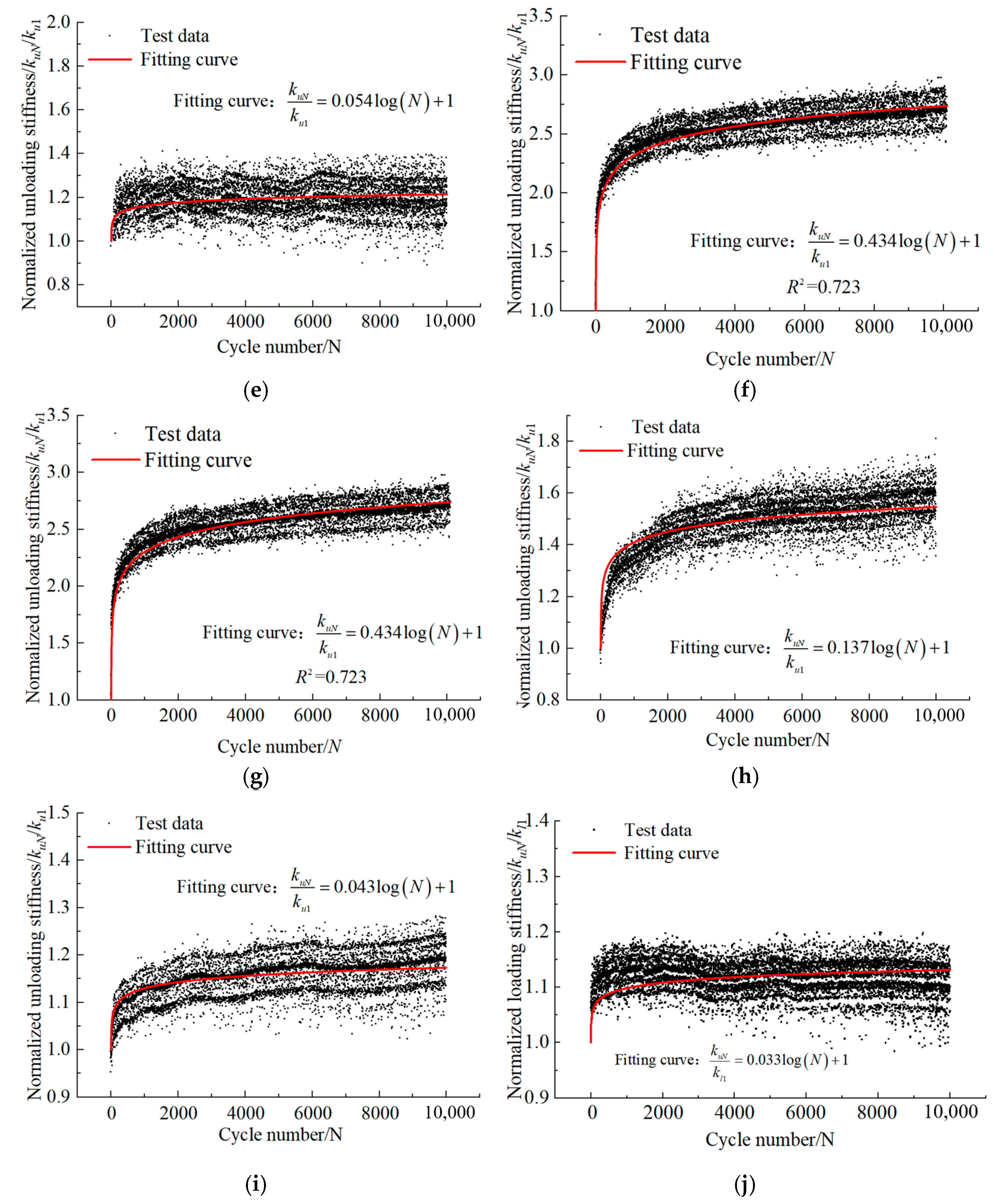
4.3. Development Law of Inclined Cyclic Unloading Stiffness
4.4. Prediction Formula of Inclined Cyclic Unloading Stiffness
5. Conclusions
- A smaller cyclic load angle (θL) or larger pile–soil relative stiffness (T/L) results in a greater range and deeper depth of settlement of sandy soil at the pile–soil interface after 10,000 cyclic loadings.
- The cumulative deformation, loading stiffness klN/kl1, and unloading stiffness kuN/ku1 of the pile under inclined cyclic loading increase with the number of cycles N, but the rate of increase slows down over time. The larger the θL, the faster the initial development of all.
- As θL increases from 0° to 80°, the initial peak displacement at the pile top decreases, while the final cumulative displacement first decreases and then increases. Additionally, after 10,000 cycles, the klN/kl1 and kuN/ku1 values of slender piles first decrease and then increase, while the klN/kl1 and kuN/ku1 values of semi-rigid piles gradually decrease. When θL = 80°, klN/kl1 and kuN/ku1 values peaked at the initial loading stage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Dai, G.; Zhu, M.; Wang, L.; Liu, H. A Simplified Method for Estimating the Initial Stiffness of Monopile—Soil Interaction Under Lateral Loads in Offshore Wind Turbine Systems. China Ocean Eng. 2023, 37, 165–174. [Google Scholar] [CrossRef]
- Qin, W.; Gao, J.; Chang, K.; Dai, G.; Wei, H. Set-up effect of large-diameter open-ended thin-walled pipe piles driven in clay. Comput. Geothecnics. 2023, 159, 105459. [Google Scholar] [CrossRef]
- Qin, W.; Ye, C.; Gao, J.; Dai, G.; Wang, D.; Dong, Y. Pore water pressure of clay soil around large-diameter open-ended thin-walled pile (LOTP) during impact penetration. Comput. Geotech. 2025, 180, 107065. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, M.; Li, X.; Dai, G.; Yin, Q.; Liu, J.; Ling, C. Experimental study on shear behavior of interface between different soil materials and concrete under variable normal stress. Appl. Sci. 2022, 12, 11213. [Google Scholar] [CrossRef]
- Qin, W.; Li, X.; Dai, G.; Hu, P. Analytical Penetration Solutions of Large-Diameter Open-Ended Piles Subjected to Hammering Loads. J. Mar. Sci. Eng. 2022, 10, 885. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, M.M.; Li, X.; Lin, C.; Wang, T.F. The Shear Effect of Large-Diameter Piles under Different Lateral Loading Levels: The Transfer Matrix Method. Buildings 2024, 14, 1448. [Google Scholar] [CrossRef]
- Li, X.; Dai, G.; Zhu, M.; Zhu, W.; Zhang, F. Investigation of the soil deformation around laterally loaded deep foundations with large diameters. Acta Geotech. 2024, 19, 2293–2314. [Google Scholar] [CrossRef]
- Hettler, A. Deformations of Stiff and Elastic Foundation Structures in Sand Under Monotonous and Cyclic Loading; Bodenmechanik und Felsmechanik der Universität Fridericiana: Karlsruhe, Germany, 1981; p. 9. [Google Scholar]
- Lin, S.; Liao, J. Permanent strains of piles in sand due to cyclic lateral loads. J. Geotech. Geoenviron. Eng. 1999, 125, 798–802. [Google Scholar] [CrossRef]
- Bai, X.Y.; Zhang, Y.J.; Yan, N.; Liu, J.W.; Zhang, Y.M. Experimental investigation on bearing capacity of rock-socketed bored piles in silty clay stratum in beach areas. Appl. Ocean Res. 2025, 154, 104336. [Google Scholar] [CrossRef]
- Huang, L.; Qin, W.; Dai, G.; Zhu, M.; Liu, L.; Huang, L.; Yang, S.; Ge, M. Ground settlement prediction for highway subgrades with sparse data using regression Kriging. Sci. Rep. 2024, 14, 24594. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Jin, T.; Qin, W.; Zhang, F. Performance evaluation of post-grouting for bored piles installed in inhomogeneous gravel pebble stratum overlaid by deep and soft soil layers. Geomech. Geoengin. Int. J. 2024, 19, 77–95. [Google Scholar] [CrossRef]
- Qin, W.; Cai, S.; Dai, G.; Wang, D.; Chang, K. Soil Resistance during Driving of Offshore Large-Diameter Open-Ended Thin-Wall Pipe Piles Driven into Clay by Impact Hammers. Comput. Geotech. 2023, 153, 105085. [Google Scholar] [CrossRef]
- LeBlanc, C.; Houlsby, G.T.; Byrne, B.W. Response of stiff piles in sand to long-term cyclic lateral loading. Géotechnique 2010, 60, 79–90. [Google Scholar] [CrossRef]
- Leblanc, C.; Byrne, B.W.; Houlsby, G.T. Response of stiff piles to random two-way lateral loading. Géotechnique 2010, 60, 715–721. [Google Scholar] [CrossRef]
- Lin, J.Y. Study on the Evolution of Bearing Performance and Cumulative Deformation Characteristics of Monopiles Under Horizontal Cyclic Loading. Master’s Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Wang, Y.; Zhu, M.X.; Dai, G.L.; Gong, W.M.; Lin, J.Y. Characteristics of cumulative deformation and prediction method for pile foundation under cyclic lateral loading considering influences of pile-soil relative stiffness. J. Geotech. Eng. 2022, 44, 220–225. [Google Scholar]
- Rathod, D.; Nigitha, D.; Krishnanunni, K.T. Experimental Investigation of the Behavior of Monopile under Asymmetric Two-Way Cyclic Lateral Loads. Int. J. Geomech. 2021, 21, 06021001. [Google Scholar] [CrossRef]
- Liang, R.; Yuan, Y.; Fu, D.S.; Liu, R. Cyclic response of monopile-supported offshore wind turbines under wind and wave loading in sand. Mar. Georesources Geotechnol. 2021, 39, 1230–1243. [Google Scholar] [CrossRef]
- Li, Q.; Askarinejad, A.; Gavin, K. Lateral response of rigid monopiles subjected to cyclic loading: Centrifuge modelling. Proc. Inst. Civ. Eng.-Geotech. Eng. 2020, 175, 426–438. [Google Scholar] [CrossRef]
- Chen, J.; Shu, J.; Xi, S.; Gu, X.; Zhu, M.; Li, X. A New Method for Predicting Dynamic Pile Head Stiffness Considering Pile-Soil Relative Stiffness Under Long-Term Cyclic Loading Conditions. Buildings 2024, 14, 3483. [Google Scholar] [CrossRef]
- Li, X.; Zhu, M.; Dai, G.; Wang, L.; Liu, J. Interface Mechanical Behavior of Flexible Piles Under Lateral Loads in OWT Systems. China Ocean Eng. 2023, 37, 484–494. [Google Scholar] [CrossRef]
- Li, X.; Dai, G. Closure to “Energy-Based Analysis of Laterally Loaded Caissons with Large Diameters under Small-Strain Conditions”. Int. J. Geomech. 2023, 23, 07023008. [Google Scholar] [CrossRef]
- Reese, L.C.; Cox, W.R.; Koop, F.D. Analysis of Laterally Loaded Piles in Sand. In Proceedings of the 6th Annual Offshore Technology Conference, Houston, TX, USA, 5–7 May 1974; pp. 473–483. [Google Scholar]
- Reese, L.C.; Welch, R.C. Lateral loading of deep foundations in stiff clay. J. Geotech. Geoenviron. Eng. 1975, 101, 633–649. [Google Scholar] [CrossRef]
- Cuéllar, P. Pile foundations for offshore wind turbines: Numerical and Experimental Investigations on the Behaviour Under Short-Term and Long-Term Cyclic Loading. Ph.D. Thesis, der Technischen Universität Berlin, Berlin, Germany, 2011. [Google Scholar]
- Abadie, C.N.; Byrne, B.W.; Houlsby, G.T. Rigid pile response to cyclic lateral loading: Laboratory tests. Géotechnique 2019, 69, 863–876. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, M.S.; Hu, Z.P. Modeling test of horizontal cyclic cumulative deformation characteristics of single pile in sandy soil. Geotechnics 2019, 40, 933–941. [Google Scholar]
- Sun, Y.X. Horizontal Bearing Characteristics Test and Numerical Analysis of Large Diameter Single Pile for Offshore Wind Turbine. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2017. [Google Scholar]











| Soil Characteristics | Parameter Values |
|---|---|
| The average particle size D50 (mm) | 0.17 |
| Maximum dry weight ρmin (kN/m3) | 1.978 |
| Minimum dry weight ρmax (kN/m3) | 1.495 |
| Moisture content | 2% |
| Specific gravity of soil particles Gs | 2.632 |
| Relative density Dr | 62% |
| ID | Length L (cm) | Diameter D (cm) | Pile Wall Thickness T (cm) | T/L |
|---|---|---|---|---|
| A | 60 | 2 | 0.1 | 0.190 |
| B | 60 | 5 | 0.2 | 0.375 |
| ID | Load Type | Cyclic Amplitude Ratio (ζb) | Cyclic Load Ratio (ζc) | Cycle Number (N) |
|---|---|---|---|---|
| A-1 | 0° | 0.5 | 0.2 | 10,000 |
| A-2 | 20° | 0.5 | 0.2 | 10,000 |
| A-3 | 40° | 0.5 | 0.2 | 10,000 |
| A-4 | 60° | 0.5 | 0.2 | 10,000 |
| A-5 | 80° | 0.5 | 0.2 | 10,000 |
| B-1 | 0° | 0.5 | 0.2 | 10,000 |
| B-2 | 20° | 0.5 | 0.2 | 10,000 |
| B-3 | 40° | 0.5 | 0.2 | 10,000 |
| B-4 | 60° | 0.5 | 0.2 | 10,000 |
| B-5 | 80° | 0.5 | 0.2 | 10,000 |
| ID | ζc | T/L | θL (rad) | αad | αcd | αcd/αad |
|---|---|---|---|---|---|---|
| A-1 | 0.2 | 0.190 | 0 | 0.145 | 0.118 | 0.814 |
| A-2 | 0.2 | 0.190 | 0.349 | 0.145 | 0.145 | 1 |
| A-3 | 0.2 | 0.190 | 0.698 | 0.145 | 0.197 | 1.359 |
| A-4 | 0.2 | 0.190 | 1.047 | 0.145 | 0.231 | 1.593 |
| A-5 | 0.2 | 0.190 | 1.396 | 0.145 | 0.260 | 1.793 |
| B-1 | 0.2 | 0.375 | 0 | 0.209 | 0.197 | 0.943 |
| B-2 | 0.2 | 0.375 | 0.349 | 0.209 | 0.212 | 1.014 |
| B-3 | 0.2 | 0.375 | 0.698 | 0.209 | 0.189 | 0.904 |
| B-4 | 0.2 | 0.375 | 1.047 | 0.209 | 0.237 | 1.134 |
| B-5 | 0.2 | 0.375 | 1.396 | 0.209 | 0.281 | 1.344 |
| A-2 | N | Test Data yN | Equation (19) yN | Error Rate (%) | A-3 | N | Test Data yN | Equation (19) yN | Error Rate (%) |
| 1000 | 29.03 | 30.38 | 4.65 | 1000 | 25.52 | 22.24 | 12.85 | ||
| 2000 | 31.39 | 33.88 | 7.93 | 2000 | 28.87 | 25.21 | 12.68 | ||
| 5000 | 35.03 | 39.13 | 11.7 | 5000 | 34.22 | 29.75 | 13.06 | ||
| 10,000 | 38.23 | 43.64 | 14.15 | 10,000 | 38.52 | 33.72 | 12.46 | ||
| B-2 | N | Test Data yN | Equation (19) yN | Error Rate (%) | B-4 | N | Test Data yN | Equation (19) yN | Error Rate (%) |
| 1000 | 32.44 | 26.97 | −16.86 | 1000 | 19.63 | 22.19 | 13.04 | ||
| 2000 | 37.24 | 30.75 | −17.43 | 2000 | 23.51 | 26.45 | 12.51 | ||
| 5000 | 44.49 | 36.56 | −17.82 | 5000 | 29.15 | 33.37 | 14.48 | ||
| 10,000 | 50.84 | 41.68 | −18.02 | 10,000 | 33.5 | 39.78 | 18.75 |
| ID | ζb | ζc | T/L | θL (rad) | βl | Fitting Formula | βL | βL/βl |
|---|---|---|---|---|---|---|---|---|
| A-1 | 0.5 | 0.2 | 0.190 | 0 | 0.778 | 0.721 | 0.927 | |
| A-2 | 0.5 | 0.2 | 0.190 | 0.349 | 0.778 | 0.388 | 0.499 | |
| A-3 | 0.5 | 0.2 | 0.190 | 0.698 | 0.778 | 0.372 | 0.478 | |
| A-4 | 0.5 | 0.2 | 0.190 | 1.047 | 0.778 | 0.333 | 0.428 | |
| A-5 | 0.5 | 0.2 | 0.190 | 1.396 | 0.778 | 0.568 | 0.730 | |
| B-1 | 0.5 | 0.2 | 0.375 | 0 | 1.08 | 1.181 | 1.092 | |
| B-2 | 0.5 | 0.2 | 0.375 | 0.349 | 1.08 | 0.504 | 0.466 | |
| B-3 | 0.5 | 0.2 | 0.375 | 0.698 | 1.08 | 0.223 | 0.206 | |
| B-4 | 0.5 | 0.2 | 0.375 | 1.047 | 1.08 | 0.16 | 0.148 | |
| B-5 | 0.5 | 0.2 | 0.375 | 1.396 | 1.08 | 0.165 | 0.152 |
| ID | ζb | ζc | T/L | θL (rad) | γu | Fitting Formula | γα | γα/γu |
|---|---|---|---|---|---|---|---|---|
| A-1 | 0.5 | 0.2 | 0.190 | 0 | 0.355 | 0.392 | 1.103 | |
| A-2 | 0.5 | 0.2 | 0.190 | 0.349 | 0.355 | 0.207 | 0.582 | |
| A-3 | 0.5 | 0.2 | 0.190 | 0.698 | 0.355 | 0.116 | 0.326 | |
| A-4 | 0.5 | 0.2 | 0.190 | 1.047 | 0.355 | 0.045 | 0.127 | |
| A-5 | 0.5 | 0.2 | 0.190 | 1.396 | 0.355 | 0.054 | 0.152 | |
| B-1 | 0.5 | 0.2 | 0.375 | 0 | 0.293 | 0.434 | 1.479 | |
| B-2 | 0.5 | 0.2 | 0.375 | 0.349 | 0.293 | 0.222 | 0.757 | |
| B-3 | 0.5 | 0.2 | 0.375 | 0.698 | 0.293 | 0.137 | 0.467 | |
| B-4 | 0.5 | 0.2 | 0.375 | 1.047 | 0.293 | 0.043 | 0.147 | |
| B-5 | 0.5 | 0.2 | 0.375 | 1.396 | 0.293 | 0.033 | 0.112 |
| Verify the Summary Table of Equation (19) | Verify the Summary Table of Equation (26) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A-1 | N | Test Data klN/kl1 | Equation (19) klN/kl1 | Error Rate (%) | A-3 | N | Test Data kuN/ku1 | Equation (26) kuN/ku1 | Error Rate (%) |
| 1000 | 3.413 | 3.124 | −8.47 | 1000 | 1.253 | 1.173017 | 11.05 | ||
| 2000 | 3.494 | 3.337 | −4.49 | 2000 | 1.335 | 1.190379 | 7.25 | ||
| 5000 | 3.762 | 3.619 | −3.8 | 5000 | 1.55 | 1.213329 | −4.29 | ||
| 10,000 | 3.689 | 3.832 | 3.88 | 10,000 | 1.497 | 1.23069 | 1.74 | ||
| A-2 | N | Test Data klN/kl1 | Equation (19) klN/kl1 | Error Rate (%) | A-4 | N | Test Data kuN/ku1 | Equation (26) kuN/ku1 | Error Rate (%) |
| 1000 | 2.048 | 2.304 | 12.49 | 1000 | 1.171 | 1.173 | 0.13 | ||
| 2000 | 2.158 | 2.435 | 12.82 | 2000 | 1.093 | 1.190 | 8.91 | ||
| 5000 | 2.377 | 2.608 | 9.69 | 5000 | 1.111 | 1.213 | 9.22 | ||
| 10,000 | 2.628 | 2.738 | 4.19 | 10,000 | 1.271 | 1.231 | −3.16 | ||
| B-1 | N | Test Data klN/kl1 | Equation (19) klN/kl1 | Error Rate (%) | B-2 | N | Test Data kuN/ku1 | Equation (26) kuN/ku1 | Error Rate (%) |
| 1000 | 4.863 | 4.44 | −8.69 | 1000 | 1.54 | 1.654 | 7.46 | ||
| 2000 | 5.246 | 4.786 | −8.78 | 2000 | 1.655 | 1.720 | 3.96 | ||
| 5000 | 4.993 | 5.242 | −5 | 5000 | 1.839 | 1.807 | −1.73 | ||
| 10,000 | 5.556 | 5.587 | 0.5 | 10,000 | 1.885 | 1.873 | −0.64 | ||
| B-3 | N | Test Data klN/kl1 | Equation (19) klN/kl1 | Error Rate (%) | B-4 | N | Test Data kuN/ku1 | Equation (26) kuN/ku1 | Error Rate (%) |
| 1000 | 1.682 | 1.677 | −0.3 | 1000 | 1.088 | 1.143 | 5.03 | ||
| 2000 | 1.831 | 1.745 | −4.69 | 2000 | 1.188 | 1.157 | −2.64 | ||
| 5000 | 1.839 | 1.835 | −0.2 | 5000 | 1.173 | 1.176 | 0.25 | ||
| 10,000 | 1.737 | 1.903 | 9.58 | 10,000 | 1.224 | 1.190 | −2.77 | ||
| B-5 | N | Test Data klN/kl1 | Equation (19) klN/kl1 | Error Rate (%) | B-5 | N | Test Data kuN/ku1 | Equation (26) kuN/ku1 | Error Rate (%) |
| 1000 | 1.638 | 1.634 | −0.3 | 1000 | 1.132 | 1.112 | −1.78 | ||
| 2000 | 1.621 | 1.697 | 4.7 | 2000 | 1.164 | 1.123 | −3.46 | ||
| 5000 | 1.691 | 1.781 | 5.33 | 5000 | 1.134 | 1.138 | 3.95 | ||
| 10,000 | 1.625 | 1.845 | 13.57 | 10,000 | 1.138 | 1.15 | 1.04 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; Li, X.; Xi, S.; Gong, W.; Zhu, M. A New Method for Predicting Pile Accumulated Deformation and Stiffness of Evolution Under Long-Term Inclined Cyclic Loading. Buildings 2025, 15, 591. https://doi.org/10.3390/buildings15040591
Pan X, Li X, Xi S, Gong W, Zhu M. A New Method for Predicting Pile Accumulated Deformation and Stiffness of Evolution Under Long-Term Inclined Cyclic Loading. Buildings. 2025; 15(4):591. https://doi.org/10.3390/buildings15040591
Chicago/Turabian StylePan, Xiangwen, Xia Li, Shuang Xi, Weiming Gong, and Mingxing Zhu. 2025. "A New Method for Predicting Pile Accumulated Deformation and Stiffness of Evolution Under Long-Term Inclined Cyclic Loading" Buildings 15, no. 4: 591. https://doi.org/10.3390/buildings15040591
APA StylePan, X., Li, X., Xi, S., Gong, W., & Zhu, M. (2025). A New Method for Predicting Pile Accumulated Deformation and Stiffness of Evolution Under Long-Term Inclined Cyclic Loading. Buildings, 15(4), 591. https://doi.org/10.3390/buildings15040591









