Planar Cross-Sectional Fitting of Structural Members to Numerical Simulation Results Obtained from Finite Element Models with Solid or Shell Elements
Abstract
:1. Introduction
2. Least Squares Approximation Fitting Method
2.1. Equation for Fitting Planar Cross-Sections
2.2. Explicit Solution of the Cubic Determination Equation
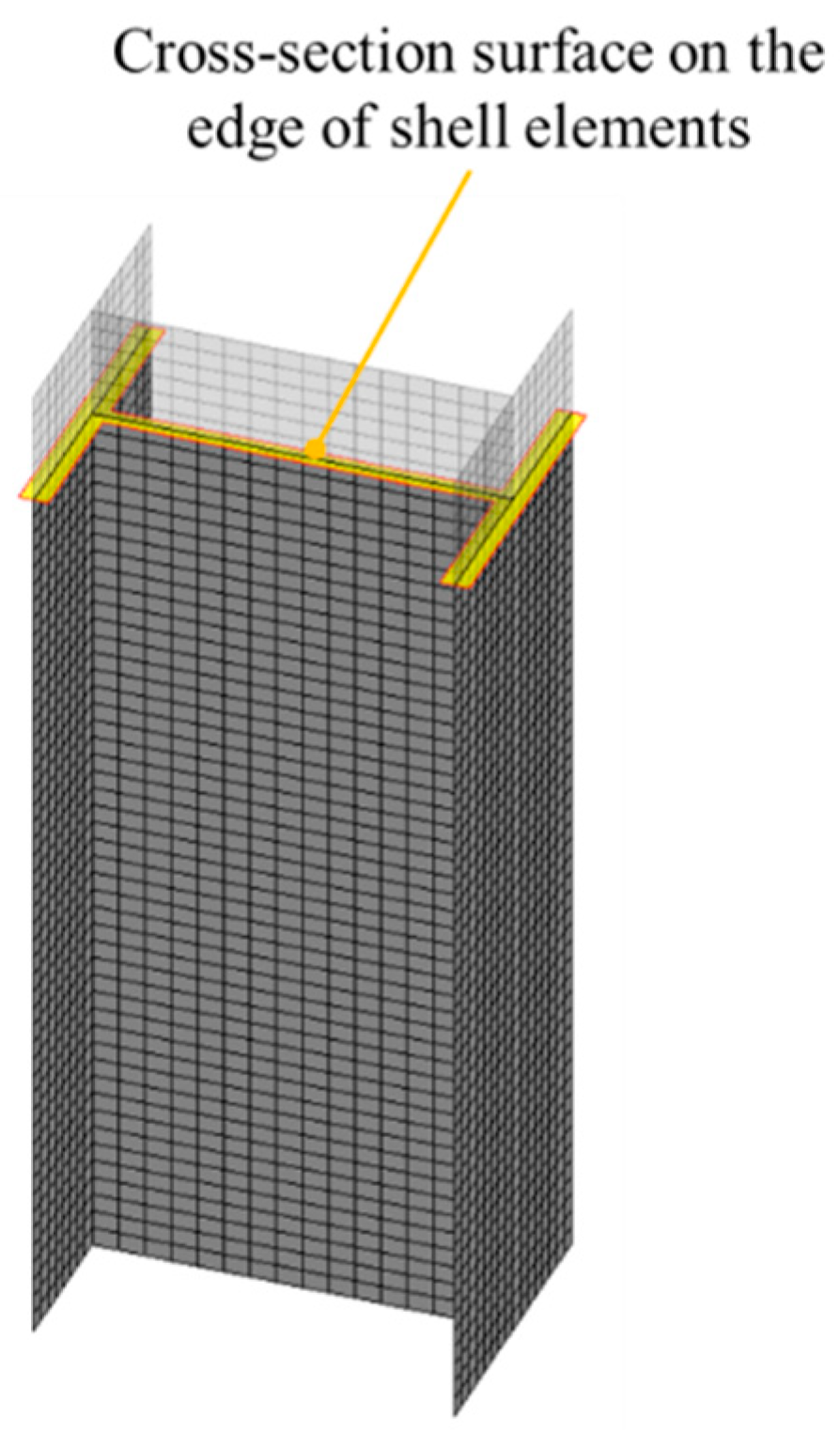
3. Integration over the Deformed Cross-Section Surface
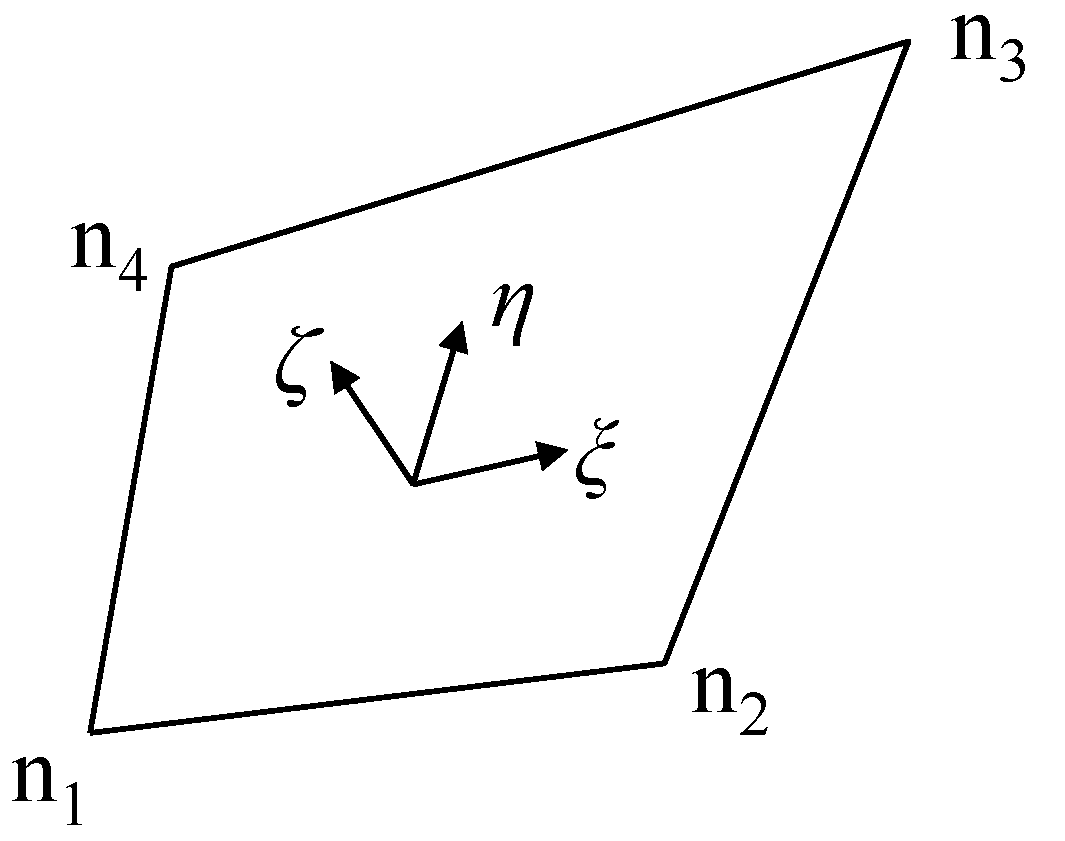
3.1. Integration of Four-Node Finite-Strain Shell Elements
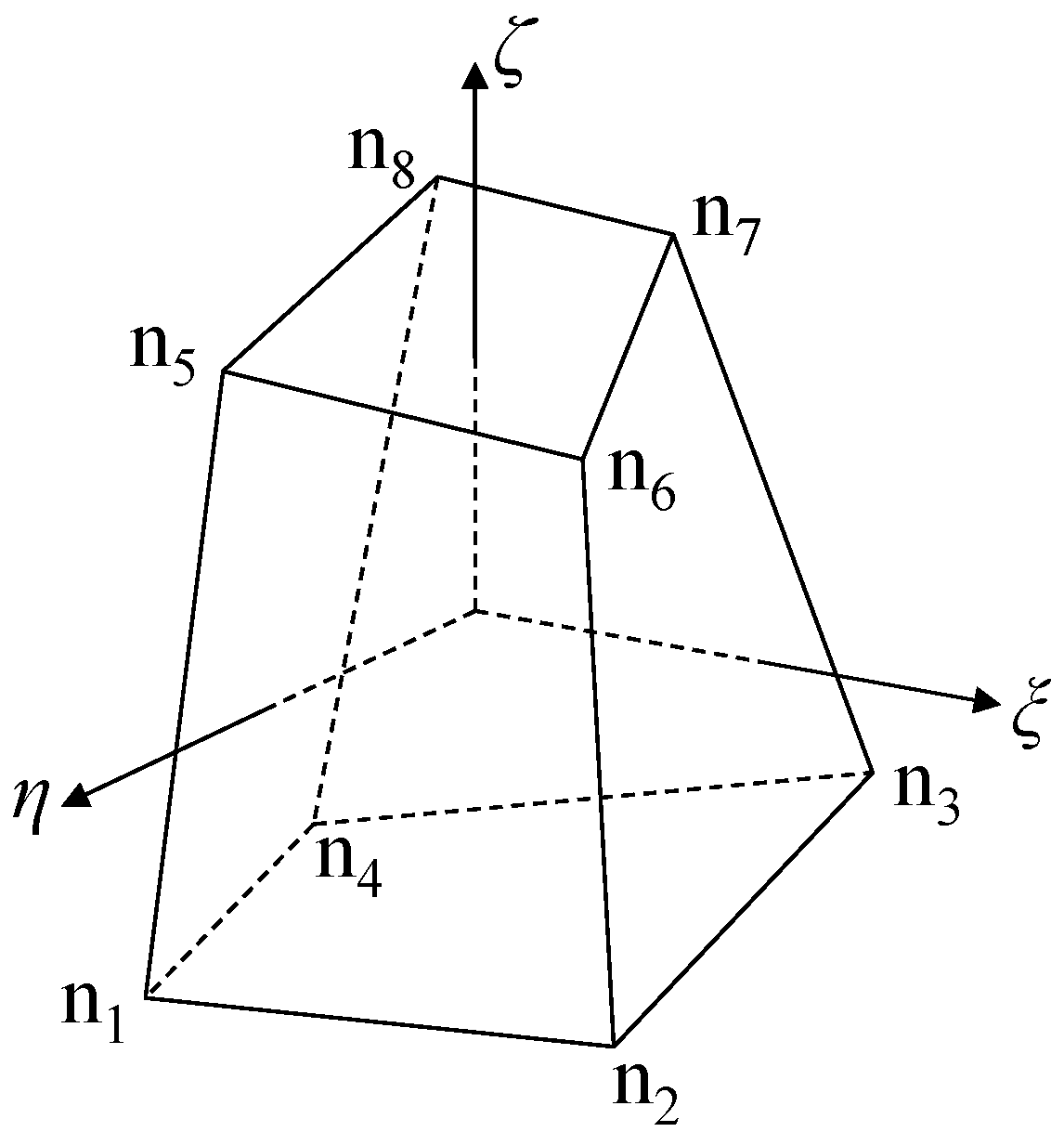
3.2. Integration of Eight-Node Solid Elements
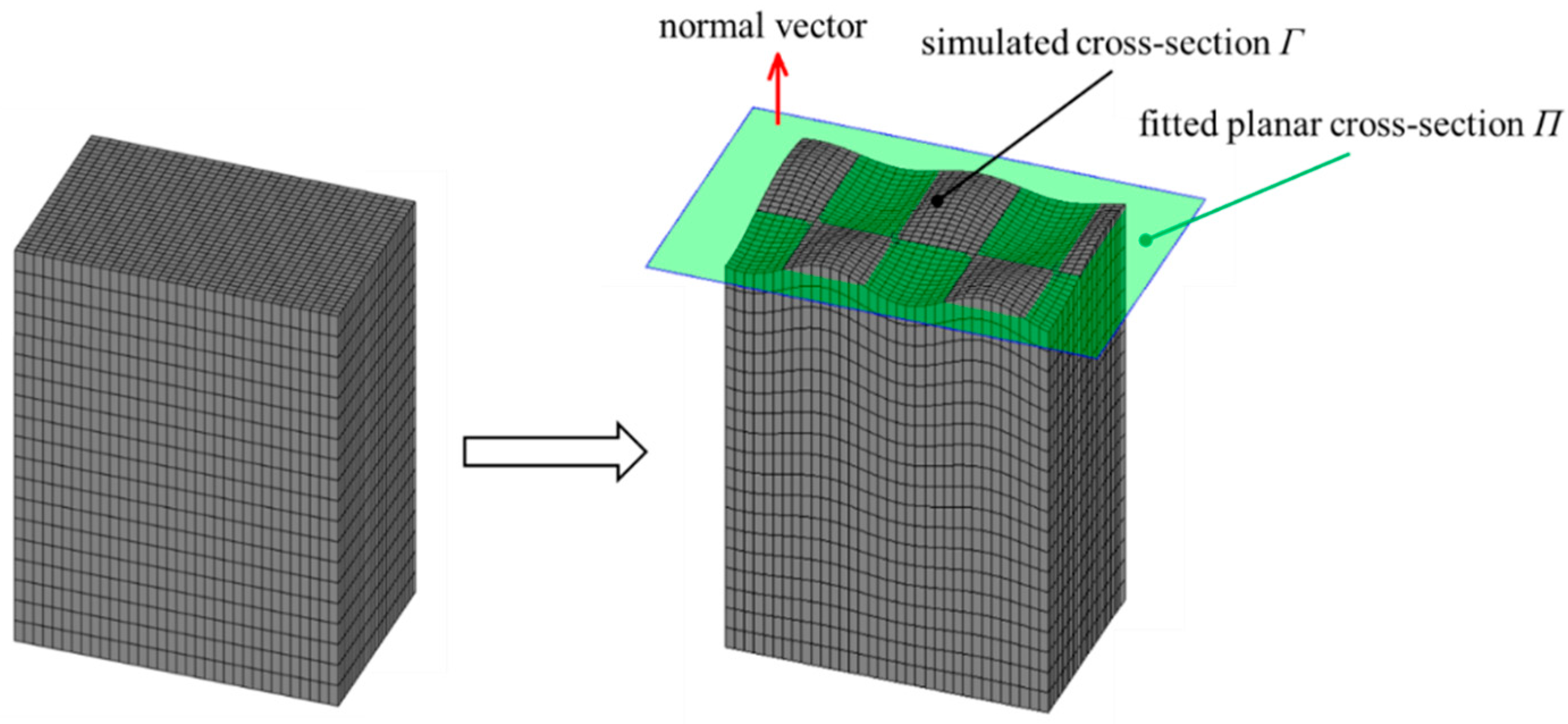
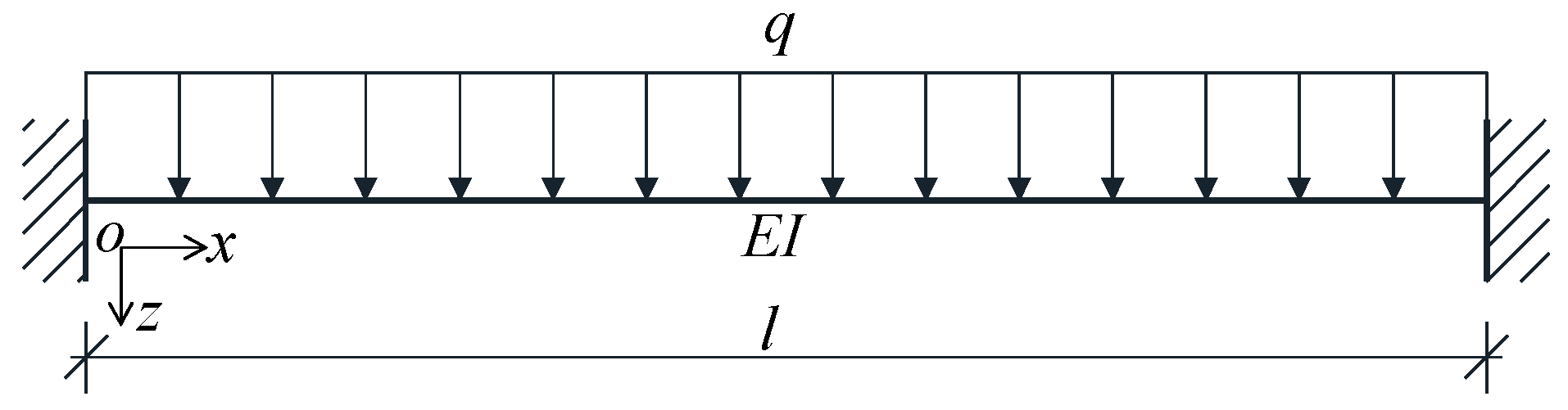
4. Validation and Applications
4.1. Validation
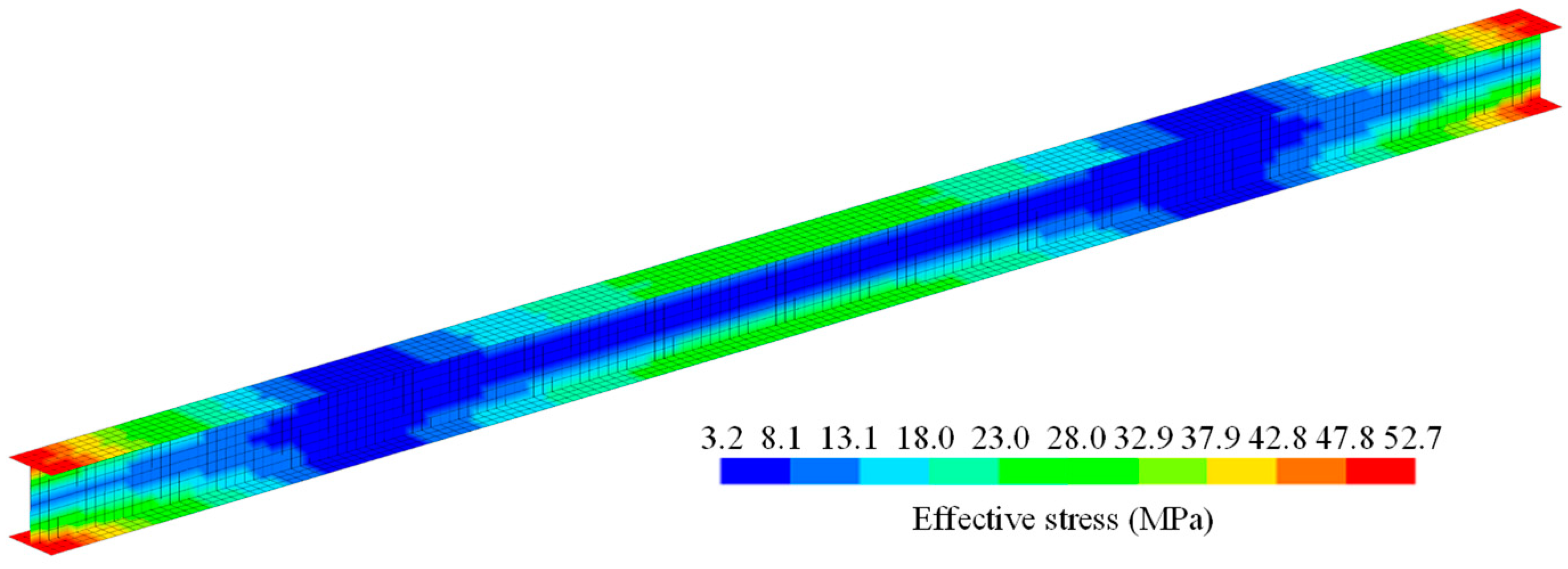
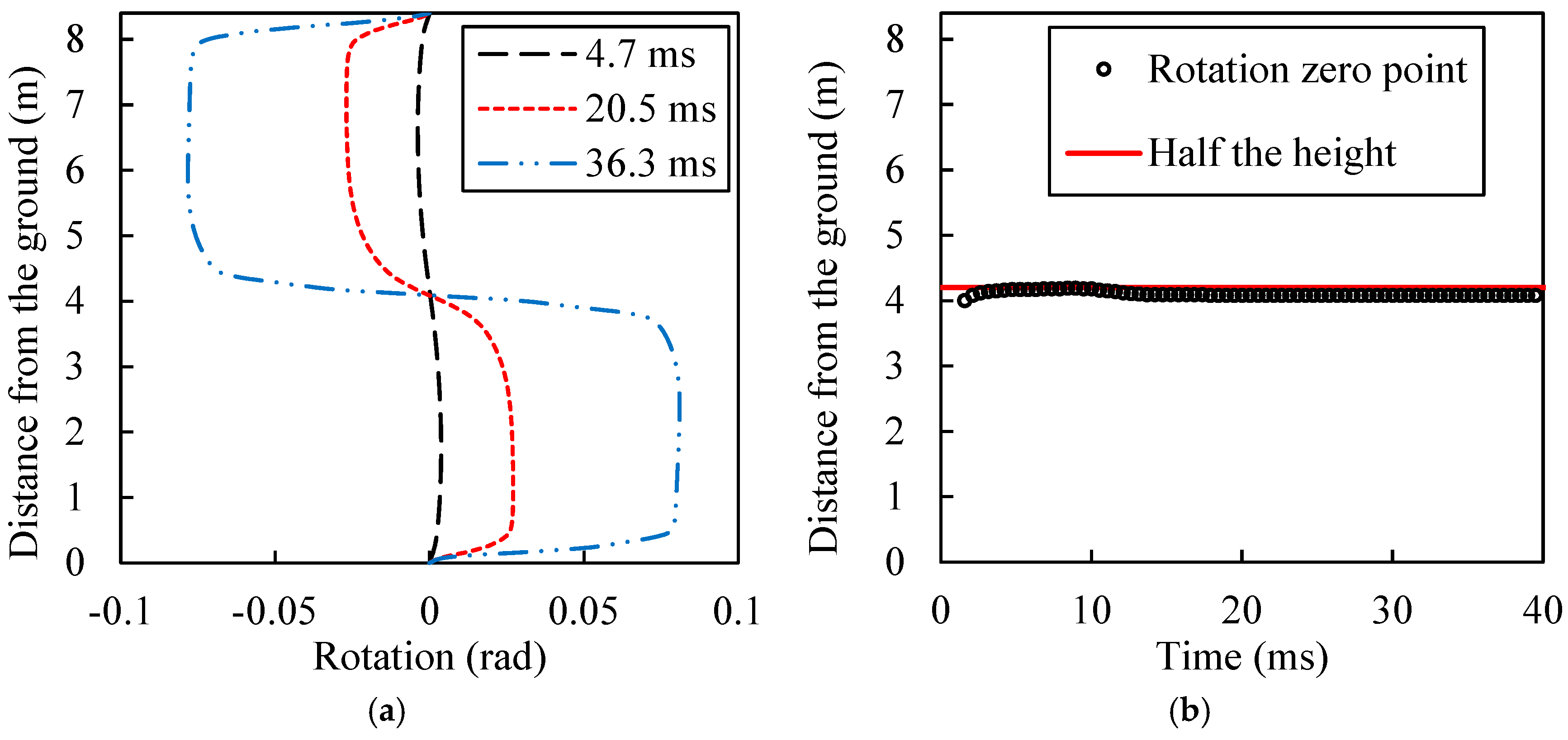
4.2. Symmetrical Mechanical Behavior of a Steel Column
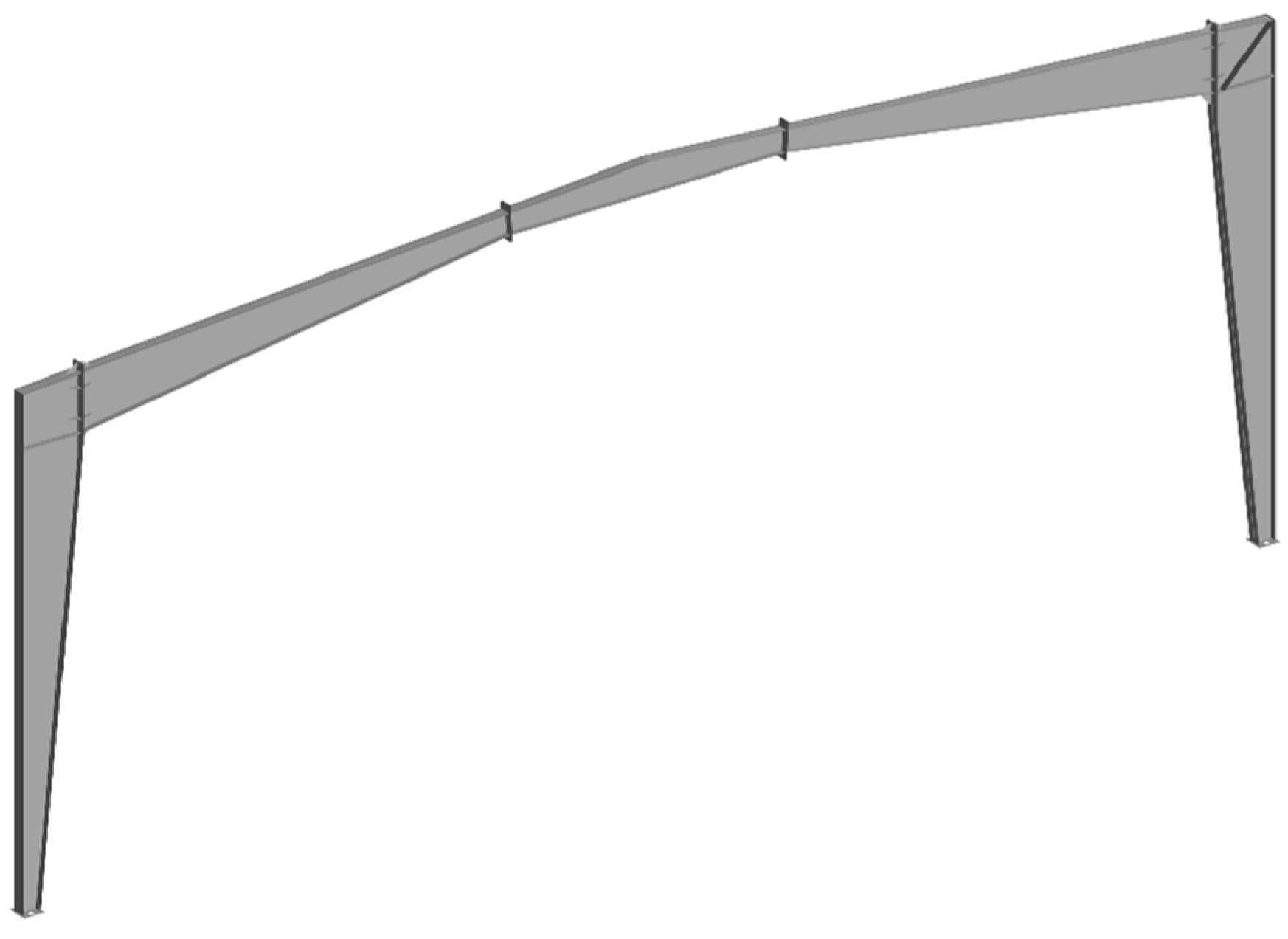
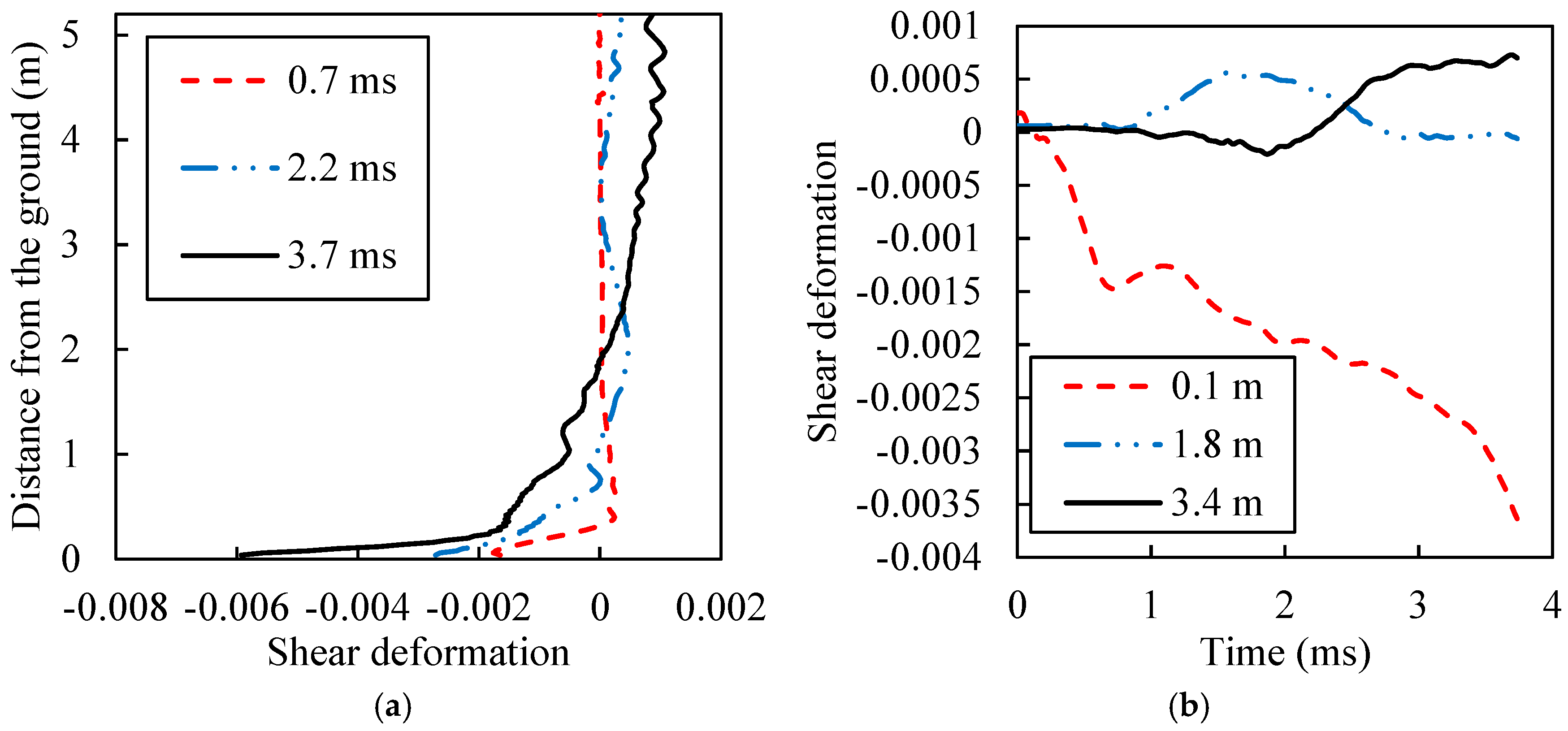
4.3. Shear Deformation of a Tapered I-Section Column
4.4. Moment–Curvature Relationship of a Tapered I-Section Column
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Domaneschi, M.; Cimellaro, G.P.; Scutiero, G. A simplified method to assess generation of seismic debris for masonry structures. Eng. Struct. 2019, 186, 306–320. [Google Scholar] [CrossRef]
- Meguro, K.; Tagel-Din, H. Applied Element Method for Structural Analysis: Theory and Application for Linear Materials. Doboku Gakkai Ronbunshu 2000, 17, 21–35. [Google Scholar] [CrossRef]
- Sediek, O.A.; El-Tawil, S. Impact of Earthquake-Induced Debris on the Seismic Resilience of Road Networks. In Proceedings of the 17th World Conference of Earthquake Engineering, Sendai, Japan, 13–18 September 2020. [Google Scholar]
- Zhang, F.; Wu, C.; Zhao, X.-L.; Li, Z.-X. Numerical derivation of pressure-impulse diagrams for square UHPCFDST columns. Thin-Walled Struct. 2017, 115, 188–195. [Google Scholar] [CrossRef]
- Nawar, M.T.; Arafa, I.T.; Elhosseiny, O.M. Numerical damage evaluation of perforated steel columns subjected to blast loading. Def. Technol. 2022, 18, 735–746. [Google Scholar] [CrossRef]
- El Khouri, I.; Garcia, R.; Mihai, P.; Budescu, M.; Taranu, N.; Toma, I.O.; Guadagnini, M.; Escolano-Margarit, D.; Entuc, I.S.; Oprisan, G.; et al. Behaviour of short columns made with conven-tional or FRP-confined rubberised concrete: An experimental and numerical investigation. Eng. Struct. 2024, 307, 117885. [Google Scholar] [CrossRef]
- Zhou, M.; Song, J.; Yin, S.; Zhu, G.; Lu, W.; Lee, G.C. Cyclic performance of severely earthquake-damaged RC bridge columns repaired using grouted UHPC jacket. Eng. Struct. 2023, 280, 115615. [Google Scholar] [CrossRef]
- Martins, A.D.; Gonçalves, R.; Camotim, D. Numerical simulation and design of stainless steel columns under fire conditions. Eng. Struct. 2021, 229, 111628. [Google Scholar] [CrossRef]
- Lorkowski, P.; Gosowski, B. Experimental and numerical research of the lateral buckling problem for steel two-chord columns with a single lacing plane. Thin-Walled Struct. 2021, 165, 107897. [Google Scholar] [CrossRef]
- Nikolić, Ž.; Živaljić, N.; Smoljanović, H.; Balić, I. Numerical modelling of reinforced-concrete structures under seismic loading based on the finite element method with discrete inter-element cracks. Earthq. Eng. Struct. Dyn. 2017, 46, 159–178. [Google Scholar] [CrossRef]
- Thiagarajan, G.; Kadambi, A.V.; Robert, S.; Johnson, C.F. Experimental and finite element analysis of doubly reinforced concrete slabs subjected to blast loads. Int. J. Impact Eng. 2015, 75, 162–173. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, H.; Wu, J.; Fang, Q. Experimental study on the residual seismic resistance of ultra high performance cementitious composite filled steel tube (UHPCC-FST) after contact explosion. Thin-Walled Struct. 2020, 154, 106852. [Google Scholar] [CrossRef]
- Blomfors, M.; GBerrocal, C.; Lundgren, K.; Zandi, K. Incorporation of pre-existing cracks in finite element analyses of reinforced concrete beams without transverse reinforcement. Eng. Struct. 2021, 229, 111601. [Google Scholar] [CrossRef]
- Seok, S.; Haikal, G.; Ramirez, J.A.; Lowes, L.N.; Lim, J. Finite element simulation of bond-zone behavior of pullout test of reinforcement embedded in concrete using concrete damage-plasticity model 2 (CDPM2). Eng. Struct. 2020, 221, 110984. [Google Scholar] [CrossRef]
- Nassr, A.A.; Razaqpur, A.G.; Tait, M.J.; Campidelli, M.; Foo, S. Strength and stability of steel beam columns under blast load. Int. J. Impact Eng. 2013, 55, 34–48. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Uy, B. Explosive testing and modelling of square tubular steel columns for near-field detonations. J. Constr. Steel Res. 2014, 101, 290–303. [Google Scholar] [CrossRef]
- Grimsmo, E.L.; Clausen, A.H.; Aalberg, A.; Langseth, M. A numerical study of beam-to-column joints subjected to impact. Eng. Struct. 2016, 120, 103–115. [Google Scholar] [CrossRef]
- Wang, F.; Yang, J.; Pan, Z. Progressive collapse behaviour of steel framed substructures with various beam-column connections. Eng. Fail. Anal. 2020, 109, 104399. [Google Scholar] [CrossRef]
- Heidarpour, A.; Bradford, M.A. Beam–column element for non-linear dynamic analysis of steel members subjected to blast loading. Eng. Struct. 2011, 33, 1259–1266. [Google Scholar] [CrossRef]
- Park, K.; Kim, H.; Kim, D. Generalized Finite Element Formulation of Fiber Beam Elements for Distributed Plasticity in Multiple Regions. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 146–163. [Google Scholar] [CrossRef]
- Pang, R.; Sun, Y.-Y.; Xu, Z.; Xu, K.; Cui, J.; Dang, L.-J. Shaking table test and numerical simulation of a precast frame-shear wall structure with innovative untopped precast concrete floors. Eng. Struct. 2024, 300, 117162. [Google Scholar] [CrossRef]
- Sha, H.; Chong, X.; Xie, L.; Huo, P.; Yue, T.; Wei, J. Seismic performance of precast concrete frame with energy dissipative cladding panel system: Half-scale test and numerical analysis. Soil Dyn. Earthq. Eng. 2023, 165, 107712. [Google Scholar] [CrossRef]
- Doeva, O.; Masjedi, P.K.; Weaver, P.M. Static deflection of fully coupled composite Timoshenko beams: An exact analytical solution. Eur. J. Mech. A/Solids 2020, 81, 103975. [Google Scholar] [CrossRef]
- Luo, Y. An Efficient 3D Timoshenko Beam Element with Consistent Shape Functions. Adv. Theor. Appl. Mech. 2008, 1, 95–106. [Google Scholar]
- Pokhrel, M.; Bandelt, M.J. Plastic hinge behavior and rotation capacity in reinforced ductile concrete flexural members. Eng. Struct. 2019, 200, 109699. [Google Scholar] [CrossRef]
- Park, G.-K.; Kwak, H.-G.; Filippou, F.C. Blast Analysis of RC Beams Based on Moment-Curvature Relationship Considering Fixed-End Rotation. J. Struct. Eng. 2017, 143, 04017104. [Google Scholar] [CrossRef]
- Liew, A.; Gardner, L.; Block, P. Moment-Curvature-Thrust Relationships for Beam-Columns. Structures 2017, 11, 146–154. [Google Scholar] [CrossRef]
- Li, W.; Ma, H. A nonlinear cross-section deformable thin-walled beam finite element model with high-order interpolation of warping displacement. Thin-Walled Struct. 2020, 152, 106748. [Google Scholar] [CrossRef]
- He, X.; Xiang, Y.; Chen, Z. Improved method for shear lag analysis of thin-walled box girders considering axial equilib-rium and shear deformation. Thin Wall Struct 2020, 151, 106732. [Google Scholar] [CrossRef]
- Qin, F.; Shigang, Y.; Li, C.; Jinchun, L.; Yadong, Z. Analysis on the building damage, personnel casualties and blast energy of the“8·12”explosion in Tianjin port. China Civ. Eng. J. 2017, 50, 12–18. [Google Scholar]
- Cannon, L.; Clubley, S.K. Structural response of simple partially-clad steel frames to long-duration blast loading. Structures 2021, 32, 1260–1270. [Google Scholar] [CrossRef]
- Lin, S.-C.; Yang, B.; Kang, S.-B.; Xu, S.-Q. A new method for progressive collapse analysis of steel frames. J. Constr. Steel Res. 2019, 153, 71–84. [Google Scholar] [CrossRef]
- Kumar, A.; Matsagar, V. Blast Fragility and Sensitivity Analyses of Steel Moment Frames with Plan Irregularities. Int. J. Steel Struct. 2018, 18, 1684–1698. [Google Scholar] [CrossRef]
- Denny, J.W.; Clubley, S.K. Long-duration blast loading & response of steel column sections at different angles of incidence. Eng. Struct. 2019, 178, 331–342. [Google Scholar] [CrossRef]
- Xing, Z.; Shen, Y.; Li, X. Performance analysis of grounded three-element dynamic vibration absorber. Chin. J. Theor. Appl. Mech. 2019, 51, 1466–1475. [Google Scholar]
- Zhan, F.; Li, M.; Yang, J.; Huang, W. The finite deformation theory and finite element formulation of plate and shell. Acta. Mech. Solida Sin. 2001, 22, 343–350. [Google Scholar]
- Hasheminejad, S.M.; Rezaei, S.; Shakeri, R. Flexural transient response of elastically supported elliptical plates under in-plane loads using Mathieu functions. Thin-Walled Struct. 2013, 62, 37–45. [Google Scholar] [CrossRef]
- DoD, U.S. Structures to Resist the Effects of Accidental Explosions UFC 3-340; National Institute of Building Sciences: Washington, DC, USA, 2008. [Google Scholar]
- Tyas, A.; Warren, J.A.; Bennett, T.; Fay, S. Prediction of clearing effects in far-field blast loading of finite targets. Shock. Waves 2011, 21, 111–119. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, Y.; Shi, Y. Numerical simulation of far-field blast loads arising from large TNT equivalent explosives. J. Loss Prev. Process. Ind. 2021, 70, 104432. [Google Scholar] [CrossRef]






| k | 0 | 1, 2 |
| ξk/ηk | 0 | ±0.7745966692 |
| Ak | 8/9 | 5/9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xia, S.; Li, H.; Shi, F.; Deng, E.-F.; Li, M. Planar Cross-Sectional Fitting of Structural Members to Numerical Simulation Results Obtained from Finite Element Models with Solid or Shell Elements. Buildings 2025, 15, 797. https://doi.org/10.3390/buildings15050797
Zhang X, Xia S, Li H, Shi F, Deng E-F, Li M. Planar Cross-Sectional Fitting of Structural Members to Numerical Simulation Results Obtained from Finite Element Models with Solid or Shell Elements. Buildings. 2025; 15(5):797. https://doi.org/10.3390/buildings15050797
Chicago/Turabian StyleZhang, Xuan, Shifa Xia, Huanchen Li, Fengwei Shi, En-Feng Deng, and Meng Li. 2025. "Planar Cross-Sectional Fitting of Structural Members to Numerical Simulation Results Obtained from Finite Element Models with Solid or Shell Elements" Buildings 15, no. 5: 797. https://doi.org/10.3390/buildings15050797
APA StyleZhang, X., Xia, S., Li, H., Shi, F., Deng, E.-F., & Li, M. (2025). Planar Cross-Sectional Fitting of Structural Members to Numerical Simulation Results Obtained from Finite Element Models with Solid or Shell Elements. Buildings, 15(5), 797. https://doi.org/10.3390/buildings15050797







