Numerical Simulation Analysis of Lead Rubber Bearings (LRBs) Damage and Superstructure Response Under Near-Fault Earthquakes †
Abstract
1. Introduction
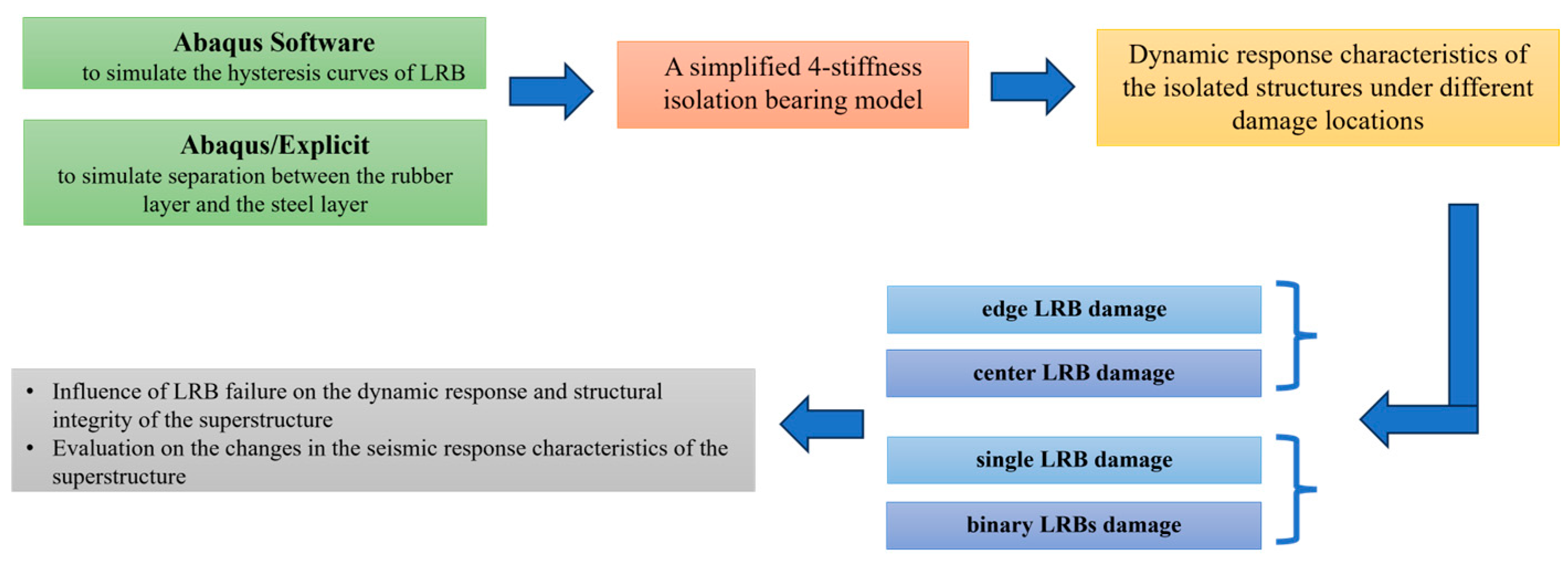
2. Materials and Methods: Finite Element Analysis Methodology for LRB Damage
2.1. Finite Element Model Parameters
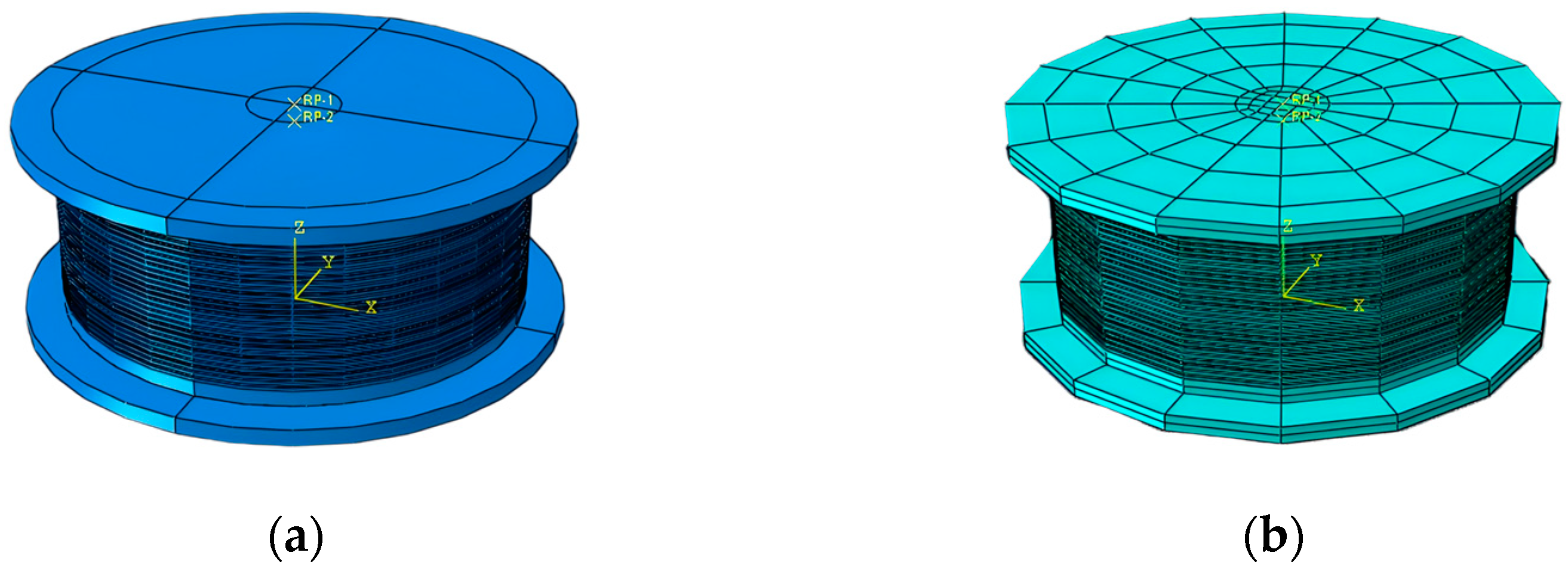
2.1.1. Unit Definition
2.1.2. Calculation Equation of Compressive Shear State
2.2. Material Selection and Parameters
2.3. Contact and Constraint Settings
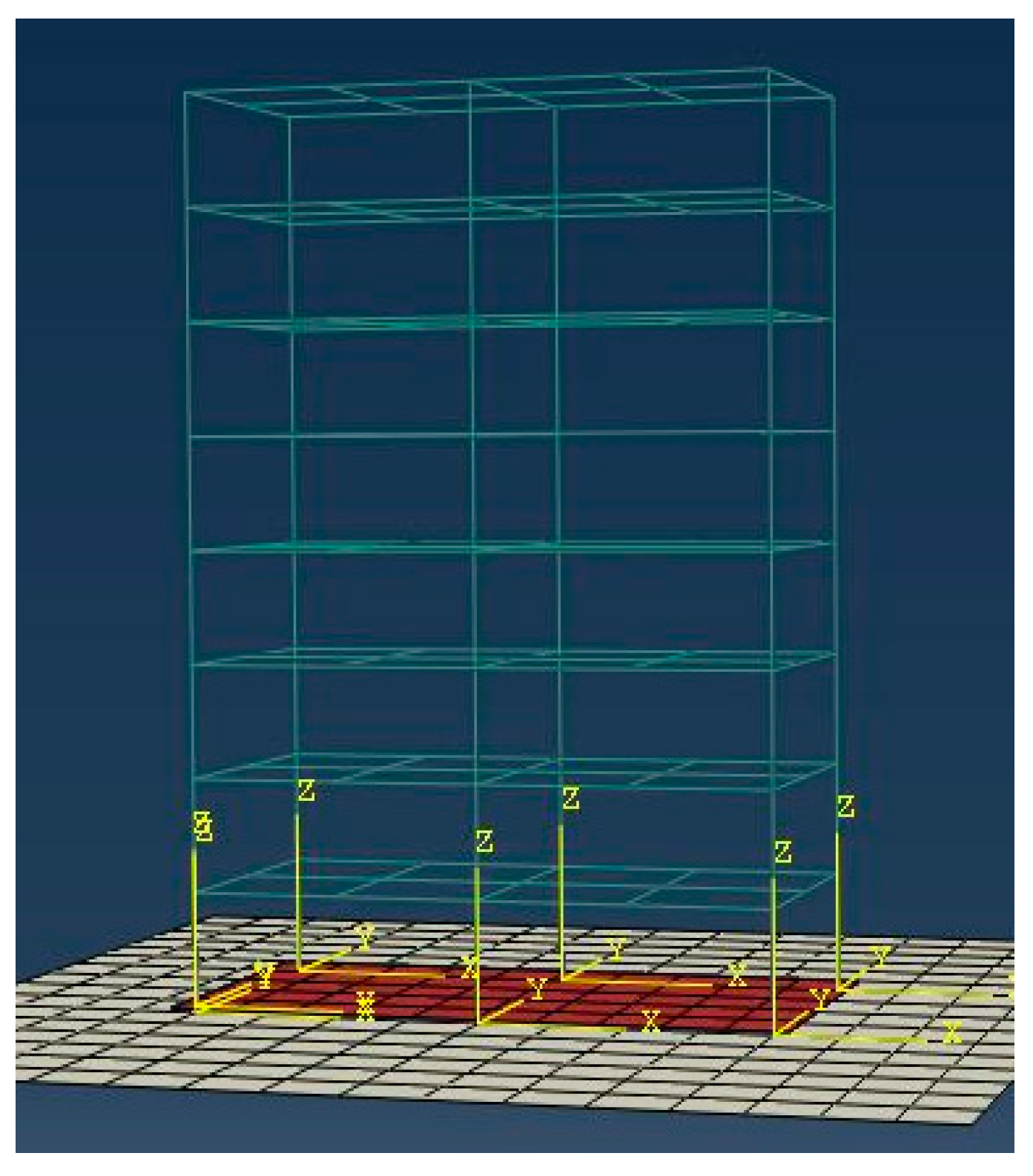
2.4. General Engineering Design
3. Results
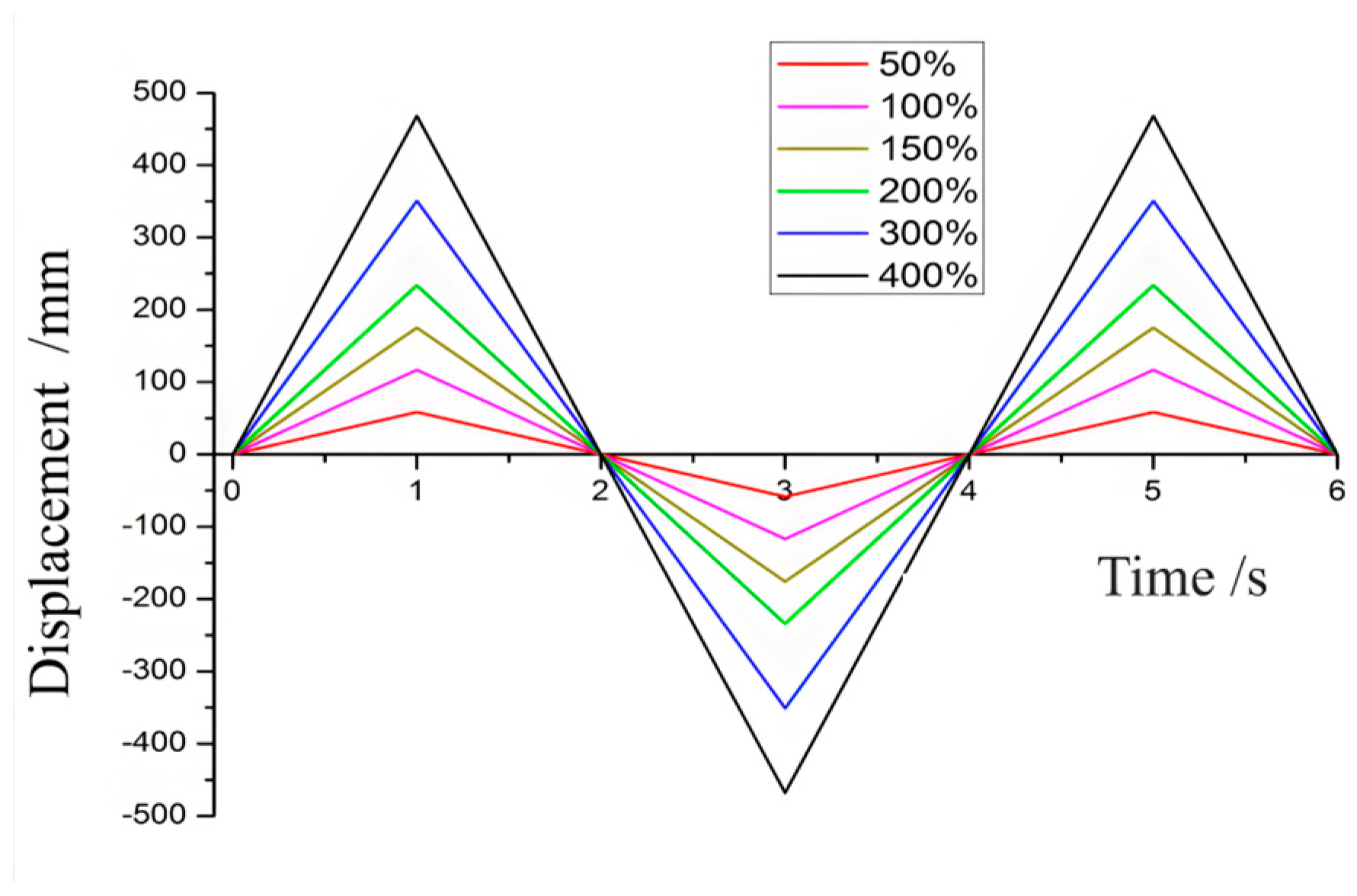
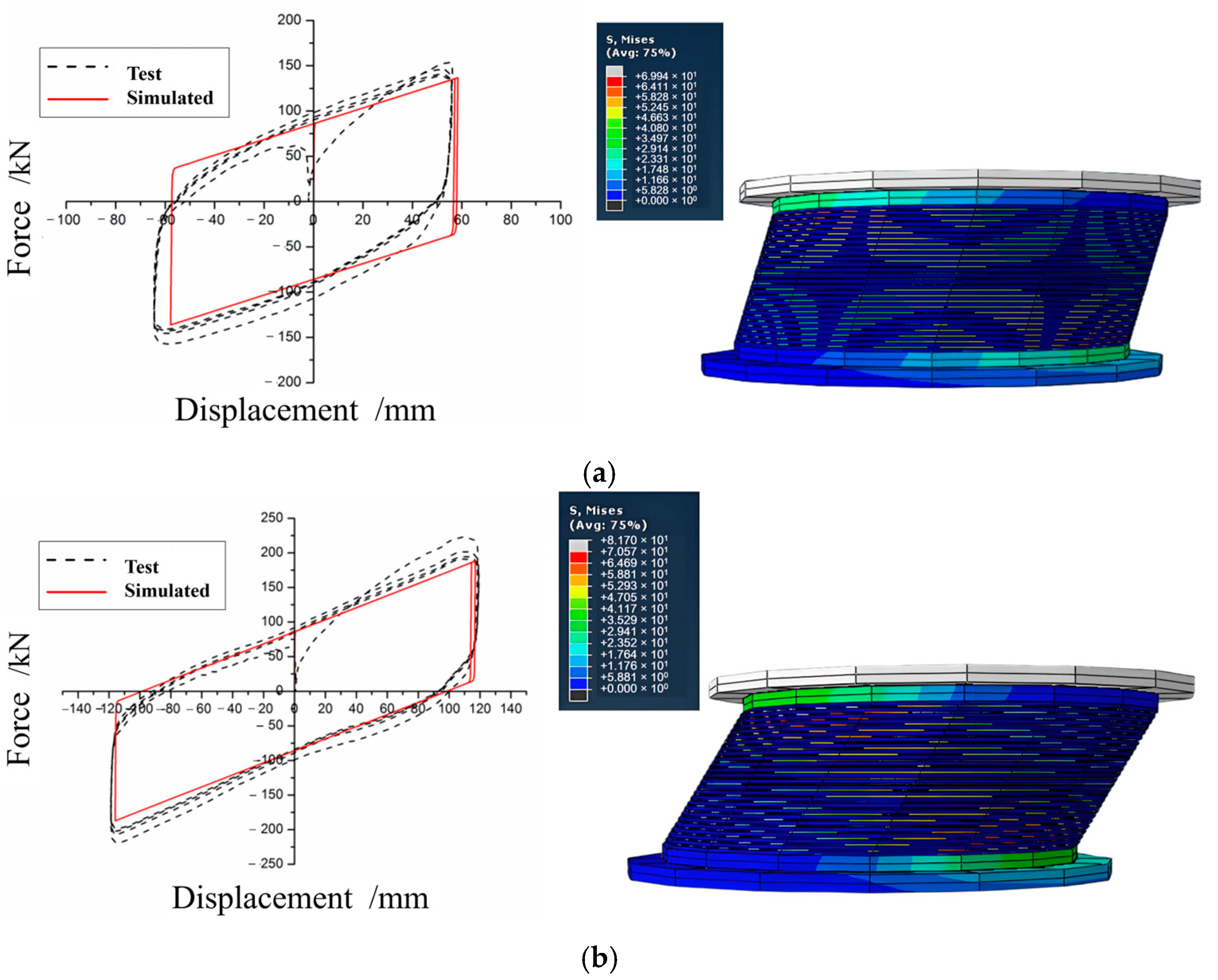
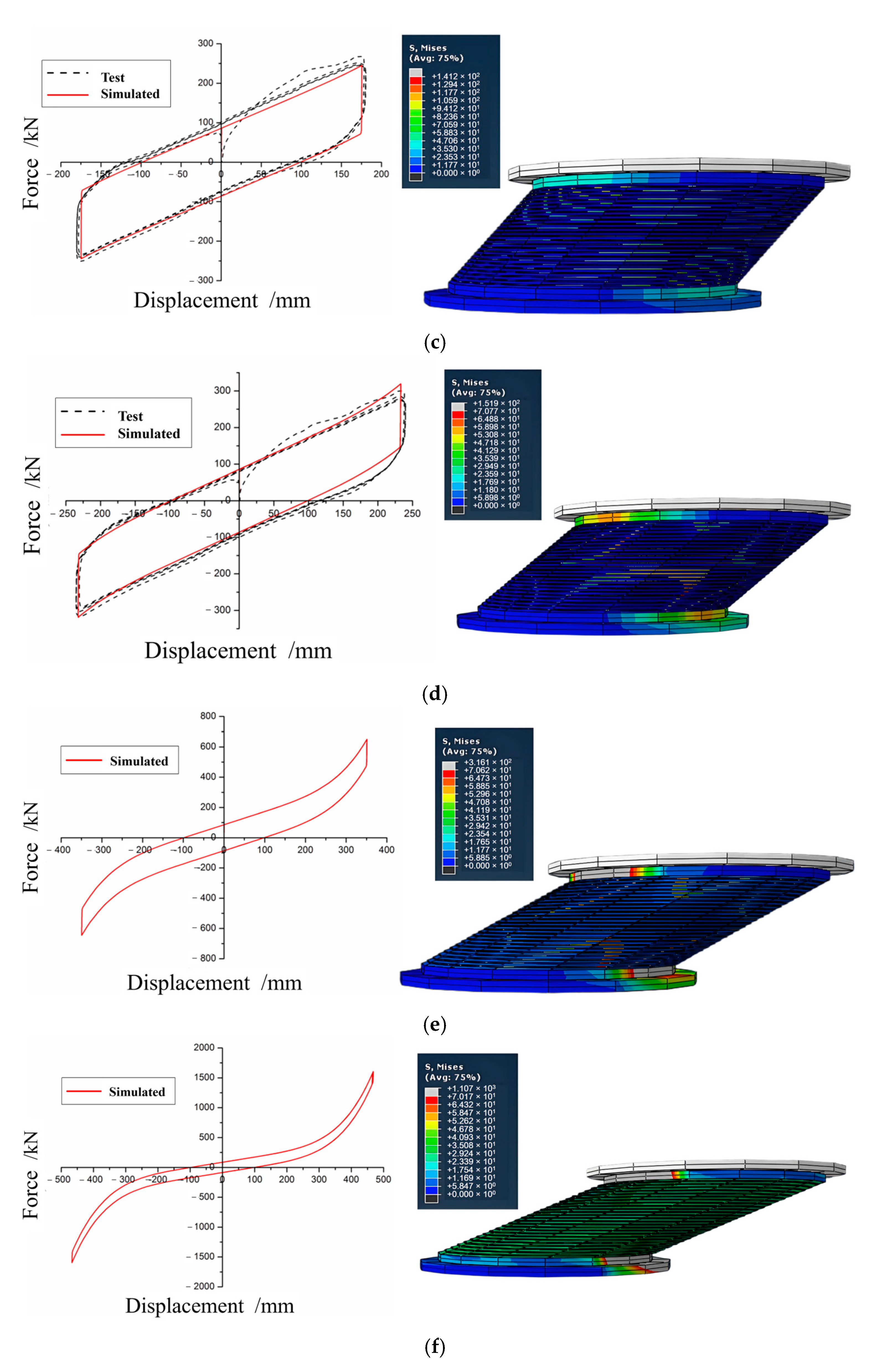
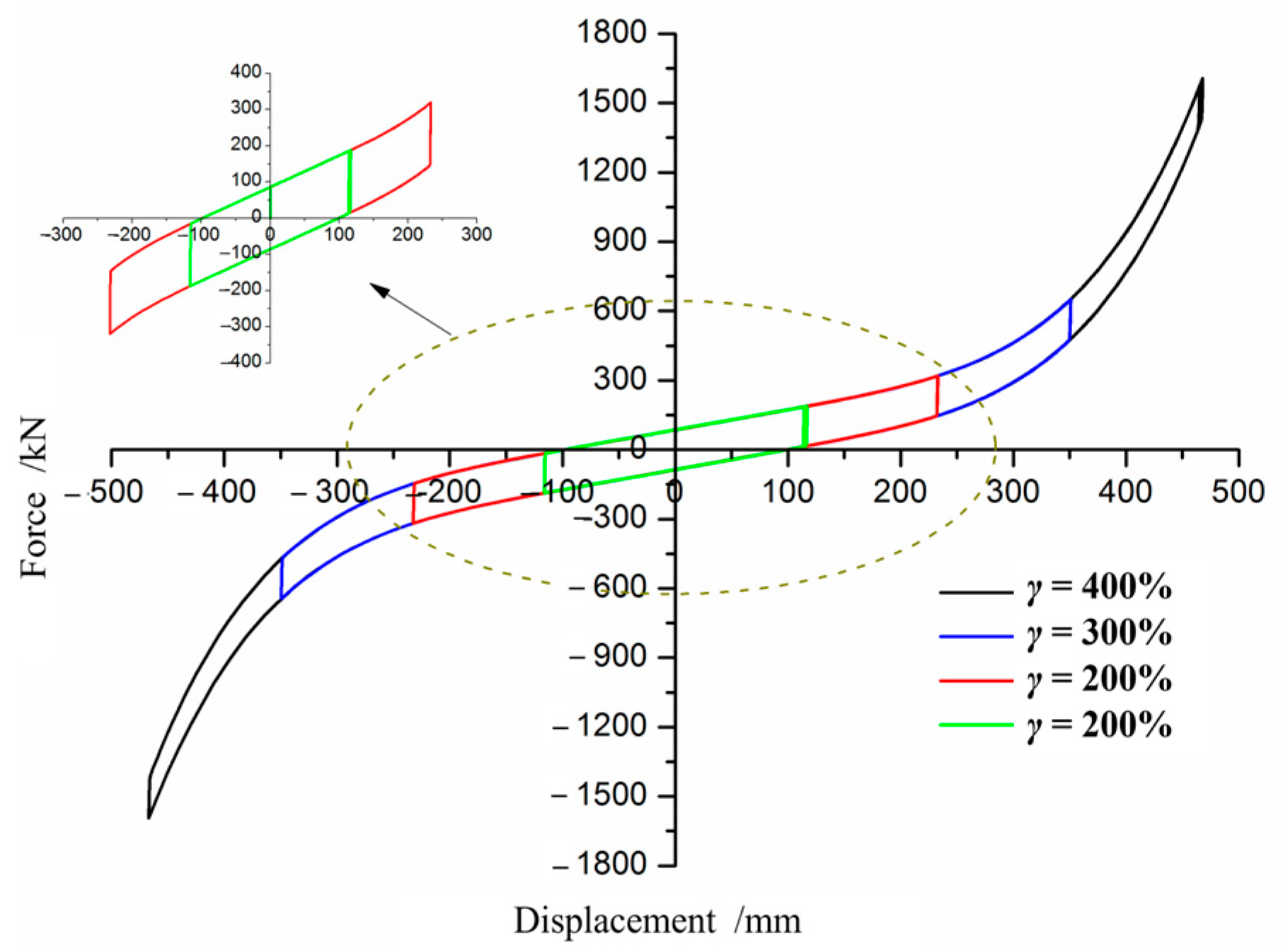
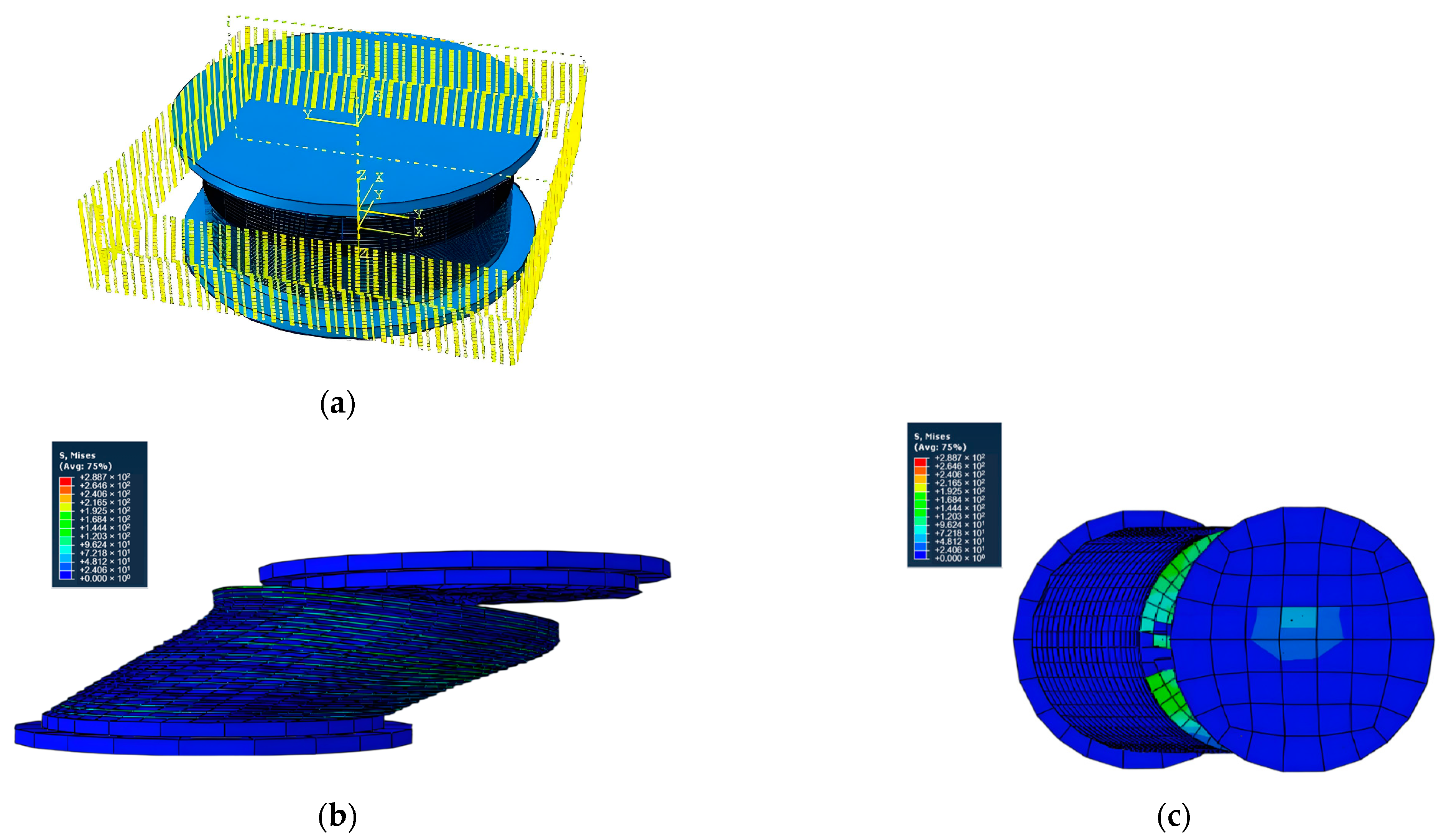
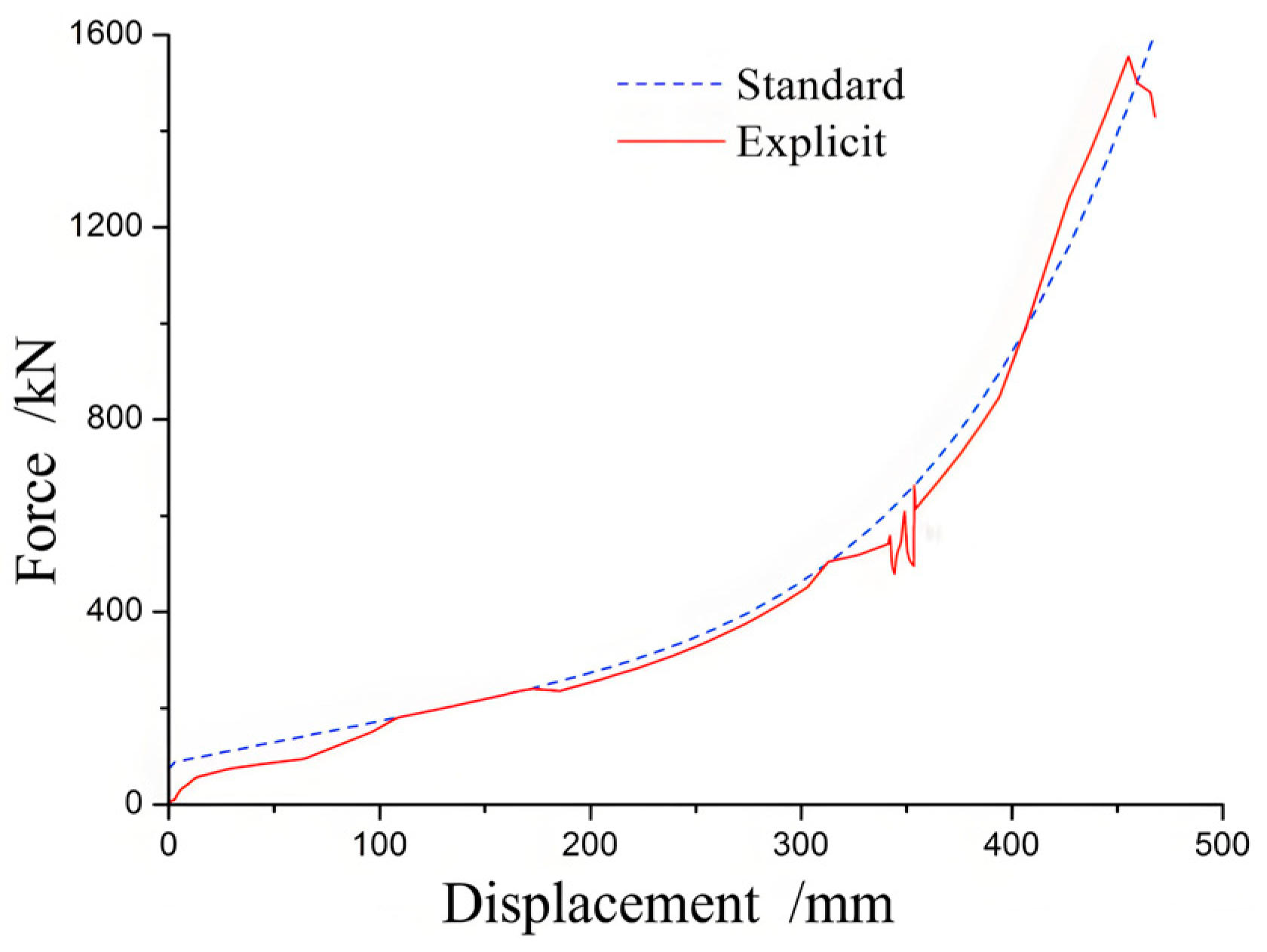
3.1. Finite Element Analysis Results of LRBs Under Compression Shear State
3.2. Numerical Simulation of LRB Damage
3.3. Analysis of the Impact of Damage to LRBs on the Superstructure
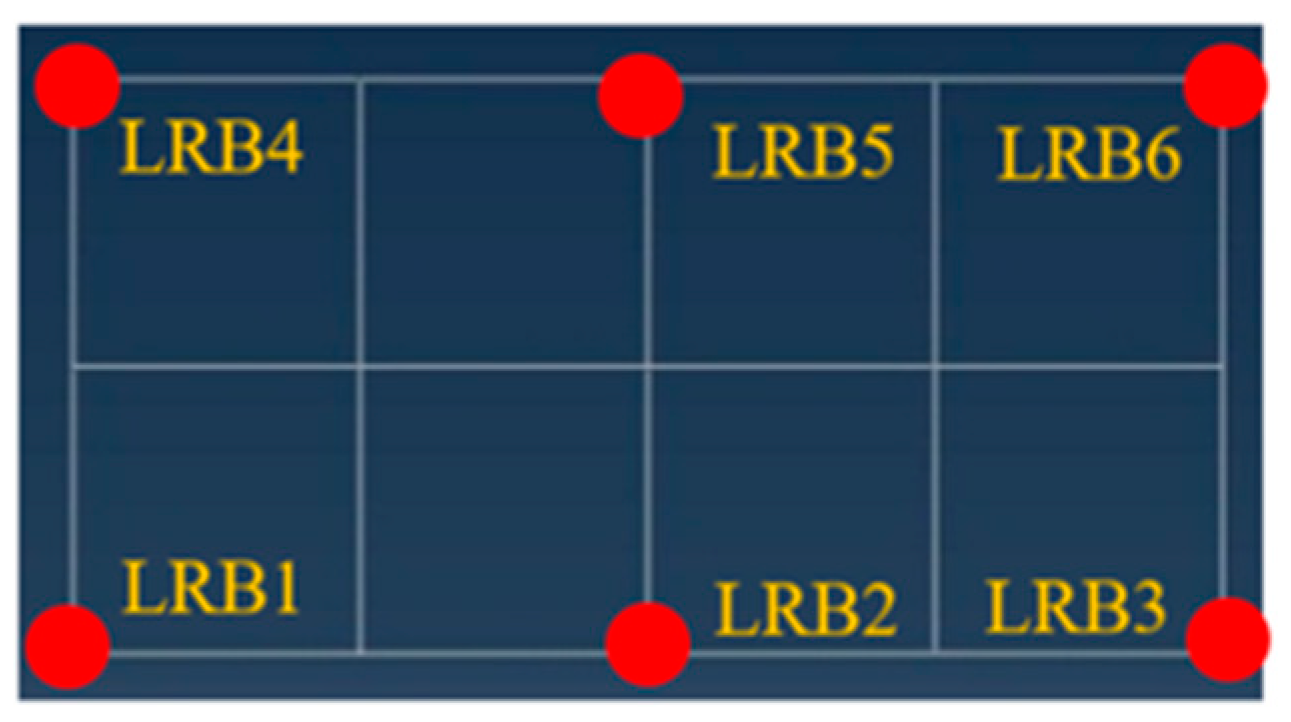
3.3.1. Working Condition
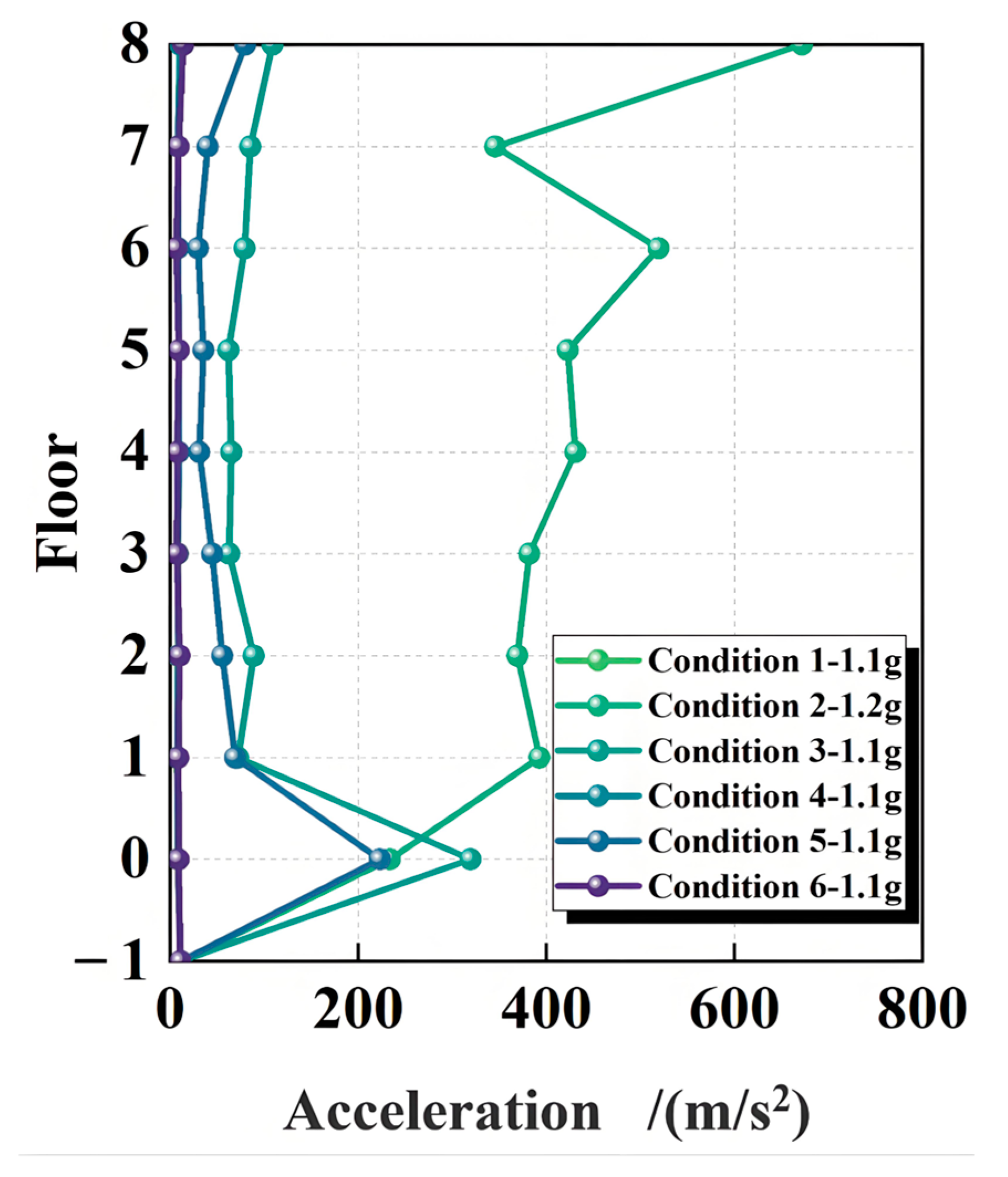
3.3.2. Peak Acceleration Results
3.3.3. Story Drift Results
4. Discussion
4.1. LRBs Under Compression Shear State
4.2. LRB Damage
4.3. Comparison of Peak Acceleration
4.4. Comparison of Story Drift
5. Conclusions
- (1)
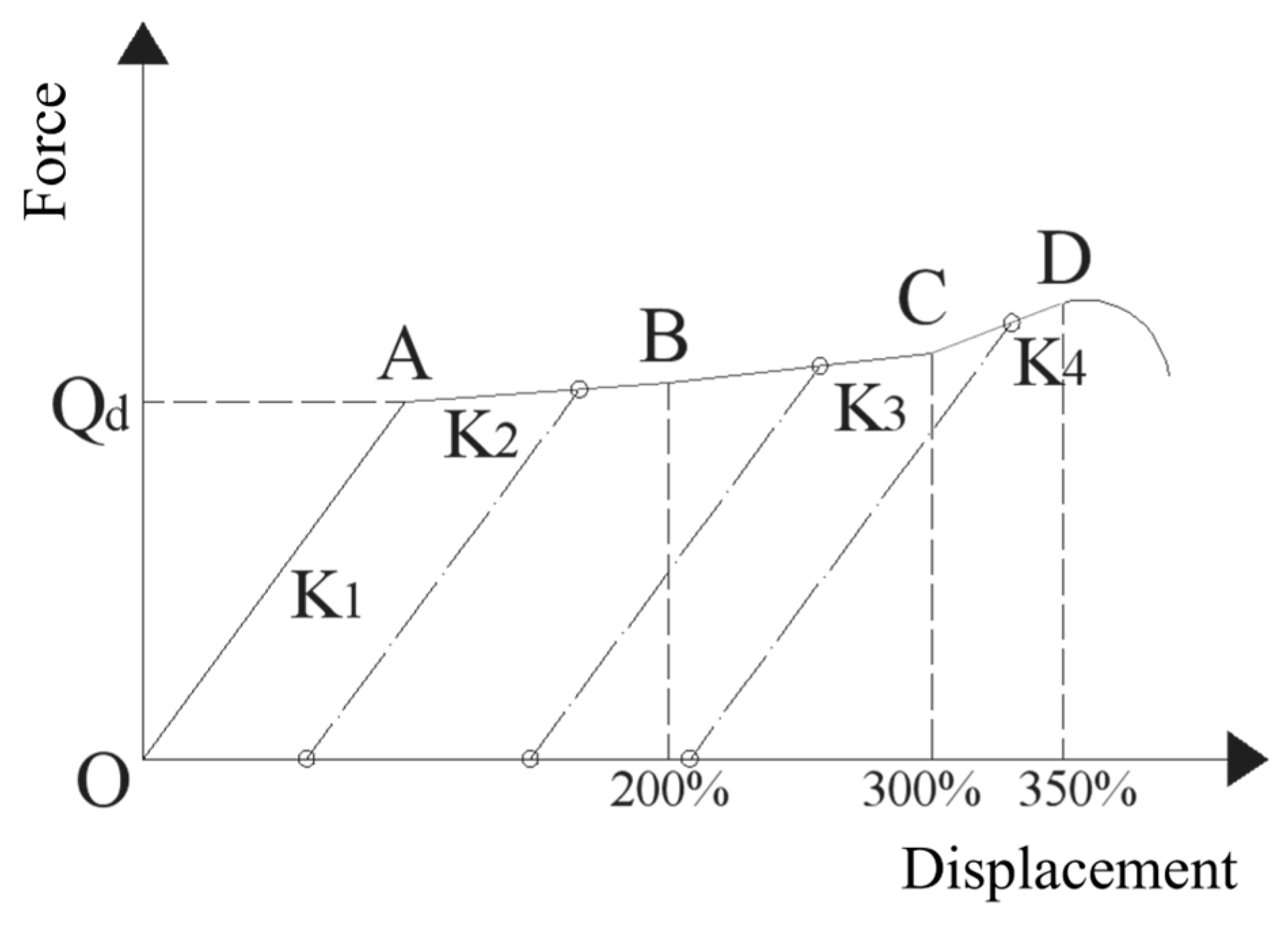
- The numerical simulation results show that under the compressive and shearing state, when the horizontal deformation of the isolator exceeds 300%, the stiffness enhancement section appears.
- (2)
- It is found that in comparison with seismic isolation structure without any damage, the damage of all LRBs show the most significant scale-up effect on acceleration. Edge-bearing damage shows greater damage than the center position. For edge bearing, the single edge damage shows more powerful damage than binary. In the center position, the damage effect shows the reverse effect.
- (3)
- The seismic isolation structure damage on story drift was simulated. Similar to the effect on acceleration, the edge-bearing damage is larger than the center position damage. While for edge and center position bearings, the single edge bearing also shows a larger story drift than binary.
- (4)
- For finite element analysis, it is found that the polynomial model performs better than the traditional Mooney–Rivlin (MR) model in the simulation of rubber reinforcement during the large deformation of LRBs. To simulate more accurately, it is recommended to use the tie element and select the reasonable parameters to deal with the bond between the rubber layer and the steel plate. If the appropriate accuracy is selected, the hysteresis performance of the lead rubber bearing in large horizontal deformations could be simulated with accepted accuracy, which fits well with the experimental data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dora, F. Response of frames seismically protected with passive systems in near-field areas. Int. J. Struct. Eng. 2014, 5, 326–345. [Google Scholar]
- Mavroeidis, G.P. A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 2003, 93, 1099–1131. [Google Scholar] [CrossRef]
- Dora, F. On the seismic response of protected and unprotected middle-rise steel frames in far-field and near-field areas. Shock. Vib. 2014, 2014, 393870. [Google Scholar]
- Jitendra, G.; Kumar, G.P. Comparative analysis of T-shaped base isolated building under far-fault and near-fault earthquake. Asian J. Civ. Eng. Build. Hous. 2024, 25, 2333–2344. [Google Scholar]
- ASCE. Post-Earthquake Damage Assessment. In Guidelines for Seismic Evaluation & Design of Petrochemical Facilities; ASCE: Reston, VA, USA, 2011. [Google Scholar]
- Weni, L.; Loh, C.; Wan, S. Dynamic responses of bridges subjected to near-fault ground motions. J. Chin. Inst. Eng. 2020, 23, 455–464. [Google Scholar]
- Fulin, Z. Seismic Control of Engineering Structures; Earthquake Publishing House: Beijing, China, 1997; pp. 2–16. [Google Scholar]
- Robinson, W.H. Lead-rubber hysteretic bearings suitable for protecting structures during earthquakes. Earthq. Eng. Struct. Dynamics 1982, 10, 593–604. (In Chinese) [Google Scholar] [CrossRef]
- Wenfu, H.; Wenguang, L.; Da, H. Flat ring phenomenon and restoring force model of hysteresis curve of lead rubber bearings. J. Zhengzhou Univ. 2006, 27, 71–74. (In Chinese) [Google Scholar]
- Wenguang, L.; Fulin, Z. Basic mechanical properties of lead core laminated rubber isolation. Earthq. Eng. Eng. Vib. 1999, 19, 93–99. (In Chinese) [Google Scholar]
- Tsai, H.C. Dynamic analysis of base-isolated shear beams bumping against stops. Earthq. Eng. Struct. Dyn. 1997, 26, 515–528. [Google Scholar] [CrossRef]
- Malhotra, P.K. Dynamics of seismic impacts in base-isolated buildings. Earthq. Eng. Struct. Dyn. 1997, 26, 797–813. [Google Scholar] [CrossRef]
- Yang, D.X.; Li, G.; Cheng, G.D. Seismic analysis of base-isolated structures subjected to near-fault pulse-like ground motions. Earthq. Eng. Eng. Vib. 2005, 25, 119–124. (In Chinese) [Google Scholar]
- Yunfei, X.; Yang, L.; Wenfu, H. Research on damage control of isolation systems under near fault earthquakes. Vib. Impact 2018, 37, 183–189+216. (In Chinese) [Google Scholar]
- Jiao, Y. Damage Modes and Control of Isolated Structures Under Near Fault Earthquake Action. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2019. (In Chinese). [Google Scholar]
- Junjie, C. Seismic Response Analysis and Isolation Effect Study of RC Frame Structures Under Multidimensional Near-Field Earthquake Action. Ph.D. Thesis, North University of China, Taiyuan, China, 2021. (In Chinese). [Google Scholar]
- Heaton, T.H.; Hall, J.F.; Wald, D.J. Response of High-rise and Base Isolated Buildings to a Hypothetical MW 7∙0 Blind Thrust Earthquake. Science 1995, 267, 206–211. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.X.; Li, G.; Cheng, G.D. Integrated Dynamic optimum design of base-isolated structure subjected to near-fault pulse-like ground motions. J. Build. Struct. 2006, 27, 42–49. (In Chinese) [Google Scholar]
- Yuxiang, W.; Kun, Y.; Boyu, Z. Seismic performance analysis of base-isolated Structures based on the direct design method under Extreme earthquakes: A case study of 2023 Turkey earthquake. Eng. Mech. 2024, S1, 104–111. (In Chinese) [Google Scholar]
- Yuhong, M.; Guifeng, Z.; Ning, Z.H. Static performance correction of lead rubber isolation bearings based on earthquake simulation vibration table test. Earthq. Eng. Eng. Vib. 2019, 39, 78–85. [Google Scholar]
- Mingjun, Z.; Wenjing, W.; Zhengnan, C.; Lijun, W. Determination of Mechanical Constants of Rubber Mooney-Rivlin Model. Rubber Ind. 2003, 50, 263–265. [Google Scholar]
- Meng, L. Determination of Material Constants of Rubber Mooney-Rivlin Model. Rubber Ind. 2011, 58, 241–245. [Google Scholar]
- Zhixiong, Y.; Li, L.; Sufei, N.; Yicheng, J. Explicit Finite Element Study of Mechanical Parameters of Lead-rubber Bearing. Earthq. Resist. Eng. Retrofit. 2006, 28, 53–60. (In Chinese) [Google Scholar]
- Lichu, F. Bridge Seismic Resistance; Tongji University Press: Shanghai, China, 2001; pp. 35–36. (In Chinese) [Google Scholar]
- Ministry of Housing and Urban-Rural Development. Standard for Seismic Isolation Design of Buildings GB/T 51408-2021; China Planning Press: Beijing, China, 2021.
- Yue, R.; Ruidong, W.; Wenguang, L.; Wenfu, H. Numerical Simulation Analysis of Collapse Process of Isolated Structure in Strong Earthquakes. In Proceedings of the ICAEER Advances in Energy and Environment Research Conference, Guilin, China, 10–12 August 2018; p. 02017. [Google Scholar]
- Wenguang, L. Recommendation for the Design of Base Isolated Buildings; Earthquake Publishing House: Beijing, China, 2006; pp. 137–140. (In Chinese) [Google Scholar]
- Endo, M.; Uryu, M.; Imazuka, Y.; Yamazaki, T.; Yoshida, S.; Nakanishi, R. Fragility Evaluation of Base-Isolated Building Part1: Evaluation of Fragility Curve Considering Bumping Against Retaining Wall; Architectural Institute of Japan: Tokyo, Japan, 2007; Volume 30, pp. 941–942. [Google Scholar]
- Manabu, L. Fragility Evaluation of Base-Isolated Building Part2: Evaluation of Fragility Curve Considering Bumping Against Retaining Wall; Architectural Institute of Japan: Tokyo, Japan, 2007; Volume 30, pp. 943–944. [Google Scholar]
- Zhijian, H. Research on Seismic Response Calculation Method for Seismic and Isolation Structures Based on Random Vibration Time Domain Explicit Method. Ph.D. Thesis, South China University of China, Guangzhou, China, 2019. (In Chinese). [Google Scholar]
- Zhuo, Z. Finite Element Analysis and Application Based on Abaqus; Tsinghua University Press: Beijing, China, 2009; pp. 56–59. (In Chinese) [Google Scholar]
- Asgarkhani, N.; Kazemi, F.; Jankowski, R. Machine learning-based prediction of residual drift and seismic risk assessment of steel moment-resisting frames considering soil-structure interaction. Comput. Struct. 2003, 289, 107181. [Google Scholar] [CrossRef]




| Model | Diameter mm | Lead Diameter mm | Internal Rubber Materials n·tr/mm | Internal Steel Plate n·ts/mm | Height in Total mm | S1 | S2 |
|---|---|---|---|---|---|---|---|
| LRB600 | 600 | 120 | 26 × 4.5 mm = 117 | 25 × 3 mm = 75 | 276 | 33.33 | 5.13 |
| Rubber Model | C10 MPa | C01 MPa | C20 MPa | C11 MPa | C02 MPa | C30 MPa | C21 MPa | C12 MPa | C03 MPa |
|---|---|---|---|---|---|---|---|---|---|
| Polynomial | 0.193407 | −0.0001449 | −0.0008073 | 0.0001794 | −0.00000345 | 0.00069279 | 0.193407 | 0.0001794 | −0.00000345 |
| Material | Elastic Modulus GPa | Poisson’s Ratio | Yield Stress Mpa | Tangent Modulus Mpa |
|---|---|---|---|---|
| Steel plate | 206.00 | 0.30 | 235.0 | 0 |
| Lead | 16.46 | 0.44 | 13.5 | 0 |
| Type | Section Size mm × mm | Material | Strength Grade | Elastic Modulus GPa |
|---|---|---|---|---|
| Frame beam | 400 × 850 | concrete | C30 | 30 |
| Secondary beam | 400 × 750 | concrete | C30 | 30 |
| Frame column | 600 × 600 | concrete | C30 | 30 |
| Type | Quantity | Axial Force kN | Surface Pressure MPa | Yield Force kN | Post-Yielding Stiffness kN/mm | Vertical Compression Stiffness kN/mm | Vertical Tensile Stiffness kN/mm |
|---|---|---|---|---|---|---|---|
| LRB400 | 4 | 596.65 | 4.75 | 42.724 | 0.848 | 1816.300 | 233.150 |
| LRB400 | 2 | 827.21 | 6.58 | 42.724 | 0.848 | 1816.300 | 233.150 |
| Type | A (Elastic Stage) | B (Yielding Stage) | C (First Reinforcement Stage) | D (Second Reinforcement Stage) |
|---|---|---|---|---|
| Force/kN | 42.724 | 176.083 | 278.568 | 449.375 |
| Displacement (mm) | 3.877 | 161.200 | 241.800 | 282.100 |
| Type | K1 | K2 | K3 | K4 |
| Stiffness (kN/mm) | 11.019 | 0.848 | 1.272 | 4.238 |
| Working Condition | Peak Acceleration | Failure Bearing | Failure Location | Horizontal Deformation |
|---|---|---|---|---|
| 1 | 1.1g | none | no | 300–350% |
| 2 | 1.2g | all | whole | >350% |
| 3 | 1.1g | 1 | edge | >350% |
| 4 | 1.1g | 2 | center | >350% |
| 5 | 1.1g | 1, 4 | edge | >350% |
| 6 | 1.1g | 2, 5 | center | >350% |
| Working Condition | Peak Acceleration of Each Floor/(m/s2) | ||||
|---|---|---|---|---|---|
| −1F (Ground) | 0F (−Isolation Layer) | 1F | 2F | 3F | |
| 1 | 11.00 | 8.09 | 7.53 | 8.42 | 8.53 |
| 2 | 12.00 | 233.87 | 392.76 | 369.24 | 381.96 |
| 3 | 11.00 | 319.54 | 72.45 | 89.00 | 63.15 |
| 4 | 11.00 | 8.73 | 7.34 | 9.22 | 8.04 |
| 5 | 11.00 | 223.03 | 69.30 | 55.66 | 44.72 |
| 6 | 11.00 | 9.16 | 8.73 | 10.34 | 7.40 |
| Working condition | Peak acceleration of each floor/(m/s2) | ||||
| 4F | 5F | 6F | 7F | 8F | |
| 1 | 9.50 | 9.45 | 8.48 | 8.30 | 10.62 |
| 2 | 430.99 | 422.83 | 519.38 | 345.81 | 672.03 |
| 3 | 65.13 | 62.28 | 79.26 | 85.43 | 108.96 |
| 4 | 9.50 | 9.45 | 8.48 | 8.30 | 10.78 |
| 5 | 31.13 | 35.77 | 29.75 | 40.19 | 79.94 |
| 6 | 7.85 | 9.29 | 6.89 | 9.08 | 13.99 |
| Working Condition | Story Drift of Each Floor/mm | |||||
|---|---|---|---|---|---|---|
| −1–0F (Ground-Isolation Layer) | 0–1F (Isolation Layer-1F) | 1–2F | 2–3F | |||
| 1 | 275.59 | 8.59 | 16.35 | 18.19 | ||
| 2 | 332.56 | 24.36 | 17.21 | 25.06 | ||
| 3 | 294.95 | 8.88 | 17.67 | 20.37 | ||
| 4 | 293.64 | 7.77 | 15.92 | 18.98 | ||
| 5 | 305.94 | 17.88 | 29.80 | 35.17 | ||
| 6 | 297.34 | 8.13 | 15.35 | 18.13 | ||
| Working condition | Story drift of each floor/mm | |||||
| 3–4F | 4–5F | 5–6F | 6–7F | 7–8F | ||
| 1 | 18.29 | 17.00 | 14.87 | 11.49 | 7.92 | |
| 2 | 22.80 | 21.15 | 20.69 | 18.38 | 22.24 | |
| 3 | 19.50 | 17.18 | 15.68 | 14.32 | 12.87 | |
| 4 | 18.62 | 16.80 | 14.87 | 11.49 | 7.92 | |
| 5 | 34.66 | 31.87 | 30.26 | 29.12 | 27.87 | |
| 6 | 17.48 | 16.80 | 15.20 | 12.19 | 8.47 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Wang, R.; He, W.; Liu, W. Numerical Simulation Analysis of Lead Rubber Bearings (LRBs) Damage and Superstructure Response Under Near-Fault Earthquakes. Buildings 2025, 15, 839. https://doi.org/10.3390/buildings15050839
Ren Y, Wang R, He W, Liu W. Numerical Simulation Analysis of Lead Rubber Bearings (LRBs) Damage and Superstructure Response Under Near-Fault Earthquakes. Buildings. 2025; 15(5):839. https://doi.org/10.3390/buildings15050839
Chicago/Turabian StyleRen, Yue, Ruidong Wang, Wenfu He, and Wenguang Liu. 2025. "Numerical Simulation Analysis of Lead Rubber Bearings (LRBs) Damage and Superstructure Response Under Near-Fault Earthquakes" Buildings 15, no. 5: 839. https://doi.org/10.3390/buildings15050839
APA StyleRen, Y., Wang, R., He, W., & Liu, W. (2025). Numerical Simulation Analysis of Lead Rubber Bearings (LRBs) Damage and Superstructure Response Under Near-Fault Earthquakes. Buildings, 15(5), 839. https://doi.org/10.3390/buildings15050839





