Impact of Moisture Migration on Heat Transfer Performance at Vertical Joints of ‘One-Line’ Sandwich Insulation Composite Exterior Walls
Abstract
1. Introduction
2. Model Description of Thermal–Humidity Coupling Transfer
2.1. Mathematical Model
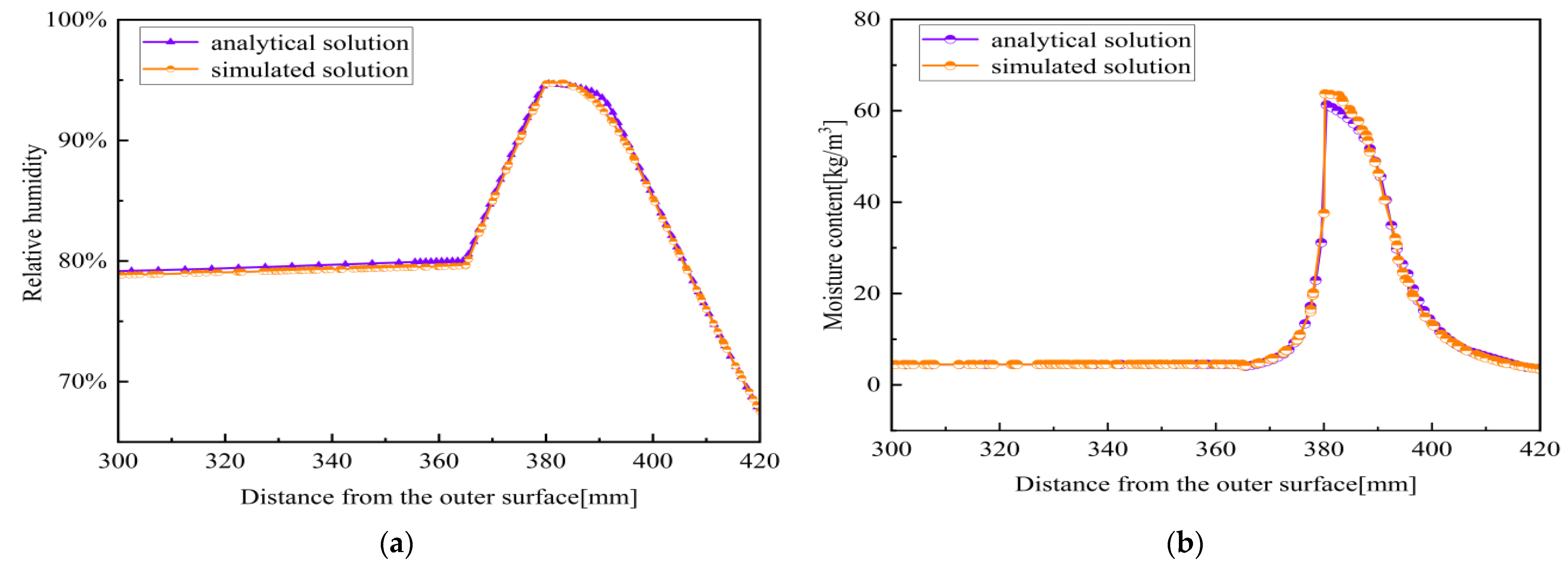
2.2. Model Verification
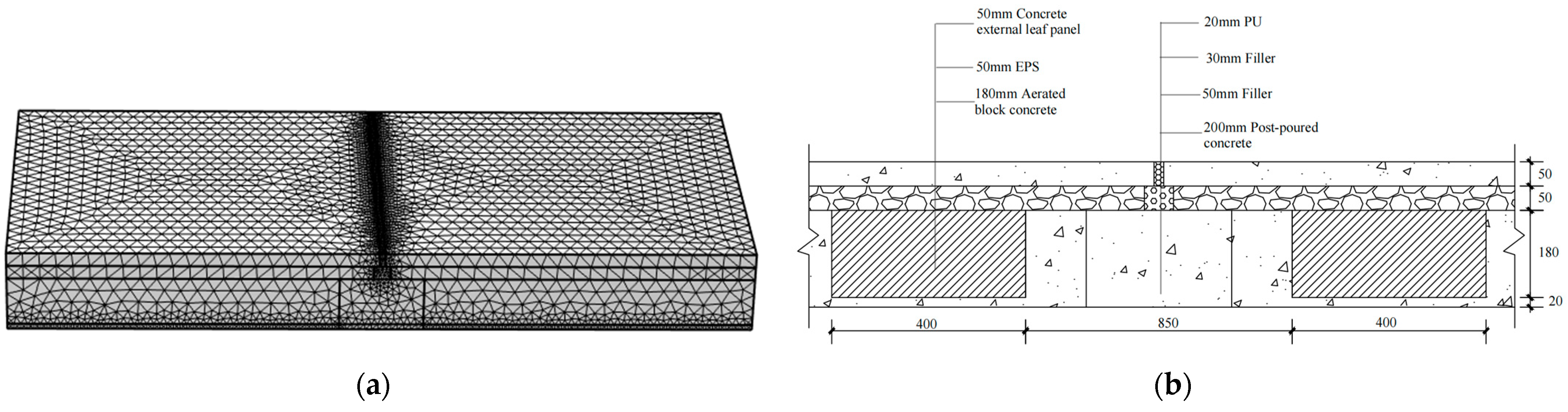
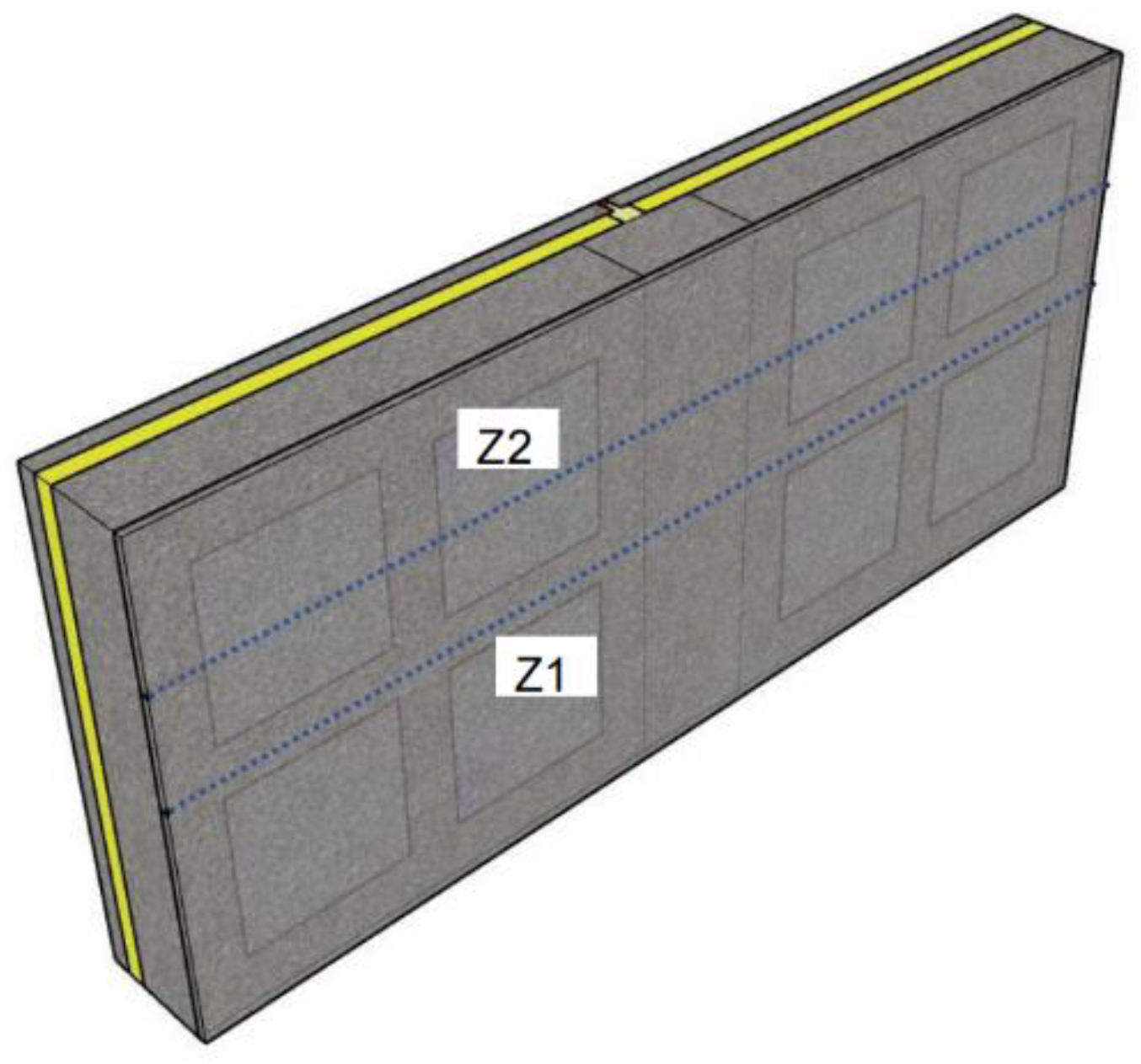
2.3. Physical Model
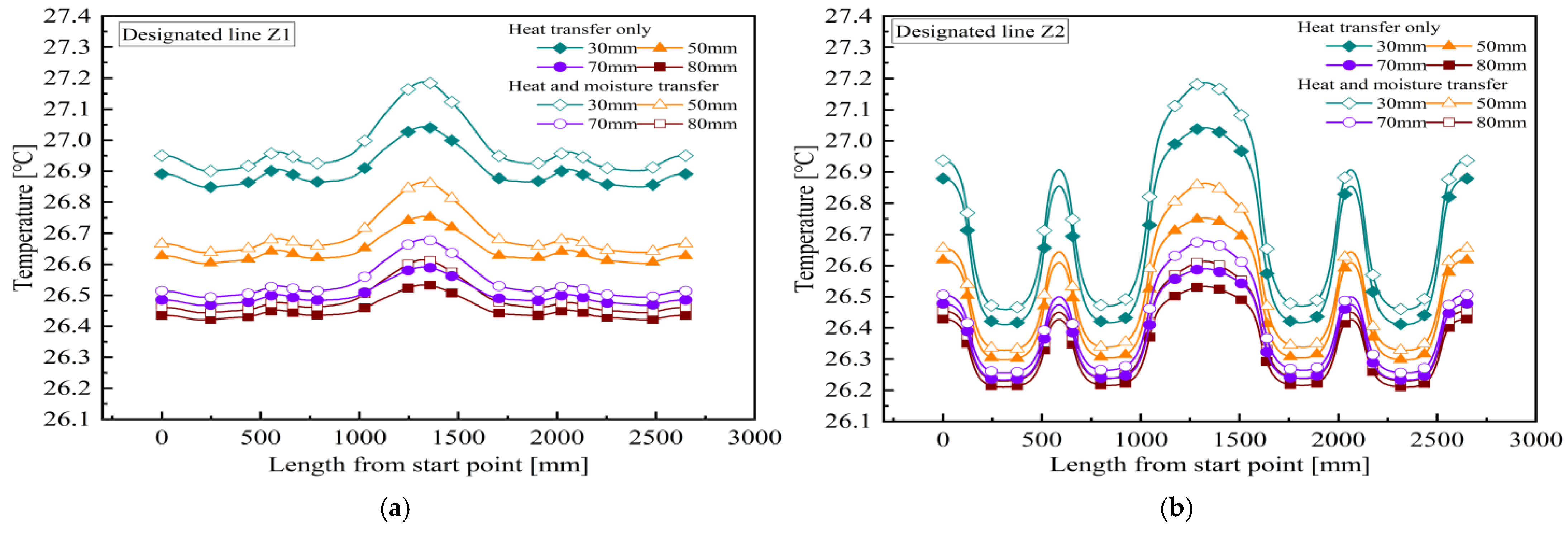
3. The Effect of Moisture Transfer on the Thermal Efficiency of Joints in ‘One-Line’ Sandwich Insulation Composite Walls
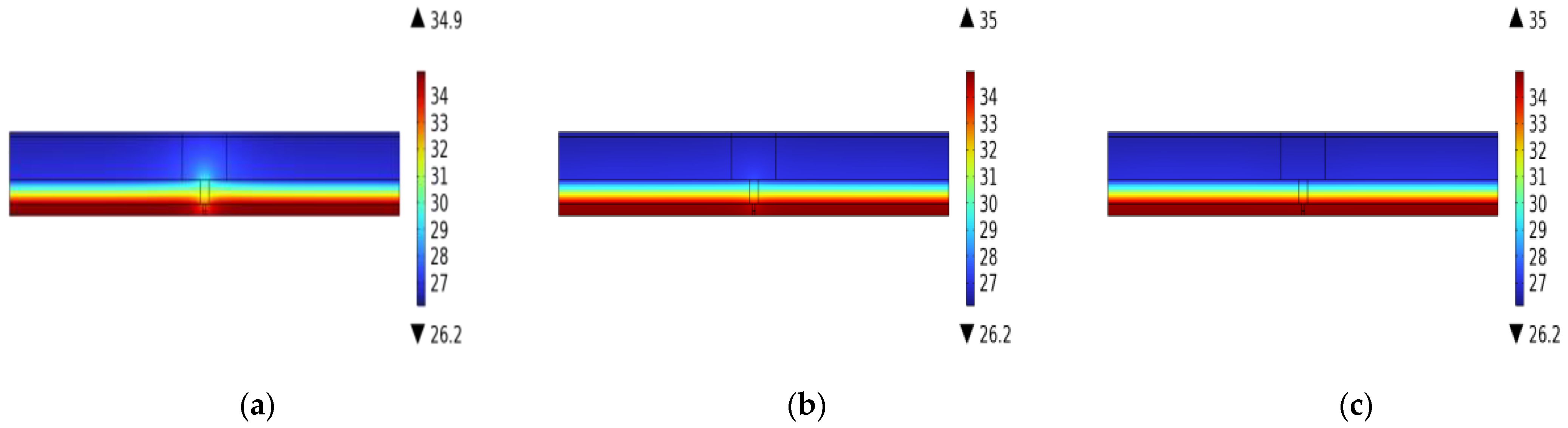
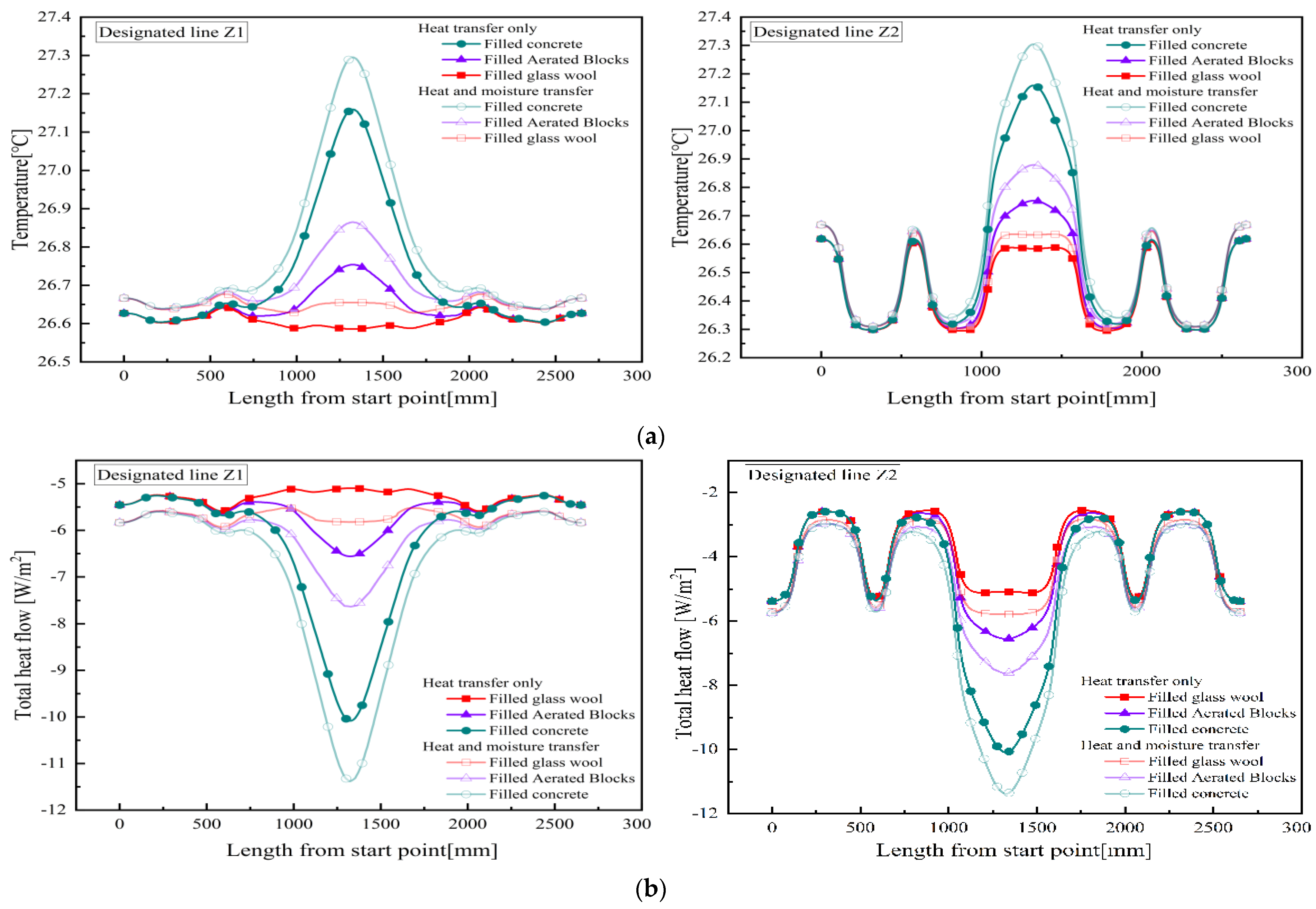
3.1. Effect of Wall Thermal Performance Using Different Fillers in Joints
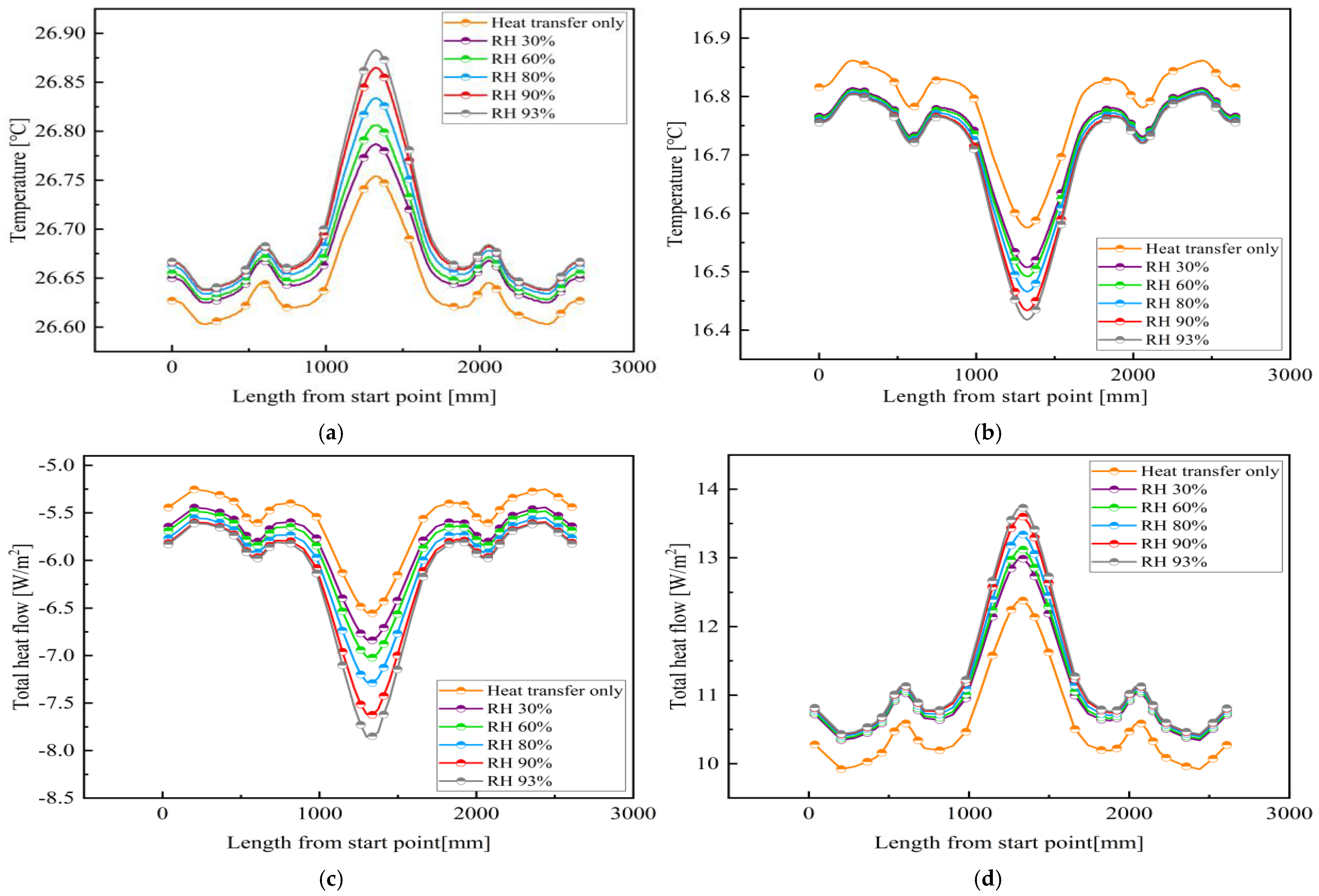
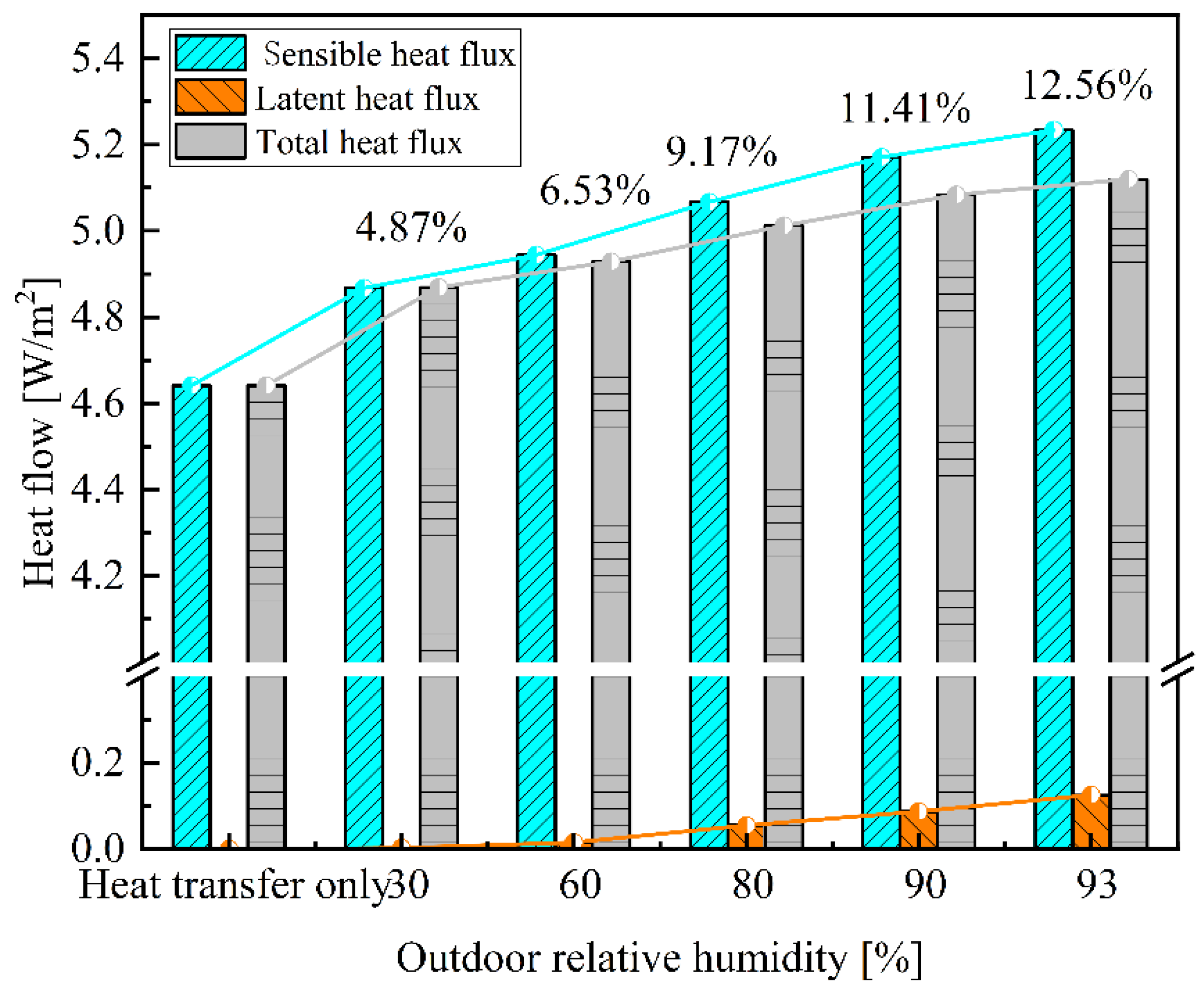
3.2. Impact of Outdoor Working Conditions on Wall Thermal Performance
- High temperature in summer:
- B.
- Low temperature in winter:
3.3. Impact of Insulation Layer Thickness on Wall Thermal Performance
4. Average Heat Transfer Coefficient and Correction for ‘One-Line’ Sandwich Insulation Composite Wall
5. Conclusions
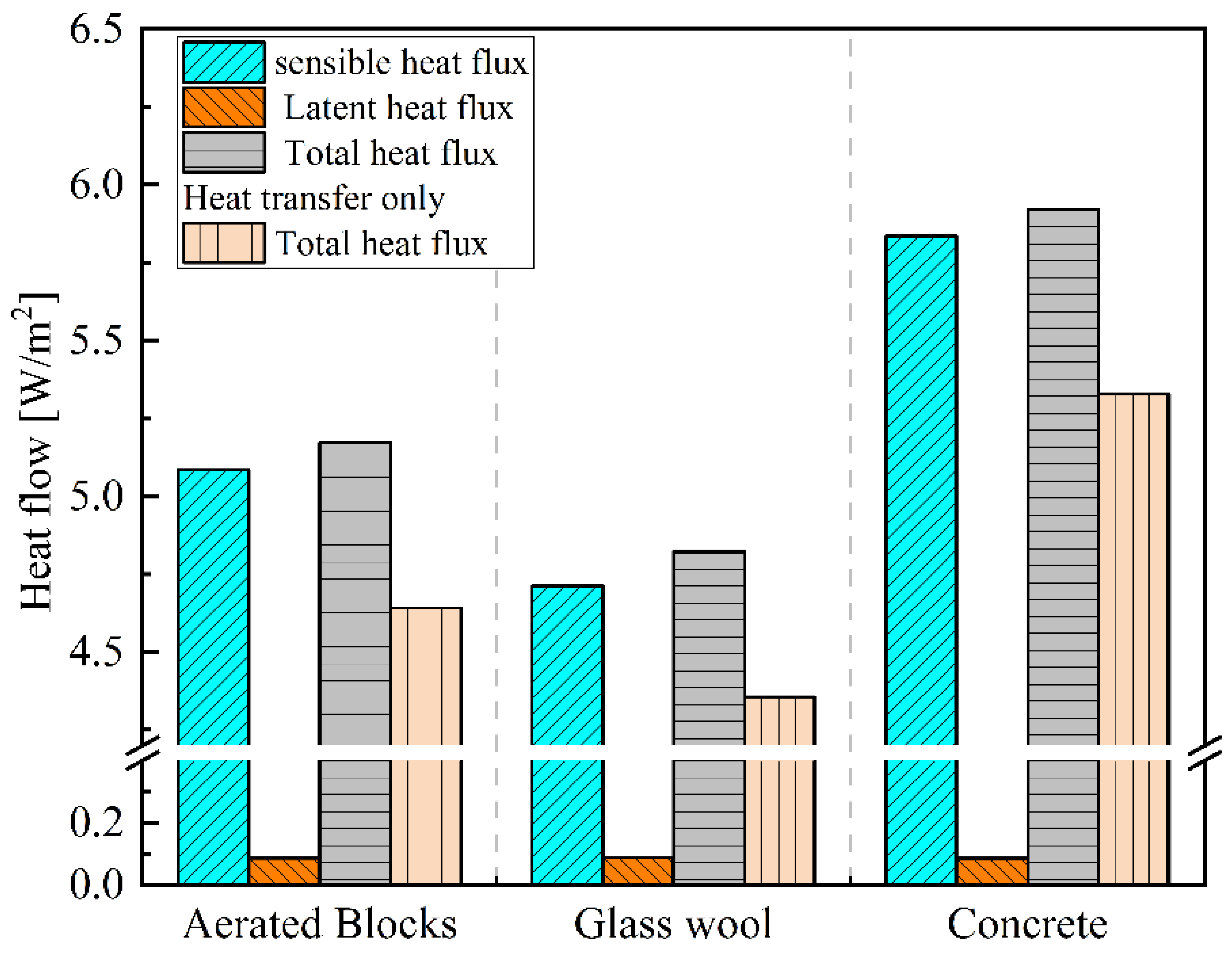
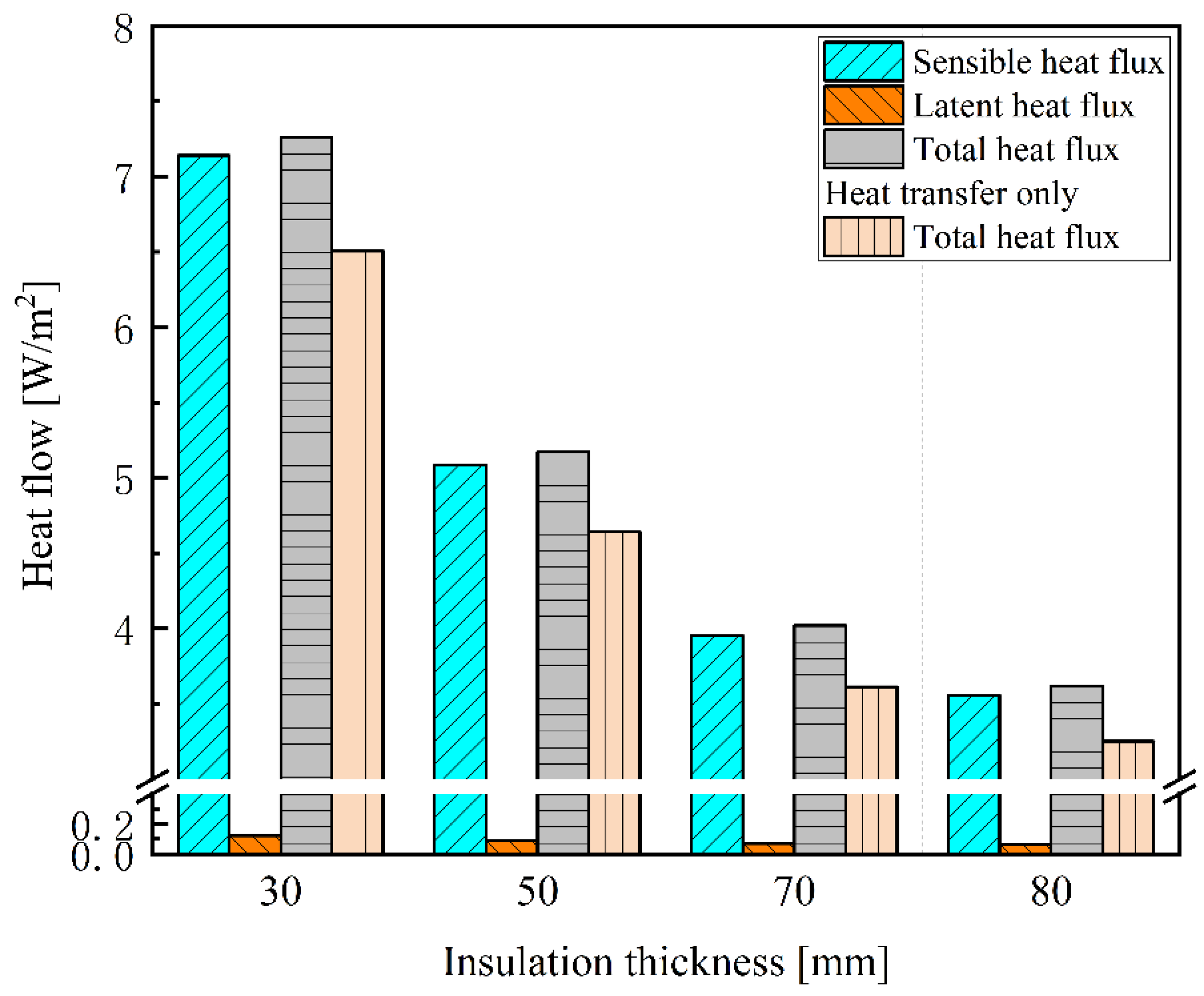
- In scenarios involving heat transfer alone, filling the joint with concrete results in the highest heat loss, with a rate of 18.65%. Conversely, when the joint is filled with glass wool, heat loss is negligible. When both heat and moisture transfer are considered, heat loss begins to occur with glass wool filling, resulting in a rate of 0.6%. Filling the joint with aerated blocks results in heat transfer being significantly influenced by moisture transfer, with a heat loss rate of 8.08%.
- In a high-humidity summer environment, moisture transfer exerts the greatest influence on the heat transfer performance at the joint of the composite wall. As the insulation layer thickness increases, the rise in surface heat flux, compared to scenarios involving heat transfer alone, diminishes; however, heat loss at the joint increases with greater insulation layer thickness. Simultaneously, an increase in insulation layer thickness contributes to reducing the ‘heterogeneity’ of the sandwich insulation composite wall. However, after accounting for moisture transfer, this degree of reduction will diminish.
- Taking into account the varying humidity conditions in summer and winter in regions characterized by hot summers and cold winters, the heat transfer coefficient of sandwich insulation composite walls with different thicknesses, filled with aerated blocks at the ‘one-line’ joint, is corrected. After accounting for the impact of the hot and humid bridge at the joint, the correction rate of the average heat transfer corrected of the wall in summer ranges from 1.10 to 1.18.
- This framework provides valuable insights for predicting coupled heat and moisture transfer through building envelopes. In the future, it will be a new research direction to further verify the authenticity of our numerical simulation through real-world experiments, which will make the work more complete.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| specific heat capacity [J/(kg·K)] | total heat flux on inner surface [W] | ||
| material density [kg/m3] | planar heat transfer coefficient of wall [W/(m2·K)] | ||
| moisture content [kg/m3] | wall plane area [m2] | ||
| latent heat of vaporization of water vapor [J/kg] | ΔT | temperature difference between indoor and outdoor [K] | |
| water vapor permeability coefficient [kg/(m·s·Pa)] | heat flow loss rate | ||
| relative humidity | average heat transfer resistance of wall [m2·K/W] | ||
| thermal conductivity coefficient [W/(m·K)] | average heat flow through wall panels [W/m2] | ||
| saturated water vapor pressure [Pa] | average temperature of inner surface [K] | ||
| slope of moisture absorption equilibrium curve | average temperature of outer surface [K] | ||
| liquid water permeability [s] | heat transfer resistance of inner surface [K/W] | ||
| density of liquid water [kg/m3] | heat transfer resistance of outer surface [K/W] | ||
| gas constant for water vapor [J/(kg·K] | heat transfer coefficient [W/(m2·K)] | ||
| thermodynamic temperature [K] | correction factor |
References
- Chen, G.X.; Chen, Y.S.; Lv, X.M. Research on seismic performance and influencing factors of lateral stiffness of composite walls with door openings and stiffening ribs. Earthq. Resist. Eng. Retrofit. 2019, 41, 26–33. (In Chinese) [Google Scholar]
- You, Y.N.; Kang, Y.T.; Ma, J.; Xing, Y.R. Research and development of key technologies for passive ultra-low energy consumption prefabricated buildings in China. Build. Sci. 2019, 35, 137–142. (In Chinese) [Google Scholar]
- Omle, I.; Kovács, E.; Bolló, B. Applying recent efficient numerical methods for long-term simulations of heat transfer in walls to optimize thermal insulation. Results Eng. 2023, 20, 101476. [Google Scholar] [CrossRef]
- Caner, G. Evaluation of the problem points that form the thermal bridge in reinforced concrete prefabricated buildings in terms of heating energy cost. Int. J. Acad. Res. 2013, 5, 28–35. [Google Scholar]
- Ge, H.; McClung, V.R.; Zhang, S. Impact of balcony thermal bridges on the overall thermal performance of multi-unit residential buildings: A case study. Energy Build. 2013, 60, 163–173. [Google Scholar]
- Zedan, M.F.; Al-Sanea, S.; Al-Mujahid, A.; Al-Suhaibani, Z. Effect of thermal bridges in insulated walls on air-conditioning loads using whole building energy analysis. Sustainability 2016, 8, 560. [Google Scholar] [CrossRef]
- Déqué, F.; Ollivier, F.; Roux, J.J. Effect of 2D modelling of thermal bridges on the energy performance of buildings: Numerical application on the Matisse apartment. Energy Build. 2001, 33, 583–587. [Google Scholar]
- de Freitas, J.R.; da Cunha, E.G. Thermal bridges modeling in South Brazil climate: Three different approaches. Energy Build. 2018, 169, 271–282. [Google Scholar]
- Viot, H.; Sempey, A.; Pauly, M.; Mora, L. Comparison of different methods for calculating thermal bridges: Application to wood-frame buildings. Build. Environ. 2015, 93, 339–348. [Google Scholar]
- Quinten, J.; Feldheim, V. Dynamic modelling of multidimensional thermal bridges in building envelopes: Review of existing methods, application and new mixed method. Energy Build. 2016, 110, 284–293. [Google Scholar]
- ISO 10211:2007(en); Thermal Bridges in Building Construction—Heat Flows and Surface Temperatures—Detailed Calculations. ISO: Geneva, Switzerland, 2007.
- GB 50176-2016; Thermal Design Code for Civil Buildings. China Architecture & Building Press: Beijing, China, 2016.
- Pásztory, Z. An overview of factors influencing thermal conductivity of building insulation materials. J. Build. Eng. 2021, 44, 102604. [Google Scholar]
- Jin, H.Q.; Yao, X.L.; Fan, L.W.; Xu, X.; Yu, Z.T. Experimental determination and fractal modeling of the effective thermal conductivity of autoclaved aerated concrete: Effects of moisture content. Int. J. Heat Mass Transf. 2016, 92, 589–602. [Google Scholar] [CrossRef]
- Qin, M.; Belarbi, R.; Aït-Mokhtar, A.; Nilsson, L.-O. Coupled heat and moisture transfer in multi-layer building materials. Constr. Build. Mater. 2009, 23, 967–975. [Google Scholar]
- Li, W.; Liu, F.; Chen, B.M.; Wei, M.F.; Gao, K.K. Influence of moisture transfer on heat transfer performance of building walls. Build. Energy Effic. 2017, 45, 57–61. [Google Scholar]
- Le, A.T.; Maalouf, C.; Mai, T.H.; Wurtz, E.; Collet, F. Transient hygrothermal behaviour of a hemp concrete building envelope. Energy Build. 2010, 42, 1797–1806. [Google Scholar]
- Maliki, M.; Laredj, N.; Bendani, K.; Missoum, H. Two-dimensional transient modeling of energy and mass transfer in porous building components using COMSOL Multiphysics. J. Appl. Fluid Mech. 2017, 10, 319–328. [Google Scholar]
- Zhao, Z.J. Study on Heat and Moisture Transfer Characteristics at Building Exterior Wall Corners with Different Structural Forms of Corner Columns. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2020. [Google Scholar]
- Wang, Y.; Liu, K.; Tian, Y.; Fan, Y.; Liu, Y. The effect of moisture transfer on heat transfer of roof-wall corner hygrothermal bridge structure. Indoor Built Environ. 2023, 32, 881–901. [Google Scholar]
- Wang, Y.; Fan, Y.; Wang, D.; Liu, Y.; Liu, J. The effect of moisture transfer on the inner surface thermal performance and the thermal transmittance of the roof-wall corner building node in high-temperature and high-humidity areas. J. Build. Eng. 2021, 44, 102949. [Google Scholar]
- Lu, J.; Xue, Y.; Wang, Z.; Fan, Y. Optimized mitigation of heat loss by avoiding wall-to-floor thermal bridges in reinforced concrete buildings. J. Build. Eng. 2020, 30, 101214. [Google Scholar]
- Li, Z.; Xing, W.; Jiang, F. Wet risk analysis on the external walls of ultra-low energy buildings in shanghai based on coupled heat and moisture transfer. J. BEE 2022, 35, 209–217. [Google Scholar]
- Wang, S.; Zhang, G.; Liu, X. Heat and moisture transfer and heat storage and release performance of assembled soil sandwich wall in solar greenhouse. Trans. Chin. Soc. Agric. Eng. 2019, 50, 100–106. [Google Scholar]
- Hagentoft, C.E. HAMSTAD–Final report: Methodology of HAM-modeling. Report R-02 2002, 8, 19–23. [Google Scholar]
- Fan, Y. Study on the Coupled Heat and Moisture Transfer Characteristics of Roof-External Wall Corner Building Nodes. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2021. [Google Scholar]
- Wang, Y.Y. Research on the Relationship Between Moisture Migration in Enclosure Structures and Indoor Thermal Environment and Air Conditioning Load. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2013. [Google Scholar]
- Wan, J.Y.; Yu, S.; Wei, J.S. The Impact of Air Layers on the Coupled Heat, Air, and Moisture Transfer Performance in Multi-Layered Walls. Energy Conserv. 2019, 42, 6–10. (In Chinese) [Google Scholar]


Density ρ [kg/m3] | Specific Heat Capacity c [J/(kg·K)] | Thermal Conductivity λ [W/(m·K)] | Moisture Content w [kg/m3] | Water Vapor Permeability Coefficient δv [s] | |
|---|---|---|---|---|---|
| Concrete [26] | 1800 | 840 | |||
| Aerated block [19] | 615 | 950 | |||
| PU [27] | 30 | 1380 | 0.028 | ||
| EPS [19] | 30 | 1470 | |||
| Glass wool [28] | 73 | 850 |
| Filled Aerated Blocks | Filled Glass Wool | Filled Concrete | ||||
|---|---|---|---|---|---|---|
| RH 90% | Heat Transfer | RH 90% | Heat Transfer | RH 90% | Heat Transfer | |
| [W] | 16.08 | 14.43 | 14.99 | 13.5 | 18.41 | 16.67 |
| [W] | 1.30 | 0.89 | 0.09 | - | 3.63 | 3.11 |
| β | 8.08% | 6.17% | 0.60% | - | 19.72% | 18.65% |
| Relative Humidity | Heat Transfer | ||||||
|---|---|---|---|---|---|---|---|
| 93% | 90% | 80% | 60% | 30% | |||
| High temperature in summer | [W] | 16.25 | 16.08 | 15.76 | 15.38 | 15.14 | 14.43 |
| [W] | 1.42 | 1.30 | 1.14 | 1.03 | 0.95 | 0.89 | |
| β | 8.74% | 8.08% | 7.23% | 6.70% | 6.28% | 6.17% | |
| Low temperature in winter | [W] | 29.42 | 29.32 | 29.11 | 28.91 | 28.77 | 27.26 |
| [W] | 2.20 | 2.12 | 1.98 | 1.87 | 1.80 | 1.56 | |
| β | 7.48% | 7.23% | 6.80% | 6.47% | 6.25% | 5.72% | |
| 30 mm | 50 mm | 70 mm | 80 mm | |||||
|---|---|---|---|---|---|---|---|---|
| RH 90% | Heat Transfer | RH 90% | Heat Transfer | RH 90% | Heat Transfer | RH 90% | Heat Transfer | |
| [W] | 22.58 | 20.23 | 16.08 | 14.43 | 12.51 | 11.23 | 11.26 | 10.11 |
| [W] | 1.50 | 1.00 | 1.30 | 0.89 | 1.12 | 0.75 | 1.04 | 0.71 |
| β | 6.64% | 4.97% | 8.08% | 6.17% | 8.95% | 6.62% | 9.23% | 7.0% |
| Summer | Winter | ||
|---|---|---|---|
| Indoor | Outdoor | Indoor | Outdoor |
| Summer | Winter | |||||||
|---|---|---|---|---|---|---|---|---|
| Insulation Layer Thickness | ||||||||
| 30 mm | 3.56 | 2.75 | 1.29 | 0.694 | 15.15 | 11.68 | 1.30 | 0.690 |
| 40 mm | 3.64 | 2.27 | 1.6 | 0.571 | 15.47 | 9.65 | 1.60 | 0.571 |
| 50 mm | 3.70 | 1.94 | 1.91 | 0.485 | 15.69 | 8.23 | 1.90 | 0.488 |
| 60 mm | 3.74 | 1.69 | 2.21 | 0.424 | 15.86 | 7.18 | 2.21 | 0.424 |
| 70 mm | 3.76 | 1.50 | 2.51 | 0.376 | 15.99 | 6.36 | 2.51 | 0.376 |
| 80 mm | 3.79 | 1.34 | 2.82 | 0.337 | 16.09 | 5.72 | 2.81 | 0.338 |
| 90 mm | 3.81 | 1.22 | 3.13 | 0.305 | 16.17 | 5.19 | 3.12 | 0.306 |
| RH 40% | RH 50% | RH 60% | RH 70% | RH 80% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Insulation Layer Thickness | ||||||||||
| 30 mm | 0.765 | 1.10 | 0.768 | 1.11 | 0.773 | 1.11 | 0.779 | 1.12 | 0.793 | 1.14 |
| 40 mm | 0.636 | 1.11 | 0.639 | 1.12 | 0.643 | 1.13 | 0.650 | 1.14 | 0.659 | 1.15 |
| 50 mm | 0.544 | 1.12 | 0.547 | 1.13 | 0.552 | 1.14 | 0.557 | 1.15 | 0.564 | 1.16 |
| 60 mm | 0.476 | 1.12 | 0.479 | 1.13 | 0.482 | 1.14 | 0.486 | 1.15 | 0.493 | 1.16 |
| 70 mm | 0.422 | 1.12 | 0.425 | 1.13 | 0.429 | 1.14 | 0.433 | 1.15 | 0.439 | 1.17 |
| 80 mm | 0.381 | 1.13 | 0.384 | 1.14 | 0.386 | 1.15 | 0.390 | 1.16 | 0.395 | 1.17 |
| 90 mm | 0.346 | 1.13 | 0.348 | 1.14 | 0.351 | 1.15 | 0.354 | 1.16 | 0.359 | 1.18 |
| RH 60% | RH 70% | RH 80% | RH 85% | |||||
|---|---|---|---|---|---|---|---|---|
| Insulation Layer Thickness | ||||||||
| 30 mm | 0.772 | 1.12 | 0.774 | 1.12 | 0.777 | 1.13 | 0.779 | 1.13 |
| 40 mm | 0.641 | 1.12 | 0.643 | 1.13 | 0.645 | 1.13 | 0.648 | 1.13 |
| 50 mm | 0.549 | 1.13 | 0.551 | 1.13 | 0.553 | 1.13 | 0.555 | 1.14 |
| 60 mm | 0.480 | 1.13 | 0.482 | 1.14 | 0.484 | 1.14 | 0.486 | 1.15 |
| 70 mm | 0.427 | 1.14 | 0.428 | 1.14 | 0.430 | 1.14 | 0.432 | 1.15 |
| 80 mm | 0.384 | 1.14 | 0.385 | 1.14 | 0.387 | 1.14 | 0.389 | 1.15 |
| 90 mm | 0.349 | 1.14 | 0.350 | 1.14 | 0.352 | 1.15 | 0.354 | 1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Mao, C.; Chen, G.; He, Y. Impact of Moisture Migration on Heat Transfer Performance at Vertical Joints of ‘One-Line’ Sandwich Insulation Composite Exterior Walls. Buildings 2025, 15, 1084. https://doi.org/10.3390/buildings15071084
Chen Y, Mao C, Chen G, He Y. Impact of Moisture Migration on Heat Transfer Performance at Vertical Joints of ‘One-Line’ Sandwich Insulation Composite Exterior Walls. Buildings. 2025; 15(7):1084. https://doi.org/10.3390/buildings15071084
Chicago/Turabian StyleChen, Yingjie, Chenyu Mao, Guoxin Chen, and Yating He. 2025. "Impact of Moisture Migration on Heat Transfer Performance at Vertical Joints of ‘One-Line’ Sandwich Insulation Composite Exterior Walls" Buildings 15, no. 7: 1084. https://doi.org/10.3390/buildings15071084
APA StyleChen, Y., Mao, C., Chen, G., & He, Y. (2025). Impact of Moisture Migration on Heat Transfer Performance at Vertical Joints of ‘One-Line’ Sandwich Insulation Composite Exterior Walls. Buildings, 15(7), 1084. https://doi.org/10.3390/buildings15071084






