Stress Measurement and Analysis of Structural Parameters of Flat Arm Tower Crane Under Different Working Conditions
Abstract
1. Introduction
2. Research Methodology
2.1. Project Overview and Test Arrangement
2.2. Testing Instruments and Measurement Point Arrangements
3. Results
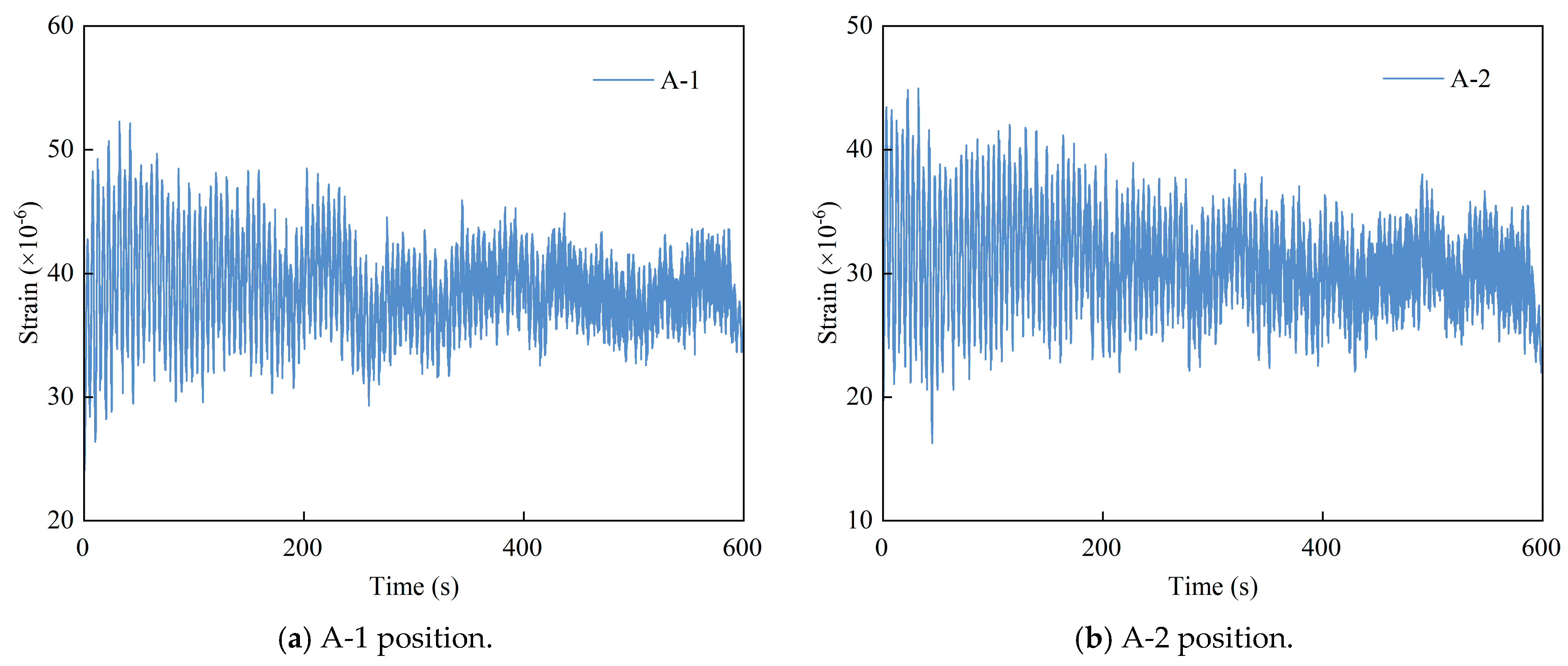
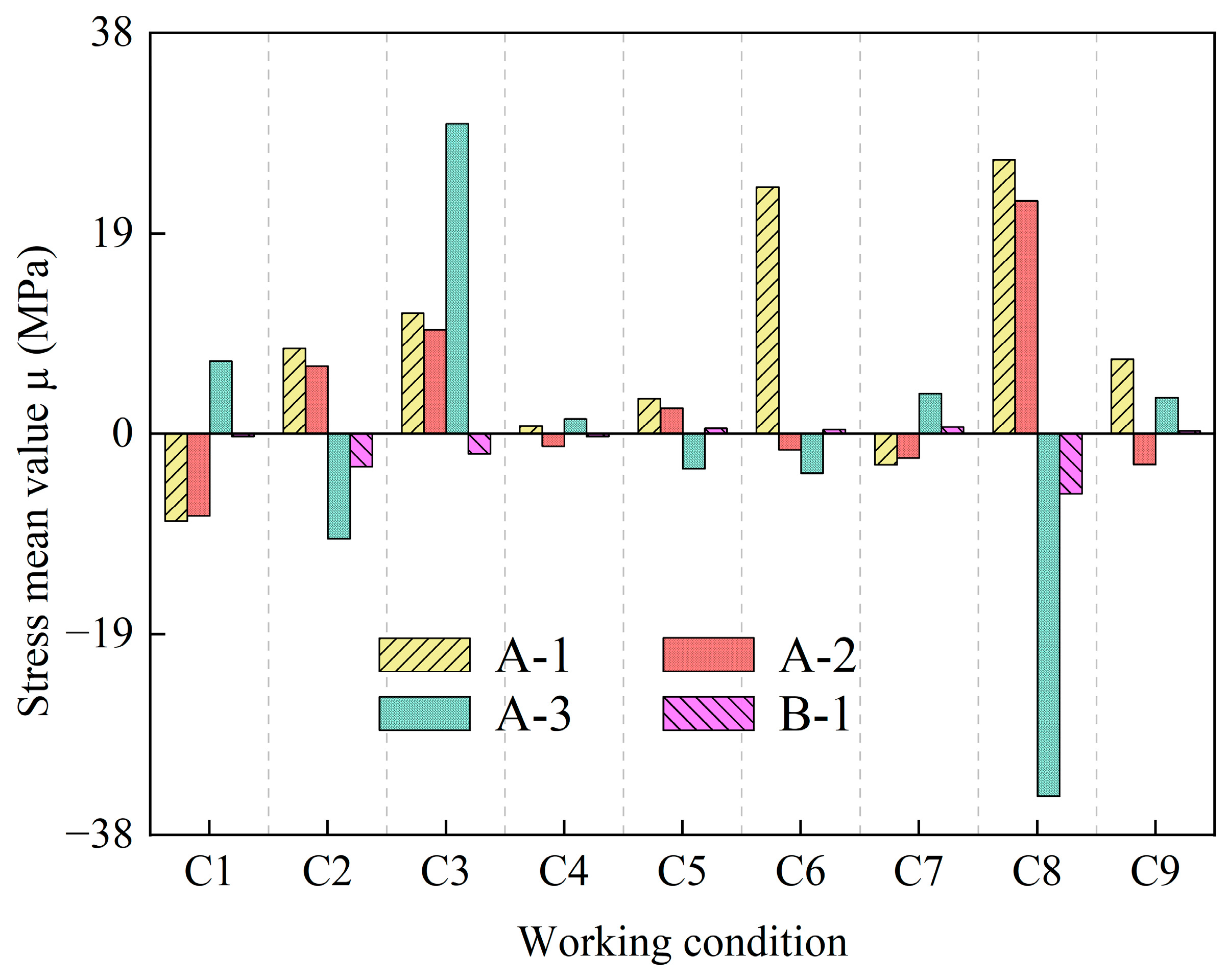
3.1. Stress Measurement Results
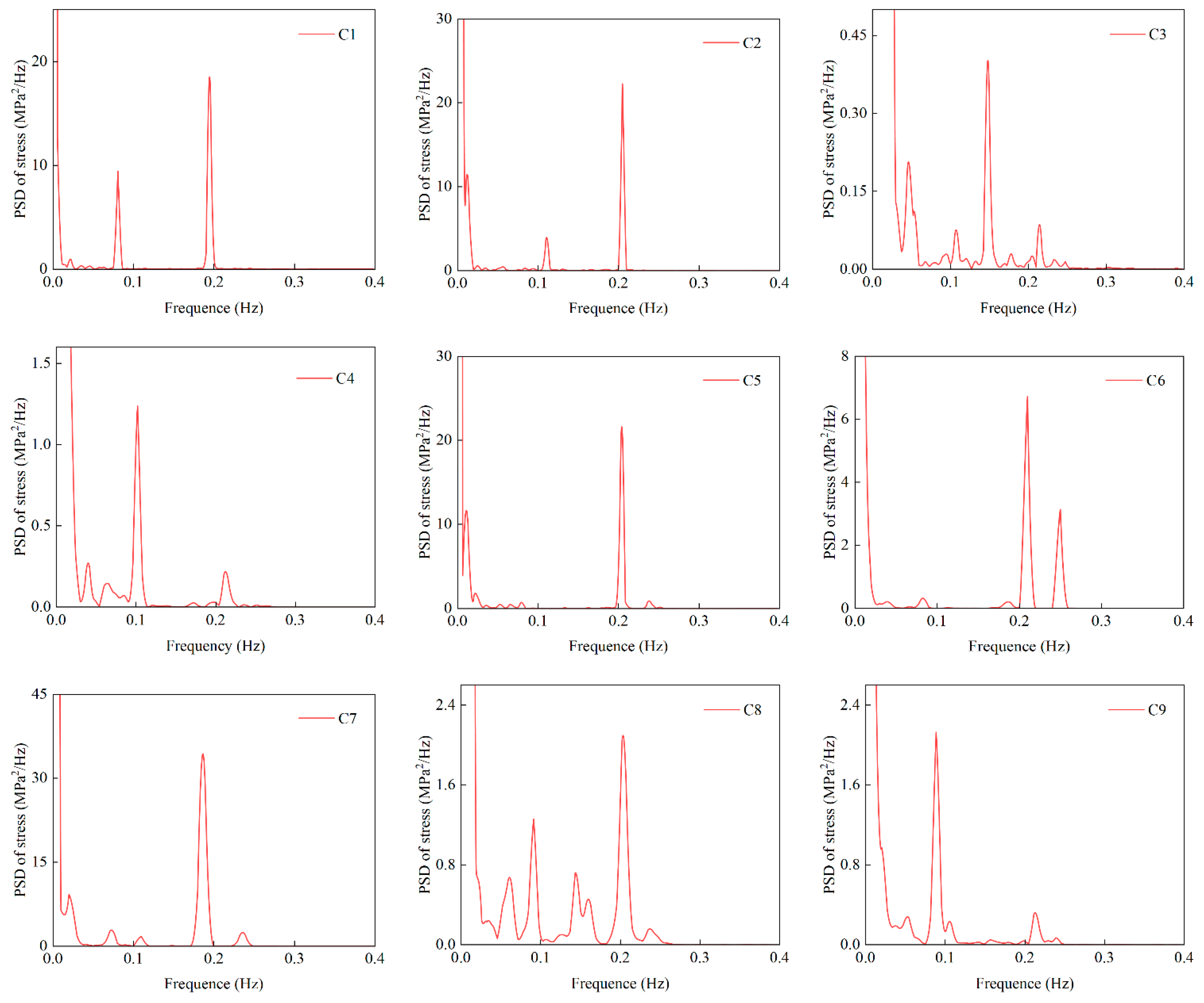
3.2. Stress Response Spectrum
3.3. Orthogonal Experimental Analysis of Stress
3.3.1. Range Analysis
3.3.2. Variance Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadeghi, S.; Soltanmohammadlou, N.; Rahnamayiezekavat, P. A systematic review of scholarly works addressing crane safety requirements. Saf. Sci. 2021, 133, 105002. [Google Scholar] [CrossRef]
- Jeong, I.; Hwang, J.; Kim, J.; Chi, S.; Hwang, B.; Kim, J. Vision-based productivity monitoring of tower crane operations during curtain wall installation using a database-free approach. J. Comput. Civ. Eng. 2023, 37, 04023015. [Google Scholar] [CrossRef]
- Hu, S.; Fang, Y.; Moehler, R. Estimating and visualizing the exposure to tower crane operation hazards on construction sites. Saf. Sci. 2023, 160, 106044. [Google Scholar] [CrossRef]
- Jiang, W.; Ding, L. Unsafe hoisting behavior recognition for tower crane based on transfer learning. Autom. Constr. 2024, 160, 105299. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, Q.; Zheng, X.; Shao, B.; Jin, L. Safety supervision of tower crane operation on construction sites: An evolutionary game analysis. Saf. Sci. 2022, 152, 105578. [Google Scholar] [CrossRef]
- Ali, A.; Zayed, T.; Wang, R.; Kit, M. Tower crane safety technologies: A synthesis of academic research and industry insights. Autom. Constr. 2024, 163, 105429. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, M.; Wan, N.; Deng, Z.; He, Z.; Luo, J. Missing measurement data recovery methods in structural health monitoring: The state, challenges and case study. Measurement 2024, 231, 114528. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The current development of structural health monitoring for bridges: A review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, X. Fatigue life prediction for tower cranes under moving load. J. Mech. Sci. Technol. 2023, 37, 6461–6466. [Google Scholar] [CrossRef]
- Yang, M.; Chang, Z.; Xu, G.; Wang, C.; Wang, P. Analysis on fatigue life of overhead travelling crane girder under impact load for sustainable transport system. IET Intell. Transp. Syst. 2020, 14, 1426–1432. [Google Scholar] [CrossRef]
- Lehner, P.; Krejsa, M.; Parenica, P.; Krivy, V.; Brozovsky, J. Fatigue damage analysis of a riveted steel overhead crane support truss. Int. J. Fatigue 2019, 128, 105190. [Google Scholar] [CrossRef]
- Li, Y.; Jin, A.; Dai, Y.; Yang, D.; Zheng, B.; Correia, J. Prediction of remaining fatigue life of in-service bridge cranes. Appl. Sci. 2023, 13, 12250. [Google Scholar] [CrossRef]
- Dong, Q.; Yu, Y.; Xu, G. Fatigue residual life estimation of jib structure based on improved v-SVR algorithm obtaining equivalent load spectrum. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1083–1099. [Google Scholar] [CrossRef]
- Jeongwoo, H.; Geun-Ho, L. Fatigue life prediction of the carrier of slewing reducer for tower crane. J. Korean Soc. Manuf. Process Eng. 2015, 14, 131–140. [Google Scholar] [CrossRef]
- Hectors, K.; Chaudhuri, S.; De Waele, W. Fracture mechanics and hot spot stress-based fatigue life calculation: Case study for a crane runway girder. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2662–2675. [Google Scholar] [CrossRef]
- Moskvichev, V.; Chaban, E. Analysis of propagation of fatigue cracks in crane girders. Inorg. Mater. 2019, 55, 1496–1502. [Google Scholar] [CrossRef]
- He, Z.; Gao, M.; Liang, T.; Lu, Y.; Lai, X.; Pan, F. Tornado-affected safety assessment of tower cranes outer-attached to super high-rise buildings in construction. J. Build. Eng. 2022, 51, 104320. [Google Scholar] [CrossRef]
- Lu, Y.; Gao, M.; Liang, T.; He, Z.; Feng, F.; Pan, F. Wind-induced vibration assessment of tower cranes attached to high-rise buildings under construction. Autom. Constr. 2022, 135, 104132. [Google Scholar] [CrossRef]
- Chen, W.; Qin, X.; Yang, Z.; Zhang, P. Wind-induced tower crane vibration and safety evaluation. J. Low Freq. Noise Vib. Act. Control. 2020, 39, 297–312. [Google Scholar] [CrossRef]
- Pástor, M.; Lengvarsky, P.; Hagara, M.; Kulka, J. Experimental investigation of the fatigue life of a bridge crane girder using S-N method. Appl. Sci. 2022, 12, 10319. [Google Scholar] [CrossRef]
- Xi, Y.; Li, H.; Sun, L.; Wang, Z. Extreme load extrapolation and long-term fatigue assessment of offshore wind turbine tower based on monitoring data. Ocean Eng. 2024, 300, 117180. [Google Scholar] [CrossRef]
- Park, Y.; Cho, S.; Han, J.; Shim, S. Fatigue life prediction of planet carrier in slewing reducer for tower crane based on model validation and field test. Int. J. Precis. Eng. Manuf. 2017, 18, 435–444. [Google Scholar] [CrossRef]
- Liu, F.; Yang, J.; Wang, J.; Liu, P. Tower Crane Effect on the Vibration Response of Elastic Foundation. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 3839–3850. [Google Scholar] [CrossRef]
- Xu, B.; Wu, Q. Stress fatigue crack propagation analysis of crane structure based on acoustic emission. Eng. Fail. Anal. 2020, 109, 104206. [Google Scholar] [CrossRef]
- Li, Q.; Fan, W.; Huang, M.; Jin, H.; Zhang, H.; Ma, J. Machine learning-based prediction of dynamic responses of a tower crane under strong coastal winds. J. Mar. Sci. Eng. 2023, 11, 803. [Google Scholar] [CrossRef]
- Wei, G.Q.; Yin, Q.Z.; Zhao, Y.; Dang, Z.; Lu, Z.W. Fatigue failure analysis and life prediction of wheel load local area of ladle crane. Meas. Sci. Technol. 2024, 35, 126120. [Google Scholar] [CrossRef]
- Dai, S.; Wang, H.; An, S.; Yuan, L. Mechanical properties and microstructural characterization of metakaolin geopolymers based on orthogonal tests. Materials 2022, 15, 2957. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Z.; Yang, H.; Zhao, J.; Xu, Y. Field Test and Analysis of Influence Factors on the Dynamic Characteristics of Self-Supporting Flat Arm Tower Crane Under Multiple Working Conditions. J. Vib. Eng. 2024, 1–9. Available online: http://kns.cnki.net/kcms/detail/32.1349.TB.20240829.1811.006.html (accessed on 20 February 2025). (In Chinese).
- Chen, M.; Zhang, Z.; Deng, Q.; Feng, Y.; Wang, X. Optimization of underfloor air distribution systems for data centers based on orthogonal test method: A case study. Build. Environ. 2023, 232, 110071. [Google Scholar] [CrossRef]
- Li, Y.; She, L.; Wen, L.; Zhang, Q. Sensitivity analysis of drilling parameters in rock rotary drilling process based on orthogonal test method. Eng. Geol. 2020, 270, 105576. [Google Scholar] [CrossRef]
- Li, X.; Hao, J. Orthogonal test design for optimization of synthesis of super early strength anchoring material. Constr. Build. Mater. 2018, 181, 42–48. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Zhang, Z.; Taylor, S.; Chen, M.; Wang, X. Experimental investigation on thermal performance of self-service cold storage cabinet based on the orthogonal test. Appl. Therm. Eng. 2024, 242, 122315. [Google Scholar] [CrossRef]

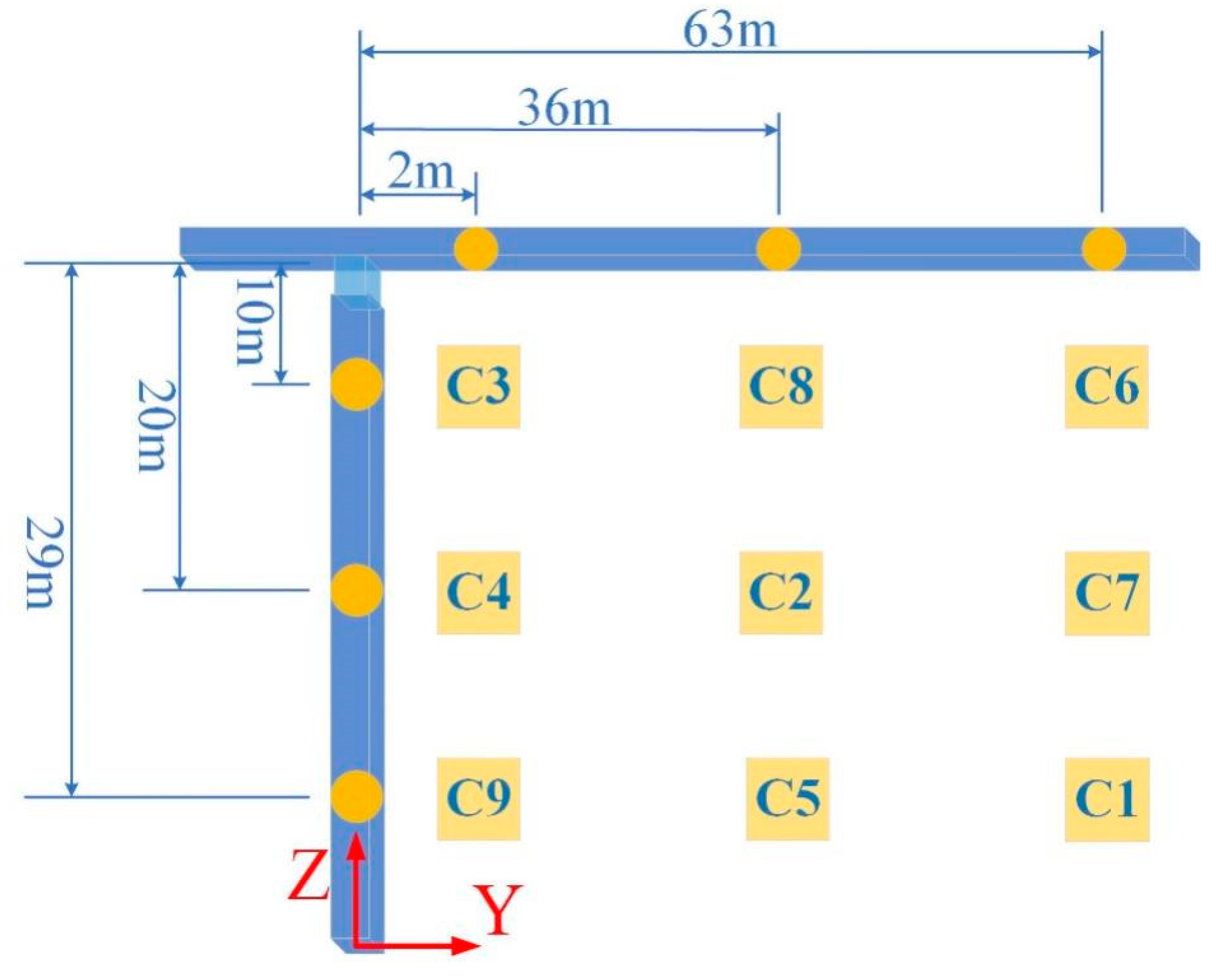



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Operating range (m) | 2.5~65 | Independent working height (m) | 46 |
| Maximum lifting weight (kg) | 1.00 × 104 | Measured tower crane height (m) | 40 |
| Balance weight (kg) | 1.86 × 104 | Rated lifting moment (kN·m) | 1600 |
| Lift arm length (m) | 66.8 | Maximum lifting moment (kN·m) | 1920 |
| Balance arm length (m) | 15.5 | Lifting speed (m·min−1) | 0~95 |
| Level | Factors | ||
|---|---|---|---|
| Lifting Position (m) | Rope Length (m) | Lifting Weight (kg) | |
| 1 | 63 | 29 | 520 |
| 2 | 36 | 20 | 750 |
| 3 | 2 | 10 | 1300 |
| No. | Lifting Position (m) | Rope Length (m) | Lifting Weight (kg) |
|---|---|---|---|
| C1 | 63 | 29 | 520 |
| C2 | 36 | 20 | 520 |
| C3 | 2 | 10 | 520 |
| C4 | 2 | 20 | 750 |
| C5 | 36 | 29 | 750 |
| C6 | 63 | 10 | 750 |
| C7 | 63 | 20 | 1300 |
| C8 | 36 | 10 | 1300 |
| C9 | 2 | 29 | 1300 |
| No. | The Root of the Tower Body (MPa) | The Root of the Jib (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|
| A-1 | A-2 | A-3 | B-1 | |||||
| µ | σ | µ | σ | µ | σ | µ | σ | |
| C1 | −8.284 | 0.714 | −7.807 | 0.713 | 6.885 | 0.784 | −0.260 | 0.367 |
| C2 | 8.106 | 0.658 | 6.427 | 0.614 | −9.935 | 0.781 | −3.123 | 0.331 |
| C3 | 11.446 | 0.751 | 9.898 | 0.677 | 29.385 | 11.804 | −1.901 | 0.225 |
| C4 | 0.722 | 0.414 | −1.183 | 0.491 | 1.427 | 0.510 | −0.269 | 0.589 |
| C5 | 3.347 | 0.587 | 2.459 | 0.639 | −3.303 | 0.744 | 0.492 | 0.638 |
| C6 | 23.384 | 1.465 | −1.537 | 0.602 | −3.733 | 0.754 | 0.387 | 0.366 |
| C7 | −2.909 | 1.298 | −2.283 | 1.205 | 3.821 | 1.656 | 0.635 | 0.589 |
| C8 | 25.988 | 1.566 | 22.065 | 1.358 | −34.335 | 2.083 | −5.656 | 0.455 |
| C9 | 7.077 | 0.614 | −2.907 | 0.734 | 3.427 | 0.637 | 0.255 | 0.664 |
| No. | Natural Frequency Results in This Document/Hz | Natural Frequency Results/Hz [28] | Error/% | |||
|---|---|---|---|---|---|---|
| First Order | Second Order | First Order | Second Order | First Order | Second Order | |
| C1 | 0.081 | 0.194 | 0.114 | 0.195 | −28.95 | −0.51 |
| C2 | 0.110 | 0.205 | 0.124 | 0.205 | −11.29 | 0 |
| C3 | 0.108 | 0.148 | 0.107 | 0.147 | 0.93 | 0.68 |
| C4 | 0.102 | 0.214 | 0.107 | 0.206 | −4.67 | 3.88 |
| C5 | / | 0.204 | 0.110 | 0.204 | / | 0 |
| C6 | 0.083 | 0.210 | 0.085 | 0.209 | −2.35 | 0.48 |
| C7 | 0.073 | 0.187 | 0.073 | 0.186 | 0 | 0.54 |
| C8 | 0.091 | 0.202 | 0.091 | 0.205 | 0 | −1.46 |
| C9 | 0.089 | 0.213 | 0.088 | 0.212 | 1.14 | 0.47 |
| No. | Lifting Position A | Rope Length B | Lifting Weight C | Mean Value of Stress (MPa) | ||
|---|---|---|---|---|---|---|
| A-1 | A-2 | B-1 | ||||
| C1 | 1 | 1 | 1 | −8.284 | −7.807 | −0.260 |
| C2 | 2 | 2 | 1 | 8.106 | 6.427 | −3.123 |
| C3 | 3 | 3 | 1 | 11.446 | 9.898 | −1.901 |
| C4 | 3 | 2 | 2 | 0.722 | −1.183 | −0.269 |
| C5 | 2 | 1 | 2 | 3.347 | 2.459 | 0.492 |
| C6 | 1 | 3 | 2 | 23.384 | −1.537 | 0.387 |
| C7 | 1 | 2 | 3 | −2.909 | −2.283 | 0.635 |
| C8 | 2 | 3 | 3 | 25.988 | 22.065 | −5.656 |
| C9 | 3 | 1 | 3 | 7.077 | −2.907 | 0.255 |
| Position | Parameter | Lifting Position A | Rope Length B | Lifting Weight C | Order of Importance |
|---|---|---|---|---|---|
| A-1 | K1 | 4.06 | 0.71 | 3.76 | |
| K2 | 12.48 | 1.97 | 9.15 | ||
| K3 | 6.41 | 20.27 | 10.05 | ||
| R | 8.42 | 19.56 | 6.30 | B > A > C | |
| A-2 | K1 | −3.88 | −2.75 | 2.84 | |
| K2 | 10.32 | 0.99 | −0.09 | ||
| K3 | 1.94 | 10.14 | 5.63 | ||
| R | 14.19 | 12.89 | 5.71 | A > B > C | |
| B-1 | K1 | 0.25 | 0.16 | −1.76 | |
| K2 | −2.76 | −0.92 | 0.20 | ||
| K3 | −0.64 | −2.39 | −1.59 | ||
| R | 3.02 | 2.55 | 1.96 | A > B > C |
| Position | Source | The Sum of Squared Deviations | Degrees of Freedom | F | p |
|---|---|---|---|---|---|
| A-1 | A | 113.157 | 2 | 0.878 | 0.533 |
| B | 719.032 | 2 | 5.577 | 0.152 | |
| C | 69.557 | 2 | 0.539 | 0.650 | |
| Error | 128.938 | 2 | |||
| R2 | 0.875 | ||||
| A-2 | A | 305.448 | 2 | 13.919 | 0.067 |
| B | 264.038 | 2 | 12.032 | 0.077 | |
| C | 48.950 | 2 | 2.231 | 0.310 | |
| Error | 21.945 | 2 | |||
| R2 | 0.966 | ||||
| B-1 | A | 14.406 | 2 | 2.824 | 0.262 |
| B | 9.848 | 2 | 1.930 | 0.341 | |
| C | 7.101 | 2 | 1.392 | 0.418 | |
| Error | 5.101 | 2 | |||
| R2 | 0.860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Mei, B.; Yang, H.; Hu, X.; An, W.; Yue, Y.; Xu, Y.; Wang, Z. Stress Measurement and Analysis of Structural Parameters of Flat Arm Tower Crane Under Different Working Conditions. Buildings 2025, 15, 1137. https://doi.org/10.3390/buildings15071137
Zhang Q, Mei B, Yang H, Hu X, An W, Yue Y, Xu Y, Wang Z. Stress Measurement and Analysis of Structural Parameters of Flat Arm Tower Crane Under Different Working Conditions. Buildings. 2025; 15(7):1137. https://doi.org/10.3390/buildings15071137
Chicago/Turabian StyleZhang, Qinghua, Bohao Mei, Hui Yang, Xin Hu, Wei An, Yanpeng Yue, Yanwei Xu, and Zhihao Wang. 2025. "Stress Measurement and Analysis of Structural Parameters of Flat Arm Tower Crane Under Different Working Conditions" Buildings 15, no. 7: 1137. https://doi.org/10.3390/buildings15071137
APA StyleZhang, Q., Mei, B., Yang, H., Hu, X., An, W., Yue, Y., Xu, Y., & Wang, Z. (2025). Stress Measurement and Analysis of Structural Parameters of Flat Arm Tower Crane Under Different Working Conditions. Buildings, 15(7), 1137. https://doi.org/10.3390/buildings15071137





