Bearing Capacity and Deformation of Micropiles Considering Plastic Hinge

Abstract

This study systematically investigates the plastic deformation behavior and load-bearing mechanisms of micropiles through integrated scaled physical modeling and nonlinear finite element analysis, with particular emphasis on quantifying plastic hinge characteristics. The development of plastic deformation in laterally loaded micropiles was analytically described using plastic hinge theory, complemented by experimental-numerical validation. The key findings demonstrate the following points. (1) Existing empirical formulas for plastic hinge length, based on sectional parameters, show significant discrepancies, with experimental calibration establishing an optimized length of 2D. (2) Parametric FEM studies of three diameter groups (3–7% longitudinal reinforcement ratio) reveal that cross-sectional geometry and reinforcement configuration collectively govern nonlinear ultimate capacity, where ≤0.1% reinforcement ratio variation induces <5% bearing capacity deviation. (3) Square sections exhibit 12–18% higher capacity than circular equivalents of the equivalent dimensions, with this advantage amplifying with increasing pile size. (4) While excessive reinforcement ratios (>6%) impair structural performance, emergent scale effects effectively mitigate associated capacity reduction. These findings provide critical insights for optimizing micropile design in geotechnical applications through coordinated consideration of geometric, material, and scale parameters.

1. Introduction

Micropiles have emerged as a transformative innovation in geotechnical engineering, serving not only as an effective solution for shallow foundation reinforcement but also as a reliable method for landslide mitigation, owing to their structural adaptability, space efficiency, and operational versatility [1,2,3]. Although their design principles are grounded in traditional structures, micropiles exhibit distinct mechanical behaviors—such as reduced cross-sectional dimensions, higher reinforcement density, and shear strength limitations—that often challenge conventional reinforced concrete design codes. These unique characteristics result in fundamentally different load-bearing mechanisms and deformation patterns compared to rigid anti-sliding systems, necessitating the development of specialized analytical frameworks.

As flexible, slender structural elements, micropiles experience complex bending-shear interactions under lateral loads. Large-scale slope tests conducted by Yan et al. [4] revealed asymmetric stress distributions, with compressive and tensile stresses concentrated on the rear and front faces, respectively. This stress dichotomy induces transverse brittle cracks within narrow zones adjacent to the sliding surface (ranging from 1.74D to 2.8D above and 2.6D to 3.5D below), while the remainder of the pile maintains structural integrity. Such localized damage patterns are consistent with combined bending-shear failure mechanisms, which serve as precursors to the development of plastic hinges [5,6]. Li et al. [7] observed that micropiles mainly resist flexure deformation in the process of supporting the landslide, and the deformation curve follows a reverse S-shape. This deformation pattern concentrates bending moments at specific depths, forming plastic hinges as material yielding initiates. Sun et al. [8,9] further demonstrated that anchorage length governs deformation modes: shallow embedment restricts movement to rigid rotation, whereas deeper embedment allows lateral bending, amplifying hinge formation risks. Numerical simulations corroborate these findings, showing slope failure along plasticized shear planes accompanied by pile-top rotation, mid-section lateral deformation, and base uplift under horizontal loading. Micropile performance is ultimately dictated by two competing failure modes: (1) brittle fracture of the pile body, controlled by material strength limits, and (2) yield failure of the surrounding soil-rock matrix at the embedded interface [10]. Crucially, the plastic failure zone is not fixed but shifts dynamically with loading conditions and soil–pile interactions [11], in other words, soil conditions determine the location of plastic hinges, usually at the location of the maximum moment. However, the location of plastic hinges can be affected by a variety of factors [12]. This unpredictability underscores the need for configuration-specific analysis, particularly when addressing shear-tensile failure transitions or hinge-driven collapse.

The plastic hinge represents a section of a structure in a plastic deformation state, where the sectional ultimate bending moment remains constant while the rotation angle changes abruptly, or curvature increases indefinitely. Potini and Coti [13] derived the theoretical failure domain of a single long pile under generalized loading and reproduced the plastic hinge in single pile, showing zero plastic hinges in short pile, one plastic hinge in the case of medium long pile and two plastic hinges in long pile. Chang and Hutchinson [14] adopted curvature profiles coupled with back-calculation of the plastic hinge length and post-test physical observations and indicated that the plastic region spread over a length of 1.5 times pile diameter (1.5D). Choi and Kimwoo [15] stated that in reinforced concrete structures, a critical section reaching flexural strength does not always cause failure. Moment redistribution during plastic hinge formation occurs, with plastic hinge length mainly determined by material properties, allowing force redistribution and preventing immediate collapse. Most existing plastic theory studies [16,17,18] focus on traditional structures like beams or pillars with slenderness ratios below 10, while micropiles in slope stabilization can reach ratios up to 30. This highlights the need for comprehensive research on micropile plastic deformation under lateral landslide loading.

During slope sliding process, evolving pile–soil relative displacements trigger redistribution of bending moment patterns along the pile shaft, potentially altering failure mechanisms (e.g., transition from flexural to shear-dominated failure). The micropile–soil system, characterized by stiff elastic pile interacting with discrete soil masses, exhibits significant spatiotemporal heterogeneity in pile internal forces due to nonlinear coupling effects at the contact interface. While current research predominantly employs physical model tests and numerical simulations to investigate their mechanical behavior, both methodologies face inherent limitations: physical experiments struggle to precisely characterize deformation evolution under complex boundary conditions, whereas numerical models often oversimplify pile–soil constitutive relationships (e.g., assuming the pile as an elastic body or neglecting anisotropic concrete cracking), leading to inaccuracies in inelastic response predictions. This study, based on scaled physical model tests under simplified loading conditions, investigates plastic deformation in micropiles under different geometric and structural parameters. Finite element numerical modeling is also employed to verify plastic hinge length, and key factors influencing nonlinear bearing capacity and ductile deformation are explored.

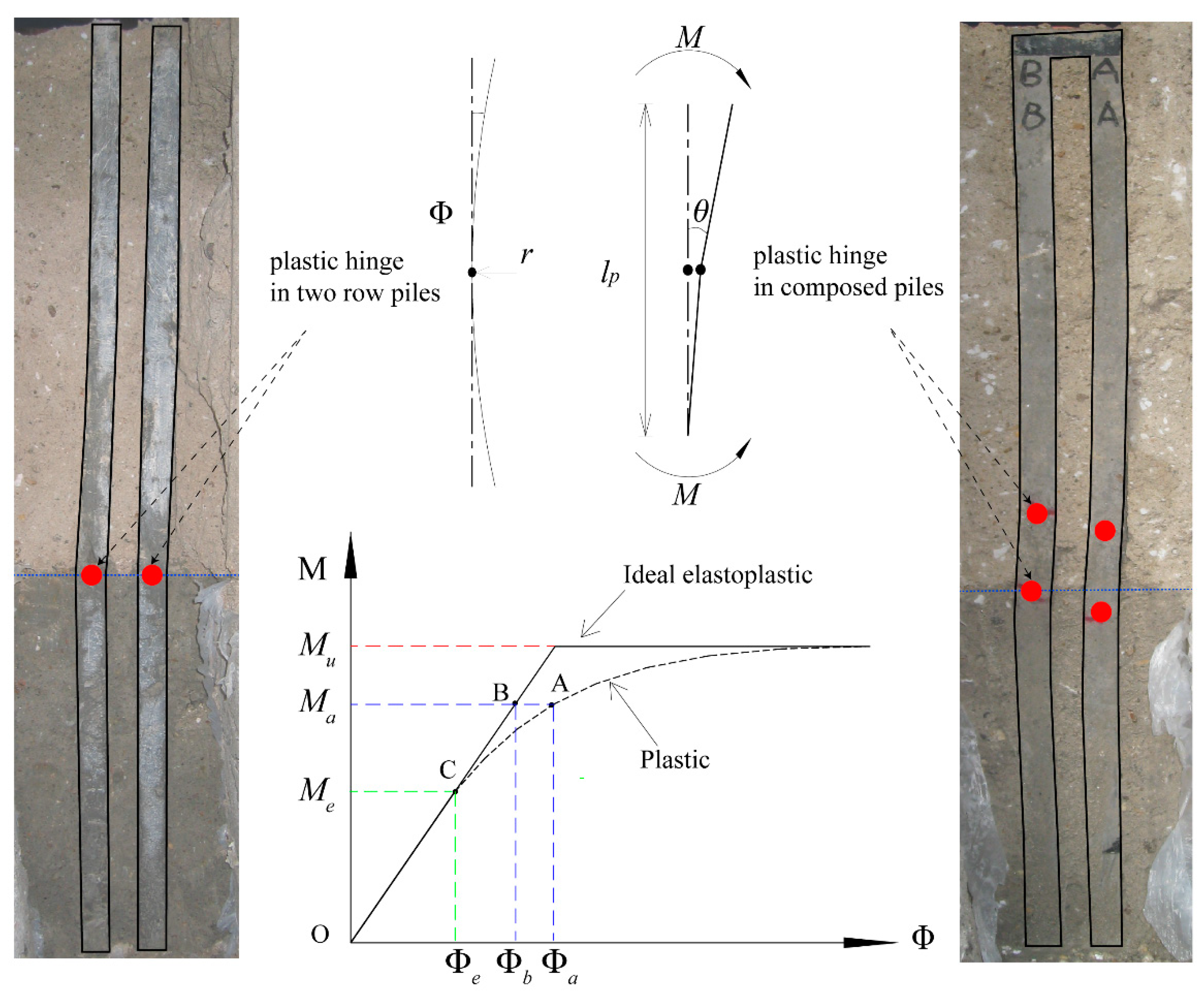
2. Plastic Hinge

2.1. The Definition of Plastic Hinge

Plastic flow is assumed to occur within a localized region along the structure, where all pile sections exhibit uniform plastic curvature. The cast-in situ bored pile prototype depicted in Figure 1 features a 10 m-long shaft with a nominal diameter of 300 mm. Constructed using C30-grade concrete (characteristic compressive strength 30 MPa as per GB/T 50010 [19]), the pile incorporates longitudinal reinforcement consisting of four 25 mm-diameter steel bars (yield strength 400 MPa). When scaled down at a 1:10 ratio and subjected to lateral loading within a slope model, the micropiles demonstrated significant plastic deformation localization within the shear band. Notably, this failure mechanism mirrors the deformation patterns observed near sliding surfaces in large-scale physical modeling tests (scale factor 1:3) [4], indicating mechanistic consistency across different scaling ratios. This alignment underscores the universality of strain concentration phenomena in geotechnical systems, validating the scalability of plastic deformation behavior from reduced scale to prototype configurations. However, the location and number of plastic hinges are closely related to the structure’s properties. Focusing on the plastic deformation zone, the linear relationship between the bending moment and curvature offers a straightforward approach to quantifying plastic hinges in concrete micro piles.

Typically, the capacity of a structure to resist flexural deformation is characterized by the curve of bending moment M as a function of curvature Φ. Based on the deflection equation of a pure bending beam and the definition of curvature, the elastic curvature is derived:

$${\Phi }_e={\displaystyle \frac{1}{r}}=-{\displaystyle \frac{{{\rm M}}_e}{{\rm E}{\rm I}}},$$

(1)

where r is the radius of curvature;

${{\rm M}}_e$ is the yield moment;

EI is the stiffness of concrete structures.

The plastic curvature is:

$${\Phi }_p=\Phi -{\displaystyle \frac{{{\rm M}}_e}{{\rm E}I}}.$$

(2)

The OC segment of bending moment–curvature curve in Figure 1. represents the elastic deformation phase before the onset of yielding, after which plastic deformation begins to develop. At point A, the plastic curvature is determined as the difference between the total curvature at that point and the elastic curvature, expressed as Φ_p = Φ_a − Φ_e. If the elastic moment is assumed to be equal to the first yield moment, this calculation holds. However, if elastic rebound occurs during the plastic deformation phase, Φ_p may be overestimated. In this case, using the bending moment corresponding to point B, the plastic curvature is adjusted to Φ_p = Φ_a − Φ_b. For an ideal elastic-plastic material, the moment–curvature relationship curve remains unaffected by this discrepancy.

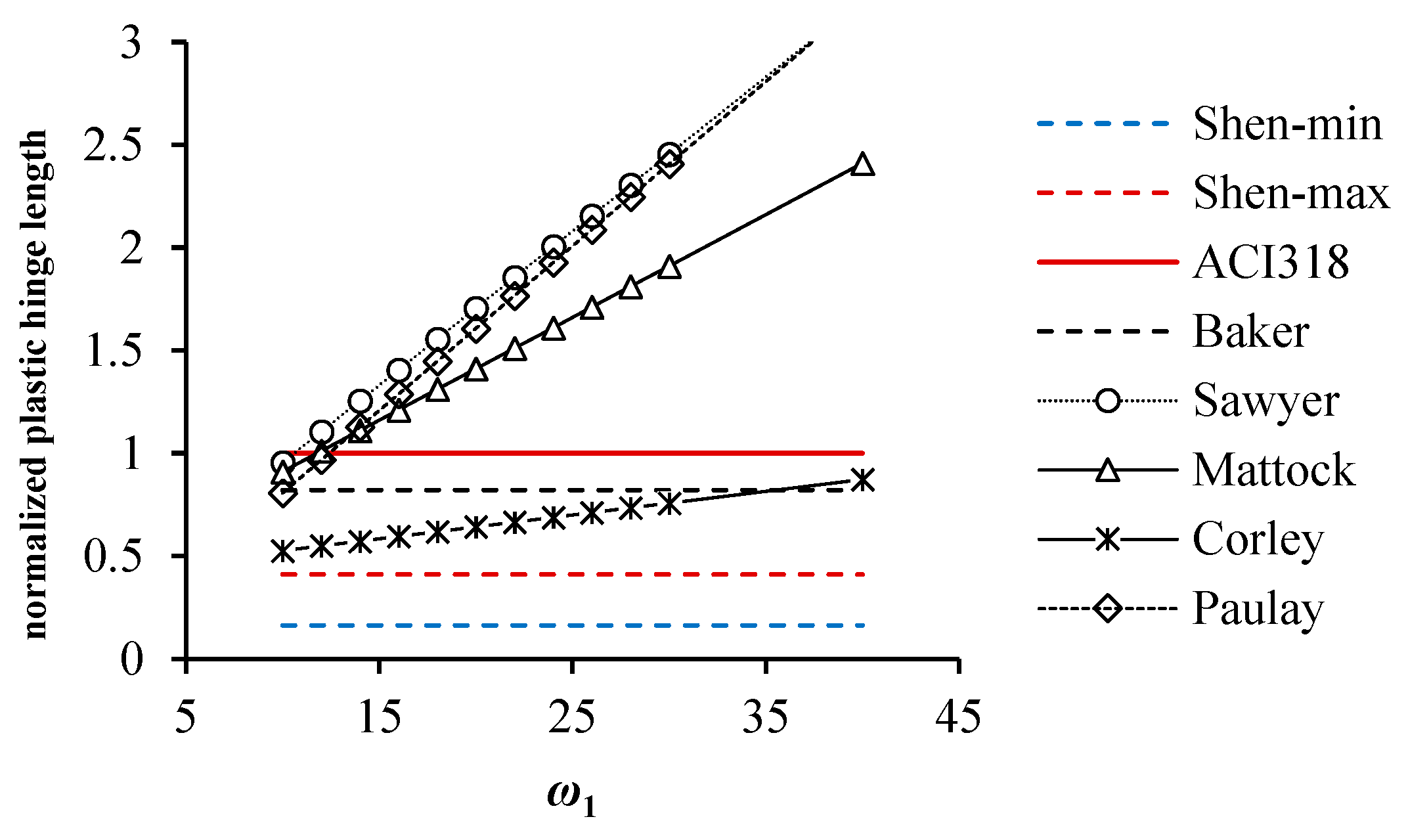
2.2. Plastic Hinge Length Calculation

Micropiles, such as steel tubes or I-beams, utilize the ductility of metal materials to enhance deformation resistance. Their behavior is typically analyzed using ideal elastic or elastic-plastic beam models to assess large-curvature deformation. In contrast, reinforced concrete friction piles exhibit more complex failure mechanisms due to material brittleness, concrete–steel bond capacity, and the restraining effects of surrounding soil, which limit plastic zone expansion. At the most critical cross-section of a reinforced concrete pile, when the outermost concrete reaches its yield strength, the ultimate bending moment remains constant while plastic deformation propagates toward the neutral axis. As the longitudinal curvature increases indefinitely, the section reaches its full resistance to plastic deformation, leading to the formation of tensile cracks that extend toward the neutral axis. As bending cracks develop, stress redistribution weakens the section’s flexural resistance. Consequently, the load previously carried by the concrete transfers to the steel reinforcement, which has a higher resistance to plastic deformation. This leads to continued curvature increase, forming new plastic hinge deformations.

Extensive experimental studies [20,21,22] on concrete component damage indicate that plastic deformation distribution in flexural members primarily depends on geometric parameters, such as cantilever segment length and section height. Various empirical formulas have been developed to describe the response and deformation of reinforced concrete beam–column structures under different loading conditions, incorporating factors like axial load-induced additional bending moments and material yield strength. Given variations in unit scales and formulations across different countries, this study adopts a normalized plastic hinge length, as defined in Equation (3), with existing empirical formulas summarized in Table 1.

$$\overline{l_p}=\left\{C\right\}\times {\left[\begin{array}{cc}{\displaystyle \frac{l_D}{D}}& {\displaystyle \frac{h_0}{D}}\end{array}\right]}^{{\rm T}}=\left\{C\right\}\times {\left[\begin{array}{cc}{\omega }_1& {\omega }_2\end{array}\right]}^{{\rm T}},$$

(3)

where $l_D$ is the distance from the plastic hinge (critical section) to the inflection point (or column cantilever length);

D is the section height perpendicular to the neutral axis;

h₀ is the effective section height;

{C} is a constant parameter;

${\omega }_1$ is the shear span ratio factor;

${\omega }_2$ is the section height factor.

Table 1. Dimensionless empirical formula of plastic hinge length.

Academia	$\overline{{\mathit{l}}_{\mathit{p}}}$		Structure	Note
Sawyer [23]	$0.075\hspace{0.33em}{\omega }_1+0.25{\omega }_2$	(4a)	Beam	${\rho }_s$—Longitudinal reinforcement ratio
Mattock [24]	$0.05{\omega }_1+0.5{\omega }_2$	(4b)	Beam	${\mathrm{f}}_{\mathrm{c}}$—Concrete compressive strength, MPa
Corley [25]	$0.2/\sqrt{h}\hspace{0.33em}{\omega }_1+0.5{\omega }_2$	(4c)	Beam	${\mathrm{f}}_{\mathrm{y}}$—Yield strength of longitudinal reinforcement, MPa
Shen [26]	$\left(0.2~0.5\right){\omega }_2$	(4d)	Beam and pillar	d—Longitudinal reinforcement diameter, mm
Baker [27]	${\omega }_2$	(4e)	Beam and pillar	${\mathrm{P}}_{\mathrm{N}}$—Axial load
ACI-318 [28]	$0.5$	(4f)	Beam and pillar	${\mathrm{P}}_{\mathrm{c}}$—Compressive load capacity
Paulay [29]	$0.08{\omega }_1+0.022f_{y}d/\mathrm{D}$	(4g)	Bridge pier column	${\mathrm{A}}_{\mathrm{s}}$—Area of longitudinal reinforcement
Bae [30]	$\left|0.3{\displaystyle \frac{P_N}{P_C}}+3{\displaystyle \frac{A_s}{A_g}}-1\right|{\omega }_1+0.25$	(4h)	Pillar	${\mathrm{A}}_{\mathrm{g}}$—Total area of concrete

Table 1. Dimensionless empirical formula of plastic hinge length.

Academia	$\overline{{\mathit{l}}_{\mathit{p}}}$		Structure	Note
Sawyer [23]	$0.075\hspace{0.33em}{\omega }_1+0.25{\omega }_2$	(4a)	Beam	${\rho }_s$—Longitudinal reinforcement ratio
Mattock [24]	$0.05{\omega }_1+0.5{\omega }_2$	(4b)	Beam	${\mathrm{f}}_{\mathrm{c}}$—Concrete compressive strength, MPa
Corley [25]	$0.2/\sqrt{h}\hspace{0.33em}{\omega }_1+0.5{\omega }_2$	(4c)	Beam	${\mathrm{f}}_{\mathrm{y}}$—Yield strength of longitudinal reinforcement, MPa
Shen [26]	$\left(0.2~0.5\right){\omega }_2$	(4d)	Beam and pillar	d—Longitudinal reinforcement diameter, mm
Baker [27]	${\omega }_2$	(4e)	Beam and pillar	${\mathrm{P}}_{\mathrm{N}}$—Axial load
ACI-318 [28]	$0.5$	(4f)	Beam and pillar	${\mathrm{P}}_{\mathrm{c}}$—Compressive load capacity
Paulay [29]	$0.08{\omega }_1+0.022f_{y}d/\mathrm{D}$	(4g)	Bridge pier column	${\mathrm{A}}_{\mathrm{s}}$—Area of longitudinal reinforcement
Bae [30]	$\left|0.3{\displaystyle \frac{P_N}{P_C}}+3{\displaystyle \frac{A_s}{A_g}}-1\right|{\omega }_1+0.25$	(4h)	Pillar	${\mathrm{A}}_{\mathrm{g}}$—Total area of concrete

Existing empirical formulations exhibit significant variability, as they often prioritize distinct influencing factors under specific loading scenarios. To facilitate a comparative analysis, eight distinct empirical models [23,24,25,26,27,28,29,30] were integrated into the generalized structure of Equation (3), generating a standardized series denoted as Equation (4a–h) (Table 1). A key observation emerged: Equation (4a–c) explicitly incorporate both shear-span ratio factor ω₁ and effective cross-sectional factor ω₂, whereas Equation (4d,e) omit the shear-span ratio term. This disparity arises because the latter models were derived from beam–column experiments that did not account for shear-span effects. To rigorously assess the applicability of these formulas to micropiles, the prototype dimensions and material properties (Figure 1) were substituted into Equation (4a–h). The comparative results are presented in Figure 2.

As the effective cross-section height approaches unity, the calculated plastic hinge length converges with the 0.5D recommendation for flexible beam–columns in the American Seismic Structural Design Code [28]. While both Equation (4g,h) incorporate cross-sectional reinforcement parameters-explicitly accounting for rebar strength effects on component plasticity—their predictions diverge regarding whether increased steel strength enhances or diminishes plastic deformation capacity.

The axial force’s role in plastic zone development introduces additional complexity. For bridge pile foundations, eccentric axial loading necessitates specialized consideration of plastic hinge length. Chinese design specifications [31] adopt an approach analogous to Equation (4g) for pier analysis, whereas Equation (4h) employs the axial compression ratio as the governing parameter for high-axial-load columns in seismic contexts. Significantly, most empirical formulas derive from tests on specimens with shear-span ratios <10 (beam structures) or cantilever lengths <10 (columns/piers), resulting in limited applicability. Disparities in original test conditions, including loading regimes and boundary constraints, frequently yield contradictory predictions across formulas.

As laterally loaded micropiles functionally resemble vertically oriented beams with combined axial–flexural action, this study adapts the plastic hinge framework to analyze their deformation mechanisms. The strong reinforcement configuration (characteristic of micropiles) necessitates particularized evaluation of steel-concrete interaction effects under high stress gradients.

Micropiles, as highly reinforced concrete structures, behave similarly to cantilever structures under landslide thrust. Considering the effect of steel reinforcement parameters, Equation (5) (referenced from Zhu and Wu [32]) was applied to estimate the plastic hinge length of micropiles.

$$l_p=2\left(1-0.5\rho f_y/f_c\right)h_0,$$

(5)

where $l_p$ is the length of the plastic hinge.

For circular micropiles, the influence of longitudinal bar diameter (d = 6–28 mm), quantity (n = 1–6 bars), and pile section dimensions (D = 100–300 mm) was analyzed, with the results presented in Figure 3 and Figure 4.

The findings indicate a negative correlation between plastic hinge length and reinforcement parameters, where increased longitudinal reinforcement content restricts plastic zone development. Under varying geometric and construction conditions for the prototype laterally loaded micropiles, the plastic hinge length along the pile shaft by means of the above empirical calculation ranges from 0.4D to 1.6D.

3. Experimental Model

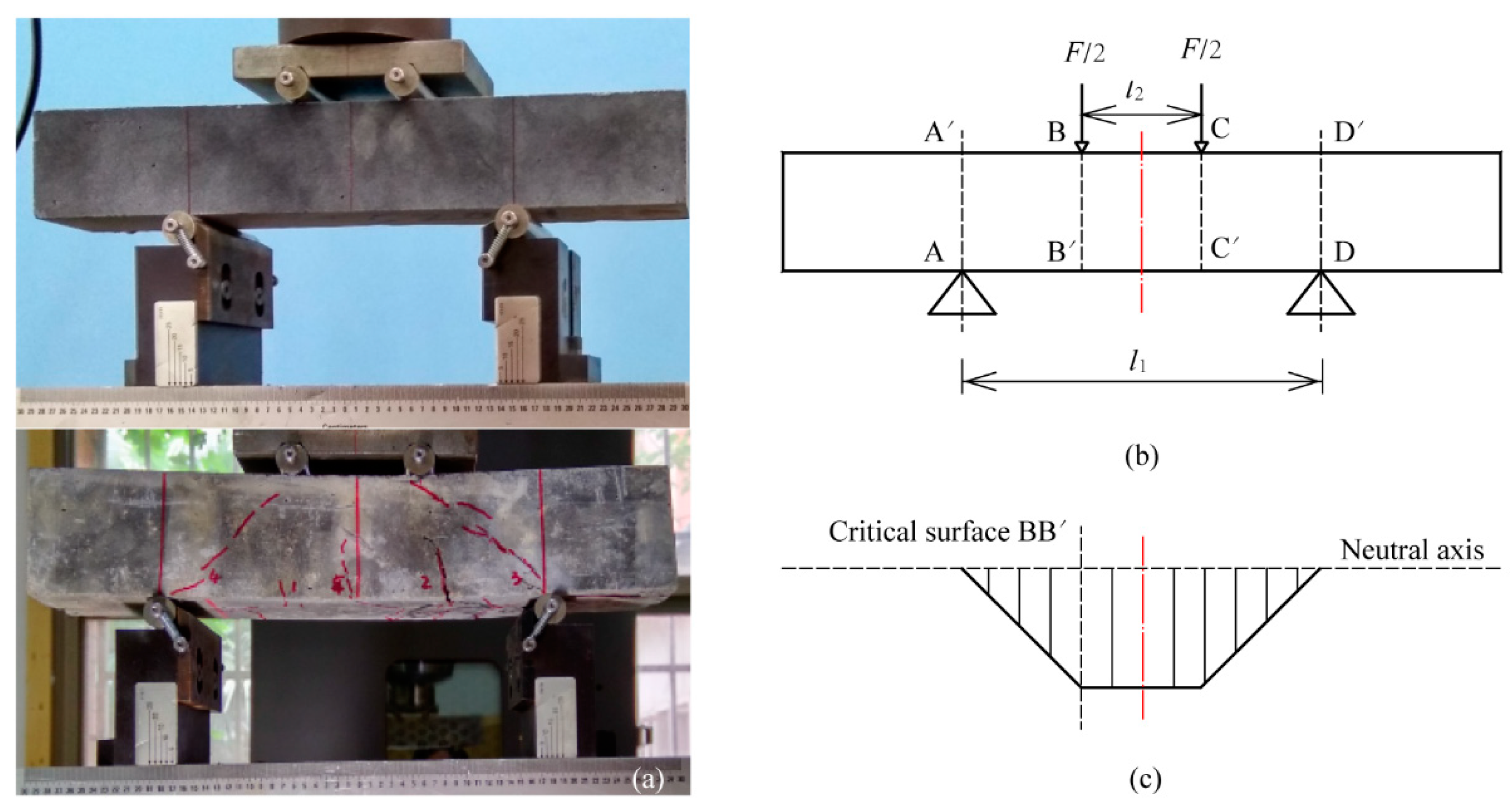
3.1. Materials

Parametric sensitivity analyses confirmed that the 1:4 scaling ratio optimally balances experimental constraints and field applicability, maintaining model pile diameters approximately within 50–70 mm while accommodating 10–14 mm rebars to replicate realistic reinforcement variability. To optimize practical implementation, the circular prototype pile was converted to an equivalent square section through cross-sectional area equivalence, preserving second moment of inertia compatibility (detailed dimensions in

Table 2. Properties of modeled micropiles.

Prototype Circular Pile Diameter/cm	Prototype Pile Cross-Section S/cm2	Equivalent Square Sectional Dimension/mm	Scaled Factor	Model Pile Cross-Sectional Dimension/mm	Area-Similarity Ratio
22.5	393.9	49.95 × 49.95	4	50 × 50	15.8
27.0	572.3	59.82 × 59.82	4	60 × 60	15.9
32.0	803.8	70.896 × 70.896	4	70 × 70	16.4

). Dimensional analysis using Buckingham π theorem established rigorous scaling relationships for bending moments, deflections, and shear forces, ensuring mechanical response fidelity between prototype and model. Scale effects were mitigated through normalized physical quantities based on shear strength equivalence, with density and gravitational acceleration scaling factors fixed at unity to preserve stress similitude (

Table 3. Similarity parameters of modeled micropiles.

Variable		Density	Length	Area	Force	Stress	Strain	Elastic Modulus	Shear Modulus	Bending Stiffness	Shear Rigidity	Time	Internal Friction Angle	Cohesion
Notation		ρ	L	A	F	σ	ε	E	Gs	EI	Gs A	t	$\varphi$	c
Basic dimension	M	1	0	0	1	1	0	1	1	1	1	0	0	1
	L	−3	1	2	1	−1	0	−1	−1	3	1	0	0	−1
	T	0	0	1	−2	−2	0	−2	−2	−2	0	1	0	−2
ni		1	4	16	16	1	1	1	1	256	16	1	1	1

).

Concrete mixtures were proportioned according to Chinese standards (GB/T 50080) [33] using graded aggregates (water:cement:sand:gravel): C20: 0.51:1:1.81:3.68; C25: 0.44:1:1.42:3.17; C30: 0.38:1:1.11:2.72; C35: 0.44:1:1.225:2.485. Reinforcement configuration achieved longitudinal reinforcement ratios of 3–7% through controlled placement of Grade HRB400 rebars.

The anti-slide pile model test employed a 1:4 geometric scaling ratio following similarity theory and Buckingham’s π theorem, maintaining prototype elastic modulus for stiffness equivalence while reducing loads by 1:16 (geometric ratio squared). Material density scaling (theoretically 1:4) was impractical due to inherent constraints (e.g., concrete aggregates), prompting adoption of prototype materials with unity density ratio, prioritizing geometric, stiffness, and force similarity over strict gravitational compliance. Derived scaling ratios governed displacement (1:4), bending moment (1:64), and stress (1:16), with post-processing corrections (multiplied by 4, 64, 16) mitigating gravity-related deviations. Despite introducing scale effects (e.g., nonlinear material behavior), this approach ensures representative deformation and internal forces for bending-critical piles, balancing practicality and accuracy in engineering design.

3.2. Test Scheme

Based on the characteristics of prototype micropiles with diameters of 225–320 mm, reinforcement ratios of 3–7%, concrete strengths of C20–C35, and longitudinal rebars of 10–14 mm, this study fabricated 20 geometrically scaled reinforced concrete specimens (30 cm length, cross-sections of 50 × 50, 60 × 60, or 70 × 70 mm). A parametric experimental matrix was established by systematically varying pile cross-section (50/60/70 mm), concrete strength (C20/C25/C30/C35), and longitudinal reinforcement ratio (3~7%). Specimens were fabricated using ±0.5 mm-tolerance steel molds with 10/12/14 mm steel rebar as reinforcement, molded and fabricated using standardized procedures and cured under standard conditions (20 ± 2 °C) for 28 days. Modeled micropiles were loaded in four-point bending tests using the MTS Landmark testing system (MTS Systems Corporation, Eden Prairie, MN, USA) (100 kN capacity, ±0.5% accuracy) under displacement control at a rate of 0.03 mm/s. The loading frame featured self-aligning spherical seats to minimize eccentricity and ensure pure bending within the inner span (100 mm) and outer span (200 mm). Meanwhile, the test specimen was supported at two bottom points located 5 cm from each end (1/3 of the specimen length), and downward concentrated loads were applied at the top points positioned 5 cm from the midpoint of the pile shaft (Figure 5a).

Applied load was monitored in real time via the MTS actuator’s integrated load cell. Vertical displacements were recorded using Harbin HLC-2 dial indicators (Harbin Measuring & Cutting Tool Group Co., Ltd., Harbin, China) (25 mm range, ±0.01 mm accuracy) mounted symmetrically at critical sections.

Bending moment at the critical section was calculated using static equilibrium M = F (L₁ − L₂)/4, as shown in Figure 5b, and maximum bending stress was subsequently derived using beam theory: σ_max = 6 M/D³, where D is the side length of the square cross-section.

3.3. Numerical Calculation

Plastic deformation analysis of prototype piles was conducted through finite element modeling to validate the reliability of model pile test results. Cross-sectional simulations of reinforced concrete micropiles were performed using XTRACT 3.05, enabling quantitative determination of ultimate bearing capacity and plastic curvature. This established methodology has been successfully applied in modeling nonlinear behavior of reinforced concrete structural members, as well documented by Chadwell [34]. The numerical framework employs the Mander constitutive model [35] with differentiated material parameters for confined concrete, unconfined concrete, and reinforcing steel with yield strength of 400 MPa.

The simulation process accounts for progressive damage mechanisms in composite sections under combined loading conditions. Tensile cracking initiates when principal stress exceeds the concrete’s tensile strength, with residual tensile stress maintained at 1 MPa in the unconfined concrete constitutive relationship to ensure computational continuity. Final failure occurs when confined concrete reaches its crushing strain limit, terminating the calculation sequence. Notably, the model incorporates two critical simplifications, namely reinforcement activation exclusively in tension and pure bending assumption (axial force exclusion).

4. Results

This study establishes a 2D finite model to simulate multi-material progressive failure under combined loads, capturing critical features like concrete spalling and steel rebar’s stress redistribution. During cross-sectional design and structural analysis, reinforcement should be uniformly distributed within the section and aligned with the principal moment direction to maximize the ultimate moment capacity of the section. Comparative analyses reveal that 45° loading optimally balances axial/transverse bending components, synchronizing concrete–steel strength development to enhance stress uniformity, delay concrete crushing, and maximize bearing capacity. Load angles of 45° demonstrate superior material utilization and energy dissipation, replacing prior model-specific claims with generalized conclusions for dynamic loading investigations. This optimized loading configuration was consequently adopted to minimize numerical artifacts, particularly addressing potential underestimation errors in conventional analytical approaches.

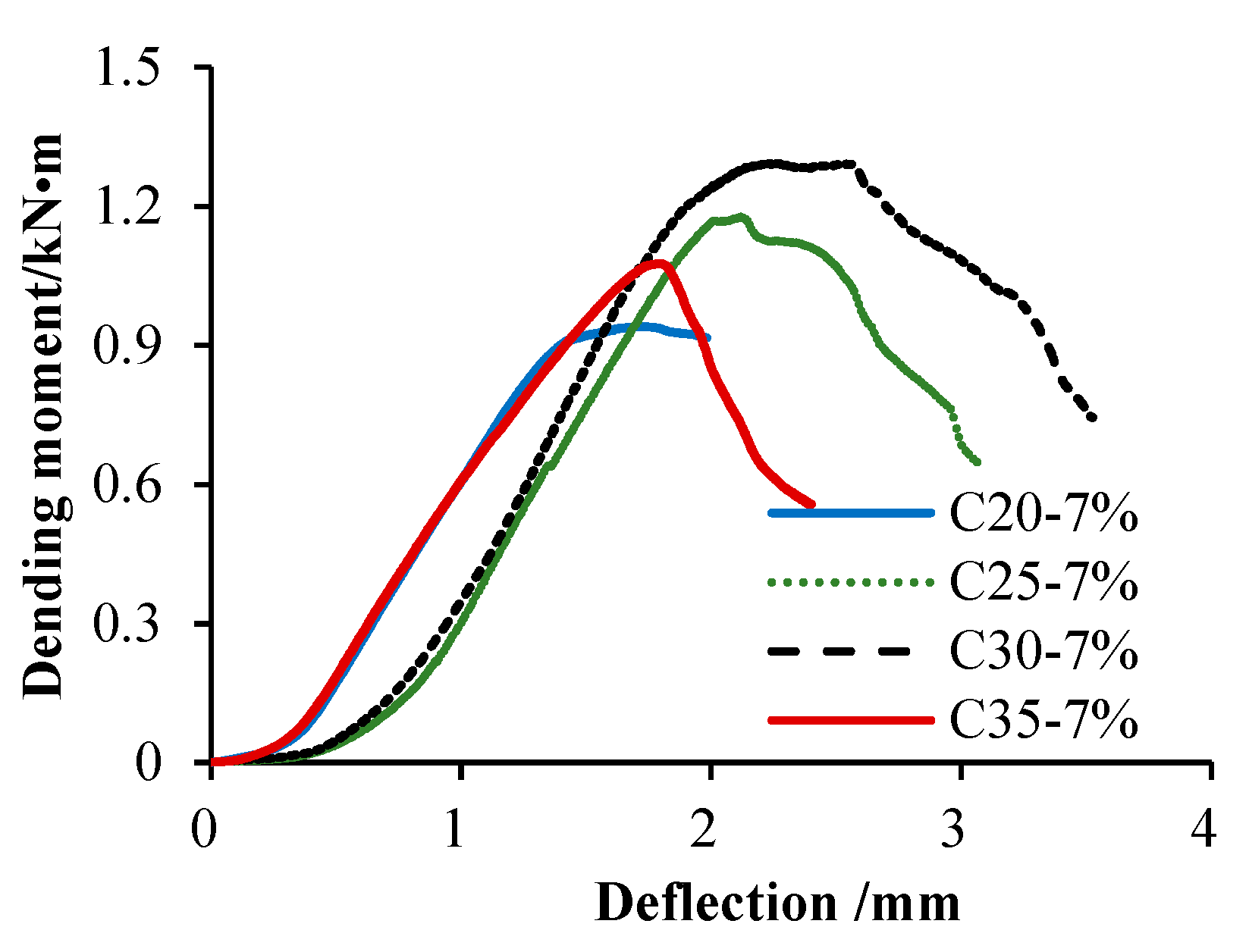
4.1. Failure of Micropiles

Vertical concentrated loads are applied to the surface of the model pile, as shown in Figure 5a, with force points B and C at the top of the component and support points A and D at the bottom, forming an inclined equilibrium force system. The segment of the pile AA′D′D undergoes bending deformation under the action of the two concentrated forces, initially generating one or more tensile cracks near the central axis of symmetry. These cracks are approximately perpendicular to the neutral axis and extend upwards as the load increases. Subsequently, inclined cracks appear at the simply supported points A and D, extending toward the force points B and C. As the load progresses, the tensile cracks along the central axis of symmetry begins to close. The inclined cracks then extend toward the force points B and C. Longitudinal splitting cracks develop at the central axis of the lower end face of the specimen and rapidly propagate towards the left and right ends, eventually splitting through the ends and extending to the upper surface, preventing the inclined cracks from closing into an arch. The typical bending moment distribution diagram for the bent component, shown in Figure 5b, is compared with the experimental schematic. The critical section BB′ (CC′), located at the force application points, experiences no shear force and exhibits the maximum bending moment. The bending moment in section BC is equal to the maximum moment M_max of the section. The displacement recorded in the direction of the applied force at the critical section corresponds to the deflection value at the force application point. This leads to the establishment of the moment–deflection curve.

Figure 6 presents the results of the bending test for a model pile with a cross-sectional size of 60 mm × 60 mm, concrete grades C20~C35, and a 7% reinforcement rate. The characteristic load values are determined based on the curve characteristics. As the surface of the model pile becomes compressed under the action of the indenter and enters the bending deformation stage, the pile’s bearing capacity reaches the elastic starting point load F1. This is characterized by the development of diagonal cracks at the pivot points A and D (as shown in Figure 5b), leading to bending shear in the AB′ (C′D) section. The load at which diagonal cracks first appear is considered the initial shear load F2.

When the reinforcement and concrete deform uncoordinatedly, and tensile cracking occurs along the longitudinal axis, the load is defined as the tensile cracking load F3. As the load–deflection curve enters the yield stage or softens beyond the strength limit, F2 is less than the initial yield load (F4) or ultimate load (F5), though tensile cracking occurs after the peak load. In the residual strength stage after plastic damage, the reinforcement bond layer begins to deteriorate. At 59.3% of the ultimate load, with a deflection of 53.7% of the ultimate deflection, flexural cracking is observed on the B′C′ tension surface. When the load is reduced to 88.1% of the ultimate load, and the deflection reaches 112.0% of the ultimate deflection, oblique cracks penetrating the cross-section are observed. These observations indicate that under transverse loading, concrete cracks first initiated on the flexural-tensile side of the pile shaft, followed by shear damage. As bending continues, the main reinforcement undergoes bending and tensile deformation, leading to bond cracks with the concrete and eventually causing longitudinal cracking in the pile concrete. The flexural strength required for longitudinal cracking of the pile is greater than the shear strength needed for concrete bending and tension cracking, as well as the shear strength. The eigenvalues of the bending stresses for the different test pile sections are derived from the load eigenvalues F1 to F5, as shown in Figure 7.

The bending capacity of the micropile cross-section generally increases with higher reinforcement ratios, but when the ratio exceeds 6%, the weakening effect of flexural rigidity in concrete during the transition from elastic deformation to ultimate failure becomes pronounced. For concrete grades not exceeding C30, although the ultimate bending strength peaks at a 7% reinforcement ratio, excessive reinforcement disrupts the synergy between steel and concrete: the dense spacing of the main bars reduces concrete’s bond strength, increasing interfacial slippage, while the compression zone concrete prematurely reaches its ultimate compressive strain (~0.0033), triggering brittle crushing failure. Lower-grade concrete has a reduced elastic modulus, leading to a faster reduction in compression zone height under high reinforcement ratios. Once the reinforcement ratio surpasses the critical threshold, the concrete fails before steel yielding, causing strength degradation. This nonlinear interaction stems from the dynamic balance between concrete’s ductility reserves and steel reinforcement’s strengthening effects, with lower concrete grades exacerbating strain incompatibility and limiting reinforcement effectiveness.

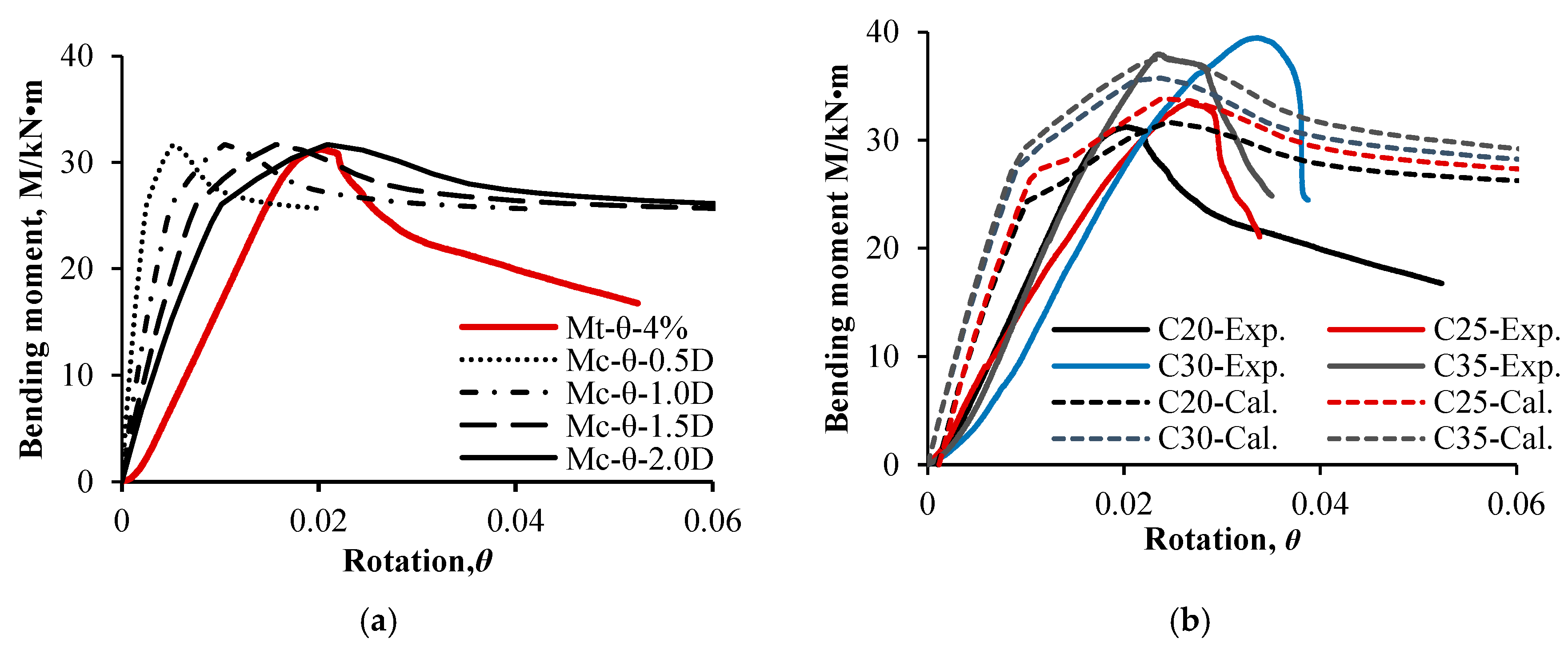
4.2. Plastic Hinge Length of Micropiles

To directly compare experimental values with prototype numerical analysis results and simplify the solution of mathematical models, such as differentiation, further processing of the model test results was conducted. Firstly, the moment–curvature data output from the finite element program were calculated and converted into sectional moment–angle curves (M_c–θ) using plastic hinge lengths of 0.5D, 1.0D, 1.5D, and 2.0D, respectively. Then, based on the physical model test’s measured deflection, the critical surface angle of rotation was identified, and a similar transformation was applied to solve the prototype’s flexural capacity, constructing the measured curve (M_t–θ).

As shown in Figure 8a, the turning angle of the model pile was larger than the theoretical value, and the deformation stiffness modulus of the model pile was lower than the theoretical value for the circular pile with a diameter of 225 mm under the same bending moment. The peak bending moments of the model pile load–deflection curves were very close to the theoretical values. Upon comparison, it was found that the peak bearing capacity fit was highest when the plastic hinge length of the finite element model was assumed to be 2.0D. Therefore, assuming that the length of the plastic hinge for the micropile is equal to two times the diameter of the pile or the height of the cross-section, the curves for different concrete strengths (M_c–θ) were calculated and compared with the test results (M_t–θ). As shown in Figure 8b, the theoretical bending moment–rotation curve of concrete piles follows a nonlinear trend with an initial rapid rise followed by gradual stabilization, reflecting the transition from elastic to plastic behavior until failure. As the rotation angle θ increases, the bending moment grows rapidly in the elastic stage (stable stiffness), slows near peak (yielding stage with microcrack-induced stiffness degradation), and stabilizes post-peak (plastic deformation or localized failure). The varying concrete material strength of the model pile from C20 to C35 leads to a theoretical increase in the cross-section’s ultimate load by a maximum of 20%. The experimental results, however, show a sharp post-peak decline. This divergence stems from reduced post-peak ductility in core-reinforced configurations compared to steel cage systems, where interfacial slip between reinforcement and concrete weakens deformation compatibility, resulting in deviations between theoretical and experimental bending resistance post-peak. Despite deviations caused by the size effect in reinforcement configuration design, the bearing capacity–deformation curves of model piles with varying concrete strengths remained closely aligned with the theoretical peaks. Consequently, a plastic hinge length of 2.0D was recommended for micropiles under bending conditions.

5. Discussion

In contrast to conventional “stubby” reinforced concrete structures [36], micropiles demonstrate enhanced plastic hinge length characteristics. The equivalent plastic hinge length of ordinary reinforced concrete piers shows significant variability (0.29–1.27D [37]). Nevertheless, due to fundamental differences between micropiles and conventional piers in structural parameters (diameter-to-length ratio, reinforcement ratio) and load-bearing mechanisms (flexure-dominated vs. combined axial-flexural behavior), direct comparisons hold limited engineering relevance. Notably, when considering pile–soil interaction, the plastic hinge length at pile failure reaches 1.02–1.48D [38]. This indirectly suggests that under unconfined conditions (without soil restraint), the plastic hinge length might exceed 1.5D. It must be explicitly stated that this study focuses on the influence mechanisms of micropile material parameters (concrete strength, steel yield point) and structural parameters (diameter-to-length ratio, reinforcement configuration) on plastic zone development, with soil constraint effects intentionally excluded from the analytical framework.

Based on these premises, with the plastic hinge length of the prototype pile established as 2D, subsequent investigations systematically examine the effects of various influencing factors on pile deformation and bearing capacity characteristics.

(1)

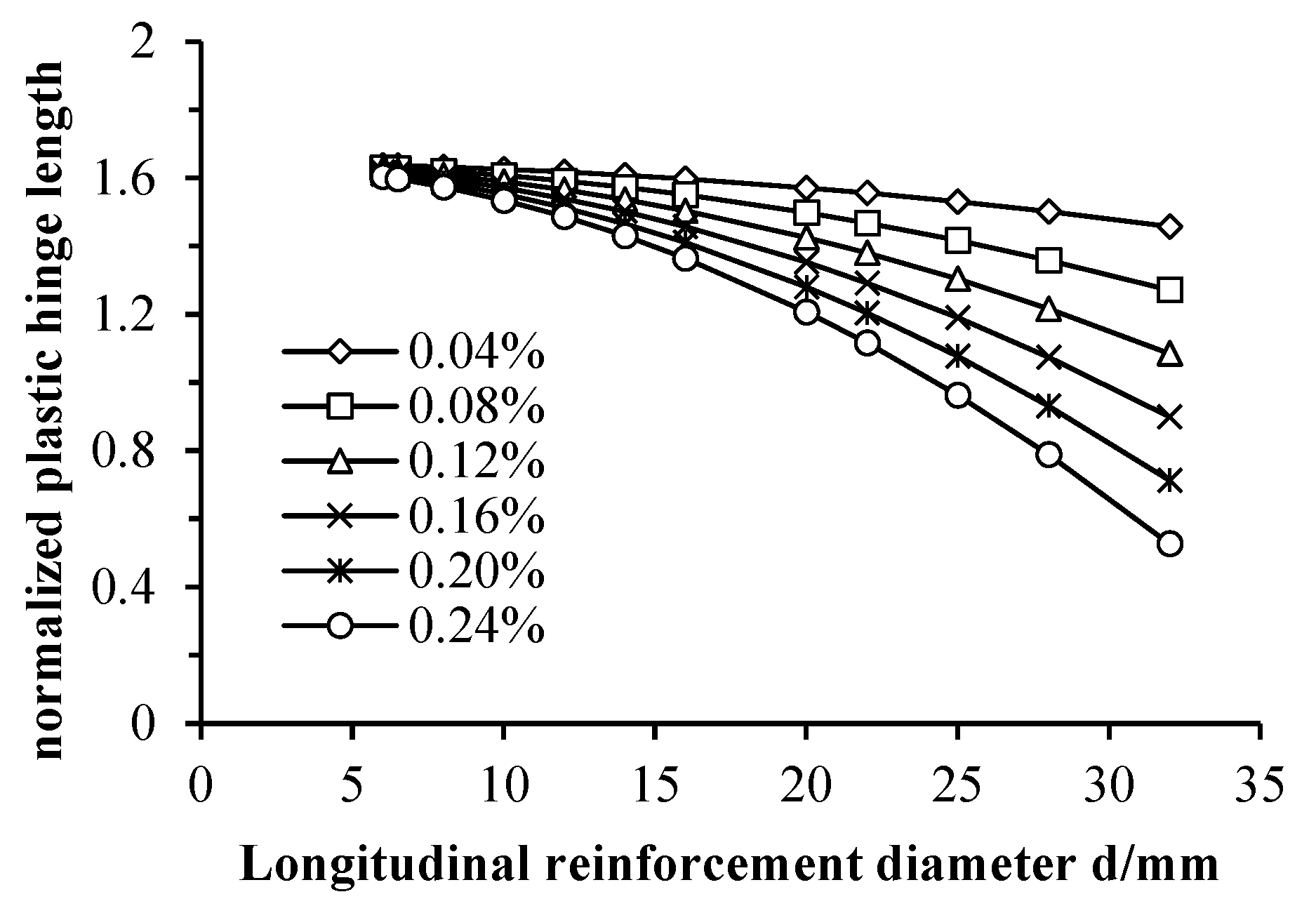
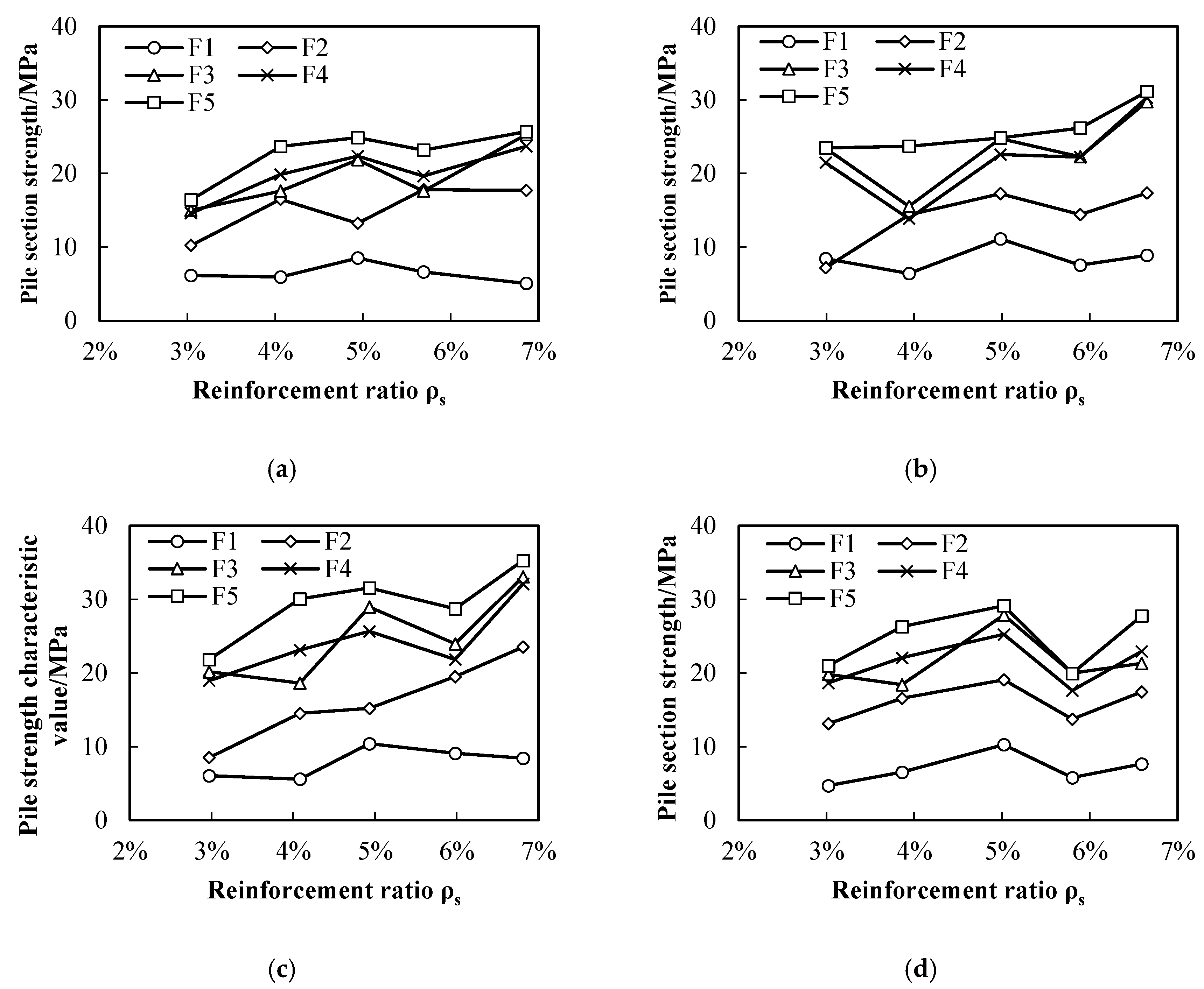
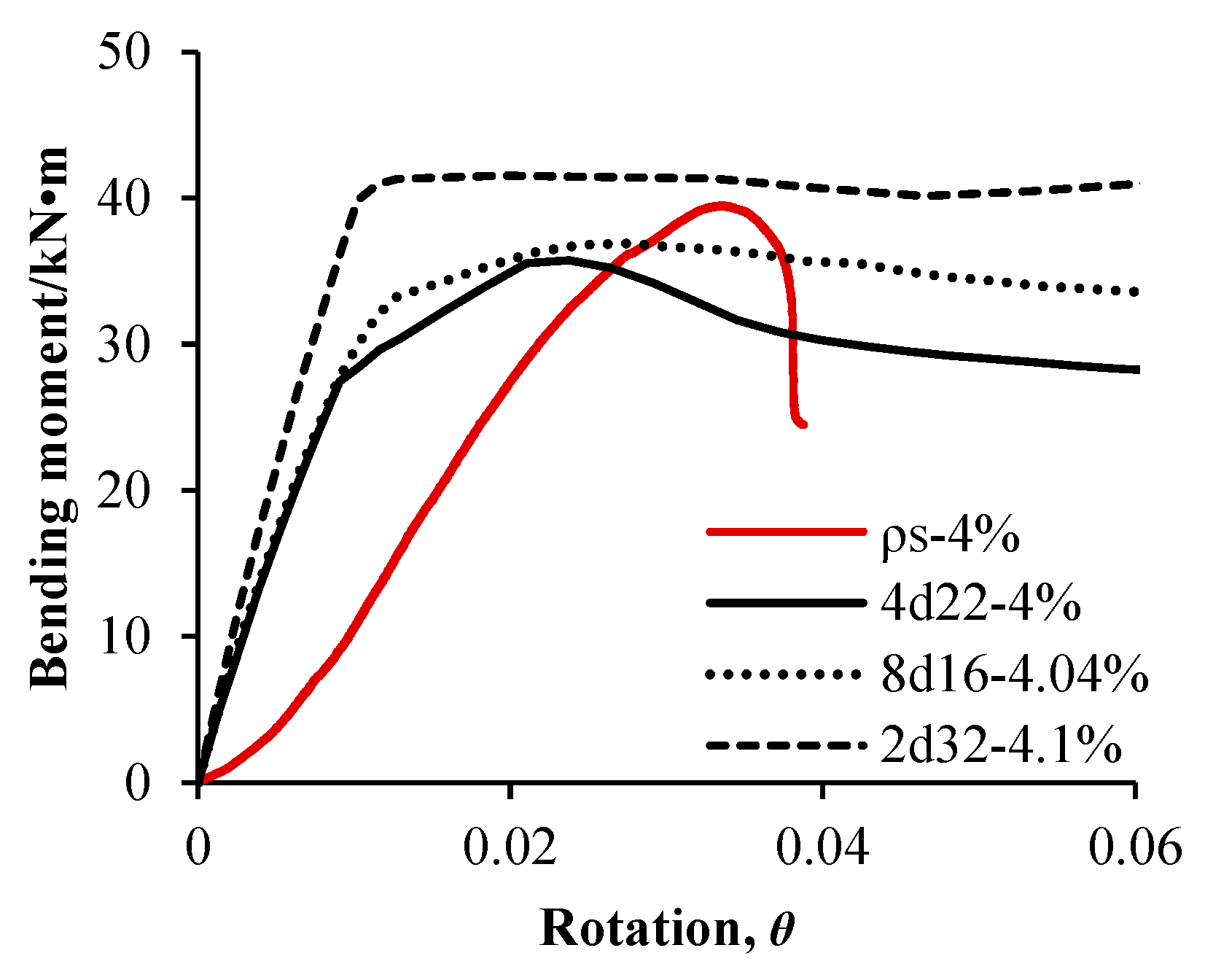
Reinforcement Ratio: In the design of longitudinal reinforcement for pile shafts, variations in nominal steel area may lead to discrepancies between actual and designed reinforcement ratios. This study conducted sensitivity analyses on reinforcement configurations through numerical simulations under a target reinforcement ratio of 4%. The measured core reinforcement of test piles and the theoretical reinforcement cage (comprising 4 × 22 mm, 8 × 16 mm, and 2 × 32 mm bars) exhibited actual reinforcement ratios deviating within ±0.1% of the target value. Structural parameters, such as reinforcement type and layout, induced fluctuations in the reinforcement ratio within the target range. Despite identical target ratios, variations in bar diameter selection, quantity, and spatial arrangement resulted in bending capacity differences among micropiles, with reinforcement ratio errors up to 1%. As shown in Figure 9, when the deviation between actual and target reinforcement ratios was ≤0.1%, the error in the section’s ultimate bending moment remained within ±5%. This demonstrates that minor deviations in reinforcement ratios (≤0.1%) have negligible practical impacts on ultimate bending capacity, provided the actual ratio closely approximates the design target.

(2)

Concrete Material Strength: Traditional theory suggests that improvements in compressive strength are often accompanied by reductions in structural ductility. Li et al. [39] demonstrated that for every 10 MPa increase in concrete strength, the section modulus of resistance increases by 8–12%, while the ductility coefficient decreases by 0.15, indicating that pursuing high strength alone may exacerbate the risk of brittle structural failure. The experiments in this study revealed that for every 5 MPa increase in strength, the peak bending resistance of the section increased by 6.8–9%. However, test results showed maximum performance at C30 concrete strength, exhibiting nonlinear characteristics in the low-to-medium strength range. Simply increasing concrete strength cannot effectively enhance load-bearing capacity of flexible piles, it is recommended to optimize strength matching based on the synergistic performance between steel reinforcement and concrete materials. This can be achieved through material parameter selection to ensure balanced development of structural performance.

(3)

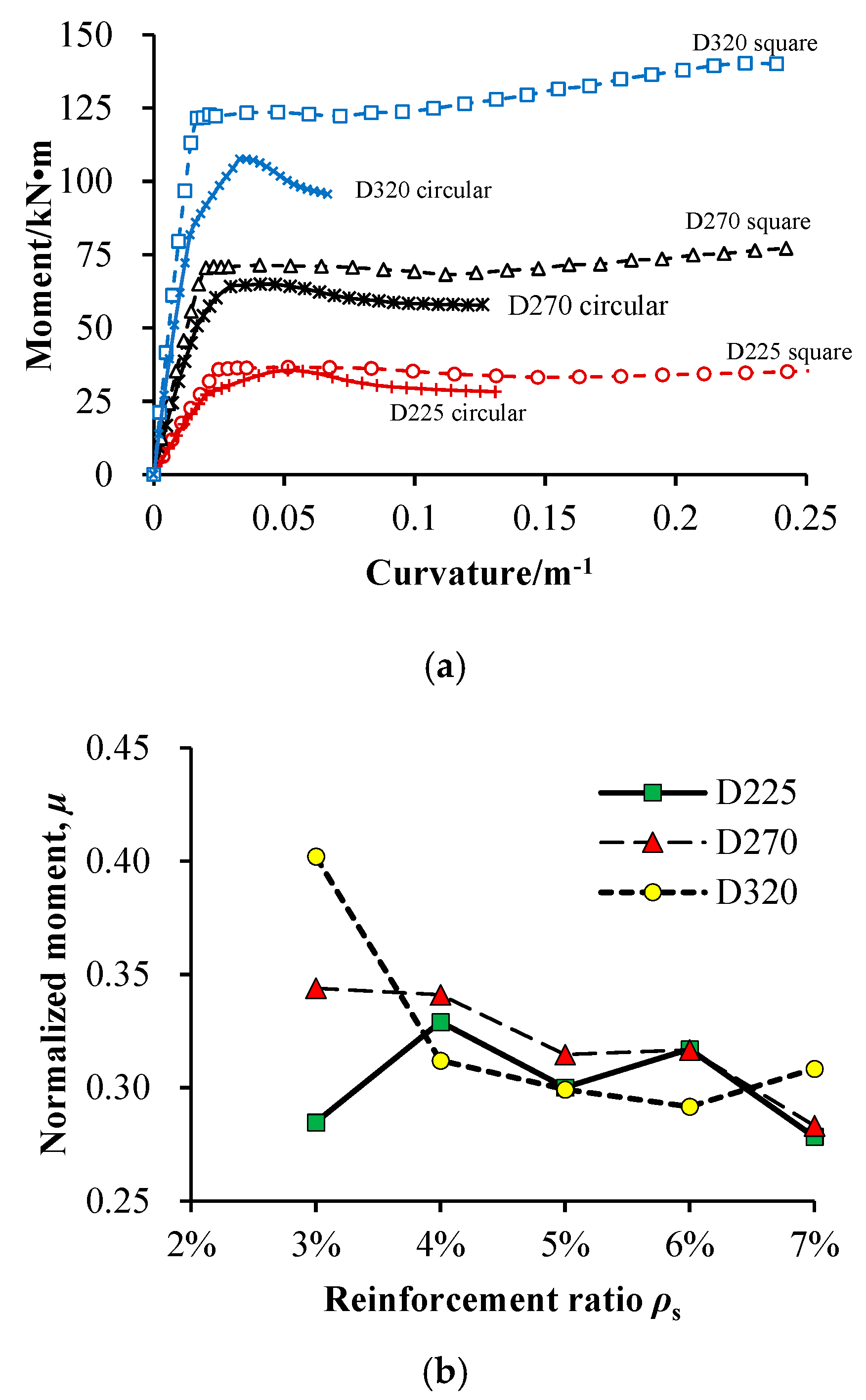
Geometric Features: Physical model experiments were conducted on prototype piles with area equivalence and scaled-down conversion to meet the test apparatus requirements and improve operability. This allows for examining the sensitivity of the pile’s moment–curvature curve to two factors, namely the size and shape of the pile cross-section. The calculation results are shown in Figure 10.

Figure 10a shows that square piles exhibit higher resistance to bending deformation compared to circular piles, subject to area equivalence. When the cross-sectional area is small, the difference in ultimate capacity between the two types is minimal. However, when the pile’s cross-sectional diameter exceeds 300 mm, the bending capacity of the pile with a square cross-section shows an error of up to 15%. The increase in cross-sectional dimensions (whether it is the diameter D of circular piles or the height of square piles) influences the pile’s bearing capacity. As the pile diameter increases, the maximum section bending moment increases slightly. However, when the ratio of effective height to section height is relatively high, the section’s ultimate bearing capacity tends to soften, which may be related to structural size effects. In practical slope or foundation works, the diameter of micropiles generally does not exceed 300 mm. Therefore, if the pile cross-section satisfies the area-equivalence condition, the influence of the pile’s cross-sectional shape on flexural bearing capacity is limited.

Square piles demonstrate superior flexural rigidity compared to circular piles due to their enhanced moment of inertia. Experimental data reveal that square-section piles exhibit up to 20% higher bending resistance under lateral loads than their circular counterparts of equivalent dimensions. Their geometric configuration induces a stress redistribution effect that mitigates stress concentration at the corners. As substantiated by Makkil et al. [40], the higher axial compression stiffness of square piles results in a 10–15% reduction in elastic compressive deformation under identical loading conditions. Crucially, within soil-structure interaction systems, the capacity advantage of square piles is amplified through optimized stress diffusion among soil particles. This enhancement mechanism primarily stems from two factors: the improved stress distribution pattern in the surrounding soil matrix and the frictional reinforcement at the pile–soil interface [40,41]. These findings collectively underscore the positive influence of square pile geometry on soil mechanical responses, particularly in optimizing load transfer efficiency and structural resilience.

To investigate the relationship further, the normalized cross-sectional bending moment, was used to establish a dimensionless bending moment-reinforcement ratio curve, as shown in Figure 10b.

$$\mu =M_{max}/A_y{f}_y{h}_0$$

(6)

When the reinforcement ratio is between 4% and 6%, changes in the pile diameter have little effect on the weakening influence of the reinforcement ratio on the cross-section’s nonlinear bearing capacity. However, when the reinforcement ratio is below 4% or above 7%, increasing the cross-sectional dimension benefits the improvement of the pile’s bearing capacity.

6. Conclusions

This study presents a systematic investigation into the influence of material properties on micropile flexural performance through an integrated approach combining theoretical analysis, numerical modeling, and experimental validation. Employing plastic hinge theory grounded in limit equilibrium principles—which assumes rotational hinge formation at critical sections upon reaching ultimate bending moments, the methodology successfully predicts flexural failure modes in micropiles. The proposed framework strategically simplifies earth pressure distributions into fundamental mechanical conditions while excluding soil nonlinearity, offering practical advantages for preliminary design optimization. This controlled analytical approach facilitates efficient parametric evaluation of material properties (e.g., concrete strength grades) and structural configurations (e.g., reinforcement ratios), establishing a systematic pathway for developing cost-effective micropile solutions. The key findings include the following points.

(1)

Micropile failure predominantly manifests as shear failure and tension-shear failure along slip surfaces. Shear resistance enhancement can be achieved through three strategic interventions, namely (1) implementation of high-strength concrete materials, (2) optimization of reinforcement ratios, and (3) localized reinforcement at critical slip zones. Mechanical analysis demonstrates that targeted strengthening within plastic hinge regions effectively mitigates risks of premature structural collapse.

(2)

The plastic hinge length in reinforced concrete flexural members serves as an indicator of plastic zone development. While existing empirical formulas derived from beam–column damage tests provide initial estimates, their applicability to micropile structures requires further validation. Comparative analysis of physical tests and numerical simulations reveals that a plastic hinge length assumption of 2D (where D represents pile diameter) optimally predicts peak load capacity when considering cross-sectional dimensions and longitudinal reinforcement conditions. Notably, soil–pile interaction reduces this length proportionally to soil stiffness characteristics.

(3)

Reinforcement configuration variations induce minimal deviations in longitudinal reinforcement ratios (<0.1%) and pile capacity calculation errors (<5%). However, concrete strength variations combined with insufficient stirrups in physical models compromise core concrete confinement, resulting in up to 15% measurement discrepancies in ultimate load predictions.

(4)

Finite element modeling incorporating stirrup confinement effects demonstrates that micropile’s geometric characteristics significantly influence ultimate load capacity under a 2.0 h plastic hinge assumption. Diameter increases amplify cross-sectional shape impacts, while empirical formulas reveal an inverse relationship between plastic hinge length and reinforcement ratio. Both experimental measurements and numerical results indicate that pile size effects modify this correlation through cross-sectional scaling mechanisms.

Critical limitations emerge from the decoupled soil–pile interaction model, which neglects stress redistribution in actual slope systems and potentially overestimates safety factors under large deformation conditions. Future research should adopt a phased implementation strategy. Initial efforts must quantify plastic zone propagation under distributed loads (e.g., triangular/trapezoidal lateral pressures) to establish failure mode transition criteria. Subsequent phases should prioritize developing nonlinear soil–pile interaction models that numerically simulate interface degradation and soil softening effects, validated through field monitoring to elucidate multifactor synergies. This progressive integration of numerical simulations and empirical data will enable the development of lifecycle-oriented design frameworks for micropile systems.