Approximate Analytical Algorithm for Pull-Out Resistance–Displacement Relationship of Series—Connected Anchor Plate Anchorage System
Abstract
1. Introduction
2. Theoretical Research Methodology
2.1. Fundamental Assumptions
- (1)
- During the pull-out process, the soil pressure is effectively distributed and borne by the multiple anchor plates, thereby significantly enhancing the overall structural load-bearing performance. Under the same conditions, the ultimate bearing capacity of the series-connected anchor plates, with double plates, is approximately 70% higher than that of a single anchor plate.
- (2)
- When dealing with high-fill engineering projects, series-connected anchor plates can significantly reduce the negative impact of the “group anchorage effect”. This effect refers to the mutual interaction between adjacent anchor plates (i.e., those in multiple rows and columns), resulting in a reduced stability of the entire support system. The series-connected anchor plates effectively increases the vertical and horizontal spacing between anchor plates, thereby mitigating the impact of this effect.
- (3)
- The series-connected anchor plates, which are lightweight and possess strong bearing capacity, make them more suitable for use in complex and special construction environments. Installing multiple anchor plates on the same rod not only simplifies the construction process, but also reduces the material and labor costs, further enhancing both the economic and social benefits of the project
- (1)
- Assume absolute rigidity of the anchor plate and neglect the frictional resistance between the steel rod and the surrounding soil.
- (2)
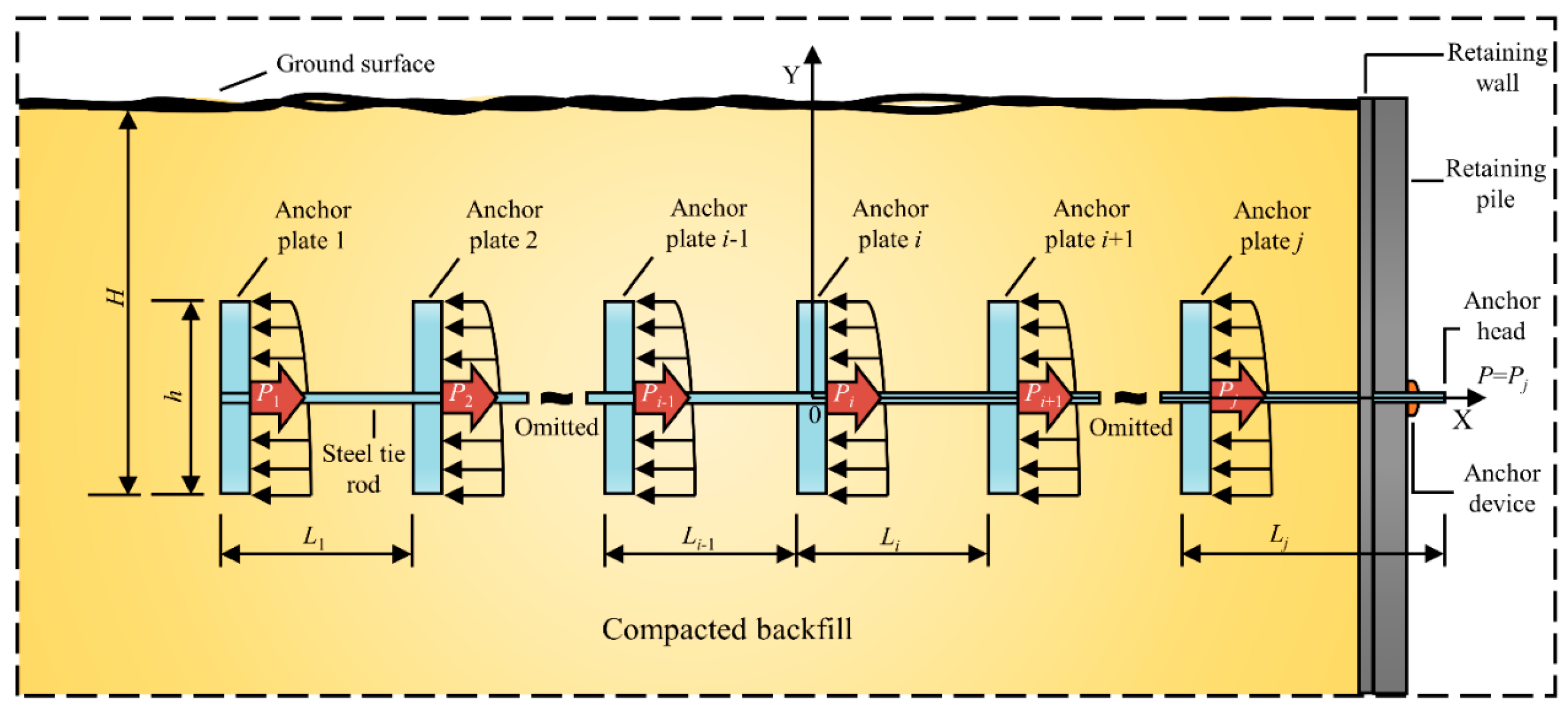
- The series-connected anchor plates consist of j anchor plates and tie rod (as shown in Figure 1). Assume that the spacing between the adjacent anchor plates is sufficiently large (i.e., the mutual influence between adjacent anchor plates is not considered).
- (3)
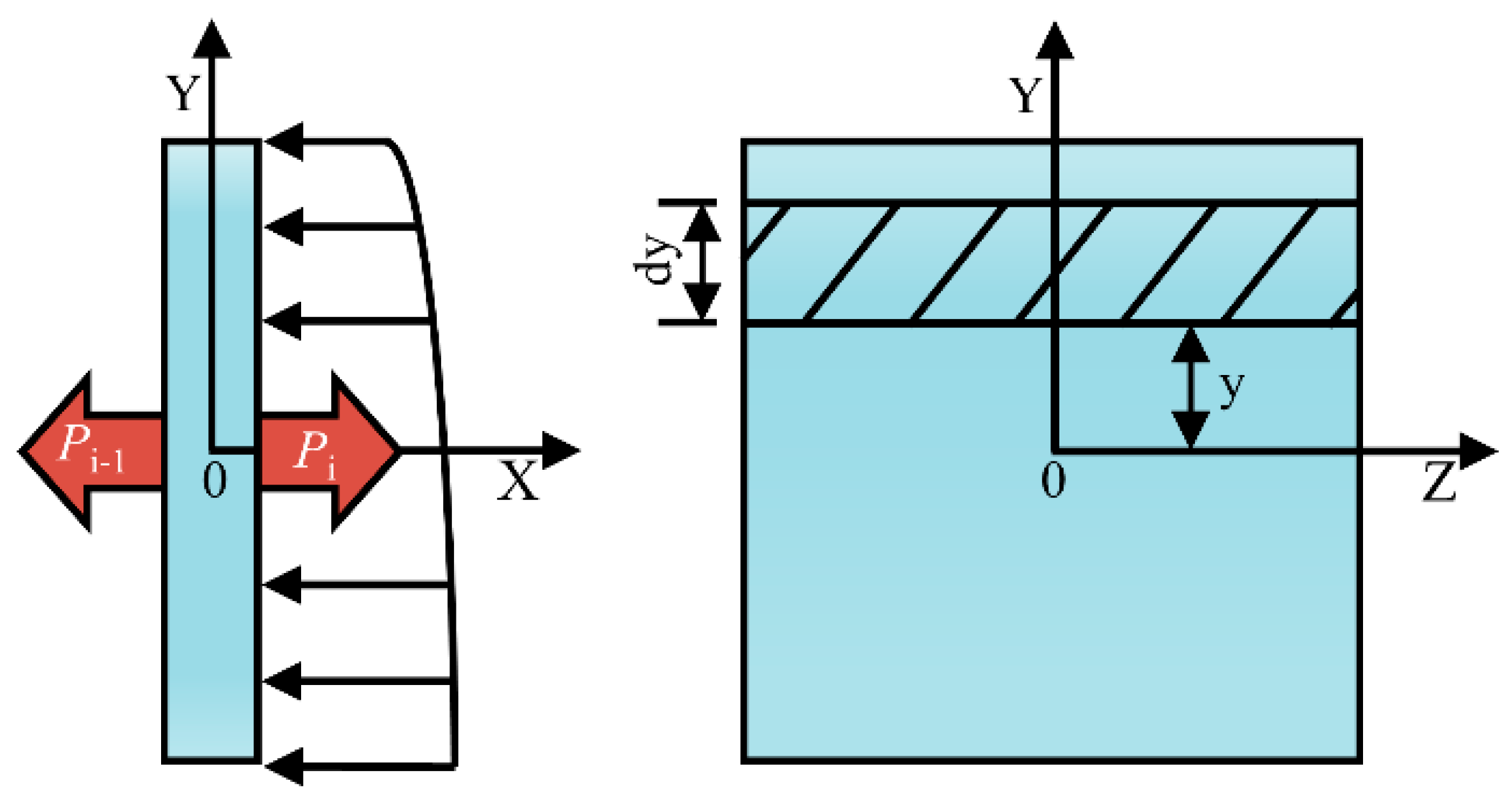
- After the application of tension force, the anchor plate undergoes displacement, causing compression of the soil in front of the anchor plate. The soil in front of the anchor plate exerts horizontal resistance on the anchor plate, known as the elastic resistance of the soil. According to the Winkler assumption, the magnitude of elastic resistance σ is proportional to the displacement of the anchor plate, as shown in Equation (1):where k represents the coefficient of the horizontal subgrade reaction of the soil in front of the anchor plate (kN/m3); x represents the horizontal displacement of the anchor plate (m); y is the distance of the calculation point from the x-axis (as shown in Figure 2), (m); θ represents the rotation angle of the anchor plate around its center (rad).
- (4)
- The anchor plate support system is generally used in fill projects. The scaling factor m of the subgrade reaction coefficient is influenced by various factors including the type of backfill material, compaction degree, and others. In engineering practice, determining this factor m, especially for compacted fill soils, is challenging. However, determining the cohesion and internal friction angle of compacted fill soil is comparatively simpler than determining the factor m. To achieve this, the study referenced the empirical equation for the parameter m, which is related to the soil’s cohesion and internal friction angle. This equation is recommended in the Chinese industry standard, Technical Specification for Retaining and Protection of Building Foundation Excavation (2012) [22]. Additionally, considering the influence of the anchor plate’s horizontal displacement on the parameter m, this paper proposed the following relationship between m and the horizontal displacement of the anchor plate:
2.2. The Formula for Pull-Out Resistance–Displacement Relationship
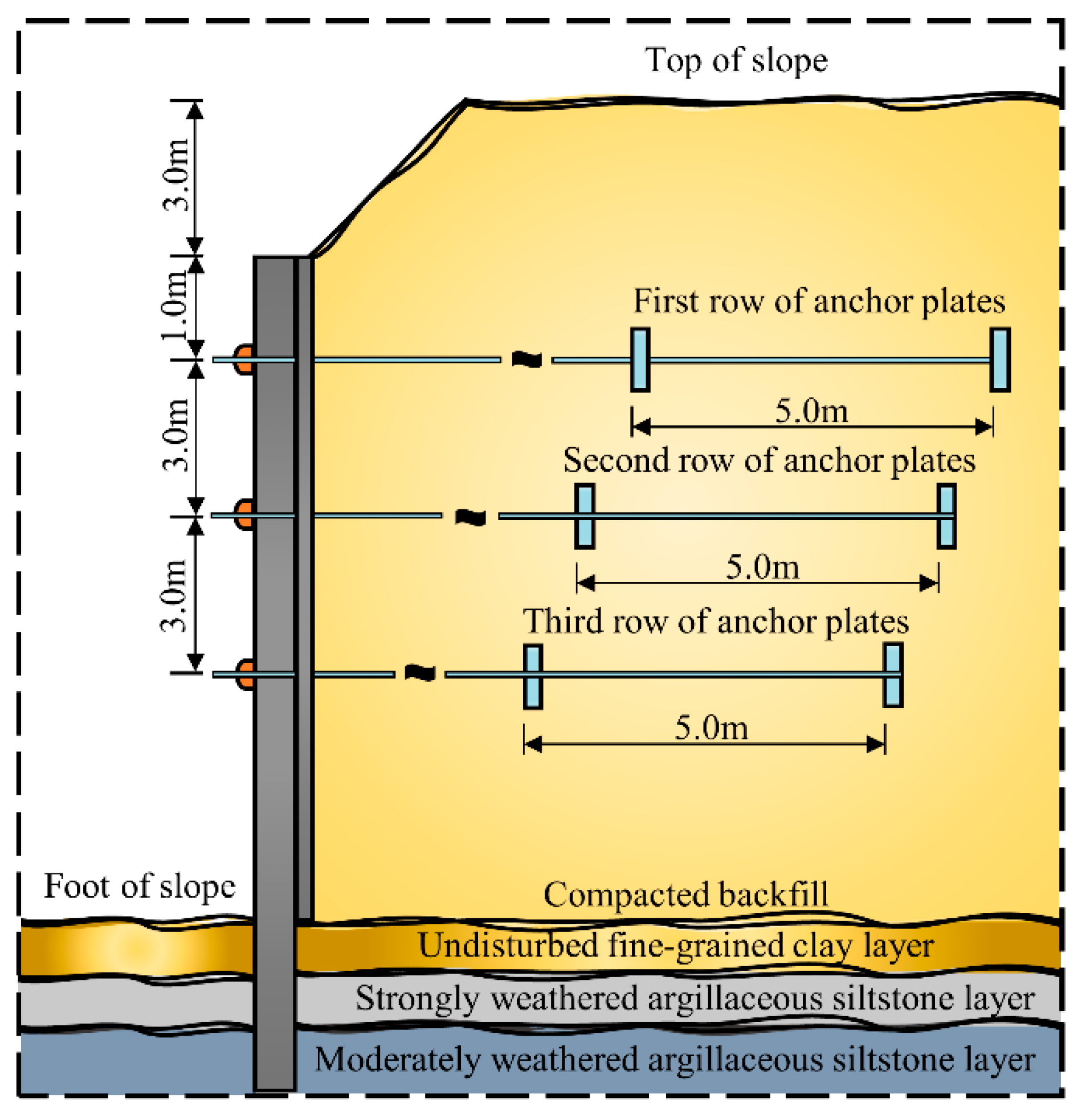
2.3. Applied to Series-Connected Anchor Plates
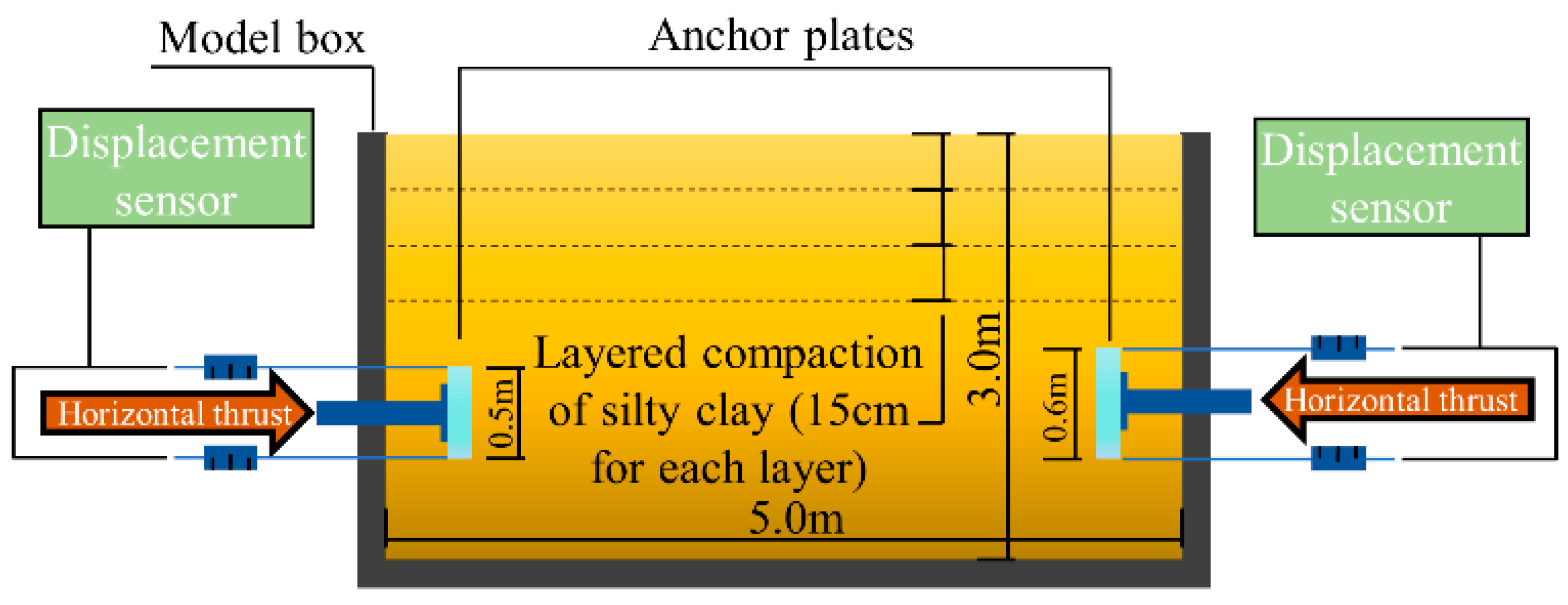
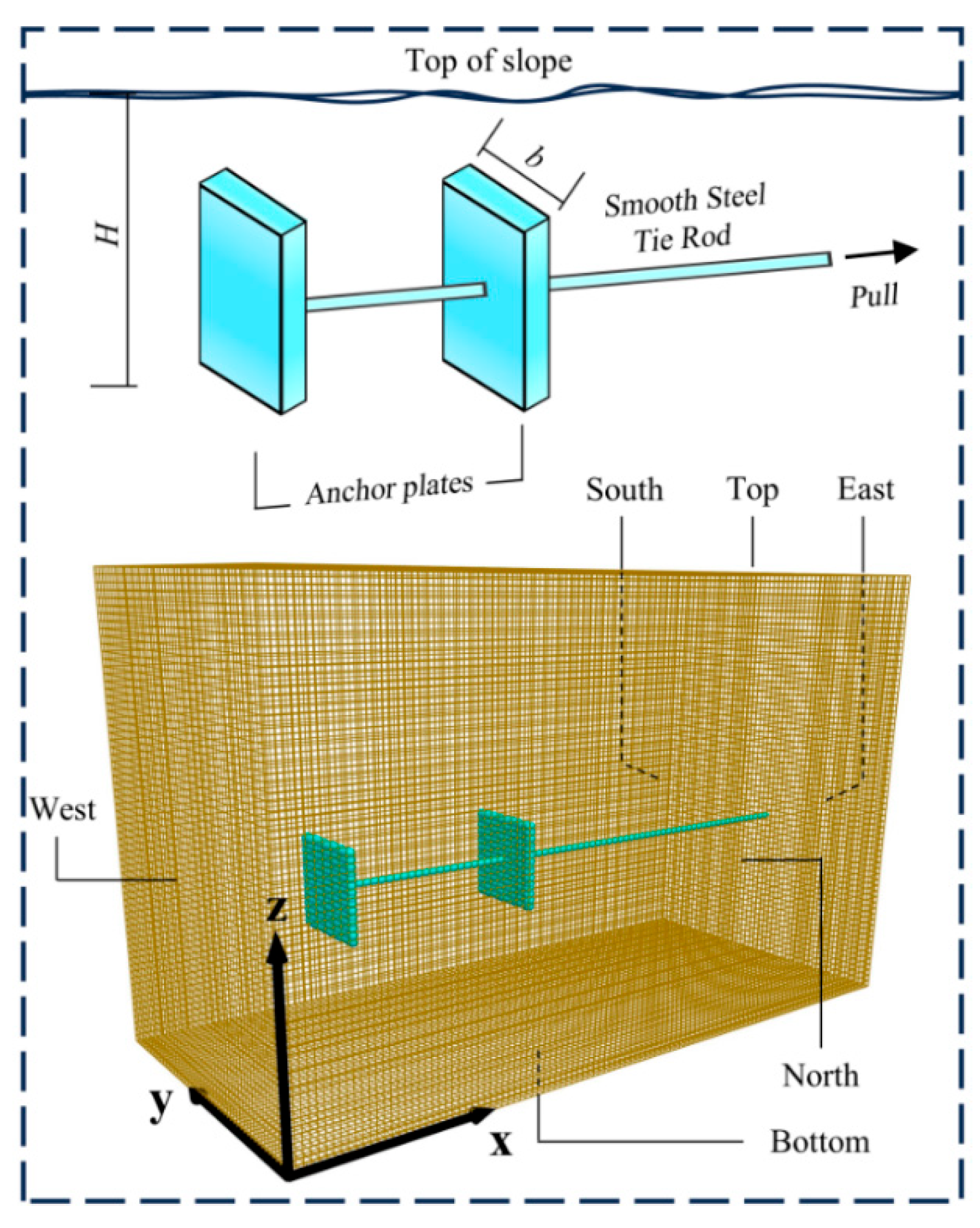
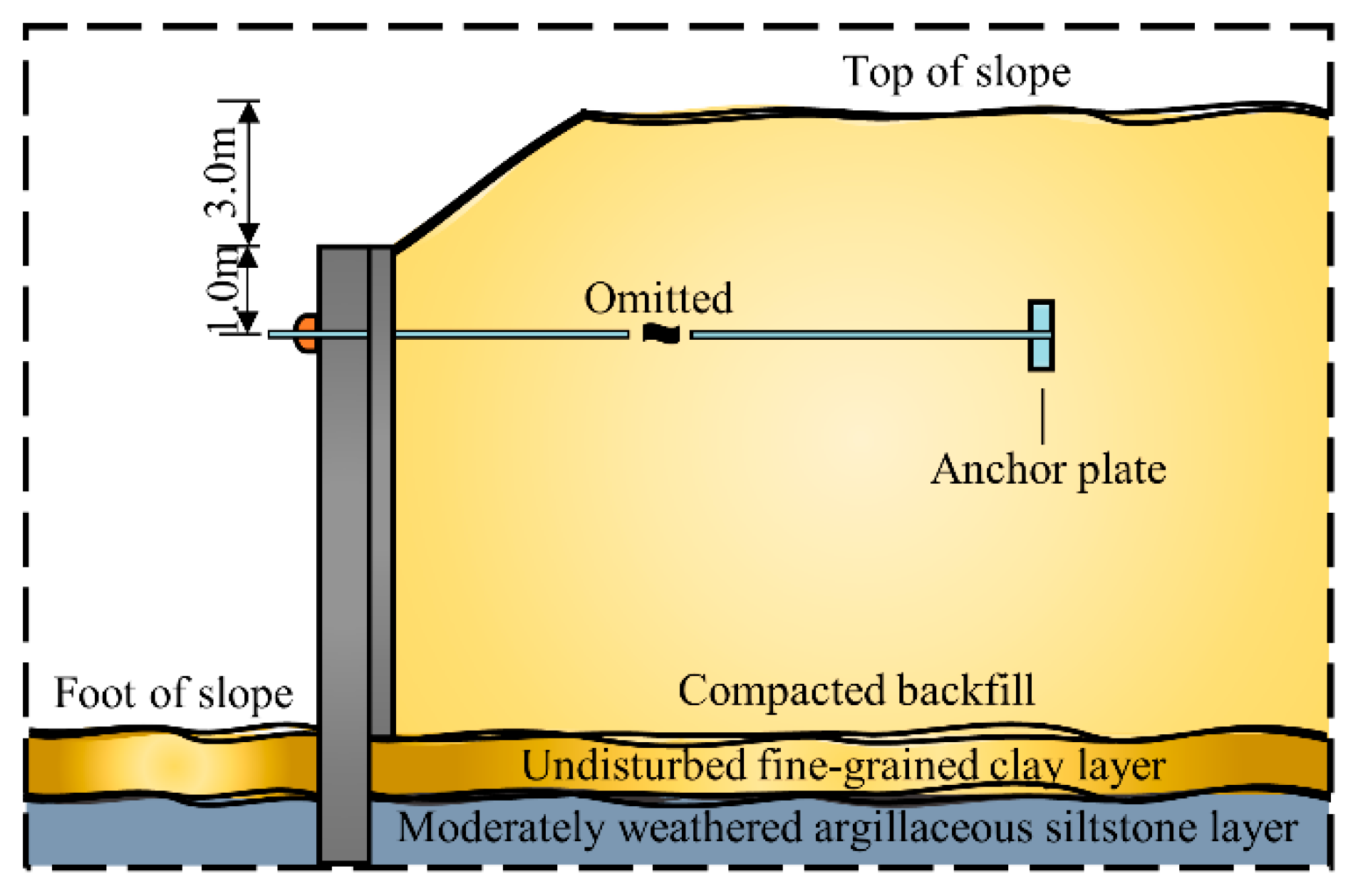
3. Model Test and Numerical Simulation of Anchor Plate
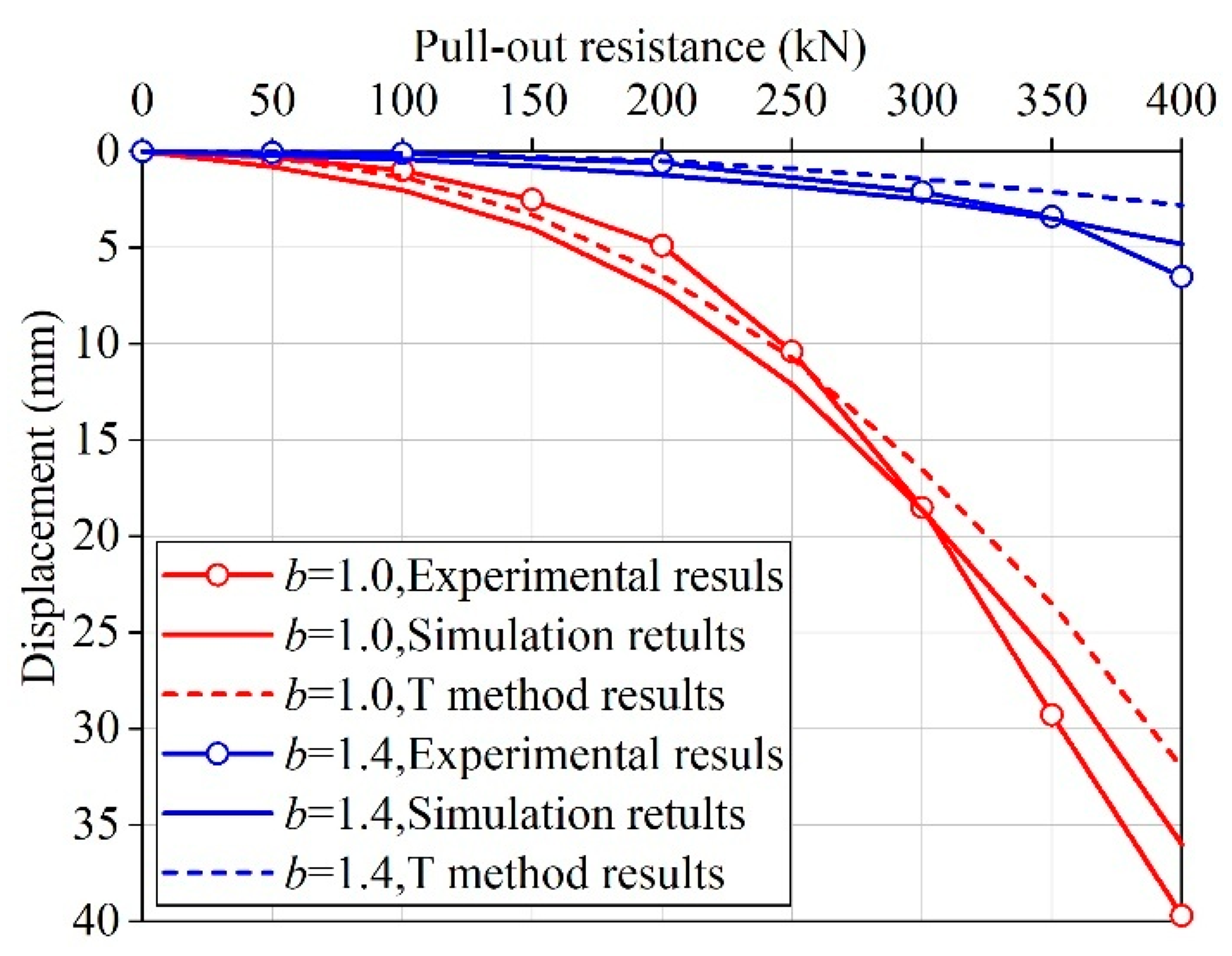
3.1. Comparison of Numerical Simulation and Theoretical Analysis Results
3.2. Establishment of Three-Dimensional Simulation Model
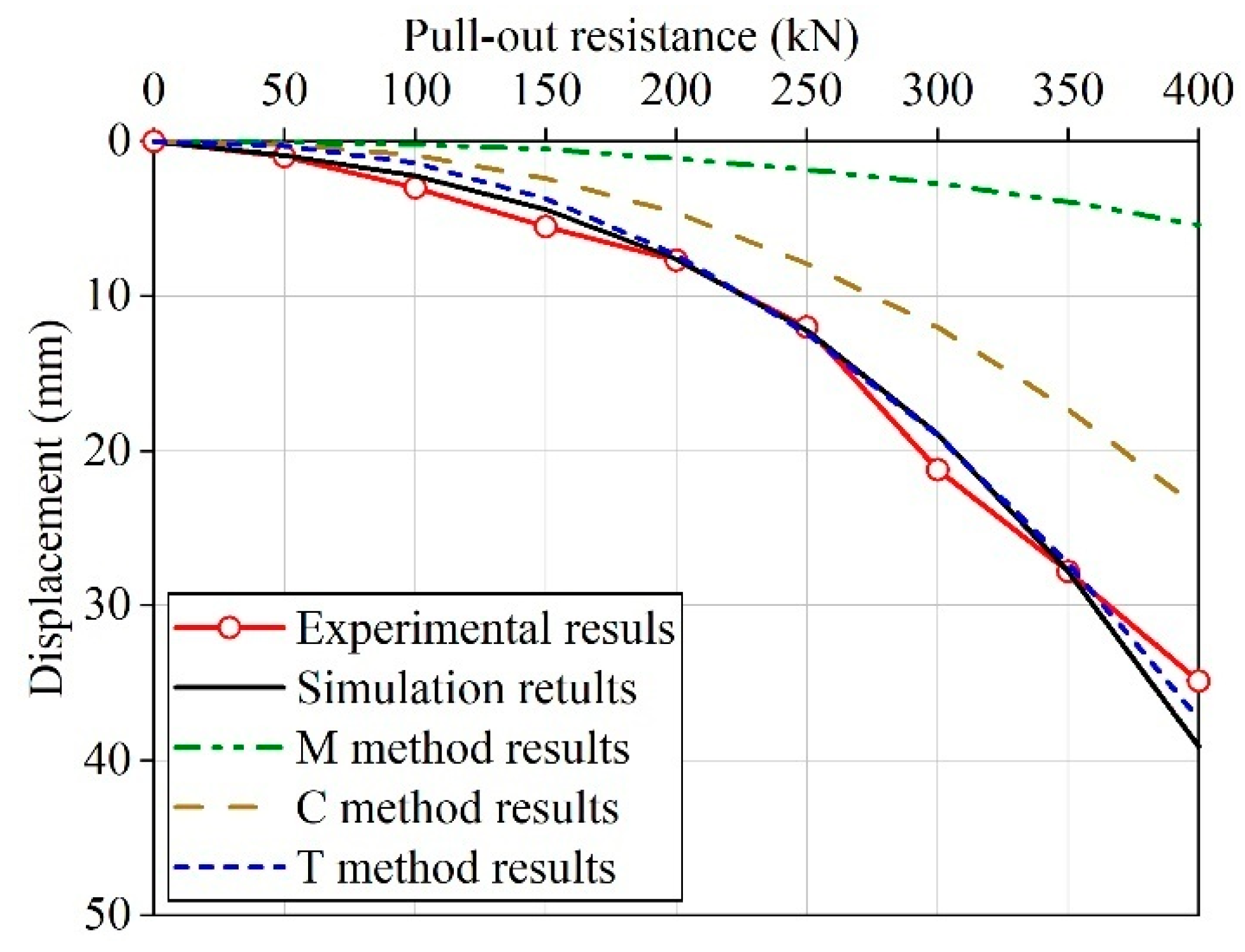
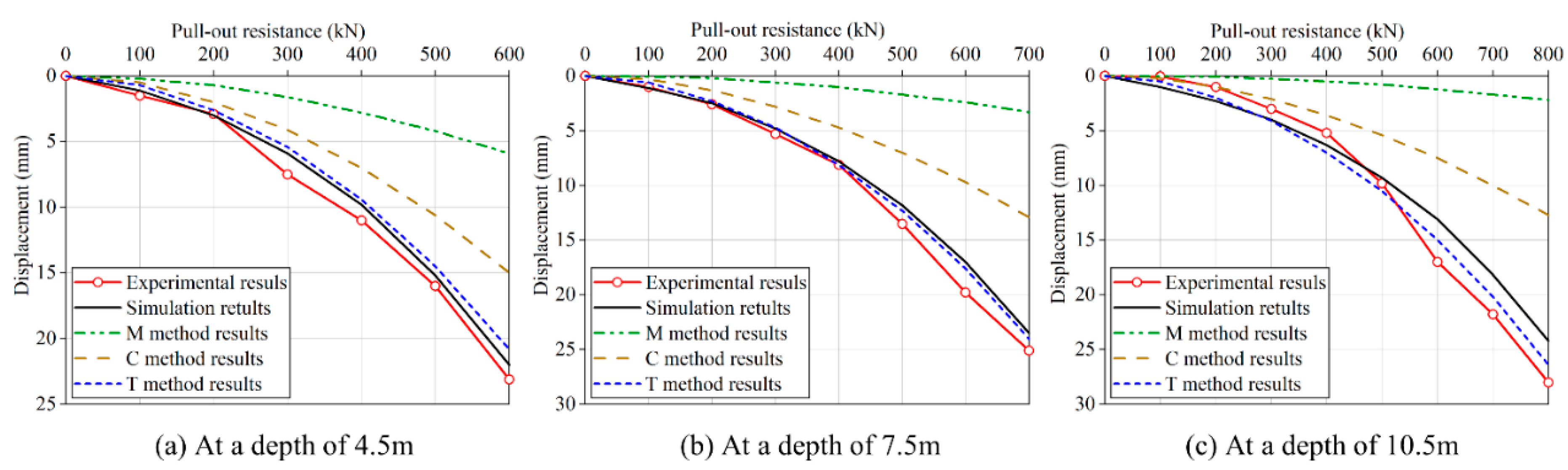
3.3. Comparison of Results
4. Parameters Fitting
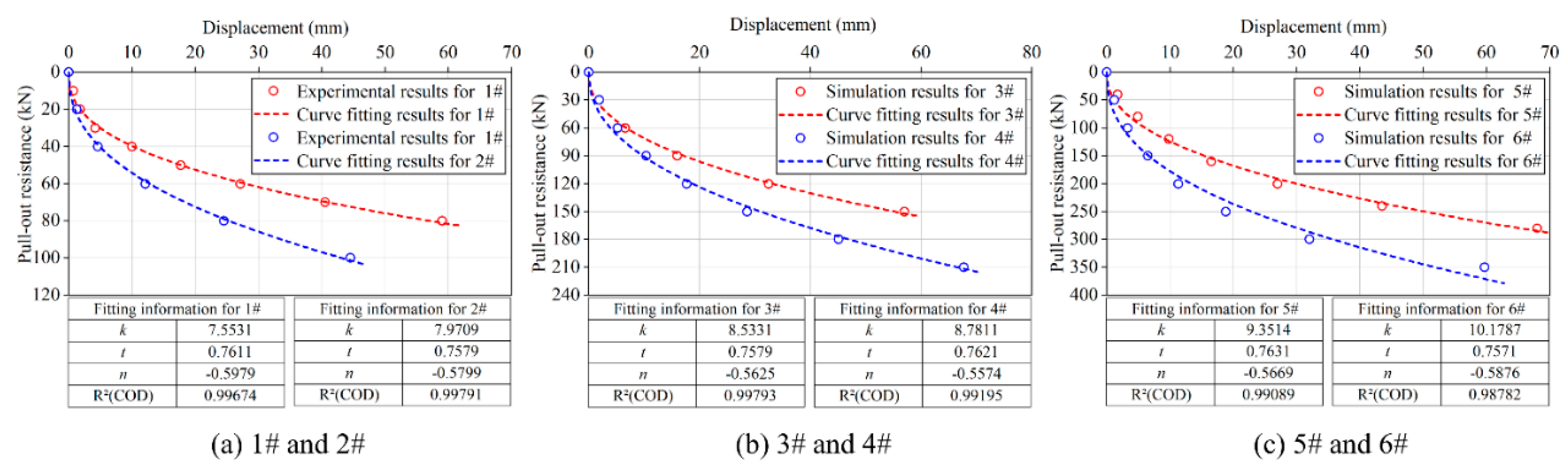
4.1. The Determination of Fitting Samples
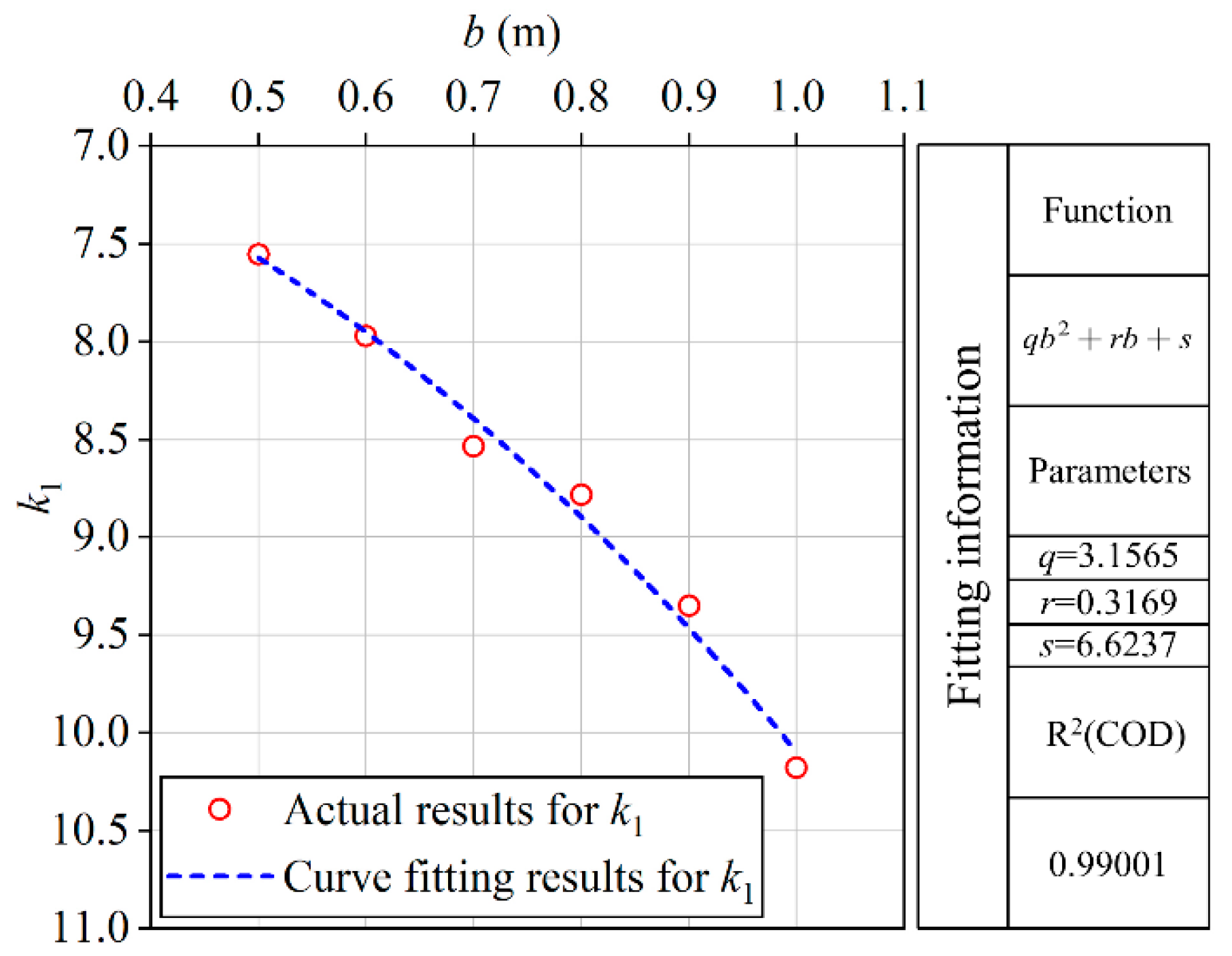
4.2. Fitting of Regression Parameters k1, t, and n for Anchor Plates with Different Sizes
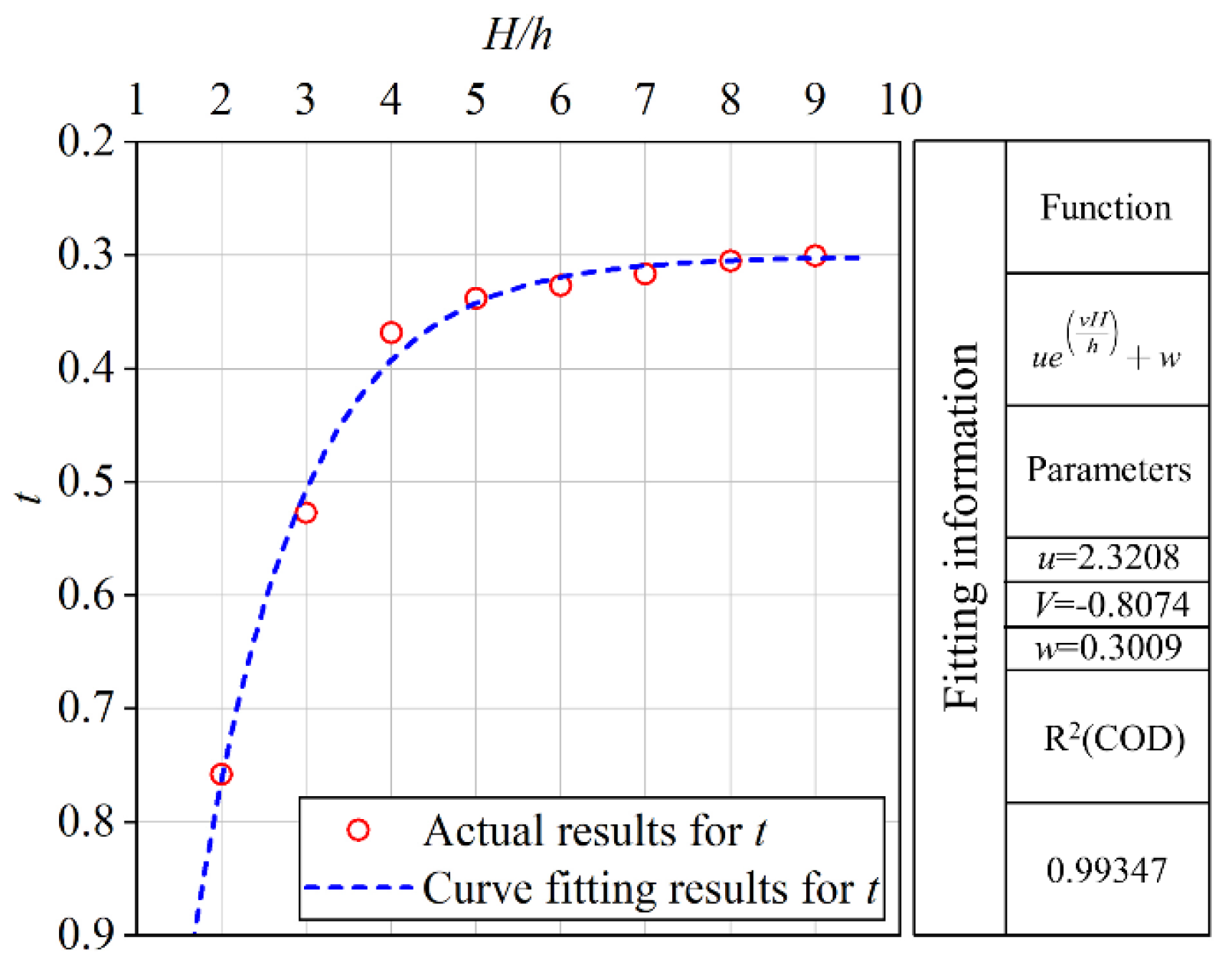
4.3. Fitting of Regression Parameters t and n for Anchor Plates with Different Burial Depths
5. M Method and C Method
6. Examples and Verifications
6.1. Engineering Case 1
6.2. Engineering Case 2
6.3. Engineering Case 3
7. Factors Influencing the Pull-Out Bearing Capacity
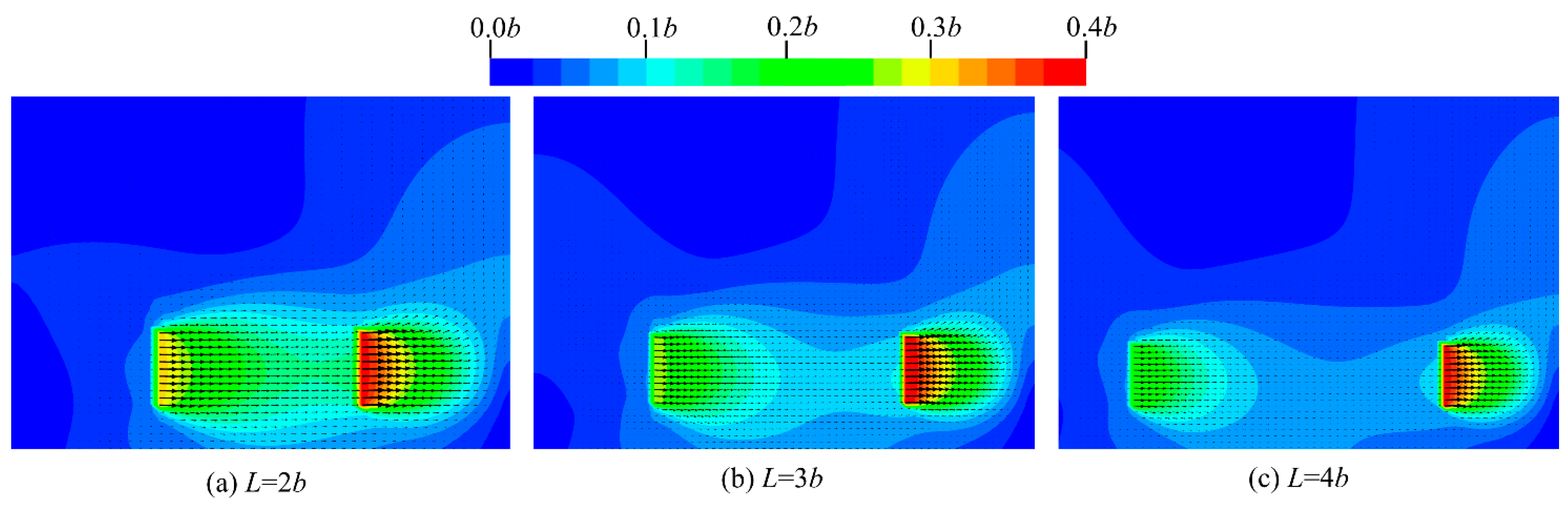
7.1. The Minimum Spacing Between Adjacent Anchor Plates
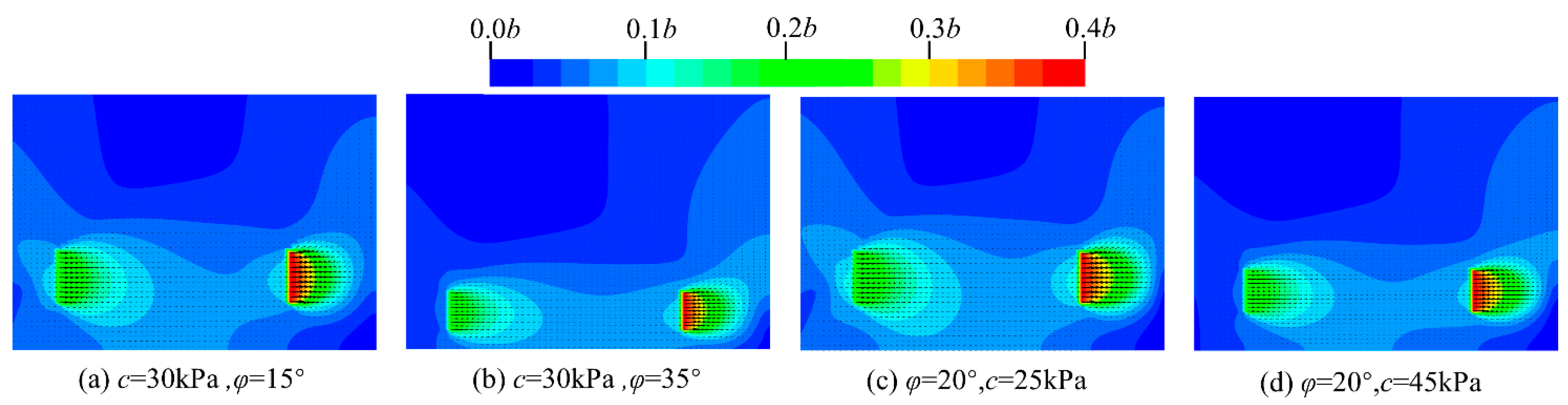
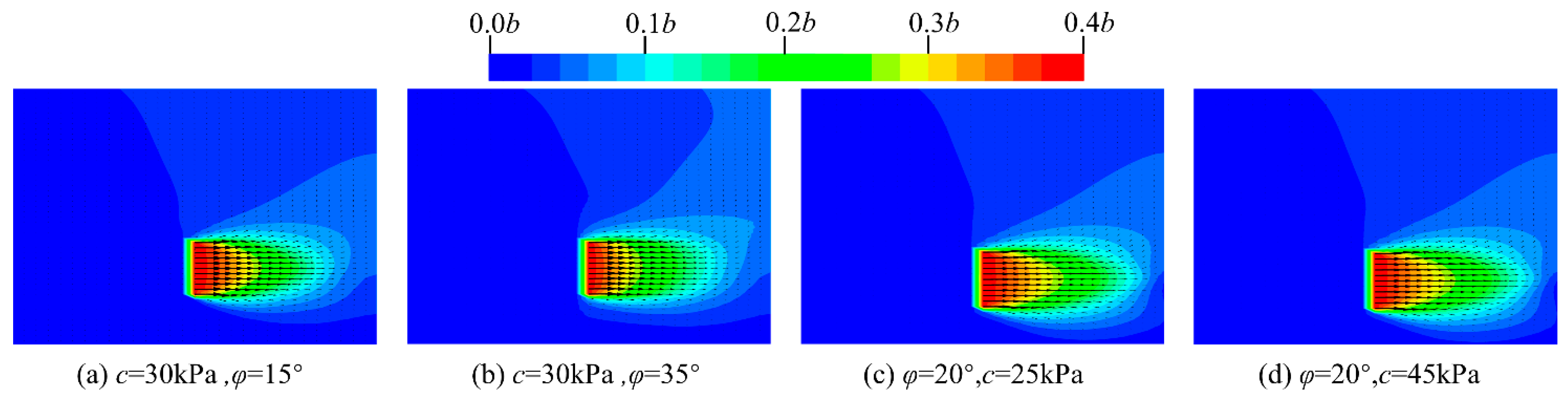
7.2. The Influence of Soil Strength Parameters on the Minimum Spacing of Anchor Plates
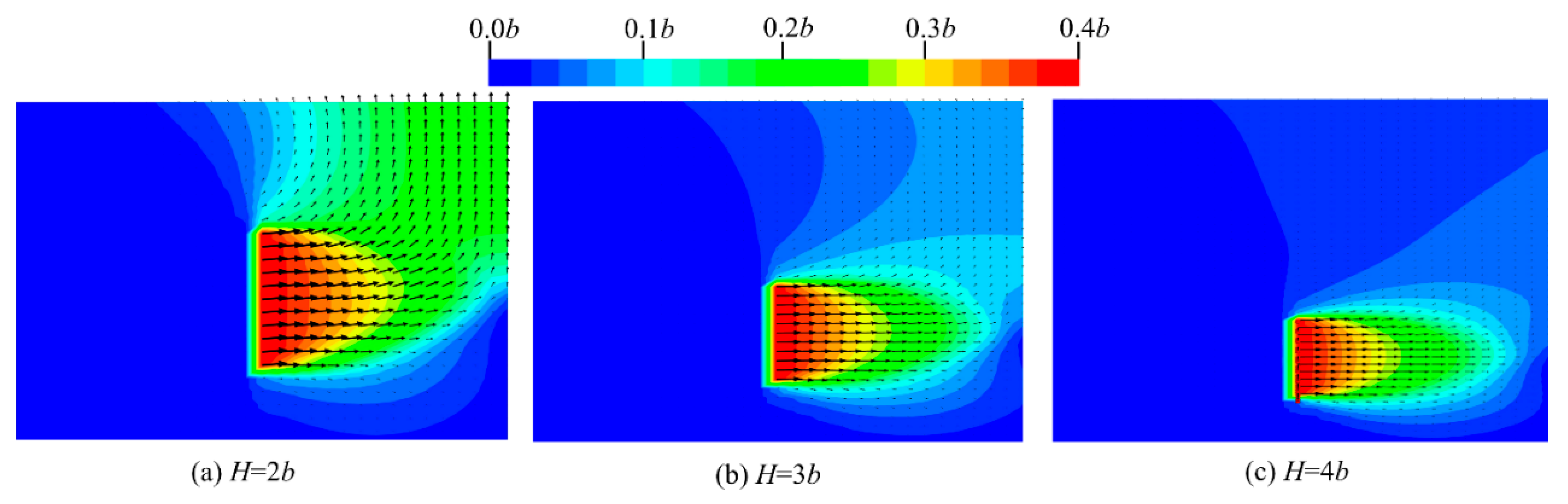
7.3. The Critical Depth Between Deeply Buried and Shallowly Buried Anchor Plates
7.4. The Influence of Soil Strength Parameters on the Critical Depth of Anchor Plate
8. Conclusions
- (1)
- To enhance the pull-out bearing capacity of the anchor plate support system, a series-connected anchor plate support system was proposed. A theoretical analysis method for the pull-out resistance–displacement relationship of series-connected anchor plates was established. Utilizing the findings from large-scale model experiments, along with numerical simulation results and via fitting analysis, approximate analytical solutions for the pull-out resistance–displacement relationship of series-connected anchor plates were obtained. This lays the theoretical foundation for achieving the dual control of both displacement and pull-out resistance in the design of the anchor plate support system.
- (2)
- Through the analysis of various engineering cases, it was conclusively demonstrated that the proposed T method for analyzing the pull-out resistance–displacement relationship of anchor plates is not only effective, but also feasible. Furthermore, it exhibits remarkable accuracy and rationality, thus providing valuable insights for engineering practice.
- (3)
- For vertically shallow-buried anchor plates, their pull-out bearing capacity increased notably as the burial depth increased. Pulling out the anchor plate can cause surface upheaval, and the failure mode exhibited the characteristics typical of shallow-buried anchor plates. On the contrary, for vertically deep-buried anchor plates, their pull-out bearing capacity increased only slightly with the increase in burial depth. The critical depth between deeply buried and shallowly buried anchor plates was approximately 4b (where b represents the side length of the square anchor plate).
- (4)
- For the series-connected anchor plates, in order to avoid mutual interference between adjacent anchor plates and reduce the pull-out bearing capacity of the support system, the minimum spacing between adjacent anchor plates should satisfy L ≥ 4b. For typical cohesive soils, the magnitude of cohesion and the internal friction angle have little influence on the critical depth between deeply buried and shallowly buried anchor plates as well as on the minimum spacing between adjacent anchor plates.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| k | Coefficient of horizontal subgrade reaction |
| σ | The elastic resistance of the soil |
| x | Horizontal displacement of the anchor plate |
| y | The distance of the calculation point from the x-axis |
| yh | The depth of the calculation point |
| θ | Rotation angle |
| m | Scaling factor of the subgrade reaction coefficient |
| φ | Internal friction angle |
| c | Cohesion |
| k1 | Regression parameter |
| n | Regression parameter |
| b | The width of the rectangular anchor plate |
| h | The height of the rectangular anchor plate |
| k2 | Equals to 0.2φ2-φ + c |
| k3 | Regression parameter |
| L | Tie rod length |
| E | Elastic modulus |
| S | Cross-sectional area of the steel tie rod |
| F | The large load |
| D | Diameter of the specimen |
| Ε | Equals to Δl/l |
| K | Bulk modulus |
| G | Shear modulus |
| V | Poisson’s ratio |
References
- Randolph, M.; Gourven1ec, S. Offshore Geotechnical Engineering; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Das, B.M.; Shukla, S.K. Earth Anchors; J. Ross Publishing: Plantation, FL, USA, 2013. [Google Scholar]
- Murray, E.J.; Geddes, J.D. Resistance of passive inclined anchors in cohesionless medium. Géotechnique 1989, 39, 417–431. [Google Scholar]
- Ilamparuthi, K.; Dickin, E.A.; Muthukrisnaiah, K. Experimental investigation of the uplift behaviour of circular plate anchors embedded in sand. Can. Geotech. J. 2002, 39, 648–664. [Google Scholar]
- Gaudin, C.; O’Loughlin, C.D.; Randolph, M.F.; Lowmass, A.C. Influence of the installation process on the performance of suction embedded plate anchors. Géotechnique 2006, 56, 381–391. [Google Scholar]
- Liu, J.; Liu, M.; Zhu, Z. Sand deformation around an uplift plate anchor. J. Geotech. Geoenviron. Eng. 2012, 138, 728–737. [Google Scholar]
- Han, C.; Wang, D.; Gaudin, C.; O’Loughlin, C.D.; Cassidy, M.J. Behaviour of vertically loaded plate anchors under sustained uplift. Géotechnique 2016, 66, 681–693. [Google Scholar]
- Basudhar, P.K.; Singh, D.N. Discussion: A generalized procedure for predicting optimal lower bound break-out factors of strip anchors. Géotechnique 1995, 45, 345–347. [Google Scholar]
- Khatri, V.N.; Kumar, J. Effect of anchor width on pullout capacity of strip anchors in sand. Can. Geotech. J. 2011, 48, 511–517. [Google Scholar]
- Kumar, J. Seismic horizontal pullout capacity of vertical anchors in sands. Can. Geotech. J. 2002, 39, 982–991. [Google Scholar]
- Merifield, R.S.; Sloan, S.W.; Yu, H.S. Stability of plate anchors in undrained clay. Géotechnique 2001, 51, 141–153. [Google Scholar]
- Merifield, R.S.; Lyamin, A.V.; Sloan, S.W.; Yu, H.S. Three-dimensional lower bound solutions for stability of plate anchors in clay. J. Geotech. Geoenviron. Eng. 2003, 129, 243–253. [Google Scholar]
- Merifield, R.S.; Lyamin, A.V.; Sloan, S.W. Stability of inclined strip anchors in purely cohesive soil. J. Geotech. Geoenviron. Eng. 2005, 131, 792–799. [Google Scholar]
- Bhattacharya, P.; Kumar, J. Pullout capacity of inclined plate anchors embedded in sand. Can. Geotech. J. 2014, 51, 1365–1370. [Google Scholar]
- Sahoo, J.P.; Ganesh, R. Vertical uplift resistance of rectangular plate anchors in two layered sand. Ocean. Eng. 2018, 150, 167–175. [Google Scholar]
- Xu, Z.D.; Wu, K.Y. Damage detection for space truss structures based on strain mode under ambient excitation. J. Eng. Mech. 2012, 138, 1215–1223. [Google Scholar]
- Xu, Z.D.; Wu, Z. Energy damage detection strategy based on acceleration responses for long-span bridge structures. J. Eng. Struct. 2007, 29, 609–617. [Google Scholar]
- Bu, G.; Chen, K.; Zhou, J.; Ma, X.; Xu, C.; Liu, F.; He, A. Seismic fragility assessment of eccentric gravity column-core tube structures subjected to pulse-like ground motions. Structures 2024, 69, 107406. [Google Scholar]
- Ghaly, A.M.; Hanna, A. Ultimate pullout resistance of single vertical anchors. Can. Geotech. J. 1994, 31, 661–672. [Google Scholar]
- White, D.J.; Take, W.A.; Bolton, M.D. The uplift resistance of pipes and plate anchors buried in sand. Géotechnique 2003, 58, 771–779. [Google Scholar]
- Tho, K.K.; Chen, Z.; Leung, C.F.; Chow, Y.K. Pullout behaviour of plate anchor in clay with linearly increasing strength. Can. Geotech. J. 2014, 51, 92–102. [Google Scholar]
- JGJ 120-2012; Technical Specification for Retaining and Protection of Building Foundation Excavation. China Architecture & Building Press: Beijing, China, 2012. (In Chinese)
- Liu, J.; Yang, Q.; Tan, X.; Ma, Y. Research on Analysis Method of Load-Displacement Relationship of Series Anchor Plates. J. For. Chem. Rev. 2021, 1536–1553. [Google Scholar]
- Rowe, R.K. Soil Structure Interaction Analysis and its Application to the Prediction of Anchor Plate Behaviour. Ph.D. Thesis, University of Sydney, Sydney, Australia, 1978. [Google Scholar]
- Rowe, R.K.; Davis, E.H. The behaviour of anchor plates in clay. Géotechnique 1982, 32, 9–23. [Google Scholar]
- Gunn, M.J. Limit analysis of undrained stability problems using a very small computer. In Symposium on Computer Applications in Geotechnical Problems in Highway Engineering; University Engineering Department: Cambridge, UK, 1980. [Google Scholar]
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. China Communication Press: Beijing, China, 2017. (In Chinese)
- Liang, L.; Zou, X.; Liu, J. Approximate analytical algorithm for pull-out resistance-displacement relationship of combined anchor system. J. Eng. Fail. Anal. 2024, 166, 108827. [Google Scholar]
- Zhang, X.; Wu, X. Theory and Practice of Anchor Plate Retaining Structures; China Railway Publishing House: Beijing, China, 1996. [Google Scholar]
- Mokhbi, H.; Mellas, M.; Mabrouki, A.; Pereira, J.M. Three-dimensional numerical and analytical study of horizontal group of square anchor plates in sand. Acta Geotech. 2018, 13, 159–174. [Google Scholar]
- Choudhary, A.K.; Pandit, B.; Sivakumar Babu, G.L. Experimental and numerical study on square anchor plate groups in geogrid reinforced sand. Geosynth. Int. 2019, 26, 657–671. [Google Scholar]
- Dickin, E.A.; Leung, C.F. Evaluation of design methods for vertical anchor plates. J. Geotech. Eng. 1985, 111, 500–520. [Google Scholar]
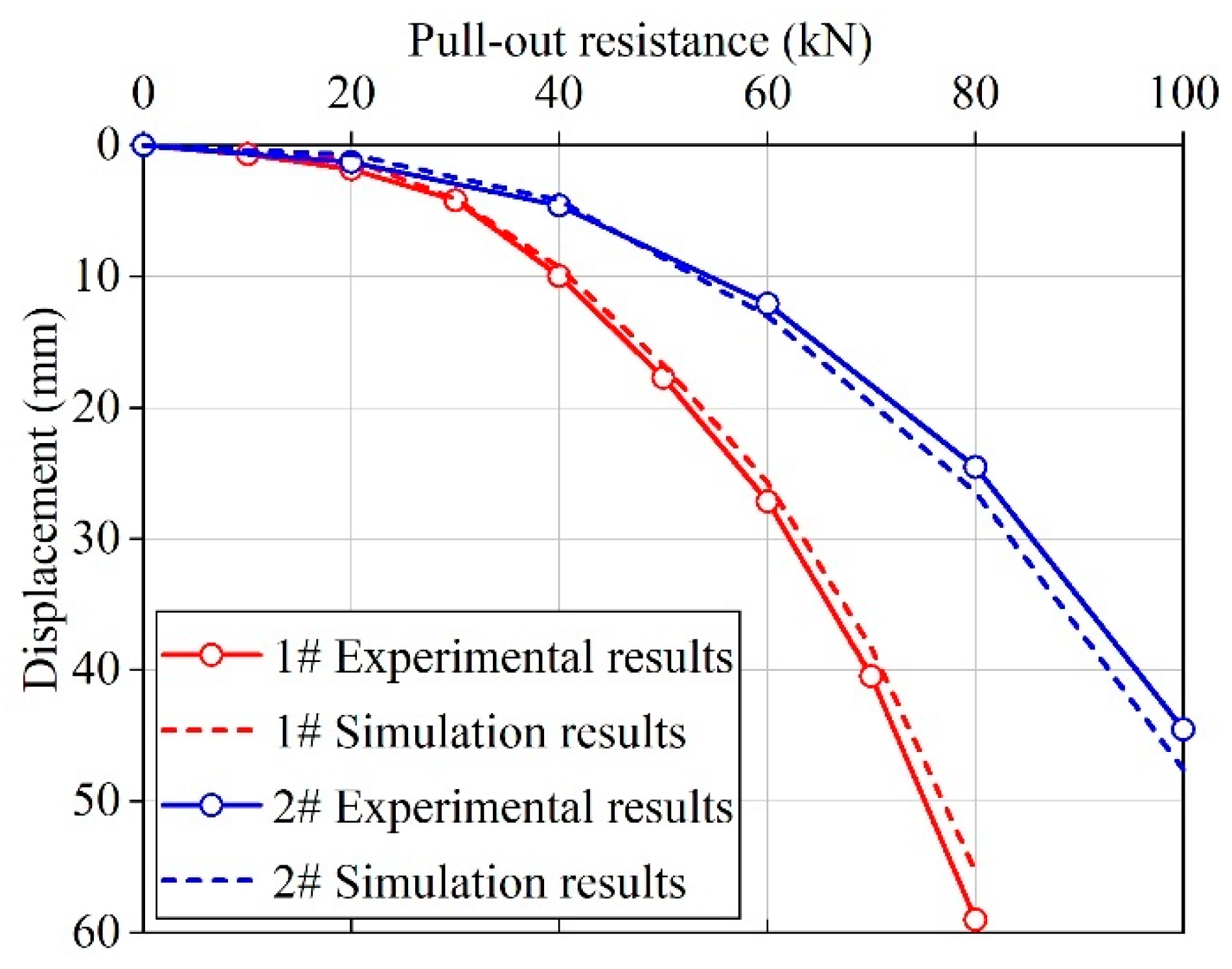



| Label Number | b (m) | Thickness (m) | H (m) |
|---|---|---|---|
| #1 | 0.5 | 0.2 | 2.0 |
| #2 | 0.6 | 0.2 | 2.0 |
| Soil Name | γ (kN/m3) | Compaction (%) | c (kPa) | φ (°) |
|---|---|---|---|---|
| compacted silty clay | 19.5 | 93 | 30.7 | 19.6 |
| Label Number | k1 | t | n |
|---|---|---|---|
| #1 | 7.5531 | 0.7611 | −0.5979 |
| #2 | 7.9709 | 0.7579 | −0.5799 |
| #3 | 8.5331 | 0.7679 | −0.5625 |
| #4 | 8.7811 | 0.7621 | −0.5574 |
| #5 | 9.3514 | 0.7631 | −0.5669 |
| #6 | 10.1787 | 0.7571 | −0.5876 |
| Label Number | t | n |
|---|---|---|
| #6 | 0.7583 | −0.5897 |
| #7 | 0.5274 | −0.5633 |
| #8 | 0.3681 | −0.5749 |
| #9 | 0.3377 | −0.5733 |
| #10 | 0.3267 | −0.5703 |
| #11 | 0.3162 | −0.5716 |
| #12 | 0.3049 | −0.5723 |
| #13 | 0.3003 | −0.5751 |
| Label Number | k1 | n |
|---|---|---|
| #1 | 6.6142 | −0.5979 |
| #2 | 7.0302 | −0.5799 |
| #3 | 7.6002 | −0.5625 |
| #4 | 7.9033 | −0.5574 |
| #5 | 8.5085 | −0.5669 |
| #6 | 9.6356 | −0.5876 |
| Label Number | k1 | n |
|---|---|---|
| #1 | 8.7187 | −0.5979 |
| #2 | 9.1032 | −0.5799 |
| #3 | 9.6641 | −0.5625 |
| #4 | 9.8718 | −0.5574 |
| #5 | 10.4011 | −0.5669 |
| #6 | 11.1764 | −0.5876 |
| Soil Name | γ (kN/m3) | Compaction (%) | c (kPa) | φ (°) |
|---|---|---|---|---|
| Compacted silty clay | 19.5 | 95.1 | 35.3 | 20.3 |
| Soil Name | γ (kN/m3) | Compaction (%) | c (kPa) | φ (°) |
|---|---|---|---|---|
| Compacted silty clay | 19.9 | 96.1 | 36.2 | 21.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Nie, C.; Tang, X.; Zou, X. Approximate Analytical Algorithm for Pull-Out Resistance–Displacement Relationship of Series—Connected Anchor Plate Anchorage System. Buildings 2025, 15, 1177. https://doi.org/10.3390/buildings15071177
Liu J, Nie C, Tang X, Zou X. Approximate Analytical Algorithm for Pull-Out Resistance–Displacement Relationship of Series—Connected Anchor Plate Anchorage System. Buildings. 2025; 15(7):1177. https://doi.org/10.3390/buildings15071177
Chicago/Turabian StyleLiu, Jie, Chuang Nie, Xiya Tang, and Xiquan Zou. 2025. "Approximate Analytical Algorithm for Pull-Out Resistance–Displacement Relationship of Series—Connected Anchor Plate Anchorage System" Buildings 15, no. 7: 1177. https://doi.org/10.3390/buildings15071177
APA StyleLiu, J., Nie, C., Tang, X., & Zou, X. (2025). Approximate Analytical Algorithm for Pull-Out Resistance–Displacement Relationship of Series—Connected Anchor Plate Anchorage System. Buildings, 15(7), 1177. https://doi.org/10.3390/buildings15071177





