Structural Damage Detection Based on Sparrow Search Algorithm
Abstract
:1. Introduction
2. Theoretical Development
- Step 1.
- Group location initialization is done by
- Step 2.
- Explorer location update is done by
- Step 3.
- The follower location update is performed as follows:
- Step 4.
- Investigator location updates are performed as follows:
3. Numerical Examples
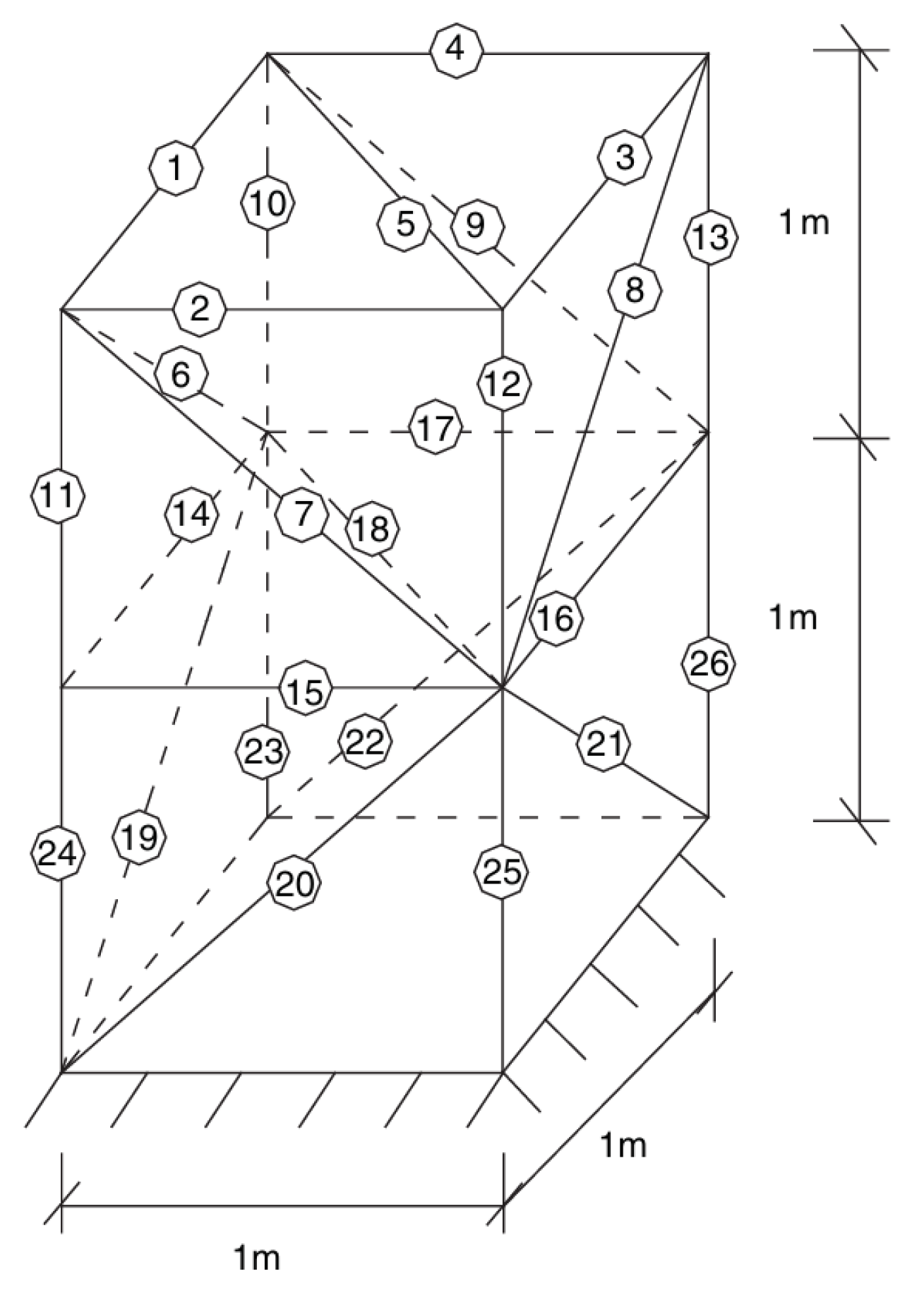
3.1. A Space Truss Structure
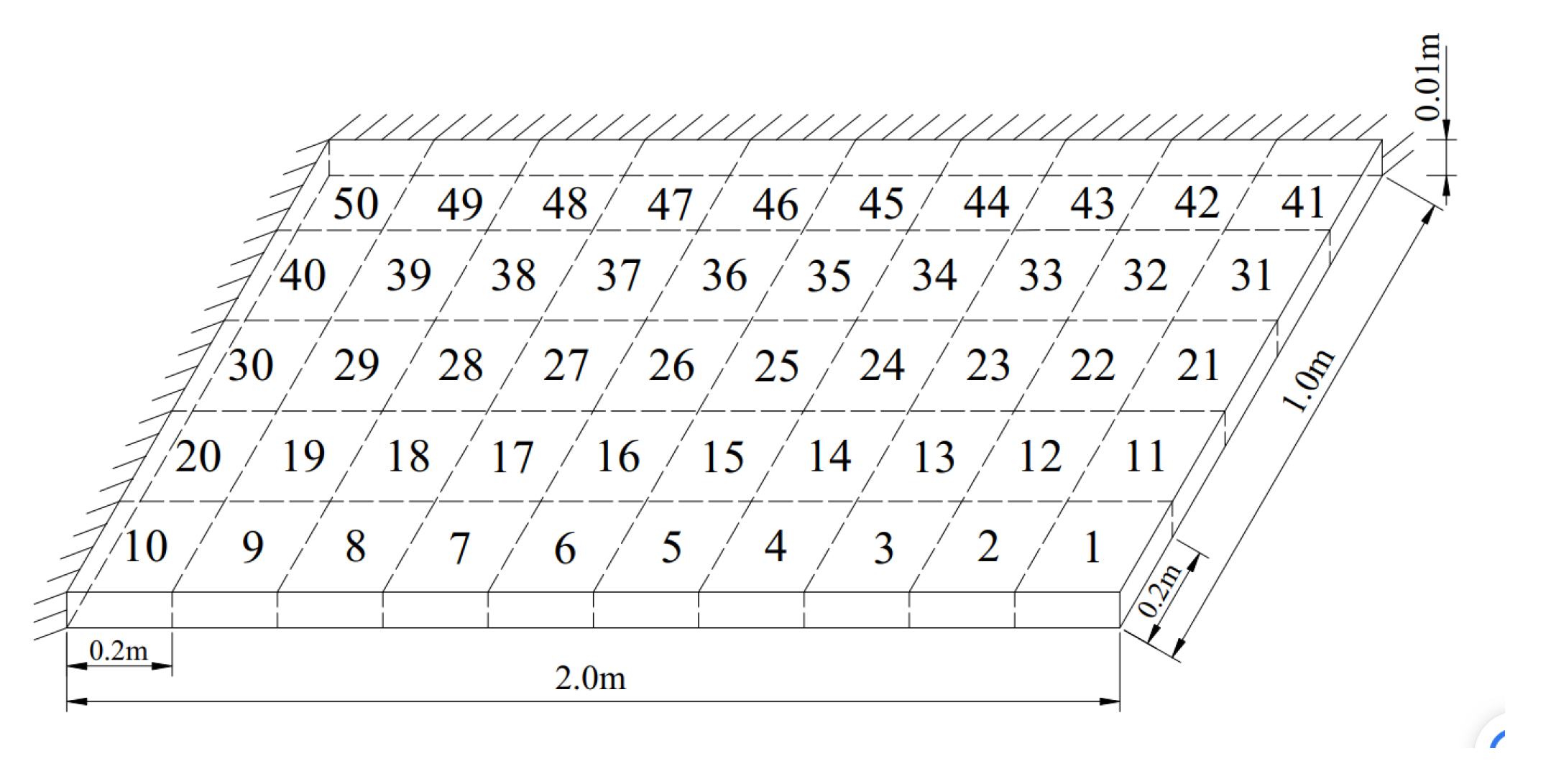
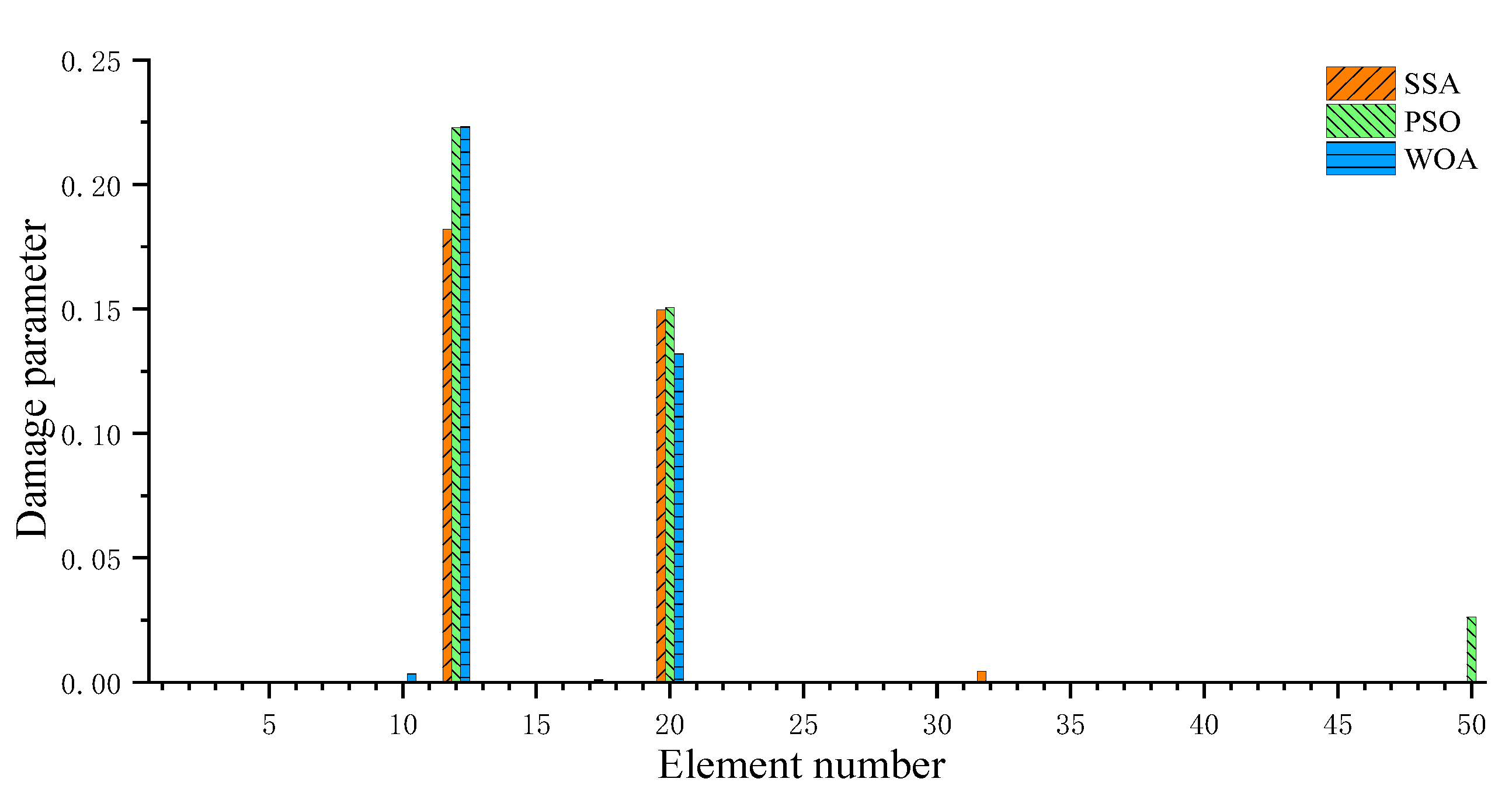
3.2. A Plate Structure
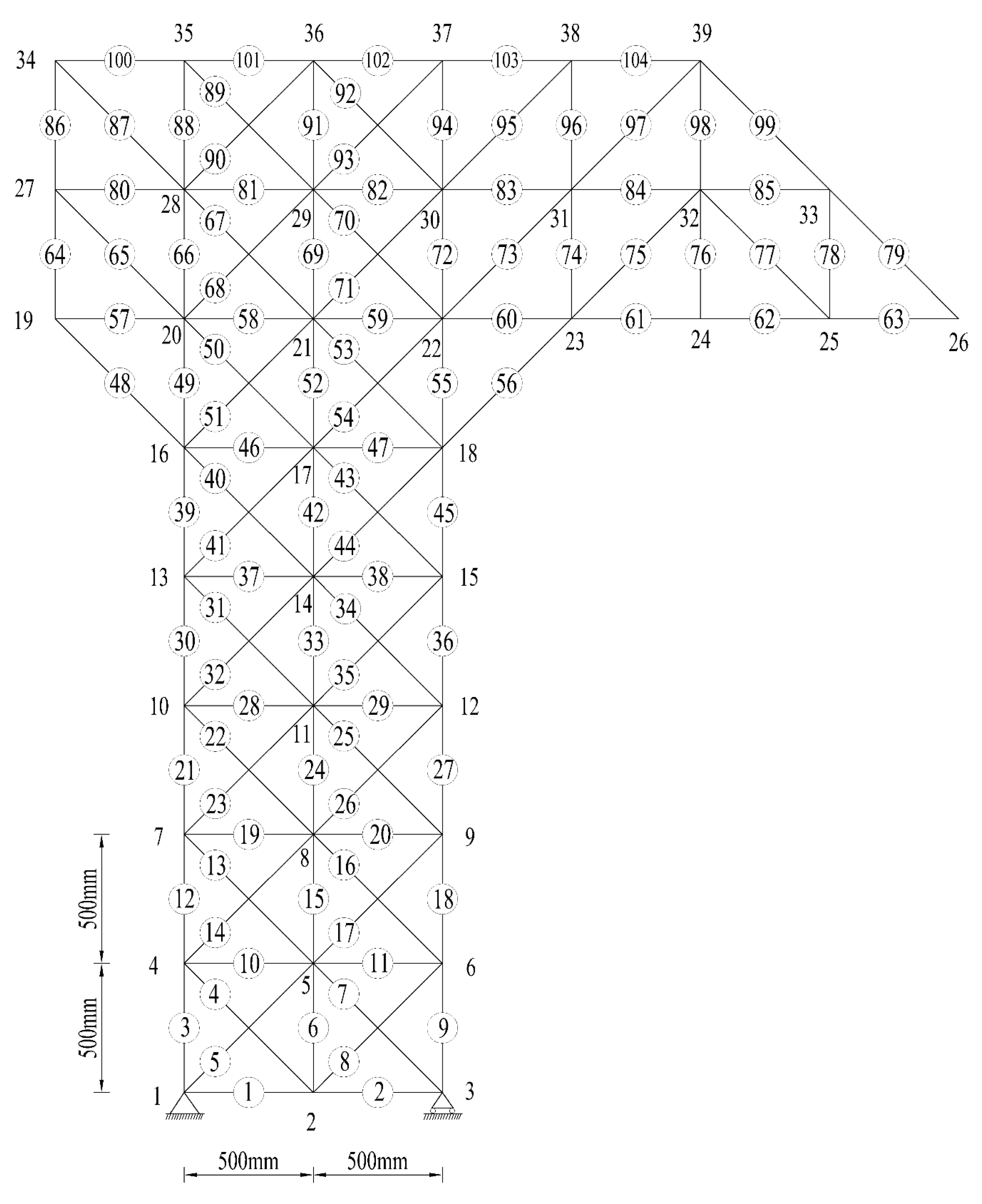
3.3. A Lattice Structure
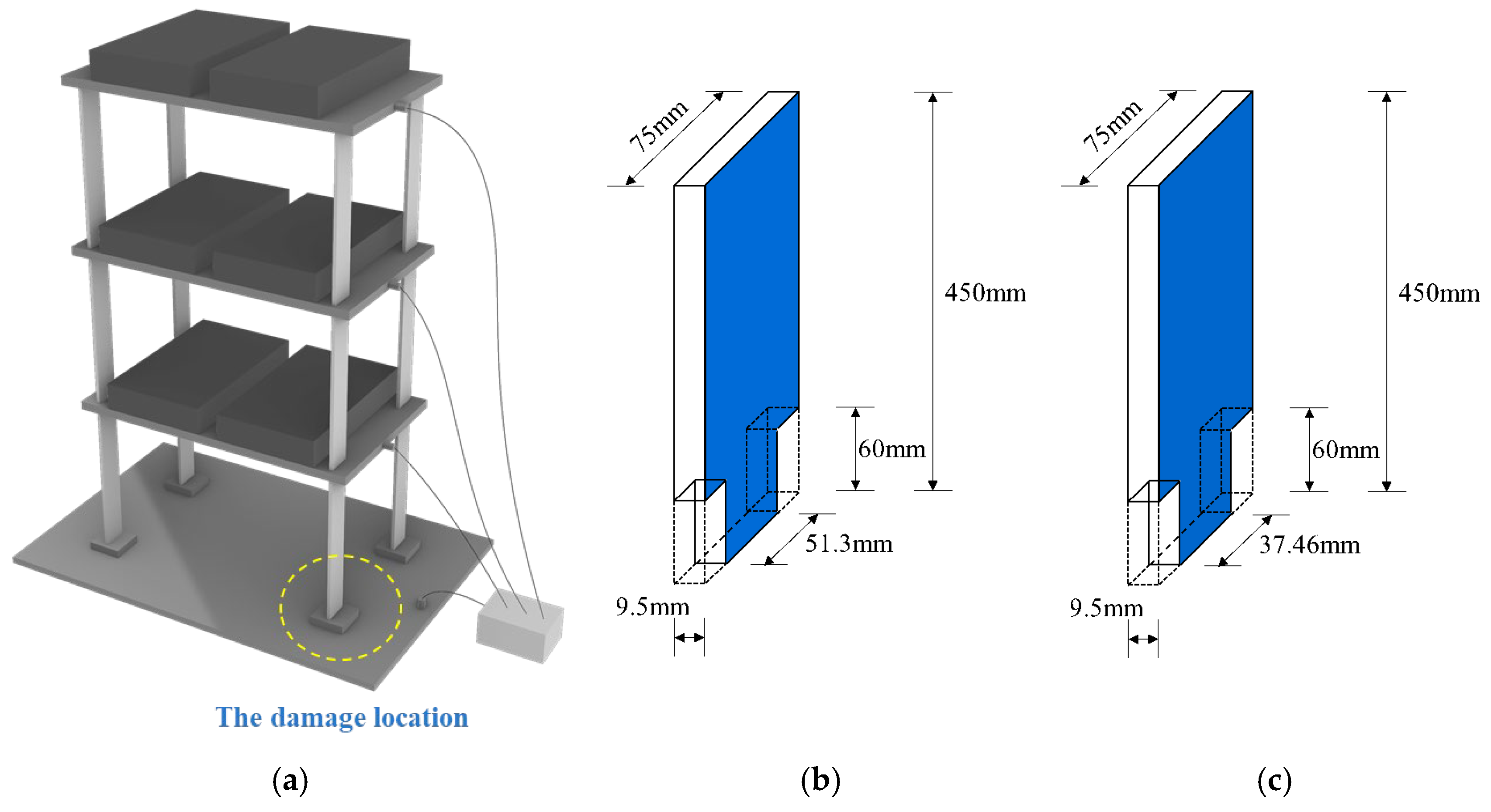
4. Experimental Validation
4.1. Cantilever Beam
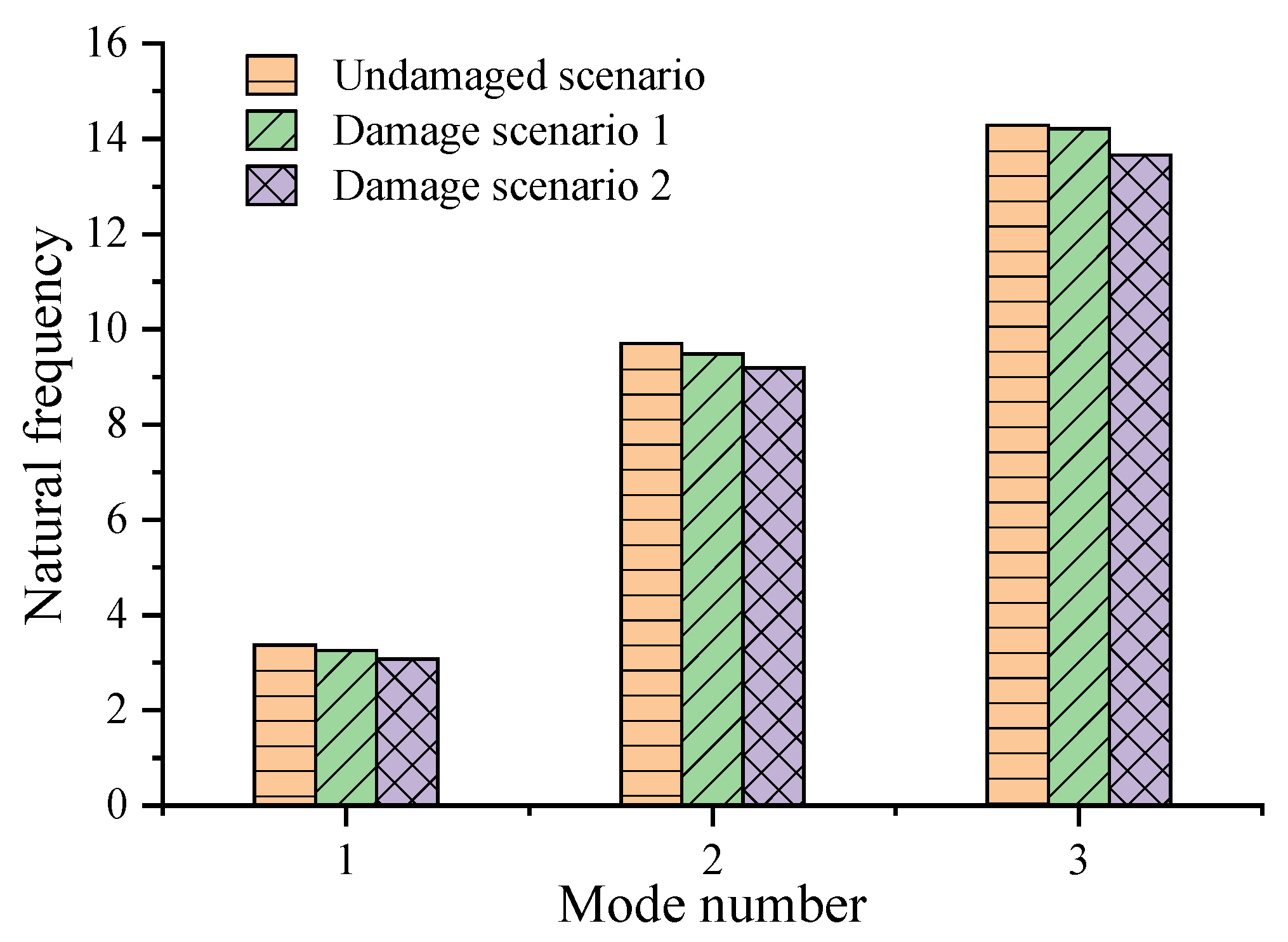
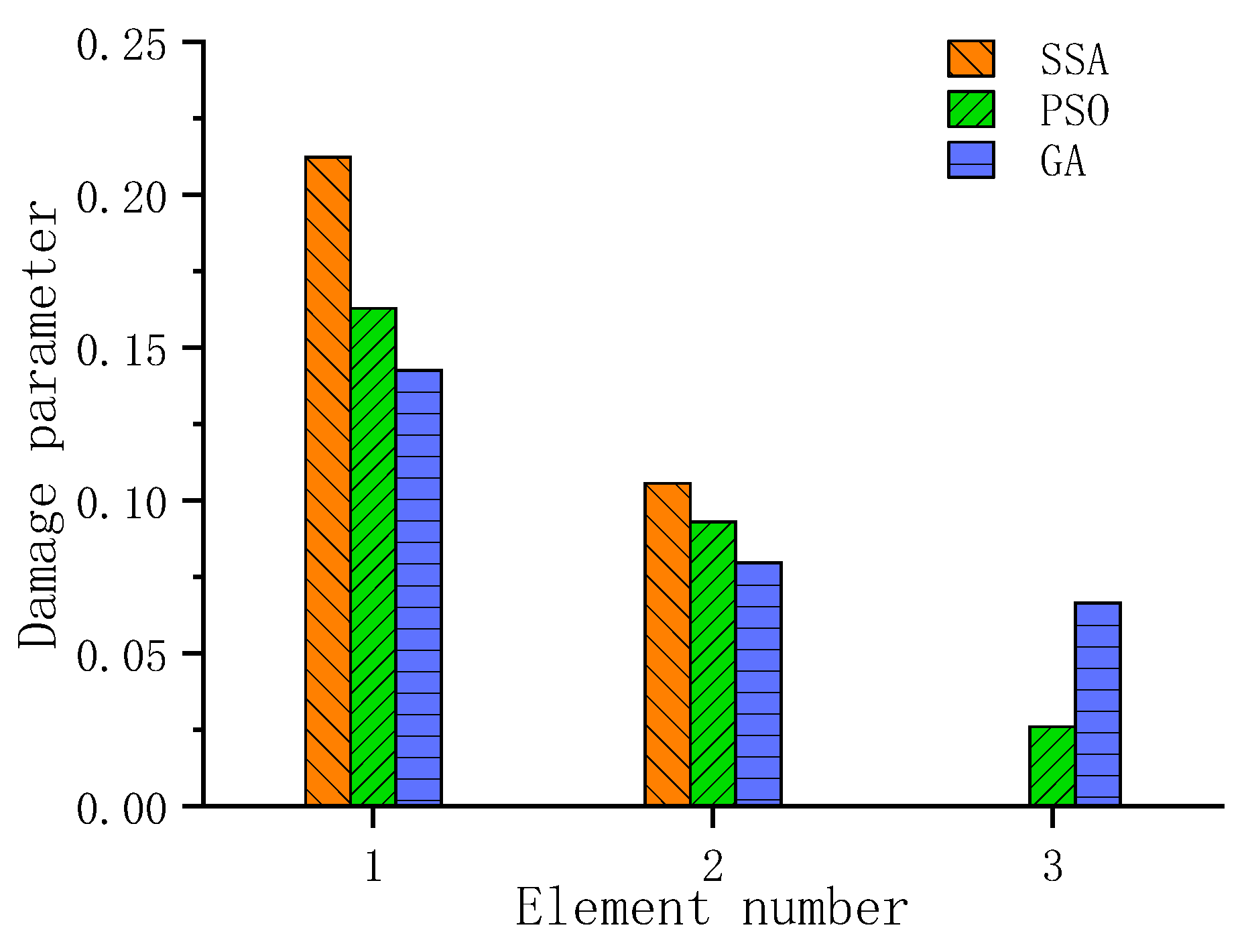
4.2. Shear Frame Structure
5. Conclusions
- (1)
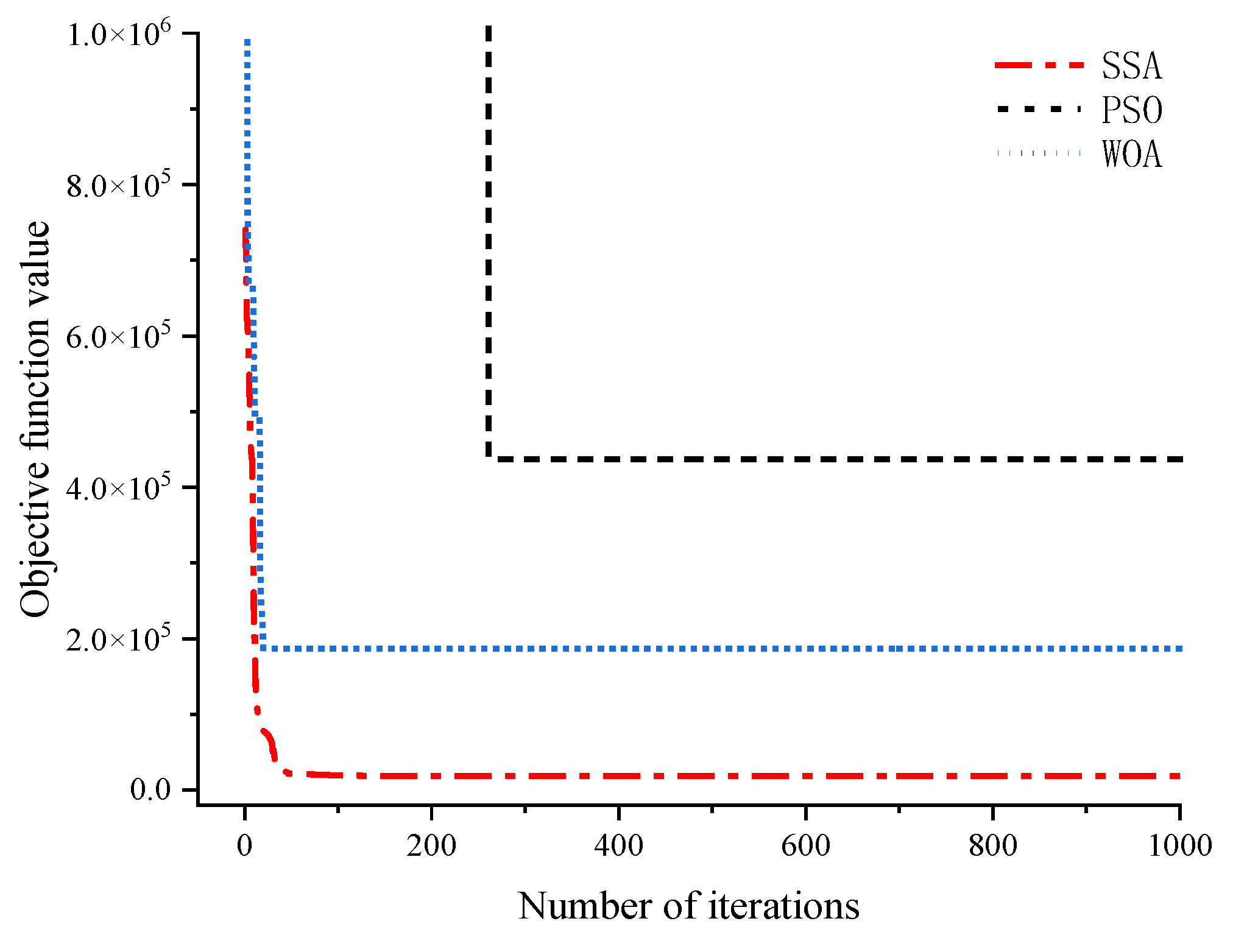
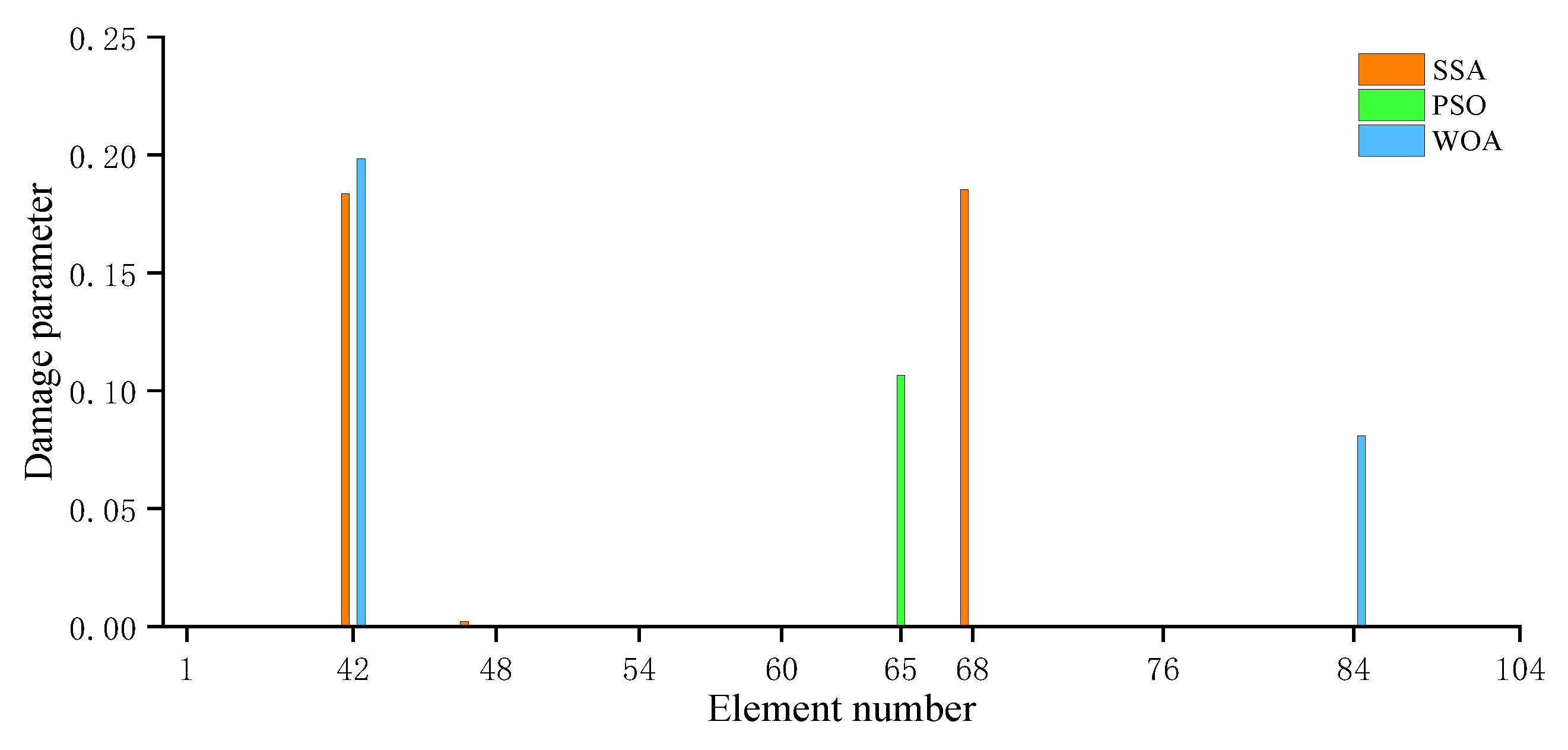
- For the numerical example of a spatial truss structure, the proposed method accurately locates the two damage locations and calculates the damage degrees of the two damaged elements to be 14.6% and 20.5%, respectively (while the actual damage degrees are 15% and 20%). These results are almost identical to the actual damage. The PSO method has a slower convergence speed than the proposed method and produces a significant misjudgment in the calculation results. Although the WOA can also achieve a 0% error rate like the SSA, its recognition accuracy is lower than that of the SSA.
- (2)
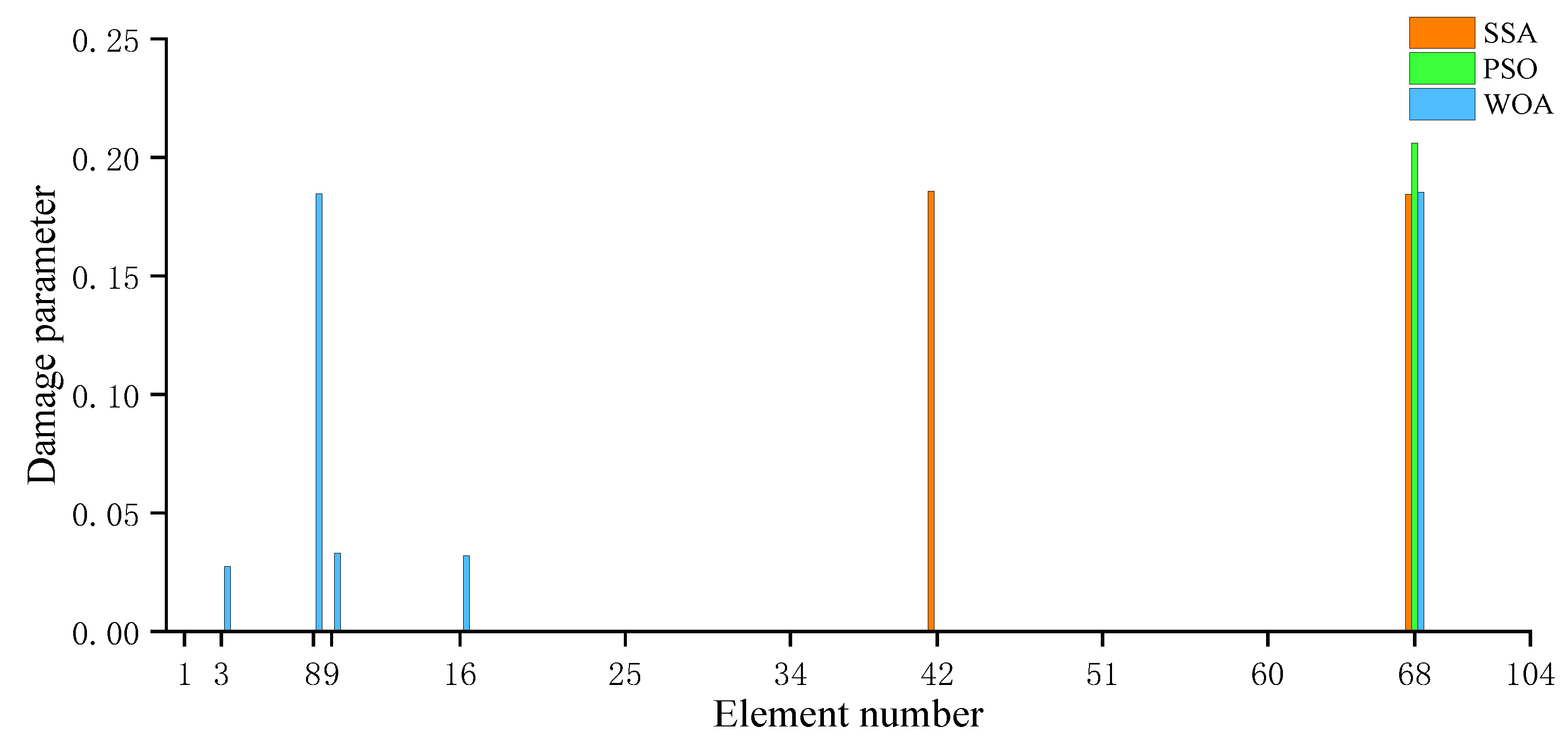
- For the numerical example of a plate structure, the proposed method can accurately locate multiple damage locations and precisely assess the degree of damage. The calculated damage degrees obtained by the proposed method are 18.2% and 15% for the two units, respectively, which are very close to the actual values of 20% and 15%. The convergence speed and computational accuracy of the proposed method are superior to those of PSO and WOA.
- (3)
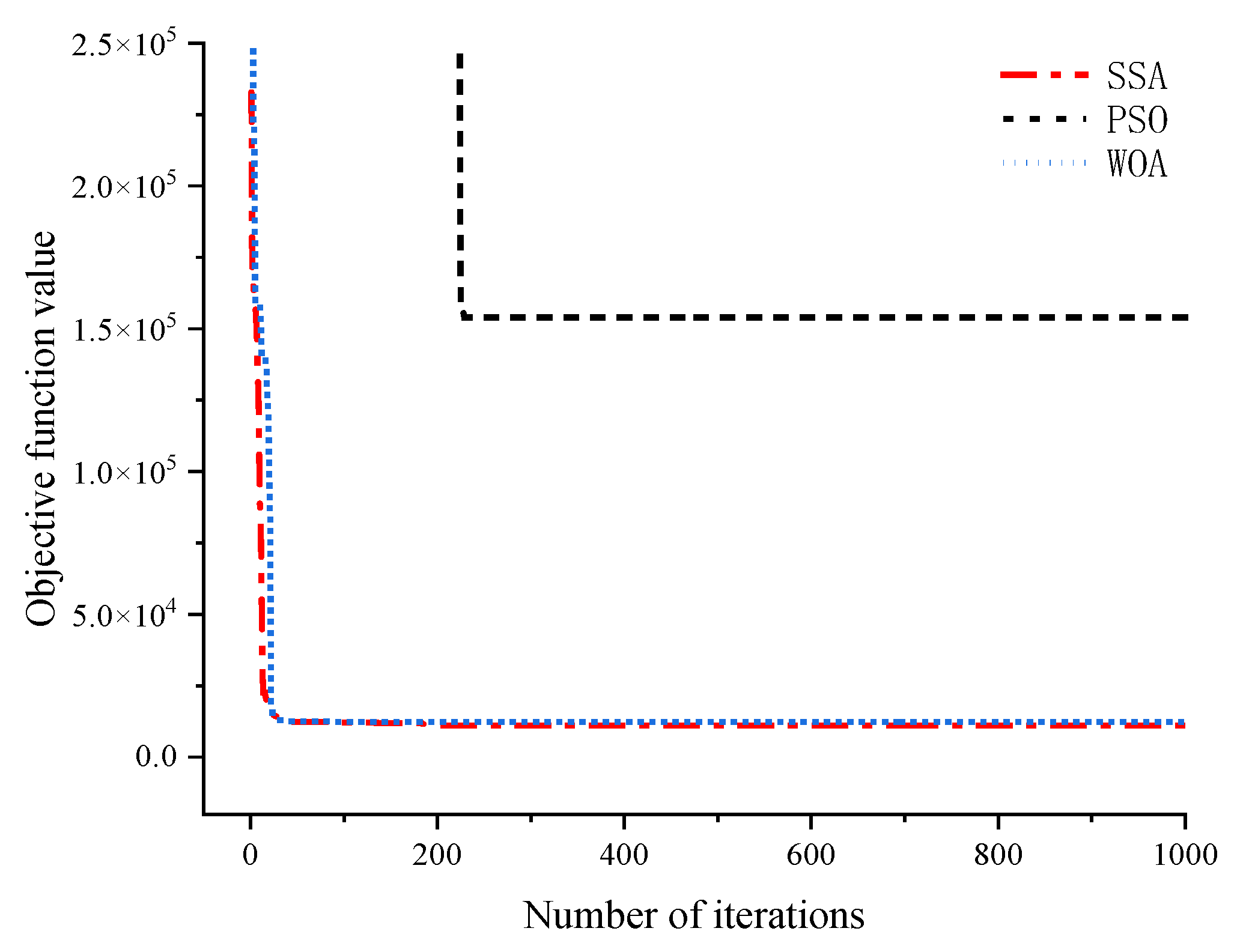
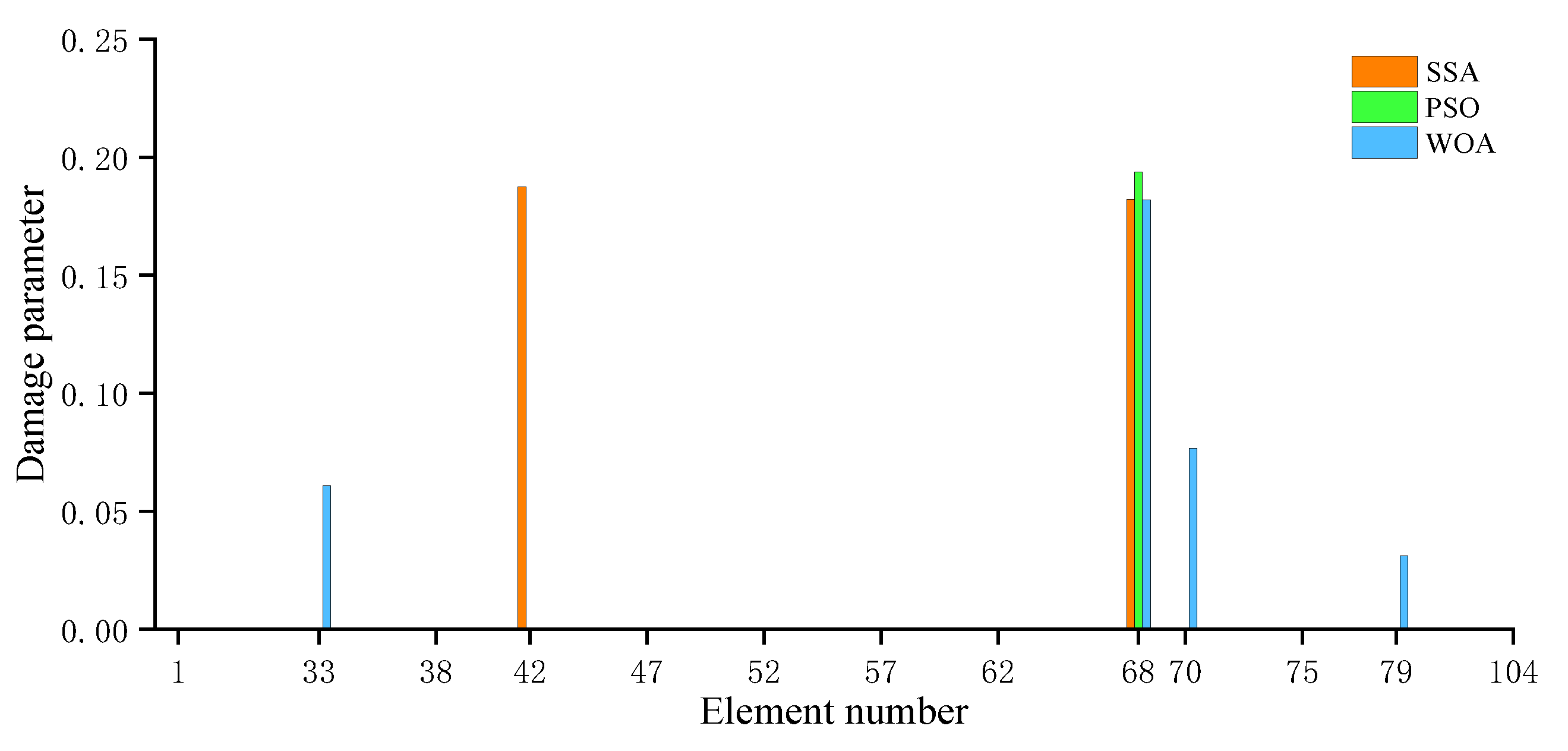
- For the large lattice structure, regardless of whether the data contains noise or not, the objective function values of the SSA after multiple iterations are significantly smaller than those of the PSO and WOA. This indicates that the SSA significantly outperforms the other two algorithms in terms of global convergence performance. In various simulated damage scenarios, only the SSA achieves a 0% error rate across all scenarios, and its recognition accuracy is notably higher than that of the PSO and WOA. It has been demonstrated that the SSA exhibits excellent robustness even in the presence of data noise interference.
- (4)
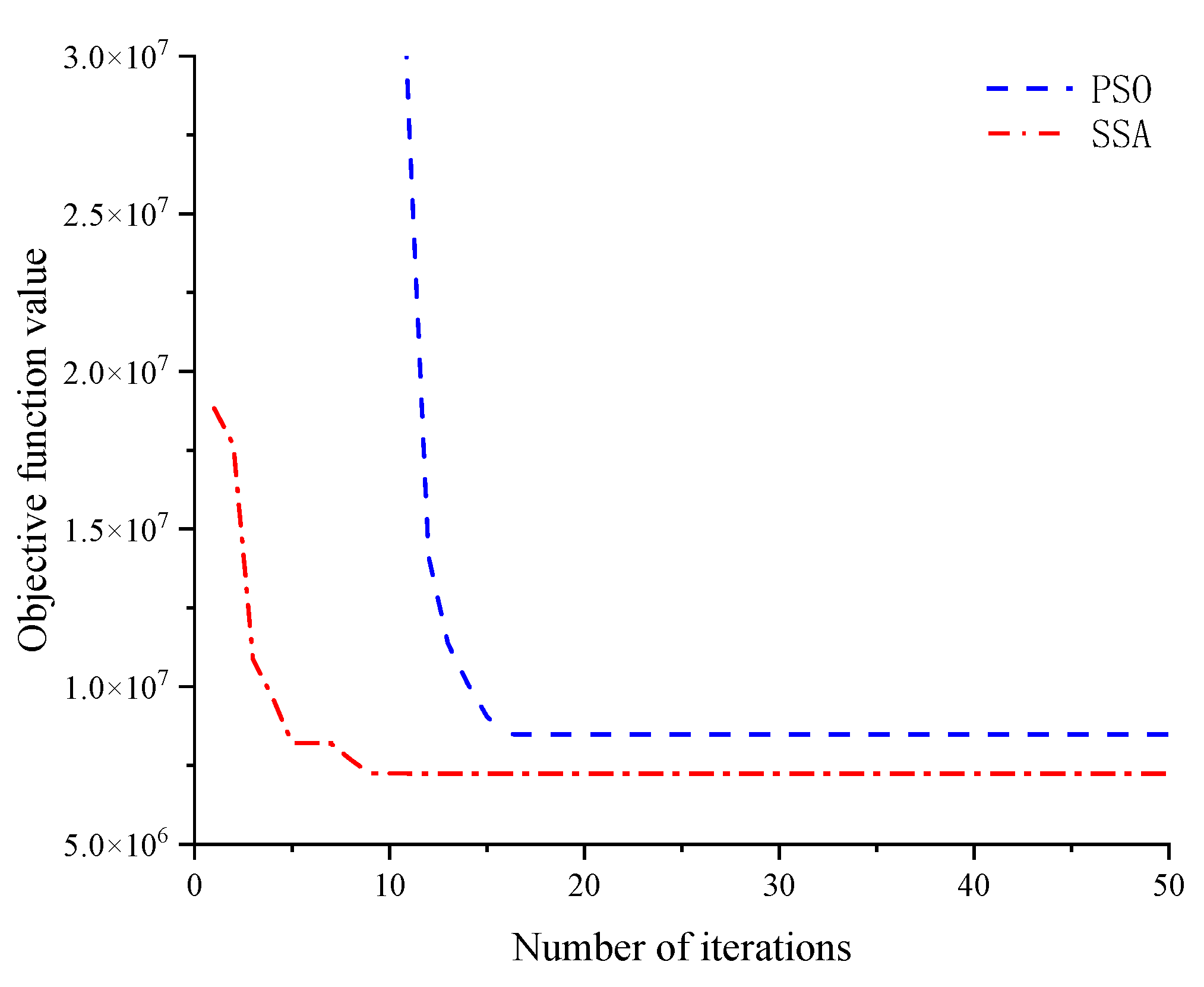
- For the example of the experimental beam, only the proposed method accurately identified the damage, while the PSO, CS, and GA all exhibited significant misjudgments. In terms of convergence speed, the proposed method requires fewer iterations than the other three methods. In terms of computational accuracy, the damage degree calculated by the proposed method, which is 86.9%, is closest to the actual value of 93.75%, while the errors of the other three methods are relatively large.
- (5)
- For the experimental example of a three-layer steel frame, the proposed method outperforms both the PSO and GA in terms of convergence speed and computational accuracy. In the scenario involving multiple damage locations (damage present on the first and second floors), both the PSO and GA exhibited significant misjudgments, falsely indicating the presence of some degree of damage on the third floor. Only the method proposed in this paper clearly identified that damage was only present in the first and second layers, with the calculated damage parameter values deviating minimally from the actual values.
- (6)
- Compared to existing swarm intelligence optimization algorithms, such as PSO, GA, CS, and WOA, the SSA has a simpler algorithmic structure, superior global search and optimization capabilities, and enhanced robustness. The introduction of the SSA into damage detection can improve the calculation efficiency and resistance to noise interference, with results that are more consistent with the actual degree of damage. For all cases presented in this paper, only the SSA achieved a 0% error rate, and in the vast majority of scenarios, its computational accuracy surpassed that of the other algorithms, particularly in complex situations where multiple damages exist within the structure. The limitation of the SSA is that, in a few simple cases, when the objective function values are similar, the computation time of the SSA is slightly higher than that of the PSO.
- (7)
- In practical applications, the proposed method is effective for various structural damage scenarios, such as material fatigue or corrosion, as long as these damages result in observable frequency changes. However, the method proposed in this paper cannot effectively identify damage scenarios that do not cause significant changes in the vibration frequency, which is a limitation of this approach. Therefore, in future studies, the following research directions can be explored. The first is to combine SSA with mode shape data for multi-parameter detection, in order to address damage detection problems that do not cause significant frequency changes. The second is to validate the proposed method by testing it on nonlinear structures (e.g., cracked beams), thereby refining the theory of damage detection under nonlinear vibrations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bicanic, N.; Chen, H.P. Damage identification in framed structures using natural frequencies. Int. J. Numer. Methods Eng. 1997, 40, 4451–4468. [Google Scholar]
- Yang, Z.; Wang, L. Structural damage detection by changes in natural frequencies. J. Intell. Mater. Syst. Struct. 2010, 21, 309–319. [Google Scholar]
- Hassiotis, S. Identification of damage using natural frequencies and Markov parameters. Comput. Struct. 2000, 74, 365–373. [Google Scholar] [CrossRef]
- Liu, W.; Ying, H. Research on damage localization method through rate of frequency change. J. Vib. Shock 2004, 23, 30–32+19+126. [Google Scholar]
- Zhong, J.; Dong, C.; Xia, K. Structural damage identification method based on frequency and mode shape parameters. J. Huazhong Univ. Sci. Technol. (Urban Sci. Ed.) 2009, 26, 1–4+9. [Google Scholar]
- Wang, X.; Yang, C.; Wang, L.; Yang, H.; Qiu, Z. Membership-set identification method for structural damage based on measured natural frequencies and static displacements. Struct. Health Monit. 2013, 12, 23–34. [Google Scholar] [CrossRef]
- Kim, J.-T.; Ryu, Y.-S.; Cho, H.-M.; Stubbs, N. Damage identification in beam-type structures: Frequency-based method vs. mode-shape-based method. Eng. Struct. 2003, 25, 57–67. [Google Scholar]
- Liu, W.; Guo, L.; He, H.; Yan, L. Damage identification method for breathing cracked beams based on natural frequencies. China Mech. Eng. 2017, 28, 702–707+713. [Google Scholar]
- Du, S.; Yin, X.; Chen, H. Structural damage identification method based on second-order frequency perturbation. Chin. J. Appl. Mech. 2006, 23, 613–617+699. [Google Scholar]
- Casas, J.R.; Aparicio, A.C. Structural damage identification from dynamic-test data. J. Struct. Eng. 1994, 120, 2437–2450. [Google Scholar]
- Ditommaso, R.; Ponzo, F.C. Automatic evaluation of the fundamental frequency variations and related damping factor of reinforced concrete framed structures using the Short Time Impulse Response Function (STIRF). Eng. Struct. 2015, 82, 104–112. [Google Scholar] [CrossRef]
- Xiang, C.; Shi, H.; Yang, R. Research on bridge damage identification method based on modal frequency strain energy entropy and Tent-SSA-BP neural network. Highway 2023, 68, 143–150. [Google Scholar]
- Ren, Y.; Weng, P. Research on structural damage identification method based on improved Hilbert-Huang transform. J. Vib. Shock 2015, 34, 195–199. [Google Scholar]
- Foti, D.; Gattulli, V.; Potenza, F. Output-only identification and model updating by dynamic testing in unfavorable conditions of a seismically damaged building. Comput.-Aided Civ. Infrastruct. Eng. 2014, 29, 659–675. [Google Scholar]
- Chen, H.; Kurt, M.; Lee, Y.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Experimental system identification of the dynamics of a vibro-impact beam with a view towards structural health monitoring and damage detection. Mech. Syst. Signal Process. 2014, 46, 91–113. [Google Scholar]
- Krishnanunni, C.; Raj, R.S.; Nandan, D.; Midhun, C.K.; Sajith, A.S.; Ameen, M. Sensitivity-based damage detection algorithm for structures using vibration data. J. Civ. Struct. Health Monit. 2019, 9, 137–151. [Google Scholar] [CrossRef]
- Liu, Y. Research on Structural Damage Identification Using Wavelet-Particle Swarm Genetic Optimization Algorithm. Master’s Thesis, Changsha University of Science and Technology, Changsha, China, 2018. [Google Scholar]
- Xie, S.; Wu, B.; Zhao, X.; Zou, M.; Lin, D. Structural damage identification based on improved grey wolf optimization algorithm. Chin. J. Comput. Mech. 2024, 41, 256–262. [Google Scholar]
- Pooya, M.; Reza, M.M.; Beheshti, A.S.B. A Two-Stage Method for Damage Identification in Concrete Gravity Dams by Using a Modal Curvature-Based Index and Pathfinder Algorithm. Arab. J. Sci. Eng. 2023, 49, 5927–5947. [Google Scholar]
- Qin, S.; Su, S.; Yang, R. Structural damage identification based on multi-label convolutional neural networks. J. Build. Sci. Eng. 2024, 41, 108–119. [Google Scholar]
- Chen, Z.; Wang, W.; Liu, Q.; Wu, J. Two-stage beam-like structure damage identification based on hybrid PSO algorithm and damage probability mean. Chin. J. Comput. Mech. 2024, 41, 525–533. [Google Scholar]
- Begambre, O.; Laier, J.E. A hybrid Particle Swarm Optimization–Simplex algorithm (PSOS) for structural damage identification. Adv. Eng. Softw. 2009, 40, 883–891. [Google Scholar]
- Huang, M.; Cheng, X.; Lei, Y. Structural damage identification based on substructure method and improved whale optimization algorithm. J. Civ. Struct. Health Monit. 2021, 11, 351–380. [Google Scholar]
- Zenzen, R.; Belaidi, I.; Khatir, S.; Wahab, M.A. A damage identification technique for beam-like and truss structures based on FRF and Bat Algorithm. C. R. Méc. 2018, 346, 1253–1266. [Google Scholar]
- Zhang, P.; Ma, T. Application research on improved BP neural network in damage identification of concrete bridges. Constr. Mach. 2024, 44, 122–129. [Google Scholar]
- Hao, H.; Xia, Y. Vibration-based damage detection of structures by genetic algorithm. J. Comput. Civ. Eng. 2002, 16, 222–229. [Google Scholar] [CrossRef]
- Xiong, C.; Lian, S. Structural damage identification based on improved fruit fly optimization algorithm. KSCE J. Civ. Eng. 2021, 25, 985–1007. [Google Scholar]
- Li, J.; Yu, L.; Qi, T.; Chen, Y. Structural Damage Identification Based on Quadratic Optimization of Objective Functions with Modal Residual Force and Weighting Strategy. J. Aerosp. Eng. 2024, 37, 04023089. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar]
- Peng, X.; Yang, Q. A fast analysis algorithm for structural vibration modal sensitivity. Structures 2024, 64, 106623. [Google Scholar]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Damage localization by directly using incomplete mode shapes. J. Eng. Mech. 2000, 126, 656–660. [Google Scholar]
- Impollonia, N.; Muscolino, G. Interval analysis of structures with uncertain-but-bounded axial stiffness. Comput. Methods Appl. Mech. Eng. 2011, 200, 1945–1962. [Google Scholar] [CrossRef]
- Yang, Q.; Peng, X. Dynamic Modal Reanalysis Using Flexibility Disassembly Perturbation Method. AIAA J. 2024, 62, 3474–3490. [Google Scholar] [CrossRef]
- Yang, J.C.S.; Tsai, T.; Pevlin, V.; Chen, J.; Tsai, W.H. Structural damage detection by the system identification technique. Shock Vib. Inf. Cent. Shock Vib. Bull. 1985, 55, 57–65. [Google Scholar]
- Li, L. Numerical and Experimental Studies of Damage Detection for Shear Buildings. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2005. [Google Scholar]

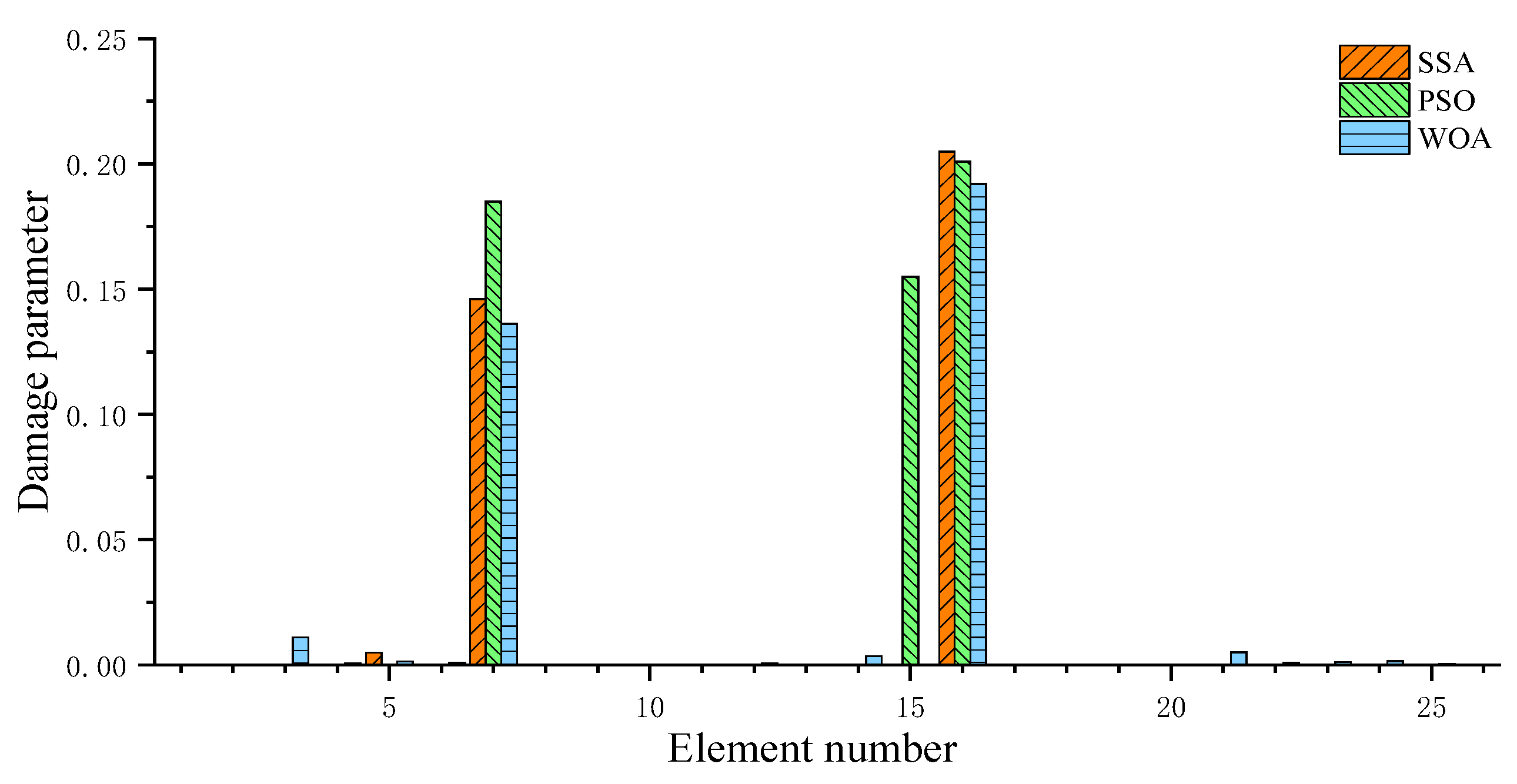


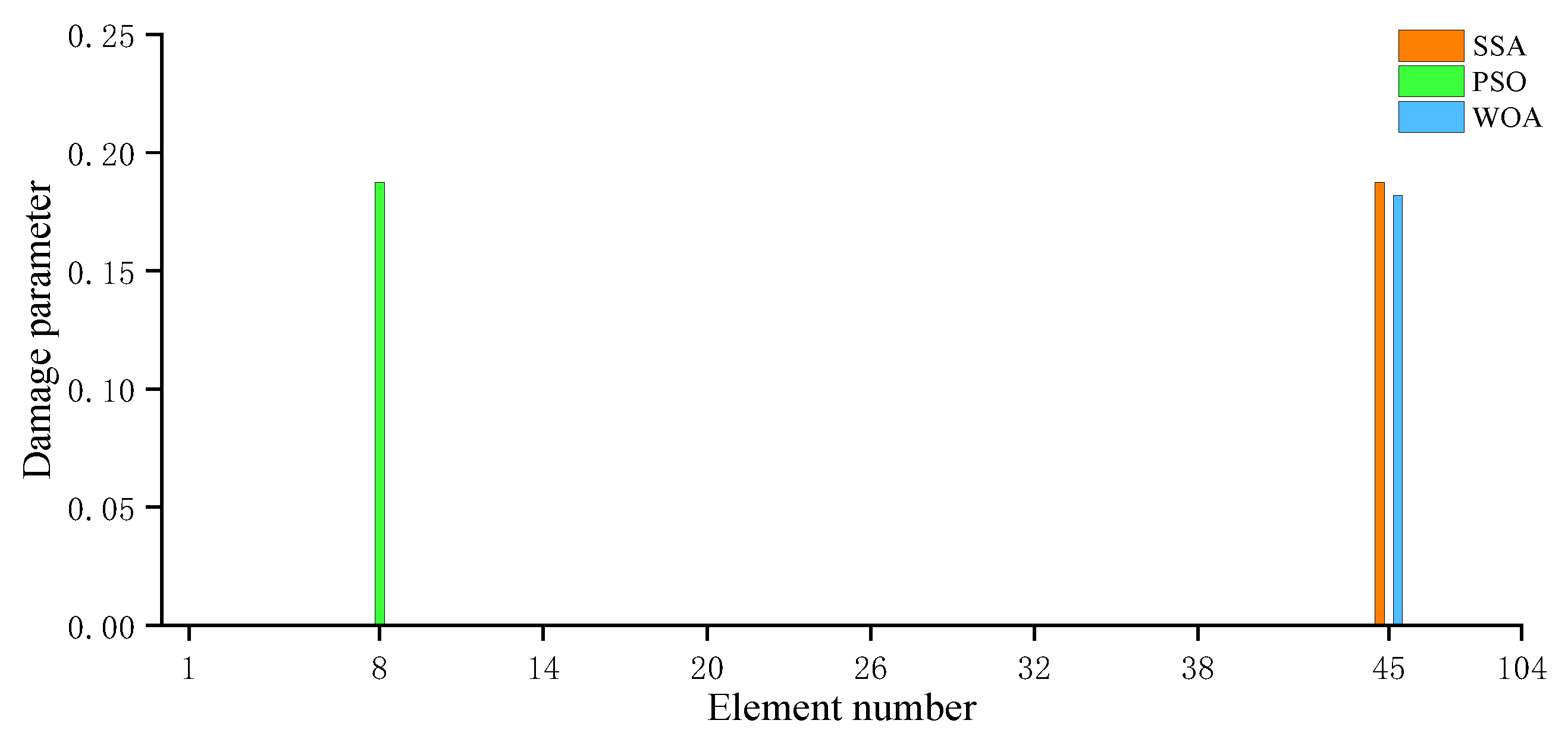











| Algorithm | Error Rate (%) | False Positive | False Negative | Accuracy of Element 7 (%) | Accuracy of Element 16 (%) |
|---|---|---|---|---|---|
| PSO | 33.3 | 1 | 0 | 76.7 | 99.5 |
| WOA | 0 | 0 | 0 | 90.8 | 96.0 |
| SSA | 0 | 0 | 0 | 97.3 | 97.6 |
| Algorithm | Error Rate (%) | False Positive | False Negative | Accuracy of Element 12 (%) | Accuracy of Element 20 (%) |
|---|---|---|---|---|---|
| PSO | 33.3 | 1 | 0 | 88.5 | 99.6 |
| WOA | 0 | 0 | 0 | 88.4 | 88.0 |
| SSA | 0 | 0 | 0 | 91.1 | 99.8 |
| Noise Level | Algorithm | Error Rate (%) | False Positive | False Negative | Accuracy of Element 45 (%) |
|---|---|---|---|---|---|
| 0% | PSO | 100 | 1 | 1 | 0 |
| WOA | 0 | 0 | 0 | 91.0 | |
| SSA | 0 | 0 | 0 | 94.4 | |
| 5% | PSO | 100 | 1 | 1 | 0 |
| WOA | 50 | 1 | 0 | 94.2 | |
| SSA | 0 | 0 | 0 | 94.3 | |
| 10% | PSO | 100 | 1 | 1 | 0 |
| WOA | 50 | 1 | 0 | 94.4 | |
| SSA | 0 | 0 | 0 | 95.6 |
| Noise Level | Algorithm | Error Rate (%) | False Positive | False Negative | Accuracy of Element 42 (%) | Accuracy of Element 68 (%) |
|---|---|---|---|---|---|---|
| 0% | PSO | 50 | 0 | 1 | 0 | 96.8 |
| WOA | 80 | 3 | 1 | 0 | 90.9 | |
| SSA | 0 | 0 | 0 | 93.8 | 91.1 | |
| 5% | PSO | 100 | 1 | 2 | 0 | 0 |
| WOA | 66.7 | 1 | 1 | 99.2 | 0 | |
| SSA | 0 | 0 | 0 | 91.8 | 92.7 | |
| 10% | PSO | 50 | 0 | 1 | 0 | 97.0 |
| WOA | 83.3 | 4 | 1 | 0 | 92.6 | |
| SSA | 0 | 0 | 0 | 94.3 | 92.2 |
| Natural Frequencies | Analytical Values (HZ) | Experimental Values (Undamaged) | Experimental Values (Damaged) |
|---|---|---|---|
| 1 | 23.7 | 19.53 | 19.00 |
| 2 | 148.5 | 122.05 | 115.85 |
| 3 | 415.7 | 339.26 | 332.36 |
| 4 | 814.2 | 661.73 | 646.91 |
| 5 | 1345.3 | 1085.22 | 1037.46 |
| 6 | 2008.7 | 1594.59 | 1591.36 |
| Natural Frequencies | Analytical Values of Original FEM (HZ) | Experimental Values (Undamaged Beam) | Analytical Values of Modified FEM (HZ) |
|---|---|---|---|
| 1 | 23.7 (21.4%) * | 19.53 | 19.0 (2.7%) |
| 2 | 148.5 (21.7%) | 122.05 | 119.8 (1.8%) |
| 3 | 415.7 (22.5%) | 339.26 | 333.7 (1.6%) |
| 4 | 814.2 (23.0%) | 661.73 | 651.2 (1.6%) |
| 5 | 1345.3 (24.0%) | 1085.22 | 1068.7 (1.5%) |
| 6 | 2008.7 (26.0%) | 1594.59 | 1582.6 (0.8%) |
| Algorithm | Error Rate (%) | False Positive | False Negative | Accuracy of Element 9 (%) |
|---|---|---|---|---|
| PSO | 50 | 1 | 0 | 90.0 |
| GA | 66.7 | 2 | 0 | 46.6 |
| CS | 75 | 3 | 0 | 79.9 |
| SSA | 0 | 0 | 0 | 93.0 |
| Algorithm | Error Rate (%) | False Positive | False Negative | Accuracy of Floor 1 (%) | Computing Time(s) |
|---|---|---|---|---|---|
| PSO | 0 | 0 | 0 | 94.7 | 0.19 |
| GA | 50 | 1 | 0 | 60.3 | 2.87 |
| SSA | 0 | 0 | 0 | 94.7 | 0.50 |
| Algorithm | Error Rate (%) | False Positive | False Negative | Accuracy of Floor 1 (%) | Accuracy of Floor 2 (%) | Computing Time(s) |
|---|---|---|---|---|---|---|
| PSO | 33.3 | 1 | 0 | 80.0 | 80.2 | 0.19 |
| GA | 33.3 | 1 | 0 | 67.5 | 68.6 | 3.03 |
| SSA | 0 | 0 | 0 | 99.4 | 90.9 | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Peng, X.; Qin, F.; Yang, Q.; Xu, B. Structural Damage Detection Based on Sparrow Search Algorithm. Buildings 2025, 15, 1179. https://doi.org/10.3390/buildings15071179
Ma Z, Peng X, Qin F, Yang Q, Xu B. Structural Damage Detection Based on Sparrow Search Algorithm. Buildings. 2025; 15(7):1179. https://doi.org/10.3390/buildings15071179
Chicago/Turabian StyleMa, Ziyan, Xi Peng, Fengjiang Qin, Qiuwei Yang, and Bin Xu. 2025. "Structural Damage Detection Based on Sparrow Search Algorithm" Buildings 15, no. 7: 1179. https://doi.org/10.3390/buildings15071179
APA StyleMa, Z., Peng, X., Qin, F., Yang, Q., & Xu, B. (2025). Structural Damage Detection Based on Sparrow Search Algorithm. Buildings, 15(7), 1179. https://doi.org/10.3390/buildings15071179









