Creep Deformation Characteristics and Damage Unified Creep Constitutive Model of Undisturbed Structural Loess Under Different Consolidation Conditions

Abstract

In the loess-filling project, the original structural loess under the filling will produce creep deformation under the isometric consolidation stress state, affecting the upper building’s safe construction and later operation. Therefore, studying the creep deformation characteristics of structural loess under different consolidation coefficients is significant. In this paper, the following results are obtained by combining test and theoretical analysis. In view of the structural loess under the filling, the triaxial creep test of undisturbed loess under different isometric consolidation coefficients, confining pressures and shear stress levels was completed, and the creep deformation law of structural loess was obtained. The creep characteristics of undisturbed loess are found to be diversified under different coefficients, confining pressures, and shear stresses, including initial instantaneous deformation, subsequent creep attenuation deformation, and final stable creep deformation. The damage creep constitutive model of undisturbed loess is established, taking the binary medium model as the framework, the cementation element adopts the Nishihara model, the friction element introduces the overstress model and considers the isometric consolidation effect, and the damage creep constitutive model of undisturbed loess is established. The theoretical model is obtained by determining the relevant parameters of the constitutive model. The theoretical curve is compared with the experimental curve and shows that the damage creep model established in this paper can better reflect the creep of structural loess under isometric consolidation conditions well. The research results can provide systematic theoretical support and an experimental basis for the deformation problems involved in the filling project in the loess area.

1. Introduction

In filling, the underlying foundation soil will produce settlement deformation under upper stress [1], and there are more and more problems with loess engineering construction. In particular, the problem of consolidation settlement deformation of structural loess is becoming increasingly severe, which may eventually lead to engineering disasters in loess areas, resulting in engineering problems such as foundation settlement and roadbed cracking [2]. The filling projects in the northwest region often use loess as the filling medium, and the original foundation is mostly loess foundation. At present, through the existing loess-filling engineering construction process and post-operation results, it can be seen that the filling and post-construction deformation are key problems that cannot be avoided in this kind of project. Among them, it is crucial to study the deformation caused by creep to the filling project. Scholars believe that [3,4,5,6,7,8] the long-term deposition and loessization process make the loess have a strong structure in the natural state, and the internal structure determines the K₀ value of loess and the change in internal stress in loess under external load. Many scholars [9,10,11,12] have studied the creep deformation process of filling engineering in the compacted loess area. However, few scholars consider the creep damage constitutive model under the action of K₀ in the theoretical research. Therefore, this paper studies the damage creep constitutive model of undisturbed loess, considering isometric consolidation.

As a unique mechanical phenomenon, soil creep shows that deformation gradually accumulates and increases with time under constant stress level. In the loess area, engineering problems such as the slope instability of the subgrade excavation, the long-term continuous settlement of the building foundation, and the lateral displacement of the free surface of the foundation pit excavation are closely related to the creep characteristics of the loess. Instantaneous damage and creep damage will occur during the creep process of loess, both of which will have a particular impact on soil deformation and strength. Based on the Malan loess in the specific test area, Pang [13] sampled the loess subgrade after compaction of different energy levels and carried out a one-dimensional consolidation creep test. The test found that when the load was small, it was mainly elastic deformation, and when the load reached the structural yield strength, it was mainly plastic deformation. The water content and compactness of the loess also had a specific influence on the creep characteristics of the soil. Le et al. [14] conducted a multi-stage drained compression test on London clay using a special triaxial apparatus and studied the evolution of creep strain components in the triaxial stress space. Experiments show that stress conditions significantly affect creep behavior. Leng et al. [15] studied the variation in structural strength, deformation modulus, and strength parameters of undisturbed samples with different water contents by triaxial shear test. Nan [16] studied the mechanical properties of loess and carried out CU tests under different initial moisture content and confining pressure conditions. Three different failure modes (shear failure, homogeneous failure, and plastic failure) and their stress–strain responses with confining pressure levels and initial moisture content were revealed. Li [17] conducted a high-pressure consolidation creep test on remolded loess and obtained the creep deformation law of remolded loess under different compaction degrees and water content conditions.

Studying the creep constitutive model can predict the deformation law of major projects such as slopes, tunnels, and high fills in loess areas in the next few years to decades and help to propose corresponding disaster prevention and mitigation measures. As a medium with multi-phase characteristics, the soil has many complex properties, such as elastoplasticity, nonlinearity, heterogeneity, and anisotropy in mechanical behavior. These characteristics make the constitutive relationship of soil much more complex than solid materials. In order to describe the complex mechanical properties of soil based on different theoretical frameworks, scholars have constructed various constitutive models of soil. These models fully consider various characteristics of soil, including elastoplasticity, nonlinearity, heterogeneity, and anisotropy, when describing the stress–strain relationship of soil. Scholars have established many linear creep models based on one-dimensional creep tests [18,19], such as the Maxwell model and the Kelvin model. In the later stage of the study, to fully understand the deformation law of the soil, some scholars studied based on conventional triaxial tests. Presently, domestic and foreign scholars have considered many influencing factors for soil sample deformation, such as considering loading method, compaction degree, water content, etc. The creep constitutive model of loess can be divided into three categories, namely the component theory constitutive model [20,21], the empirical constitutive model [21,22], and the semi-empirical and semi-theoretical constitutive model [23,24]. Atriya [25] has extensively studied and recorded the creep behavior of cohesive soil around the world, indicating that it adversely affects the stability of structures, dams, excavations, etc. At the same time, through the multi-stage creep triaxial test under undrained conditions on the remolded soil samples, the creep parameters in the Singh–Mitchell model are used to quantify the creep potential of the Kolkata soft clay. Finally, these parameters are used to estimate the overall settlement of an old building in Kolkata. From the above analysis, it can be seen that the empirical model has few parameters and is easy to establish, but the applicability is not strong. For different working conditions and different conditions, it is usually necessary to establish different and large numbers of creep empirical model formulas. The empirical model uses mathematical formulas to summarize the changes with various conditions. The parameters are fewer, and the engineering application is more convenient, but its essential problem is that the theory is weak. Abu et al. [26] determined the fractional Burgers model under Robin-constrained boundary conditions by the Hilbert algorithm. The parameters of the empirical model are relatively few, the formula is simple and clear, and it is also convenient and fast in engineering applications. However, due to the lack of theoretical support, the model is limited by many factors. Based on the semi-theoretical and semi-empirical correction principle, Lian [27] introduced the Abel pot constructed by fractional calculus and used the nonlinear empirical formula to describe the nonlinear viscoplastic strain. Finally, a nonlinear semi-element semi-empirical model suitable for the research object was established. The semi-empirical and semi-theoretical model can not only describe the linear and nonlinear characteristics of loess but also the accelerated creep process of loess, which has certain practical value in practical engineering. The secondary anisotropy induced by K₀ consolidation is that the spatial position of soil particles will change after they are subjected to certain stress and strain, resulting in the spatial structure of the soil. At the theoretical level of the constitutive model, some scholars also introduced the K₀ consolidation condition. For the first time, OHTA et al. [28] introduced the relative stress ratio to characterize the anisotropy of saturated soft clay based on the original modified Cam-clay mode and deduced the undrained strength calculation formula of clay. Based on the modified Cambridge model, Wang et al. [29] considered the anisotropy, structure, and evolution of soft clay and the influence of plastic shear strain in the yield-surface-hardening rule and developed the traditional model into a constitutive model suitable for K₀ consolidated structured soft clay. Hou et al. [30] used undisturbed and remolded soil for isotropic compression. Based on the Cambridge model, the relative stress ratio and critical state stress ratio were introduced, reflecting the structural evolution of undisturbed loess under hydraulic coupling. However, most of the constitutive models considering K₀ consolidation in the above study are clay, and there are few constitutive models considering K₀ consolidation in the loess area. The constitutive model of K₀-consolidated structured loess: After fully understanding the influence of the structure of natural loess and the secondary anisotropy induced by K₀ consolidation on its stress and deformation, there are few studies on how to reflect these important influencing factors in the constitutive model. Although most researchers believe that the relationship between loess deformation and anisotropy is not significant and tend to use isotropic assumptions for in-depth research, in actual engineering practice, this simplification often leads to a series of safety accidents and unnecessary economic waste. In summary, it is of great engineering significance for engineering construction to study the creep characteristics and creep damage constitutive model of undisturbed loess considering the influence of isometric consolidation and to master the damage evolution of undisturbed loess. It can be seen that the current creep constitutive model does not consider the following problems, which limits its prediction accuracy when calculating the long-term settlement deformation of the original foundation of loess high fill:

(1)

In loess high-fill excavation and filling construction, the undisturbed loess will produce stress paths of vertical unloading and horizontal loading, and consolidation deformation and subsequent creep deformation will occur under these stress states (isometric consolidation). However, few creep tests and constitutive models consider the influence of isometric consolidation.

(2)

Undisturbed loess is a geotechnical engineering material with a cemented structure. When subjected to external loads, local damage will occur in the internal cementation, which creates creepy characteristics of undisturbed loess on the macro scale shared by the internal complete cementation structure and the damaged structure. However, the existing creep models rarely consider this local dynamic damage mechanism.

Therefore, this paper will establish a damage mechanism creep constitutive model of undisturbed loess, considering the influence of isometric consolidation. To this end, the main work carried out in this paper is as follows: 1. For the structural loess under the fill, the triaxial creep test of undisturbed loess under different isometric consolidation conditions was completed to explore the creep deformation law of structural loess. Based on the deformation characteristics of undisturbed loess under the isometric consolidation condition, a damage creep constitutive model of undisturbed loess considering the secondary anisotropy of isometric consolidation is derived based on the binary medium model. The Nishihara model describes the constitutive relationship of the cementation element, the friction element, and the overstress model, respectively, and the volume damage rate considering the creep condition and the damage constitutive equation of the friction element under the isometric consolidation condition are proposed, and the rationality of the model established in this paper is verified.

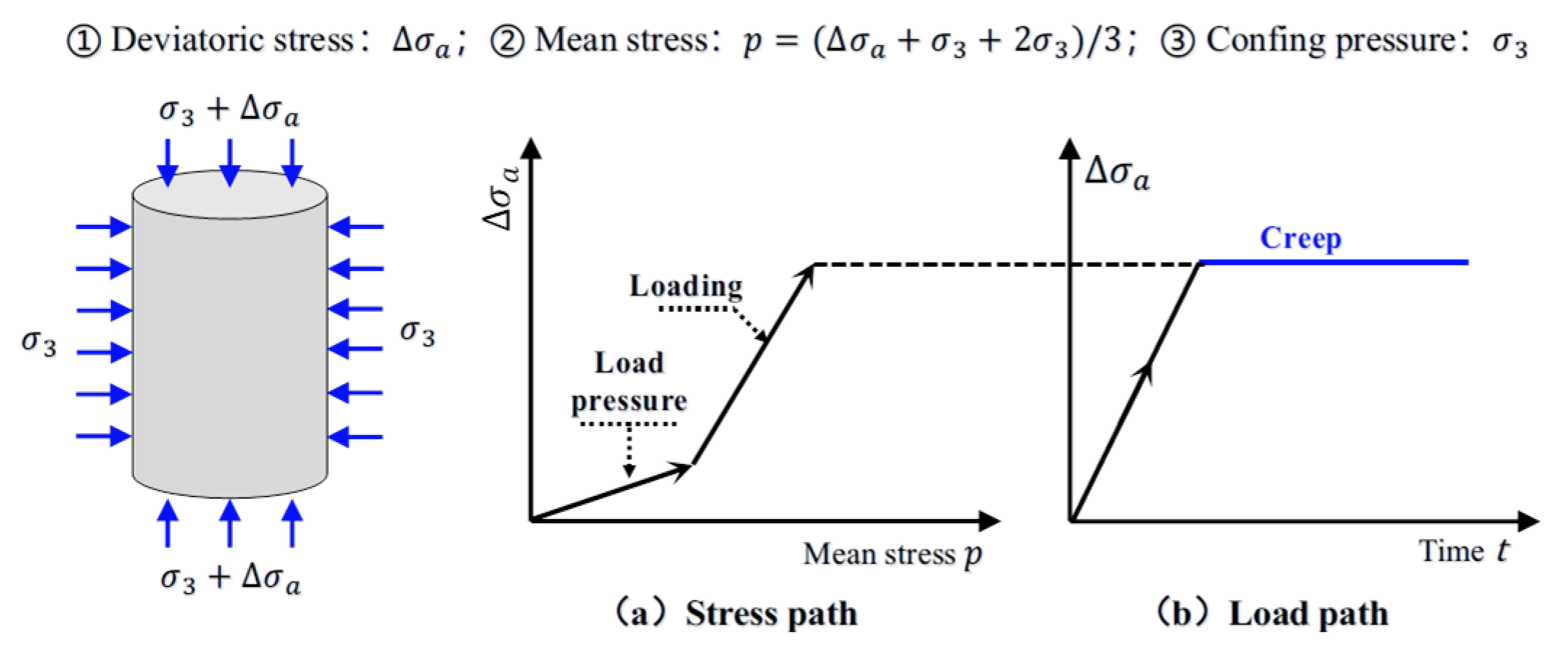
2. Test Scheme

2.1. Test Soil Sample

The sampling site is the construction site of a high-fill project, and the soil-sampling method is manual excavation. Based on the analysis of the results of field sampling observation and geotechnical test (according to geotechnical test method standard [31]), the essential physical and mechanical characteristics are shown in

Table 1. Physical and mechanical indexes of soil samples.

Water Content w	Void Ratio e	Liquid Limit WL	Plastic Limit WP	Density	Dry Density
12.56%	0.983	28.8%	18.6%	1.82 g/cm3	1.62 g/cm3

.

2.2. Test Scheme and Instruments

In order to study the influence of different isometric consolidation and confining pressure conditions on the creep deformation characteristic. The creep tests of undisturbed loess are carried out, and the strain–time relationship and isochronous curve relationship of the loess are analyzed. The sample loading scheme is shown in Figure 1. The test is terminated when the axial strain reaches 15% or the creep time reaches 24 h. Three parallel tests were performed on each group of tests to ensure the reliability of the test data. The test process should be operated strictly with the geotechnical specifications, and the test plan is shown in

Table 2. Triaxial creep test scheme of undisturbed loess.

Consolidation Coefficient	Confining Pressure (kPa)	Shear Stress Level
0.5	50, 200, 400	0.4, 0.6, 0.8, 0.95
0.8	50, 200, 400	0.4, 0.6, 0.8, 0.95
1.0	50, 200, 400	0.4, 0.6, 0.8, 0.95

.

The required soil samples were prepared according to the geotechnical test specifications. The sample size was 39.1 mm in diameter and 80 mm in height. The test instrument is a TKA-TTS-1WS automatic temperature control triaxial instrument, as shown in Figure 2.

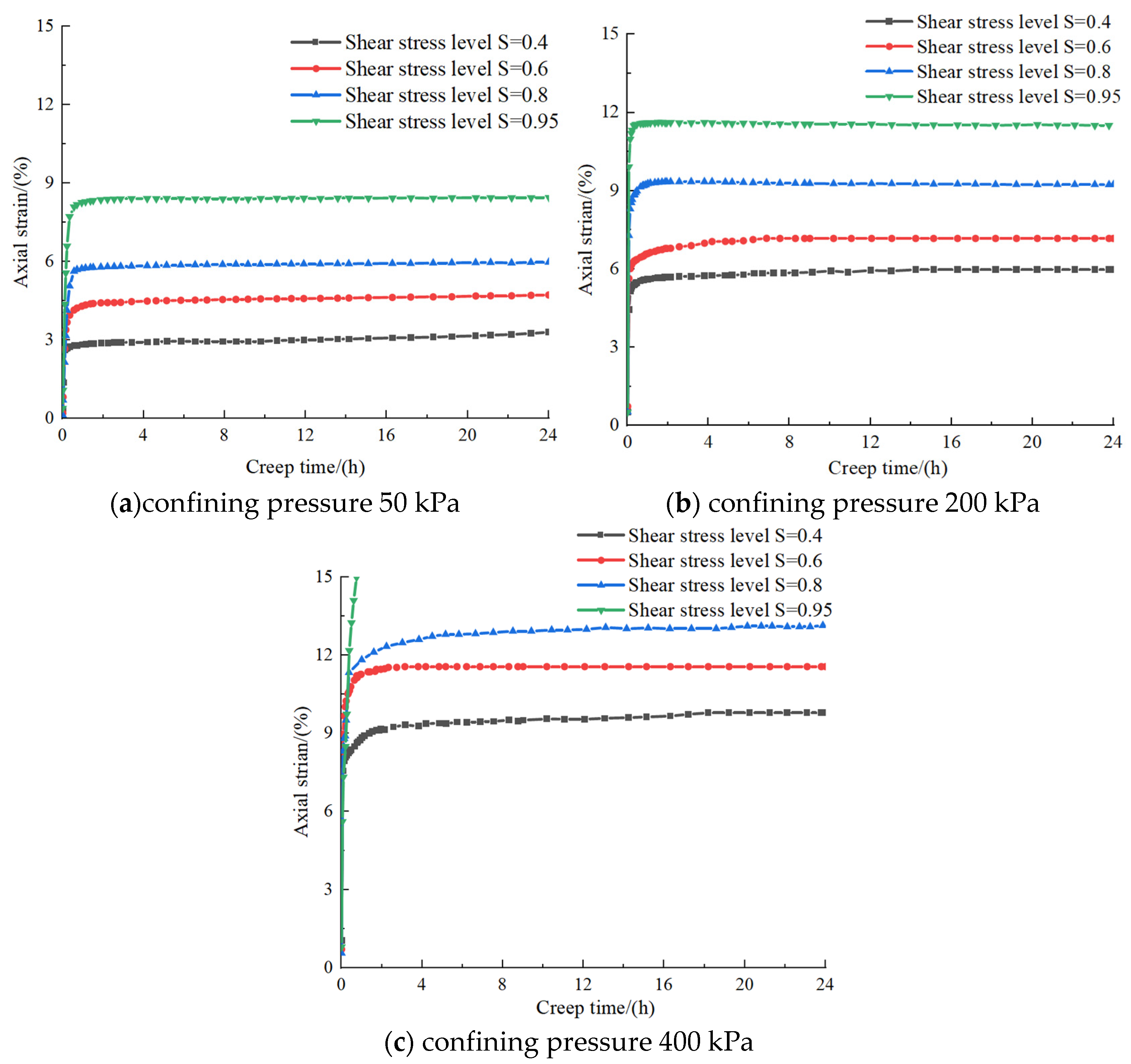
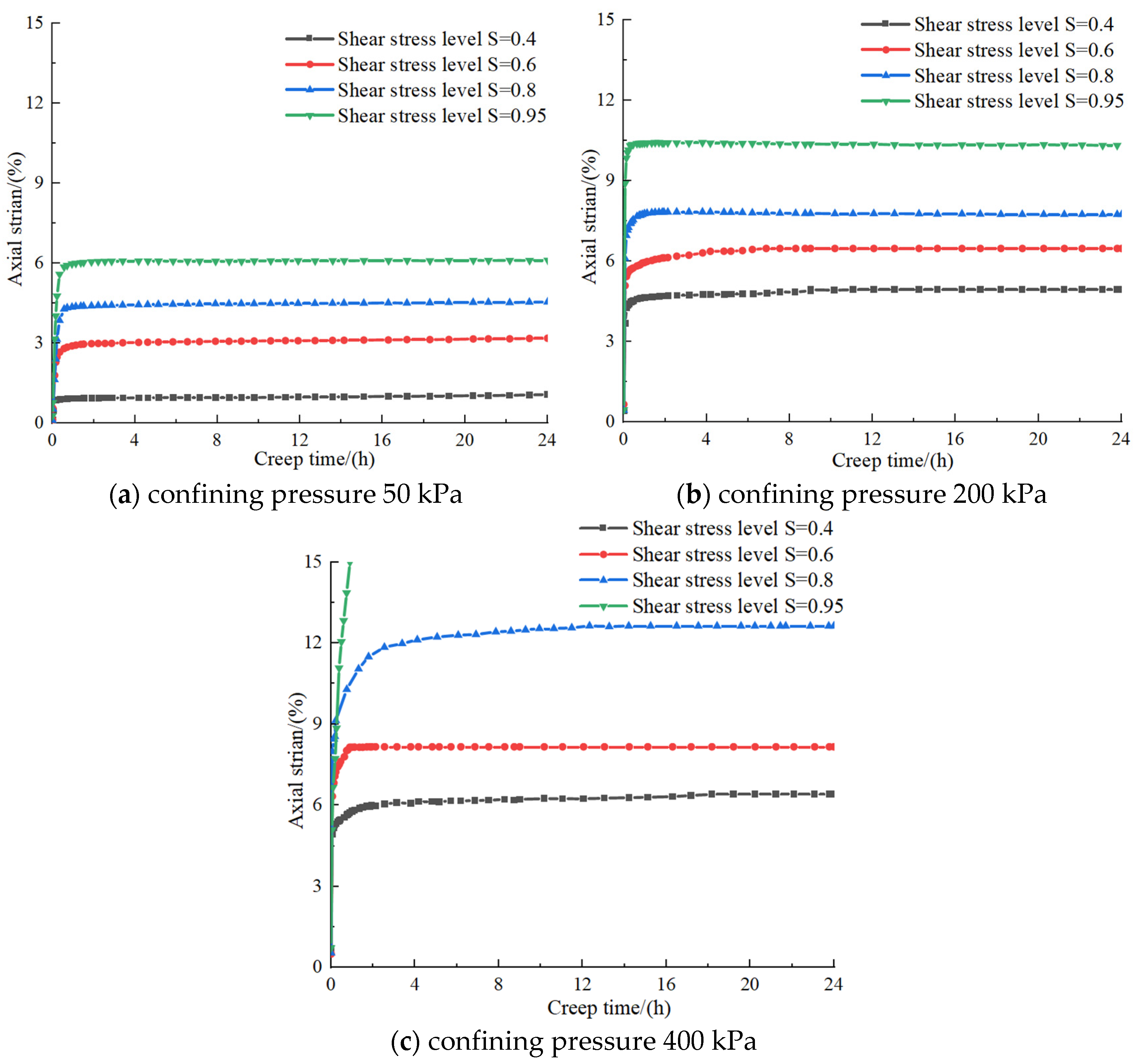
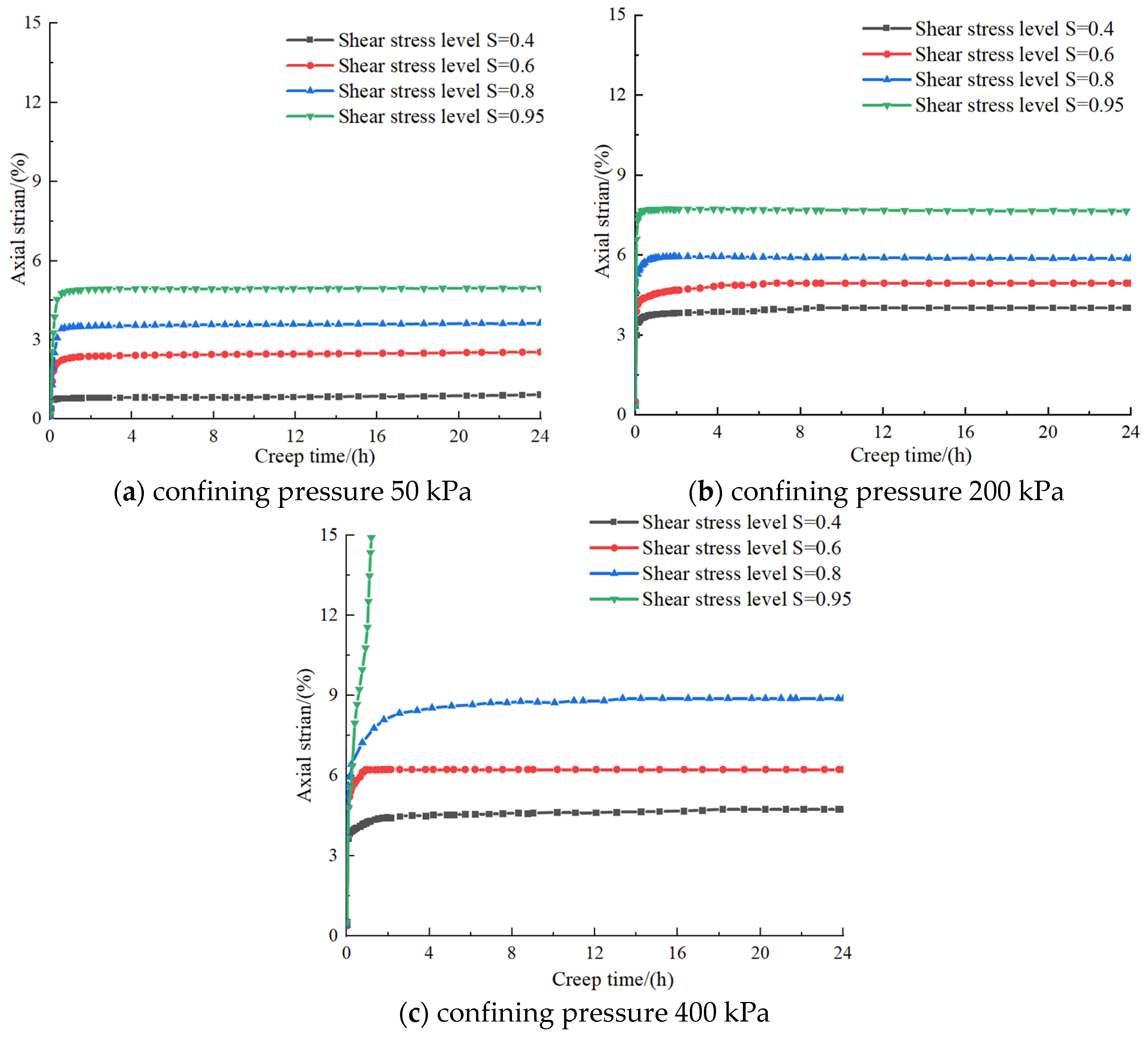
3. Analysis of Triaxial Creep Test Results

The triaxial creep test of saturated undisturbed loess under different isometric consolidation and confining pressure conditions shows the test results in Figure 3, Figure 4 and Figure 5.

Figure 3, Figure 4 and Figure 5 show the undisturbed loess’s triaxial creep test results under different isometric consolidation coefficients and confining pressures. The time–strain curve is obtained by conventional triaxial creep test of saturated undisturbed loess. This paper applies four creep loads level (0.4, 0.6, 0.8, 0.95) to the creep test. When the isometric consolidation coefficient is constant, the axial strain generated by the soil sample under different stress levels is not the same, and the corresponding total creep deformation is also different. The test results show that the curve has the following characteristics: under the same isometric consolidation coefficient and confining pressure, the more significant the principal stress difference, the more pronounced the instantaneous deformation and creep deformation of loess, and the more significant the creep effect. Under the same isometric consolidation coefficient and principal stress difference, the larger the confining pressure, the smaller the instantaneous deformation and creep deformation of loess, and the weaker the creep effect.

Under the same confining pressure and deviatoric stress level, the larger the isometric consolidation coefficient, the smaller the instantaneous deformation and creep deformation of loess, and the weaker the creep effect. When the isometric consolidation coefficient and confining pressure are constant, the soil sample will rapidly produce instantaneous deformation quickly when the load is applied to the soil sample. After the instantaneous deformation is completed, the deformation gradually increases with time, and the deformation rate gradually decreases and tends to a particular value. When the confining pressure of the sample increases, the corresponding instantaneous deformation increases, and the final creep deformation value gradually increases. When the isometric consolidation coefficient is 1.0, the confining pressure of the sample increases, and the instantaneous deformation of the load at different stress levels increases. When the isometric consolidation coefficient decreases, the instantaneous deformation gradually increases. When the confining pressure increases, the creep deformation stability time gradually increases; when the isometric consolidation coefficient decreases, the creep stability time gradually decreases, but the change range is small, and the total creep deformation gradually increases. The influence of the isometric consolidation coefficient on the creep characteristics of saturated undisturbed loess is also prominent. With the decrease in the isometric consolidation coefficient, it is easier for saturated undisturbed loess to enter the failure stage. Moreover, the larger the isometric consolidation coefficient is, the longer the development time of the creep curve of the saturated undisturbed loess enters the accelerated failure stage, and its essentially viscoplastic deformation characteristics are more prominent. The sudden increase in strain increment when the stress increment is the same is because the load on the sample has exceeded its yield stress, the soil structure is destroyed, and the viscoplastic deformation is generated. The soil structure bears deviatoric stress for the first few loads and produces viscoelastic deformation.

4. Creep Constitutive Model for Undisturbed Loess

4.1. Creep Mechanism

Loess is a unique soil deposit in nature. In the process of its natural or artificial external force deposition, it will be subjected to stress from all directions. The properties given by this stress are called anisotropy of soil. In order to simplify the calculation and design process, researchers in the field of geotechnical engineering tend to treat loess as an isotropic material [25]. However, it cannot be ignored that many practical studies have revealed that the influence of anisotropy on soil is exceptionally significant. Therefore, ignoring this point may lead to a significant deviation between the design calculation results and the actual situation, affecting the stability and safety of the project.

The anisotropy of natural soil affects its deformation and strength. According to the anisotropy of genetic soil, it can be divided into primary anisotropy and secondary anisotropy. The former is caused by the structural anisotropy of the soil skeleton, and the effect is difficult to quantify; the latter is caused by the unequal stress state in the consolidation process of in situ soil, which can be considered using inclined yield surface. Although most researchers reveal the anisotropic characteristics of loess through deformation indexes, these indexes are often based on elastic assumptions and fail to fully consider the nonlinear characteristics of soil and the influence of creep. However, in practice, the effect of creep on secondary anisotropy cannot be ignored, and the current research on this aspect is not detailed enough. Therefore, it is particularly urgent and necessary to deeply explore the influence of secondary anisotropy and local bonding breakage under creep under isometric consolidation, which will help scholars understand loess’s engineering characteristics more comprehensively and provide a more accurate and scientific basis for engineering design and construction.

4.2. Creep Model Framework

The creep breakage mechanism of loess has been analyzed, and it is considered that loess is a binary medium model composed of two parts: cementation elements and frictional elements. Therefore, for a representative volume element at time t or RVE, the total creep and local strain are denoted as follows: ${\epsilon }_{ij}\left(t\right)$ and ${\epsilon }_{ij}^{local}\left(t\right)$. The creep strain of the cementation and frictional elementss is expressed by ${\epsilon }_{ij}^b\left(t\right)$ and ${\epsilon }_{ij}^f\left(t\right)$, respectively. Therefore, the total strain ${\epsilon }_{ij}\left(t\right)$ of the two can be expressed as follows:

$${\epsilon }_{ij}\left(t\right)={\displaystyle \frac{1}{\nu }}\int {\epsilon }_{ij}^{locd}d\nu ={\displaystyle \frac{1}{\nu }}\int {\epsilon }_{ij}^{locd}d\left({\nu }_b+{\nu }_f\right)={\displaystyle \frac{1}{\nu }}\int {\epsilon }_{ij}^{locd}d{\nu }_b+{\displaystyle \frac{1}{\nu }}\int {\epsilon }_{ij}^{local}d{\nu }_f$$

(1)

In Formula (1): $v$ represents the volume of RVE, $v_b$ represents the volume of cementation elements, and $v_f$ represents the volume of frictional elements.

$${\epsilon }_{ij}^b\left(t\right)={\displaystyle \frac{1}{{\nu }_b}}\int {\epsilon }_{ij}^{local}d{\nu }_b$$

(2)

$${\epsilon }_{ij}^f\left(t\right)={\displaystyle \frac{1}{{\nu }_f}}\int {\epsilon }_{ij}^{local}d{\nu }_f$$

(3)

By Formulas (1)–(3), we can obtain the following:

$${\epsilon }_{ij}\left(t\right)={\displaystyle \frac{{\nu }_b}{\nu }}\int {\epsilon }_{ij}^{local}d{\nu }_b+{\displaystyle \frac{{\nu }_f}{\nu }}\int {\epsilon }_{ij}^{local}d{\nu }_f$$

(4)

The volume fraction of the frictional element in a RVE unit is defined as the volume breakage ratio ${\lambda }_v$, which can be expressed as follows:

$${\lambda }_v={\displaystyle \frac{v_f}{v}}$$

(5)

Substituting Formula (5) into Formula (4), we can obtain the following:

$${\epsilon }_{ij}\left(t\right)=\left(1-{\lambda }_v\right){\epsilon }_{ij}^b\left(t\right)+{\lambda }_v{\epsilon }_{ij}^f\left(t\right)$$

(6)

Formula (6) is the general strain relationship of creep model for loess.

By differentiating Formula (6) with time, the volume homogenization equation is as follows:

$${\dot{\epsilon }}_{ij}(t)=\left(1-{\lambda }_v\right)d{\epsilon }_{ij}^b\left(t\right)+{\lambda }_{v}d{\epsilon }_{ij}^f\left(t\right)+d{\lambda }_v\left({\epsilon }_{ij}^f\left(t\right)-{\epsilon }_{ij}^b\left(t\right)\right)$$

(7)

According to Formula (7), the macroscopic strain rate consists of three parts: ① the strain rate of the cementation elements $\left(1-{\lambda }_v\right)d{\epsilon }_{ij}^b\left(t\right)$; ② strain rate of frictional elements ${\lambda }_{v}d{\epsilon }_{ij}^f\left(t\right)$; ③ strain rate of local damage $d{\lambda }_v\left({\epsilon }_{ij}^f\left(t\right)-{\epsilon }_{ij}^b\left(t\right)\right)$.

4.3. Creep Constitutive Model for Cemented Element

As the Nishihara model can better reflect the elastic–viscoelastic–viscoplastic rheological properties of rock and soil, many scholars choose to improve the accuracy of the model by changing the characteristics or types of components in the Nishihara model. The viscosity coefficient of the viscoplastic element in the Nishihara model increases with time, so an improved Nishihara creep constitutive model suitable for the loess cementation element is proposed.

The one-dimensional creep equation of the Nishihara model is as follows:

$$\left\{\begin{array}{l}\mathrm{When}\sigma \mathrm{is}\mathrm{less}\mathrm{than}{\sigma }_s,\epsilon \left(t\right)={\displaystyle \frac{{\sigma }_0}{E_1}}+{\displaystyle \frac{{\sigma }_0}{E_2}}\left(1-e^{-{\displaystyle \frac{E_2}{{\eta }_1}}t}\right)\\ \mathrm{When}\sigma \mathrm{is}\mathrm{greater}\mathrm{than}\mathrm{or}\mathrm{equal}\mathrm{to}{\sigma }_s,\epsilon (t)={\displaystyle \frac{{\sigma }_0}{E_1}}+{\displaystyle \frac{{\sigma }_0-{\sigma }_s}{{\eta }_2}}t+{\displaystyle \frac{{\sigma }_0}{E_2}}(1-e^{-{\displaystyle \frac{E_2}{{\eta }_1}}t})\end{array}\right.$$

(8)

When $\sigma$ is less than ${\sigma }_s$, the model is reduced to a generalized Kelvin three-element model, and the nonlinear damage variable in the model does not play its role. According to the superposition principle, the one-dimensional creep equation is as follows:

$${\epsilon }_1^b\left(t\right)={\displaystyle \frac{\sigma }{E_1}}+{\displaystyle \frac{\sigma }{E_2}}\left[1-\exp (-{\displaystyle \frac{E_2}{{\eta }_1}}t)\right]$$

(9)

In Formula (9), ${\epsilon }_1^b\left(t\right)$ is the strain; $E_1$, $E_2$ are the elastic moduli; ${\eta }_1$ is the Kelvin viscosity coefficient; and t is time.

In the three-dimensional stress state, it is necessary to convert the one-dimensional constant stress ${\sigma }_0$ into a constant deviatoric stress ${(S_{ij})}_0$; then, we obtain the following:

$${\epsilon }_{ij}^b\left(t\right)={\displaystyle \frac{{(S_{ij})}_0}{2G_1}}+{\displaystyle \frac{{(S_{ij})}_0}{2G_2}}\left(1-e^{-{\displaystyle \frac{E_2}{{\eta }_1}}t}\right)$$

(10)

G₁ and G₂ in Formula (10) are the shear modulus corresponding to E₁ and E₂ in the model, respectively.

4.4. Creep Constitutive Model for Frictional Element

When $\sigma$ it is more significant than ${\sigma }_s$$\left({(S_{ij})}_0\ge {\sigma }_s\right)$, due to the plastic flow of the rock and soil mass at this time, the plastic potential function Q and the yield surface F need to be introduced. At this time, the viscous plastic deformation rate of the third part (plastic element and viscous element in parallel) in the Nishihara model can be used for reference from the overstress model in soil mechanics:

$${\epsilon }_{ij}^f(t)=\left({\displaystyle \frac{\langle F\rangle }{2{\eta }_2}}\right){\displaystyle \frac{\partial Q}{\partial {\sigma }_{ij}}}$$

(11)

$$\langle F\rangle =\left\{\begin{array}{l}0\left(f\le 0\right)\\ f(f>0)\end{array}\right.$$

(12)

In Formula (12), f refers to the yield function, and f = Q when using the relevant flow rule. Therefore, when (f > 0), the creep constitutive equation is as follows:

$${\epsilon }_{ij}^f(t)=\left({\displaystyle \frac{f}{2{\eta }_2}}\right){\displaystyle \frac{\partial f}{\partial {\sigma }_{ij}}}t$$

(13)

In order to reasonably reflect the stress-induced anisotropy and breakage caused by the initial isometric consolidation state, this paper uses the existing research results as the loess yield function proposed by Hou [31], as shown in Formula (14).

$$f=1+{({\displaystyle \frac{\eta }{M^{*}}})}^2-{\displaystyle \frac{p_c}{p}}=0$$

(14)

In Formula (14):

$$\eta ={\displaystyle \frac{q}{p}}$$

(15)

$${\eta }_g={\displaystyle \frac{{\sigma }_g-p{\delta }_g}{p}}$$

(16)

$${\eta }_{go}={\displaystyle \frac{{\sigma }_{go}-p_0{\delta }_{ij}}{p_0}}$$

(17)

$$M^{*}=\sqrt{M^2-{\eta }_0^2}$$

(18)

$${\eta }_0=\left|{\displaystyle \frac{3\left(1-K_0\right)}{2K_0+1}}\right|$$

(19)

In the above formula, ${\eta }_{ij}$ and ${\eta }_{ij0}$ are the normalized stress ratio tensors during the loading process and after consolidation, respectively; ${\sigma }_{ij}$ and ${\sigma }_{ij0}$ are the tensor forms of the mean stress under the loading process and the initial state, respectively; $p_0$ is the initial mean stress; ${\delta }_{ij}$ is the Kronecker symbol; ${\eta }_0$ is the initial stress ratio; $K_0$ is the lateral pressure coefficient; $p_c$ is the initial yield stress; $q$ is the shear stress; $p^{\prime }$ is the mean stress.

$$f=1+{\left({\displaystyle \frac{\frac{q}{p}}{\sqrt{M^2-{\left|\frac{3\left(1-K_0\right)}{2K_0+1}\right|}^2}}}\right)}^2-{\displaystyle \frac{p_c}{p}}$$

(20)

In Formula (20), q: shear stress; p_c is the initial yield stress; p is the average stress; and M is the critical stress ratio of undisturbed loess. $K_0$ is the coefficient.

$${\displaystyle \frac{\partial f}{\partial q}}={\displaystyle \frac{2q}{p^2\left|M^2-\frac{{(3-3K_0)}^2}{{(2K_0+1)}^2}\right|}}$$

(21)

$${\epsilon }_{\mathrm{s}}^f(t)=\left({\displaystyle \frac{1+{\left(\frac{\frac{q}{p}}{\sqrt{M^2-{\left|\frac{3\left(1-K_0\right)}{2K_0+1}\right|}^2}}\right)}^2-\frac{p_c}{p}}{2{\eta }_2}}\right){\displaystyle \frac{2qt}{p^2\left|M^2-\frac{{(3-3K_0)}^2}{{(2K_0+1)}^2}\right|}}$$

(22)

$${\epsilon }_s^f(t)={\displaystyle \frac{2}{3}}\left({\epsilon }_1^f(t)-{\epsilon }_3(t)\right)$$

(23)

$${\epsilon }_1^f(t)={\displaystyle \frac{3}{2}}{\epsilon }_s^f(t)$$

(24)

$${\epsilon }_1\left(t\right)=\left(1-{\lambda }_v\right){\epsilon }_1^b\left(t\right)+{\lambda }_v{\epsilon }_1^f\left(t\right)$$

(25)

$$\begin{array}{l}{\epsilon }_1\left(t\right)=(1-{\lambda }_v){\displaystyle \frac{\sigma }{E_1}}+(1-{\lambda }_v){\displaystyle \frac{\sigma }{E_2}}\left[1-\exp (-{\displaystyle \frac{E_2}{{\eta }_1}}t)\right]+{\displaystyle \frac{3}{2}}{\lambda }_v\left({\displaystyle \frac{1+{\left(\frac{\frac{q}{p}}{\sqrt{M^2-{\left|\frac{3\left(1-K_0\right)}{2K_0+1}\right|}^2}}\right)}^2-\frac{p_c}{p}}{2{\eta }_2}}\right){\displaystyle \frac{2q}{p^2\left|M^2-\frac{{(3-3K_0)}^2}{{(2K_0+1)}^2}\right|}}t\\ =(1-{\lambda }_v){\displaystyle \frac{\sigma }{E_1}}+(1-{\lambda }_v){\displaystyle \frac{\sigma }{E_2}}\left[1-\exp (-{\displaystyle \frac{E_2}{{\eta }_1}}t)\right]+{\displaystyle \frac{3{\lambda }_{v}qt\left[1+\left(\frac{\frac{q^2}{p^2}}{\left|M^2-{\left|\frac{3\left(1-K_0\right)}{2K_0+1}\right|}^2\right|}\right)-\frac{p_c}{p}\right]}{2{\eta }_2{p}^2\left|M^2-\frac{{(3-3K_0)}^2}{{(2K_0+1)}^2}\right|}}\\ =(1-{\lambda }_v){\displaystyle \frac{\sigma }{E_1}}+(1-{\lambda }_v){\displaystyle \frac{\sigma }{E_2}}\left[1-\exp (-{\displaystyle \frac{E_2}{{\eta }_1}}t)\right]+{\displaystyle \frac{3{\lambda }_{v}qt\left[1+{\left(\frac{\eta }{M^{*}}\right)}^2-\frac{p_c}{p}\right]}{2{\eta }_2{p}^2(M^{*}{)}^2}}\end{array}$$

(26)

4.5. Breakage Ratio

Since the breakage ratio cannot be directly reflected from the macro scale for loess, the rationality of the proposed breakage ratio is verified by the first assumption and then verification. The analysis of the damage law of undisturbed loess is as follows:

(1)

Under the condition of low confining pressure, it shows attenuation creep under the condition of low stress. Under applying high stress, it shows non-attenuation creep, and the time of each stage of the creep curve under different conditions is different. When the load is large, the stable creep stage in the non-attenuation creep curve is not apparent, and it quickly transforms into the acceleration stage, and the damage rate of rock and soil increases.

(2)

With the increase in confining pressure, the creep acceleration stage is less obvious, showing a decreasing trend.

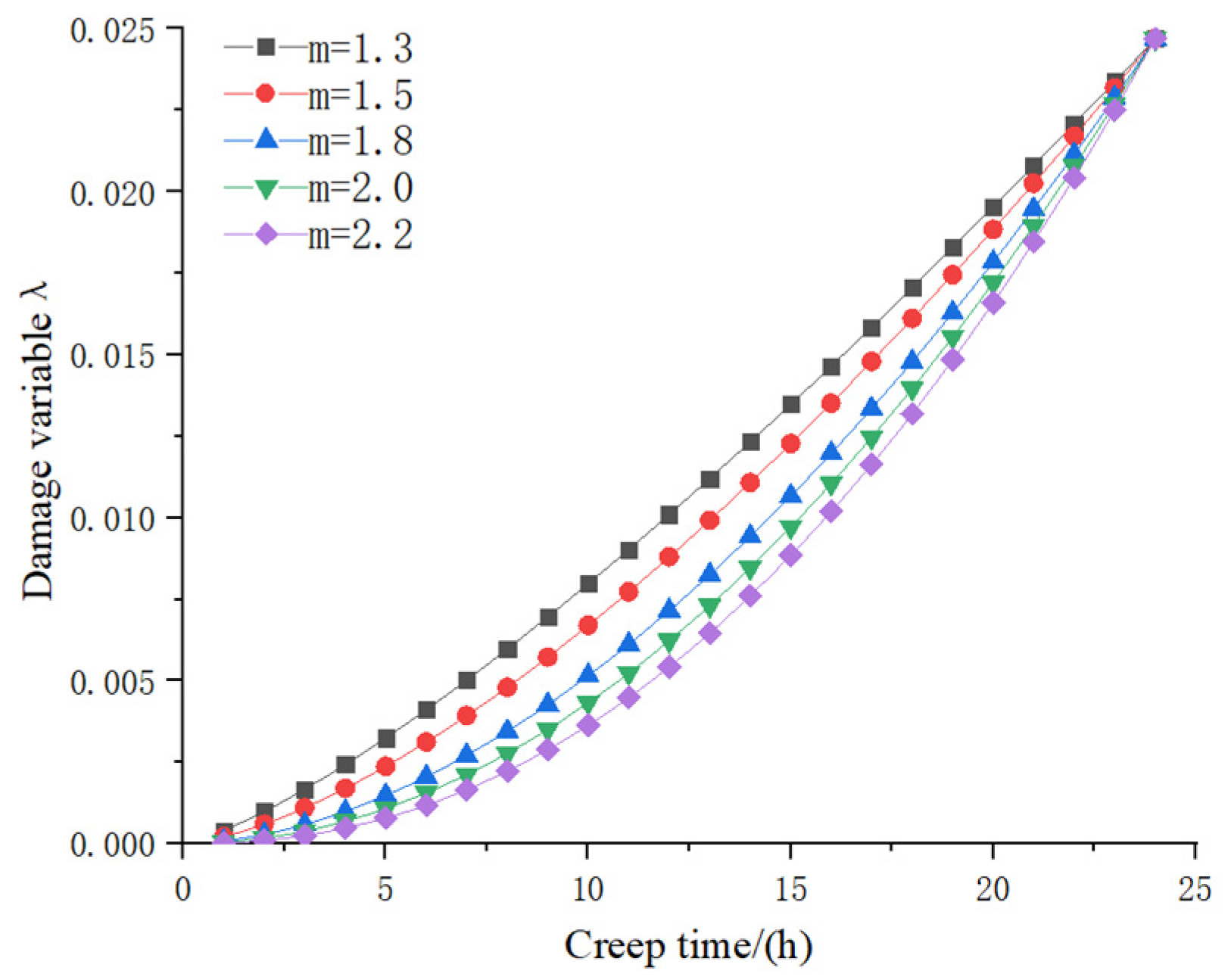
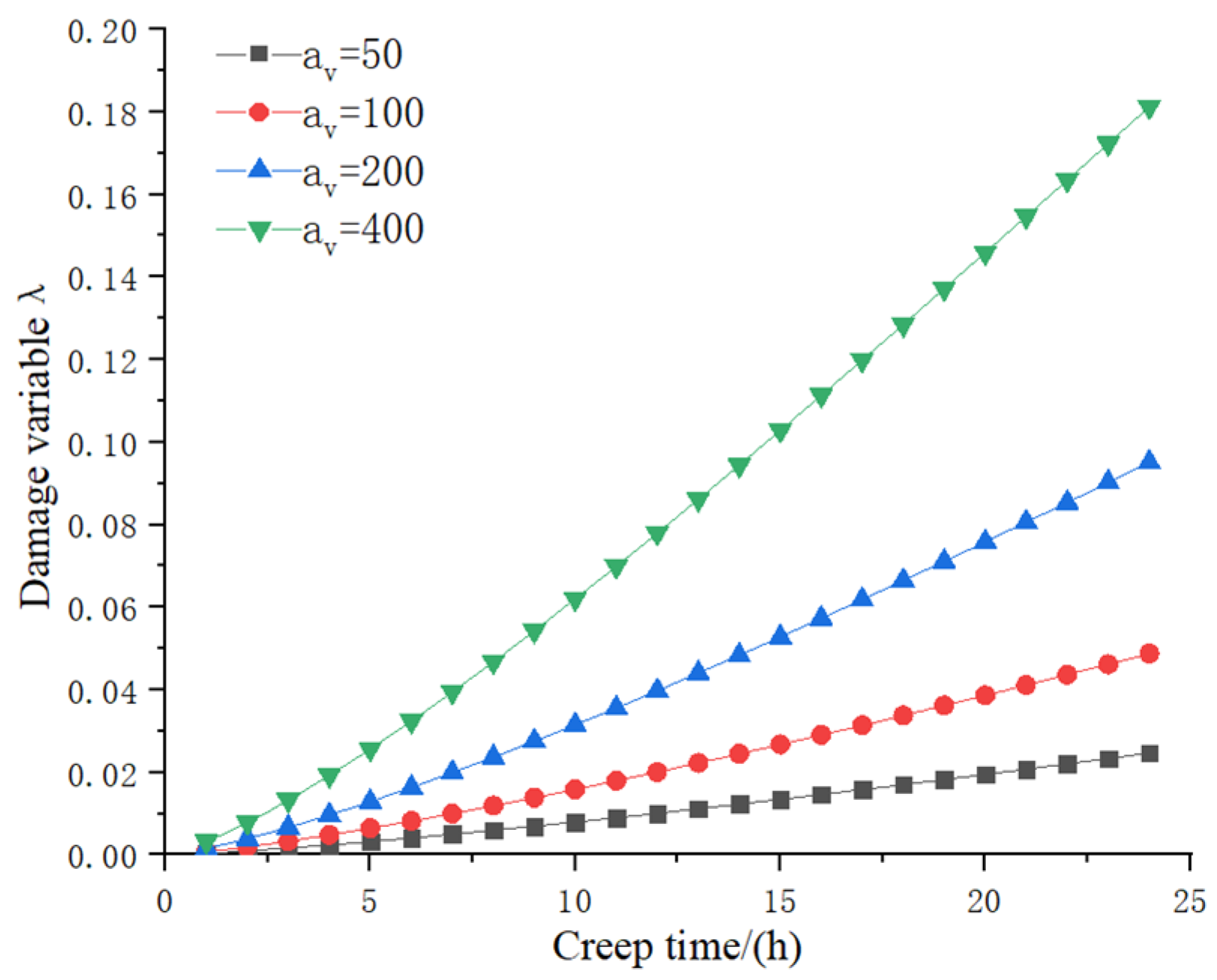
(3)

With the increase in loading time, the damage rate of loess increases first and then tends to be stable. Its value changes from a value slightly greater than 0 to a value less than 1.

Considering that the damage variable is related to stress, confining pressure, and time, an equation is established to better simulate the creep damage rate of geotechnical materials. The expression is as follows:

$${\lambda }_v=1-exp\left[-a_v\left({\displaystyle \frac{{\sigma }_3}{10Pa}}\right)\left({\displaystyle \frac{q}{q_0}}\right){\left({\displaystyle \frac{t}{t_0}}\right)}^m\right]\left(F-F_0\right)>0$$

(27)

In Formula (27), $Pa$ is the standard atmospheric pressure, 101.01 kPa; $q$ is the shear stress under the condition of conventional triaxial stress, and $q_0$ is the stress reference value; this paper takes 1 kPa. t is the creep time, and t₀ is the time reference value; this paper takes 24 h; $a_v$ and $m$ for the material parameters.

4.6. Determination Method of Model Parameters

In the above constitutive model established in this paper, the parameters of cementation element, friction element, and breakage rate are included, as shown in the Table 3.

Table 3. Model parameter table.

Parameter	Implication	Determine Method
$E_1$	Elastic modulus	Determined by undisturbed loess triaxial compression test
$E_2$
${\eta }_1$	Coefficient of viscosity	The creep deformation curve of undisturbed loess under low-stress levels is simulated without considering the damage rate.
M	Critical stress ratio	Determined by undisturbed loess triaxial compression test
K0	Consolidation coefficient	K0 consolidation test
$p_{\mathrm{c}}$	Initial yield stress	Determined by undisturbed loess triaxial compression test
${\eta }_2$	Coefficient of viscosity	The non-attenuation creep curve of the simulated original loess is determined.
$a_v$	Breakage parameter	According to the model’s prediction of the experimental data, the inversion is determined.
$m$

Table 3. Model parameter table.

Parameter	Implication	Determine Method
$E_1$	Elastic modulus	Determined by undisturbed loess triaxial compression test
$E_2$
${\eta }_1$	Coefficient of viscosity	The creep deformation curve of undisturbed loess under low-stress levels is simulated without considering the damage rate.
M	Critical stress ratio	Determined by undisturbed loess triaxial compression test
K0	Consolidation coefficient	K0 consolidation test
$p_{\mathrm{c}}$	Initial yield stress	Determined by undisturbed loess triaxial compression test
${\eta }_2$	Coefficient of viscosity	The non-attenuation creep curve of the simulated original loess is determined.
$a_v$	Breakage parameter	According to the model’s prediction of the experimental data, the inversion is determined.
$m$

5. Model Verification

5.1. Parameter Analysis of Cementation Elements

The creep constitutive model of the cementation elements reflects the viscoelastic model. Derivation of Formula (9):

$${\dot{\epsilon }}_1^b={\displaystyle \frac{\sigma }{E_2}}\exp (-{\displaystyle \frac{E_2}{{\eta }_1}}t)$$

(28)

For the extreme value of t in Formulas (9) and (27), then:

$$\left\{\begin{array}{l}{\epsilon }_1^b(t\to 0)={\epsilon }_1={\displaystyle \frac{\sigma }{E_1}}\\ {\dot{\epsilon }}_1^b(t\to 0)={\displaystyle \frac{\sigma }{E_2}}\end{array}\right.$$

(29)

$$\left\{\begin{array}{l}{\epsilon }_3^b(t\to \infty )={\displaystyle \frac{\sigma }{E_1}}+{\displaystyle \frac{\sigma }{E_2}}\\ {\dot{\epsilon }}^b(t\to \infty )=0\end{array}\right.$$

(30)

In the above formula: $E_1,E_2,{\eta }_1$ are the three parameters in the cemented element model. ${\epsilon }_1$ represents the instantaneous elastic strain generated by the soil; ${\epsilon }_3^b(t\to \infty )$ is the final creep deformation corresponding to the Kelvin model.

Combining the above equations, we can derive the following:

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{\sigma }{{\epsilon }_1}}\\ E_2={\displaystyle \frac{\sigma }{{\epsilon }_3^b(t\to \infty )-{\epsilon }_1}}\end{array}\right.$$

(31)

The parameters determined by the test data in this paper are shown in

Table 4. Model parameter values.

Confining Pressure/kPa	${\mathit{E}}_1$/kPa	${\mathit{E}}_2$/kPa	${\mathit{\eta }}_1$/105 kPa·h
50	175.42	223.65	2.33
200	184.72	311.34	1.95
400	191.72	423.37	1.87

.

5.2. Parameter Analysis of Friction Elements

The creep constitutive model of the friction elements reflects the viscoplastic deformation model. The specific parameter determination method is shown in

Table 5. Cementing element model parameter values.

Confining Pressure/kPa	M	${\mathit{\eta }}_2$/105 kPa·h
50	1.04	1.02
200	1.04	1.79
400	1.04	2.69

.

5.3. Breakage Parameter Analysis

The damage variable curve of the same creep is also determined by assuming and verifying. The specific method is to obtain different damage variable curves by assuming the parameter values of the damage variable. Then, the damage variable is substituted into the stress–strain curve of the sample to select the appropriate damage variable curve. By substituting $a_v$ = 50 into the Formula (27), a set of damage variables with different m values can be obtained. The value of m mainly affects the damage degree of the sample, as shown in Figure 6. Substituting m = 1.3 into Formula (27), a set of damage variables with different values can be obtained. The value $a_v$ mainly affects the speed of initial damage, as shown in Figure 7.

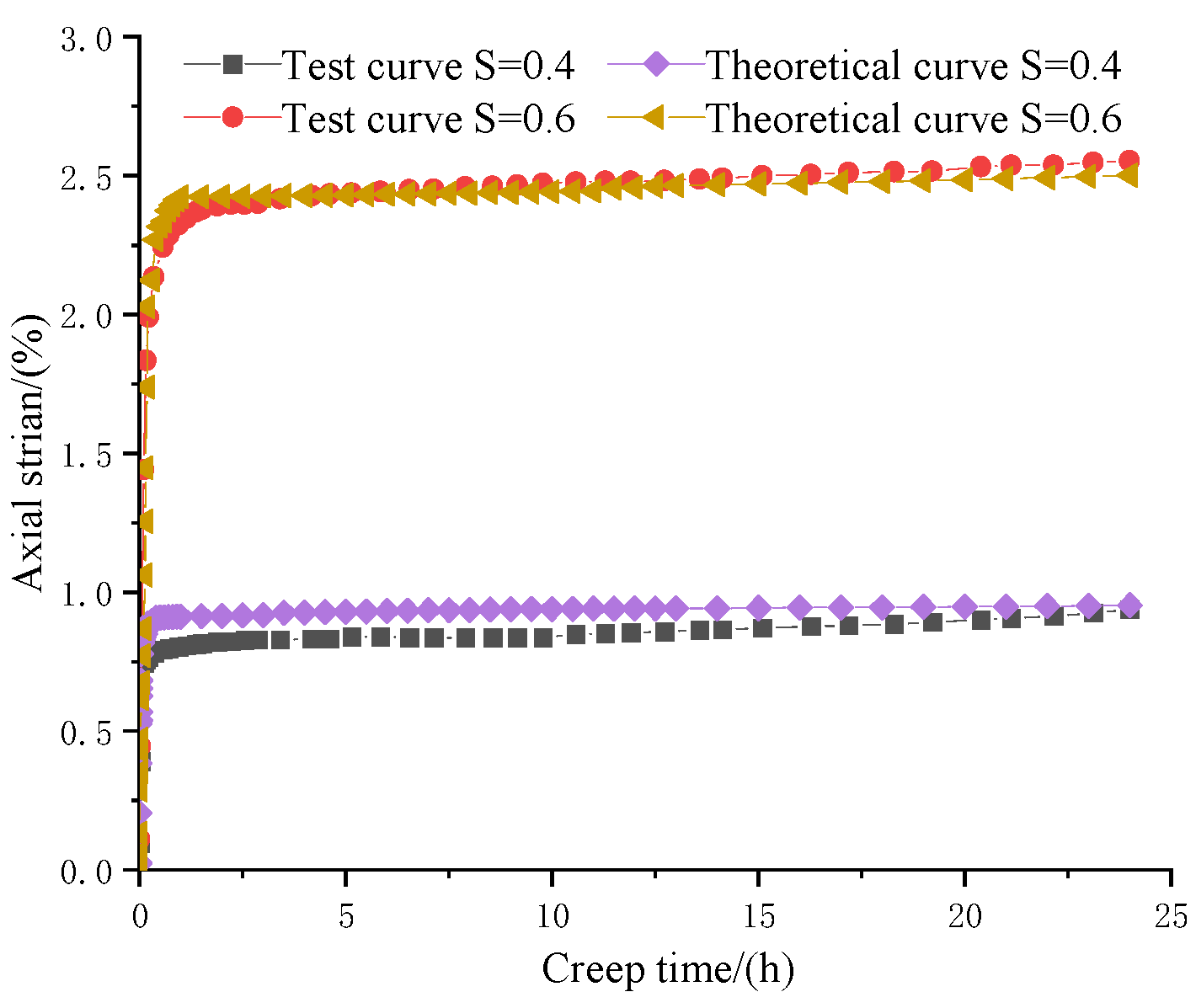
5.4. Theoretical Model Verification

The above model parameters are substituted into the creep damage constitutive model of undisturbed loess considering the rate of isometric consolidation, and the theoretical curve can be calculated, as shown in Figure 8 and Figure 9. Comparing the test curve with the theoretical curve, it can be seen that the established model accurately simulates the attenuation curve under different confining pressures and different stress levels, and the relative error is small. It simulates the characteristics of the initial creep rate reduction and the influence of creep deformation characteristics.

The comparison of theoretical and experimental data in

Table 6. Comparison of theoretical and experimental data under different test conditions.

Consolidation Coefficient	Confining Pressure/kPa	Shear Stress Level	Axial Strain for Test (%)	Axial Strain for Theoretical (%)	Relative Error (%)
0.8	50	0.4	1.07818	0.9768	9.40
		0.6	3.19184	2.96148	7.21
0.8	200	0.4	4.94257	4.88834	1.09
		0.6	6.4799	6.23682	3.758
1.0	200	0.4	0.93755	0.95218	−1.56
		0.6	2.55347	2.5006	2.07

under different experimental conditions shows that the maximum prediction error of the model in this paper is 9.4%, which can meet the requirements of engineering prediction and illustrate the rationality of the model in this paper.

6. Conclusions

In this paper, the creep constitutive model considering different isometric consolidation coefficients, confining pressures, and shear stress levels is established, and the test curve is compared with the theoretical curve to verify the rationality and validity of the model. The main conclusions are as follows:

(1)

Based on the Nishihara model, the relationship between the strain of the cementation element and the creep time is proposed. And the isometric consolidation coefficient is introduced into the overstress model in the friction element, and the relationship between the strain of the friction element and the creep time is proposed. The expression of the volume damage rate can quickly and effectively determine the mechanical parameters of the soil.

(2)

The parameters proposed in the model are calculated reasonably, and the damage law of undisturbed loess is analyzed: with the increase in loading time, the damage rate of loess increases first and then gradually tends to be stable, and the value of volume damage rate is a value between 0–1.

(3)

This paper proposes a creep damage constitutive model of undisturbed loess based on a binary medium model considering the isometric consolidation, which can better reflect the creep characteristics. By the test curve and theoretical curve, it can be obtained that the model has a good prediction effect.

In the follow-up research work, multi-scale test experimental techniques, such as CT technology, should be used to capture the evolution law of meso-cementation structure in real-time during the creep process to reveal the internal damage mechanism quantitatively and put forward the damage parameter equation related to creep deformation, to construct a multi-scale creep model to fully consider the physical mechanism of deformation and achieve better prediction accuracy.