Concrete Carbonization Prediction Method Based on Bagging and Boosting Fusion Framework
Abstract
1. Introduction
2. Dataset Description and Analysis
3. Methods
3.1. Machine Learning Algorithms
3.1.1. Random Forest Regression
3.1.2. Categorical Boosting (Catboost)
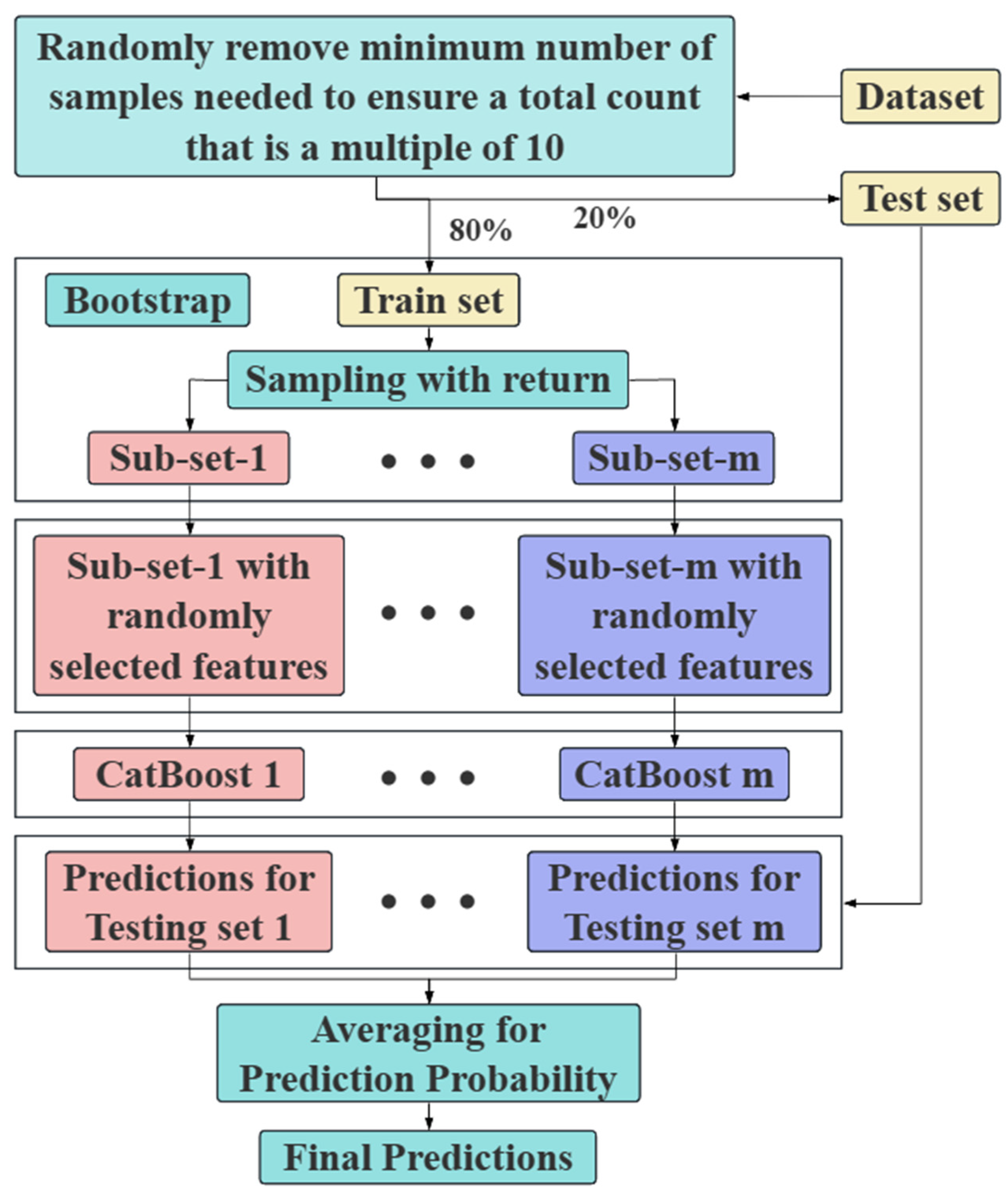
3.1.3. RF–CatBoost-Based Fusion Framework
3.2. Hyperparameter Tuning
3.3. K-Fold Cross-Validation
3.4. Performance Evaluation Indicators
3.5. Explanatory Analysis of the Best Model
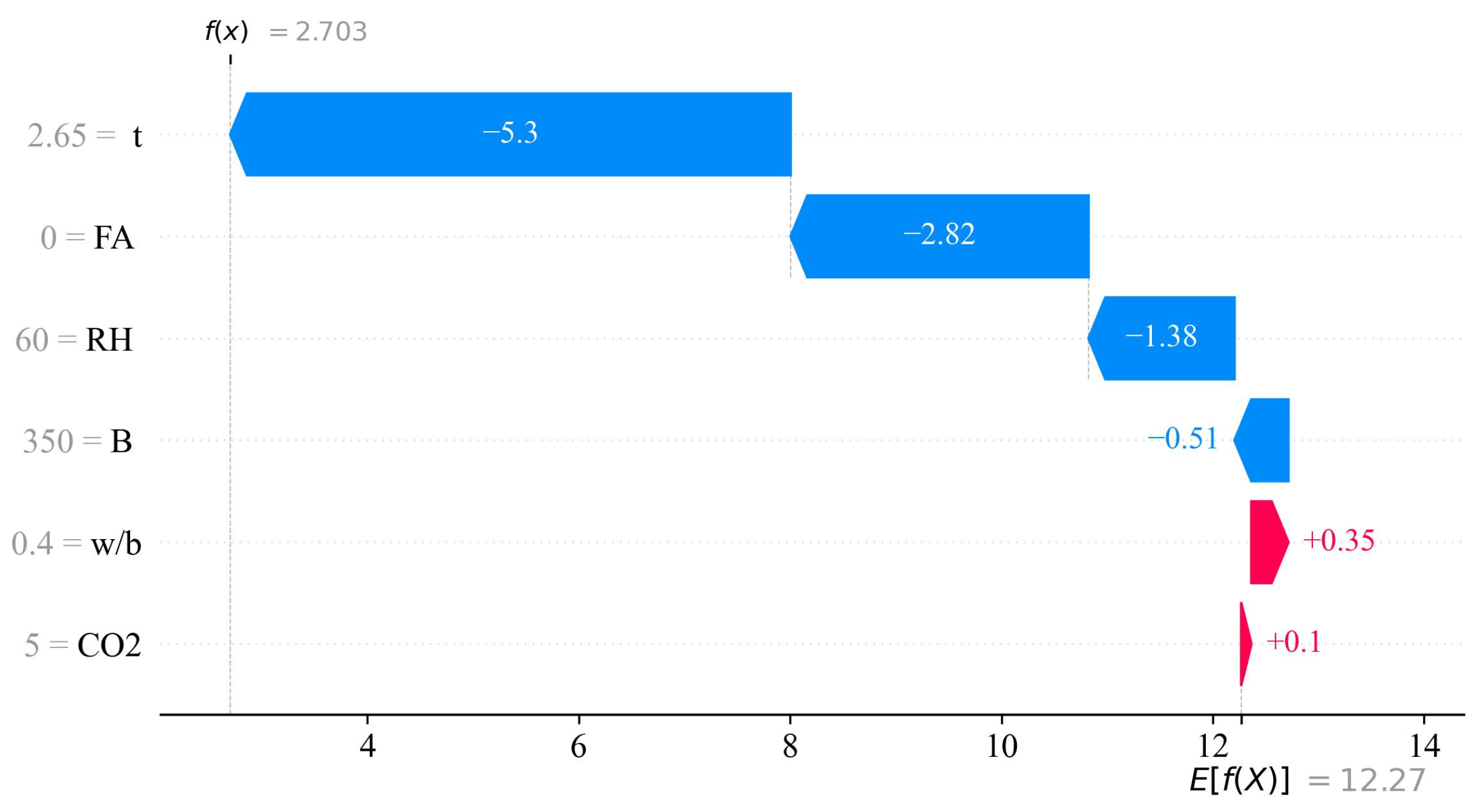
3.5.1. Global Significance Analysis and Local Output Explanation
3.5.2. Feature Interaction Analysis
3.5.3. Characteristic Importance Analysis
4. Results and Discussion
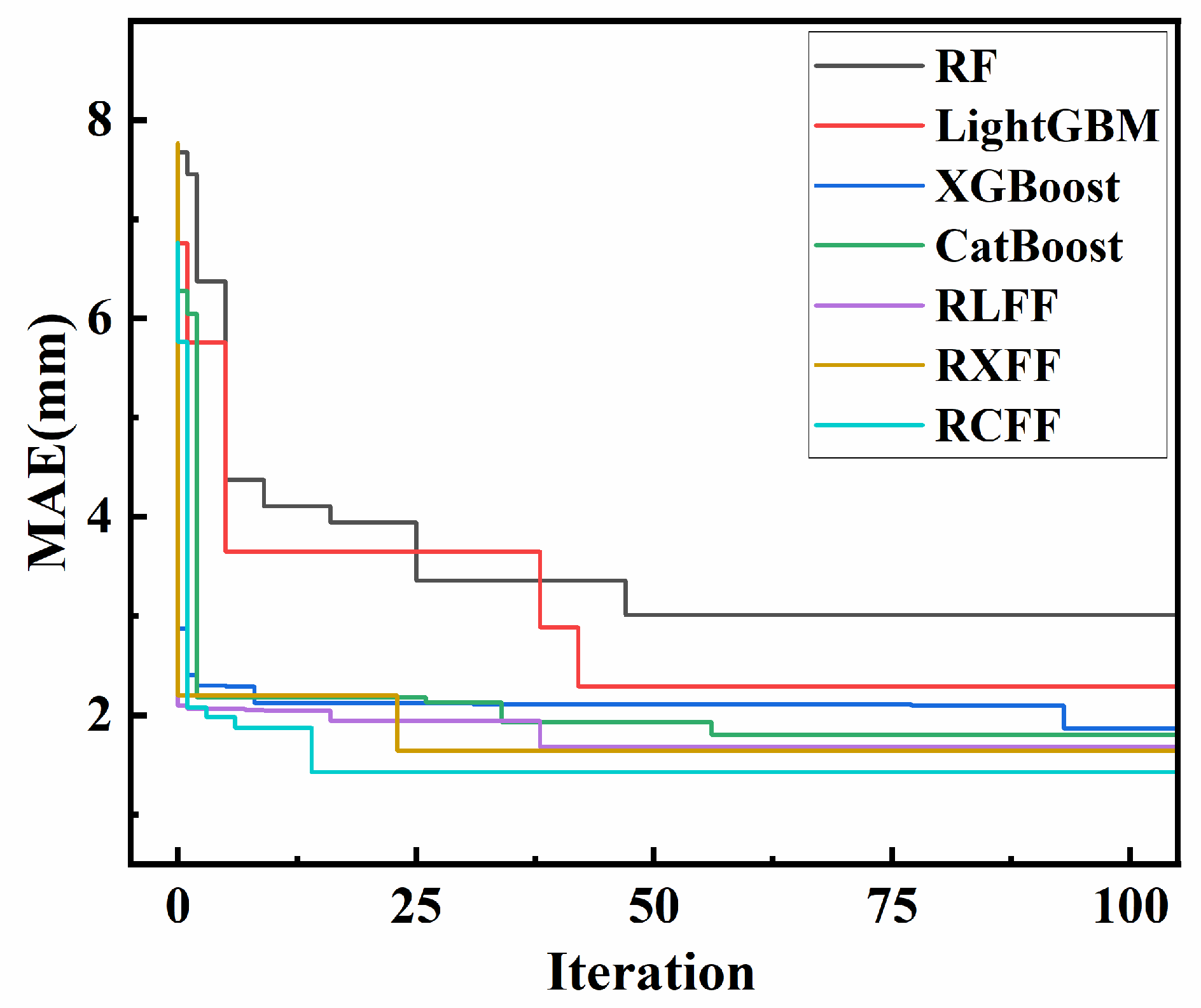
4.1. Hyperparameter Optimization
4.2. Model Prediction Results
4.3. SHAP Interpretation Analysis of the Best Model
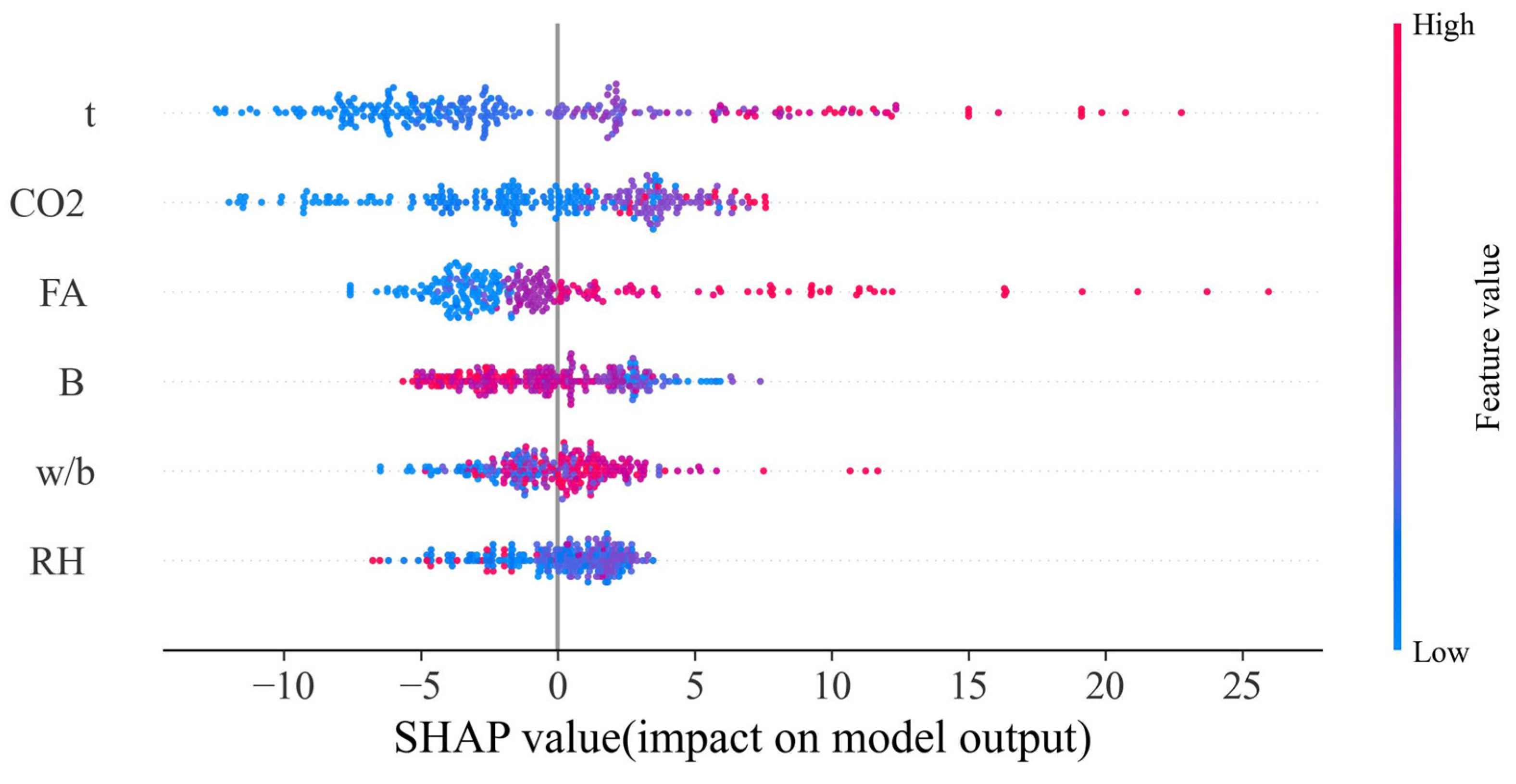
4.3.1. Global Significance Analysis
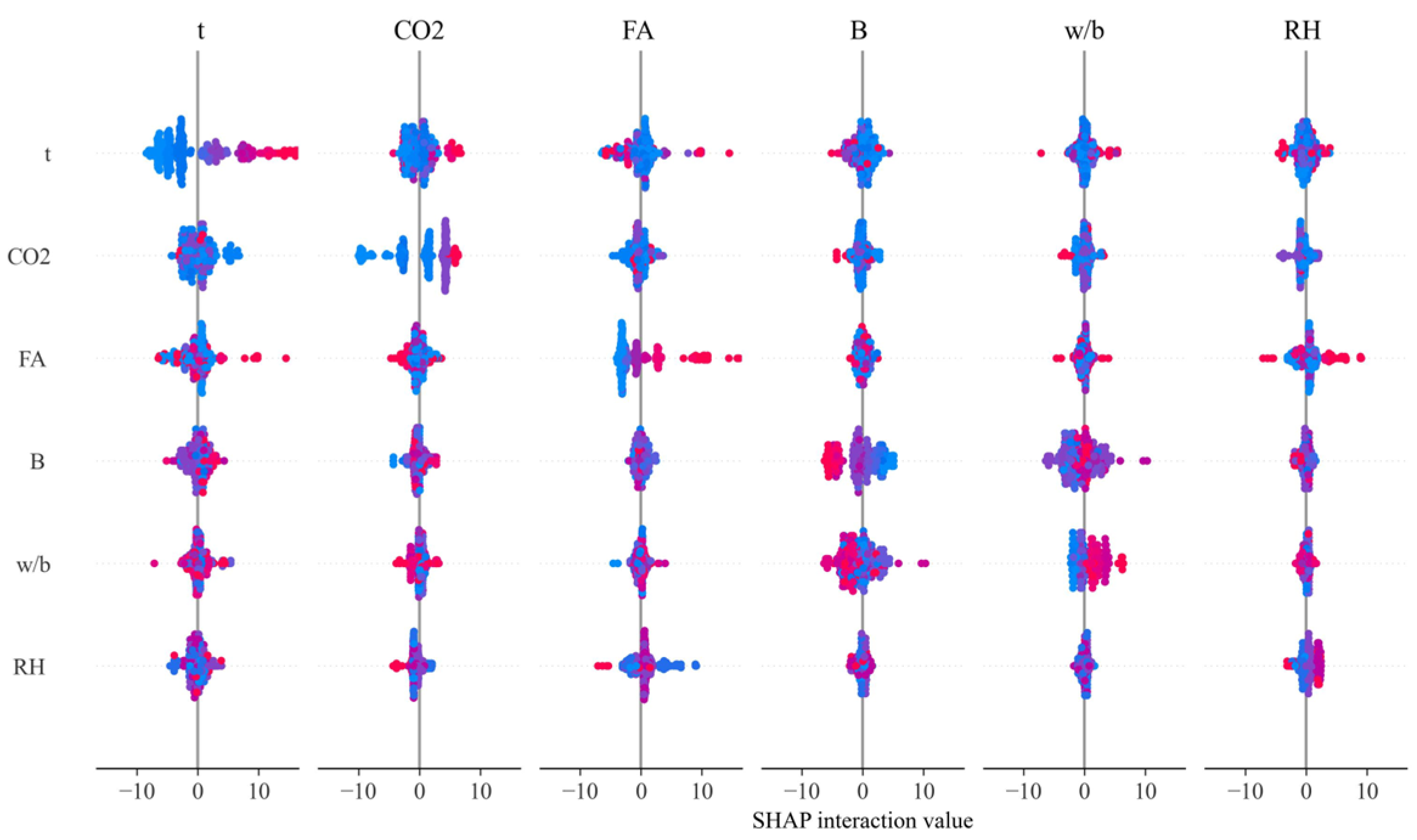
4.3.2. Analysis Results of Feature Interaction
4.3.3. Analysis Results of Characteristic Importance
4.4. Significance and Limitations of the Study
5. Conclusions
- (1)
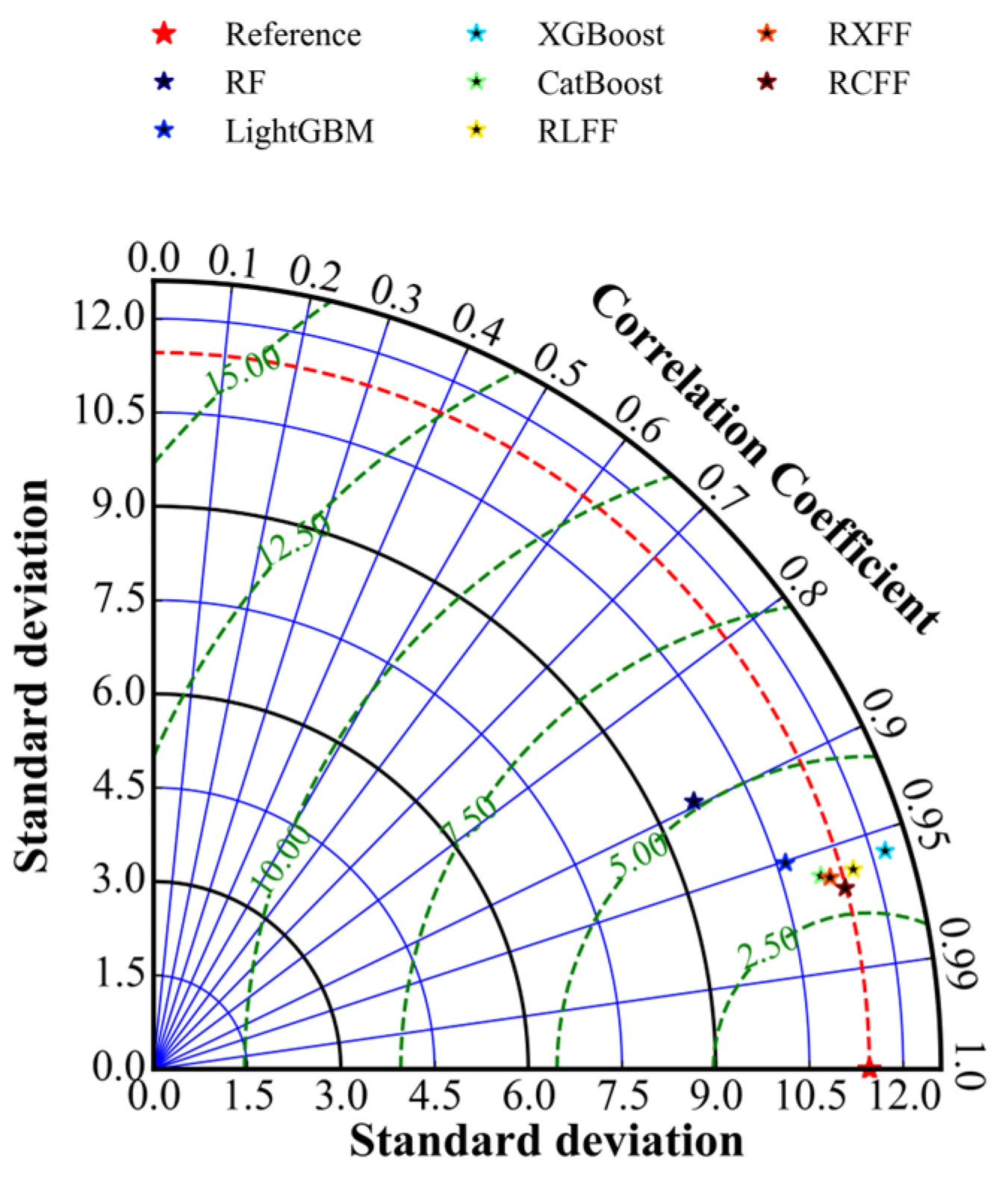
- The RCFF model outperforms single models (RF, CatBoost, LightGBM, XGBoost) and other fusion models (RLFF, RXFF) on both the training and test sets. The R2 of the test set reaches 0.9674, the MAE is 1.4199, the RMSE is 2.0648, and the VAF is 96.78%, which is significantly better than the rest of the models, indicating that RCFF effectively improves the prediction accuracy through the advantages of the fusion framework;
- (2)
- The prediction ability of each model on the test set was comprehensively evaluated and compared through the comprehensive scoring formula as well as Taylor diagrams. The results of the study show that RCFF has the highest comprehensive score. Taylor diagrams further visualize the performance of multiple performance metrics of different models, corroborating the excellent performance of the hybrid integration framework proposed in this paper in carbonation depth prediction;
- (3)
- In this paper, the RCFF model was analyzed for SHAP interpretation through three levels. Based on the SHAP analysis, it was found that exposure time and CO2 concentration were the most important factors affecting the depth of carbonation, with exposure time contributing the highest SHAP value. This indicates that prolonged exposure significantly deepens the carbonation. In addition, FA and B also had a significant effect on the depth of carbonation, while w/b and RH had the second highest but still not negligible effect. SHAP interaction analysis revealed a significant interaction between FA, CO2, and t, which suggests that fly ash admixture and CO2 concentration intensified the effect of carbonation under prolonged exposure. Whereas RH interacted weakly with other variables, relative humidity was more inclined to influence the carbonation process alone.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Papadakis, V.G.; Vayenas, C.G.; Fardis, M.N. Fundamental Modeling and Experimental Investigation of Concrete Carbonation. Mater. J. 1991, 88, 363–373. [Google Scholar]
- Papadakis, V.G.; Vayenas, C.G.; Fardis, M.N. Physical and Chemical Characteristics Affecting the Durability of Concrete. Mater. J. 1991, 88, 186–196. [Google Scholar]
- Amorim, P.; de Brito, J.; Evangelista, L. Concrete Made with Coarse Concrete Aggregate: Influence of Curing on Durability. Mater. J. 2012, 109, 195–204. [Google Scholar]
- Wierig, H. Longtime studies on the carbonation on concrete under normal outdoor exposure. In Proceedings of the Rilem Seminar Durability of Concrete Structures under Normal Outdoor Exposure, Hannover, Germany, 26–29 March 1984; pp. 239–249. [Google Scholar]
- Bahador, S.D.; Cahyadi, J.H. Modelling of carbonation of PC and blended cement concrete. IES J. Part A Civ. Struct. Eng. 2009, 2, 59–67. [Google Scholar] [CrossRef]
- Ngala, V.; Page, C. Effects of carbonation on pore structure and diffusional properties of hydrated cement pastes. Cem. Concr. Res. 1997, 27, 995–1007. [Google Scholar] [CrossRef]
- Ahmad, S. Reinforcement corrosion in concrete structures, its monitoring and service life prediction—A review. Cem. Concr. Compos. 2003, 25, 459–471. [Google Scholar] [CrossRef]
- Page, C.; Treadaway, K. Aspects of the electrochemistry of steel in concrete. Nature 1982, 297, 109–115. [Google Scholar] [CrossRef]
- Leek, D.S. The passivity of steel in concrete. Q. J. Eng. Geol. Hydrogeol. 1991, 24, 55–66. [Google Scholar] [CrossRef]
- Ghods, P.; Isgor, O.B.; Bensebaa, F.; Kingston, D. Angle-resolved XPS study of carbon steel passivity and chloride-induced depassivation in simulated concrete pore solution. Corros. Sci. 2012, 58, 159–167. [Google Scholar] [CrossRef]
- Jiang, L.; Lin, B.; Cai, Y. A model for predicting carbonation of high-volume fly ash concrete. Cem. Concr. Res. 2000, 30, 699–702. [Google Scholar] [CrossRef]
- Shen, W.; Cao, L.; Li, Q.; Zhang, W.; Wang, G.; Li, C. Quantifying CO2 emissions from China’s cement industry. Renew. Sustain. Energy Rev. 2015, 50, 1004–1012. [Google Scholar] [CrossRef]
- von Greve-Dierfeld, S.; Lothenbach, B.; Vollpracht, A.; Wu, B.; Huet, B.; Andrade, C.; Medina, C.; Thiel, C.; Gruyaert, E.; Vanoutrive, H.; et al. Understanding the carbonation of concrete with supplementary cementitious materials: A critical review by RILEM TC 281-CCC. Mater. Struct. 2020, 53, 136. [Google Scholar] [CrossRef]
- Zhang, D.; Cai, X.; Shao, Y. Carbonation curing of precast fly ash concrete. J. Mater. Civ. Eng. 2016, 28, 04016127. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, M.; Zhu, J. Carbonation depth model and prediction of hybrid fiber fly ash concrete. Adv. Civ. Eng. 2020, 2020, 9863963. [Google Scholar] [CrossRef]
- Carević, V.; Ignjatović, I.; Dragaš, J. Model for practical carbonation depth prediction for high volume fly ash concrete and recycled aggregate concrete. Constr. Build. Mater. 2019, 213, 194–208. [Google Scholar] [CrossRef]
- Te Liang, M.; Qu, W.J.; Liang, C.-H. Mathematical modeling and prediction method of concrete carbonation and its applications. J. Mar. Sci. Technol. 2002, 10, 128–135. [Google Scholar] [CrossRef]
- Bonnet, S.; Balayssac, J.-P. Combination of the Wenner resistivimeter and Torrent permeameter methods for assessing carbonation depth and saturation level of concrete. Constr. Build. Mater. 2018, 188, 1149–1165. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete. Ph.D. Thesis, Swedish Cement and Concrete Research Institute, Stockholm, Sweden, 1982. [Google Scholar]
- Long, W.; Bao, Z.; Chen, K.; Ng, S.T.; Wuni, I.Y. Developing an integrative framework for digital twin applications in the building construction industry: A systematic literature review. Adv. Eng. Inform. 2024, 59, 102346. [Google Scholar] [CrossRef]
- Liu, W.; Li, A.; Fang, W.; Love, P.E.; Hartmann, T.; Luo, H. A hybrid data-driven model for geotechnical reliability analysis. Reliab. Eng. Syst. Saf. 2023, 231, 108985. [Google Scholar] [CrossRef]
- Hou, H.; Liu, C.; Wei, R.; He, H.; Wang, L.; Li, W. Outage duration prediction under typhoon disaster with stacking ensemble learning. Reliab. Eng. Syst. Saf. 2023, 237, 109398. [Google Scholar] [CrossRef]
- Londhe, S.; Kulkarni, P.; Dixit, P.; Silva, A.; Neves, R.; de Brito, J. Tree based approaches for predicting concrete carbonation coefficient. Appl. Sci. 2022, 12, 3874. [Google Scholar] [CrossRef]
- Kellouche, Y.; Boukhatem, B.; Ghrici, M.; Tagnit-Hamou, A. Exploring the major factors affecting fly-ash concrete carbonation using artificial neural network. Neural Comput. Appl. 2019, 31, 969–988. [Google Scholar] [CrossRef]
- Akpinar, P.; Uwanuakwa, I.D. Intelligent prediction of concrete carbonation depth using neural networks. Bull. Transilv. Univ. Bras. Ser. III Math. Comput. Sci. 2016, 9, 99–108. [Google Scholar]
- Huang, X.; Liu, W.; Guo, Q.; Tan, J. Prediction method for the dynamic response of expressway lateritic soil subgrades on the basis of Bayesian optimization CatBoost. Soil Dyn. Earthq. Eng. 2024, 186, 108943. [Google Scholar] [CrossRef]
- Kumar, N.; Prakash, S.; Ghani, S.; Gupta, M.; Saharan, S. Data-driven machine learning approaches for predicting permeability and corrosion risk in hybrid concrete incorporating blast furnace slag and fly ash. Asian J. Civ. Eng. 2024, 25, 3263–3275. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, G.; Wang, M.; Xu, Y.; Wang, N. Concrete carbonation depth prediction model based on a gradient-boosting decision tree and different metaheuristic algorithms. Case Stud. Constr. Mater. 2024, 21, e03864. [Google Scholar] [CrossRef]
- Luo, L.; Chen, X. Integrating piecewise linear representation and weighted support vector machine for stock trading signal prediction. Appl. Soft Comput. 2013, 13, 806–816. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Cook, R.; Lapeyre, J.; Ma, H.; Kumar, A. Prediction of compressive strength of concrete: Critical comparison of performance of a hybrid machine learning model with standalone models. J. Mater. Civ. Eng. 2019, 31, 04019255. [Google Scholar] [CrossRef]
- Wang, M.; Mitri, H.S.; Zhao, G.; Wu, J.; Xu, Y.; Liang, W.; Wang, N. Performance comparison of several explainable hybrid ensemble models for predicting carbonation depth in fly ash concrete. J. Build. Eng. 2024, 98, 111246. [Google Scholar] [CrossRef]
- Huo, Z.; Wang, L.; Huang, Y. Predicting carbonation depth of concrete using a hybrid ensemble model. J. Build. Eng. 2023, 76, 107320. [Google Scholar] [CrossRef]
- Han, T.; Siddique, A.; Khayat, K.; Huang, J.; Kumar, A. An ensemble machine learning approach for prediction and optimization of modulus of elasticity of recycled aggregate concrete. Constr. Build. Mater. 2020, 244, 118271. [Google Scholar] [CrossRef]
- Meng, S.; Shi, Z.; Xia, C.; Zhou, C.; Zhao, Y. Exploring LightGBM-SHAP: Interpretable predictive modeling for concrete strength under high temperature conditions. Structures 2025, 71, 108134. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Abedin, M.Z.; Wang, J.; Yang, H.; Gao, Y.; Chen, Y. Profit-driven fusion framework based on bagging and boosting classifiers for potential purchaser prediction. J. Retail. Consum. Serv. 2024, 79, 103854. [Google Scholar] [CrossRef]
- Chang, C.F.; Chen, J.W. The experimental investigation of concrete carbonation depth. Cem. Concr. Res. 2006, 36, 1760–1767. [Google Scholar] [CrossRef]
- Cui, H.; Tang, W.; Liu, W.; Dong, Z.; Xing, F. Experimental study on effects of CO2 concentrations on concrete carbonation and diffusion mechanisms. Constr. Build. Mater. 2015, 93, 522–527. [Google Scholar] [CrossRef]
- Balayssac, J.P.; Détriché, C.H.; Grandet, J. Effects of curing upon carbonation of concrete. Constr. Build. Mater. 1995, 9, 91–95. [Google Scholar] [CrossRef]
- Roziere, E.; Loukili, A.; Cussigh, F. A performance based approach for durability of concrete exposed to carbonation. Constr. Build. Mater. 2009, 23, 190–199. [Google Scholar] [CrossRef]
- Hussain, S.; Bhunia, D.; Singh, S.B. Comparative study of accelerated carbonation of plain cement and fly-ash concrete. J. Build. Eng. 2017, 10, 26–31. [Google Scholar] [CrossRef]
- Younsi, A.; Turcry, P.; Aït-Mokhtar, A.; Staquet, S. Accelerated carbonation of concrete with high content of mineral additions: Effect of interactions between hydration and drying. Cem. Concr. Res. 2013, 43, 25–33. [Google Scholar] [CrossRef]
- Turcry, P.; Oksri-Nelfia, L.; Younsi, A.; AT-Mokhtar, A. Analysis of an accelerated carbonation test with severe preconditioning. Cem. Concr. Res. 2014, 57, 70–78. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, P.; Yu, Z. Effects of Environmental Factors on Concrete Carbonation Depth and Compressive Strength. Materials 2018, 11, 2167. [Google Scholar] [CrossRef]
- Khunthongkeaw, J.; Tangtermsirikul, S.; Leelawat, T. A study on carbonation depth prediction for fly ash concrete. Constr. Build. Mater. 2006, 20, 744–753. [Google Scholar] [CrossRef]
- Huang, C.; Geng, G.; Lu, Y.; Bao, G.; Lin, Z. Carbonation depth research of concrete with low-volume fly ash. In Proceedings of the International Conference on Mechanical Engineering and Green Manufacturing (MEGM 2012), Chongqing, China, 16–18 March 2012. [Google Scholar]
- Gao, Y.; Cheng, L.; Gao, Z.; Guo, S. Effects of different mineral admixtures on carbonation resistance of lightweight aggregate concrete. Constr. Build. Mater. 2013, 43, 506–510. [Google Scholar] [CrossRef]
- Zhao, Q.; He, X.; Zhang, J.; Jiang, J. Long-age wet curing effect on performance of carbonation resistance of fly ash concrete. Constr. Build. Mater. 2016, 127, 577–587. [Google Scholar] [CrossRef]
- Kurda, R.; Brito, J.D.; Silvestre, J.D. Carbonation of concrete made with high amount of fly ash and recycled concrete aggregates for utilization of CO2. J. CO2 Util. 2019, 29, 12–19. [Google Scholar] [CrossRef]
- Lu, C.F.; Wang, W.; Li, Q.T.; Hao, M.; Xu, Y. Effects of micro-environmental climate on the carbonation depth and the pH value in fly ash concrete. J. Clean. Prod. 2018, 181, 309–317. [Google Scholar] [CrossRef]
- Atis, C.D. Accelerated carbonation and testing of concrete made with fly ash. Constr. Build. Mater. 2003, 17, 147–152. [Google Scholar] [CrossRef]
- Tu, L.Q.; Xu, W.B.; Chen, W. Carbonation of Fly Ash Concrete and Micro-Hardness Analysis. Adv. Mater. Res. 2011, 378–379, 56–59. [Google Scholar]
- Felix, E.F.; Carrazedo, R.; Possan, E. Carbonation model for fly ash concrete based on artificial neural network: Development and parametric analysis. Constr. Build. Mater. 2021, 266, 121050. [Google Scholar] [CrossRef]
- Papadakis, V.G. Effect of fly ash on Portland cement systems Part I. Low-calcium fly ash. Cem. Concr. Res. 1999, 29, 1727–1736. [Google Scholar] [CrossRef]
- Dunlop, P.; Smith, S. Estimating key characteristics of the concrete delivery and placement process using linear regression analysis. Civ. Eng. Environ. Syst. 2003, 20, 273–290. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Xia, Y.; Zhao, J.; He, L.; Li, Y.; Niu, M. A novel tree-based dynamic heterogeneous ensemble method for credit scoring. Expert Syst. Appl. 2020, 159, 113615. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:181011363. [Google Scholar]
- Avrizal, R.; Wibowo, A.; Yuniarti, A.S.; Sandy, D.A.; Prihandani, K. Analysis Comparison of The Classification Data Mining Method to Predictthe Decisions of Potential Customer Insurance. Int. J. Comput. Tech. 2018, 5, 15–20. [Google Scholar]
- Alam, M.S.; Sultana, N.; Hossain, S.Z. Bayesian optimization algorithm based support vector regression analysis for estimation of shear capacity of FRP reinforced concrete members. Appl. Soft Comput. 2021, 105, 107281. [Google Scholar] [CrossRef]
- Daneshvar, K.; Moradi, M.J.; Khaleghi, M.; Rezaei, M.; Farhangi, V.; Hajiloo, H. Effects of impact loads on heated-and-cooled reinforced concrete slabs. J. Build. Eng. 2022, 61, 105328. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, G.; Liang, W.; Wang, N. A comparative study on the development of hybrid SSA-RF and PSO-RF models for predicting the uniaxial compressive strength of rocks. Case Stud. Constr. Mater. 2023, 18, e02191. [Google Scholar] [CrossRef]
- Rui, J. Exploring the association between the settlement environment and residents’ positive sentiments in urban villages and formal settlements in Shenzhen. Sustain. Cities Soc. 2023, 98, 104851. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Mai, H.-V.T.; Trinh, S.H.; Ly, H.-B. A comparative assessment of tree-based predictive models to estimate geopolymer concrete compressive strength. Neural Comput. Appl. 2023, 35, 6569–6588. [Google Scholar] [CrossRef]
- Li, Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96, 101845. [Google Scholar] [CrossRef]
- Kim, C.-M.; Jaffari, Z.H.; Abbas, A.; Chowdhury, M.F.; Cho, K.H. Machine learning analysis to interpret the effect of the photocatalytic reaction rate constant (k) of semiconductor-based photocatalysts on dye removal. J. Hazard. Mater. 2024, 465, 132995. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Li, Y.; Li, Y.; Su, L.; He, W. Investigation on compressive strength of coral aggregate concrete: Hybrid machine learning models and experimental validation. J. Build. Eng. 2024, 82, 108220. [Google Scholar] [CrossRef]
- Rahmani, P.; Gholami, H.; Golzari, S. An interpretable deep learning model to map land subsidence hazard. Environ. Sci. Pollut. Res. 2024, 31, 17448–17460. [Google Scholar] [CrossRef]
- Hastie, T. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Han, J.; Pei, J.; Tong, H. Data Mining: Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2022. [Google Scholar]
- Liu, P.; Yu, Z.; Chen, Y. Carbonation depth model and carbonated acceleration rate of concrete under different environment. Cem. Concr. Compos. 2020, 114, 103736. [Google Scholar] [CrossRef]
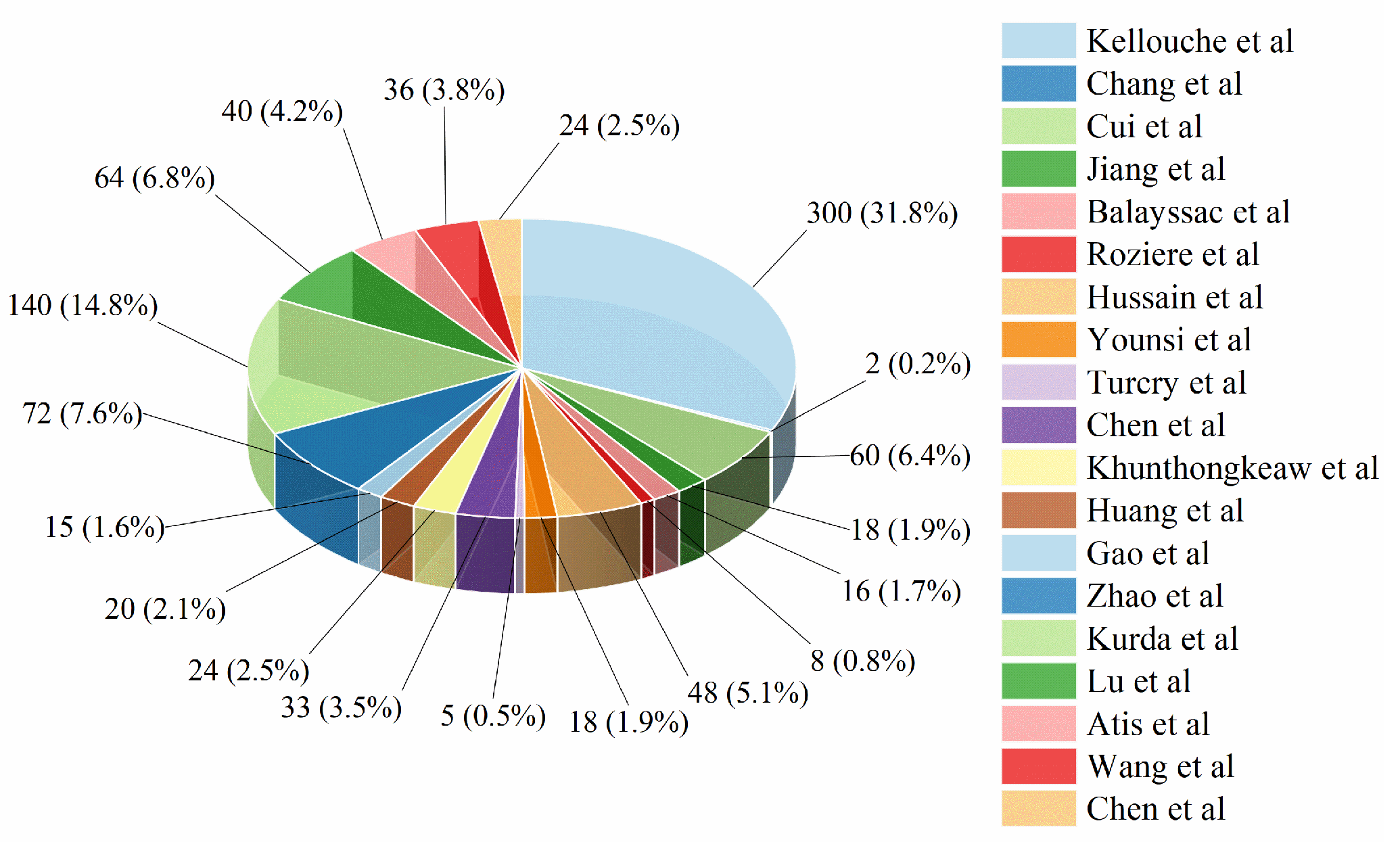
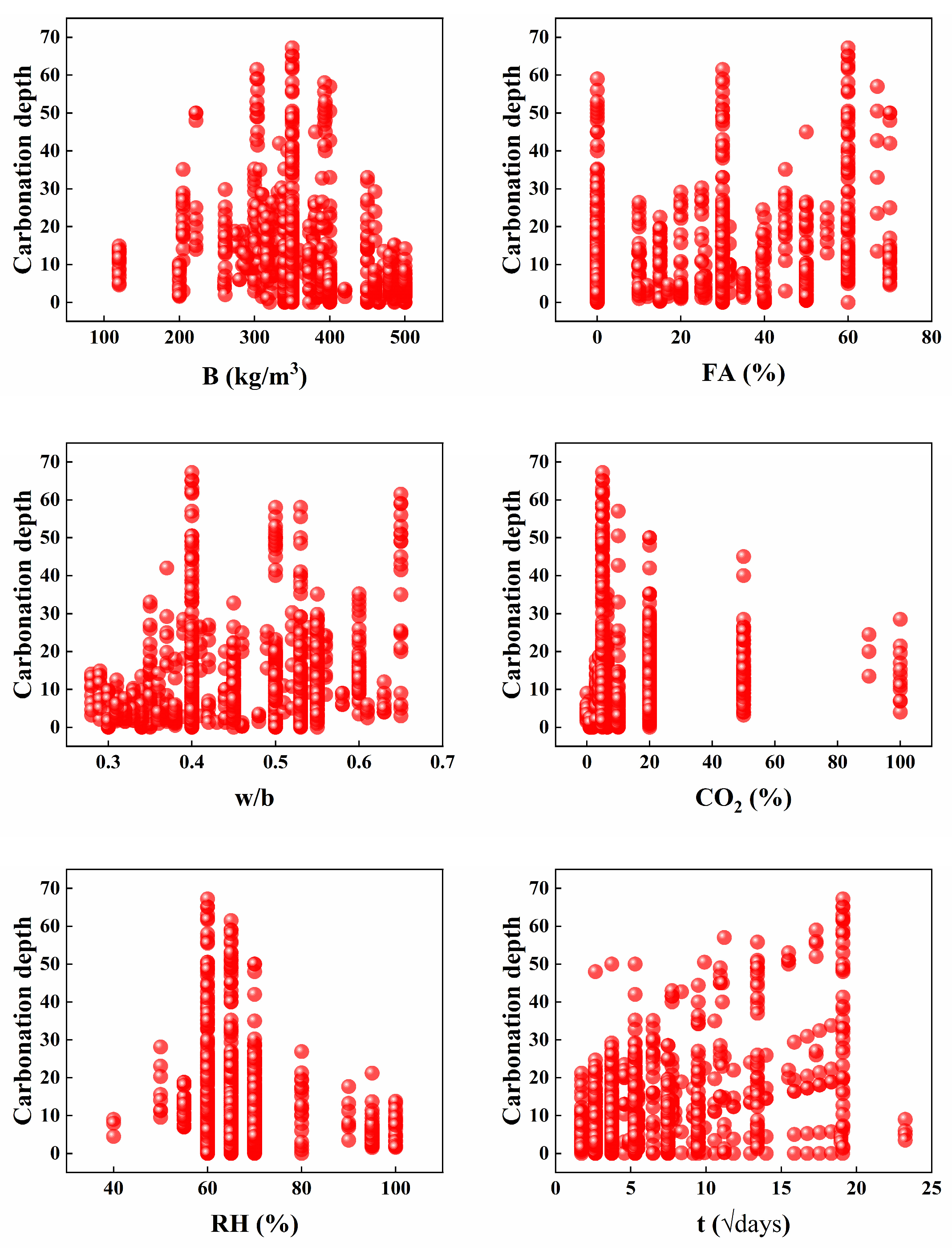




| Input | Output | ||||||
|---|---|---|---|---|---|---|---|
| B (kg/m3) | FA (%) | w/b | CO2 (%) | RH (%) | X (mm) | ||
| Count | 943 | 943 | 943 | 943 | 943 | 943 | 943 |
| Mean | 360.94 | 22.65 | 0.46 | 14.35 | 66.66 | 6.71 | 12.62 |
| STD | 74.39 | 22.18 | 0.09 | 16.30 | 9.44 | 4.71 | 12.55 |
| Min | 120.00 | 0.00 | 0.28 | 0.03 | 40.00 | 1.73 | 0.00 |
| 25% | 325.00 | 0.00 | 0.39 | 5.00 | 60.00 | 3.74 | 4.00 |
| 50% | 350.00 | 20.00 | 0.45 | 6.5 | 65.00 | 5.29 | 9.00 |
| 75% | 400.00 | 39.60 | 0.53 | 20.00 | 70.00 | 7.94 | 17.00 |
| Max | 500.00 | 70.00 | 0.65 | 100.00 | 100.00 | 23.24 | 67.20 |
| Model | Parameter | Scope | Optimal Value | Ave R2 | MAE |
|---|---|---|---|---|---|
| RF | n_estimators | [50, 500] | 282 | 0.8582 | 2.8687 |
| max_depth | [3, 10] | 9 | |||
| min_samples_leaf | [1, 20] | 1 | |||
| min_samples_split | [5, 20] | 5 | |||
| LightGBM | n_estimators | [50, 500] | 398 | 0.9401 | 2.0865 |
| learning_rate | [0.01, 1] | 0.31 | |||
| max_depth | [3, 10] | 4 | |||
| num_leaves | [20, 100] | 48 | |||
| min_child_samples | [5, 30] | 18 | |||
| XGBoost | n_estimators | [50, 500] | 487 | 0.9432 | 1.8069 |
| learning_rate | [0.01, 1] | 0.50 | |||
| max_depth | [3, 10] | 3 | |||
| reg_lambda | [1, 10] | 3 | |||
| CatBoost | iterations | [50, 500] | 427 | 0.9455 | 1.7018 |
| learning_rate | [0.01, 1] | 0.39 | |||
| max_depth | [3, 10] | 4 | |||
| l2_leaf_reg | [1, 10] | 2 | |||
| RLFF | Number of DTs inLightGBMs | [50, 500] | 234 | 0.9483 | 1.5243 |
| Nodes number of DTs in LightGBMs | [20, 100] | 20 | |||
| Learning rate in LightGBMs | [0.01, 1] | 0.20 | |||
| Maximum depth in LightGBMs | [3, 10] | 4 | |||
| Minimum value of the sum of sample weights in each node of DTs in LightGBMs | [5, 30] | 20 | |||
| RXFF | Number of DTs in XGBoosts | [50, 500] | 195 | 0.9501 | 1.5025 |
| Learning rate in XGBoosts | [0.01, 1] | 0.21 | |||
| Maximum depth of DTs in XGBoosts | [3, 10] | 4 | |||
| Minimum number of samples contained in the nodes of DTs in XGBoost | [1, 20] | 9 | |||
| RCFF | Number of DTs in CatBoosts | [50, 500] | 483 | 0.9524 | 1.4262 |
| Learning rate in CatBoosts | [0.01, 1] | 0.23 | |||
| Depth of DTs in CatBoosts | [3, 10] | 4 | |||
| Minimum number of samples contained in the nodes of DTs in CatBoosts | [1, 20] | 12 |
| Model | R2 | MAE | RMSE | VAF | Si | |
|---|---|---|---|---|---|---|
| Training | RF | 0.9453 | 2.0026 | 2.8428 | 94.53% | 0.8930 |
| LightGBM | 0.9852 | 0.8515 | 1.4449 | 98.52% | 0.9554 | |
| XGBoost | 0.9865 | 0.7849 | 1.3808 | 98.65% | 0.9583 | |
| CatBoost | 0.9871 | 0.7982 | 1.3831 | 98.71% | 0.9583 | |
| RLFF | 0.9877 | 0.6908 | 1.3209 | 98.77% | 0.9616 | |
| RXFF | 0.9881 | 0.7096 | 1.3269 | 98.81% | 0.9614 | |
| RCFF | 0.9884 | 0.6727 | 1.3112 | 98.84% | 0.9625 | |
| Testing | RF | 0.8960 | 2.6786 | 3.6869 | 89.62% | 0.8432 |
| LightGBM | 0.9507 | 1.9493 | 2.7754 | 95.07% | 0.8977 | |
| XGBoost | 0.9583 | 1.7256 | 2.5506 | 95.83% | 0.9091 | |
| CatBoost | 0.9607 | 1.6105 | 2.2666 | 96.09% | 0.9166 | |
| RLFF | 0.9617 | 1.4958 | 2.2362 | 96.18% | 0.9198 | |
| RXFF | 0.9623 | 1.4826 | 2.2205 | 96.23% | 0.9205 | |
| RCFF | 0.9674 | 1.4199 | 2.0648 | 96.78% | 0.9267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Xu, A. Concrete Carbonization Prediction Method Based on Bagging and Boosting Fusion Framework. Buildings 2025, 15, 1349. https://doi.org/10.3390/buildings15081349
Li Q, Xu A. Concrete Carbonization Prediction Method Based on Bagging and Boosting Fusion Framework. Buildings. 2025; 15(8):1349. https://doi.org/10.3390/buildings15081349
Chicago/Turabian StyleLi, Qingfu, and Ao Xu. 2025. "Concrete Carbonization Prediction Method Based on Bagging and Boosting Fusion Framework" Buildings 15, no. 8: 1349. https://doi.org/10.3390/buildings15081349
APA StyleLi, Q., & Xu, A. (2025). Concrete Carbonization Prediction Method Based on Bagging and Boosting Fusion Framework. Buildings, 15(8), 1349. https://doi.org/10.3390/buildings15081349






