Experimental Study of Pre-Tensioned Polygonal Prestressed T-Beam Under Combined Loading Condition
Abstract
1. Introduction
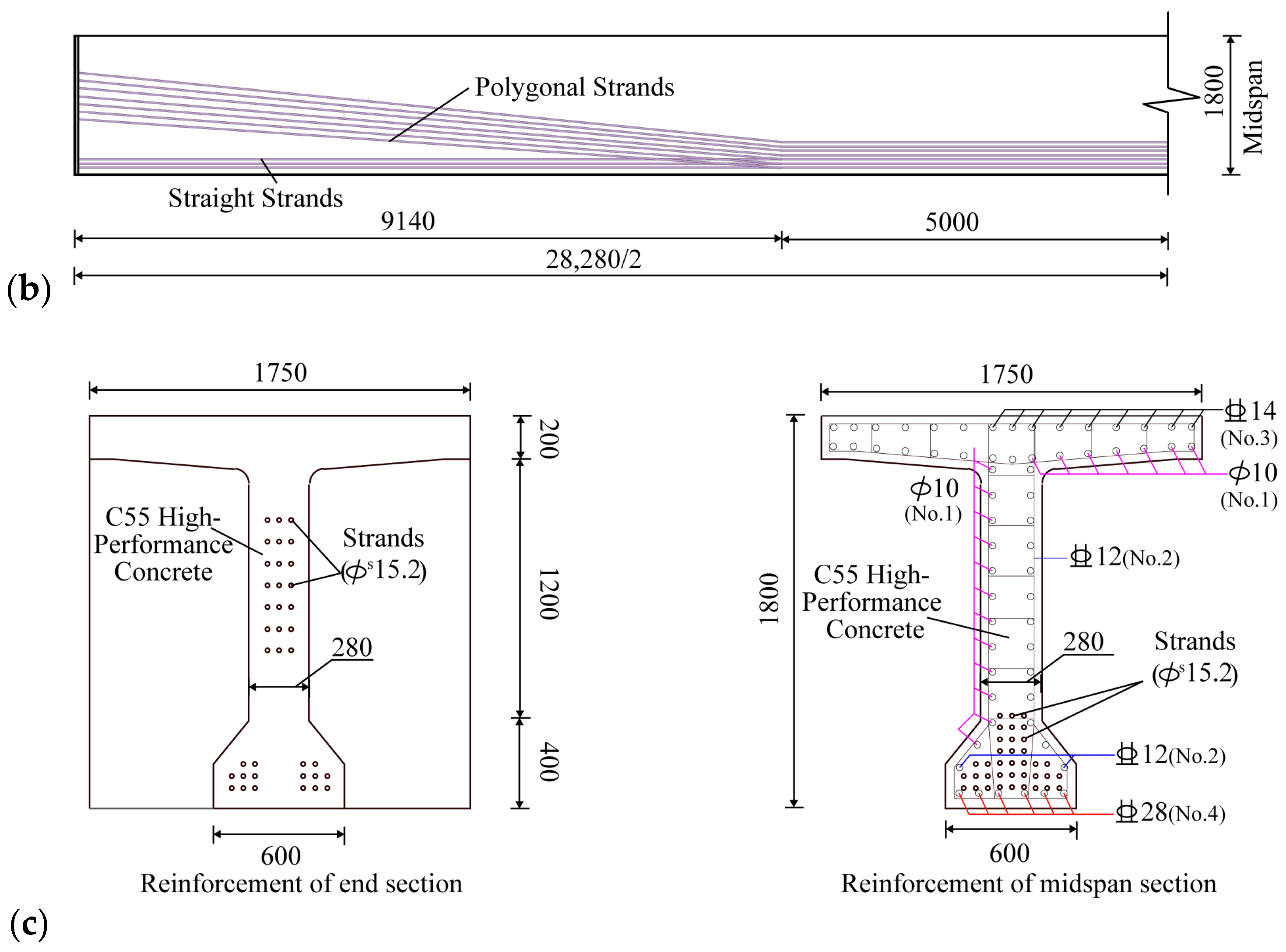
2. Full-Scale Model Parameters of Pre-Tensioned Prestressed T-Beams
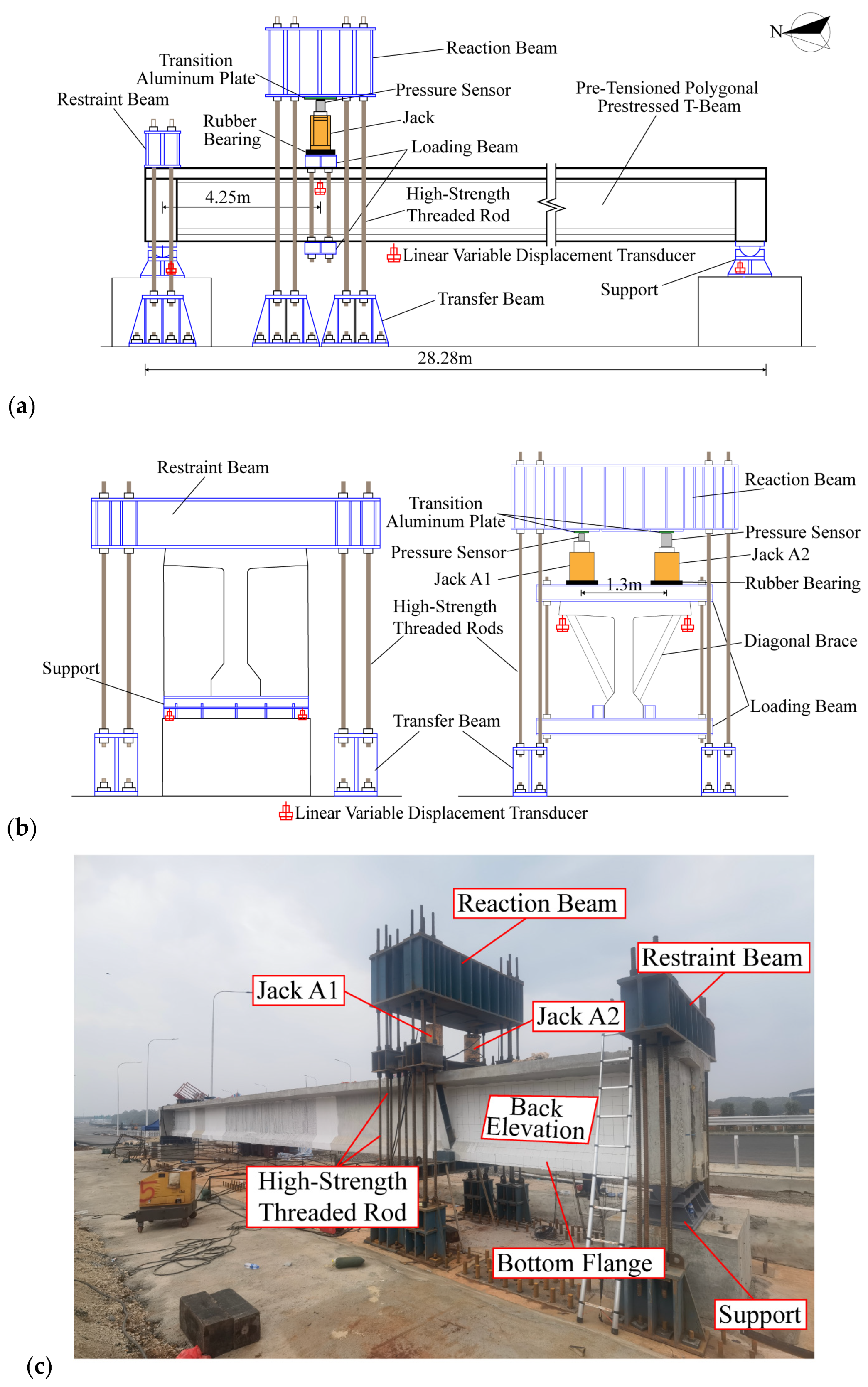
3. Full-Scale Experimental Scheme
3.1. Loading Device and Loading Scheme
3.2. Sensor Arrangement Scheme
4. Analysis of Experimental Results
4.1. Experimental Observations
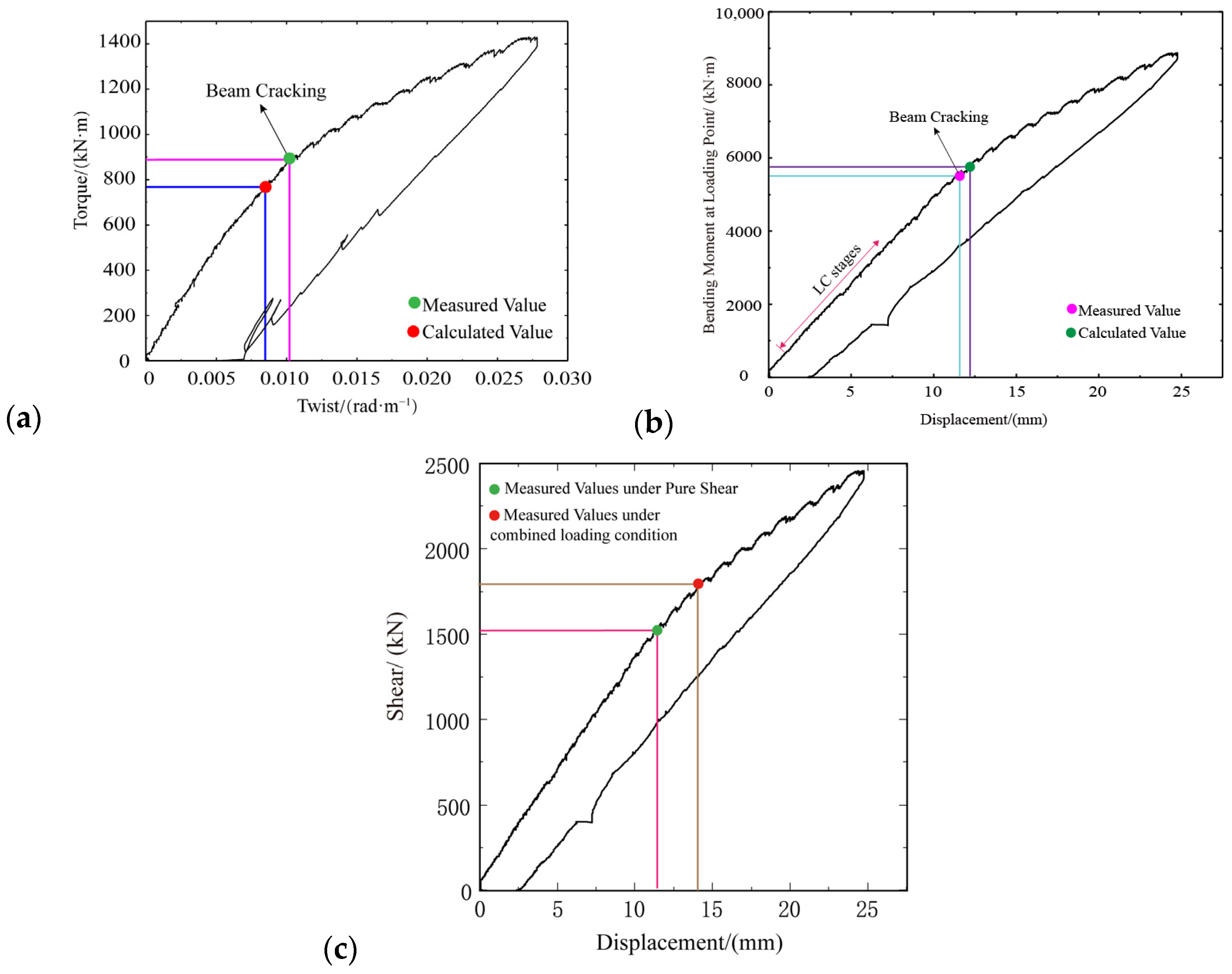
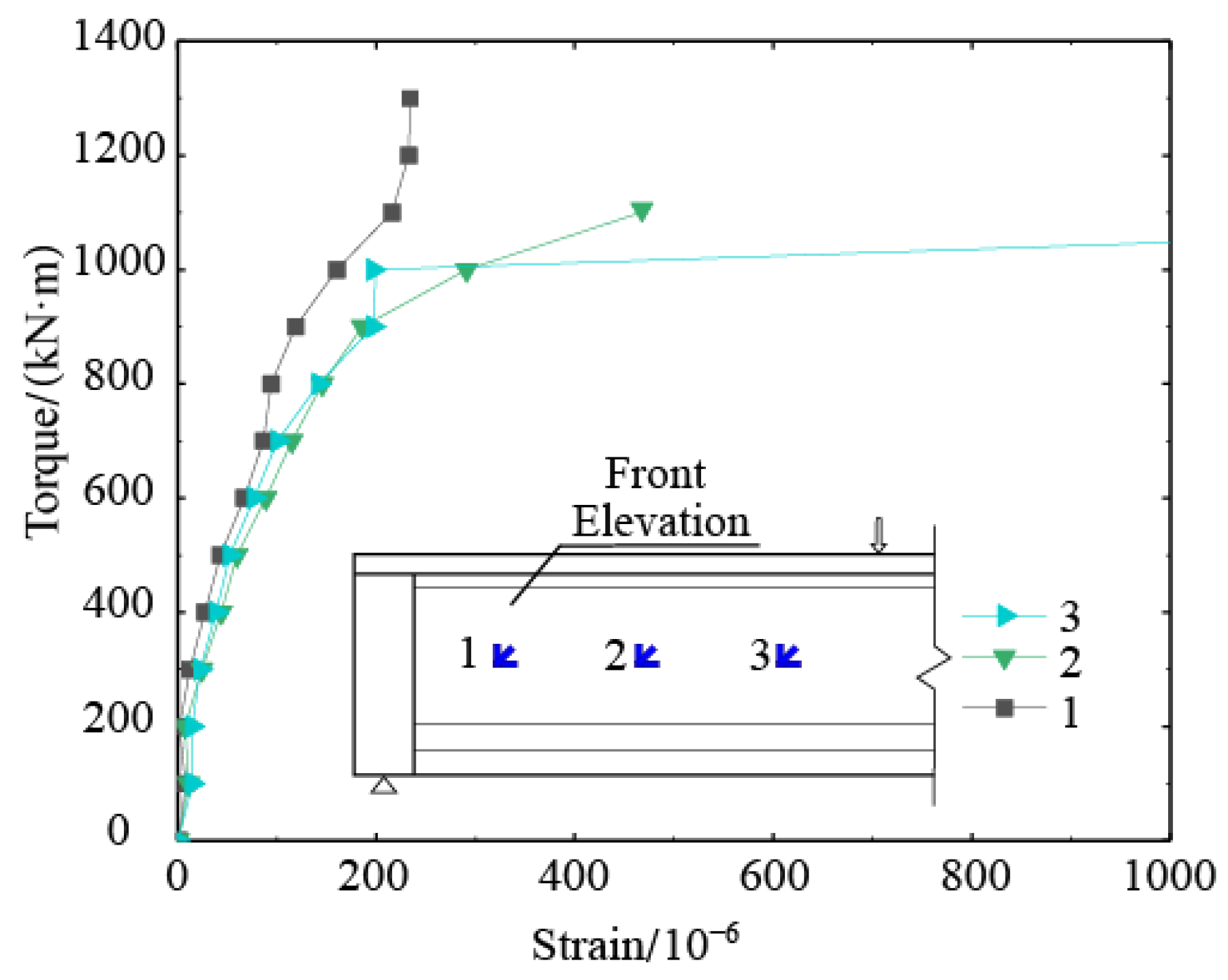
4.2. Torque-Twist Ratio Relationships
4.3. Strain Analysis
4.3.1. Principal Strain of Concrete
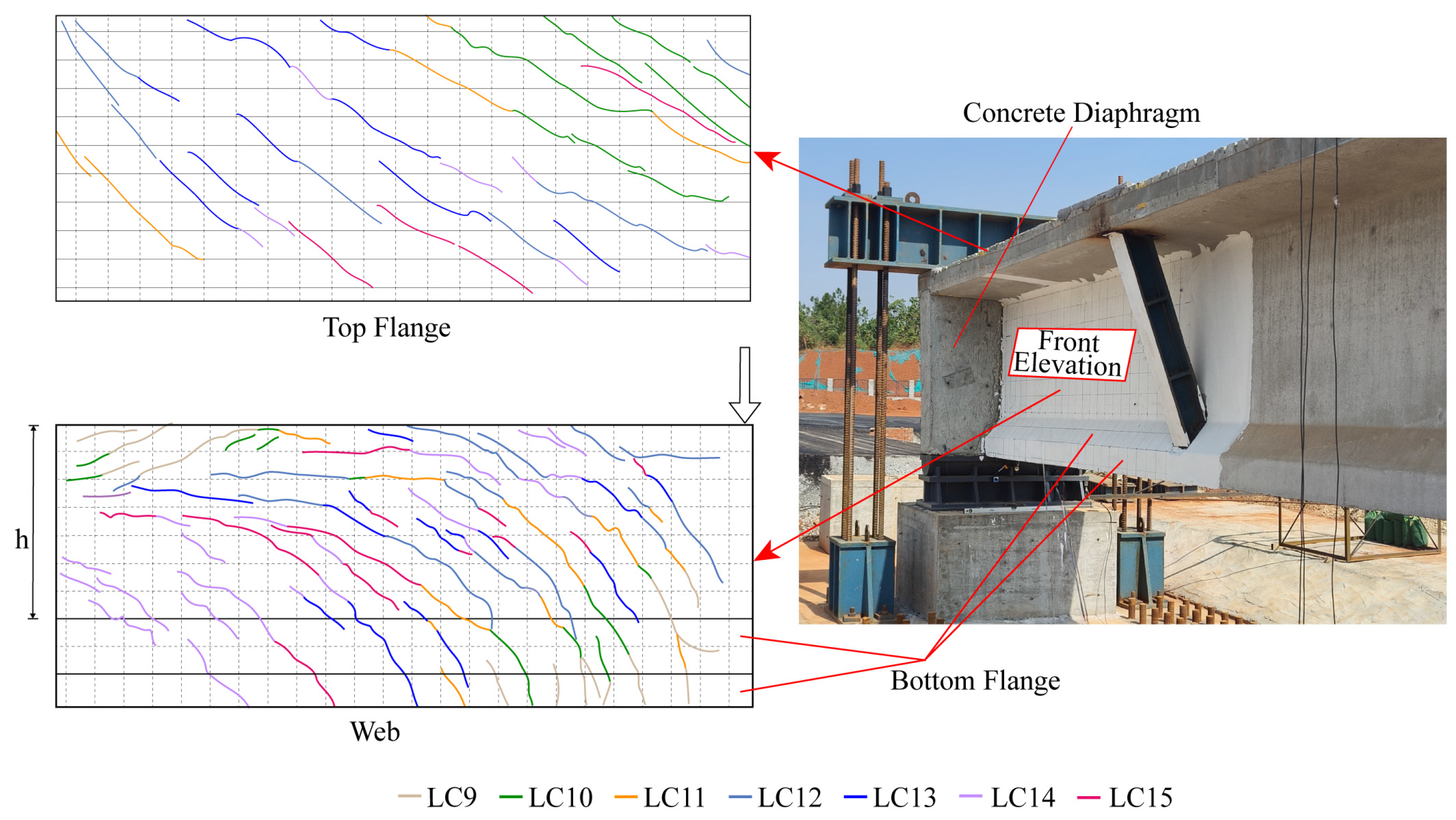
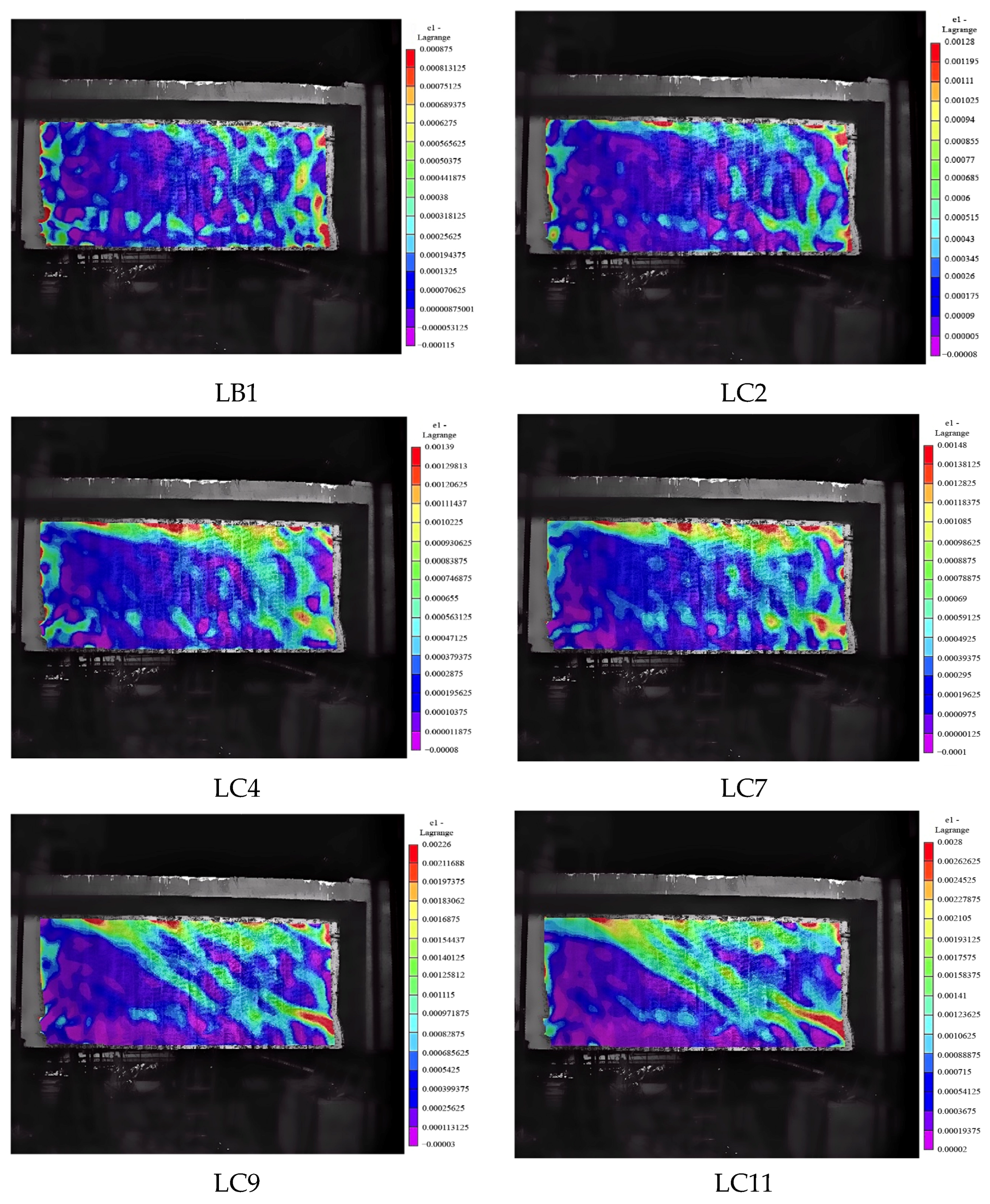
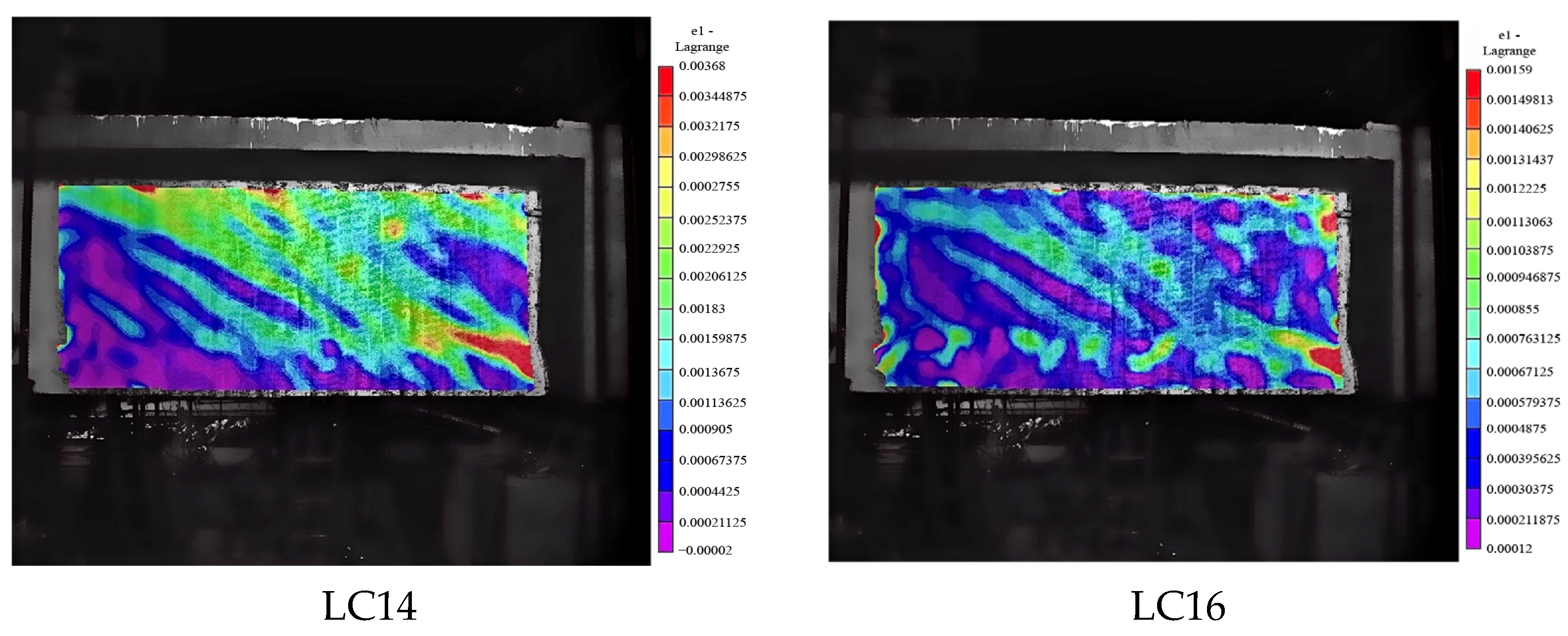
4.3.2. Strain Field Analysis of the Beam Based on VIC-3D
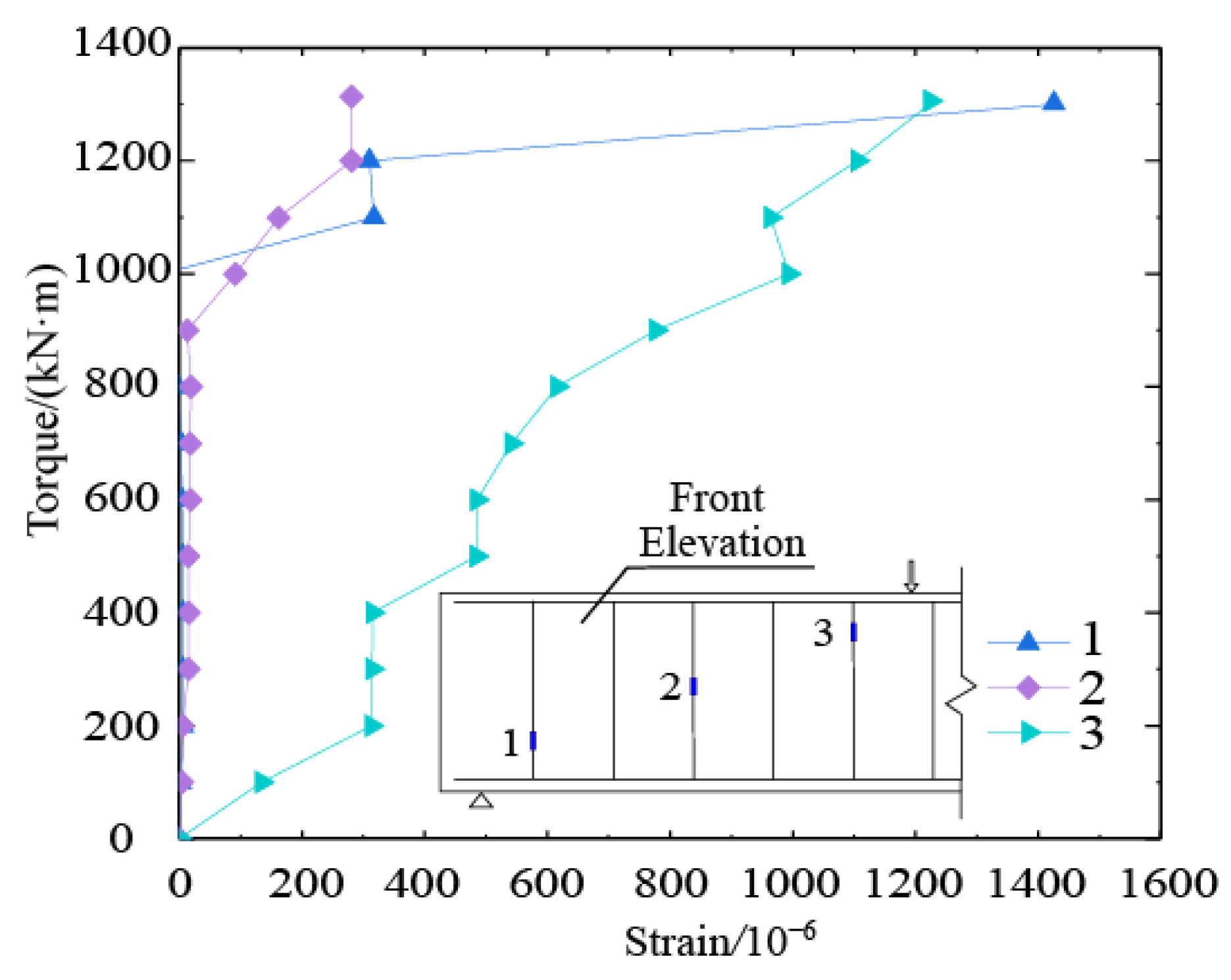
4.3.3. Stirrup Strain
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, K.L.; Qiao, L. Application of non-bonded prestressing technology in ultra-long structures. Ind. Constr. 2023, 53, 238–239. [Google Scholar]
- Xia, Y.L.; Zhang, W.; Dai, J. Study on prestress transfer length of concrete beams using self-balanced prestressed hollow tubes. Bridge Constr. 2023, 53, 33–40. [Google Scholar]
- Chen, C. Theoretical Analysis and Experimental Study of Flexural Bearing Capacity for Pretensioned Prestressed T-Shaped Concrete Beam with Bent-Tendons. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Wu, H. Construction Technology and Quality Control Analysis of Prestressed Concrete T-Beam. Metall. Collect. 2022, 7, 84–86. [Google Scholar]
- Lin, Y.; Wang, J.H.; Deng, Q.E. Research on polygonal pretensioning technology for I-beams in Xishamen Bridge. Highway 2022, 67, 218–224. [Google Scholar]
- Zhang, C.L. Research on the Application of Prestressing Technology with Pretensioned Draped Strands in Bridge Engineering. Shanghai Highw. 2020, 41–44+48+149. [Google Scholar]
- Zhang, Z.; Lin, Y.; Wang, J.; Deng, Q.; Zhang, K. Calculation method of load lateral distribution coefficient of I-beam with deviated pretensioning method and design of cross-girder. Struct. Eng. 2022, 38, 185–191. [Google Scholar]
- Wang, R.; Wang, B. Application of folded line first tensioning technology in prefabricated T girders for highway bridges. New Technol. New Prod. China 2023, 102–104. [Google Scholar] [CrossRef]
- Du, L.; Wu, D.; Wang, J.; Wang, S.; Zhao, B.; Tang, X. Experimental Study on Flexural Behavior of Retard-Bonded Prestressed UHPC Beams with Different Reinforcement Ratios. Buildings 2025, 15, 887. [Google Scholar] [CrossRef]
- Li, H.; Qiu, Y.; Pan, Z.; Yang, Y.; Tang, H.; Ma, F. Experimental Study on the Flexural Performance of the Corrosion-Affected Simply Supported Prestressed Concrete Box Girder in a High-Speed Railway. Buildings 2024, 14, 3322. [Google Scholar] [CrossRef]
- Wu, D.; Wang, H.; Wang, R.; Lv, C. Crack Resistance of Pre-Stressed Steel-Reinforced Concrete Composite Simple Supported Beams. Buildings 2024, 14, 201. [Google Scholar] [CrossRef]
- Ju, H.; Jung, C.; Cho, H.-C. Strength Model for Prestressed Concrete Beams Subjected to Pure Torsion. Buildings 2024, 14, 2690. [Google Scholar] [CrossRef]
- Al-Salim, N.H.; Jaber, M.H.; Hassan, R.F.; Mohammed, N.S.; Hussein, H.H. Experimental Investigation of Compound Effect of Flexural and Torsion on Fiber-Reinforced Concrete Beams. Buildings 2023, 13, 1347. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, N.; Wang, Q.; Li, Z.; Qin, X. Shear Behavior of T-Shaped Concrete Beams Reinforced with FRP. Buildings 2022, 12, 2062. [Google Scholar] [CrossRef]
- Jiang, H.; Mo, F.; Chen, Z.; Wu, J.; Fang, H.; Fang, Z.; Zhang, S.; Xu, Z. Full-Scale Experimental Study of Shear and Flexural Behavior of 16-m Retired Reinforced Concrete T-Beams. Buildings 2023, 13, 2075. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, T.; Zhu, Y.; Zhu, Z.; Wang, K. Analysis on Flexural Performance of Prestressed Steel-Reinforced UHPC Beams. Buildings 2024, 14, 4029. [Google Scholar] [CrossRef]
- Liu, Z.; Lei, H.P.; Luo, J.; Zhang, C.; Ma, B. Full-Scale Experimental Test on Flexural Behavior of a 30 m-Long Pretensioned Concrete Double-Tee Girder. Bridge Constr. 2022, 52, 14–20. [Google Scholar]
- Liu, Y.C. Theoretical Analysis and Experimental Study on Mechanical Properties of Simply Supported T-Beams with Single Polygonal Prestressed Tendons. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Yang, H.; Dai, M.; Wu, N.; Zheng, M.; Zhang, X. Experimental on mechanical behavior of broken line pretensioned I-beam. Sci. Technol. Eng. 2022, 22, 13484–13489. [Google Scholar]
- Hu, K.; Liu, C.; Duanmu, X.Y.; Wang, S.B. Theoretical study on shear capacity of concrete beam sections under combined bending and shear. Bridge Constr. 2023, 53, 135–141. [Google Scholar]
- Garber, D.B.; Gallardo, J.M.; Deschenes, D.J.; Bayrak, O. Nontraditional Shear Failures in Bulb-T Prestressed Concrete Bridge Girders. J. Bridge Eng. 2016, 21, 04016030. [Google Scholar] [CrossRef]
- Deifalla, A.; Ghobarah, A. Behavior and analysis of inverted T-shaped RC beams under shear and torsion. Eng. Struct. 2014, 68, 57–70. [Google Scholar] [CrossRef]
- Deifalla, A.; Awad, A.; Seleem, H.; Abdelrahman, A. Investigating the behavior of lightweight foamed concrete T-beams under torsion, shear, and flexure. Eng. Struct. 2020, 219, 110741. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China National Standardization Administration: Beijing, China, 2019.
- GB/T 228.1—2021; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. China National Standardization Administration: Beijing, China, 2021.
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- JTG 3362-2018; Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. China Architecture & Building Press: Beijing, China, 2018.
- Xue, Y.H.; Dong, Z.Q.; Li, G.; Yu, D.H.; Wang, R.; Zhang, H. Multi-mode inversion of dispersive surface-wave free fields in layered media. Earthq. Eng. Struct. Dyn. 2024, 53, 2331–2353. [Google Scholar] [CrossRef]
- Yu, D.H.; Li, G. A novel Woodbury solution method for nonlinear seismic response analysis of large-scale structures. Earthq. Eng. Struct. Dyn. 2024, 53, 261–278. [Google Scholar] [CrossRef]
- Zhang, J.L.; Li, G.; Yu, D.H.; Dong, Z.Q. Framework for seismic risk analysis of engineering structures considering the coupling damage from multi-environmental factors. J. Struct. Eng. 2024, 150, 1–15. [Google Scholar] [CrossRef]
- Li, G.; Yu, D.H. Efficient Inelasticity-Separated Finite Element Method for Material Nonlinearity Analysis. ASCE-J. Eng. Mech. 2018, 144, 04018008. [Google Scholar] [CrossRef]
- Zhang, J.L.; Yu, D.H.; Li, G.; Dong, Z.Q. Multi-hazard performance assessment of monopile offshore wind turbine considering coupled corrosion and fatigue damage. Ocean. Eng. 2025, 316, 119985. [Google Scholar] [CrossRef]
- Li, G.; Jiang, Y.M.; Yu, D.H.; Dong, Z.Q. A mixed stochastic waves model for analyzing offshore structures considering engineering characteristics correlation of wind-generated-wave and swell. Ocean. Eng. 2024, 314, 119671. [Google Scholar] [CrossRef]

| Type | Diameter (mm) | Yield Strength fy (MPa) | Ultimate Strength fu (MPa) |
|---|---|---|---|
| No. 1 bars | 10 | 332.0 | 461.2 |
| No. 2 bars | 12 | 418.0 | 595.4 |
| No. 3 bars | 14 | 446.0 | 580.4 |
| No. 4 bars | 28 | 432.0 | 614.1 |
| Prestressing strands | 15.2 | 1383.3 | 1834.6 |
| Loading Conditions | A1 Load (kN) | A2 Load (kN) | Torque (kN·m) | Note |
|---|---|---|---|---|
| LB1 | 127 | 127 | 0 | Self-weight and secondary dead loads |
| LC1 | 280 | 127 | 100 | — |
| LC2 | 435 | 127 | 200 | — |
| LC3 | 590 | 127 | 300 | — |
| LC4 | 745 | 127 | 400 | — |
| LC5 | 900 | 127 | 500 | — |
| LC6 | 1055 | 127 | 600 | — |
| LC7 | 1210 | 127 | 700 | — |
| LC8 | 1365 | 127 | 800 | — |
| LC9 | 1520 | 127 | 900 | Cracking |
| LC10 | 1620 | 127 | 970 | — |
| LC11 | 1720 | 127 | 1035 | — |
| LC12 | 1820 | 127 | 1100 | — |
| LC13 | 1920 | 127 | 1165 | — |
| LC14 | 2020 | 127 | 1230 | — |
| LC15 | 2120 | 127 | 1295 | — |
| LC16 | 0 | 0 | 0 | Unloading |
| Number | Measurement Range/kN | Sensitivity/(mV/V) | Operating Temperature Range/°C |
|---|---|---|---|
| Jack A1 | 0–3000 | 1.2437 | −10~+70 |
| Jack A2 | 0–1000 | 1.4260 | −10~+70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Z.; Wei, M.; Yan, H.; Yu, D.; Li, G.; Zhang, C.; Tao, J.; Pei, H. Experimental Study of Pre-Tensioned Polygonal Prestressed T-Beam Under Combined Loading Condition. Buildings 2025, 15, 1379. https://doi.org/10.3390/buildings15081379
Yao Z, Wei M, Yan H, Yu D, Li G, Zhang C, Tao J, Pei H. Experimental Study of Pre-Tensioned Polygonal Prestressed T-Beam Under Combined Loading Condition. Buildings. 2025; 15(8):1379. https://doi.org/10.3390/buildings15081379
Chicago/Turabian StyleYao, Zengbo, Mingguang Wei, Hai Yan, Dinghao Yu, Gang Li, Chunlei Zhang, Jinglin Tao, and Huiteng Pei. 2025. "Experimental Study of Pre-Tensioned Polygonal Prestressed T-Beam Under Combined Loading Condition" Buildings 15, no. 8: 1379. https://doi.org/10.3390/buildings15081379
APA StyleYao, Z., Wei, M., Yan, H., Yu, D., Li, G., Zhang, C., Tao, J., & Pei, H. (2025). Experimental Study of Pre-Tensioned Polygonal Prestressed T-Beam Under Combined Loading Condition. Buildings, 15(8), 1379. https://doi.org/10.3390/buildings15081379





