Seismic Performance Analysis for an Eccentrically Braced Frame (EBF) with an Innovative Self-Centering Shear Link
Abstract
1. Introduction
2. Basic Performance
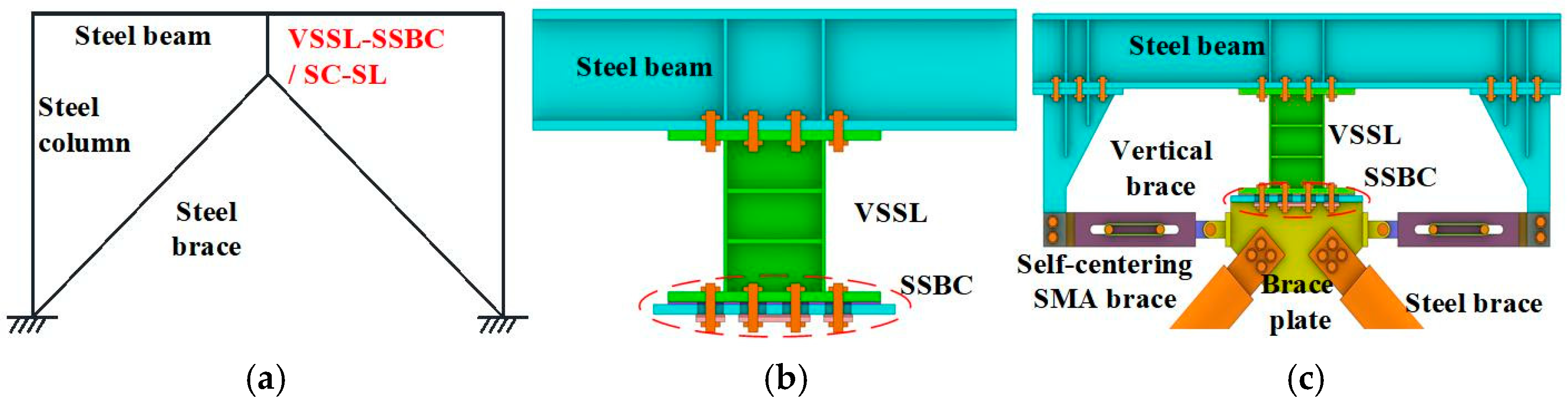
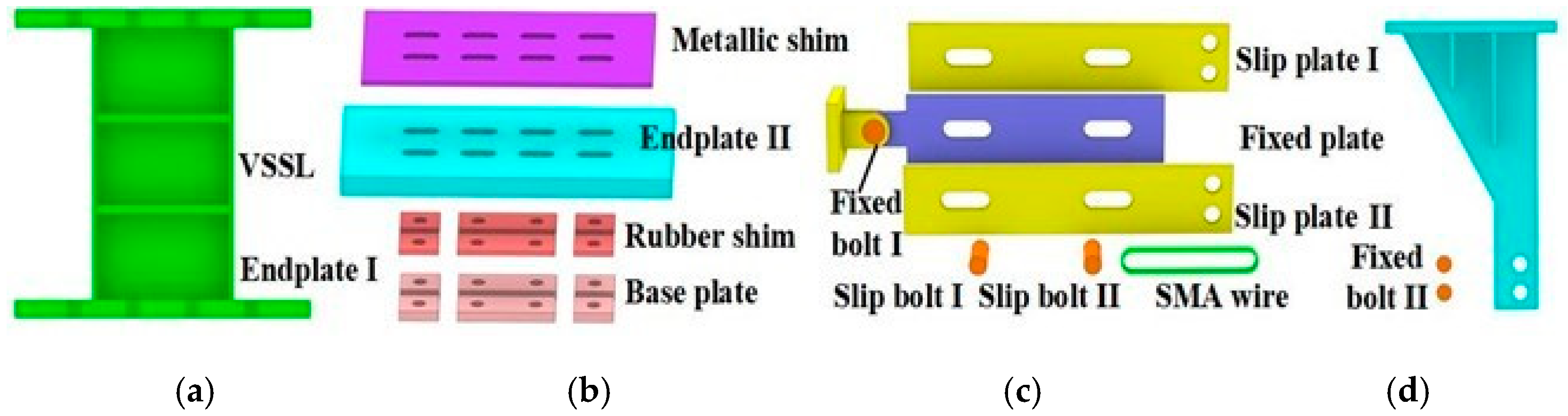
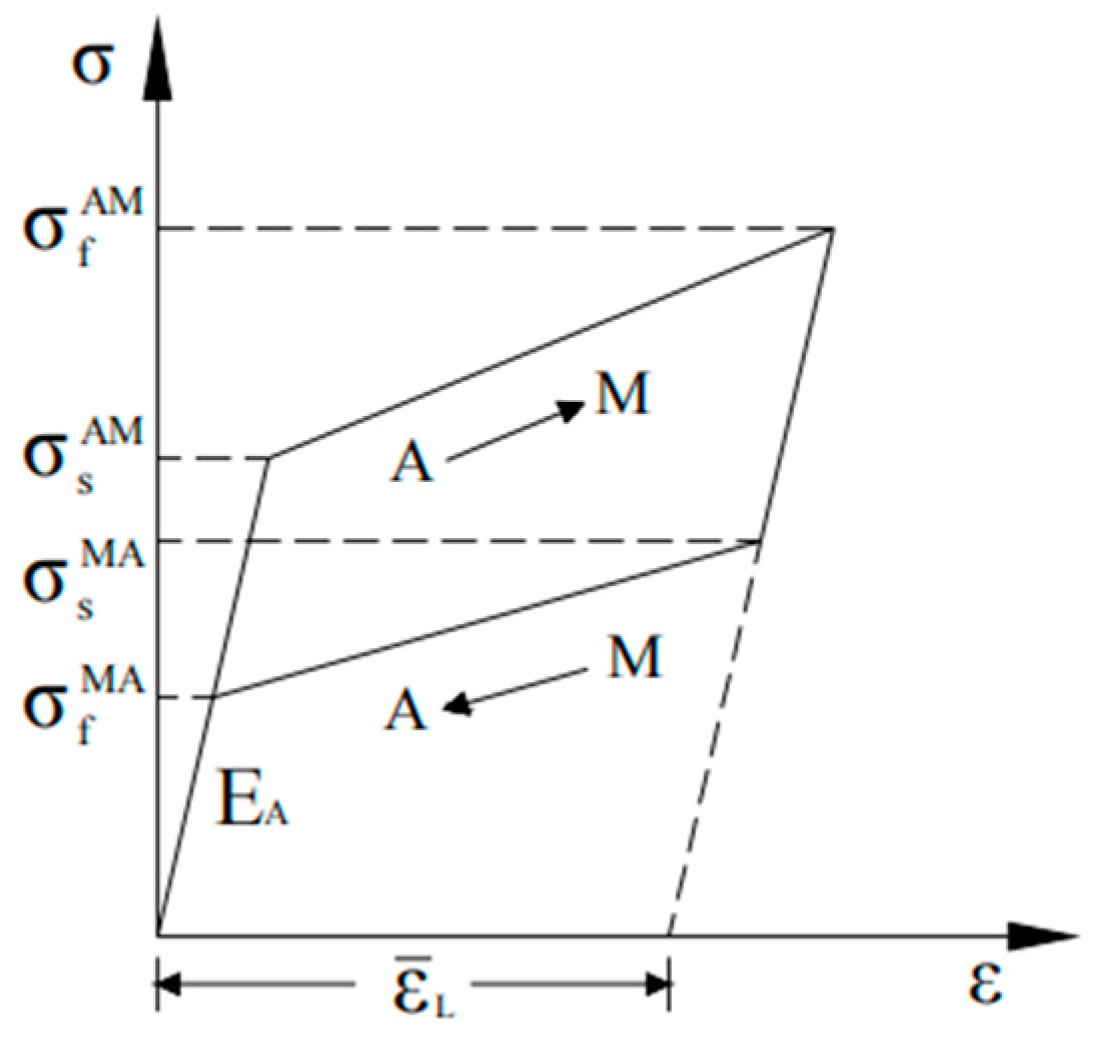
2.1. Basic Component
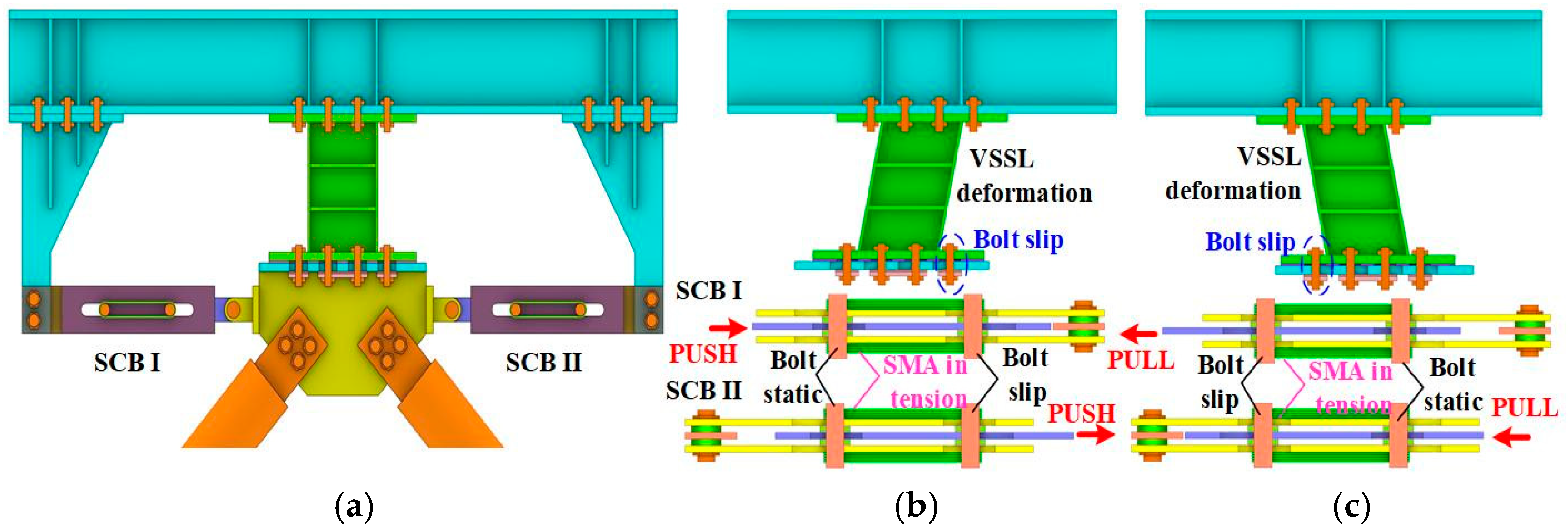
2.2. Working Mechanism
2.3. Design Method
3. Experimental Study of VSSL-SSBC and SC-SL
3.1. Test Plan
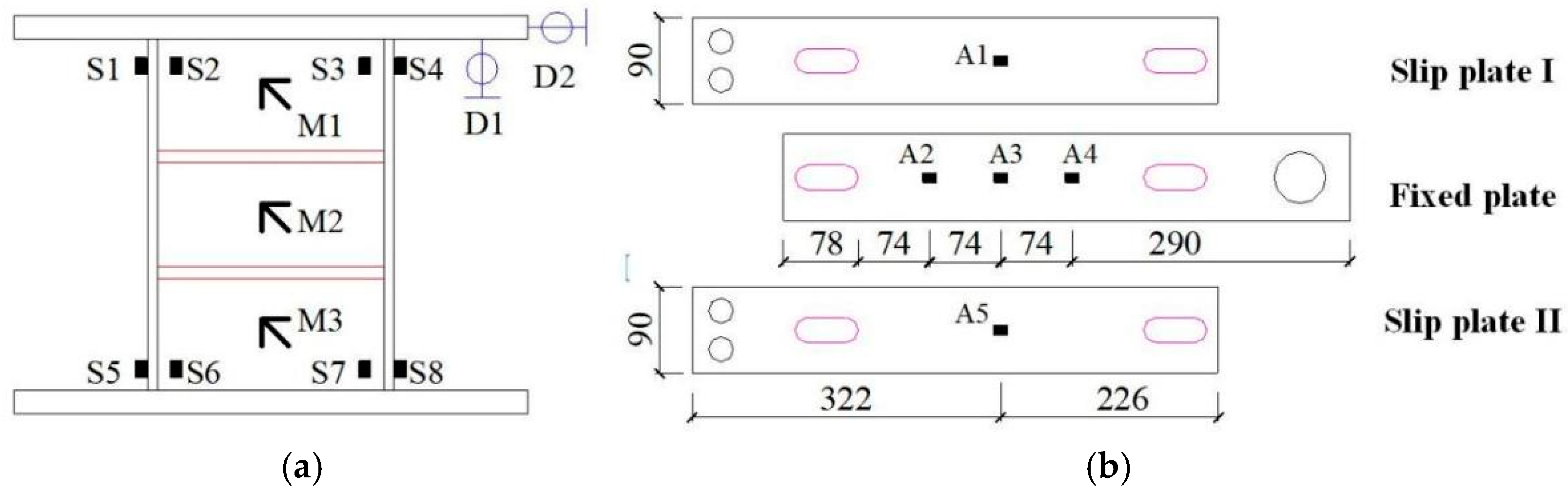
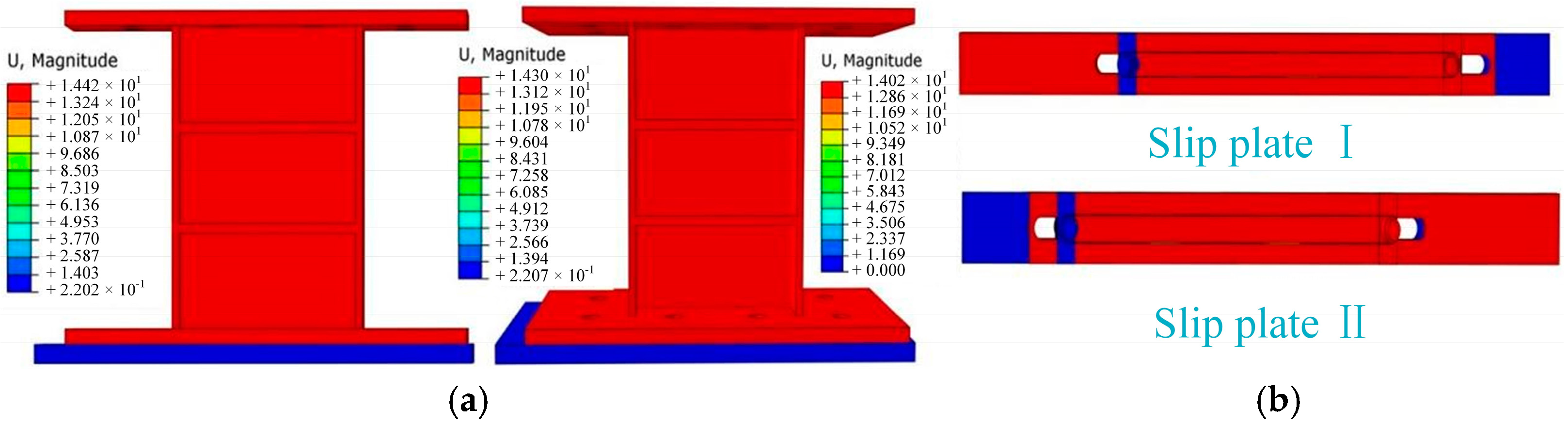
3.1.1. Specimen Design
3.1.2. Material Properties
3.1.3. Test Setup and Loading Protocol
3.1.4. Measurement Scheme
3.2. Failure Mode
3.2.1. VSSL-SSBC-1 Specimen
3.2.2. SC-SL-1 Specimen
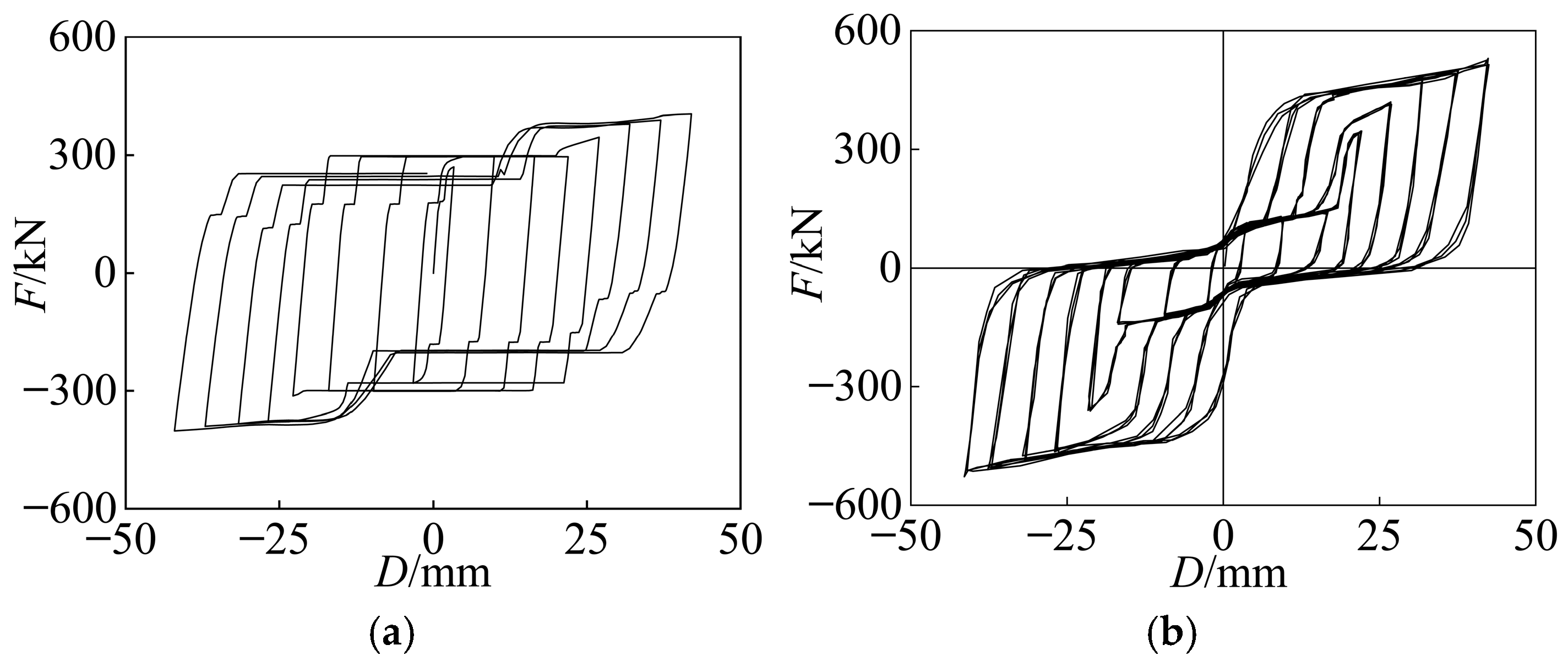
3.3. Hysteresis Performance
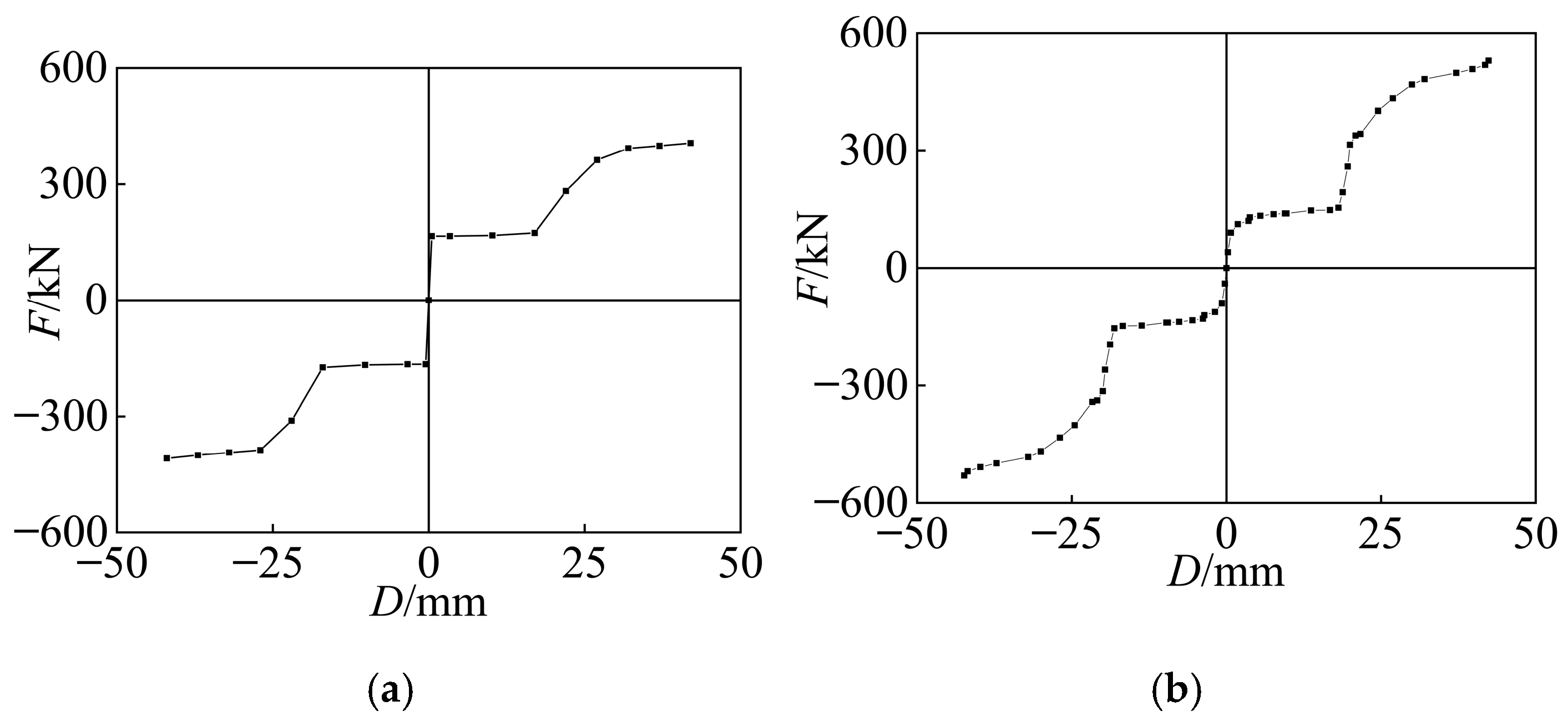
3.4. Skeleton Curves
4. Numerical Study of VSSL-SSBC and SC-SL
4.1. Numerical Analysis Method
4.1.1. Verification of the SMA
4.1.2. Numerical Method of VSSL-SSBC-1 Specimen
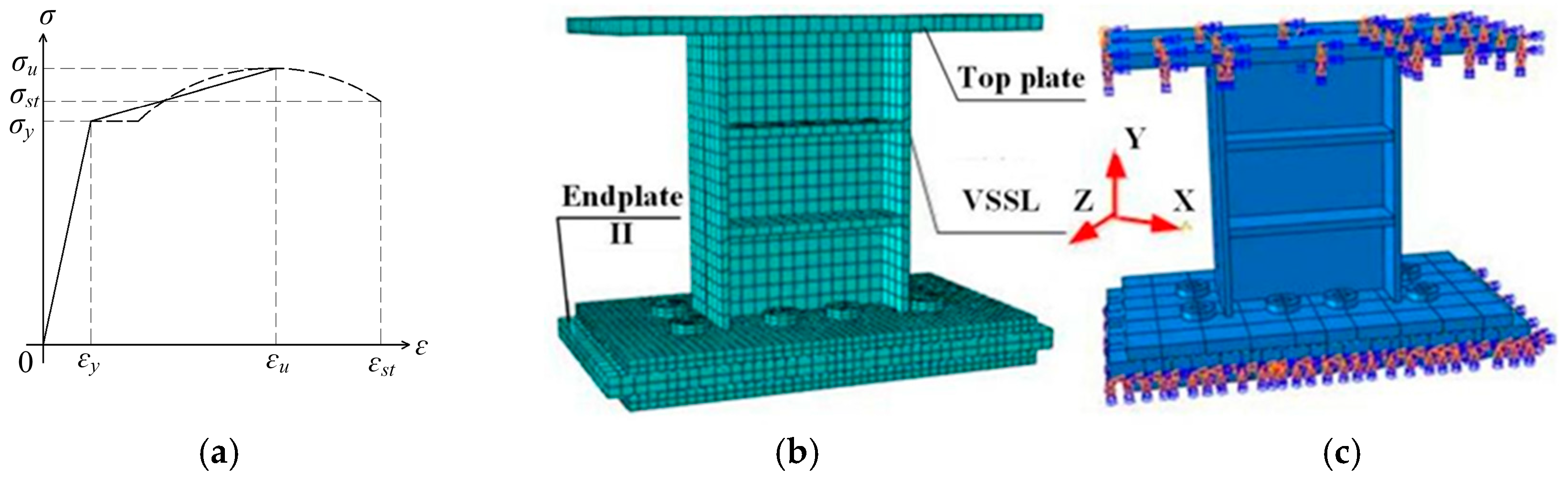
4.1.3. Numerical Method of SC-SL-1 Specimen

4.2. Comparison of VSSL-SSBC-1 Specimen
4.2.1. Hysteresis Curves
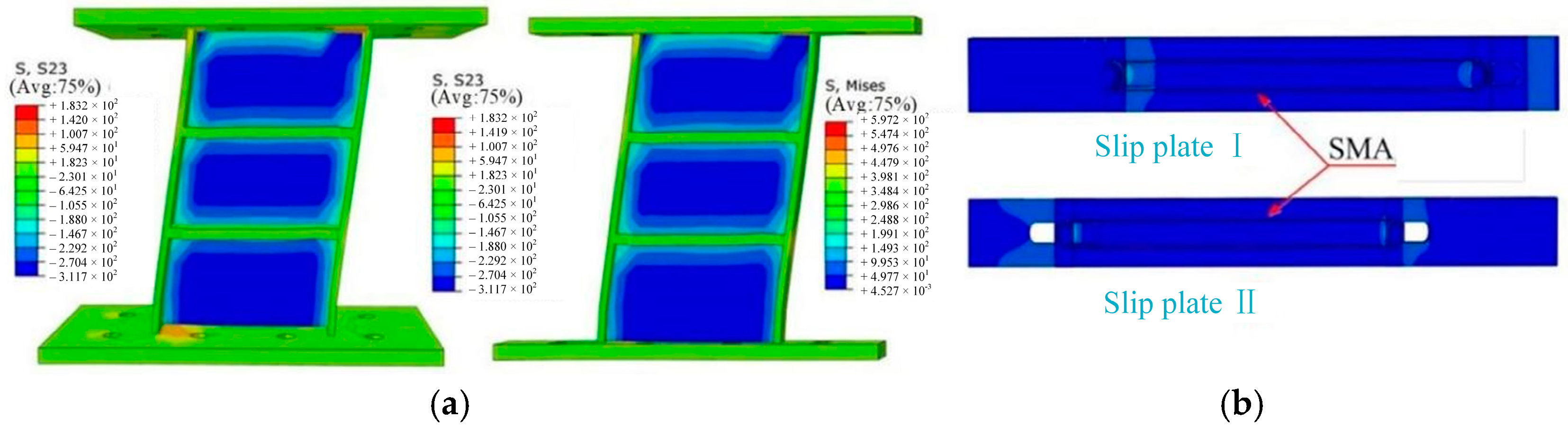
4.2.2. Failure Modes
4.3. Comparison of SC-SL-1 Specimen
4.3.1. Hysteresis Curves
4.3.2. Failure Modes
5. Seismic Performance of EBF with Self-Centering Shear Link
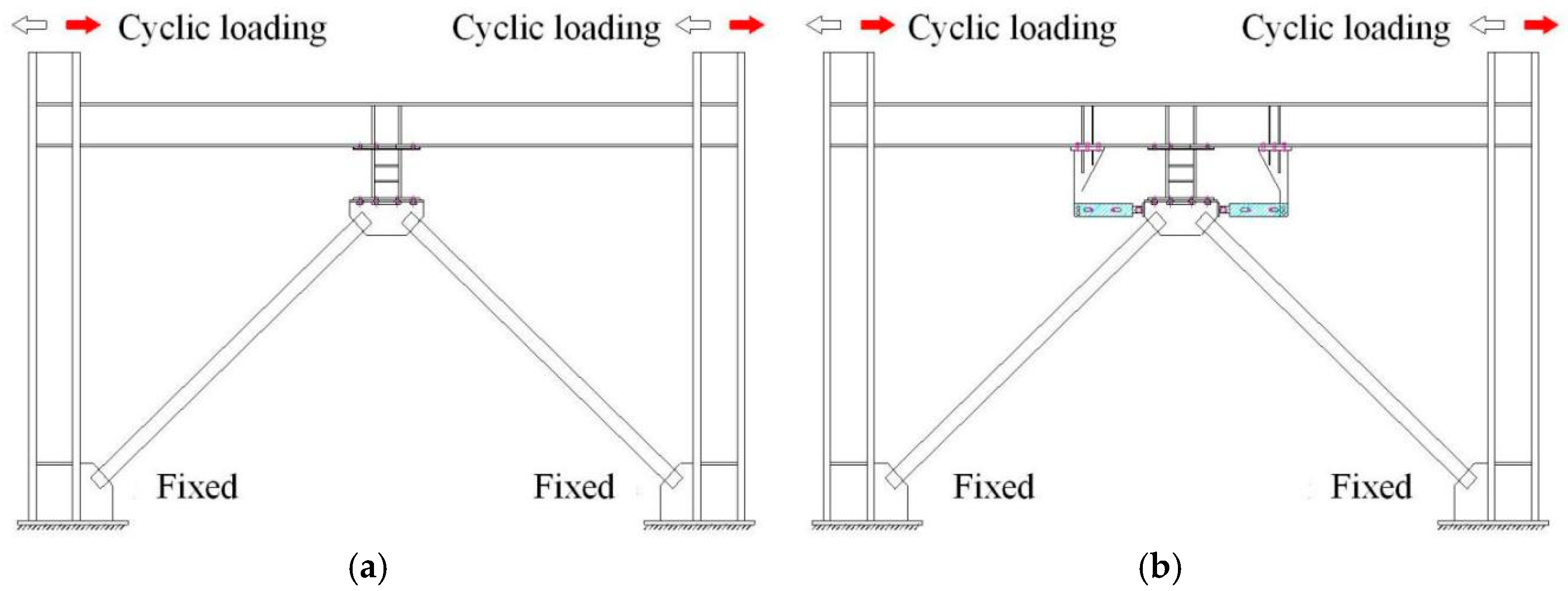
5.1. Analysis Model
5.1.1. Modeling
5.1.2. Numerical Analysis Method
5.2. Frequent Earthquakes
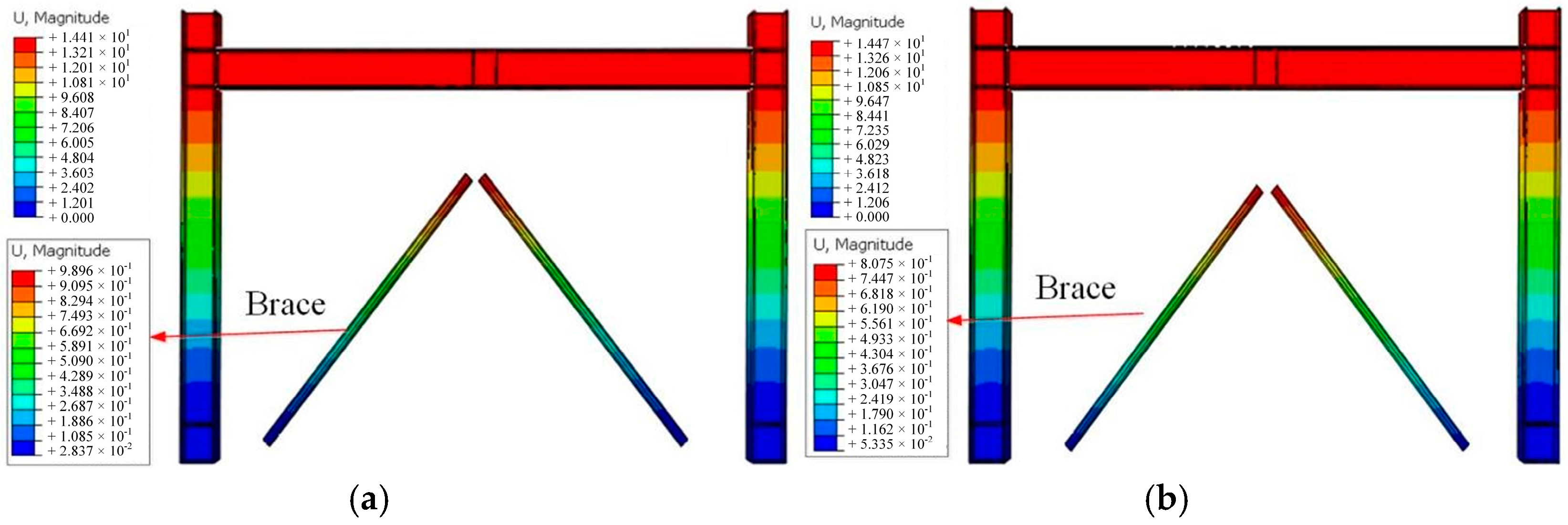
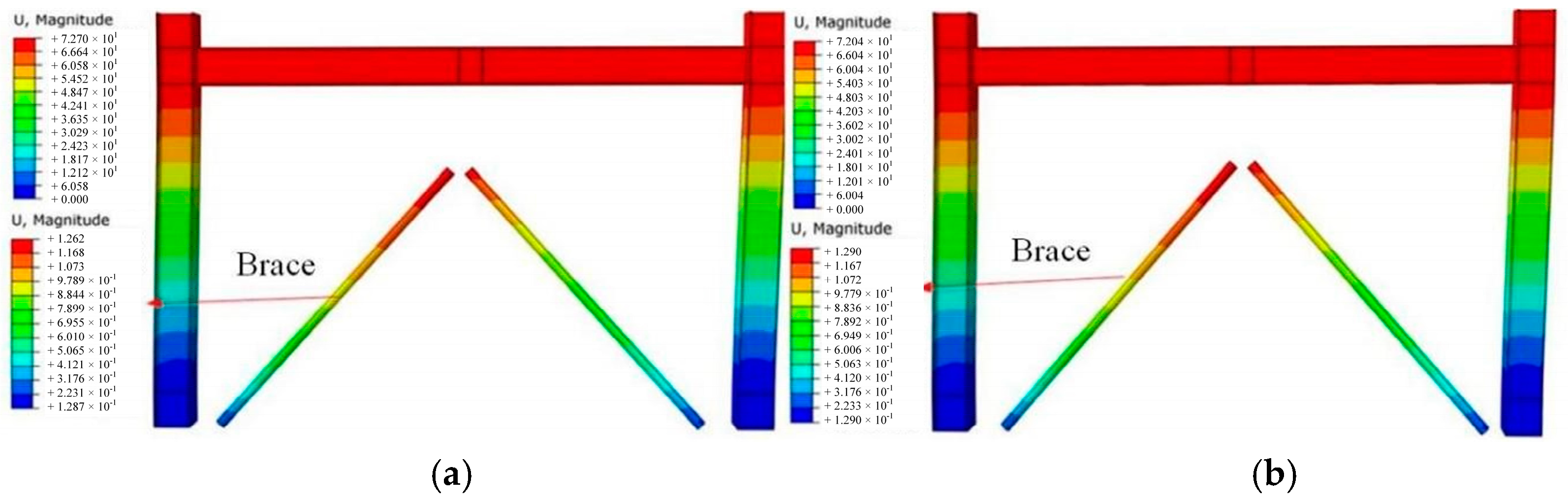
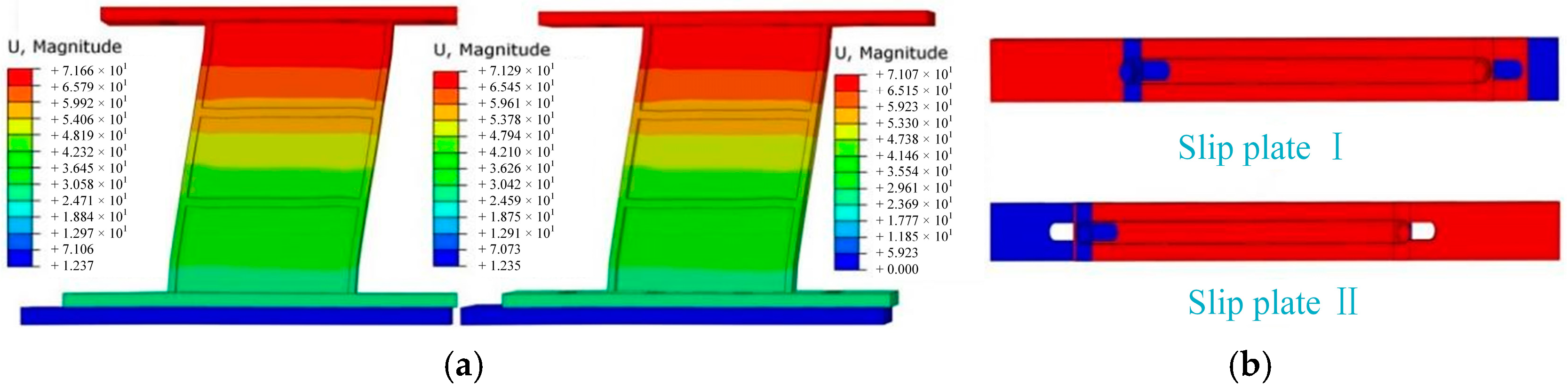
5.2.1. Deformation Modes
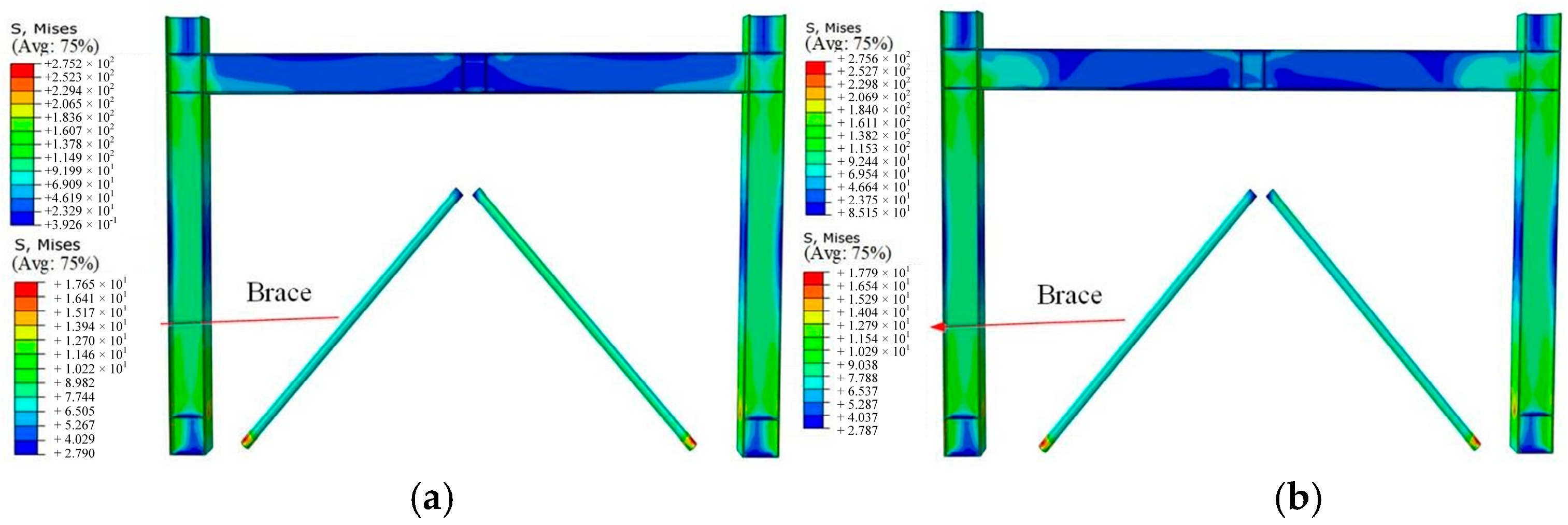
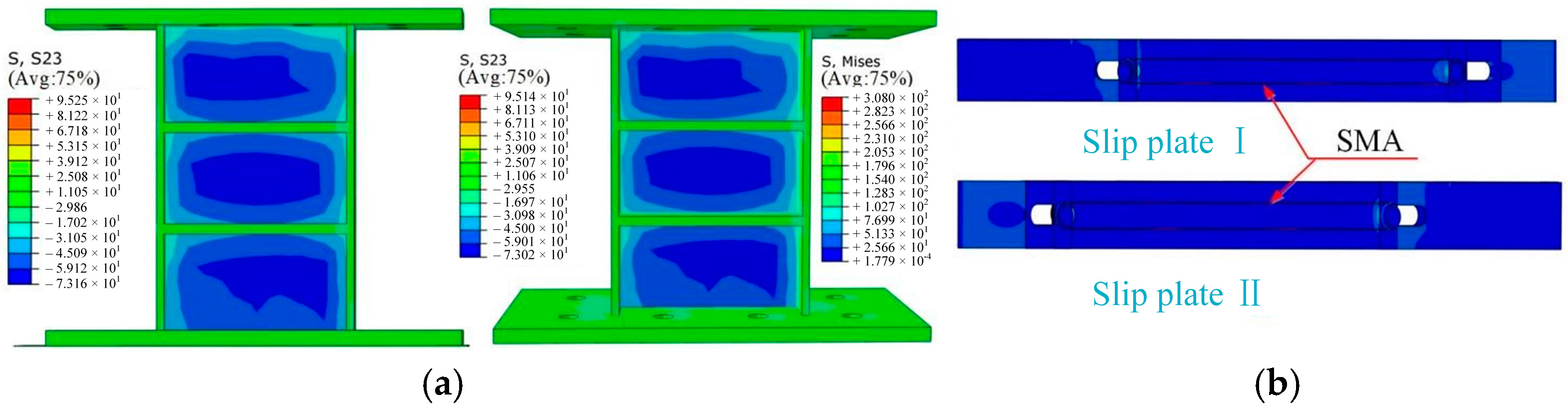
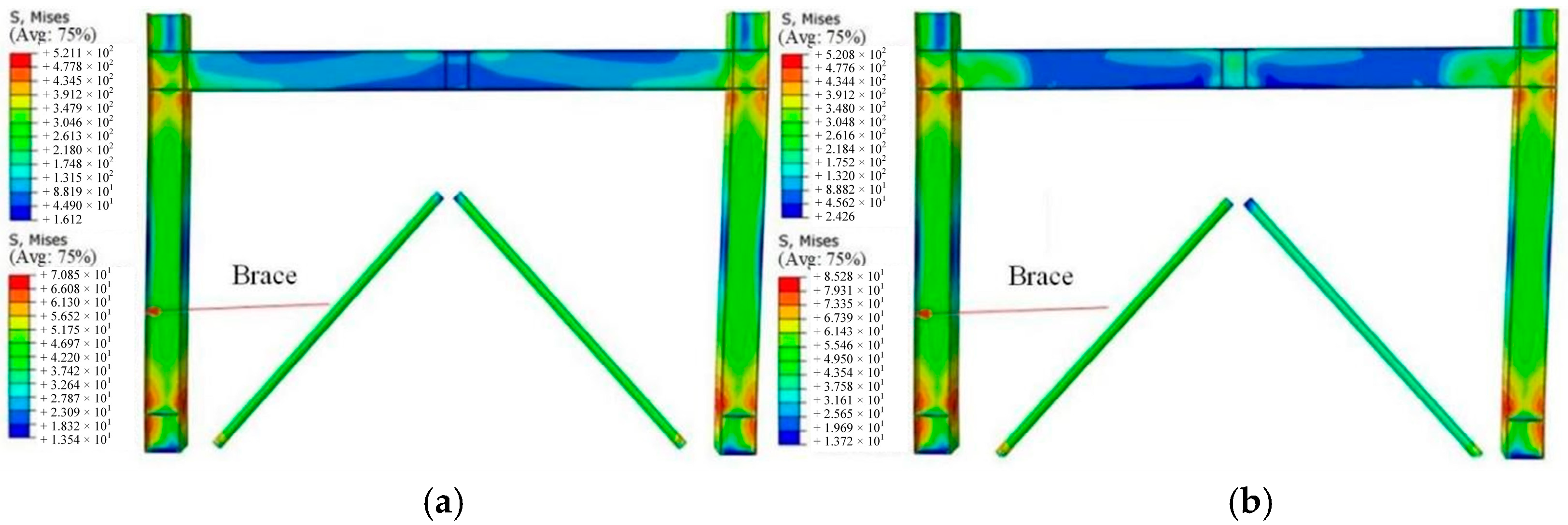
5.2.2. Stress Nephograms
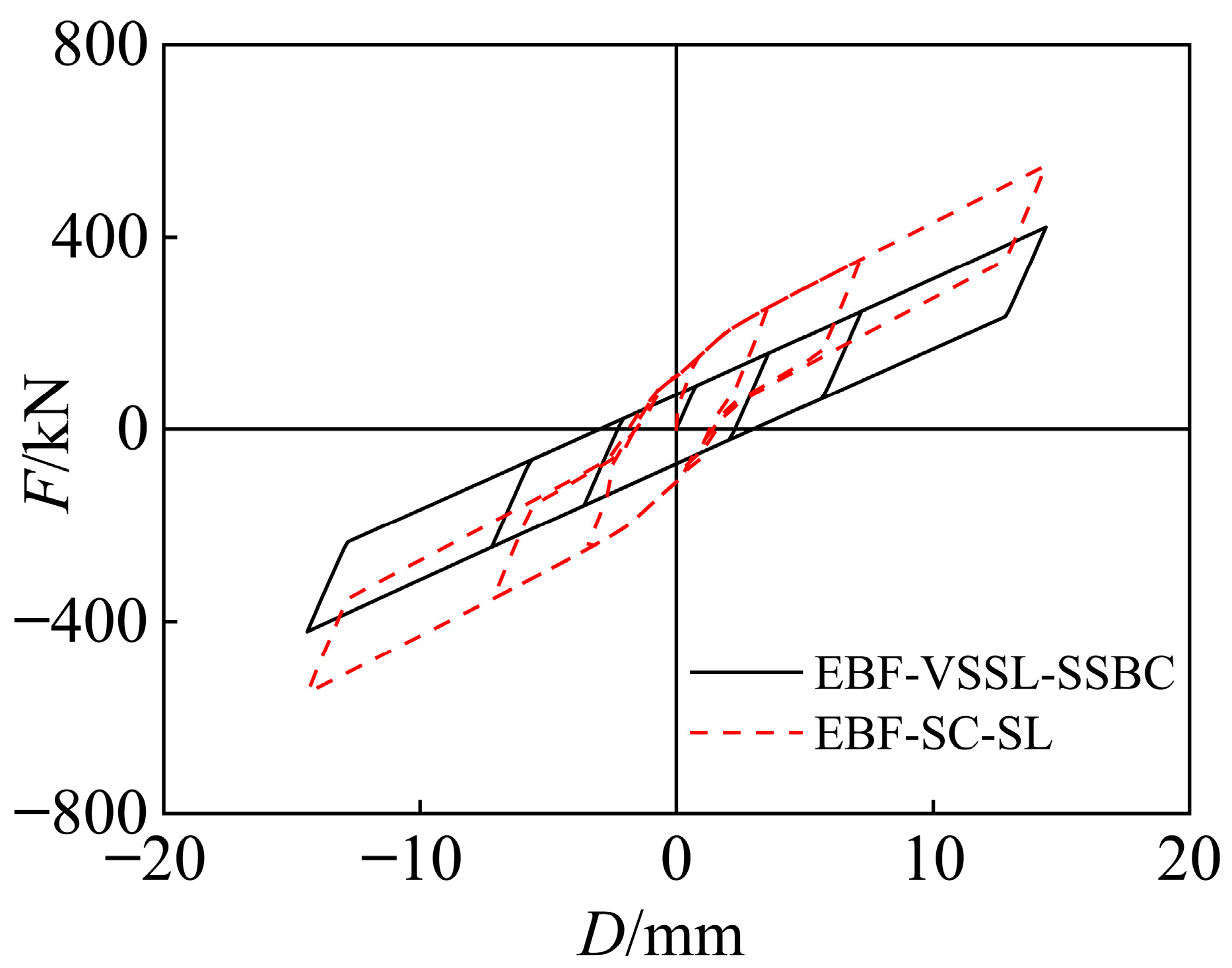
5.2.3. Hysteresis Curves
5.3. Rare Earthquakes
5.3.1. Deformation Modes
5.3.2. Stress Nephograms
5.3.3. Hysteresis Curves
5.4. Seismic Results Analysis
6. Conclusions and Future Prospects
6.1. Conclusions
- (1)
- Under seismic loading, the VSSL-SSBC mainly experienced elastic, slip, elastoplastic, and plastic stages, while the SC-SL experienced VSSL slip, yielding, and flange and web buckling, with the SMA wires in tension. The ultimate bearing capacities of the two devices are 442.30 kN and 529.18 kN, respectively.
- (2)
- The experimental and finite element results demonstrate that the SC-SL has a significant improvement in both the ultimate bearing capacity and energy dissipation capacity compared with the VSSL-SSBC. Moreover, due to the function of the SCB, it exhibits an excellent self-centering capacity.
- (3)
- Under frequent earthquakes, the frame, brace, and VSSL stresses and displacements in EBF-VSSL-SSBC and EBF-SC-SL are basically equivalent. Both frames dissipate energy through the slippage of high-strength bolts, and VSSL-SSBC remains elastic without significant yielding deformation.
- (4)
- Under rare earthquakes, the bearing force and stress of the brace of the EBF-SC-SL are slightly increased compared with EBF-VSSL-SSBC. Its ultimate load capacity is enhanced by 19.66%, and the residual deformation is reduced by 27.90%. This improvement contributes to the seismic resilience capacity of the EBF.
6.2. Outlook
- (1)
- In this paper, a method combining experiments and finite element verification is adopted to study the mechanical properties of SC-SL, which provides a reference for the design of self-centering structures. However, it is necessary to carry out frame design and experimental research for the EBF with SC-SL in the future.
- (2)
- Based on future experiments on the EBF with SC-SL, the influencing factors on its self-centering capacity, such as the circles and diameter of the SMA wires, can be investigated.
- (3)
- This paper only investigated the application of SC-SL in Y-shaped eccentrically braced frames, whereas the application of SC-SL in other types of EBFs can be expanded in the future.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okazaki, T.; Arce, G.; Ryu, H.C.; Engelhardt, M.D. Experimental study of local buckling, overstrength, and fracture of links in eccentrically braced frames. J. Struct. Eng. 2005, 131, 1526–1535. [Google Scholar] [CrossRef]
- Bosco, M.; Rossi, P.P. Seismic behaviour of eccentrically braced frames. Eng. Struct. 2009, 31, 664–674. [Google Scholar] [CrossRef]
- Azad, S.K.; Topkaya, C. A review of research on steel eccentrically braced frames. J. Constr. Steel Res. 2017, 128, 53–73. [Google Scholar] [CrossRef]
- Okazaki, T.; Engelhardt, M.D. Cyclic loading behavior of EBF links constructed of ASTM A992 steel. J. Constr. Steel Res. 2007, 63, 751–765. [Google Scholar] [CrossRef]
- Hu, S.J.; Zeng, S.Z.; Zhou, Q.; Zhi, Q.; He, K. Mechanism and seismic performance of a novel precast concrete beam-to-very short shear link joint: Experimental and numerical simulation. Structures 2023, 56, 104938. [Google Scholar] [CrossRef]
- Hu, S.J.; Liu, S.W.; Zeng, S.Z.; Shao, T.F. Mechanical properties and influence factors of ordinary shear links. Buildings 2024, 14, 160. [Google Scholar] [CrossRef]
- AISC 341; Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2010.
- Ji, X.D.; Wang, Y.D.; Ma, Q.F.; Okazaki, T. Cyclic behavior of very short steel shear links. J. Struct. Eng. 2016, 142, 04015114. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. Chinese Building Industry Press: Beijing, China, 2016.
- Hu, S.J.; Xiong, J.G.; Zhou, Q.; Lin, Z.B. Analytical and numerical investigation of overstrength factors for very short shear links in EBFs. KSCE J. Civ. Eng. 2018, 22, 4473–4482. [Google Scholar] [CrossRef]
- Chen, Z.P.; Zhu, S.; Yu, H.; Wang, B. Development of novel SMA-based D-type self-centering eccentrically braced frames. Eng. Struct. 2022, 260, 114228. [Google Scholar] [CrossRef]
- Kazaz, I.; Bilge, I.H.; Gurbuz, M. Near-fault ground motion characteristics and its effects on a collapsed reinforced concrete structure in Hatay during the February 6, 2023 Mw7.8 Kahramanmaras, earthquake. Eng. Struct. 2024, 298, 117067. [Google Scholar] [CrossRef]
- Dedeoglu, I.O.; Yetkin, M.; Tunc, G.; Ozbulut, O.E. Evaluating earthquake-induced damage in Dogansehir, Malatya after 2023 Kahramanmaras Earthquake sequence: Geotechnical and structural perspectives. J. Build. Eng. 2025, 104, 112266. [Google Scholar] [CrossRef]
- Damci, E.; Temur, R.; Kanbir, Z.; Sekerci, C.; Koroglu, E.O. Comprehensive investigation of damage due to 2023 Kahramanmaras, Earthquakes in Türkiye: Causes, consequences, and mitigation. J. Build. Eng. 2025, 99, 111420. [Google Scholar] [CrossRef]
- Hu, S.J.; Liu, S.W.; Zeng, S.Z.; Zhang, B.; Xu, Z.H. Investigating seismic performance of a novel self-centering shear link in EBF utilizing experimental and numerical simulation. J. Constr. Steel Res. 2025, 224, 109129. [Google Scholar] [CrossRef]
- Liu, S.W.; Chen, S.Y.; Zeng, S.Z.; Zhang, B.; Hu, S.J. Seismic performance analysis of K-shaped EBF with an innovative crack-resistant composition beam. J. Build. Eng. 2025, 101, 111818. [Google Scholar] [CrossRef]
- Loo, W.Y.; Quenneville, P.; Chouw, N. A new type of symmetric slip-friction connector. J. Constr. Steel Res. 2014, 94, 11–22. [Google Scholar] [CrossRef]
- Kolbadi, S.M.S.; Piri, H.; Keyhani, A.; Kolbadi, S.M.S.; Mirtaheri, M. Seismic performance evaluation of slotted-web and bolt-flange plate moment connection. J. Build. Eng. 2021, 20, 655–667. [Google Scholar] [CrossRef]
- Liu, X.C.; Chen, M.L.; Chen, X.S.; Li, Y.M.; Wang, Y.; Xu, L. Seismic behavior of bolted truss-to-column joint with oversized or slotted bolt hole. Eng. Struct. 2021, 247, 113110. [Google Scholar] [CrossRef]
- Zhang, Q.; Men, J.; Wang, J.; He, P.J.; Huang, C.H.; Li, J.F. Seismic performance evaluation of a replaceable steel beam with slotted bolted connections. J. Constr. Steel Res. 2022, 198, 107553. [Google Scholar] [CrossRef]
- Zhai, S.Y.; Lyu, Y.F.; Cao, K.; Li, G.Q.; Wang, W.Y.; Chen, C. Seismic behavior of an innovative bolted connection with dual-slot hole for modular steel buildings. Eng. Struct. 2023, 279, 115619. [Google Scholar] [CrossRef]
- Hu, S.J.; Liu, S.W.; Xu, H.W.; Zeng, S.Z.; Zhang, B.; Yu, Y.J. Experimental investigation of an innovative very short shear link with shear slotted bolted connection in eccentrically braced frames. Structures 2024, 66, 106890. [Google Scholar] [CrossRef]
- Zhang, B.; Zeng, S.Z.; Tang, F.H.; Hu, S.J.; Zhou, Q.; Jia, Y.G. Experimental and numerical analysis of the mechanical properties of a pretreated shape memory alloy wire in a self-centering steel brace. Processes 2021, 9, 80. [Google Scholar] [CrossRef]
- Feng, W.K.; Fang, C.; Wang, W. Behavior and design of top flange-rotated self-centering steel connections equipped with SMA ring spring dampers. J. Constr. Steel Res. 2019, 259, 315–329. [Google Scholar] [CrossRef]
- Qiu, C.X.; Jiang, T.Y.; Liu, J.W.; Du, X.L. Seismic performance of knee-braced frames equipped with NiTi BRBs. J. Constr. Steel Res. 2022, 197, 107480. [Google Scholar] [CrossRef]
- Sun, G.H.; Liu, H.; Liu, W.Y.; Yang, W.X. Development, simulation, and validation of sliding self-centering steel brace with NiTi SMA wires. Eng. Struct. 2022, 256, 114069. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.X.; Yu, H.F.; An, J.H. Experimental study on seismic performance of a new self-centering coupling beam. J. Constr. Steel Res. 2024, 216, 108572. [Google Scholar] [CrossRef]
- Jia, Y.G.; Zhang, B.; Zeng, S.Z.; Tang, F.H.; Hu, S.J.; Chen, W.P. Effect of loading rate and initial strain on seismic performance of an innovative self-centering SMA brace. Materials 2022, 15, 1234. [Google Scholar] [CrossRef]
- Rahgozar, N.; Pouraminian, M.; Rahgozar, N. Reliability-based seismic assessment of controlled rocking steel cores. J. Build. Eng. 2021, 44, 102623. [Google Scholar] [CrossRef]
- Chen, Z.P.; Zhu, S.Y. Seismic responses and resilience of novel SMA-based self-centring eccentrically braced frames under near-fault ground motions. Front. Struct. Civ. Eng. 2022, 16, 962–975. [Google Scholar] [CrossRef]
- Xiong, J.G.; Xiong, M.Q.; Liu, Y.Q.; Li, X.; Hu, S.J. Lateral Load Behavior of Self-centering Frame with Y-Eccentrically Braced Substructure: An Experiment and Numerical Analysis. KSCE J. Civ. Eng. 2024, 28, 715–731. [Google Scholar] [CrossRef]
- GB/T 228.1-2021; Metallic Materials—Tensile Testing. China Standards Press: Beijing, China, 2021.
- Li, P.C. Study on Seismic Performance of Friction Composite Damper Based on SMA Rod; Hebei University of Science of Technology: Shijiazhuang, China, 2022. [Google Scholar]






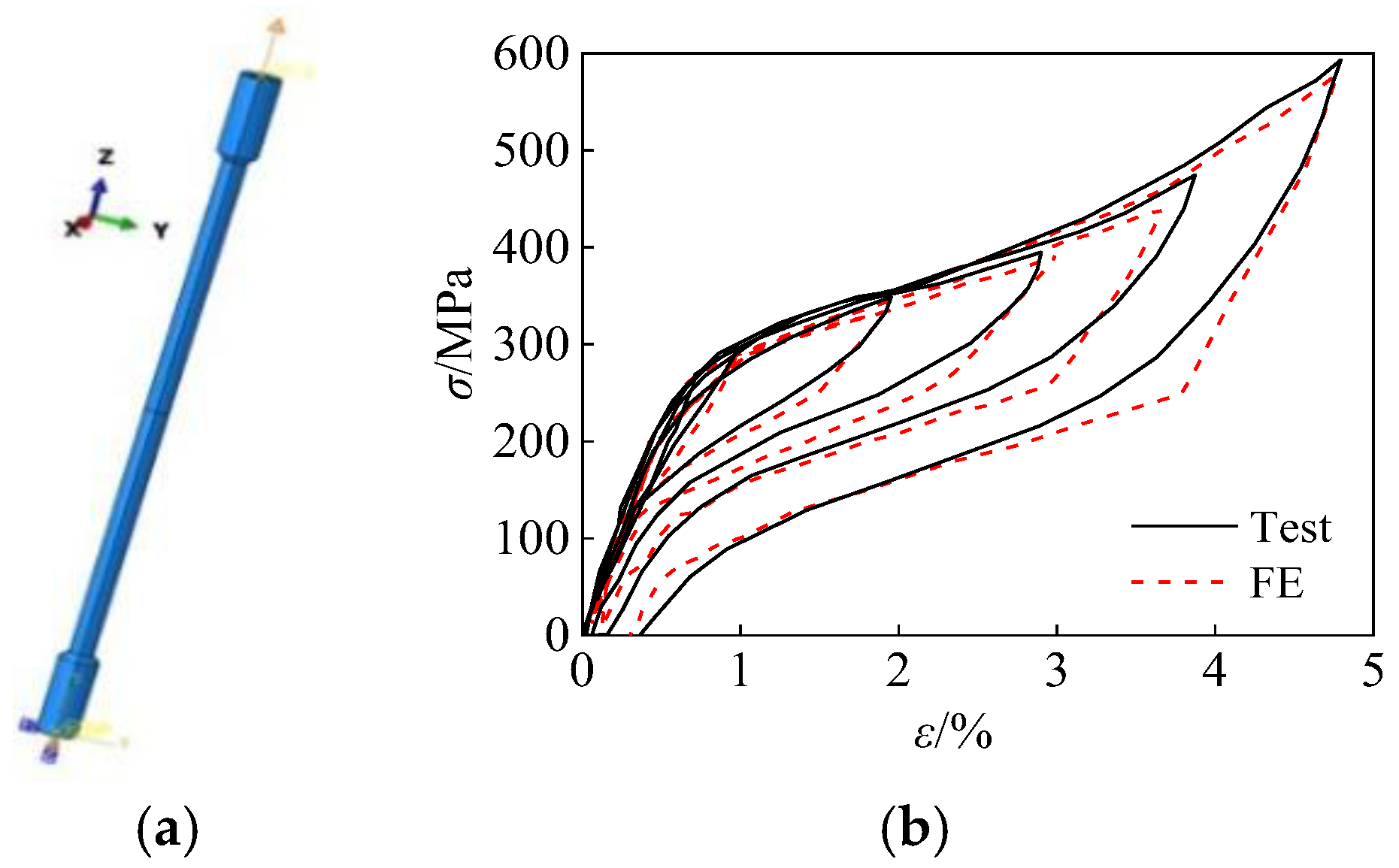
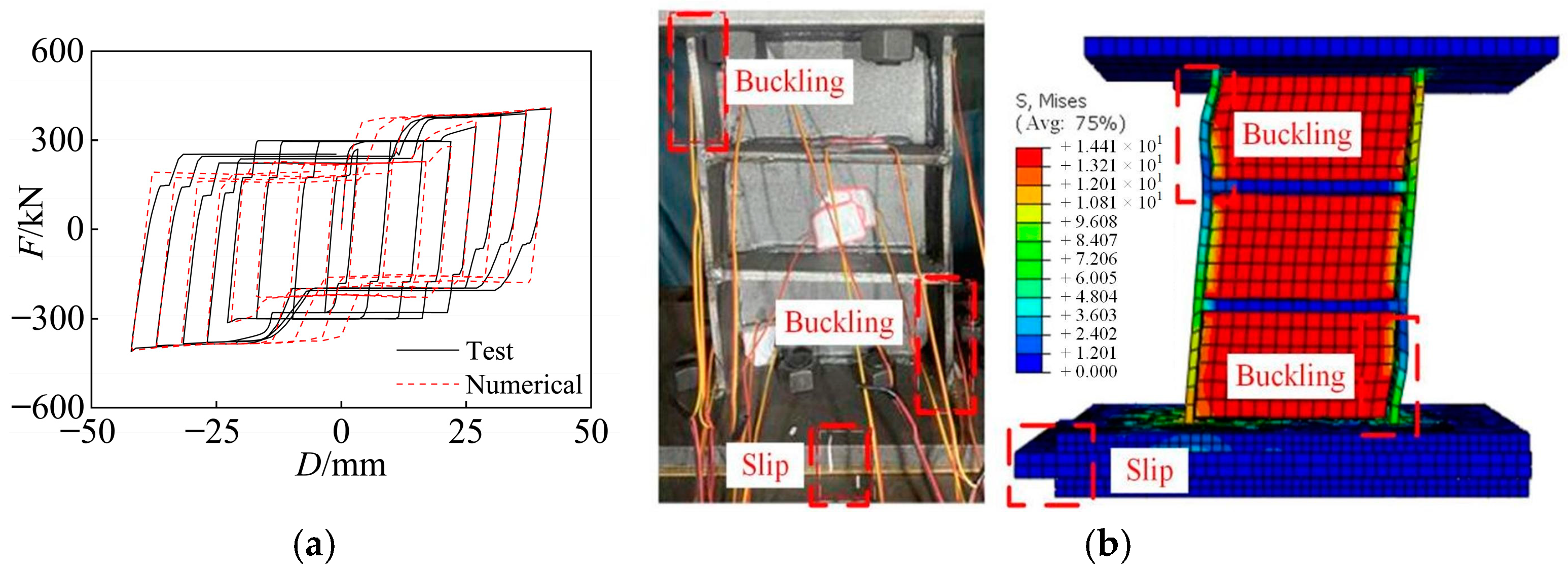
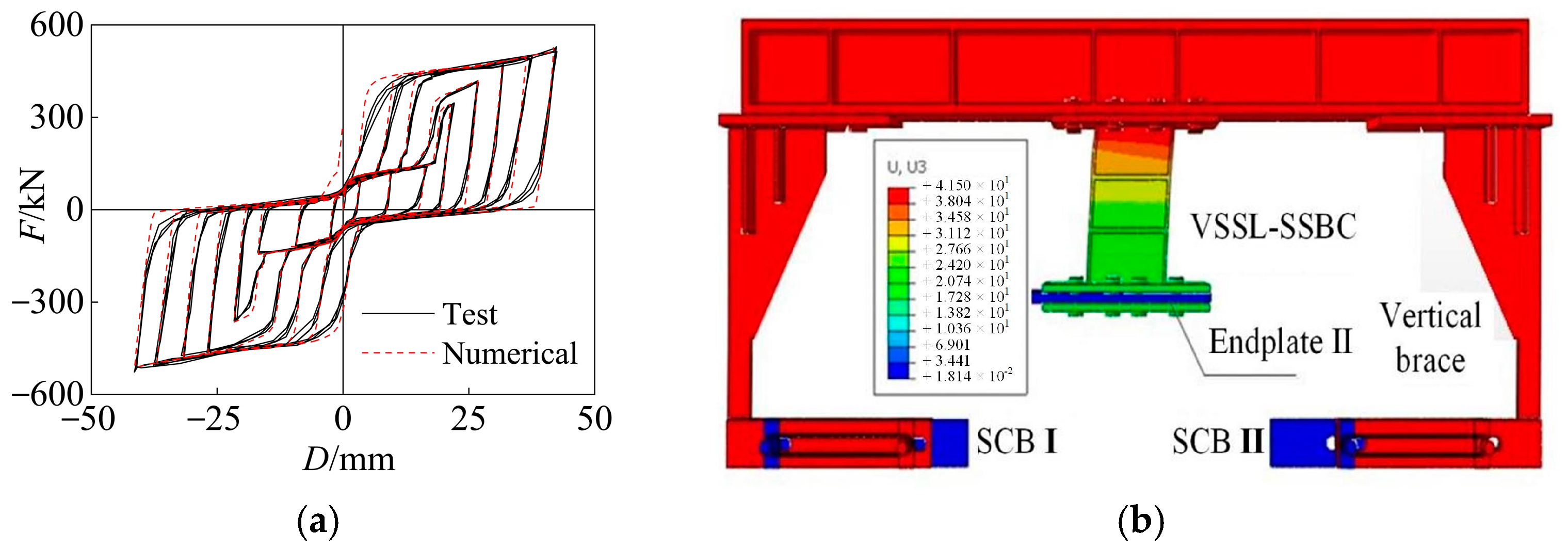
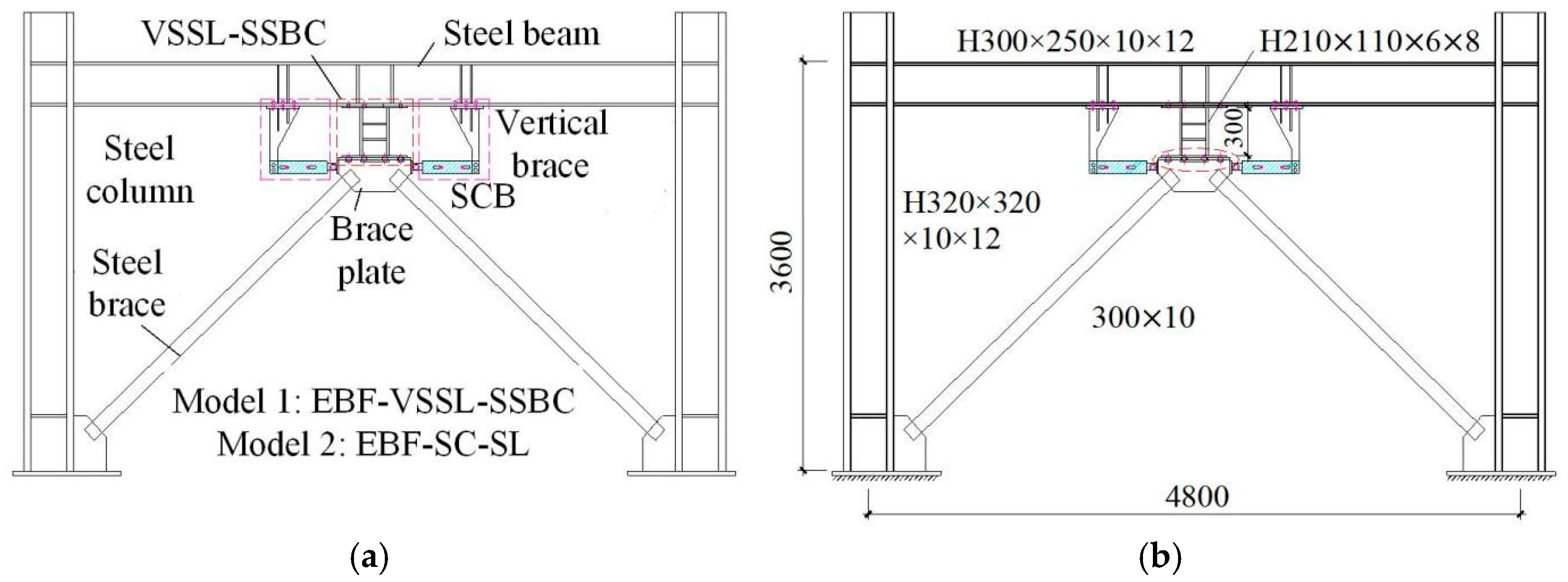

| Specimen | P /kN | μ | VSSL /mm | SMA Area /mm2 | Ps /kN | Loading Displacement/mm | Slot Hole Length/mm |
|---|---|---|---|---|---|---|---|
| VSSL-SSBC-1 | 50 | 0.30 | 210 × 110 × 6 × 8 | - | - | 40 | 34 |
| SC-SL-1 | 50 | 0.30 | 210 × 110 × 6 × 8 | 94.20 | 10 | 40 | 34 |
| Thickness t/mm | Yield Stress fy/MPa | Ultimate Stress fu/MPa | Elastic Modulus E/MPa | Elongation δ/% |
|---|---|---|---|---|
| 6 | 356 | 535 | 203 | 21.7 |
| 8 | 361 | 547 | 206 | 22.2 |
| 10 | 368 | 552 | 208 | 23.3 |
| 15 | 372 | 556 | 209 | 23.2 |
| EBF-VSSL-SSBC | EBF-SC-SL | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DF /mm | DV /mm | DB /mm | σF /MPa | τV /MPa | σB /MPa | η | DF /mm | DV /mm | DB /mm | σF /MPa | τV /MPa | σB /MPa | η | σS /MPa | |
| Frequent earthquake | 14.56 | 0 | 0.22 | 275 | 73 | 16.13 | 2.99 | 14.38 | 0 | 0.22 | 275 | 73 | 17.79 | 1.32 | 308 |
| Rare earthquake | 72.70 | 46.66 | 1.26 | 521 | 312 | 70.85 | 35.28 | 72.04 | 46.29 | 1.29 | 521 | 312 | 85.28 | 25.44 | 597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Huang, L.; Liu, S.; Zhang, B.; Hu, S. Seismic Performance Analysis for an Eccentrically Braced Frame (EBF) with an Innovative Self-Centering Shear Link. Buildings 2025, 15, 1471. https://doi.org/10.3390/buildings15091471
Xu X, Huang L, Liu S, Zhang B, Hu S. Seismic Performance Analysis for an Eccentrically Braced Frame (EBF) with an Innovative Self-Centering Shear Link. Buildings. 2025; 15(9):1471. https://doi.org/10.3390/buildings15091471
Chicago/Turabian StyleXu, Xinyu, Lifen Huang, Shangwen Liu, Bo Zhang, and Shujun Hu. 2025. "Seismic Performance Analysis for an Eccentrically Braced Frame (EBF) with an Innovative Self-Centering Shear Link" Buildings 15, no. 9: 1471. https://doi.org/10.3390/buildings15091471
APA StyleXu, X., Huang, L., Liu, S., Zhang, B., & Hu, S. (2025). Seismic Performance Analysis for an Eccentrically Braced Frame (EBF) with an Innovative Self-Centering Shear Link. Buildings, 15(9), 1471. https://doi.org/10.3390/buildings15091471






