Fire Resistance of In-Plane Compressed Log-House Timber Walls with Partial Thermal Insulation
Abstract
1. Introduction and State-of-the-Art
2. Testing
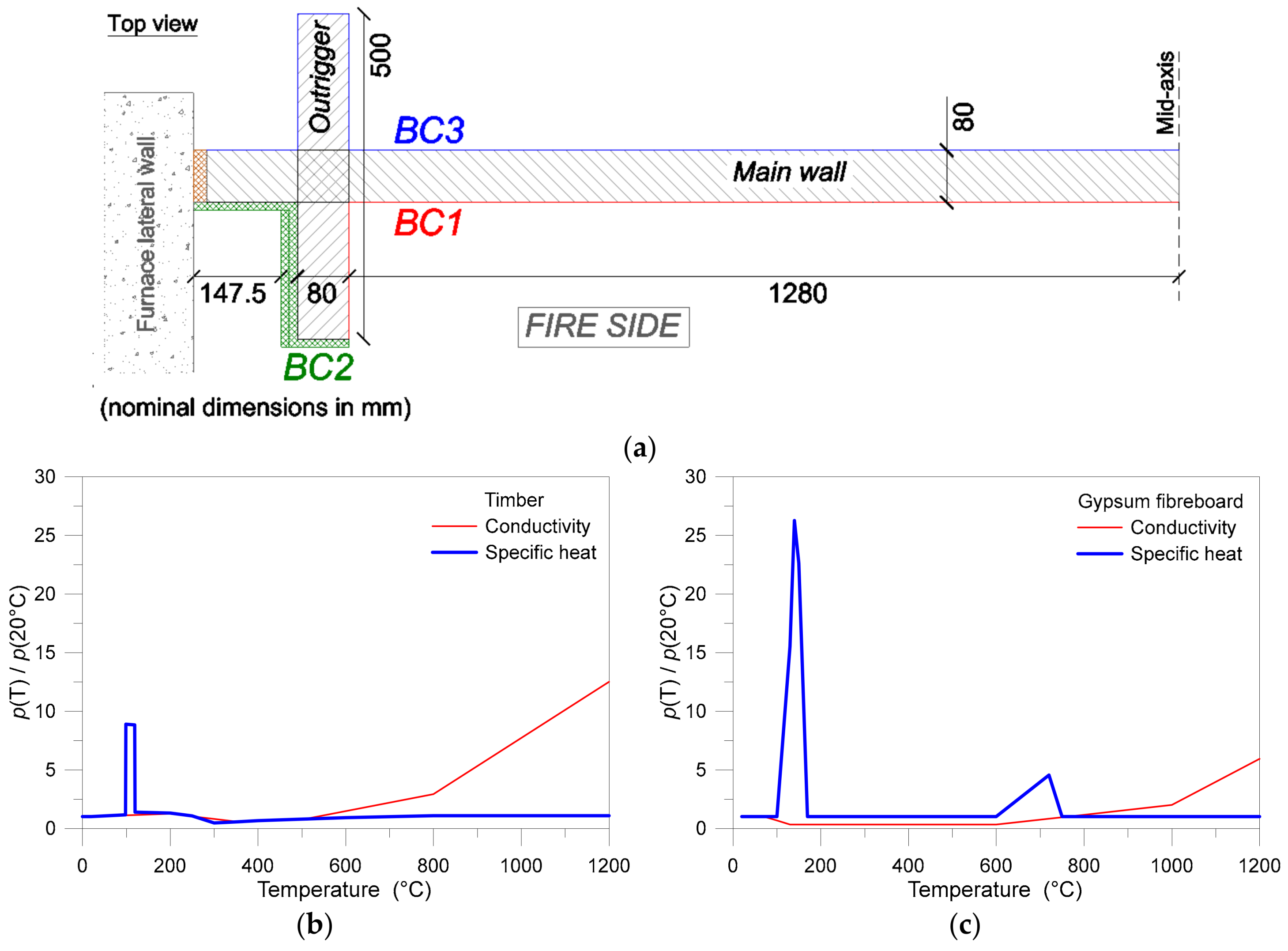
2.1. The Examined ‘W80’ Log-House Wall
2.2. Experimental Setup and Methods
2.3. Experimental Results
2.3.1. Visual Observations and Qualitative Comments
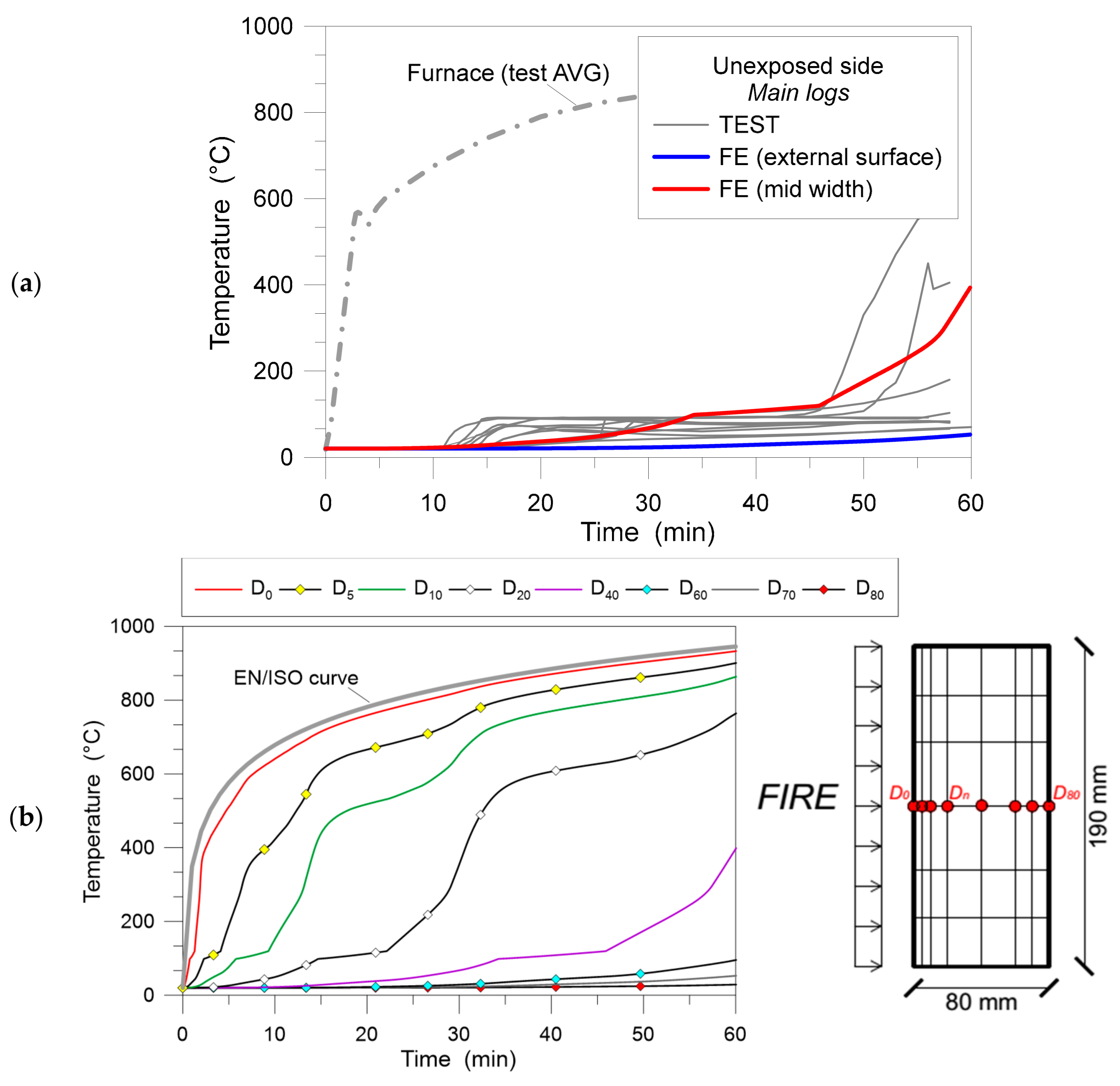
2.3.2. Temperature Measurements
2.3.3. Fire Resistance
- (a)
- Structural systems mainly loaded in bending
- (b)
- Structural systems mainly loaded in-plane
3. Finite Element Numerical Assessment of Experimental Results
3.1. Modelling Approach
3.2. Thermal Analysis in Fire Conditions
3.3. Mechanical Analysis in Fire Conditions
4. Discussion of FE Results
4.1. Thermal Simulations
4.2. Mechanical FE Simulations in Fire Conditions
- (a)
- limited residual stiffness of charred main logs, and
- (b)
- lack of robust lateral restraints for the same main logs, due to charring of outriggers and vanishing of the bracing system, see Figure 11a.
- (i)
- the high sensitivity of log-house walls to buckling phenomena,
- (ii)
- the predominant role of out-of-plane deformations in the assessment of their actual load-carrying capacity in fire conditions, as well as
- (iii)
- the lack of an appropriate number of experimental control points, to describe and monitor the global deformations of similar specimens (i.e., mid-height measurements only for out-of-plane deformations).
4.3. Parametric Study
5. Conclusions
- The actual EN 1361-1 standard provisions for the assessment of the load-carrying capacity of timber structures in fire conditions do not properly account for the typical behaviour of log-house walls Specific deflection and deformation rate limit values should be provided to assess their fire performance, especially in terms of out-of-plane phenomena.
- A key role is generally played by the corner joint components, where appropriate instrumentation should be used to account for thermal local phenomena, and related mechanical effects. Thermocouples should be placed within the thickness of logs (at least one in the mid thickness), close to the corner joints, and also at different heights of the sample.
- When thermal insulation layers are used, additional thermocouples should be placed also in their thickness (at least one), and at the interface with the timber assembly (possibly, at different heights of the wall).
- Careful consideration should be finally given to the accurate experimental analysis of the sample deformations, where critical displacements could be achieved at the mid-height as well as on the top logs. The recommendation is to monitor the out-of-plane deformations of a given log-house wall at 1/3rd height, mid-height, and top.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- EN 1363-1. Fire Resistance Tests—Part 1: General Requirements; European Committee for Standardization (CEN): Brussels, Belgium, 2012. [Google Scholar]
- Östman, B.; Esko, M.; René, S.; Andrea, F. Fire Safety in Timber Buildings—Technical Guideline for Europe; SP Report 19; RISE—Research Institutes of Sweden: Göteborg, Sweden, 2010. [Google Scholar]
- Suzuki, J.; Mizukami, T.; Naruse, T.; Araki, Y. Fire resistance of timber panel structures under standard fire exposure. Fire Technol. 2016, 52, 1015–1034. [Google Scholar] [CrossRef]
- Mindeguia, J.C.; Cueff, G.; Dréan, G.; Auguin, G. Simulation of charring depth of timber structures when exposed to non-standard fire iso-curves. J. Struct. Fire Eng. 2018, 9, 63–76. [Google Scholar] [CrossRef]
- Schmid, J.; Santomaso, A.; Brandon, D.; Wickstrom, U.; Frangi, A. Timber under real fire conditions—The influence of oxygen content and gas velocity on the charring behavior. J. Struct. Fire Eng. 2017. [Google Scholar] [CrossRef]
- Schnabl, S.; Turk, G.; Planinc, I. Buckling of timber columns exposed to fire. Fire Saf. J. 2011, 46, 431–439. [Google Scholar] [CrossRef]
- Lineham, S.A.; Thomson, D.; Bartlett, A.I.; Bisby, L.A.; Hadden, R.M. Structural response of fire-exposed cross-laminated timber beams under sustained loads. Fire Saf. J. 2016, 85, 23–34. [Google Scholar] [CrossRef]
- Schmid, J.; Klippel, M.; Just, A.; Frangi, A. Review and analysis of fire resistance tests of timber members in bending, tension and compression with respect to the Reduced Cross-Section Method. Fire Saf. J. 2014, 68, 81–99. [Google Scholar] [CrossRef]
- Franzoni, L.; Dhima, D.; Lyon, F.; Laebée, A.; Foret, G. A Stiffness-based Approach to Analyze the Fire Behaviour of Cross-Laminated Timber Floors. Struct. Eng. Int. 2017, 27, 238–245. [Google Scholar] [CrossRef]
- Ekr, J.; Caldova, E.; Vymlatil, P.; Frantisek, W.; Kuklikova, A. Timber steel-fibre-reinforced concrete floor slabs subjected to fire. Eur. J. Wood Wood Prod. 2018, 76, 201–212. [Google Scholar] [CrossRef]
- Frangi, A.; Knobloch, M.; Fontana, M. Fire design of timber-concrete composite slabs with screwed connections. J. Struct. Eng. 2010, 136. [Google Scholar] [CrossRef]
- Yue, K.; Chen, Z.; Lu, W.; Liu, W.; Li, M.; Shao, Y.; Tang, L.; Wan, L. Evaluating the mechanical and fire-resistance properties of modified fast-growing Chinese fir timber with boric-phenol-formaldehyde resin. Constr. Build. Mater. 2017, 154, 956–962. [Google Scholar] [CrossRef]
- Tiso, M.; Just, A. Design criteria for insulation materials applied in timber frame assemblies. J. Struct. Fire Eng. 2017. [Google Scholar] [CrossRef]
- Pásztory, Z.; Mohácsiné, I.R.; Börcsök, Z. Investigation of thermal insulation panels made of black locust tree bark. Constr. Build. Mater. 2017, 147, 733–735. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Q.; Xu, Y.; Wang, B.; Shang, J. A numerical study on the fire endurance of wood beams exposed to three-side fire. Appl. Phys. Eng. 2012, 13, 491–505. [Google Scholar] [CrossRef]
- Thi, V.D.; Khelifa, M.; Oudjene, M.; El Ganaoui, M.; Rogaume, Y. Finite element analysis of heat transfer through timber elements exposed to fire. Eng. Struct. 2017, 143, 11–21. [Google Scholar] [CrossRef]
- Du, H.; Hu, X.; Zhang, B.; Minli, Y. Numerical simulation on behaviour of timber-concrete composite beams in fire. IOP Conf. Ser. Earth Environ. Sci. 2017, 81, 012148. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Li, L.; Xu, Q. Thermo-mechanical behaviour of dovetail timber joints under fire exposure. Fire Saf. J. 2017. [Google Scholar] [CrossRef]
- Menis, A.; Fragiacomo, M.; Clemente, I. Numerical Investigation of the Fire Resistance of Protected Cross-Laminated Timber Floor Panels. Struct. Eng. Int. 2012, 22, 523–532. [Google Scholar] [CrossRef]
- EN 1995-1-1. Eurocode 5—Design of Timber Structures—Part 1-1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization (CEN): Brussels, Belgium, 2004. [Google Scholar]
- EN 1998-1. Eurocode 8—Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; CEN (European Committee for Standardization): Brussels, Belgium, 2004. [Google Scholar]
- EN 1995-1-2. Eurocode 5—Design of Timber Structures—Part 1-2: General—Structural Fire Design; CEN (European Committee for Standardization): Brussels, Belgium, 2004. [Google Scholar]
- Branco, J.; Araújo, J.P. Structural behaviour of log timber walls under lateral in plane loads. Eng. Struct. 2012, 40, 371–382. [Google Scholar] [CrossRef]
- Bedon, C.; Fragiacomo, M.; Amadio, C.; Sadoch, C. Experimental study and numerical investigation of Blockhaus shear walls subjected to in-plane seismic loads. J. Struct. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Piazza, M. Seismic Performance of Multi-Storey Timber Buildings—Rusticasa Building—Final Report, SERIES 227887 Timber Buildings Project. Available online: http://www.series.upatras.gr/dev (accessed on 20 September 2018).
- Bedon, C.; Fragiacomo, M. Numerical investigation of timber log-haus walls with steel dovetail reinforcements under in-plane seismic loads. Adv. Civ. Eng. 2018, 2018, 6929856. [Google Scholar] [CrossRef]
- Sciomenta, M.; Bedon, C.; Fragiacomo, M.; Luongo, A. Shear performance assessment of timber log-house walls under in-plane lateral loads via numerical and analytical modelling. Buildings 2018, 8, 99. [Google Scholar] [CrossRef]
- Bedon, C.; Fragiacomo, M. Derivation of buckling design curves via FE modelling for in-pane compressed timber log-walls in accordance with the Eurocode 5. Eur. J. Wood Wood Prod. 2016. [Google Scholar] [CrossRef]
- Bedon, C.; Fragiacomo, M. Experimental and numerical analysis of in-plane compressed unprotected log-haus timber walls in fire conditions. Fire Saf. J. 2018. [Google Scholar] [CrossRef]
- Simulia. ABAQUS v.6.14 Computer Software; Dassault Systèmes: Providence, RI, USA, 2018. [Google Scholar]
- EN 338. Structural Timber-Strength Classes; European Committee for Standardization (CEN): Brussels, Belgium, 2009. [Google Scholar]
- EN 1365-1. Fire Resistance Tests for Load Bearing Elements—Walls—Part 1: General Requirements; CEN (European Committee for Standardization): Brussels, Belgium, 2012. [Google Scholar]
- Fermacell® Gypsum Fibreboard, Technical Data Sheet. Available online: https://www.fermacell.com/fermacell_gypsum_fibreboard_1236.php (accessed on 20 September 2018).
- EN 13501. Fire Classification of Construction Products and Building Elements—Classification Using Test Data from Reaction to Fire Tests; CEN (European Committee for Standardization): Brussels, Belgium, 2007. [Google Scholar]
- Fahrni, R.; Schmid, J.; Klippel, M.; Frangi, A. Investigation of different designs and installations of temperature measurements in wood as low conductive materials. In Proceedings of the 10th International Conference on Structures in Fire (SIF’18), Belfast, UK, 6–8 June 2018. [Google Scholar]
- EN 1991-1. Eurocode 1—Actions on Structures—Part 1-5: General Actions—Thermal Actions; European Committee for Standardization (CEN): Brussels, Belgium, 2004. [Google Scholar]
- Palma, P. Fire behaviour of timber connections. Ph.D. Thesis No. 24032, ETH Zurich, Zurich, Switzerland, 2016. [Google Scholar] [CrossRef]
- König, J. Structural fire design according to Eurocode 5—Design rules and their background. Fire Mater. 2005, 29, 147–163. [Google Scholar] [CrossRef]
- König, J.; Walleij, L. One-Dimensional Charring of Timber Exposed to Standard and Parametric Fires in Initially Unprotected and Postprotection Situations; Technical Report (No. 9908029); RISE—Research Institutes of Sweden: Göteborg, Sweden, 1999; ISSN ISSN 1102-1071. [Google Scholar]
- Laplanche, K.; Dhima, D.; Racher, P. Predicting the behaviour of dowelled connections in fire: Fire test results and heat transfer modelling. In Proceedings of the 8th World Conference on Timber Engineering—WCTE2004, Lahti, Finland, 14–17 June 2004. [Google Scholar]
- Werther, N.; O’Neill, J.W.; Spellman, P.M.; Abu, A.K.; Moss, P.J.; Buchanan, A.H.; Winter, S. Parametric study of modelling structural timber in fire with different software packages. In Proceedings of the 7th International Conference on Structures in Fire, Zurich, Switzerland, 6–8 June 2012. [Google Scholar]












| Geometry | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test | Log | Outriggers | Main Wall | In-Plane Compression | |||||
| Lorto | D | H | L | L0 | N20 | Ntest | RN | ||
| (mm) | (m) | (m) | (m) | (m) | (m) | (kN/m) | (kN/m) | - | |
| W80 | 80 × 190 (h/b = 2.38) | 0.5 (0.21 symm) | 0.14 | 3 | 3 | 2.64 | 258 | 30 | 0.11 |
| W90 | 90 × 160 (h/b = 1.78) | 0.59 (unsym; 0.1 ext; 0.4 int) | 0.10 | 2.96 | 3 | 2.71 | 349 | 45 | 0.13 |
| Time (min) | Observed Phenomena | Specimen Side |
|---|---|---|
| −15 | Application of the in-plane compressive load (30 kN/m) | - |
| 0 | Fire test started | - |
| 2 | Blackening of timber surface (see Figure 2a) | I |
| 7 | Uniform charring of the timber surface | I |
| 8 | Persistent crackling pops perceived | E |
| 10 | Smoke propagating from corner joints | E |
| 14 | Crackling pops ended | E |
| 28 | Soot precipitation in the vicinity of corner joints | E |
| 32 | Limited visibility within the furnace, minor propagation of smoke and blackening in the region of joints (see Figure 3b) | I/E |
| 40 | Isolated crackling pop | E |
| 41 | Moisture propagates from notches and protrusions of main logs | E |
| 44 | Isolated gas leaks close to joints of main logs, in the upper third of the wall (Figure 3c) | E |
| 55 | Abrupt increase in out-of-plane deformation of the main wall due to buckling | - |
| 57 | Fire test stopped, due to large out-of-plane deformations | - |
| Out-of-Plane/Bending | In-Plane | ||||||
|---|---|---|---|---|---|---|---|
| Displacement (mm) | Displacement Rate (mm/min) | Displacement (mm) | Displacement Rate (mm/min) | ||||
| EN | TEST | EN | TEST | EN | TEST | EN | TEST |
| 205 | 84 | 9 | 10.6 | 30 | 30 | 9 | 4.5 |
| (57 min) | (52 min) | (56 min) | (57 min) | ||||
| Exceeded: NO | Exceeded: YES | Exceeded: YES | Exceeded: NO | ||||
| Failure Time (min) | ||||||
|---|---|---|---|---|---|---|
| FE Model | Numerical Analysis * | EN 1361-1 Regulations (mm) | ||||
| Log-House | Fully Monolithic | Log-House | Fully Monolithic | |||
| M0 | 57.3 | >100 | V & VR | 56.5 | V | 86.2 |
| M1 | 57.8 | >100 | V & VR | 56.8 | V | 88.7 |
| M2 | 58.3 | >100 | n.a. | n.a. | n.a. | n.a. |
| M3 | 21.0 | >100 | n.a. | n.a. | OR | 94.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedon, C.; Fragiacomo, M. Fire Resistance of In-Plane Compressed Log-House Timber Walls with Partial Thermal Insulation. Buildings 2018, 8, 131. https://doi.org/10.3390/buildings8100131
Bedon C, Fragiacomo M. Fire Resistance of In-Plane Compressed Log-House Timber Walls with Partial Thermal Insulation. Buildings. 2018; 8(10):131. https://doi.org/10.3390/buildings8100131
Chicago/Turabian StyleBedon, Chiara, and Massimo Fragiacomo. 2018. "Fire Resistance of In-Plane Compressed Log-House Timber Walls with Partial Thermal Insulation" Buildings 8, no. 10: 131. https://doi.org/10.3390/buildings8100131
APA StyleBedon, C., & Fragiacomo, M. (2018). Fire Resistance of In-Plane Compressed Log-House Timber Walls with Partial Thermal Insulation. Buildings, 8(10), 131. https://doi.org/10.3390/buildings8100131






