Effect of Shear Walls on the Active Vibration Control of Buildings
Abstract
:1. Introduction
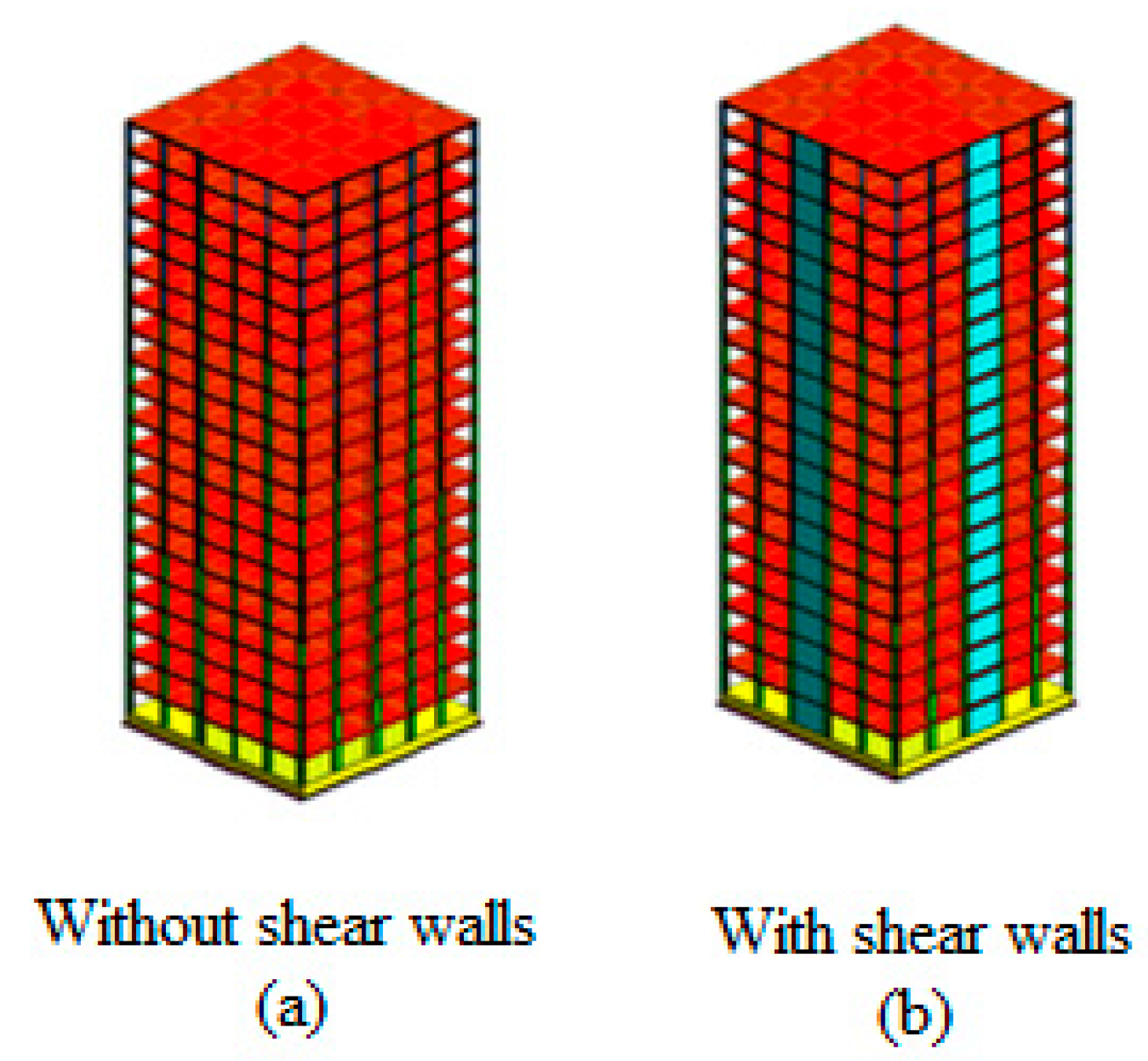
2. Modeling of the Controlled Building
- s is the Laplace variable
- u is the control input.
- is the sensor output, (the sensor is an accelerometer combined to an integrator 1/s)
- −(g/s) is the feedback control law.
3. Numerical Example
4. Results and Discussion
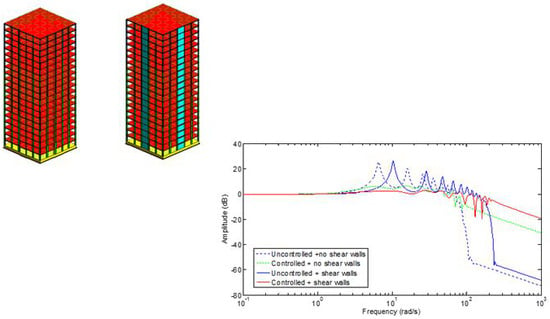
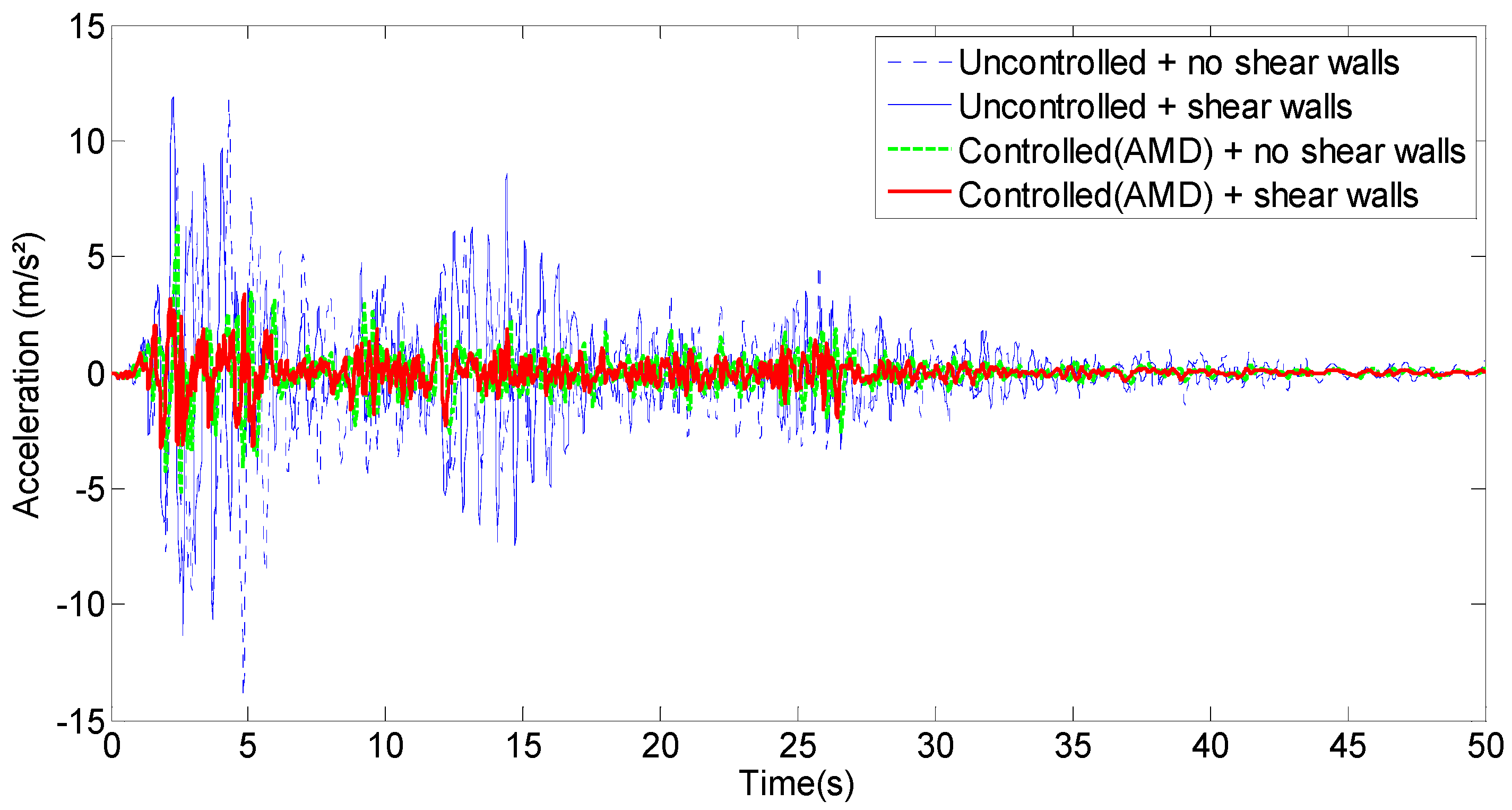
4.1. Effect of Shear Walls on the Building Response before Adding the Active Control
4.2. Comparison between Active Control Cases with and without Shear Walls
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Constantinou, M.C.; Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems for Structural Design and Retrofit; Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 1998. [Google Scholar]
- Fisco, N.R.; Adeli, H. Smart structures: Part I—Active and semi-active control. Sci. Iran. 2011, 18, 275–284. [Google Scholar] [CrossRef]
- Fisco, N.R.; Adeli, H. Smart structures: Part II—Hybrid control systems and control strategies. Sci. Iran. 2011, 18, 285–295. [Google Scholar] [CrossRef]
- Korkmaz, S. A review of active structural control: Challenges for engineering informatics. Comput. Struct. 2011, 89, 2113–2132. [Google Scholar] [CrossRef]
- Ghaedi, K.; Ibrahim, Z.; Adeli, H.; Javanmardi, A. Invited Review: Recent developments in vibration control of building and bridge structures. J. Vibroeng. 2017, 19, 3564–3580. [Google Scholar] [CrossRef]
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; Wiley and Sons Ltd.: Chichester, UK, 1997. [Google Scholar]
- Castaldo, P.; De Iulisiis, M. Optimal integrated seismic design of structural and viscoelastic bracing-damper systems. Earthq. Eng. Struct. Dyn. 2014, 43, 1809–1827. [Google Scholar] [CrossRef]
- Soong, T.T.; Constantinou, M.C. Passive and Active Structural Vibration Control in Civil Engineering; Springer: New York, NY, USA, 1994. [Google Scholar]
- De Iuliis, M.; Castaldo, P. An energy-based approach to the seismic control of one-way asymmetrical structural systems using semi-active devices. Int. J. Earthq. Eng. 2012, 29, 31–42. [Google Scholar]
- Preumont, A.; Seto, K. Active Control of Structures; Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar]
- Yao, J.T.P. Concept of structure control. ASCE J. Struct. Div. 1972, 98, 1567–1574. [Google Scholar]
- Chang, J.C.; Soong, T.T. Structural control using active tuned mass dampers. J. Eng. Mech. Div. 1980, 106, 1091–1098. [Google Scholar]
- Abdel-Rohman, M. Optimal design of active TMD for buildings control. Build. Environ. 1984, 19, 191–195. [Google Scholar] [CrossRef]
- Samali, B.; Yang, J.N.; Yeh, C.T. Control of lateral-torsional motion of wind-excited buildings. J. Eng. Mech. 1985, 111, 777–796. [Google Scholar] [CrossRef]
- Wu, J.C.; Yang, J.N. Active control of transmission tower under stochastic wind. J. Struct. Eng. 1998, 124, 1302–1312. [Google Scholar] [CrossRef]
- Yamada, Y.; Ikawa, N.; Yokoyama, H.; Tachibana, E. Active control of structures using the joining member with negative stiffness. In Proceedings of the First World Conference on Structural Control, Los Angeles, CA, USA, 3–5 August 1994. [Google Scholar]
- Ikeda, Y.; Sasaki, K.; Sakamoto, M.; Kobori, T. Active mass driver system as the first application of active structural control. Earthq. Eng. Struct. Dyn. 2001, 30, 1575–1595. [Google Scholar] [CrossRef]
- Wang, A.P.; Lin, Y.H. Vibration control of a tall building subjected to earthquake excitation. J. Sound Vib. 2007, 299, 757–773. [Google Scholar] [CrossRef]
- Guclu, R.; Yazici, H. Vibration control of a structure with ATMD against earthquake using fuzzy logic controllers. J. Sound Vib. 2008, 318, 36–49. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Xu, G. Fuzzy Control of Seismic Structure with an Active Mass Damper. In Proceedings of the 6th International Conference on Advances in Experimental Structural Engineering, Champaign, IL, USA, 1–2 August 2015. [Google Scholar]
- Tu, J.; Lin, X.; Tu, B.; Xu, J.; Tan, D. Simulation and experimental tests on active mass damper control system based on model reference adaptive control algorithm. J. Sound Vib. 2014, 333, 4826–4842. [Google Scholar] [CrossRef]
- Roffel, A.J.; Narasimhan, S. Extended Kalman filter for modal identification of structures equipped with a pendulum tuned mass damper. J. Sound Vib. 2014, 333, 6038–6056. [Google Scholar] [CrossRef]
- Roffel, A.J.; Narasimhan, S.; Haskett, T. Performance of pendulum tuned mass dampers in reducing the responses of flexible structures. J. Struct. Eng. 2012, 139, 04013019. [Google Scholar] [CrossRef]
- Tuan, A.Y.; Shang, G.Q. Vibration control in a 101-storey building using a tuned mass damper. Tamkang Univ. Sci. Technol. 2014, 17, 141–156. [Google Scholar]
- Han, B.; Li, C. Characteristics of linearly distributed parameter-based multiple-tuned mass dampers. Struct. Control Health Monit. 2008, 15, 839–856. [Google Scholar] [CrossRef]
- Li, C. Performance of multiple tuned mass dampers for attenuating undesirable oscillations of structures under the ground acceleration. Earthq. Eng. Struct. Dyn. 2000, 29, 1405–1421. [Google Scholar] [CrossRef]
- Li, C. Optimum multiple tuned mass dampers for structures under the ground acceleration based on DDMF and ADMF. Earthq. Eng. Struct. Dyn. 2002, 31, 897–919. [Google Scholar] [CrossRef]
- Aly, A.M. Proposed robust tuned mass damper for response mitigation in buildings exposed to multidirectional wind. Struct. Des. Tall Spec. Build. 2014, 23, 664–691. [Google Scholar] [CrossRef]
- Elias, S. Seismic Energy Assessment of Buildings with Tuned Vibration Absorbers. Shock Vib. 2018, 2018, 2051687. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, W.; Zhu, W.; Zheng, R.; Zhao, X. A Tuned Mass Damper with Nonlinear Magnetic Force for Vibration Suppression with Wide Frequency Range of Offshore Platform under Earthquake Loads. Shock Vib. 2018, 2018, 1505061. [Google Scholar] [CrossRef]






| Magnitude | Deaths | Location | Date |
|---|---|---|---|
| 8 | 830.000 | Shansi, China | 23 January 1556 |
| 7.5 | 255.000 | Tangshan, China | 27 July 1976 |
| 9.0 | 225.000 | Off west coast of Northern Sumatra | 26 December 2004 |
| 7.0 | 222.570 | Haiti | 12 January 2010 |
| 7.9 | 200.000 | Near Xining, Tsinghai, China | 22 May 1927 |
| 7.8 | 200.000 | Gansu, China | 16 December 1920 |
| 7.9 | 143.000 | Kwanto, Japan | 1 September 1923 |
| 7.3 | 110.000 | Ashgabat, Turkmenistan, USSR | 5 October 1948 |
| 7.2 | 100.000 | Messina, Italy | 28 December 1908 |
| 7.9 | 87.587 | Eastern Sichuan, China | 12 May 2008 |
| 7.6 | 80.361 | Pakistan | 8 October 2005 |
| 7.6 | 70.000 | Gansu, China | 25 December 1932 |
| 8.7 | 70.000 | Lisbon, Portugal | 1 November 1755 |
| 7.9 | 66.000 | Peru | 31 May 1970 |
| 7.5 | 60.000 | Quetta, Pakistan | 30 May 1935 |
| 7.7 | 50.000 | Iran | 20 June 1990 |
| Floor | Floor Mass for Building without Shear Walls (ton) | Floor Mass for Building with Shear Walls (ton) |
|---|---|---|
| 1 | 643,795 | 662,020 |
| 2 | 643,795 | 662,020 |
| 3 | 637,677 | 655,902 |
| 4 | 637,677 | 655,902 |
| 5 | 632,012 | 650,237 |
| 6 | 632,012 | 650,237 |
| 7 | 626,800 | 645,025 |
| 8 | 626,800 | 645,025 |
| 9 | 622,041 | 640,266 |
| 10 | 622,041 | 640,266 |
| 11 | 617,736 | 635,961 |
| 12 | 617,736 | 635,961 |
| 13 | 613,883 | 632,108 |
| 14 | 613,883 | 632,108 |
| 15 | 610,484 | 628,709 |
| 16 | 610,484 | 628,709 |
| 17 | 607,538 | 625,763 |
| 18 | 607,538 | 625,763 |
| 19 | 605,046 | 623,271 |
| 20 | 605,046 | 623,271 |
| Floor | Floor Stiffness for Building without Shear Walls (KN/m) | Floor Stiffness for Building with Shear Walls (KN/m) |
|---|---|---|
| 1 | 8,036,886 | 14,230,276.8 |
| 2 | 8,036,886 | 14,230,276.8 |
| 3 | 6,929,764 | 13,123,154.8 |
| 4 | 6,929,764 | 13,123,154.8 |
| 5 | 5,904,651 | 12,098,041.8 |
| 6 | 5,904,651 | 12,098,041.8 |
| 7 | 4,961,547 | 11,154,937.9 |
| 8 | 4,961,547 | 11,154,937.9 |
| 9 | 4,100,452 | 10,293,842.9 |
| 10 | 4,100,452 | 10,293,842.9 |
| 11 | 3,321,366 | 9,514,757.07 |
| 12 | 3,321,366 | 9,514,757.07 |
| 13 | 2,624,289 | 8,817,680.24 |
| 14 | 2,624,289 | 8,817,680.24 |
| 15 | 2,009,221 | 8,202,612.44 |
| 16 | 2,009,221 | 8,202,612.44 |
| 17 | 1,476,163 | 7,669,553.69 |
| 18 | 1,476,163 | 7,669,553.69 |
| 19 | 1,025,113 | 7,218,503.97 |
| 20 | 1,025,113 | 7,218,503.97 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Ouni, M.H.; Laissy, M.Y.; Ismaeil, M.; Ben Kahla, N. Effect of Shear Walls on the Active Vibration Control of Buildings. Buildings 2018, 8, 164. https://doi.org/10.3390/buildings8110164
El Ouni MH, Laissy MY, Ismaeil M, Ben Kahla N. Effect of Shear Walls on the Active Vibration Control of Buildings. Buildings. 2018; 8(11):164. https://doi.org/10.3390/buildings8110164
Chicago/Turabian StyleEl Ouni, Mohamed Hechmi, Mohamed Y. Laissy, Mohammed Ismaeil, and Nabil Ben Kahla. 2018. "Effect of Shear Walls on the Active Vibration Control of Buildings" Buildings 8, no. 11: 164. https://doi.org/10.3390/buildings8110164
APA StyleEl Ouni, M. H., Laissy, M. Y., Ismaeil, M., & Ben Kahla, N. (2018). Effect of Shear Walls on the Active Vibration Control of Buildings. Buildings, 8(11), 164. https://doi.org/10.3390/buildings8110164