Abstract
The Benedictine Monastery of São Miguel de Refojos, located in Cabeceiras de Basto (Portugal), is a monumental complex and a distinctive example of the 18th century Portuguese Baroque architecture. This study addresses the state of conservation of the church as well as the evaluation of its structural behavior and seismic performance. An initial inspection and diagnosis campaign revealed that the structure presents low to moderate damage and other non-structural issues generally associated with high levels of moisture and water infiltration. In order to study the structural performance, a three-dimensional (3D) numerical model was prepared based on the finite element method. This model was calibrated with respect to dynamic identification tests and nonlinear static analyses were then performed to evaluate the seismic behavior. Capacity curves, deformations, crack patterns, and failure mechanisms were used to characterize the structural response. Additionally, the safety evaluation for horizontal actions was verified by means of limit analysis. An overall good agreement was found between the results of the pushover and the limit analyses. To conclude, the present work provides a comprehensive evaluation of the state of conservation of the church and verifies the safety condition of the structure for seismic actions.
1. Introduction
The church of São Miguel de Refojos is a monumental building in Baroque-Rococo style and is part of the historical Benedictine Monastery located in Cabeceiras de Basto, Portugal. The monastery was founded in the 12th century by the Benedictine Order and was located in an unpopulated but geographically strategic area []. After some flourishing early years, the building underwent a ruinous period during the 15th century. However, by the end of the following century, the monastery experienced a new economic and architectural recovery with the change of administration [,]. Major works for the renovation and re-organization of the monastic complex started during the last decades of the 17th century []. In fact, the current aspect of the church is the result of the works carried out between 1675 and 1766, when it was renovated in Baroque style [].
The suppression of the Religious Orders in 1834 led to a progressive abandonment of the Monastery and the building started a new period of decay that lasted until the first half of the 20th century []. After that, the building was subjected once more to different restoration and repair works, namely filling of cracks, cleaning of stone surfaces, repainting, application of water drainage collectors, reconstruction of the roof and replacement of tiles. Nowadays, the monastery is used by the municipal authorities of Cabeceiras de Basto and it still maintains religious activities. Moreover, the church and the sacristy of the monastery have been classified as a Public Interest Building since 1933.
The church of São Miguel de Refojos stands as a historical and cultural landmark and possesses an unquestionable artistic and architectural value. However, as for many other historical structures, environmental and accidental actions always entail a major risk that may lead to degradation, severe damage, or even loss. In particular, unreinforced masonry (URM) buildings, such as the church of São Miguel, are vulnerable to the horizontal loads caused by earthquakes [,]. The seismic performance of URM structures is mainly determined by: the material properties of masonry (high-specific mass, low tensile and shear strength, brittle response), the geometrical configuration, the mass and stiffness distribution, and the type and quality of the connections between the different structural components []. In addition, the global response of this type of construction is difficult to characterize since URM structures dissipate energy by the propagation of damage (cracks), which consequently leads to isolated mechanisms and local failure modes [].
In this context, finite element (FE) modelling is a very useful tool for URM cases because it allows for an accurate simulation of the overall structural behavior under different scenarios. Therefore, numerical approaches may be used to assess the safety condition of historical buildings as well as to evaluate the need and efficiency of different retrofitting techniques. In addition, the case study presented in this paper presents a comprehensive methodology (inspection and diagnosis, numerical modelling, structural analyses, and safety assessment) that can be extrapolated and applied to similar constructions.
2. Description of the Church
The church of São Miguel de Refojos is located on the southern side of the monastery. It has a Latin-cross plan (nave, transept, and chancel) and follows a classical east–west orientation (Figure 1). In the plan, the building is about 60 m long and 24 m wide in the transept. At one and the other side of the nave and chancel, adjacent spaces with smaller dimensions are used to accommodate different ecclesiastical functions. The transept has a direct connection with the central cloister on the left side of the church and it also connects with an octagonal plan chapel located outside the main body of the church. The detached position of this volume seems to indicate that it was built in a later period [].
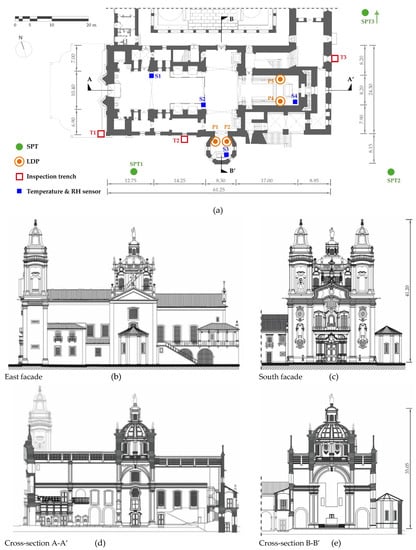
Figure 1.
Architectural definition of the church of São Miguel de Refojos: (a) ground floor plan, (b) longitudinal elevation, (c) front elevation, (d) longitudinal cross-section, (e) transversal cross-section. Dimensions in m.
The front facade has two bell towers with square plan and of about 40 m high. Inside the church, the main entrance is covered by a choir loft supported by a ribbed vault. The crossing is covered by a dome with an oval-shaped plan standing over pendentives. In turn, the body of the dome is made up by a drum, a cupola, and a lantern. The interior height of the church is about 18 m in the nave, 35 m under the dome, and 16 m in the chancel.
The ceilings of the nave, transept, and chancel are made up by barrel vaults. The spaces above the vaults are covered by gable roofs with ceramic tiles finishing, supported by timber trusses oriented in the shortest span. Due to access limitations, only the extrados of the vault and the roof structure of the nave can be inspected.
3. Inspection Works and Diagnosis
A comprehensive inspection and diagnosis campaign were carried out in order to characterize the main structural aspects and evaluate the damage condition and state of conservation of the church. The works included: geometrical and damage survey, monitoring of temperature and relative humidity inside the church, dynamic identification tests, georadar tests, and several geotechnical works.
3.1. Geometrical and Damage Survey
The identification of damage involved a detailed visual inspection of all of the structural elements, both from the outside and the inside of the building. The inspection revealed the presence of structural and non-structural problems. The non-structural damage corresponds to moisture stains, vegetation, fungi, and deterioration of plaster and stone. Additionally, the building shows low to moderate structural damage. There are cracks at the top of the south facade, on the transept walls, on the walls behind the high altar, and on the arch between the crossing and the chancel. The most significant damage appears in the connections between the front facade and the south tower, and in between this tower and the south wall of the nave. Moreover, the open cracks allow for rainwater infiltration with the subsequent deterioration of the internal elements. The floors of the high altar and the octagonal chapel present significant deformations probably caused by consolidation of the soil. Similarly, other deformations in the structure might be associated with a foundation settlement.
3.2. Monitoring of Temperature and Relative Humidity
Air temperature and relative humidity are generally associated with mechanical stresses due to thermal expansion and hygroscopic swelling, opening and closing of cracks, deformations, and other non-structural problems, such as condensation of water vapor on cold surfaces. Temperature, relative humidity, and dew point were monitored for twelve months in four different locations inside the church (Figure 1a). The average values of the temperature and relative humidity measurements is represented in Figure 2.
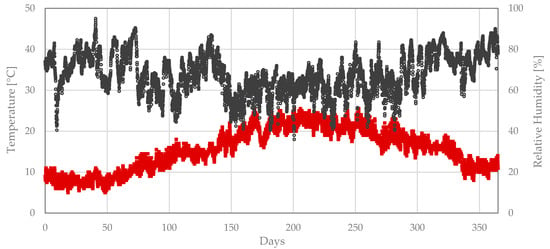
Figure 2.
Average temperature and relative humidity values measured inside the church.
Considering the entire monitoring period for the four locations, the average total, maximum and minimum temperatures are 15 °C, 27 °C, and 4 °C, respectively. On the other hand, the overall average and average maximum and minimum relative humidity values inside the church are equal to 71%, 97%, and 35%, respectively. This represents a yearly average thermal excursion of 23 °C and a yearly average humidity variation equal to 62%. Nevertheless, the daily variation of temperature and relative humidity values inside the church is less significant.
3.3. Dynamic Identification Tests
Dynamic identification tests were carried out in order to estimate the dynamic properties of the church (natural frequencies and mode shapes), which would be used later to validate the numerical model. The accelerations of the structure caused by ambient vibrations (wind, traffic, etc.) were recorded using piezoelectric accelerometers with 10 V/g sensitivity (±0.5 g pk), acquisition boards with 24-bit resolution, and a USB chassis connected to a computer. The acceleration time series were acquired with a sampling frequency equal to 200 Hz. The total duration of the signals was 30 min.
The vibrations were measured at the top of the walls of the nave, dome, and chancel, in both the transversal (X) and longitudinal (Y) directions of the church, for five different configurations (Figure 3). The setups were correlated using a reference accelerometer placed on the balcony of the dome in the transversal direction of the church. The chosen reference point was considered sufficient for the whole set of setups since the transversal direction was expected to be more flexible and therefore more representative than the longitudinal one.
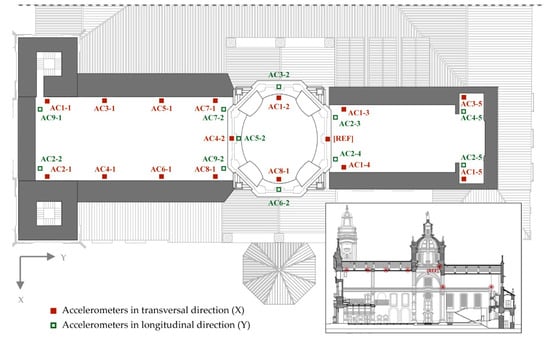
Figure 3.
Location of the accelerometers for the dynamic identification tests.
The signs of the dynamic identification tests were processed in ARTeMIS Modal software [] by using two different methods, namely: (a) Enhanced Frequency Domain Decomposition (EFDD) and (b) Stochastic Subspace Identification based on Unweighted Principal Component (SSI-UPC). Both methods allowed us to estimate six modes, with frequencies ranging from 1.79 Hz to 5.14 Hz. The six estimated modes are associated with local and global modes mainly in the transversal direction, as expected.
The vibration modes obtained by the two aforementioned methods were compared using the MAC (Model Assurance Criterion) []. In a range from 0 to 1, where 1 indicates a perfect match of the mode shapes, the MAC of the first three modes of vibration show values between 0.89 and 0.99, which indicates that the results of the two methods are very close. However, the remaining three modes associated with the higher frequencies present low MAC values, with an average equal to 0.56.
Therefore, only the first three modes are of interest for the scope of this study (Figure 4). The first mode of vibration (1.79 Hz) is associated with a local mode of the nave related to the vibration of the towers in the transversal direction. The second mode (2.75 Hz) is the first global mode, with simple curvature in the transversal direction of the church. Finally, the third vibration mode (3.72 Hz) presents double curvature, corresponding to a global translation of the church in the transversal direction.
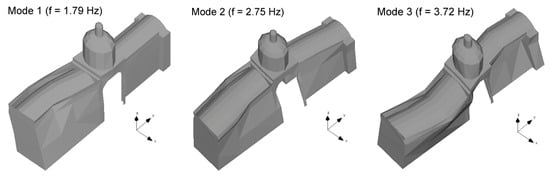
Figure 4.
First three modes of vibration estimated by the Stochastic Subspace Identification based on Unweighted Principal Component (SSI-UPC) method.
3.4. Georadar Tests
Ground Penetrating Radar (GPR) tests were performed in different parts of the monastery using equipment with 500, 800, and 1600 MHz antennas. These tests were aimed at identifying the unseen constructive elements and characterizing the material composition of the structure. The use of Ground Penetrating Radar on historical structures has already been documented by different authors [,].
In some cases, the constitution of the walls is visible at plain sight because there is no rendering layer covering the surface. That is the case of the thinner walls behind the altar, made up by a unique leaf of ashlar masonry. For the rest of the walls, the Ground Penetrating Radar was used to identify the internal composition. Thus, GPR readings were carried out, both in the horizontal and in the vertical direction, in various locations of the walls, namely the main facade, the longitudinal walls of the nave, the walls of the transept, and the walls of the octagonal chapel. In general, the results show that the structure is made up by composite walls with three masonry leaves (Figure 5): an outer layer of irregular stone blocks, a similar internal layer, and a rubble core.

Figure 5.
Horizontal georadar reading on the south wall of the nave: (a) inner surface of the interior leaf at 35–40 cm depth; (b) inner surface of the interior leaf at 55 cm depth (irregular inner surface); (c) opposite side (inner surface of the exterior leaf) at 1.20–1.25 m depth.
In addition, georadar readings were used to identify the constitution of the barrel vault of the nave. The radargrams showed that the total thickness of the vault is about 16 cm. Furthermore, the readings next to the springing line showed an irregular infill, which was characterized as a mixture of gravel and waste.
3.5. Geotechnical Survey
The geotechnical prospection plan consisted of three Standard Penetration Tests (SPT) outside the church and four Light Dynamic Penetrometer tests (LDP) inside the church, as well as several inspection trenches at the base of the walls and water table measurements, see Figure 1a. The purpose of the geotechnical prospection was manifold: characterization of the soil profile and its mechanical properties, evaluation of the type of foundation and identification of the foundation level, verification of the existence of a draining system, and detection of the water table depth.
The trenches and boreholes of the drilling tests showed that the water table is very close to the ground level of the church (summer period), less than 1.00 m depth in some cases (Figure 6). The shallow water level made it impossible to identify the actual depth of the foundations under the walls. Nonetheless, the geotechnical survey allowed us to identify the geological profile. The superficial layer is constituted by soft clay, with low resistance and very deformable, until a depth of about 4.00 m. The following layer corresponds to a transition layer of gravelly sand. Finally, the last layer of the soil consists of highly altered and fractured rock (starting at depths between 4.20 to 5.50 m).

Figure 6.
Water table visible in the inspection trenches days after the excavation (summer period). (a) Excavation 1: water level at −0.93 m below the nave floor; (b) Excavation 3: water table at −1.10 m measured from the floor of the nave.
The existence of a surface layer with poor geotechnical characteristics might be the cause of the settlements detected on the church pavements. Some of the observed structural damages could also be the result of localized foundation settlements.
4. Preparation and Calibration of the Numerical Model
The numerical Finite Element (FE) model of the church was prepared using the structural analysis software DIANA (DIsplacement ANAlyser) [].
4.1. Geometry
The geometry of the three-dimensional (3D) model included all major structural elements, namely the main volume of the church plus the annexed lateral bodies (Figure 7). The stiffness of the structural elements of the monastery adjacent to the church (orthogonal walls and columns of the cloister) was considered in the model by means of spring elements. Since it was not possible to inspect the roofs of the transept and the chancel, the truss elements in these areas were idealized according to the known roof structure above the nave.
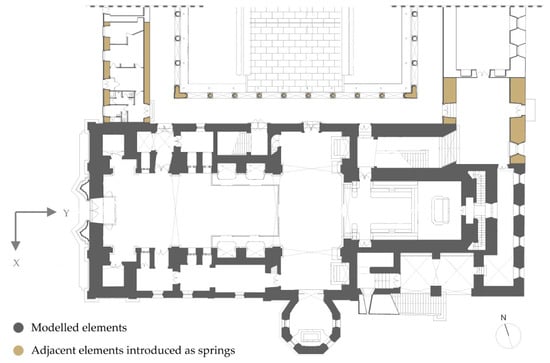
Figure 7.
Plan view with the geometry considered for the numerical model.
4.2. Type of Elements
Different elements were used to define the mesh: four-node tetrahedron solid elements (walls, arches and columns), three-node curved shell elements (vaults), three-node three-dimensional class-III beam elements (roof trusses), and spring elements (stiffness of adjacent buildings). For later nonlinear analyses, in addition, the number of integration points across the thickness of the shell elements was increased (five integration points).
4.3. Boundary Conditions
An overall base level located at −2.00 m below the nave floor was assumed for all of the walls. At that level, the foundation was considered rigid. Thus, all degrees of freedom of the nodes at the base of the masonry walls were constrained. In addition, as already mentioned, spring elements were introduced to simulate the stiffness of the adjacent structures of the monastery.
4.4. Loads
Besides the self-weight of the modelled structural elements, which is automatically calculated by the software, the weight of the roof and the infill material of the vaults was additionally applied. The weight of the roof was assumed equal to 1.00 kN/m2 and it was applied as a uniformly distributed load along the trusses. The infill material was considered up to half the height of the vaults [] and its weight was estimated equal to 12 kN/m3. The infill was modelled as a distributed superficial load applied to the extrados of the vaults, near the supports.
4.5. Material Properties
As it was mentioned before, the visual inspection and georadar tests allowed us to identify the different types of materials that compose the structure of the church, namely brick masonry (BRM–vaults), ashlar masonry (GRM–walls behind the high altar, arches in the crossing, top part of the towers, and dome), three-leaf stone masonry (STM–main walls and rest of masonry elements), granite units (lintels), and timber (roof truss structure). Figure 8 shows the material configuration considered in the model.
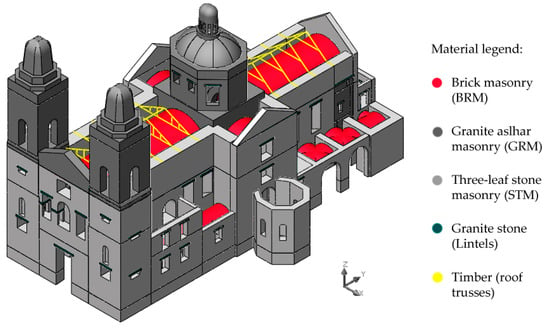
Figure 8.
Geometry of the numerical model with identification of materials.
In the first stage, the material properties were defined according to sets of data and recommendations available in specialized literature. In particular, the prescriptions of the Italian code [,] were used to determine the elastic properties of the masonry materials: average density, elastic modulus, and Poisson’s ratio calculated from the range of values proposed for each type of masonry. Similarly, the characteristics of granite and timber elements were defined as the mean value of the material properties provided by specialized studies [,].
The initial linear-elastic properties were subsequently updated during the calibration process of the numerical model. This numerical validation was done with respect to the experimental dynamic properties estimated from the dynamic identification tests, namely the frequencies of the first three modes of vibration. The calibration was performed following the Douglas-Reid method [], which involves an optimization process to minimize the difference between the experimental and numerical responses. In particular, the elastic moduli of the three masonry materials (BRM, GRM, and STM) were used as the variables to calibrate. The upper and lower limits for the variables were defined in accordance with the aforementioned Italian code, assuming the highest and lowest values of the range proposed for each masonry material.
After the optimization process, the numerical model was able to simulate the first three experimental modes of the church with an average error of the frequency values less than 2%. Moreover, the mode shapes of the numerical model were compared with the modal configurations of the experimental modes through MAC (Modal Assurance Criterion) values []. From 0 to 1, where 1 indicates a perfect match, the calibrated model of the church resulted in an average MAC value equal to 0.92. The numerical model was thus successfully validated, and it was possible to use the updated material properties for further analyses.
Using the updated linear-elastic parameters, the necessary nonlinear properties were estimated following relations established in literature or adopting values coming from similar case studies. In particular, the nonlinear behavior of the masonry materials (BRM, GRM, and STM) was described using the Total Strain Rotating Crack model, which corresponds to a smeared crack model based on the principal strains [].
An exponential function was considered for the tensile softening and a parabolic curve was assumed for compression (Figure 9). In this material model, the shear behavior is updated according to the damage which occurred during the analysis. The compressive strength () was determined as a function of the modulus of elasticity (E), where []. In turn, the compression fracture energy was determined as a function of the compressive strength and the ductility index (), where and 1.6 mm []. The tensile strength and tensile fracture energy of masonry were considered equal to 0.15 MPa and 50 N/m, respectively [].
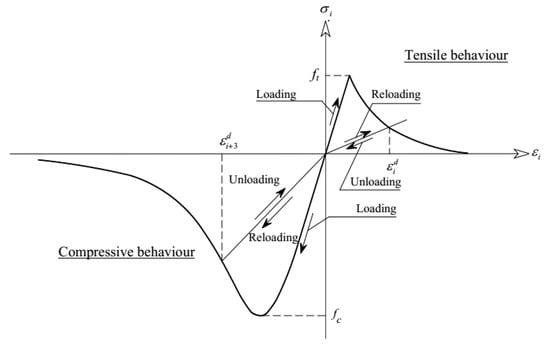
Figure 9.
Nonlinear behavior of the masonry materials in the numerical model: Total Strain Rotating Crack model [].
Table 1 presents the updated linear and nonlinear properties of the materials used in the model. It must be noted that the granite and timber elements were assumed to work always within their linear-elastic range. Finally, the crack bandwidth value (h) was automatically calculated by the software according to the type of element, namely and for shell and solid elements respectively, where and stand for the area and volume of the element.

Table 1.
Linear-elastic and nonlinear properties of materials.
5. Seismic Behavior Evaluation
5.1. Nonlinear Static Analysis
The structural performance of the church for the seismic action was initially verified using nonlinear static or pushover analysis. The use of pushover analysis for the seismic assessment of historical masonry structures has been proven to be a suitable approach and is fairly documented in the literature [,,]. In the current study, the nonlinear static analyses were carried out using a uniform unidirectional load pattern based on horizontal forces proportional to the mass of the structure at all elevations [].
This type of analysis allows for the evaluation of the nonlinear behavior by applying the action in successive load steps. The equilibrium of the system of equations for each step is guaranteed by an iterative method and a convergence criterion. In this case, the regular Newton–Raphson iterative method and an energy-based convergence criterion (10−3) were used. In addition, the Line Search algorithm and arc-length method were used as well to improve the convergence and obtain the post-peak response.
The seismic performance of the building was evaluated according to the global horizontal axes, X and Y, which correspond to the transversal and longitudinal directions of the church, respectively. The results of the pushover analyses are shown in Figure 10 in terms of capacity curves (displacement against base shear factor), using the point at the top of the south tower as a control node to plot the displacements. The base shear factor corresponds to the ratio between the sum of the horizontal forces and the total self-weight of the structure. It should be noted that the analysis in the negative transversal direction (–XX) was neglected due to the presence of the adjacent buildings introduced in the model as spring elements, which can provide a larger capacity in that direction.
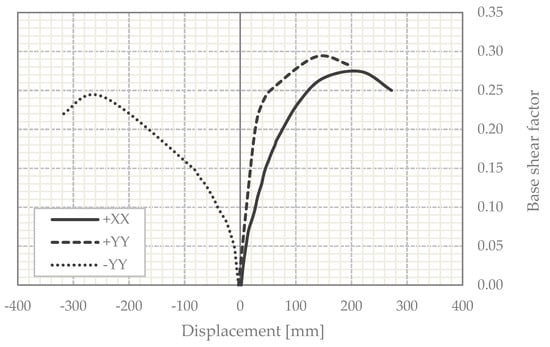
Figure 10.
Capacity curves for nonlinear static analyses. Control point at the top of the south tower. The base shear factor corresponds to the ratio between the sum of the horizontal forces and the total self-weight of the structure [dimensionless].
5.1.1. Positive Transversal Direction (+XX)
The seismic analysis in the positive transversal direction (+XX) indicates that the maximum horizontal capacity is equal to 0.28 g (Figure 10). The horizontal maximum displacement occurs at the top of the south tower. The damage pattern is characterized by shear cracks in the plane of the walls and cracks in the connections between structural elements (Figure 11). The most severe damage occurs in the main facade (diagonal cracks) and in the connections of the south tower with the orthogonal walls.
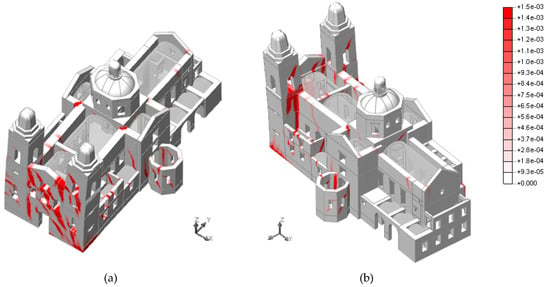
Figure 11.
Crack width associated with the maximum principal strain at the end of the capacity curve for the pushover analysis in the positive transversal direction (+XX). (a) South-West view; (b) South-East view. Units in m.
5.1.2. Positive Longitudinal Direction (+YY)
The curve for the positive longitudinal direction shows a stiffer response, with a maximum capacity equal to 0.29 g (Figure 10). The maximum displacement occurs at the top of the towers. In fact, the main failure involves the local collapse of the belfries (Figure 12). In addition, there is also damage in the connections between the rear facade and the longitudinal walls of the chancel.
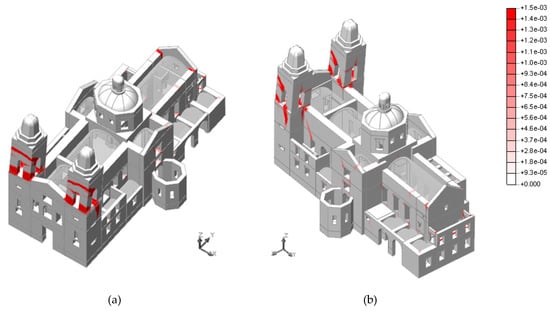
Figure 12.
Crack width associated with the maximum principal strain at the end of the capacity curve for the pushover analysis in the positive longitudinal direction (+YY). (a) South-West view; (b) South-East view. Units in m.
5.1.3. Negative Longitudinal Direction (−YY)
The pushover analysis in the negative longitudinal direction (−YY) presents a maximum base shear factor equal to 0.24 (Figure 10). This value represents the lowest capacity obtained from the different pushover analyses and therefore indicates the most vulnerable direction of the church. This response is associated with a significant deformation of the main facade and the towers in the out-of-plane direction (Figure 13). The damage pattern is characterized by cracks in the connections between the towers and the longitudinal walls of the nave as well as vertical cracks in the main facade.
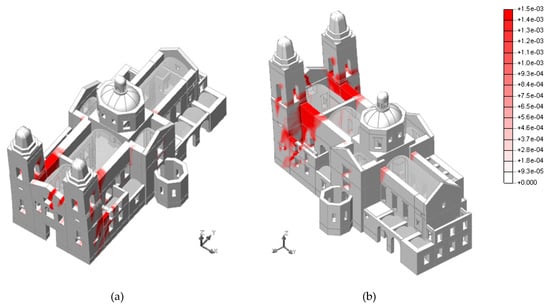
Figure 13.
Crack width associated with the maximum principal strain at the end of the capacity curve for the pushover analysis in the negative longitudinal direction (−YY). (a) South-West view; (b) South-East view. Units in m.
5.2. Safety Assessment
The verification of the structural safety for the seismic action was carried out according to the Portuguese National Annex of Eurocode 8 []. The verification must be done for each type of seismic action, i.e., Type 1 (far field) and Type 2 (near field), in both principal (longitudinal and transversal) directions of the structure.
According to the Portuguese seismic zonation, the reference acceleration values () for Cabeceiras de Basto are 0.05 g and 0.08 g for earthquakes Type 1 and Type 2, respectively. Moreover, the soil coefficient () is assumed equal to 1.0 (deep foundation on rock or other rock-like geological formation, including at most 5 m of weaker material at the surface) and the damping correction coefficient () is equal to 1.00 (5% damping).
The capacity required in terms of horizontal acceleration is determined as a function of , assuming collapse mechanisms based on macroblocks and defined taking into account the damage obtained from the numerical analyses. As presented in Table 2, the results of the pushover analyses for the seismic action indicate that the church meets the required criteria for both types of earthquake. The lowest capacity of the church occurs for the seismic action in the negative longitudinal direction (0.24 g) and is associated with a safety factor equal to 3.00. The safety factor for the seismic action is given by the relation between the base shear factor and the required capacity determined for the zone and defined in the Portuguese National Annex of Eurocode 8 (see Table 2).

Table 2.
Safety verification for seismic action by means of nonlinear static analysis.
5.3. Limit Analysis
In order to validate the seismic performance of the church, the limit analysis based on the kinematic approach was also carried out. For the limit analysis, seven local collapse mechanisms were proposed taking into account the damage patterns caused in churches by past earthquakes [], as well as the results from the pushover analyses and the existing damage in the structure. The stability for each mechanism was verified according to the methodology defined in the Italian code NTC-08 [,], in which the following criteria should be evaluated for the Ultimate Limit State:
- (a)
- Verification A – Mechanisms involving part of the structure in contact with the soil:
- (b)
- Verification B – Mechanisms involving part of the structure above the ground level:
In the previous equations, corresponds to the spectral acceleration for activation of the mechanism, and is the behavior coefficient (2.00). Additionally, in Equation (1), represents the peak ground acceleration (PGA) according to the seismic zonation (0.05 g and 0.08 g for earthquake Type 1 and Type 2, respectively) amplified by the coefficient of importance (1.00), and is the soil coefficient (1.0). For the second verification, is the spectral acceleration associated with the period (first mode of vibration of the structure in the considered direction), is the ratio between the height of the hinge at the base of the collapse block divided by the total height, and is an amplification factor that takes into account the number of floors ().
The spectral acceleration for activation of the mechanism is determined by:
where is the acceleration of gravity (9.81 m/s2), is the load factor that activates the mechanism (determined by the Principle of Virtual Works for the equilibrium between the overturning moment caused by the horizontal forces and the stabilizing moment caused by the vertical forces), is the confidence factor associated to the level of knowledge of the structure (1.00 for = 3), and corresponds to the mass participation factor of the mechanism,
where is the mass participation of the mechanism defined as:
where is the vertical force of the self-weight and is the horizontal virtual displacement of the center of gravity of the macroblock .
In the studied cases, the masonry materials were assumed to have infinite compressive strength and tensile strength equal to zero. The following collapse mechanisms were considered (Figure 14):
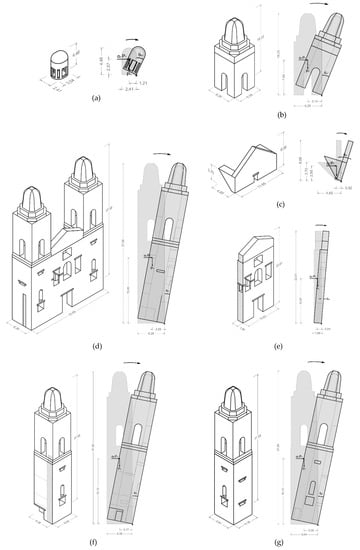
Figure 14.
Collapse mechanisms considered for limit analysis: (a) Mechanism 1, (b) Mechanism 2, (c) Mechanism 3, (d) Mechanism 4, (e) Mechanism 5, (f) Mechanism 6, (g) Mechanism 7. Units in m.
- Mechanism 1: Overturning of the lantern with rotation at the base (Figure 14a);
- Mechanism 2: Overturning of the belfry with rotation at the base (Figure 14b);
- Mechanism 3: Overturning of the gable of the rear facade (high altar) with rotation at the base and diagonal wedges from the lateral walls of the chancel (Figure 14c);
- Mechanism 4: Overturning of the main facade and towers with rotation at the base (Figure 14d);
- Mechanism 5: Overturning of the main facade with rotation at the base (Figure 14e);
- Mechanism 6: Overturning of the south tower with rotation at the base in the direction perpendicular to the facade (Figure 14f);
- Mechanism 7: Overturning of the south tower with rotation at the base in the direction parallel to the facade (Figure 14g).
It must be noted that these collapse mechanisms were defined based on expert opinions and typical failures caused by earthquakes, which can be different from the failure modes obtained from the pushover analysis. The results of the limit analysis for the seismic action are shown in Table 3. The maximum capacity of the considered mechanisms varies between 0.09 g and 0.53 g. The lowest capacity corresponds to the partial mechanism of the facade with vertical cracks in the connections with the towers (Mechanism 5). This is an extremely conservative case and implies a very poor connection between the longitudinal and transversal walls. There is no current damage or reasonable suspicion that indicates a poor-quality connection between these walls.

Table 3.
Safety verification for seismic action by means of limit analysis.
Mechanism 2 (collapse of the belfry) results in a maximum capacity equal to 0.48 g, which is significantly higher than the capacity obtained from the pushover analysis in the positive longitudinal direction (0.29 g). However, it must be noted that the collapse obtained from the pushover analysis involves diagonal cracks in the columns of the belfry (Figure 12), which differs from the mechanism proposed for the limit analysis (horizontal cracks at the base of the belfry).
Mechanism 4 (overturning of facade and towers) corresponds to a failure mode also observed in the pushover analysis (Figure 13). In this case, the maximum capacity obtained from both approaches is the same (0.24 g). Additionally, Mechanism 6 (overturning of the tower in the direction parallel to the facade) results in a maximum capacity (0.25 g) similar to the one obtained by means of the nonlinear static analysis in the positive transversal direction (0.28 g). The lower value of the limit analysis could be explained by the differences between the failure mechanisms defined for one and the other methods.
Finally, the limit analysis proves that the collapse mechanisms considered in this study comply with the stability criteria for seismic actions defined in the Italian code NTC-08 (Table 3), with a minimum safety factor of 2.30. Overall, the limit analysis results in capacity values equivalent to those obtained by means of the nonlinear static analysis, despite some differences in the damage patterns associated with the mechanisms.
6. Conclusions
A 3D FEM model was prepared and validated in order to evaluate the performance and structural stability of the church of São Miguel de Refojos (Portugal). The seismic behavior was assessed by means of nonlinear static analysis as well as limit analysis. Moreover, the safety condition of the structure was verified according to the prescribed criteria established in national and international structural codes.
In the first stage, the inspection and diagnosis campaign allowed us to identify and characterize the main structural aspects necessary to evaluate the state of conservation of the building and generate the numerical model. From these works, it was concluded that the current structural condition and the overall state of conservation are good. Then, the model was calibrated with respect to the dynamic properties estimated from the dynamic identification tests. Subsequently, the numerical and kinematic analyses allowed us to conclude that the church meets the safety requirements prescribed for the seismic action. The results showed that the negative longitudinal direction (−YY) is the most vulnerable one and is associated with the overturning mechanism of the main facade and towers with rotation at the base (out-of-plane collapse). Nonetheless, this mechanism has a safety factor equal to 3.00.
Taking into account the assumptions and results of this study, the safety condition of the structure is guaranteed. However, a set of preventive measures should be put into practice in order to guarantee a more efficient structural behavior and the necessary works for the conservation of the building, namely the filling of existing cracks, repair of deformed floors, and development and application of a monitoring plan including the revealing aspects for the structural condition, such as regular visual inspection.
Author Contributions
Investigation, R.R., N.M. and P.B.L.; Validation, N.M. and P.B.L.; Writing – original draft, R.R. and P.B.L.; Writing – review & editing, R.R. & N.M.
Funding
This research received no external funding.
Acknowledgments
The authors would like to acknowledge the contribution of the Municipality of Cabeceiras de Basto and the Regional Northern Culture Directorate of Portugal for the data that they provided and their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lemos, C.; Queiroga, F.; Vitorino, A.; Melo, L. Remodeling of the Cloister of the Monastery of S. Miguel de Refojos, Cabeceiras de Basto; Final Report of Archaeological Works; Perennia Monumenta: Oporto, Portugal, 2013. (In Portuguese) [Google Scholar]
- Sequeira, M. The Church of the Monastery of São Miguel de Refojos in Cabeceiras de Basto. In Studies in honor of Professor José Amadeu Coelho Dias; Faculdade de Letras da Universidade do Porto (FLUP): Porto, Portugal, 2006; Volume 2, pp. 223–232. (In Portuguese) [Google Scholar]
- Pereira, J.F. Baroque Architecture in Portugal; Portuguese Culture and Language Institute (Ministry of Education): Lisbon, Portugal, 1992. (In Portuguese) [Google Scholar]
- PAUTA. Study of the Edification of the Church and Sacristy of the Convent of Refojos; Municipality of Cabeceiras de Basto: Cabeceiras de Basto, Portugal, 2000. (In Portuguese)
- DGPC. Church and Sacristy of the Monastery of Refojos, as well as the Ceiling of One of the Rooms of the Old Monastery of Benedictine Friars; General Directorate of Cultural Heritage: Lisbon, Portugal, 2015. (In Portuguese) [Google Scholar]
- Castellazzi, G.; Gentilini, C.; Nobile, L. Seismic vulnerability assessment of a historical church: Limit analysis and nonlinear Finite Element Analysis. Adv. Civ. Eng. 2013, 1, 1–12. [Google Scholar] [CrossRef]
- Milani, G. Lesson learned after the Emilia-Romagna, Italy, 20–29 May 2012 earthquakes: A limit analysis insight on three masonry churches. Eng. Fail. Anal. 2013, 34, 761–778. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Mendes, N.; Ramos, L.F.; Oliveira, D.V. Analysis of masonry structures without box behavior. Int. J. Archit. Herit. 2011, 5, 369–382. [Google Scholar] [CrossRef]
- Angelillo, M.; Lourenço, P.B.; Milani, G. Masonry Behaviour and Modelling. In Mechanics of Masonry Structures; Angelillo, M., Ed.; Springer: Milan, Italy, 2014; Volume 551, pp. 1–26. [Google Scholar]
- ARTeMIS. Modal Users’ Manual; SVS–Structural Vibration Solutions: Aalborg East, Denmark, 2014. [Google Scholar]
- Ewins, D. Modal Testing: Theory, Practice and Application, 2nd ed.; Research Studies Press LTD: Baldock-Hertfordshire, UK, 2000. [Google Scholar]
- Fernandes, F. Evaluation of Two Novel NDT Techniques: Microdrilling of Clay Bricks and Ground Penetrating Radar in Masonry. Ph.D. Thesis, University of Minho, Braga, Portugal, 2006. [Google Scholar]
- Johnston, B.; Ruffell, A.; McKinley, J.; Warke, P. Detecting voids within a historical building façade: A comparative study of three high frequency GPR antenna. J. Cult. Herit. 2018, 32, 117–123. [Google Scholar] [CrossRef]
- DIANA FEA BV. DIsplacement Method ANAlyser, Release 10; DIANA FEA BV: Delft, The Netherlands, 2017. [Google Scholar]
- Gaetani, A. Seismic Performance of Masonry cross Vaults: Learning from Historical Developments and Experimental Testing. Ph.D. Thesis, University of Minho, Braga, Portugal, 2016. [Google Scholar]
- NTC-08 Guidelines. Technical Standards for Constructions; Official Journal of the Italian Republic: Rome, Italy, 2008. (In Italian) [Google Scholar]
- IMIT. Circ. 02.02.2009, n. 617: Instructions for the Application of the New Technical Standards for Construction Referred to in the Ministerial Decree of 14 January 2008; Italian Ministry of Infrastructures and Transportation: Rome, Italy, 2009. (In Italian)
- Vasconcelos, G. Experimental Investigations on the Mechanics of Stone Masonry: Characterization of Granites and Behavior of Ancient Masonry Shear Walls. Ph.D. Thesis, University of Minho, Braga, Portugal, 2005. [Google Scholar]
- Poletti, E. Characterization of the Seismic Behaviour of Traditional Timber Frame Walls. Ph.D. Thesis, University of Minho, Braga, Portugal, 2013. [Google Scholar]
- Douglas, B.M.; Reid, W.H. Dynamic tests and system identification of bridges. J. Struct. Div. 1982, 108, 2295–2312. [Google Scholar]
- Tomazevic, M. Earthquake-Resistant and Design of Masonry Buildings; Imperial College Press: London, UK, 1999. [Google Scholar]
- CEB-FIB. Material Properties. In CEB-FIP MODEL CODE 1990; T. Telford: London, UK, 1993; pp. 33–81. [Google Scholar]
- Lourenço, P.B. Recent advances in masonry modelling: Micromodelling and Homogenisation. In Multiscale Modeling in Solid Mechanics: Computational Approaches; Galvanetto, U., Ferri Aliabadi, M.H., Eds.; Imperial College Press: London, UK, 2009; Volume 3, pp. 251–294. [Google Scholar]
- Mendes, N. Seismic Assessment of Ancient Masonry Buildings: Shaking Table Tests and Numerical Analysis. Ph.D. Thesis, University of Minho, Braga, Portugal, 2012. [Google Scholar]
- Peña, F.; Lourenço, P.B.; Mendes, N.; Oliveira, D.V. Numerical models for the seismic assessment of an old masonry tower. Eng. Struct. 2010, 32, 1466–1478. [Google Scholar] [CrossRef]
- O’Hearne, N.; Mendes, N.; Lourenço, P.B. Seismic analysis of the San Sebastian Basilica (Philippines). In Proceedings of the 40th IABSE Symposium: Tomorrow’s Megastructures, Nantes, France, 19–21 September 2018. [Google Scholar]
- EN 1998-1. Eurocode 8: Design of Structures for Earthquake Resistance—General Rules, Seismic Actions and Rules for Building; European Commitee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- NIKER. Inventory of Earthquake-Induced Failure Mechanisms Related to Construction Types, Structural Elements, and Materials; POLIMI, D 3.1; Politecnico di Milano: Milan, Italy, 2010. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).