Real-Time Anti-Saturation Flow Optimization Algorithm of the Redundant Hydraulic Manipulator
Abstract
:1. Introduction
2. Model of Hydraulic Manipulator
2.1. Forward Kinematics Model
2.2. Hydraulic Cylinder Driving Model
3. Anti-Saturation Flow Optimization Algorithm
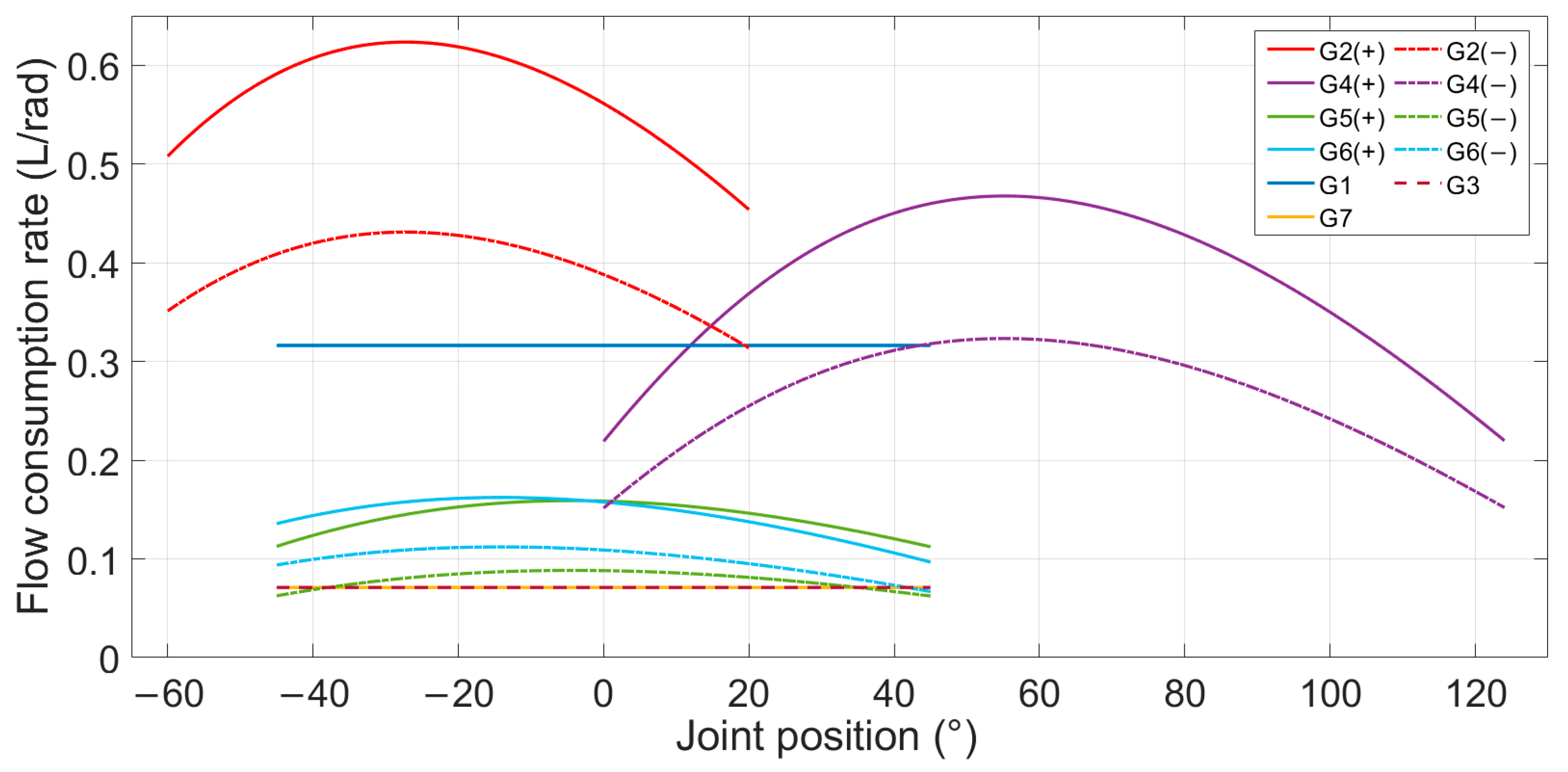
3.1. Inverse Kinematics and Flow Analysis
3.2. Anti-Flow Saturation Algorithm
3.3. Anti-Saturation Flow Optimization Algorithm
4. Experimental Verification
4.1. Introduction of the Experimental Platform
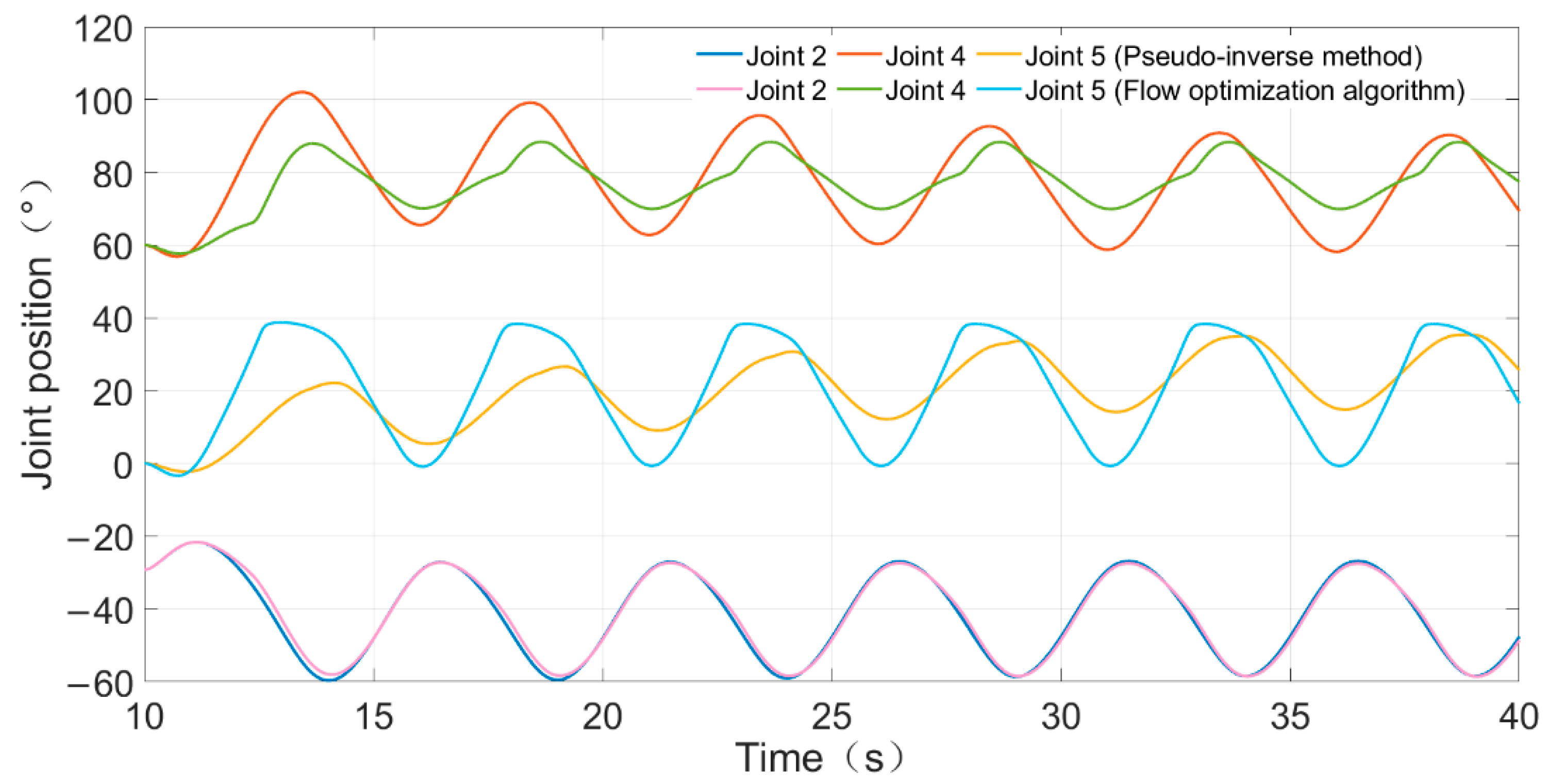
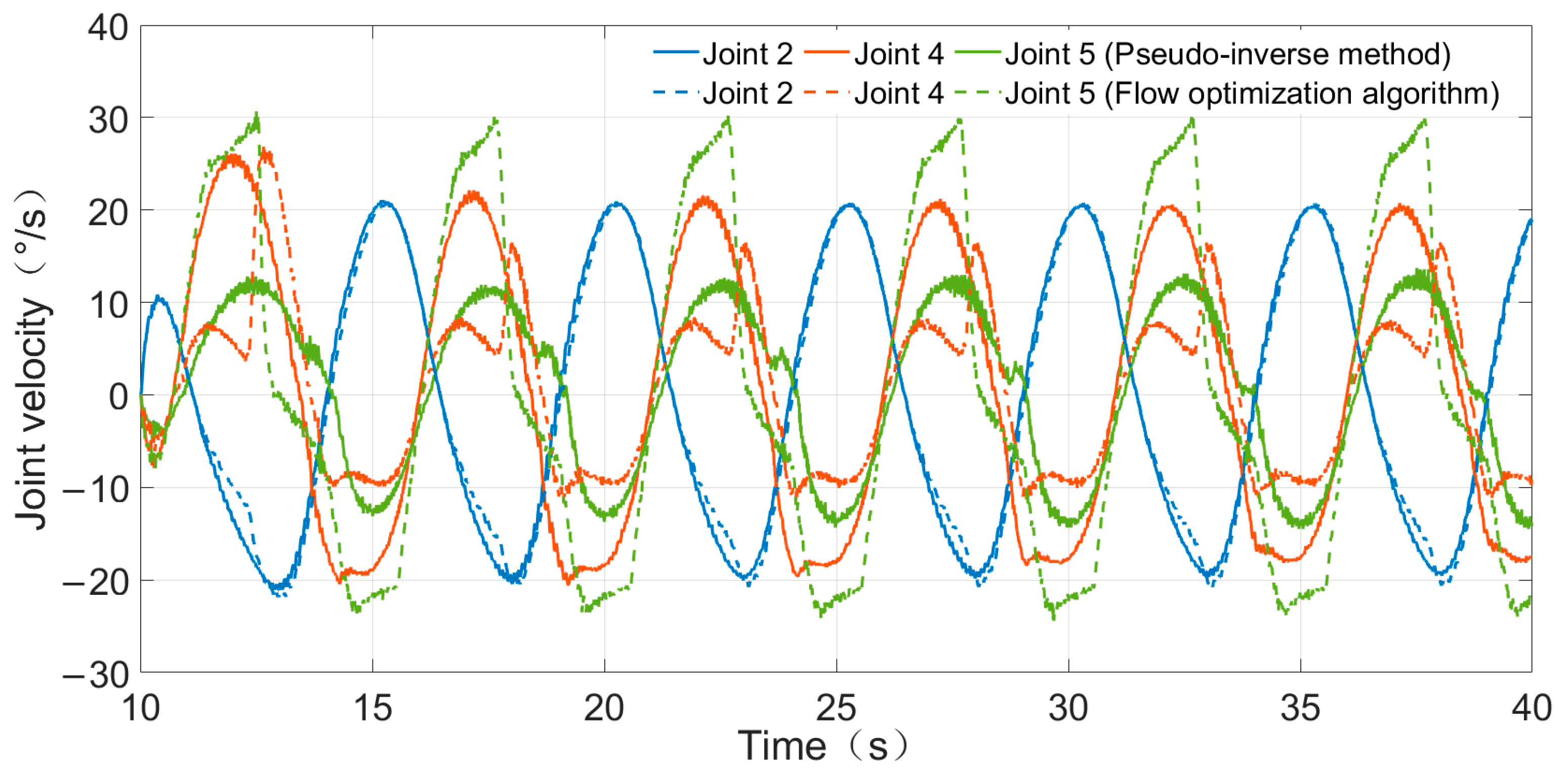
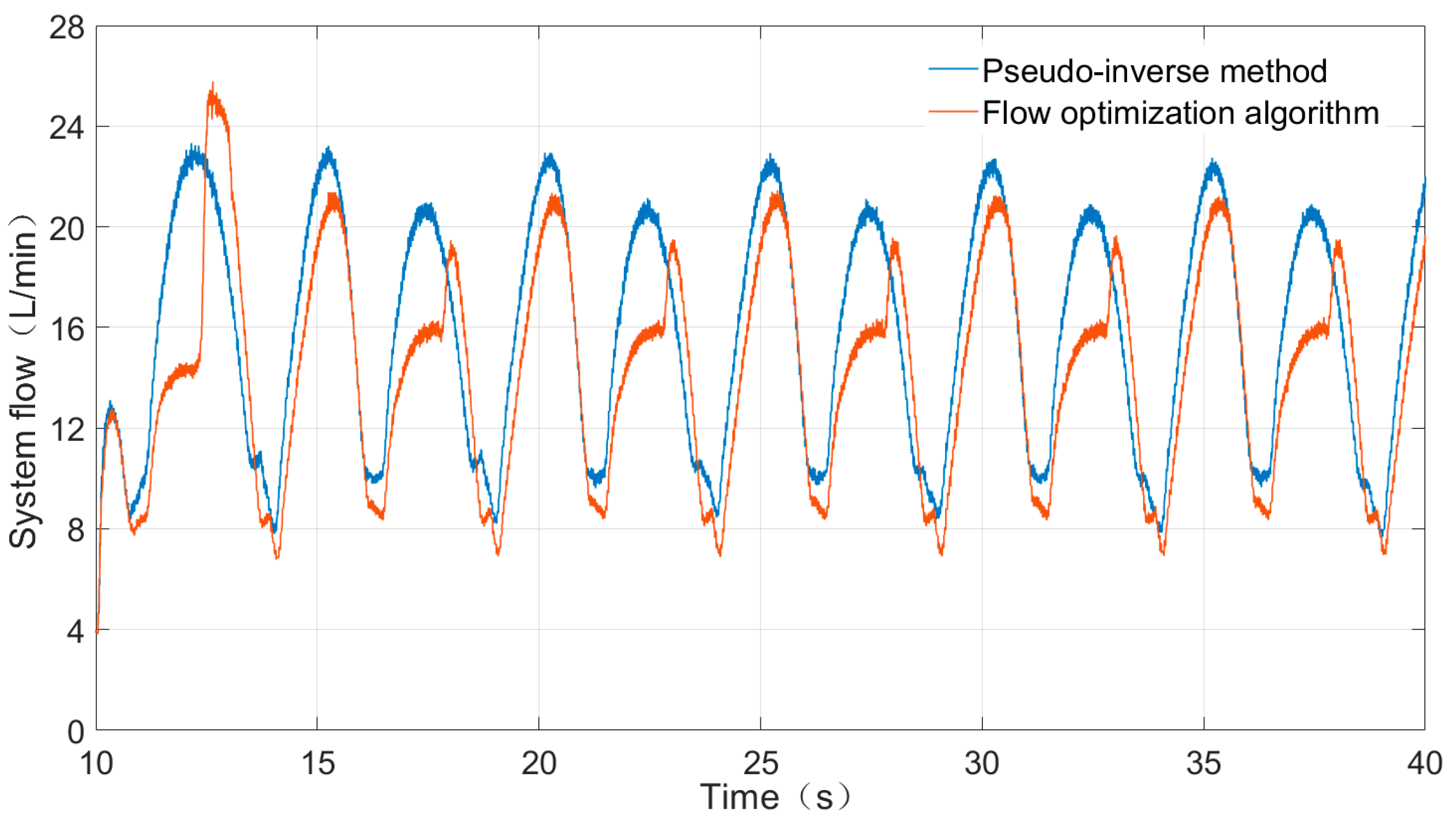
4.2. Experiment for the Flow Optimization Algorithm
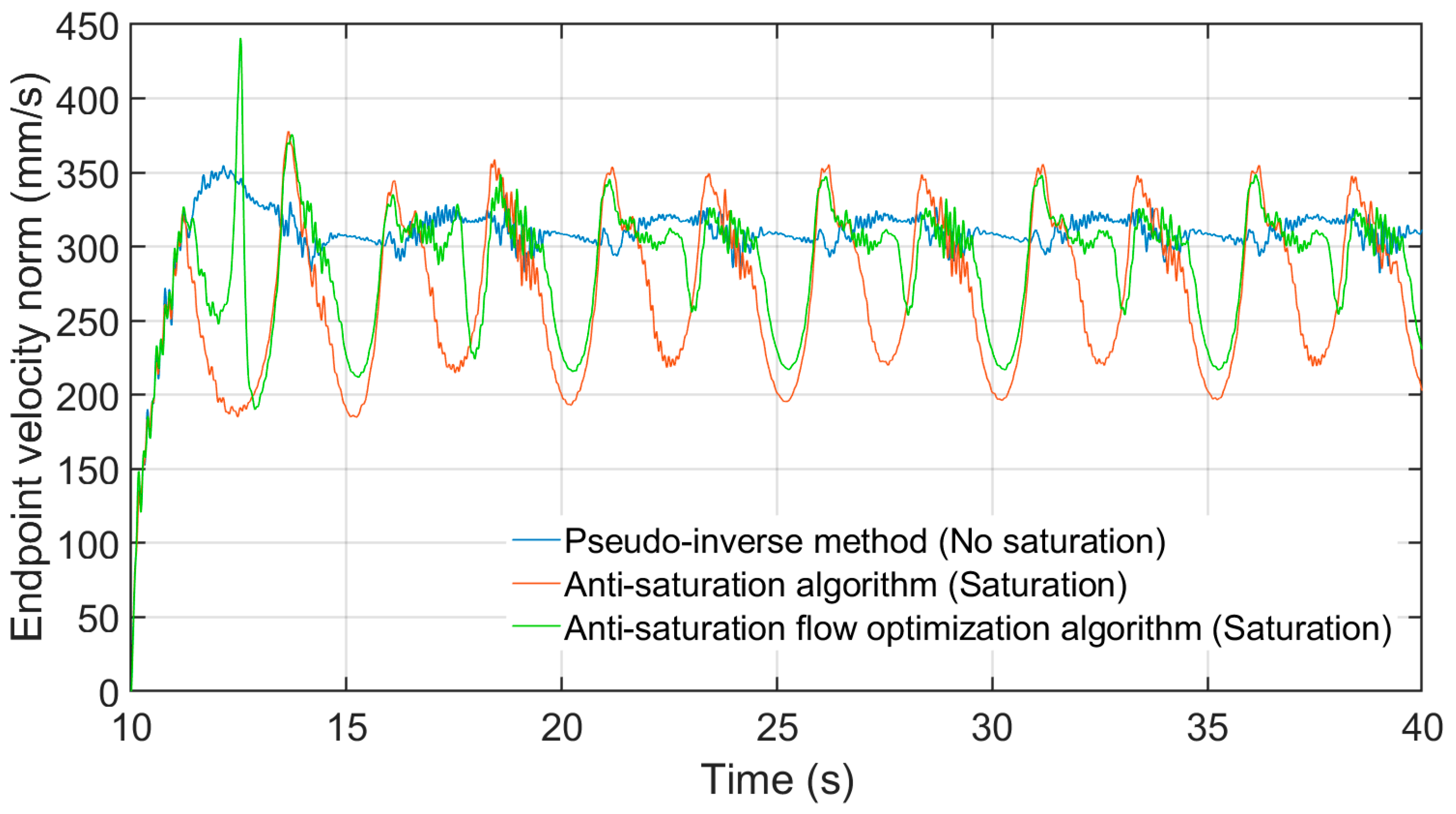
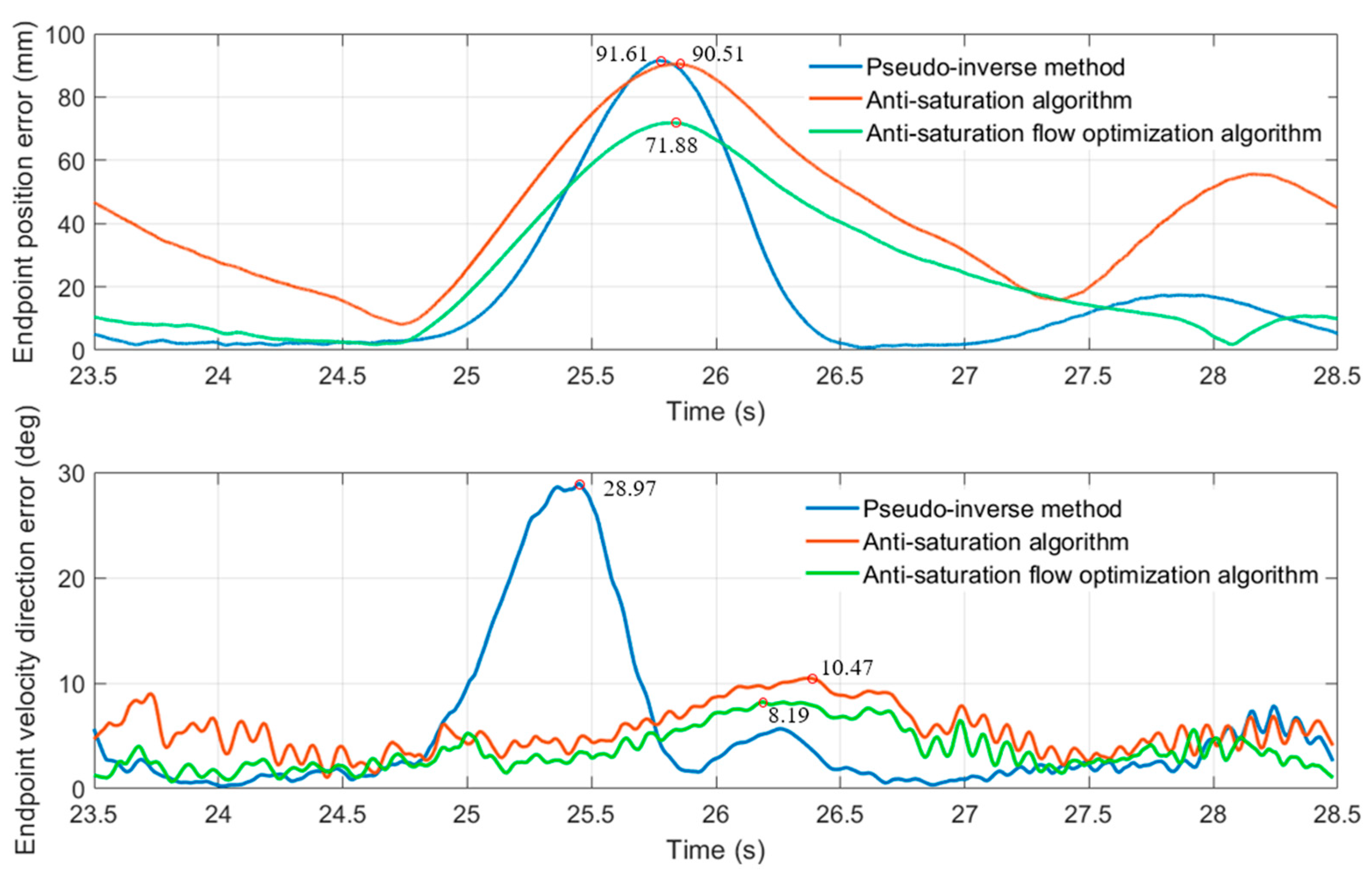
4.3. Anti-Saturation Flow Optimization Algorithm Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | Description and Unit |
|---|---|
| Joint angle (rad) | |
| Link offset (mm) | |
| Link length (mm) | |
| Link twist (rad) | |
| Joint position (rad) | |
| Length of the segments (mm) | |
| Length of the segments (mm) | |
| Joint offset (rad) | |
| Sum of joint position and joint offset (rad) | |
| Total line cylinder length (mm) | |
| Velocity of the hydraulic cylinder (mm/s or rad/s) | |
| Joint velocity calculated by pseudo-inverse method (rad/s) | |
| Hydraulic cylinder areas without the rod () | |
| Hydraulic cylinder areas with the rod () | |
| Effective displacement of cylinder () | |
| Flow of the i-th hydraulic cylinder (L/min) | |
| Demand flow of joints (L/min) | |
| Total leakage flow (L/min) | |
| Demand flow of the system (L/min) | |
| Correction coefficient | |
| Flow threshold (L/min) | |
| Corrected joint velocity (rad/s) | |
| System flow after the joint velocity is corrected (L/min) | |
| Corrected endpoint velocity (mm/s) | |
| Flow adaptive coefficient matrix | |
| optimized joint velocity solved by the flow optimization algorithm (rad/s) | |
| Joint limit avoidance coefficient | |
| Final output joint velocity (rad /s) | |
| t | Algorithm execution time (s) |
| ω | Angular velocity of the target trajectory (rad/s) |
| R | Radius of the target trajectory (mm) |
| Coordinates of the circle center (mm) | |
| Coordinates of the target point (mm) | |
| Coordinates of the endpoint (mm) | |
| Desired velocity of the endpoint at time t (mm/s) | |
| System pressure (MPa) | |
| Energy consumption (kJ) |
References
- Mattila, J.; Koivumaki, J.; Caldwell, D.G.; Semini, C. A Survey on Control of Hydraulic Robotic Manipulators with Projection to Future Trends. IEEE ASME Trans. Mechatron. 2017, 22, 669–680. [Google Scholar] [CrossRef]
- Deere, J. Intelligent Boom Control Ibc. Available online: https://www.deere.co.uk/en/forestry/ibc/ (accessed on 20 November 2020).
- HIAB CONTROL SYSTEMS. Available online: https://www.hiab.com/en/products/loader-cranes/hiab-control-systems (accessed on 20 November 2020).
- Technion. Technion Xcrane Crane Control System. Available online: https://technion.fi/wp-content/uploads/xcrane-brochure-en.pdf (accessed on 20 November 2020).
- Faroni, M.; Beschi, M.; Pedrocchi, N. Inverse Kinematics of Redundant Manipulators with Dynamic Bounds on Joint Movements. IEEE Robot. Autom. Lett. 2020, 5, 6435–6442. [Google Scholar] [CrossRef]
- Woolfrey, J.; Lu, W.J.; Liu, D.K. A Control Method for Joint Torque Minimization of Redundant Manipulators Handling Large External Forces. J. Intell. Robot. Syst. 2019, 96, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Wei, B. Adaptive Control Design and Stability Analysis of Robotic Manipulators. Actuators 2018, 7, 89. [Google Scholar] [CrossRef] [Green Version]
- Ding, R.Q.; Cheng, M.; Jiang, L.; Hu, G.L. Active Fault-Tolerant Control for Electro-Hydraulic Systems with an Independent Metering Valve Against Valve Faults. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, J.H.; Xu, B.; Ding, R. An Electrohydraulic Load Sensing System based on flow/pressure switched control for mobile machinery. ISA Trans. 2020, 96, 367–375. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, T. Foundations of Robotics: Analysis and Control; MIT Press: London, England, 1990. [Google Scholar]
- Lampinen, S.; Niemi, J.; Mattila, J. Flow-bounded trajectory-scaling algorithm for hydraulic robotic manipulators. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM 2020, Boston, MA, USA, 6–9 July 2020; pp. 619–624. [Google Scholar]
- Mononen, T.; Mattila, J.; Aref, M.M. High-Level Controller for High Productivity Earthmoving by Tracked Bulldozers. In Proceedings of the BATH/ASME 2020 Symposium on Fluid Power and Motion Control, FPMC 2020, Bath, England, 9−11 September 2020. [Google Scholar] [CrossRef]
- Hulttinen, L.; Mattila, J. Flow-limited path-following control of a double Ackermann steered hydraulic mobile manipulator. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM 2020, Boston, MA, USA, 6–9 July 2020; pp. 625–630. [Google Scholar]
- Tringali, A.; Cocuzza, S. Globally Optimal Inverse Kinematics Method for a Redundant Robot Manipulator with Linear and Nonlinear Constraints. Robotics 2020, 9, 61. [Google Scholar] [CrossRef]
- Reiter, A. Time-Optimal Trajectory Planning for Redundant Robots: Joint Space Decomposition for Redundancy Resolution in Non-Linear Optimization; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2016. [Google Scholar]
- Wang, X.Y.; Yang, C.G.; Ma, H.B. Automatic Obstacle Avoidance using Redundancy for Shared Controlled Telerobot Manipulator. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015; pp. 1338–1343. [Google Scholar]
- Flacco, F.; De Luca, A.; Khatib, O. Control of Redundant Robots Under Hard Joint Constraints: Saturation in the Null Space. IEEE Trans. Robot. 2015, 31, 637–654. [Google Scholar] [CrossRef]
- Arrichiello, F.; Chiaverini, S.; Indiveri, G.; Pedone, P. The Null-Space-based Behavioral Control for Mobile Robots with Velocity Actuator Saturations. Int. J. Robot. Res. 2010, 29, 1317–1337. [Google Scholar] [CrossRef]
- Morales, D.O.; Westerberg, S.; La Hera, P.X.; Mettin, U.; Freidovich, L.; Shiriaev, A.S. Increasing the Level of Automation in the Forestry Logging Process with Crane Trajectory Planning and Control. J. Field Robot. 2014, 31, 343–363. [Google Scholar] [CrossRef]
- Löfgren, B. Kinematic Control of Redundant Knuckle Booms with Automatic Path Following Functions. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2009. [Google Scholar]
- Beiner, L.; Mattila, J. An improved pseudoinverse solution for redundant hydraulic manipulators. Robotica 1999, 17, 173–179. [Google Scholar] [CrossRef]
- Nurmi, J.; Mattila, J. Global energy-optimised redundancy resolution in hydraulic manipulators using dynamic programming. Autom. Constr. 2017, 73, 120–134. [Google Scholar] [CrossRef]
- Nurmi, J.; Mattila, J. Global Energy-Optimal Redundancy Resolution of Hydraulic Manipulators: Experimental Results for a Forestry Manipulator. Energies 2017, 10, 647. [Google Scholar] [CrossRef] [Green Version]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB® Second, Completely Revised, Extended and Updated Edition; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Deo, A.S.; Walker, I.D. Minimum effort inverse kinematics for redundant manipulators. IEEE Trans. Robot. Autom. 1997, 13, 767–775. [Google Scholar] [CrossRef]
- Cheng, M.; Luo, S.Q.; Ding, R.Q.; Xu, B.; Zhang, J.H. Dynamic Impact of Hydraulic Systems Using Pressure Feedback for Active Damping. Appl. Math. Model. 2020, 89, 454–469. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, J.H.; Xu, B.; Hou, L.; Xiang, J.; Tang, H. A theoretical dynamic model to study the vibration response characteristics of an axial piston pump. Mech. Syst. Signal Process. 2021, 150, 107237. [Google Scholar] [CrossRef]
- Ding, R.; Cheng, M.; Zheng, S.; Xu, B. Sensor-Fault-Tolerant Operation for the Independent Metering Control System. IEEE/ASME Trans. Mechatron. 2020. [Google Scholar] [CrossRef]








| Joint Number | Joint Name | |||||
|---|---|---|---|---|---|---|
| 1 | − 90 | 1015 | 55 | −90 | [−45, 45] | Should yaw |
| 2 | − 90 | 0 | 225 | 90 | [−60, 40] | Arm pitch |
| 3 | 846 | 0 | −90 | [−45, 45] | Arm roll | |
| 4 | − 90 | 0 | 360 | 0 | [0, 120] | Elbow pitch |
| 5 | 0 | 0 | −90 | [−40, 40] | Wrist pitch | |
| 6 | + 90 | 464 | 0 | 90 | [−40, 40] | Wrist yaw |
| 7 | 277 | 0 | 0 | [−135, 135] | Wrist roll |
| Joint Number | |||||
|---|---|---|---|---|---|
| 1 | - | - | 0 | 5.52/° 1 | |
| 2 | 20 | 80.126 | 102.83 | 31.172 | 21.551 |
| 3 | - | - | 0 | 1.24/° | |
| 4 | 15 | 67.319 | 21.95 | 31.172 | 21.551 |
| 5 | 10 | 41.445 | 80.28 | 15.904 | 8.836 |
| 6 | 10.2 | 41.775 | 90 | 15.904 | 10.996 |
| 7 | - | - | 0 | 1.24/° | |
| Joint Number | PID Parameters | Joint Name | ||
|---|---|---|---|---|
| 2 | 1.07 | 0 | Arm pitch | |
| 4 | 2.27 | 0.06 | Elbow pitch | |
| 5 | 0.77 | 0.2 | Wrist pitch | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, M.; Li, L.; Ding, R.; Xu, B. Real-Time Anti-Saturation Flow Optimization Algorithm of the Redundant Hydraulic Manipulator. Actuators 2021, 10, 11. https://doi.org/10.3390/act10010011
Cheng M, Li L, Ding R, Xu B. Real-Time Anti-Saturation Flow Optimization Algorithm of the Redundant Hydraulic Manipulator. Actuators. 2021; 10(1):11. https://doi.org/10.3390/act10010011
Chicago/Turabian StyleCheng, Min, Linan Li, Ruqi Ding, and Bing Xu. 2021. "Real-Time Anti-Saturation Flow Optimization Algorithm of the Redundant Hydraulic Manipulator" Actuators 10, no. 1: 11. https://doi.org/10.3390/act10010011
APA StyleCheng, M., Li, L., Ding, R., & Xu, B. (2021). Real-Time Anti-Saturation Flow Optimization Algorithm of the Redundant Hydraulic Manipulator. Actuators, 10(1), 11. https://doi.org/10.3390/act10010011





