Performance Analysis of a Magnetorheological Shock Absorber Prototype Designed According to a Quasi-Static No-Slip Model

Abstract

The aim of this paper is to investigate the limits of the quasi-static, no-slip approach when modeling the activation of magnetorheological (MR) devices. A quasi-static model is implemented to define the hydraulic and magnetic characteristics of an MR damper prototype. Then, an FE (Finite Element) magnetic simulation activity is carried out to validate theoretical findings, and an optimization procedure is carried out to adjust nominal geometry to actual application. Furthermore, a prototype is realized re-using the maximum number of components that constitute the existing conventional shock absorber. Finally, experimental tests at bench stands are performed. The predictable results demonstrate that neglecting the transient slipping effects, the Force–Velocity performance of the device is correlated with the model findings only for low current intensities acting in the magnetic circuit.

1. Introduction

In a motorcycle, the suspensions are the set of parts that connect the sprung and unsprung masses, allowing relative motion. The unsprung masses are all those elements connected to the ground—tires, rims, the brake system, and the parts of the suspension integral with them. Instead, all the components above the suspension belong to the sprung masses, such as the chassis, engine, fairing, and driver [1]. The role of the suspension system is crucial in the vehicle design, as it performs different tasks, and its performance requirements are often conflicting: it guarantees the contact between the vehicle tires and road while isolating the vehicle body from the vibrations due to the road roughness [2].

Mechanically, a conventional shock absorber is composed of a spring and a central body that is designed as a hydraulic circuit to ensure a certain damping effect; the dynamic driving behavior can be customized by adjusting the fluid passage sections when the vehicle is stationary. When setting the suspension of a vehicle, it is necessary to satisfy different requirements such as driving comfort and good tire grip [1]. Using traditional hydraulic shock absorbers, a compromise choice must be found between comfort and safety needs; comfort riding often requires a plush, underdamped shock absorbers setting, while the search for grip and traction mostly suggests overdamped characteristics.

Magnetorheological (MR) fluids devices applied in the field of vehicle suspensions allow dynamically adjusting damping characteristics, exploiting the physical characteristics of the MR fluids [3,4,5] so as to overcome the constraint of a compromise setting. Discovered by Jacob Rabinow [6], MR fluids consist of micron-sized, magnetically polarizable ferrous particles suspended in a carrier fluid such as oil. MR fluids are smart materials, whose chemical–physical characteristics can vary in a controlled way, depending on the intensity of the magnetic field. Different design solutions of an MR damper can be chosen, according to the “fluid activation” strategy (direct shear—see Figure 1—or pressure-driven flow).

The MR devices are mainly used in the civil field [7,8,9] for the control of structural vibrations, in the automotive field [10,11,12], as well as some uses in the industrial field [13,14]. Li et al. [15] developed and tested a steering damper for motorcycle use, also taking into consideration the ease of assembly. The device by Zhang et al. [16] is equipped with a piston with an internal bypass valve and a permanent magnet. The valve serves to prevent the blockage of the fluid in case of high currents applied, while the magnet guarantees minimum safety magnetization and a wide dynamic range.

An innovation in the motorcycle field is reported by Wang et al. [17] which introduced a winding integral with the shock absorber cylinder for automatic detection of the piston position (IRDS). This system is interesting, as the piston winding simultaneously activates the MR fluid and acts as a displacement sensor.

Again, with regard to control systems, Metered et al. [18] developed a neural network-based one. These allow a low energy demand, long service life, and a minimal use of the sensors, making it the most convenient system in economic terms. Spelta et al. [12] reported the study of a control system for semi-active suspension applied to a dirt motorcycle. Regarding shock absorbers with permanent magnets, Du et al. [19] carried out studies on the flow losses in the magnetic circuit, indicating significant differences between experimental results and modeling and specifying the appropriate corrective factors for the case under consideration. Chen et al. [20] published studies on an MR shock absorber for vehicles, which were equipped with self-sensing speed and the ability to recover the mechanical energy of vibration with transformation into electricity. The main advantages are savings in terms of costs, weight, dimensions, and, of course, energy.

In this paper, a quick technical approach was used to define geometrical dimensions of the MR shock absorber, through which the minimum and maximum damping forces were determined. Subsequently, the hydraulic and magnetic circuits were dimensioned to guarantee the above forces. As a performance requirement, it was established that a semi-active damper should perform a wide range “Force vs. Velocity’’ (F₋V) diagram that is superimposable to that of a conventional high-end SuperSport shock absorber, i.e., equipped with high and low speed adjustment, both for compression and rebound. This functional prerogative represents the most challenging objective since, within the full range of hydraulic adjustments available, the traditional shock absorbers for SuperSport applications show performances which, to date, are considered as state of the art. Moreover, we also decided to keep the overall dimensions of the MR prototype unchanged with reference to the traditional device. The prototype building approach was based on the idea of re-using the maximum number of components that constitute the existing traditional passive device. In this way, any implementation on the motorcycle could take place without any mechanical intervention on the frame and suspension, at a minimal cost.

The aim of this paper is to investigate the limits of the quasi-static, no-slip approach when modeling the activation of the MR fluid of devices that must guarantee high performance for a wide spectrum of acting forces, such as in the case of shock absorbers for motorcycle use. The quasi-static approach to modeling the activation of a MR fluid, if the slip effect is neglected, is lean and essentially requires the design of the induced magnetic field, but what is the downside? The experiment described in the paper demonstrates that the range of use in which the device offers the required damping forces is predictable for low current intensities acting in the magnetic circuit. The results could be useful to understand the accuracy of the required mathematical model as a function of the desired F-V response, and this is a novelty in the field.

Therefore, the present paper is basically an overview on the whole activity, i.e., from mathematical models to the experimental comparative testing at bench stands, highlighting the limits of the quasi-static approach with no slip.

First, a quasi-static axisymmetric model is implemented in Matlab to obtain geometrical characteristics of the gap and to design the magnetic circuit. Therefore, a magnetic simulation activity is carried out to validate theoretical findings. Furthermore, an optimization procedure is carried on adjusting nominal geometry to actual application. Finally, experimental tests are proposed.

2. Materials and Methods

As hinted in Section 1, the philosophy of the present work is proposing a global view approach for MR dampers design: from the performance requirements to a prototype built by re-engineering a passive shock absorber, from the numerical modeling of the magnetic field to the choice of the material, until operational validation. The main activities can be summarized as following:

• Determination of the gap geometry: By means of geometric parameters, estimate the force from the device as a function of the fluid volume stimulated by the magnetic field.
• Calculation of the total reluctance of the equivalent magnetic circuit: By means of the definition of the equivalent RL circuit, this activity returns an estimate of the number of windings of the wire.
• Calculation of the winding configuration: According to time response issues, define the configuration of the winding.
• Design optimization by means magnetic simulation: Based on the theoretical findings, Finite Element Analysis (FEA) is employed for numerical modeling of magnetic field and stresses distribution according to the chosen geometry. Geometry itself is optimized to ensure functionality
• Manufacturing of the prototype: the MR prototype is manufactured starting from components of a traditional, passive, shock absorber. A new piston is realized, and the main cylinder housing in which the piston is engaged is replaced to ensure the closure of the magnetic field. Once the MR device is assembled, it is tested under typical working conditions.
• Final operational validation: bench tests are performed at different current intensities (including challenging limits) acting in the RL circuit, and a comparative analysis with the passive traditional shock absorber is proposed.

2.1. Design of the MR Damper

The functional characteristics of a hydraulic shock absorber for high-end SuperSport purpose, such as the F-V diagram were used as a reference. So, a characterization of a traditional shock absorber available on the market (Matris M46R) was first performed on the test bench (Figure 2). The reference to a specific product does not make the work lose generality, since the top-of-the-range products of each manufacturer show similar characteristics. Moreover, with a view to re-engineering an MR shock absorber exploiting a high number of existing components taken from a traditional device, the geometric dimensions related to the cylinder housing and the useful stroke were considered settled.

The nominal performance forces for the MR prototype were established as follows. Referring to the F₋V curves of the conventional shock absorber (see Figure 2), at maximum speed, in the condition of fluid activated with maximum current intensity, the MR shock absorber should offer a force equal to the traditional shock absorber with the hydraulic closed. Instead, the force required in the condition of deactivated fluid (zero current) should be equal to that of the conventional device with open hydraulic condition. Assuming a maximum piston velocity equal to V_MAX = 0.5 m/s, the force that the magnetic shock absorber should exert in the hydraulic closed condition is F_ON Max = 4431 N and in the condition of hydraulic open, it is F_OFF Min = 3235 N.

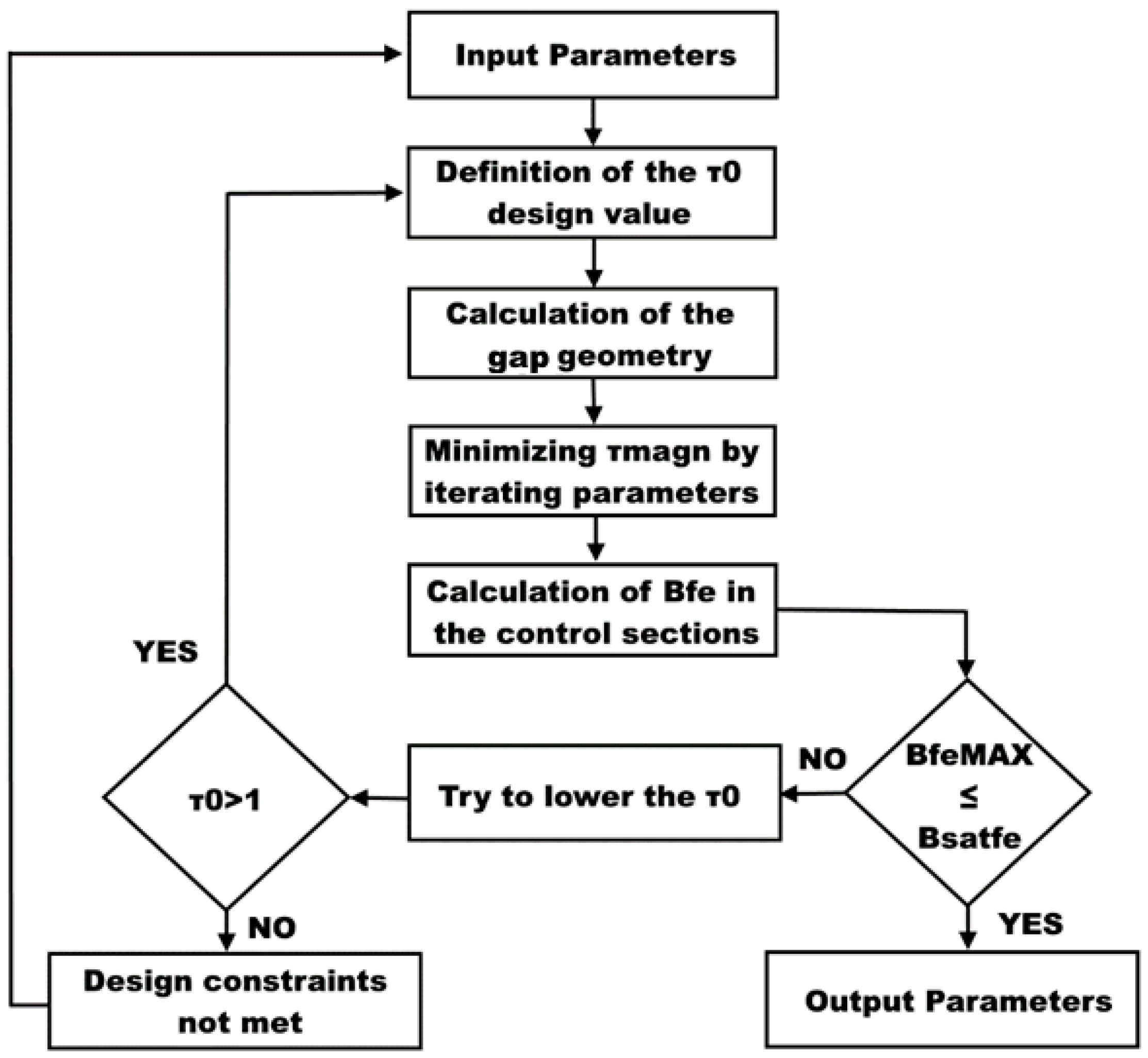
Once the performance requirements are established, a Design Algorithm (DA) was implemented in Matlab [21] exploiting the findings of a quasi-static axisymmetric model [22].

Essentially, that DA represents the sizing of the magnetic circuit as a function of the desired output forces and of the physical characteristics of the materials. The DA worked with “if” and “while” loops (see Figure 3) and proposed the geometry of the gap as a function of the maximum force required and minimum volume of activated fluid, and it iterates the process for the quantities definition to obtain the shortest magnetization time of the winding. The DA received nine constants as input and three parameters to be iterated and returned seven values that completely define the gap, piston geometry, and winding characteristics as well as the F₋V characteristics at maximum current intensity and zero current.

The geometry of the gap depends on the piston geometry, magnetic properties of the materials, and geometry of the gap. All the inputs and outputs are shown in

Table 1. Input and output data.

Name	Symbol	Unit
Inputs
Internal diameter of the cylinder	Dcint	mm
External diameter of the cylinder	Dcest	mm
Piston stroke	c	mm
Relative magnetic permeability of steel	μr fe	/
Absolute magnetic permeability of the fluid	μa fl	H/m
Magnetic permeability in vacuum	μ0	H/m
Resistivity of copper	ρ	Ω * m
Constant for minimum volume activated	α	/
Maximum current intensity	Imax	A
Solenoid diameter	Dsol	mm
Wire diameter	Φwire	mm
Number of wire passes	Npass	/
Outputs
Volume of MR fluid activated	Vmin	mm3
Length of gap	g	mm
Gap thickness	h	mm
Gap width	w	mm
Piston length	Lpist	mm
Piston diameter	Dp	mm
Number of turns	Nsp	/

.

Other input data were the magnetic permeability values of the MR fluid and the steel, which were necessary to characterize the magnetic circuit, the maximum current intensity applicable to the winding, the resistivity of the copper, and the curves B = B (H) and τ₀ = τ₀ (H) related to the fluid. In addition, other parameters were used such as the diameter of the copper wire of the winding, the number of wire passes, and the internal diameter of the piston.

In order to obtain a short time magnetic response in the gap [23], an economic and easily workable ferromagnetic material (AISI 1018) was chosen for the piston prototype. According to the experimental B(H) curve of the AISI 1018 steel, it was set as the limit value for the magnetic induction B_{sat Fe} = 1.5 T, which is the magnetic field saturation.

The B_{sat Fe} value was a constraint condition in the DA and acted as a control parameter to check the piston geometry. Whenever the design flow did not lead to a geometry that allows compliance with the saturation limits in the gap, the tangential stress value τ₀, that is the nominal τ obtainable by magnetizing the MR fluid in the gap, was decreased.

In the block called “Calculation of the gap geometry”, the direct shear (see Figure 1) activation mode for MR fluids was implemented within a while loop; exiting the while loop was allowed if the damping force in the activated fluid condition F_outON exceeded the F_ONMax, which is the maximum exerted damping force for the traditional device experimentally observed. To obtain this result, the height of the gap g was increased in steps of a tenth of a millimeter.

The calculation of the minimum volume of activated fluid V_min occurred with following equation [24]:

$$V_{min}=\alpha \ast \left(\frac{\eta }{{\tau }_y^2}\right)\ast \left(\frac{F_{on}}{F_{off}}\right)\ast F_{on}\ast V_{max}$$

(1)

where the V_min becomes a reference value (V_{min ref}), which is used when changing the τ₀ to calculate the initial V_min according to the following equation:

$$V_{\min start}= V_{\min ref}\ast \left(\frac{{\tau }_{0max}^2}{{\tau }_0^2}\right).$$

(2)

In the first geometry definition attempt, all the values were calculated according to the V_min starting point. Subsequently, having a first attempt geometry of the gap available, at the end of each cycle, V_min was recalculated according to (1) to be reused in the next step, as long as F_{out ON} remained below the F_{ON Max}.

Having to vary the response of the shock absorber in relation to the speed with which it is compressed, it is important that the fluid magnetizes to the desired value in a short time. Since the fluid needs a few tens of milliseconds to react to the applied magnetic field, it follows that its response times depends on the time constant (τ_mg) of the equivalent RL electric circuit (see Figure 4).

2.2. Determination the τ_mg

Inside the block “Choice of the configuration of the parameters to be iterated with the criterion of the minor τ_mg“, the magnetic circuit was modeled. In compliance with the tangential stress required in the fluid (τ₀) and the necessary B_fl value, and given the geometry of the gap, the magnetic flow ϕ that must take place in the magnetic circuit defined by the piston, gap, and cylinder housing is univocally defined. By the reluctance method, one can define the number of turns N_sp:

$$N_{sp}\ast I_{max}= R_{tot}\ast \varphi$$

(3)

where I_max is the maximum intensity current and R_tot is the total reluctance.

The schematic representation of the magnetic circuit (see Figure 4), which is necessary to define the reluctances of the actual application, was also revised considering the observations in [25].

Reluctance R₁ and section S₁ relate to the central body of the piston, while R₂ and sections S₂ and S₃ relate to the piston wings. R_tr and S_tr relate to the MR fluid, and R₄ and S₄ refer to the cylinder housing.

$$S_1=\frac{\pi }{4}\ast D_{sol}^2$$

(4)

$$S_2=\pi \ast D_{sol}\ast g$$

(5)

$$S_3=2\pi \ast R_{pist}\ast g$$

(6)

$$S_{tr}=1.05\ast S_{3 }$$

(7)

$$S_4= \frac{\pi }{4} \left(D_{cest}^2-D_{cint}^2\right)$$

(8)

To calculate the reluctance of the piston wings that have a variable section from S₂ to S₃, the reluctance expressed in infinitesimal terms (9) was integrated by D_sol/2 to R_pist, which is based on the heat conduction model through the cylindrical wall.

$$dR= \frac{dr}{{\mu }_{afl}\ast 2\pi \ast r\ast g}=>R= {{\displaystyle \int }}_{R_i}^{R_e}\frac{dr}{{\mu }_{afl}\ast 2\pi \ast r\ast g}$$

(9)

$$R_1=\frac{\frac{N_{sp}}{N_{pass}}\ast {\varphi }_{wire}+g}{{\mu }_{aFe}\ast S_1}$$

(10)

$$R_2=\frac{1}{{\mu }_{afl}\ast 2\pi \ast g}\ast \ln \frac{2R_{pist}}{D_{sol}}$$

(11)

$$R_{tr}= \frac{h}{{\mu }_{afl}\ast S_{tr}}$$

(12)

$$R_4=\frac{\frac{N_{sp}}{N_{pass}}\ast {\varphi }_{wire}+g}{{\mu }_{aFe}\ast S_4}$$

(13)

As shown, N_sp appears in (10). Total reluctance depends on physical constants (absolute magnetic permeability of steel and MR fluid), and the geometric values (lengths l and areas of sections S of the circuit) are all known or calculable, except for the number of turns of the winding; therefore, Equation (3) can be rewritten by specifying N_sp.

Considering:

$$R_{tot}=R_1+2R_2+2R_{tr}+R_4$$

(14)

One can obtain:

$$N_{sp}= \frac{\varphi \left(g\ast A+B\right)}{\left(I-\varphi \right)\ast {\varphi }_{wire}\ast \frac{A}{N_{pass}}}$$

(15)

where A and B are equal, respectively:

$$A=4\left(\frac{1}{{\mu }_{aFe}\ast \pi \ast D_{sol}{}^2}+\frac{1}{{\mu }_{aFe}\ast \pi \ast (D_{cest}^2-D_{cint}^2)}\right)$$

(16)

$$B=\frac{\ln \left(2R_{pist}/D_{sol}\right)}{{\mu }_{aFe}\ast \pi \ast g}+\frac{h}{1.05\ast {\mu }_{afl}\ast \pi \ast R_{pist}\ast g} .$$

(17)

Once the winding magnetization time was determined, an RL equivalent circuit was resolved to determine the length of the wire:

$$L_{wire}= \pi \ast N_{sp}\ast \left(D_{sol}+N_{pass}\ast {\varphi }_{wire}\right).$$

(18)

Since the piston geometry and the winding characteristics are all determined, therefore, B_Fe was calculated in the control sections S₁, S₂, and S₄. In addition, since the magnetic flux is constant, in correspondence of section S₃, the maximum magnetic induction value of the ferromagnet was obtained. If its value was less than the B_{sat Fe} limit, the design process was finished; otherwise, the algorithm reduced the τ₀ and restarted from the determination of the gap geometries.

2.3. FEA and Optimization

To validate the theoretical findings, a magnetic FE analysis was performed. A two-dimensional axisymmetric model was implemented in Ansys. According to the Direct Shear activation (Figure 2), an FE model (Figure 5) was designed to evaluate the magnetic field of the MR fluid in the gap. To model the magnetic properties of the various materials, which were subsequently assigned to the appropriate areas of the model, the B(H) curve of the MR fluid was introduced, while for copper, insulation resin, and steel, the relative magnetic permeability μ was considered.

The magnetization curve of AISI 1018 steel (cylinder housing), Fe 360 steel (piston), and MR fluid were implemented by points in the pre-processing phase of the analysis. The model consisted of about 91,000 nodes and 35,000 elements (PLANE53 of Ansys library). Boundary conditions were set as amagnetic for the outer regions.

Simulation activity allowed us also to estimate the shear stress τ to be used in the direct shear model for the calculation of the force applied and to check that the magnetic induction values in the steel parts did not exceed the imposed limit.

The DA of the MR shock absorber was performed by acting on the parameters to be iterated (Table 1) and on the B_{sat Fe} magnetic induction limit.

A first analysis was carried out by setting B_{sat Fe} = 1.4 T, keeping its constraint control limit equal to 1.5 T. The first run of the DA with the input data values shown in Table 1 did not produce satisfying results; the magnetic induction values in the section S₄, i.e., the cross-section of the shock absorber cylinder housing, exceeded the control limits. Since S₄ is constant and univocally determined by the internal and external diameters of the cylinder, the input data were varied, increasing the D_cest diameter. By performing the DA, the solution shown in

Table 2. Program output data.

Parameter	Value	Unit
τ0	35.7	kPa
Dsol	24	mm
g	4.8	mm
Npass	3	/
h	0.3	mm
ϕwire	0.57	mm

was obtained.

However, with these geometrical parameters, the total length of the piston exceeded the axial overall dimension available, which is equal to 25 mm. Therefore, some input parameters were varied, as shown in

Table 3. New input values for sizing.

Parameter	Value	Unit
Dsol	26-27-28	mm
Dcest	51	mm
Bsat fe	1.4	T
Npass	5-8-10	/
ϕwire	0.57	mm

.

To limit the piston axial length, both the number of passages (N_pass) and the diameter of the solenoid were considered. The diameter of the wire has a significant influence only on the resistance, so it was set equal to ϕ wire = 0.57 mm.

The magnetic analysis solution showed high induction values in the control section S₂ and in some parts of the cylinder housing (see Figure 6); moreover, we noticed a difference of about 0.25 T with respect to the average values calculated by the DA.

The variation of the magnetic induction was further investigated by varying only one parameter at a time. Magnetic induction deriving from the dimensions chart in Table 3 was explored, considering N_pass values of 10, 12, and 15 and finding a slight deterioration of the magnetic field and a much more marked increase in terms of magnetization time. These trends suggested keeping lower the number of passages N_pass. By fixing the number of passages N_pass = 8, B_fe was analyzed by varying D_sol. As D_sol increased, the magnetic induction B_fe estimated by DA decreased in the control sections S₁ and S₄, increased in S₃, and remained approximately unchanged in S₂. The same trends were observed from the results of the magnetic analysis (see Figure 7), which stands at average values greater than 0.2–0.3 T. Therefore, B_{sat limit fe} = 1.2 T was set.

The trends of some fundamental geometric dimensions and physical characteristics as a function of the N_pass and D_sol parameters can be deduced from the data listed in

Table 4. Output data as N_pass and D_sol vary.

Npass	h [mm]	g [mm]	τ0 [kPa]	Lpist [mm]	Nsp	τmg [s]
5	0.3	4.2	38.3	22.1	120	0.47
8	0.3	4.2	38.3	16.4	112	0.58
10	0.3	4.2	38.3	14.7	110	0.86
Dsol [mm]
26	0.3	4.2	38.3	16.4	112	0.58
30	0.2	3.1	41.7	11.9	80	0.67
34	0.2	2.3	43.5	10.3	80	0.78

.

The solenoid diameter D_sol exhibited the greatest influence on the magnetic induction values, while the effect of changing the number of passes mainly influenced the magnetization time. By examining the possible combinations between D_sol variables from 30 to 36 mm and N_pass from 2 to 5, a solution was obtained only by considering D_sol ≥ 32 and N_pass ≥ 3. Since a least number of wire passes guarantees lower τ_mg, numerical analyses were performed keeping this constraint, fully exploiting the available space in the axial direction L_pistMAX = 25 mm.

Three further cases (D_sol = 32, 34, 36 mm, N_pass = 3) were investigated, and magnetic induction values were always lower than the limit of 1.5 T, except for the internal corners of the piston where local peaks of about 1.8 T were noted. Given the local character of the phenomenon (see Figure 8), the results have been considered acceptable.

According to the quasi-static parallel plate model, for each of these design options, the MR shock absorber showed oversized F-V curves if compared to the hydraulic shock absorber reference. The most critical data were the performance at zero current intensity (F_{MR OFF}), since it did not allow the device to fully cover the speed field below 0.25 m/s, as shown in Figure 9.

In order to further optimize the model, the clearance between the piston and cylinder was increased, without excessively deteriorating the performance at maximum current intensity (F_{MR ON}). In this contest, geometric solutions with D_sol = 33, 35, and 36 mm were considered, also varying the gap height in steps of 0.3 mm, which is approximately 10% of the initial value, and the gap thickness of 0.05 mm, corresponding to a variation of 0.1 mm in the piston diameter. The h-g combinations that guaranteed F-V curves with the best compromise between covering the area at low speed and achieving adequate force in the activated fluid condition were obtained with h = 0.3 mm and g = 3.4 mm (Figure 10).

Finally, D_sol = 33 mm was considered the best compromise, since it allowed holding the magnetic induction limits, especially in the cylinder housing section (see Figure 11).

3. Manufacturing the MR Prototype

For the prototyping of the magnetorheological shock absorber, a hydraulic shock absorber was used, keeping unchanged most of the overall dimensions and damping characteristics. The MR shock absorber was realized maintaining the same piston rod, piston guide, and compensation tank. The main cylinder housing was replaced by a ferromagnetic one. As for the piston, the lamellar pack was removed, keeping the disc perforated to ensure the coaxiality of the new piston with the cylinder: this feature guarantees a space through which the fluid can flow and can be magnetized.

The material used for the piston is a Fe 360 steel, which was chosen for the good compromise it offers between magnetic characteristics and workability. To avoid MR fluid contact-winding and MR fluid-upper and lower surfaces of the piston, the epoxy resin produced by Dolph’s was interposed as an insulator, mixing hardener, and resin with a 10:1 ratio.

The new MR piston was built in three phases:

• Realization of the piston and protections (caps);
• Realization of the wire winding; and
• Application of the resin in parallel with the assembly of the pieces.

On the upper surface, two holes were made for the winding wires. Finally, the insulating resin was applied, and the following were installed: internal spring, seal, O-ring, cylinder cap, and lower uniball (Figure 12). Figure 13 shows the fundamental dimensional parameters of the MR shock absorber.

4. Experimental Testing

To validate the F-V curves of the model, tests at the bench stands were performed at 300 mm/s.

The test bench is a rod–crank type with adjustable stroke up to 120 mm and equipped with a data logger. The test bench is equipped with a load cell with 1000 kg of full scale, a magnetoresistive position transducer with a stroke of 200 mm, a contact thermocouple with a measuring range from −200 to +400 °C, and accuracy of 1 °C.

4.1. Zero Current Intensity Tests

At a first instance, three tests with zero current intensity for the MR shock absorber were performed, with a central time of 15 s and sinusoidal forcing at 1, 2, 3, and 4 Hz were considered (Figure 14).

4.2. Increasing Current Tests

In a second instance, tests at 0.5 Hz were performed with the current intensity varying from 0 to 1.8 A with an increase of 0.3 A. Passing from 0 to 0.3 A, it was possible to highlight an increase in the force exerted by the MR shock absorber, while the graphs maintained the overall shape (Figure 15).

5. Results and Discussion

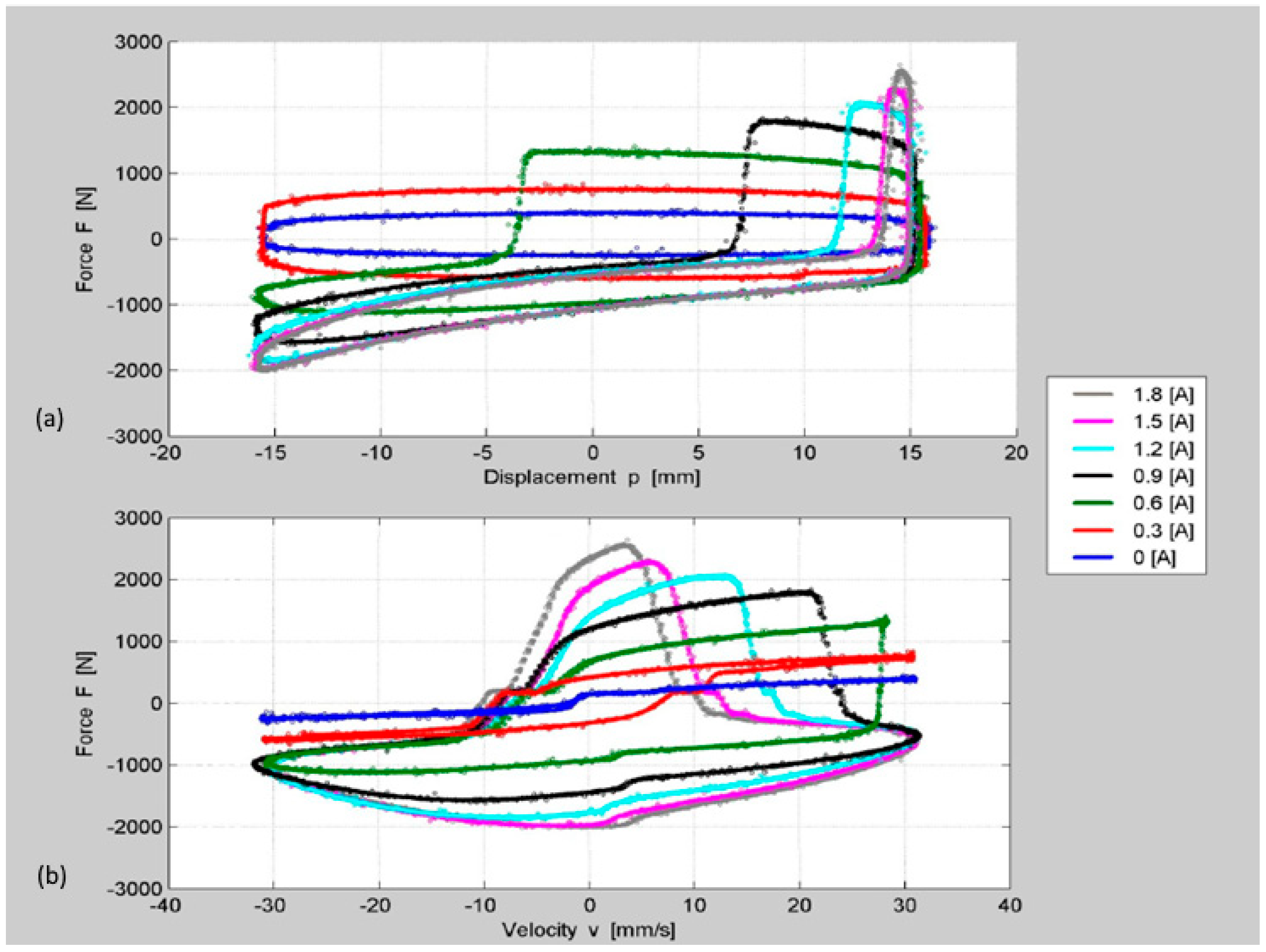
As it is known from the literature, such MR devices often show a non-linear behavior: in our activity, when the power supply for the magnetic circuit exceeded 0.3 A, the trends in the F₋S plane took on a pipe shape that was accentuated more and more as the current intensity increased (Figure 16).

The divergence of the F₋S of the MR damper from a traditional device can be explained as follows [26].

Within a certain displacement range, the ferrite particle chains act as springs that stick both to the piston and the inner housing surface, because all particle chains along the entire radius have not yet reached the sliding angle γ [27].

The force growth due to the slip effect occurs between pre-yield and post-yield regions when ferrite chains start to slide relative to the peripheral area of the piston and relative to the outer surface of the cylinder, generating the friction force (Section C–A in Figure 16).

The friction force steadily increases to level B (Section A–B in Figure 16) within the transition zone due to the increasing sliding area on the piston with increasing stroke. When all particle chains along the entire radius are in the sliding regime and the migration process of particles is finished, the friction force (Section B–D in Figure 16) is generated by the MR damper [27,28].

This physical interpretation of the observed force response was confirmed by rheometer tests on MR fluid samples [29]. Compression behavior is much less sensitive to the slip effect, since the compensation circuit in this phase is not subject to cavitation.

As the current intensity increased, the cycle became increasingly deformed (Figure 17a,b). Analyzing the F₋S plot obtained at 0.5 Hz (Figure 17a), it is noted that the response of the MR device changed when the power supply for the magnetic circuit exceeded 0.3 A; in the last part of the rebound stroke, damping forces seem to agree with the F₋S curve of a standard device. As a result, the increase in the supply current of the magnetic circuit causes, during the extension phase, the displacement of point B (Figure 15) toward the reversal stroke point; when this current is 1.8 A, the point of damping force restoring, in essence, coincides with the beginning of the compression phase.

A different shape from the usual one of a traditional shock absorber one can also be noted in the F₋V curve (Figure 17b), on which the same reference points used can still be traced. It is well known that the maxima of damping force, both in compression and rebound, consequently tends to move from the extremes of the velocity range (midpoints of the stroke) to the center (stroke reversal points).

If one considers the damping force value in the velocity range under exam (+32 mm/s/−30.5 mm/s), when varying the current intensity, the values of force exerted increase by a variable quantity from 300 to 500 N, unlike the plate-parallel no slip model. This implies that the model underestimates the experimental data for currents from 0.3 to 1.8 A, unlike what happens at the extremes. Therefore, it is only from 0 to 0.3 A of input current that the quasi-static parallel no-slip model can be considered descriptive (Figure 17a,b).

The experimental tests show how the hysteretic behavior is highly frequency-dependent: F₋V performance correlation between the model and the experimental tests (Figure 18) when varying the forcing frequency becomes much more evident.

Since the plate-parallel model is quasi-static, it is possible to compare only the extreme points of the experimental curves, which correspond to quasi-static behaviors. In fact, the velocity at extremes is closest to the quasi-static condition, being a = dv/dt = 0.

It is evident that a device with the aforementioned dynamic characteristics essentially becomes unusable for vehicle applications; in this regard, it is sufficient to observe that, passing for example from 0.3 to 0.6 A in the graph F₋V (Figure 17a), for a stroke equal to, say, −10 mm, the damping force changes sign. This proves that the quasi-static parallel model in which the slip prediction is not included proves to be predictive only for low supply currents. The restoring force (point B) can be modeled by a modified Bouc–Wen–Baber–Nory model [28,29], which considers the slip effect. That given, our intent is to implement a reviewed model to redesign the magnetic circuit of the prototype.

6. Conclusions

In order to overcome the limits of the traditional hydraulic shock absorber, a magnetorheological shock absorber has been designed and built, trying to replicate the performance of the reference traditional device. A DA was implemented based on the quasi-static no slip mathematical model of the parallel plate geometry, which is capable of providing the characteristic dimensions of the damper as output. Subsequently, a prototype of a magnetorheological damper has been realized, using a traditional shock absorber as the starting point. The comparison between the experimental and theoretical damping characteristics, with current intensity equal to zero, shows an excellent correspondence. Good correlation is maintained for low current intensities tests. In fact, the current prototype shows good performances only in the context of a reduced stroke, say from −3 to + 5mm, from 0 to 0.6 A of supply current. As the current intensity increases, the mathematical model tends to overestimate the rebound damping force while underestimating the compression one. Moreover, correlation is strictly dependent on forcing frequency. As the testing velocity and intensity of the current grown up, both the experimental F-S and F-V of the MR device show damping force lacks during both compression and rebound phases. Based on these observations, a review of the DA is in progress, implementing in the calculation both the effect of the slip, according to the Bouc–Wen model [30,31], and the determination of the contribution due to the pressure acting in the compensation tank [32] Furthermore, since it is challenging to match F₋D and F₋V of the traditional model for a wide range of current intensities, it is planned to develop an algorithm-based non-linear control strategy [33] exploiting the feedback loop.

On balance, the no-slip parallel plate model is slender, since it is almost based on the search for the maximum and minimum damping force obtainable from τ0, neglecting the transient effects. On the other hand, it is not suitable for demanding dynamical applications, making it useful mostly for applications requiring minor adjustments of damping performance. The results of this research could be a useful reference for designers to understand the complexity of the mathematical model to adopt according to the expected performance.