Adaptive Shell Spherical Reflector Actuated with PVDF-TrFE Thin Film Strain Actuators
Abstract
:1. Introduction
2. Electrostrictive Materials
2.1. Material Model
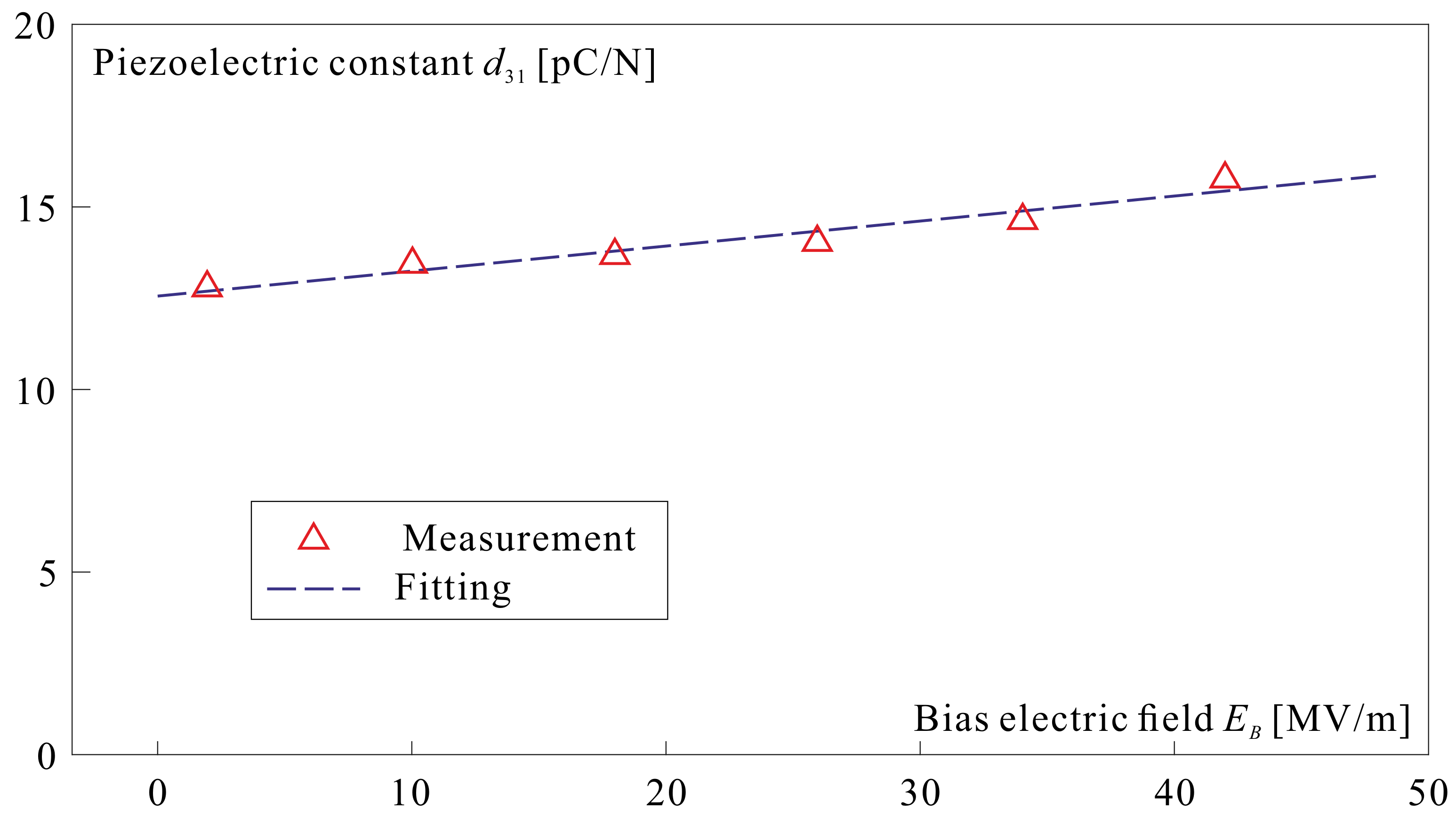
2.2. Material Properties
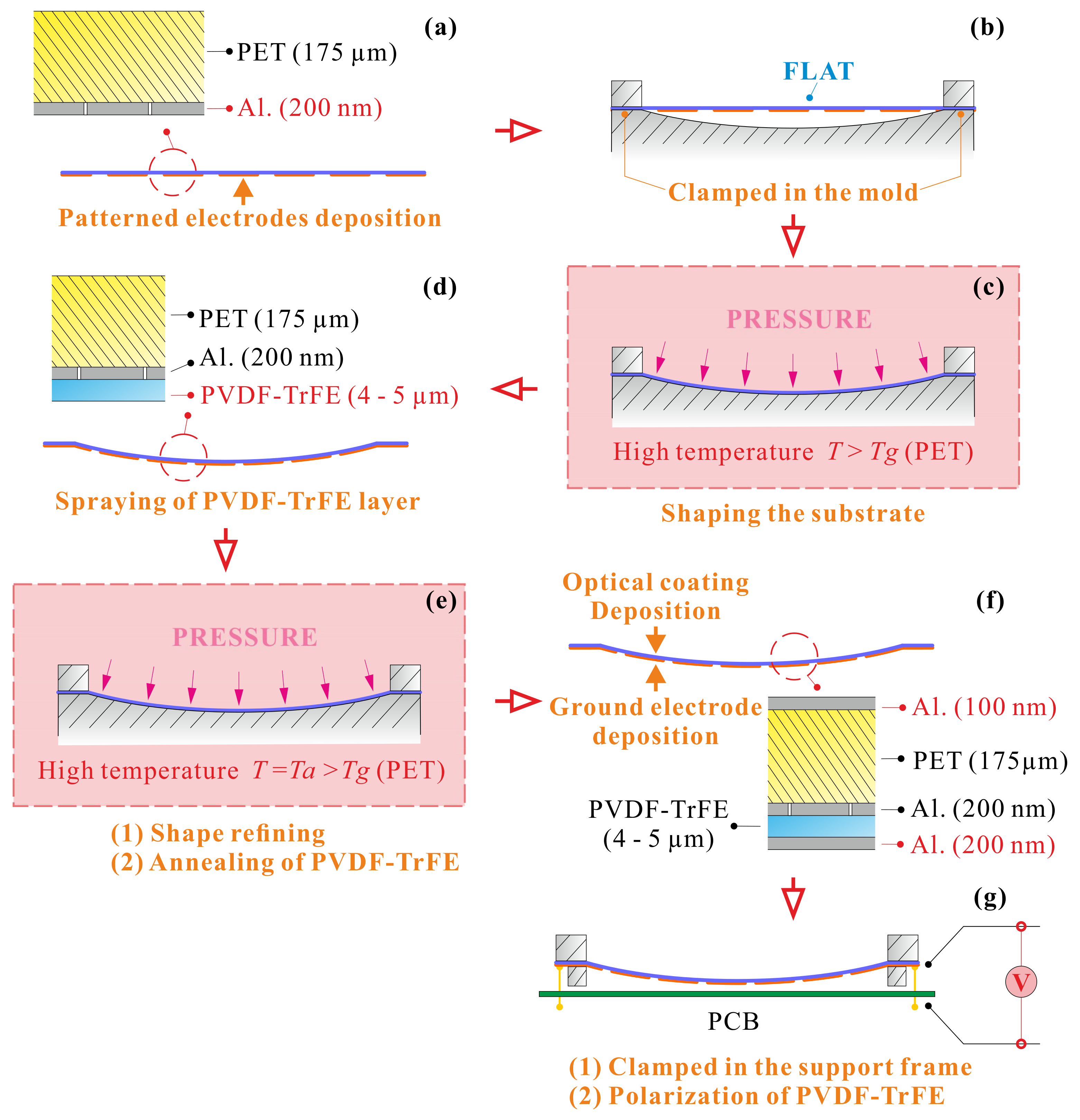
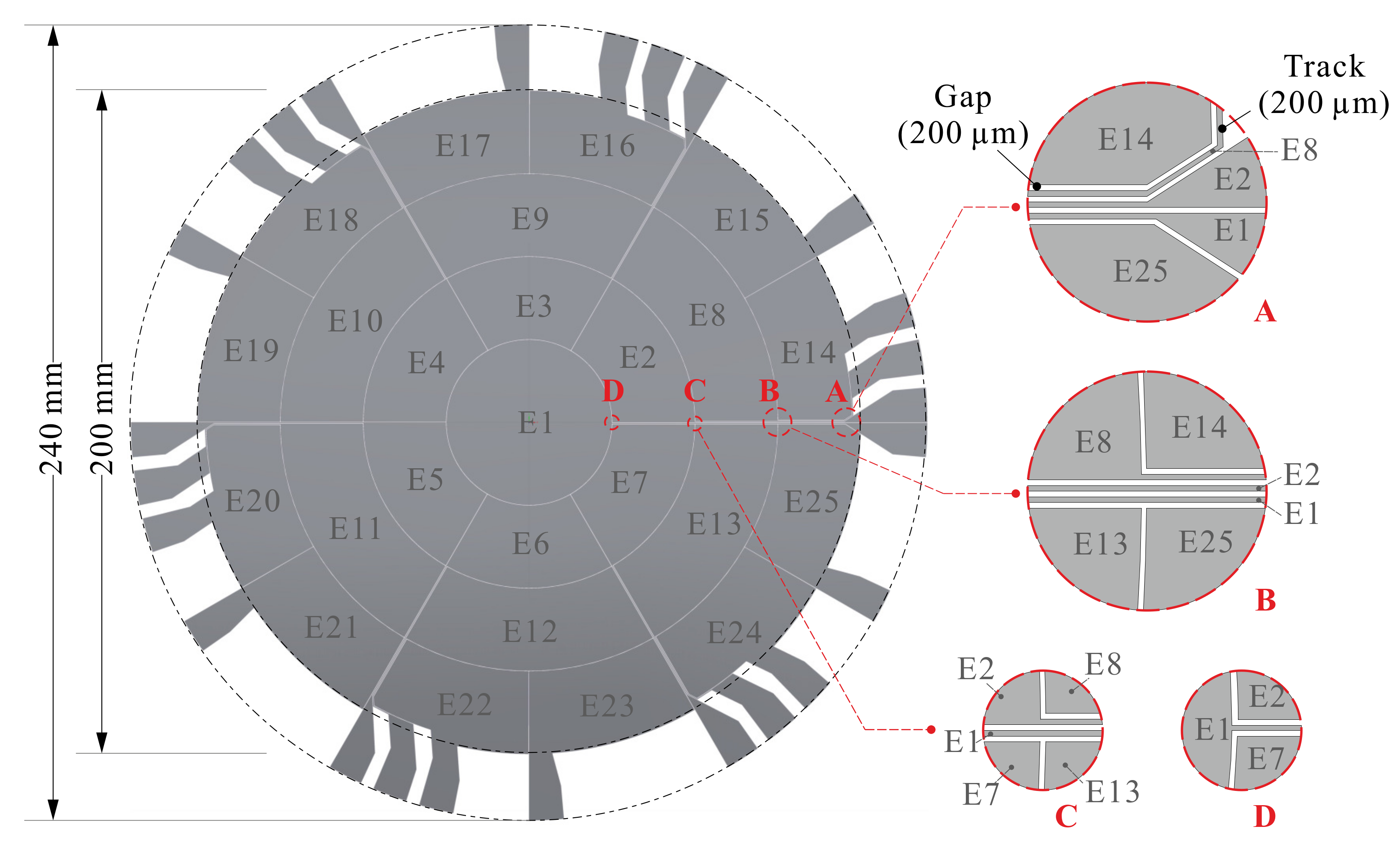
3. Manufacturing of the Demonstrator
4. Shape Control
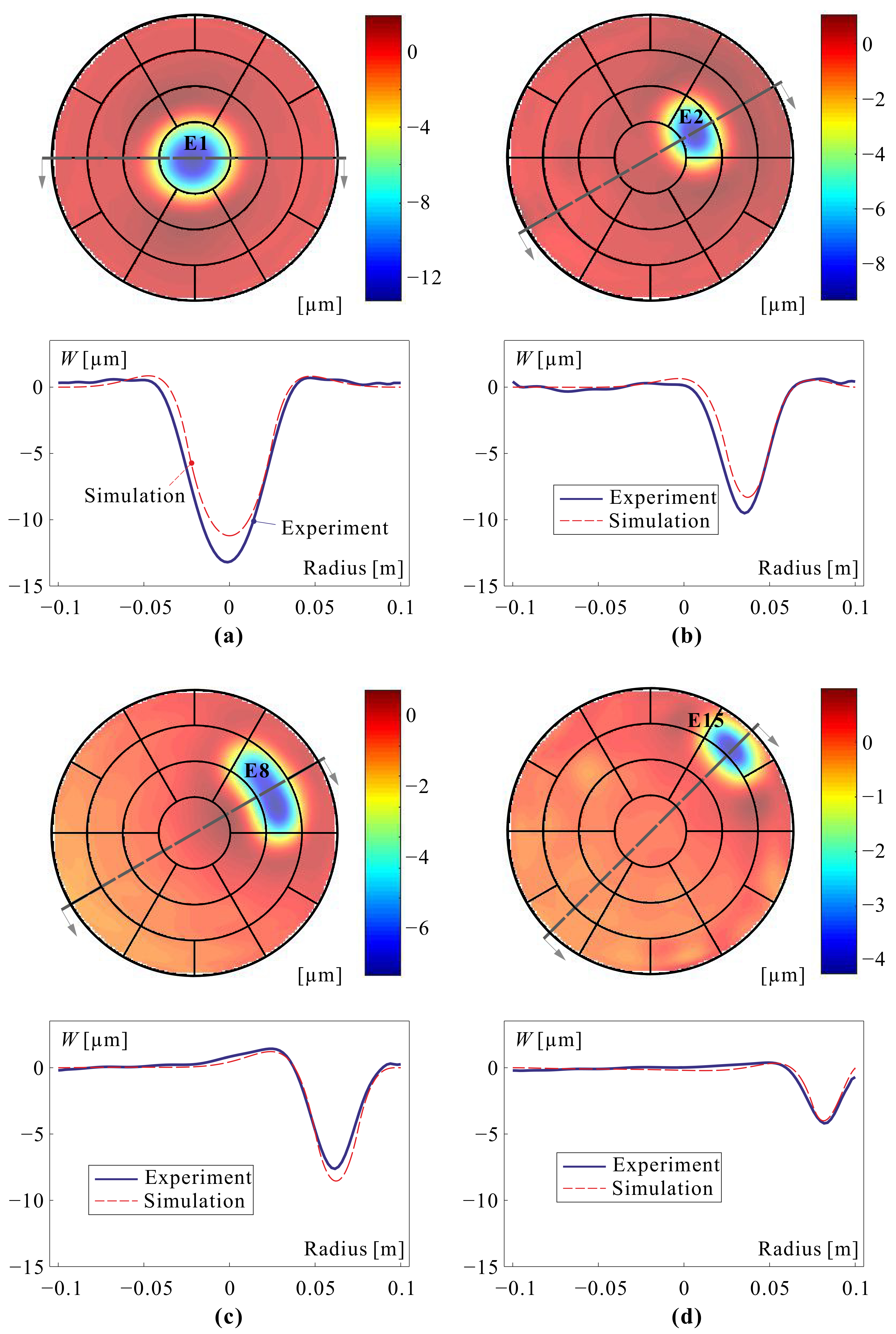
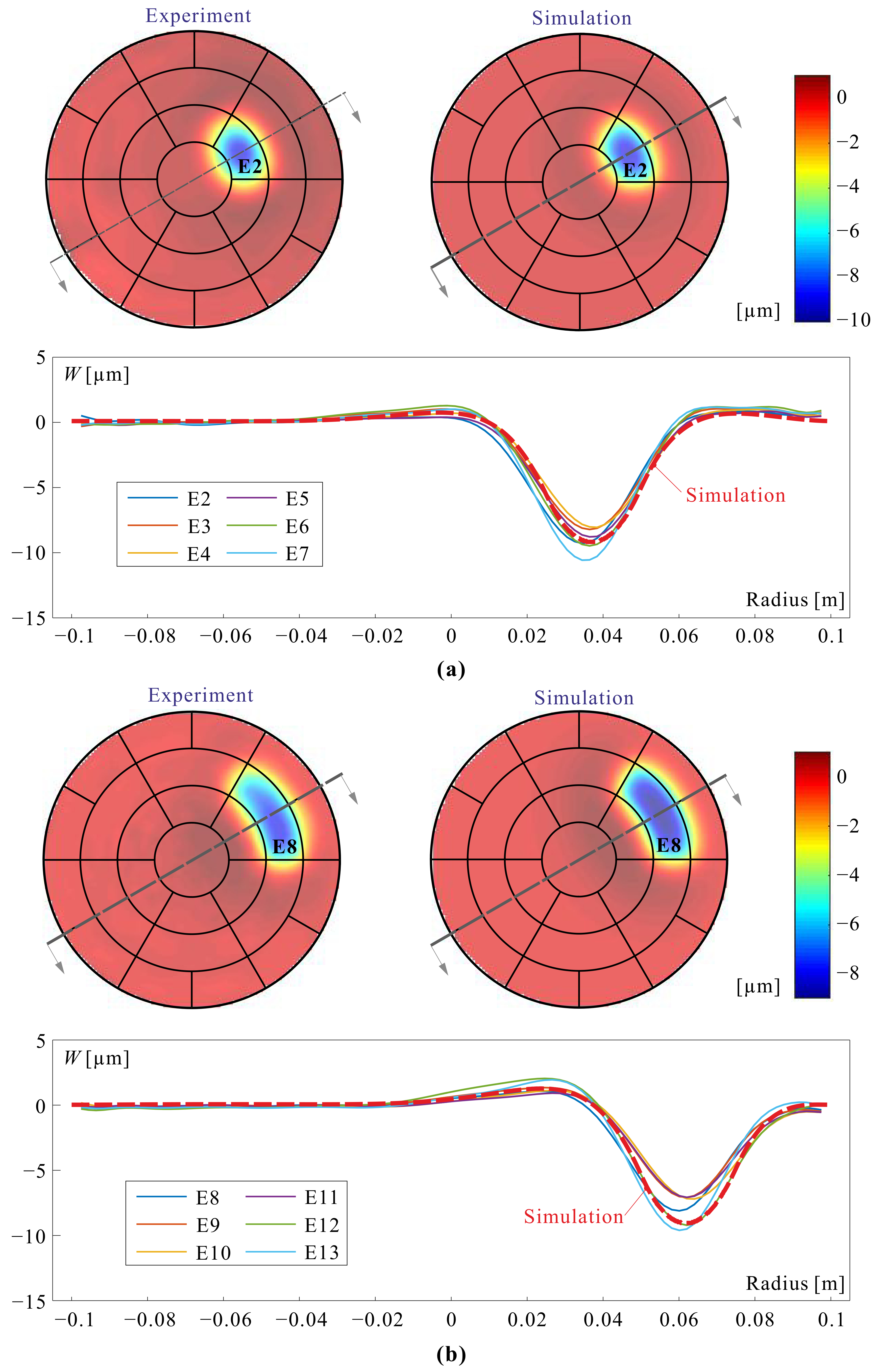
4.1. Influence Functions
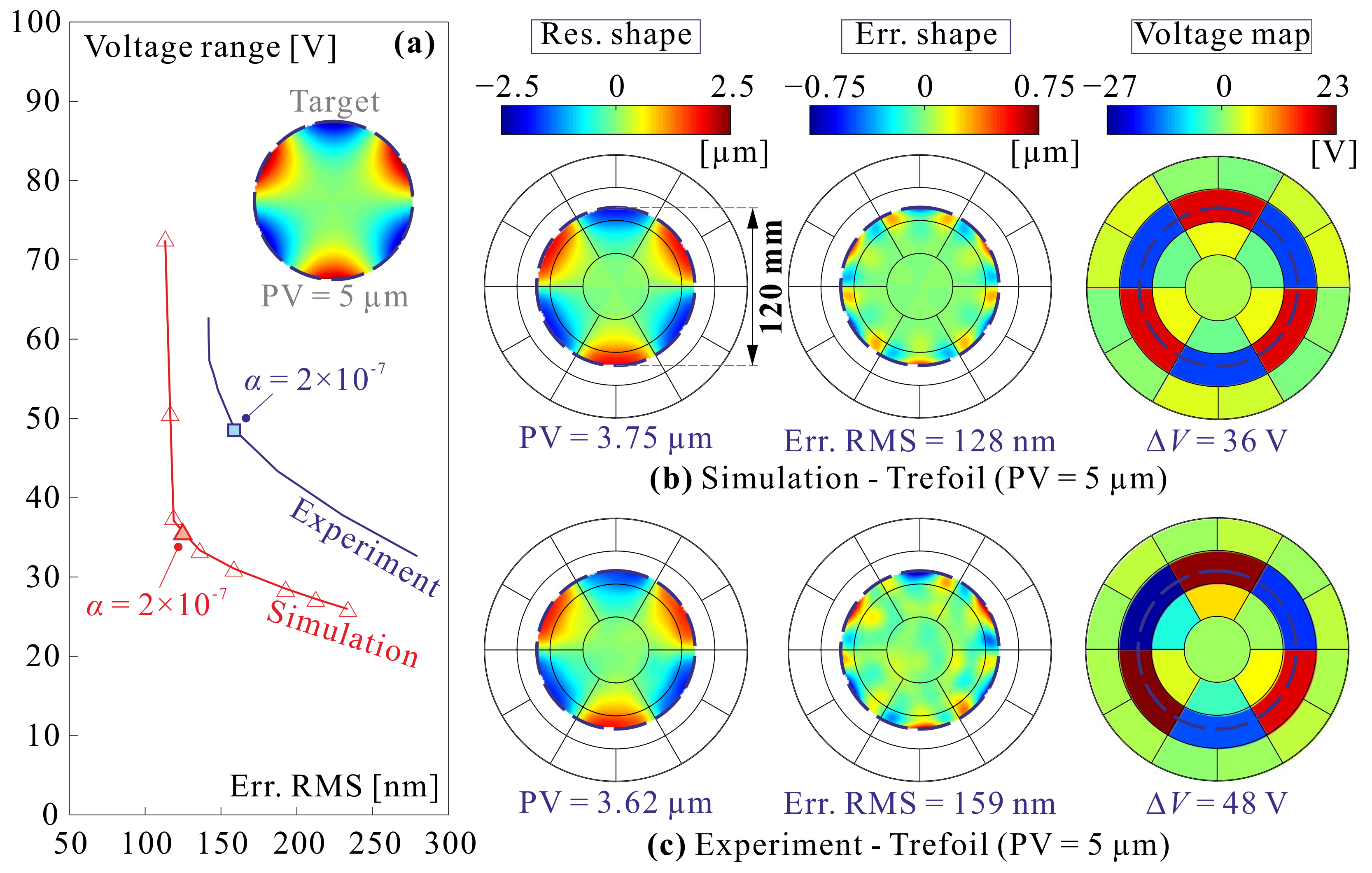
4.2. Optical Modes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ESA | European Space Agency |
| DLS | Damped Least Squares |
| GSTP | General Support Technology Programme |
| MATS | Multilayer Adaptive Thin Shell Reflectors for Future Space Telescopes |
| MEK | Methyl ethyl ketone |
| MIBK | Methyl isobutyl ketone |
| PDCMS | Pulse DC Magnetron Sputtering |
| PET | Polyethylene terephthalate |
| PV | Peak to Valley |
| PVDF-TrFE | Poly(vinylidene fluoride-co-trifluoroethylene) |
| PZT | Lead Zirconate Titanate |
| RMS | Root mean square |
| ULB | Université Libre de Bruxelles |
References
- Hedgepeth, J.M. Accuracy potentials for large space antenna reflectors with passive structure. J. Spacecr. Rocket. 1982, 19, 211–217. [Google Scholar] [CrossRef]
- Bekey, I. Advanced Space System Concepts and Technologies: 2010–2030+; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar]
- Jenkins, C.H. Gossamer Spacecraft: Membrane and Inflatable Structures Technology for Space Applications; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar]
- Marker, D.K.; Jenkins, C.H. Surface precision of optical membranes with curvature. Opt. Express 1997, 1, 324–331. [Google Scholar] [CrossRef] [PubMed]
- Flint, E.; Lindler, J.; Hall, J.; Rankine, C.; Regelbrugge, M. Overview of form stiffened thin film shell characteristic behavior. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006; p. 1900. [Google Scholar]
- Flint, E.; Bales, G.; Glaese, R.; Bradford, R. Experimentally characterizing the dynamics of 0.5 m diameter doubly curved shells made from thin films. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003; p. 1831. [Google Scholar]
- Chodimella, S.; Moore, J.; Otto, J.; Fang, H. Design evaluation of a large aperture deployable antenna. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006; p. 1603. [Google Scholar]
- Haftka, R.T.; Adelman, H.M. An analytical investigation of shape control of large space structures by applied temperatures. AIAA J. 1985, 1, 450–457. [Google Scholar] [CrossRef]
- Fang, H.; Quijano, U.; Bach, V.; Hill, J.; Wang, K.W. Experimental study of a membrane antenna surface adaptive control system. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011; p. 1828. [Google Scholar]
- Wang, K.; Godfroid, T.; Robert, D.; Preumont, A. Electrostrictive PVDF-TrFE thin film actuators for the control of adaptive thin shell reflectors. Actuators 2020, 9, 53. [Google Scholar] [CrossRef]
- Wang, K.; Alaluf, D.; Preumont, A. Thermal balance and active damping of a piezoelectric deformable mirror for adaptive optics. Actuators 2019, 8, 75. [Google Scholar] [CrossRef] [Green Version]
- Preumont, A.; Alaluf, D.; Wang, K.; Rodrigues, G. Adaptive thin shell reflectors for future space telescopes. In Proceedings of the 14th European Conference on Spacecraft Structures, Materials and Environmental Testing (ECSSMET), Toulouse, France, 27–30 September 2016. [Google Scholar]
- Wang, K. Piezoelectric Adaptive Mirrors for Ground-Based and Space Telescopes. Ph.D. Thesis, Active Structures Laboratory, Université Libre de Bruxelles, Brussels, Belgium, 2019. [Google Scholar]
- Preumont, A. Vibration Control of Active Structures, an Introduction, 4th ed.; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Wang, K.; Alaluf, D.; Rodrigues, G.; Preumont, A. Precision shape control of ultra thin shells with strain actuators. J. Appl. Comput. Mech. 2020, in press. [Google Scholar]
- Li, F.; Jin, L.; Xu, Z.; Zhang, S. Electrostrictive effect in ferroelectrics: An alternative approach to improve piezoelectricity. Appl. Phys. Rev. 2014, 1, 011103. [Google Scholar] [CrossRef] [Green Version]
- Buss, S.R. Introduction to inverse kinematics with jacobian transpose, pseudoinverse and damped least squares methods. IEEE Robot. Autom. 2004, 17, 16. [Google Scholar]


| Deposition Technique | Spin Coating | Spray Coating |
|---|---|---|
| Dielectric constant [/] | 11.86 | 9.6 |
| Piezoelectric constant () | 13.54 | 12.54 |
| Electrostrictive constant | −12.65 | −13.81 |
| Remnant polarization | 0.0152 | 0.0157 |
| 0.0163 | 0.0144 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Godfroid, T.; Robert, D.; Preumont, A. Adaptive Shell Spherical Reflector Actuated with PVDF-TrFE Thin Film Strain Actuators. Actuators 2021, 10, 7. https://doi.org/10.3390/act10010007
Wang K, Godfroid T, Robert D, Preumont A. Adaptive Shell Spherical Reflector Actuated with PVDF-TrFE Thin Film Strain Actuators. Actuators. 2021; 10(1):7. https://doi.org/10.3390/act10010007
Chicago/Turabian StyleWang, Kainan, Thomas Godfroid, Damien Robert, and André Preumont. 2021. "Adaptive Shell Spherical Reflector Actuated with PVDF-TrFE Thin Film Strain Actuators" Actuators 10, no. 1: 7. https://doi.org/10.3390/act10010007
APA StyleWang, K., Godfroid, T., Robert, D., & Preumont, A. (2021). Adaptive Shell Spherical Reflector Actuated with PVDF-TrFE Thin Film Strain Actuators. Actuators, 10(1), 7. https://doi.org/10.3390/act10010007







