An Actuator Concept for Adaptive Concrete Columns
Abstract
:1. Introduction
1.1. Adaptive Engineering Structures
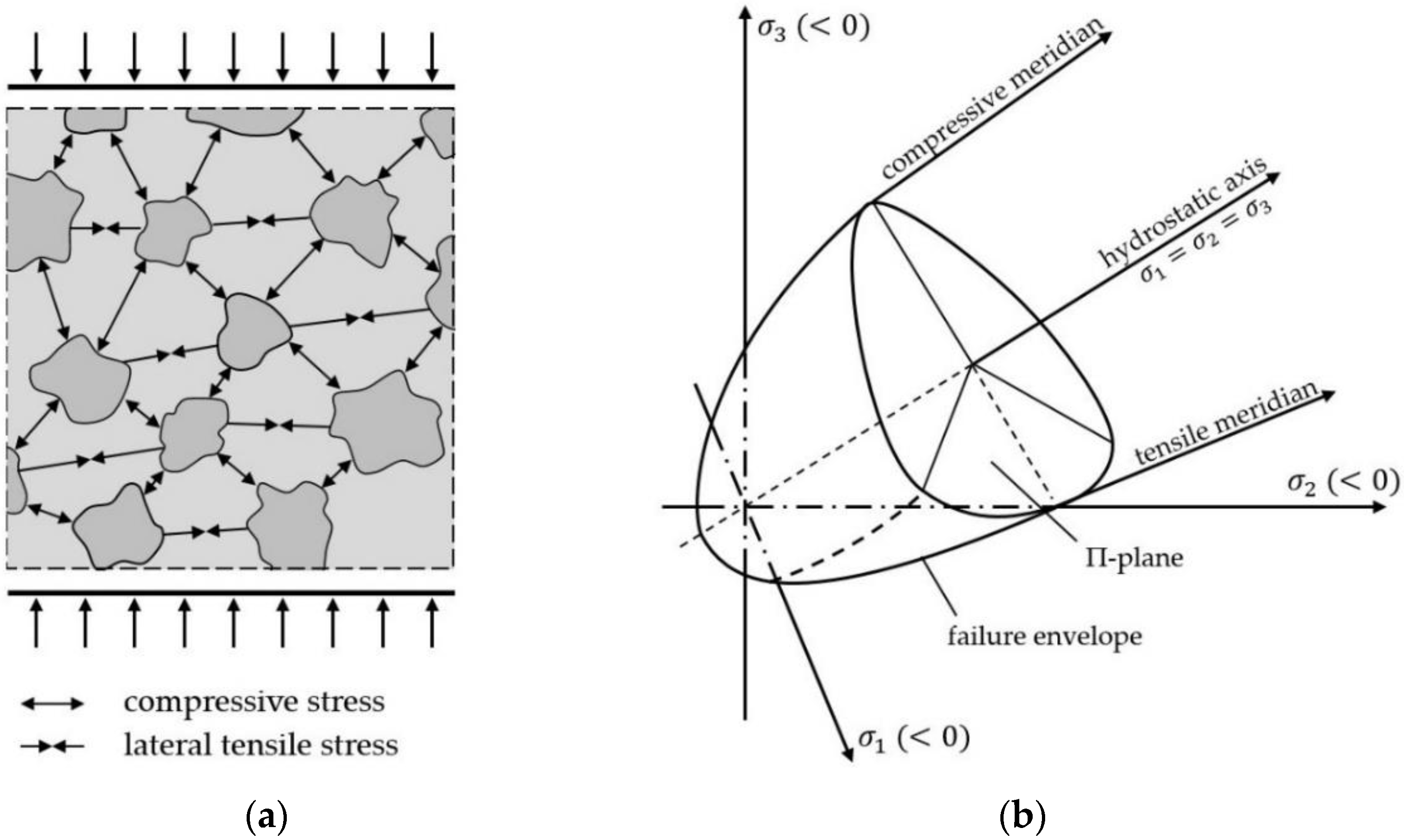
1.2. Material Properties of Concrete
2. Concepts for Adaptive Concrete Columns
2.1. Basic Concepts
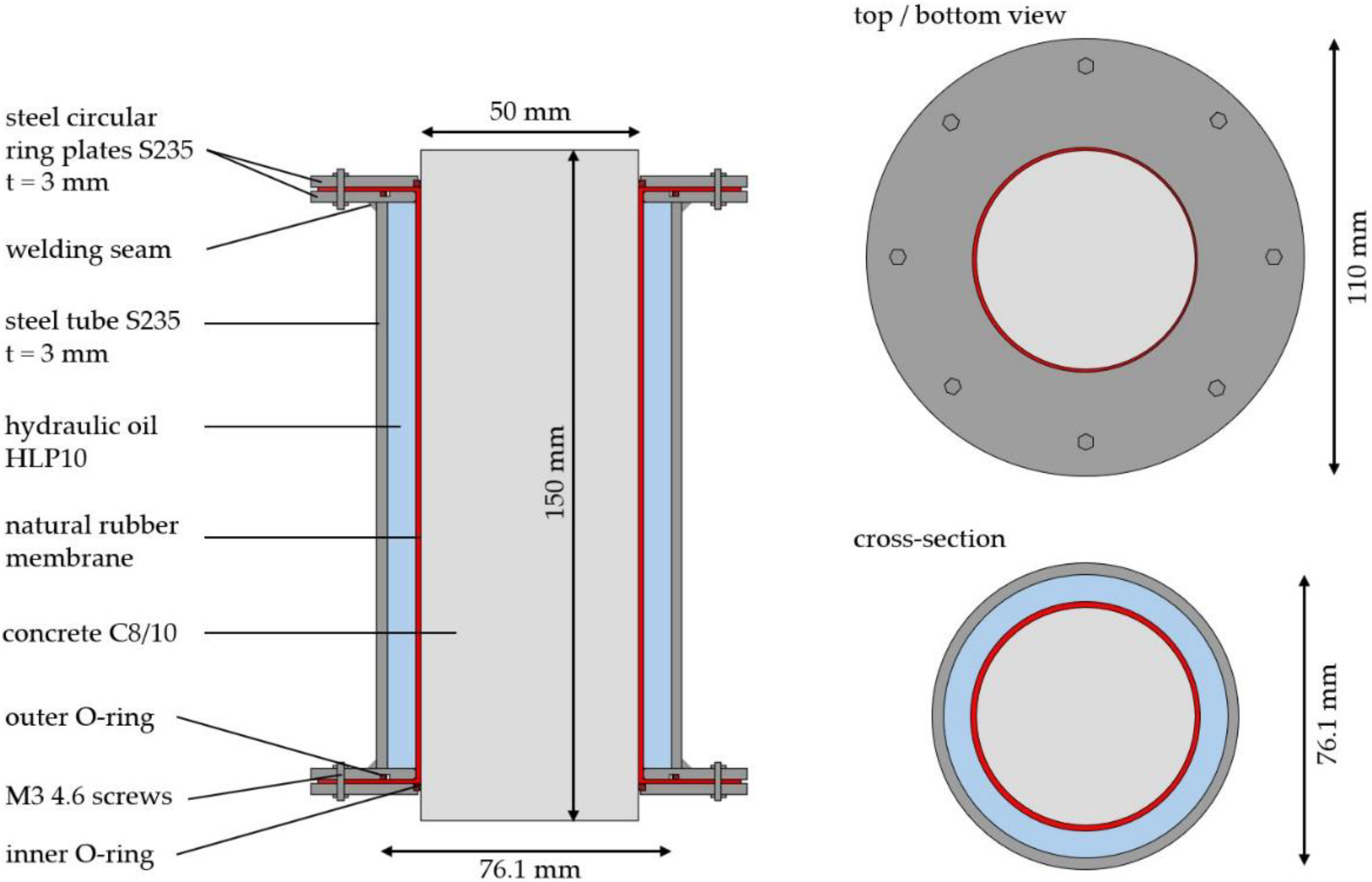
2.2. Prototype of an Externally Compressed Adaptive Concrete Column
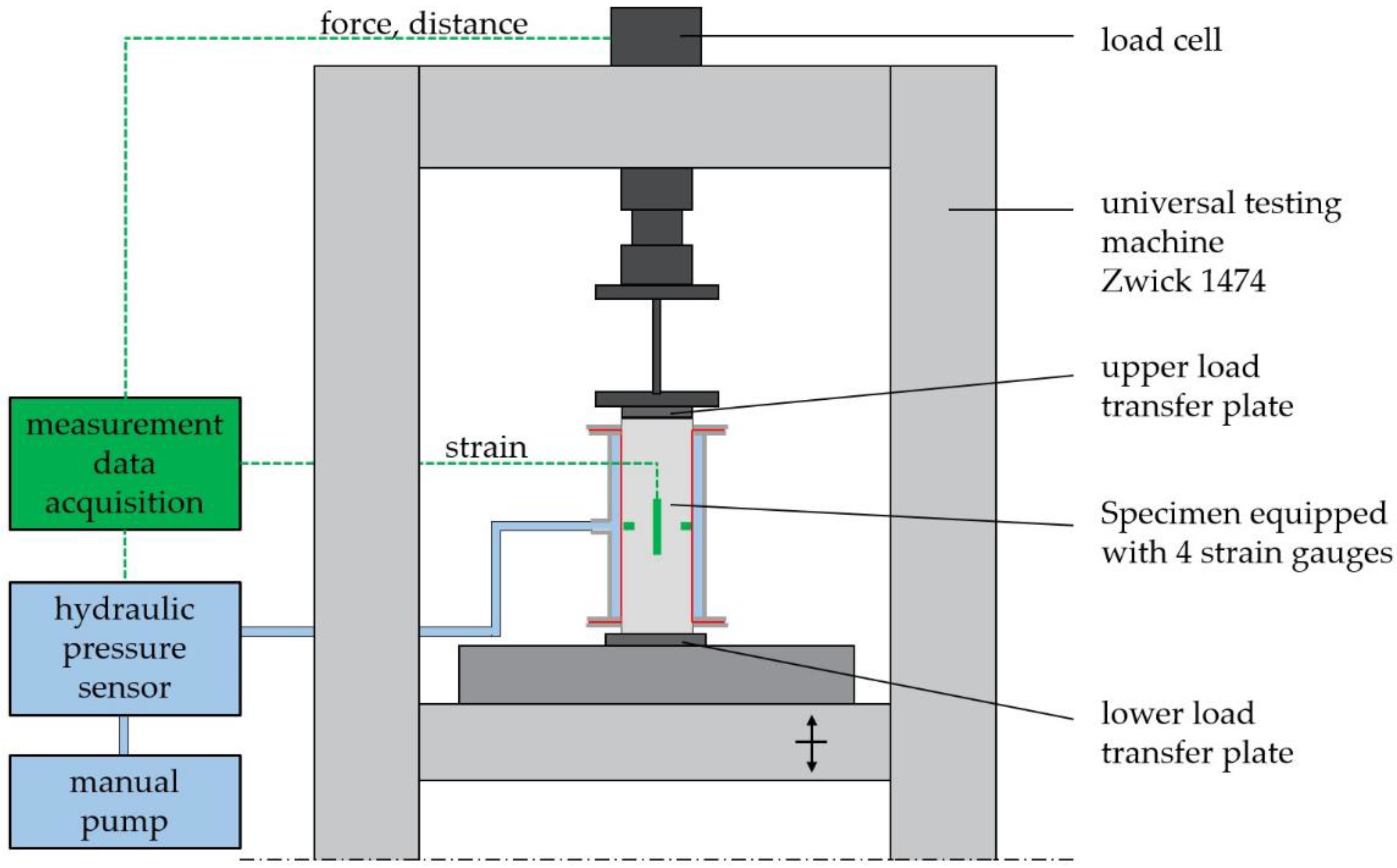
2.3. Experimental Setup and Procedure
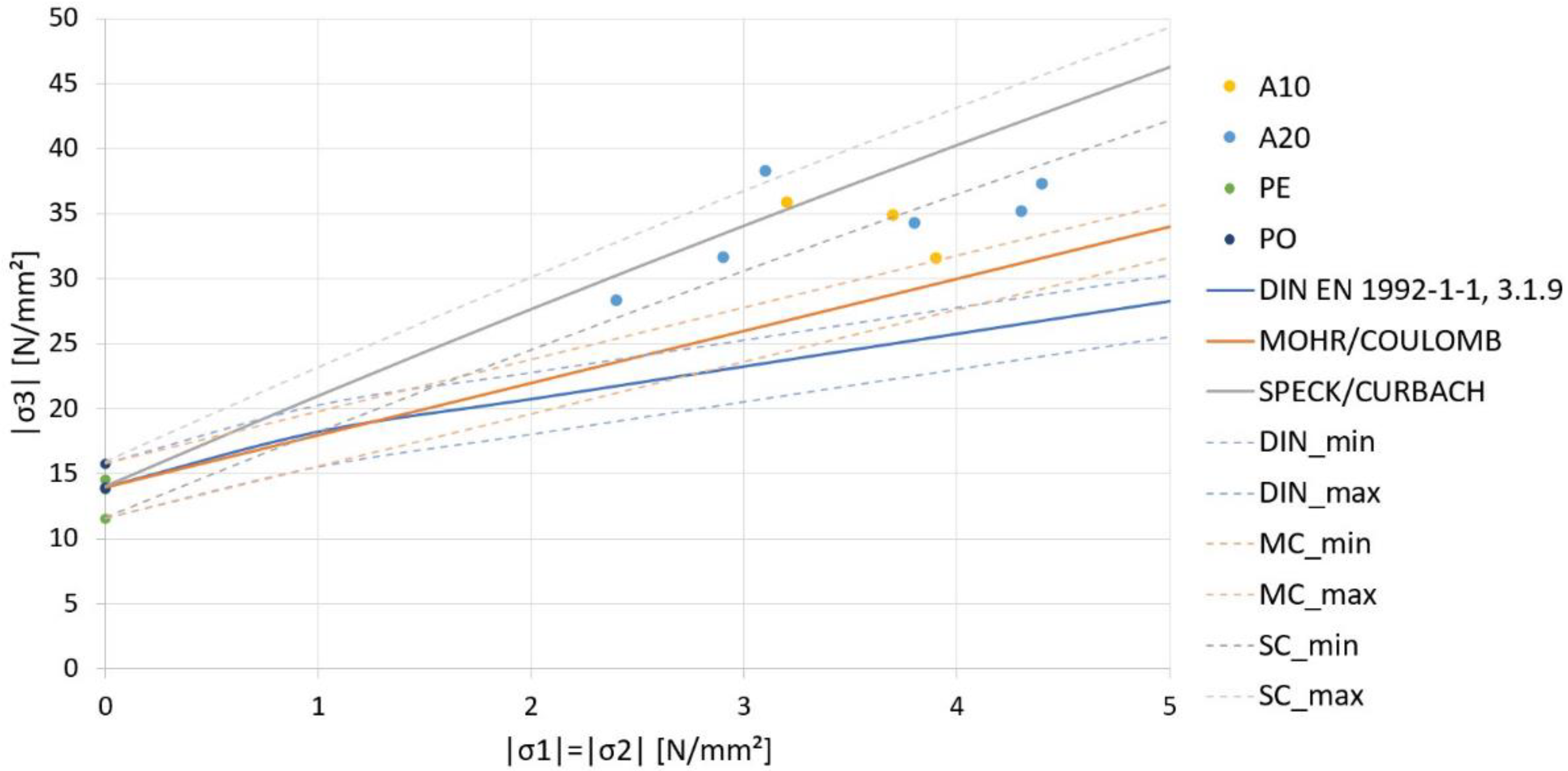
- Can a higher compressive strength be achieved?
- Which fracture criterion is applicable?
- Which strains occur in the actuated, adaptive state (actuator travel)?
- Does the enveloping construction (rubber membrane and steel) influence the stiffness or strain? Does it participate in the passive load transfer?
- Are there differences in the fracture behavior?
3. Experimental Results
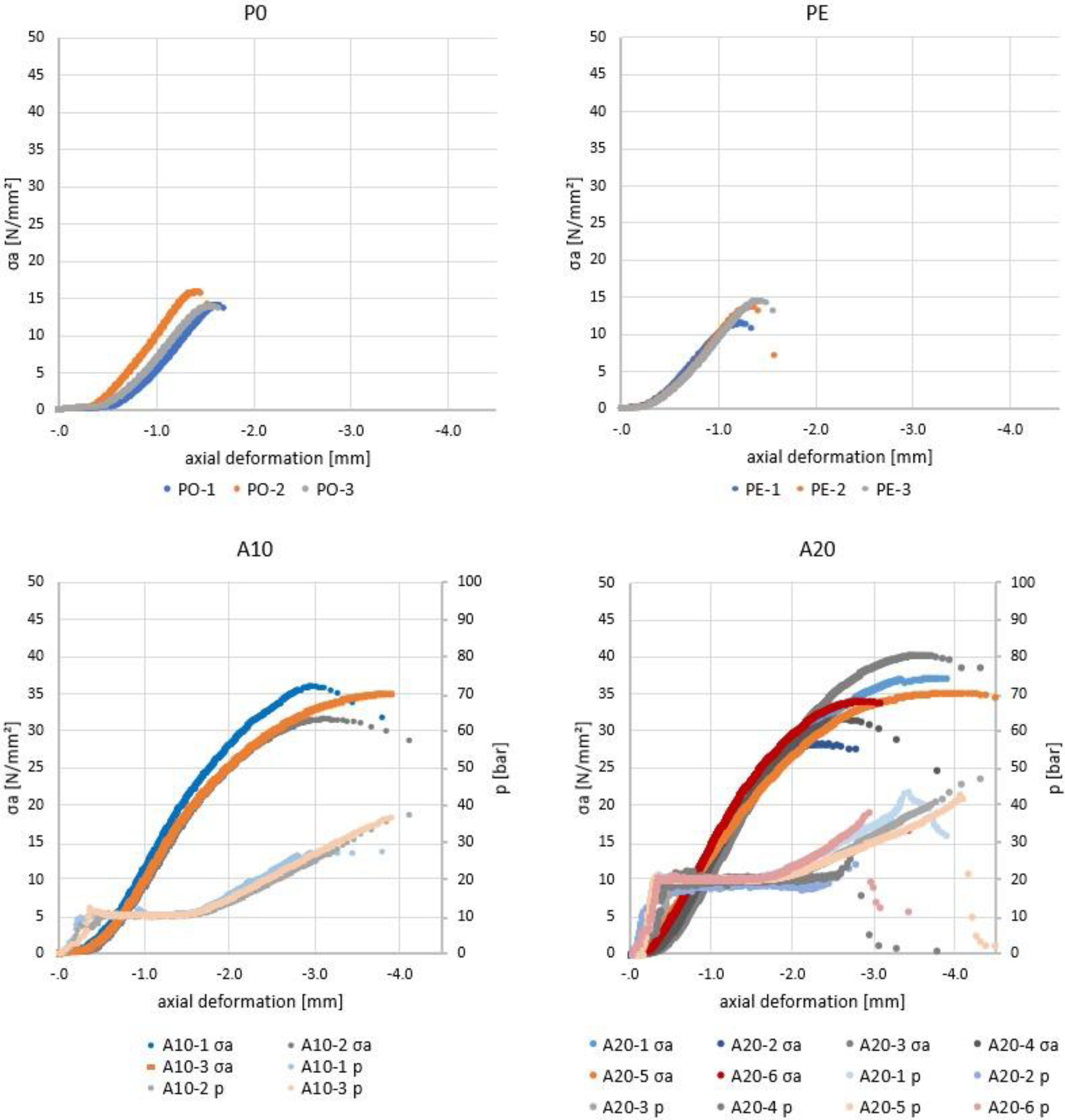
3.1. Mechanisms of Failure and Failure Stresses
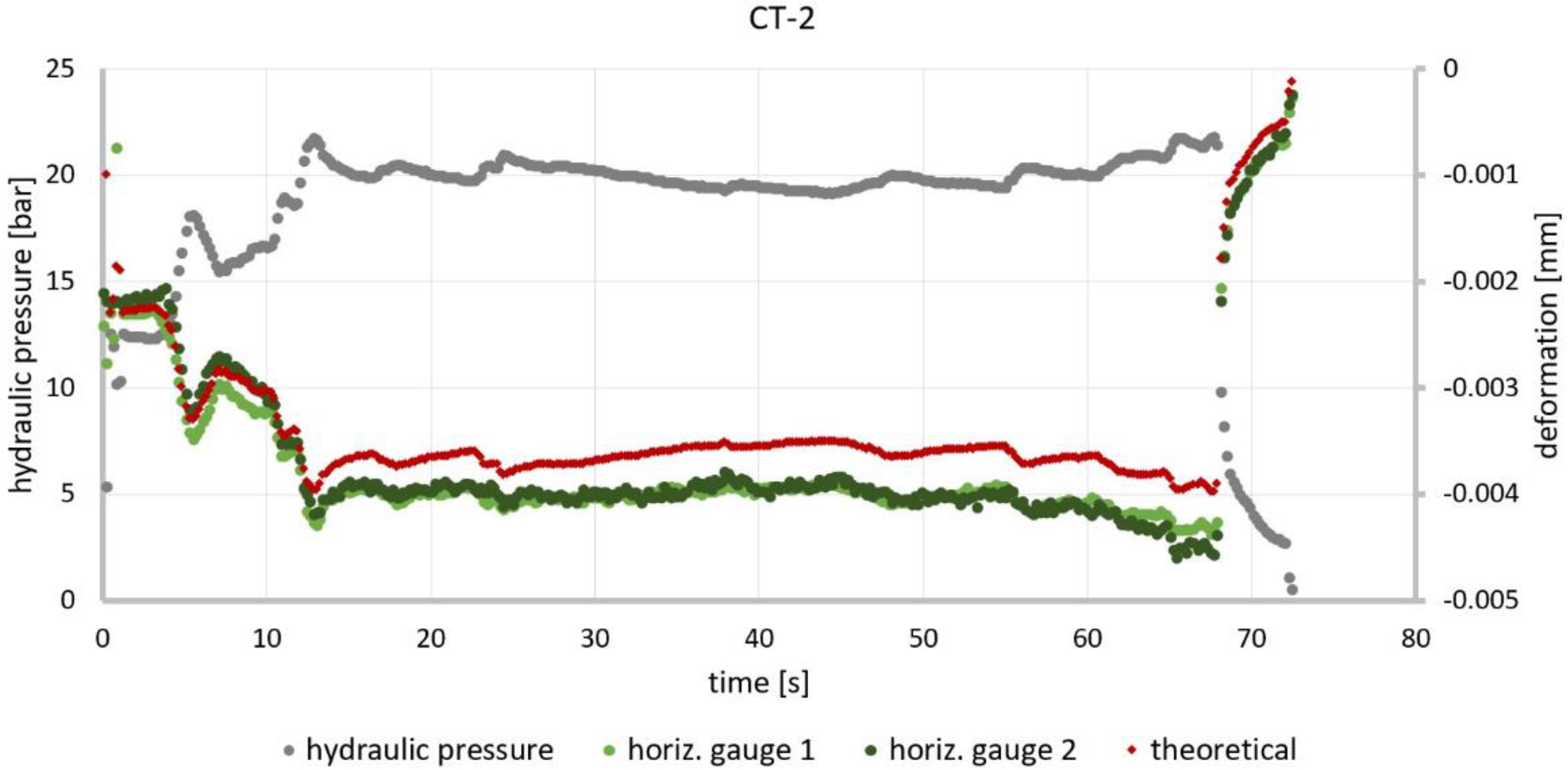
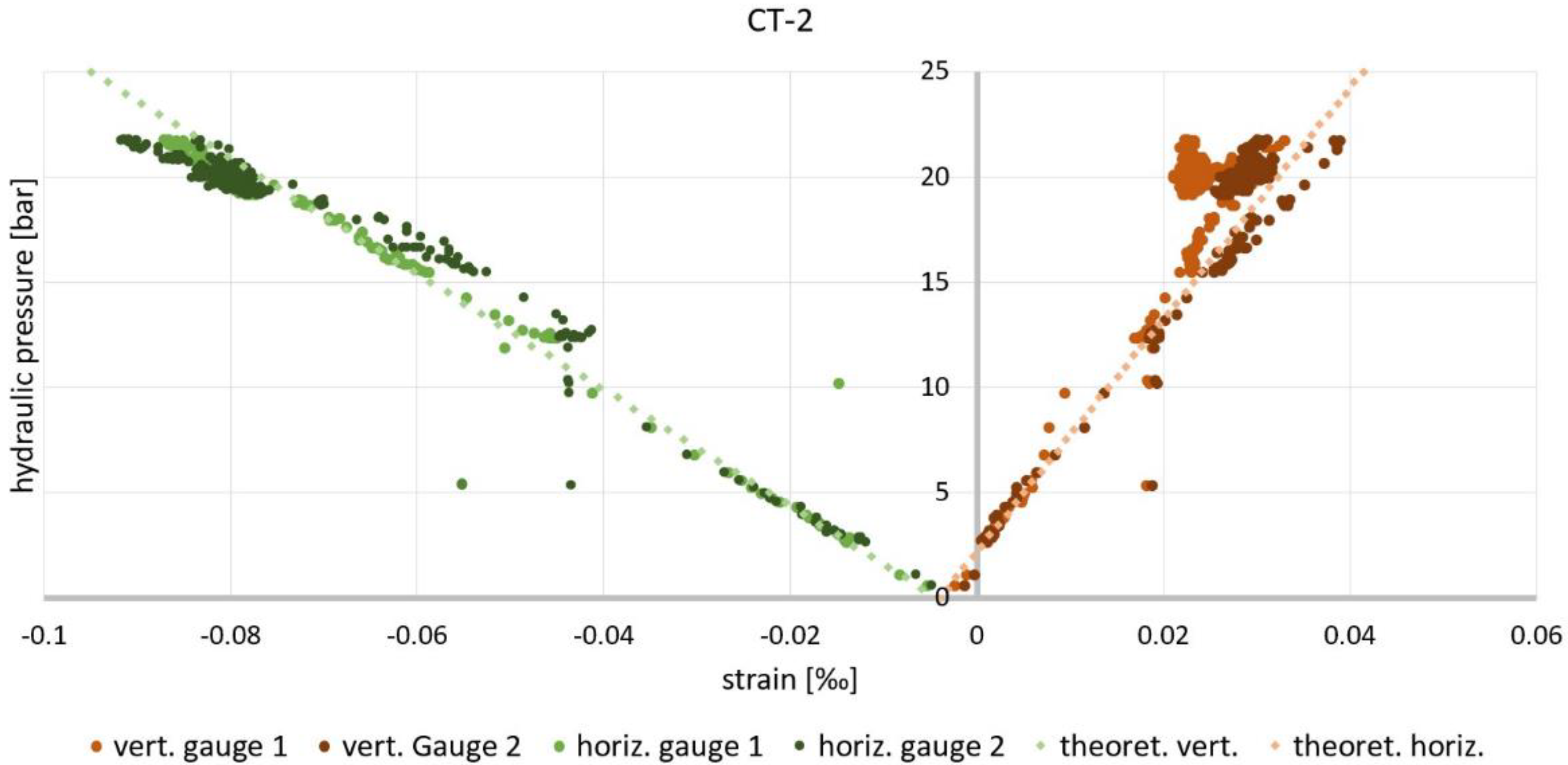
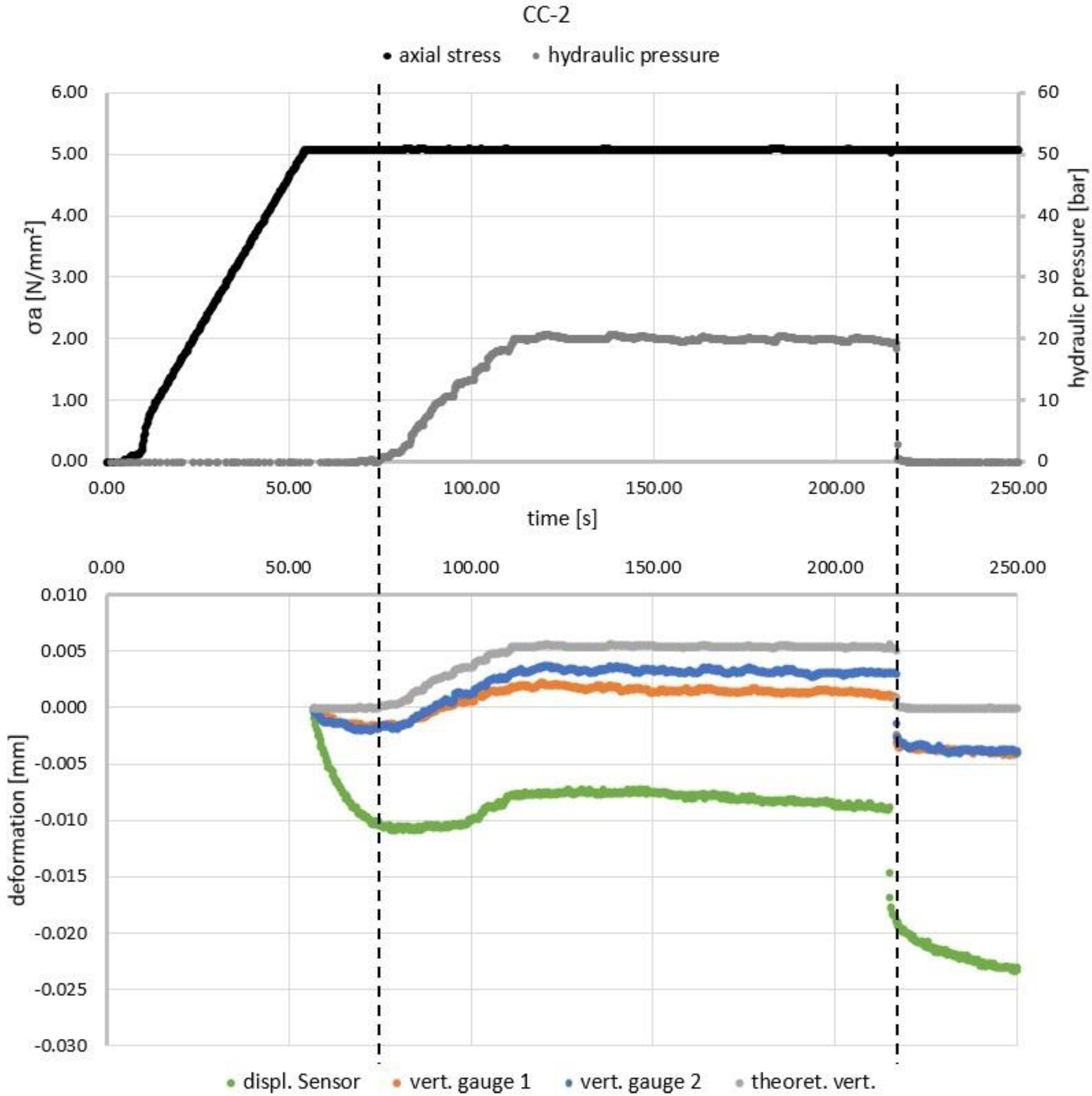
3.2. Deformations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scrivener, K.L.; Kirkpatrick, R.J. Innovation in Use and Research on Cementitious Material. Cem. Concr. Res. 2008, 38, 128–136. [Google Scholar] [CrossRef]
- Scrivener, K.L.; John, V.M.; Gartner, E.M. Eco-Efficient Cements: Potential Economically Viable Solutions for a Low-CO2 Cement-Based Materials Industry. Cem. Concr. Res. 2018, 114, 2–26. [Google Scholar] [CrossRef]
- Peduzzi, P. Sand, Rarer than One Thinks. UNEP Global Environ. Alert Serv. (GEAP) 2014, 11, 208–218. [Google Scholar]
- Weidner, S.; Mrzigod, A.; Bechmann, R.; Sobek, W. Graue Emissionen im Bauwesen—Bestandsaufnahme und Optimierungsstrategien. Beton- und Stahlbetonbau 2021. [Google Scholar] [CrossRef]
- Sobek, W. Ultra-Lightweight Construction. Int. J. Space Struct. 2016, 31, 74–80. [Google Scholar] [CrossRef]
- International Resource Panel. Decoupling Natural Resource Use and Environmental Impacts from Economic Growth; UNEP, Ed.; UNEP: Nairobi, Kenya, 2011; ISBN 978-92-807-3167-5. [Google Scholar]
- United Nations Environment Programme The Emissions Gap Report 2019; UNEP: Nairobi, Kenya, 2019; ISBN 978-92-807-3766-0.
- Geiger, F.; Gade, J.; von Scheven, M.; Bischoff, M. A Case Study on Design and Optimization of Adaptive Civil Structures. Front. Built Environ. 2020, 6, 94. [Google Scholar] [CrossRef]
- Senatore, G.; Duffour, P.; Winslow, P. Synthesis of Minimum Energy Adaptive Structures. Struct. Multidisc. Optim. 2019, 60, 849–877. [Google Scholar] [CrossRef] [Green Version]
- Reksowardojo, A.P.; Senatore, G.; Smith, I.F.C. Design of Structures That Adapt to Loads through Large Shape Changes. J. Struct. Eng. 2020, 146, 04020068. [Google Scholar] [CrossRef]
- Ostertag, A.; Dazer, M.; Bertsche, B.; Schlegl, F.; Albrecht, S.; Leistner, P.; Gienger, A.; Wagner, J.; Tarín, C.; Sawodny, O. Reliable Design of Adaptive Load-Bearing Structures with Focus on Sustainability. In Proceedings of the 30th European Safety and Reliability Conference and 15th Probabilistic Safety Assessment and Management Conference, Venice, Italy, 1–5 November 2020; pp. 4703–4710. [Google Scholar]
- Zilch, K.; Zehetmaier, G. Bemessung im Konstruktiven Betonbau; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-540-70637-3. [Google Scholar]
- Senatore, G.; Duffour, P.; Winslow, P.; Wise, C. Shape Control and Whole-Life Energy Assessment of an ‘Infinitely Stiff’ Prototype Adaptive Structure. Smart Mater. Struct. 2018, 27, 015022. [Google Scholar] [CrossRef] [Green Version]
- Sobek, W.; Teuffel, P. Adaptive Systems in Architecture and Structural Engineering. In Proceedings of the SPIE 8th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 4–8 March 2001; pp. 36–45. [Google Scholar]
- Senatore, G.; Duffour, P.; Winslow, P. Energy and Cost Assessment of Adaptive Structures: Case Studies. J. Struct. Eng. 2018, 144, 04018107. [Google Scholar] [CrossRef]
- Neuhaeuser, S.; Weickgenannt, M.; Witte, C.; Haase, W.; Sawodny, O.; Sobek, W. Stuttgart SmartShell—A Full Scale Prototype of an Adaptive Shell Structure. J. Int. Assoc. Shell Spat. Struct. 2013, 54, 259–270. [Google Scholar]
- Reksowardojo, A.P.; Senatore, G.; Smith, I.F.C. Experimental Testing of a Small-Scale Truss Beam That Adapts to Loads Through Large Shape Changes. Front. Built Environ. 2019, 5, 93. [Google Scholar] [CrossRef]
- Sobek, W.; Teuffel, P.; Landauer, A. Stuttgarter Träger; Institute for Lightweight Structures (ILEK), University of Stuttgart: Stuttgart, Germany, 2002. [Google Scholar]
- Senatore, G.; Duffour, P.; Winslow, P. Exploring the Application Domain of Adaptive Structures. Eng. Struct. 2018, 167, 608–628. [Google Scholar] [CrossRef]
- Kelleter, C.; Burghardt, T.; Binz, H.; Blandini, L.; Sobek, W. Adaptive Concrete Beams Equipped with Integrated Fluidic Actuators. Front. Built Environ. 2020, 6, 91. [Google Scholar] [CrossRef]
- Weidner, S.; Steffen, S.; Sobek, W. The Integration of Adaptive Elements into High-Rise Structures. Int. J. High-Rise Build. 2019, 8, 95–100. [Google Scholar] [CrossRef]
- Bleicher, A. Aktive Schwingungskontrolle einer Spannbandbrücke mit pneumatischen Aktuatoren. Bautechnik 2012, 89, 89–101. [Google Scholar] [CrossRef] [Green Version]
- Burghardt, T.; Kelleter, C.; Bosch, M.; Bachmann, M.; Binz, H.; Blandini, L.; Sobek, W. Adaptive Beams with Integrated Thermal Actuator. In Proceedings of the International Conference and Exhibition on New Actuator Systems and Applications 2021, Online Event, 17 February 2021; VDE Verlag GmbH: Berlin, Germany, 2021; Volume 98, pp. 341–343. [Google Scholar]
- DIN. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings (Includes Corrigendum AC:2010) Englisch Translation of DIN EN 1992-1-1:2011-01; DIN: Berlin, Germany, 2011. [Google Scholar]
- Jonas, F.; Knippers, J. Tragverhalten von Betondruckgliedern mit Umschnürung durch geflochtene und gewickelte Carbonrohre: Tragfähigkeitssteigerung durch Aktivierung eines mehraxialen Spannungszustands im Beton. Beton-Und Stahlbetonbau 2017, 112, 517–529. [Google Scholar] [CrossRef]
- Käseberg, S.; Holschemacher, K.; Curbach, M. Zum Tragverhalten CFK-umschnürter Stahlbetonstützen mit Kreisquerschnitt. Beton-Und Stahlbetonbau 2018, 113, 505–514. [Google Scholar] [CrossRef]
- Janke, L.; Czaderski, C.; Ruth, J.; Motavalli, M. Experiments on the Residual Load-Bearing Capacity of Prestressed Confined Concrete Columns. Eng. Struct. 2009, 31, 2247–2256. [Google Scholar] [CrossRef]
- Kaeseberg, S.; Messerer, D.; Holschemacher, K. Assessment of Standards and Codes Dedicated to CFRP Confinement of RC Columns. Materials 2019, 12, 2390. [Google Scholar] [CrossRef] [Green Version]
- Hampel, T.; Speck, K.; Scheerer, S.; Ritter, R.; Curbach, M. High-Performance Concrete under Biaxial and Triaxial Loads. J. Eng. Mech. 2009, 135, 1274–1280. [Google Scholar] [CrossRef]
- Speck, K.; Curbach, M. Ein einheitliches dreiaxiales Bruchkriterium für alle Betone. BUST 2010, 105, 233–243. [Google Scholar] [CrossRef]
- Ottosen, N.S. A Failure Criterion for Concrete. J. Eng. Mech. Div. 1977, 103, 527–535. [Google Scholar] [CrossRef]
- Rogge, A. Materialverhalten von Beton Unter Mehrachsiger Beanspruchung; Technische Universität München: München, Germany, 2003. [Google Scholar]
- Steffen, S.; Weidner, S.; Blandini, L.; Sobek, W. Using Influence Matrices as a Design and Analysis Tool for Adaptive Truss and Beam Structures. Front. Built Environ. 2020, 6, 83. [Google Scholar] [CrossRef]
- Weidner, S.; Kelleter, C.; Sternberg, P.; Haase, W.; Geiger, F.; Burghardt, T.; Honold, C.; Wagner, J.; Böhm, M.; Bischoff, M.; et al. The Implementation of Adaptive Elements into an Experimental High-Rise Building. Steel Constr. 2018, 11, 109–117. [Google Scholar] [CrossRef]
- Böhm, M.; Wagner, J.L.; Steffen, S.; Gade, J.; Geiger, F.; Sobek, W.; Bischoff, M.; Sawodny, O. Input Modeling for Active Structural Elements—Extending the Established FE-Work? Ow for Modeling of Adaptive Structures. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 1595–1600. [Google Scholar]
- Zupan, M.; Ashby, M.F.; Fleck, N.A. Actuator Classification and Selection—The Development of a Database. Adv. Eng. Mater. 2002, 4, 933–940. [Google Scholar] [CrossRef]
- Isermann, R. Mechatronische Systeme: Grundlagen, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-32336-5. [Google Scholar]
- Dahl, K.K. The Calibration and Use of a Triaxial Cell; Technical University of Denmark, Department of Civil Engineering: Lyngby, Denmark, 1992; ISBN 978-87-7740-105-3. [Google Scholar]
- Hobbs, D.W. Strength of Concrete under Combined Stress. Cem. Concr. Res. 1971, 1, 41–56. [Google Scholar] [CrossRef]
- Speck, K. Beton unter Mehraxialer Beanspruchung (Concrete under Multiaxial Loading Conditions); Universität Dresden: Dresden, Germany, 2007. [Google Scholar]
- Simsch, G. Tragverhalten von Hochbeanspruchten Druckstützen Aus Hochfestem Normalbeton (B 65-B 115); VDI Verlag: Düsseldorf, Germany, 1995; ISBN 3-18-312704-0. [Google Scholar]



| C20/25 | C30/37 | C40/50 | C50/60 | |
|---|---|---|---|---|
| 20 | 30 | 40 | 50 | |
| 2.2 | 2.9 | 3.5 | 4.1 | |
| 30,000 | 33,000 | 35,000 | 37,000 |
| Test Series | Description | Test Procedure (Over Time t) |
|---|---|---|
| P0 | passive; concrete cylinder only; axially loaded (F) until failure | 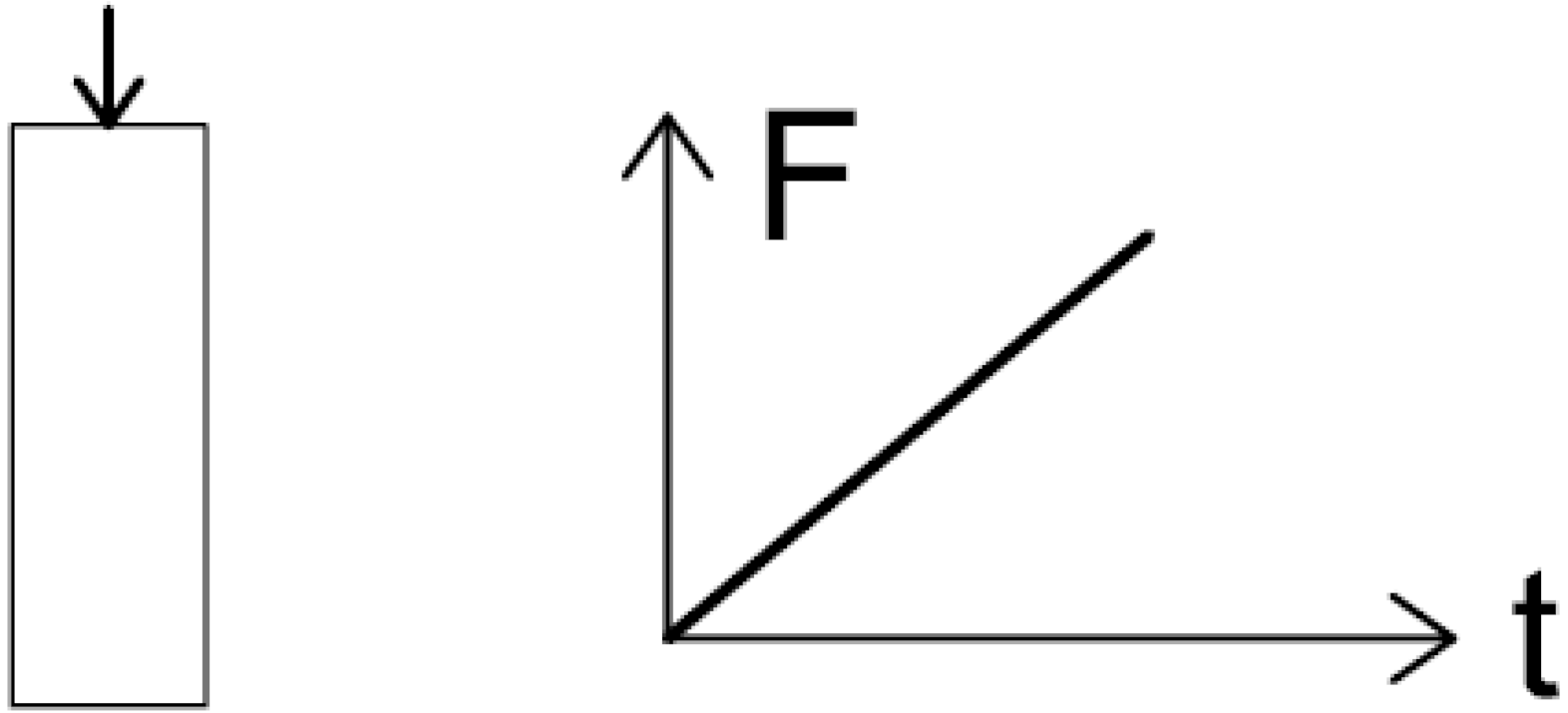 |
| PE | passive; concrete cylinder integrated into envelope; axially loaded (F) until failure | 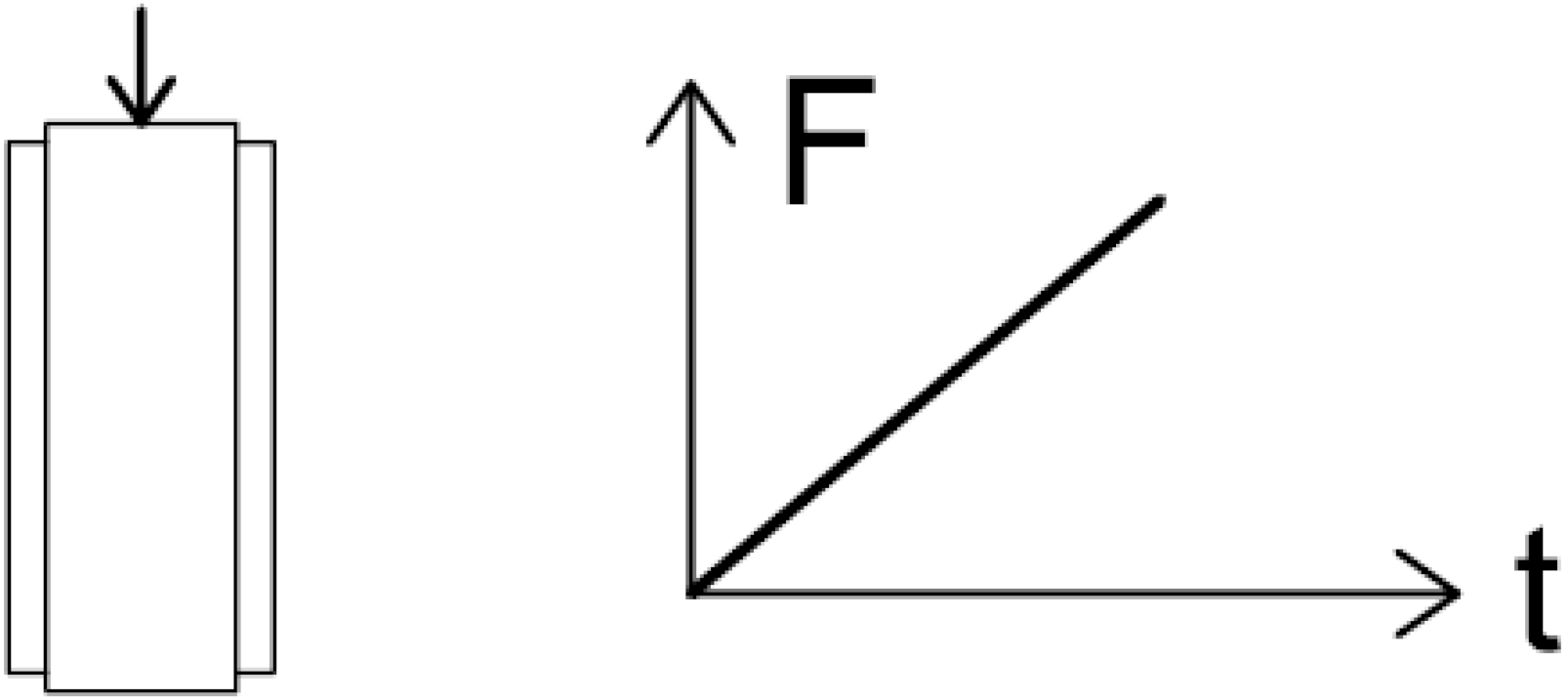 |
| A10 | adaptive; lateral hydraulic pressure (p) of 10 bar; axially loaded (F) until failure | 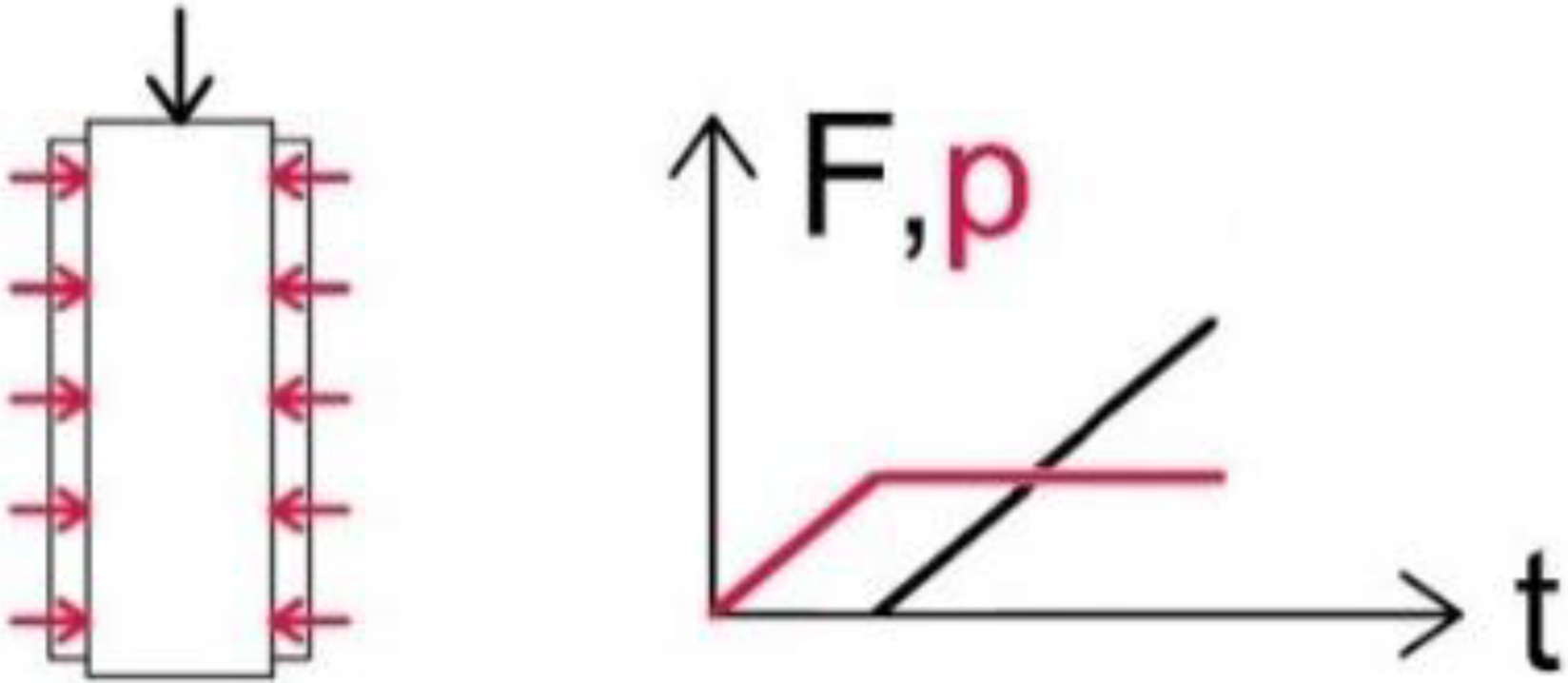 |
| A20 | adaptive; lateral hydraulic pressure (p) of 20 bar; axially loaded (F) until failure | 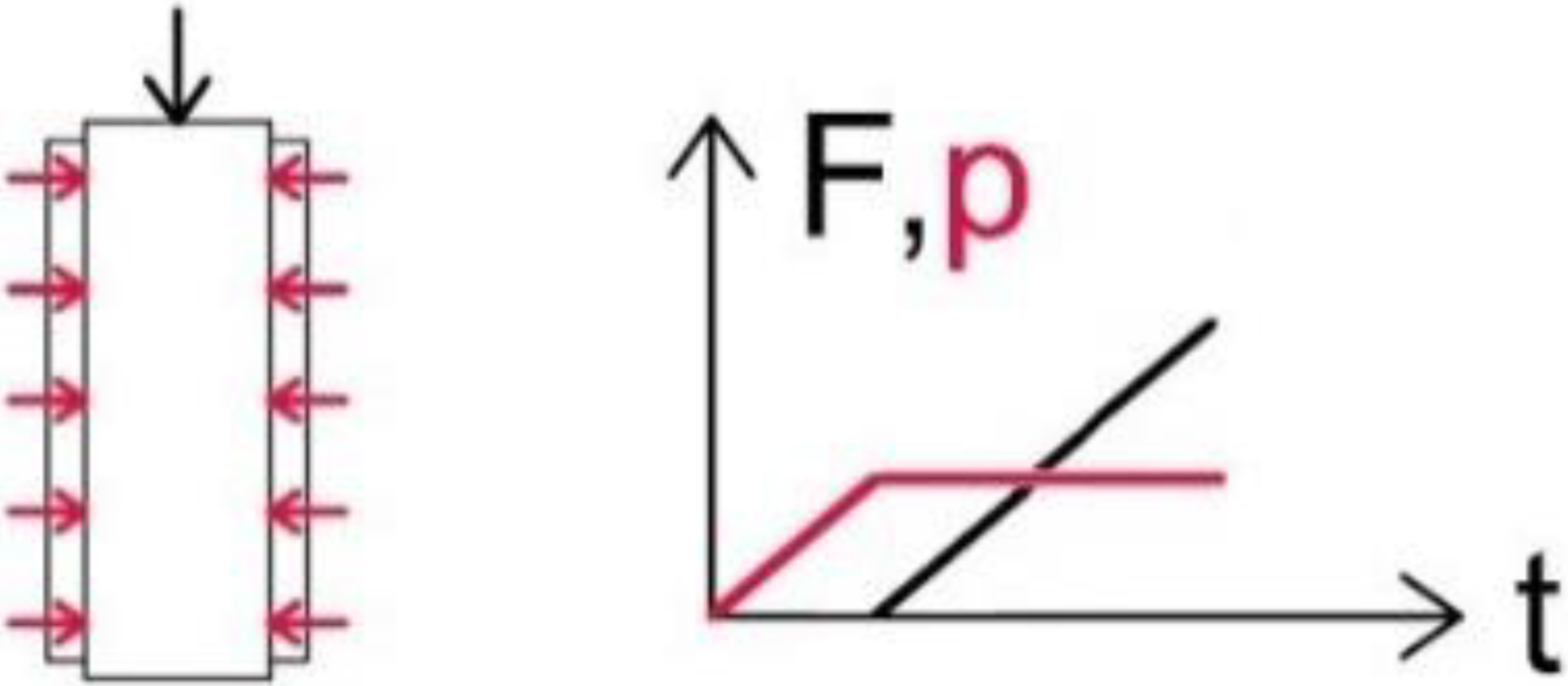 |
| CT | hydraulic pressure (p) of 20 bar only; elastic range | 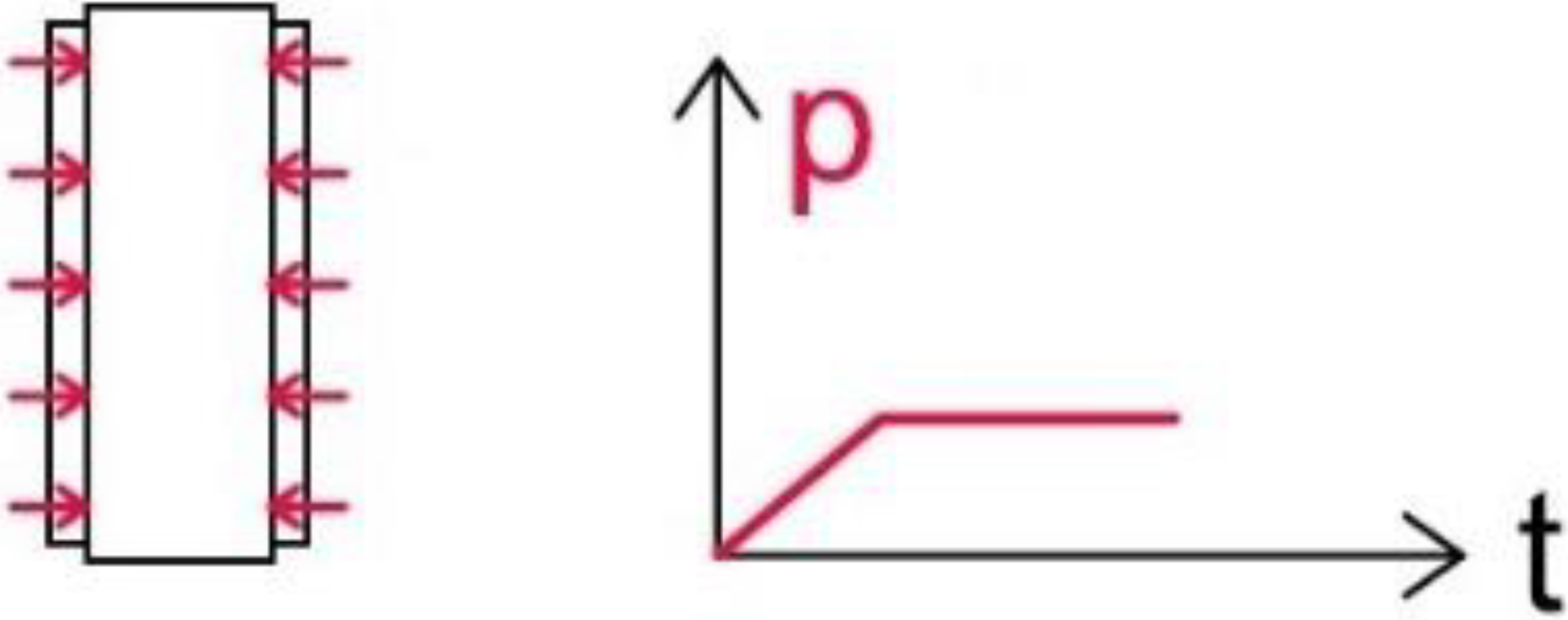 |
| CC | combined axial load (F) of ~10 N (5 MPa) and lateral hydraulic pressure (p) of 20 bar; elastic range | 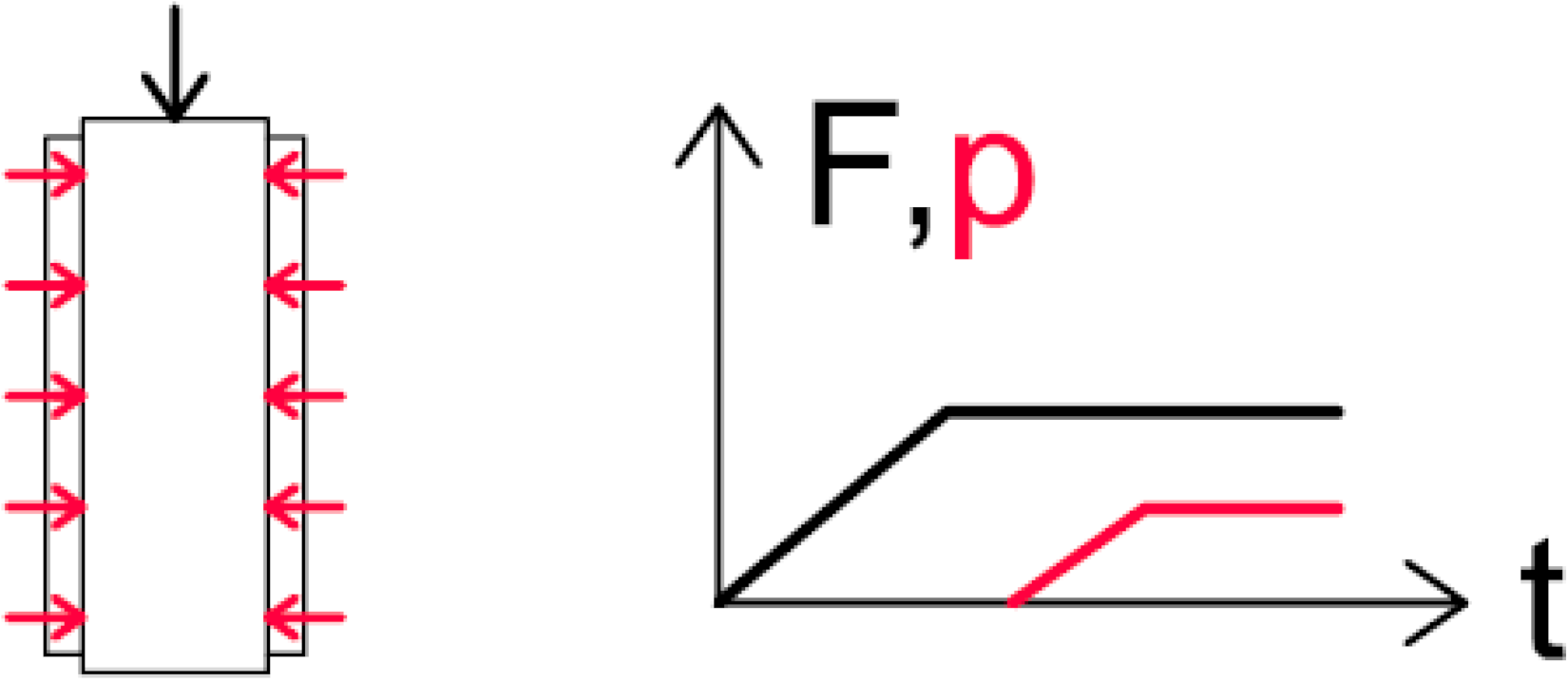 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steffen, S.; Nitzlader, M.; Burghardt, T.; Binz, H.; Blandini, L.; Sobek, W. An Actuator Concept for Adaptive Concrete Columns. Actuators 2021, 10, 273. https://doi.org/10.3390/act10100273
Steffen S, Nitzlader M, Burghardt T, Binz H, Blandini L, Sobek W. An Actuator Concept for Adaptive Concrete Columns. Actuators. 2021; 10(10):273. https://doi.org/10.3390/act10100273
Chicago/Turabian StyleSteffen, Simon, Markus Nitzlader, Timon Burghardt, Hansgeorg Binz, Lucio Blandini, and Werner Sobek. 2021. "An Actuator Concept for Adaptive Concrete Columns" Actuators 10, no. 10: 273. https://doi.org/10.3390/act10100273
APA StyleSteffen, S., Nitzlader, M., Burghardt, T., Binz, H., Blandini, L., & Sobek, W. (2021). An Actuator Concept for Adaptive Concrete Columns. Actuators, 10(10), 273. https://doi.org/10.3390/act10100273







