Large Stepwise Discrete Microsystem Displacements Based on Electrostatic Bending Plate Actuation
Abstract
:1. Introduction
2. Concept
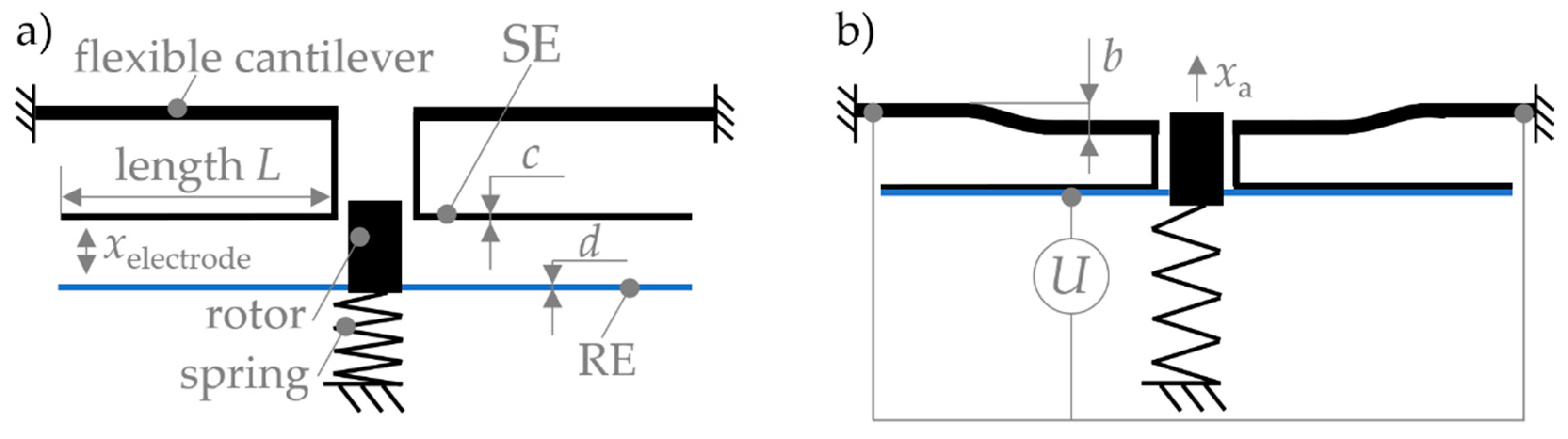
2.1. Flexible Electrostatic Bending Plate Actuators
2.2. System Function
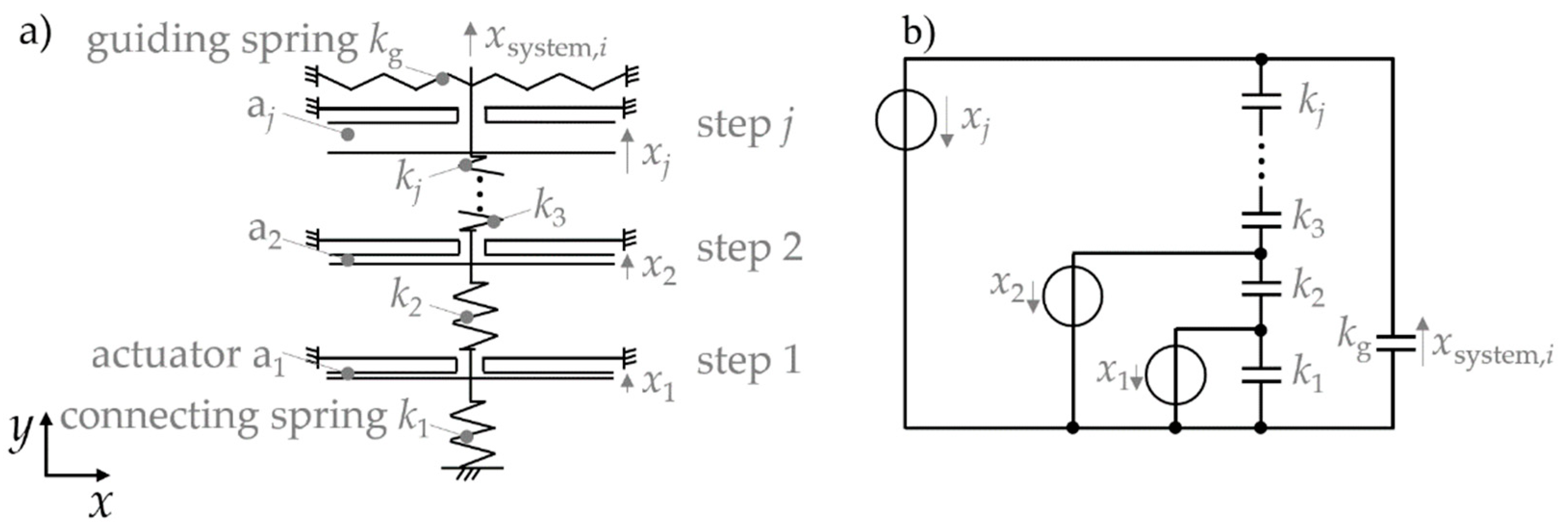
2.3. Step-by-Step and Collective Actuation
2.4. System Setup Based on Modelling and Simulation
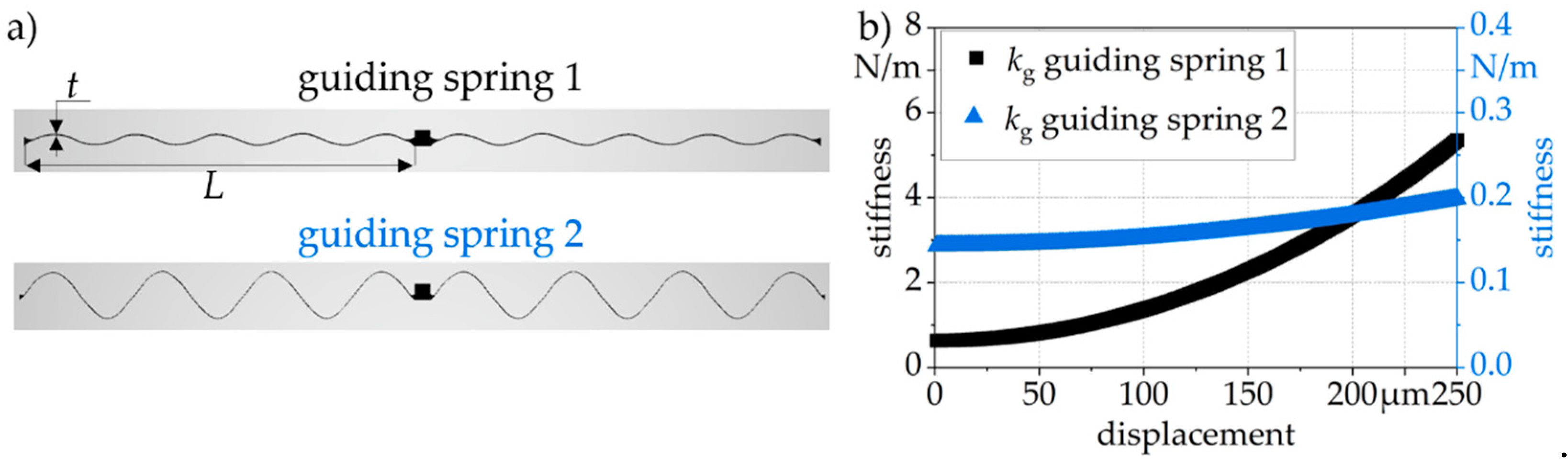
2.4.1. System Design Based on the Guiding Spring
2.4.2. System Design for Different Step Numbers
2.4.3. Overview of the Modelled Systems
3. Fabrication
4. System Characterization
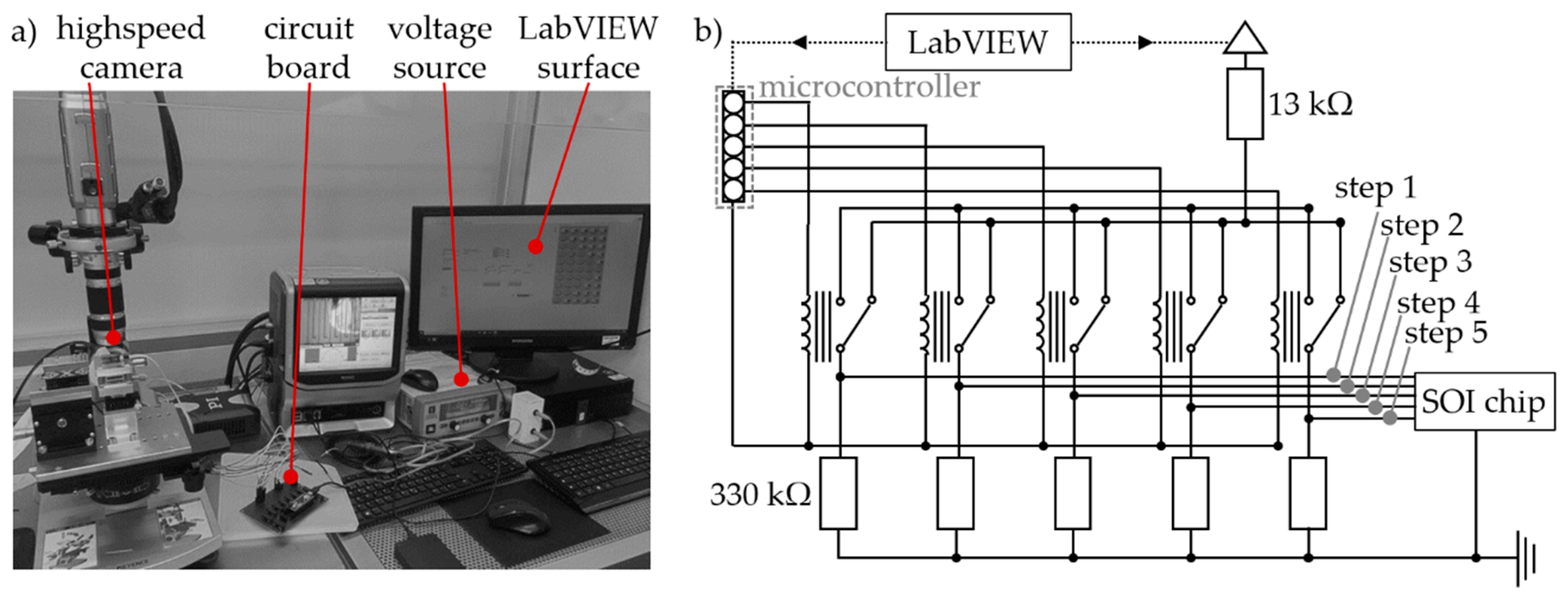
4.1. Experiment and Characterization Setup
4.2. System Characterization Results
4.2.1. Overview of Results
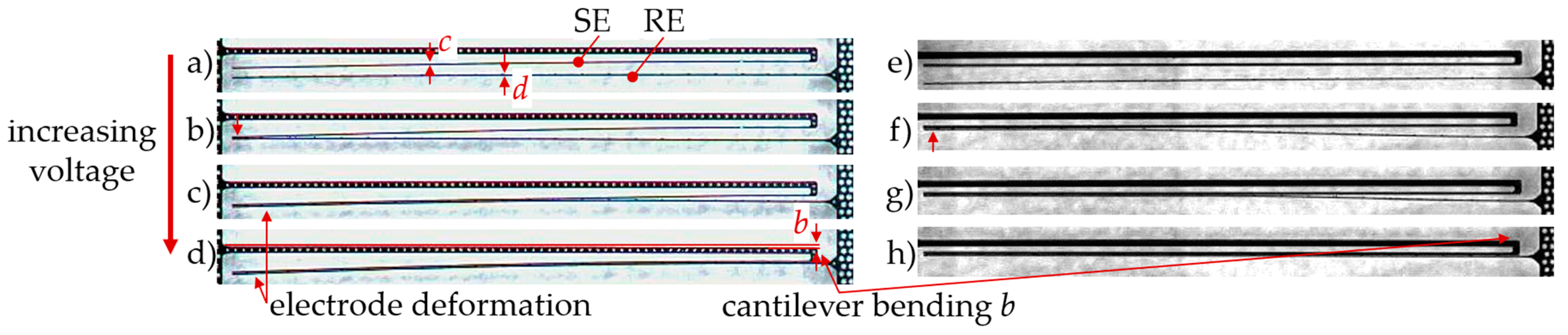
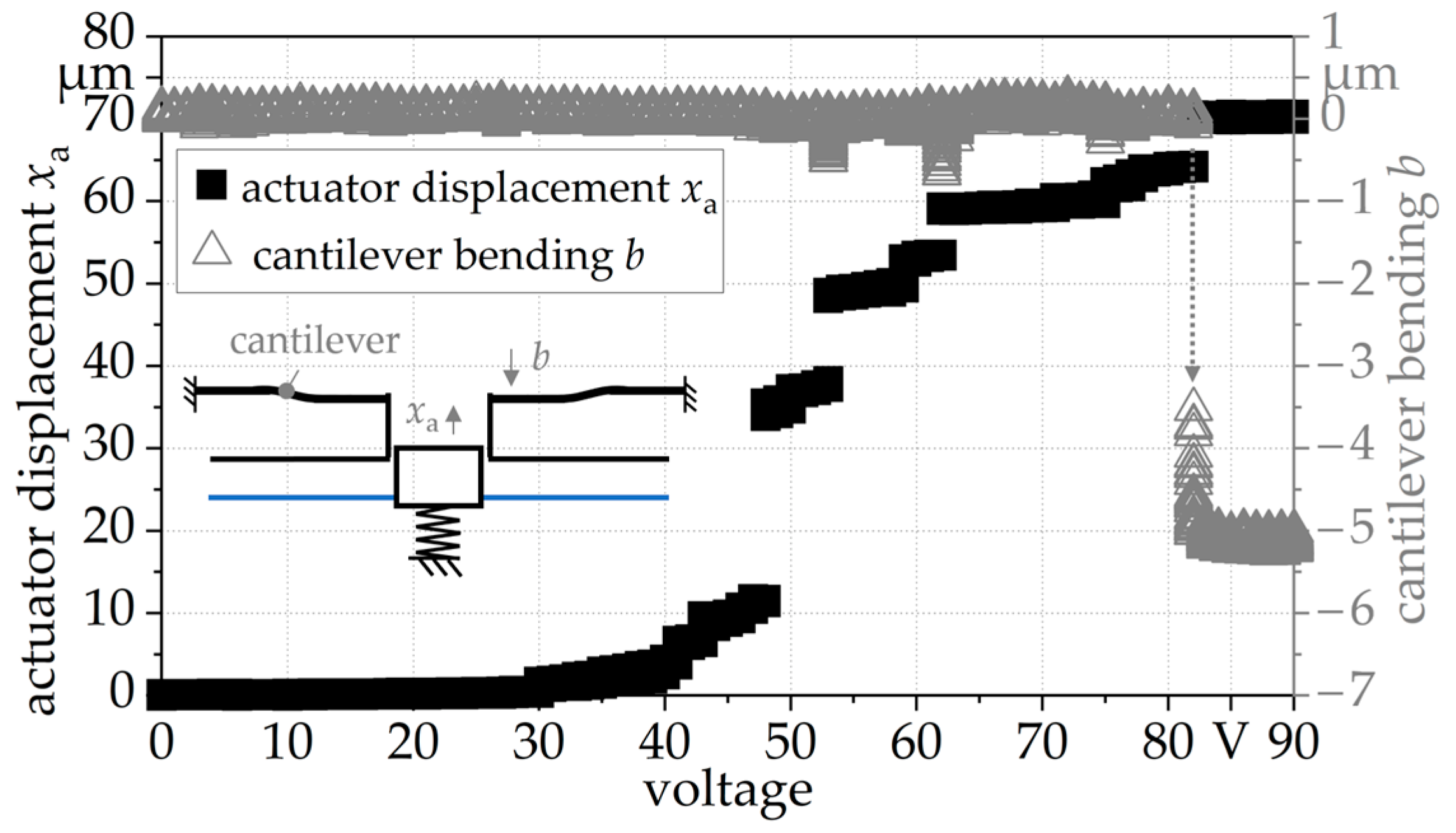
4.2.2. Design-Based Electrostatic Bending Plate Actuator Behavior
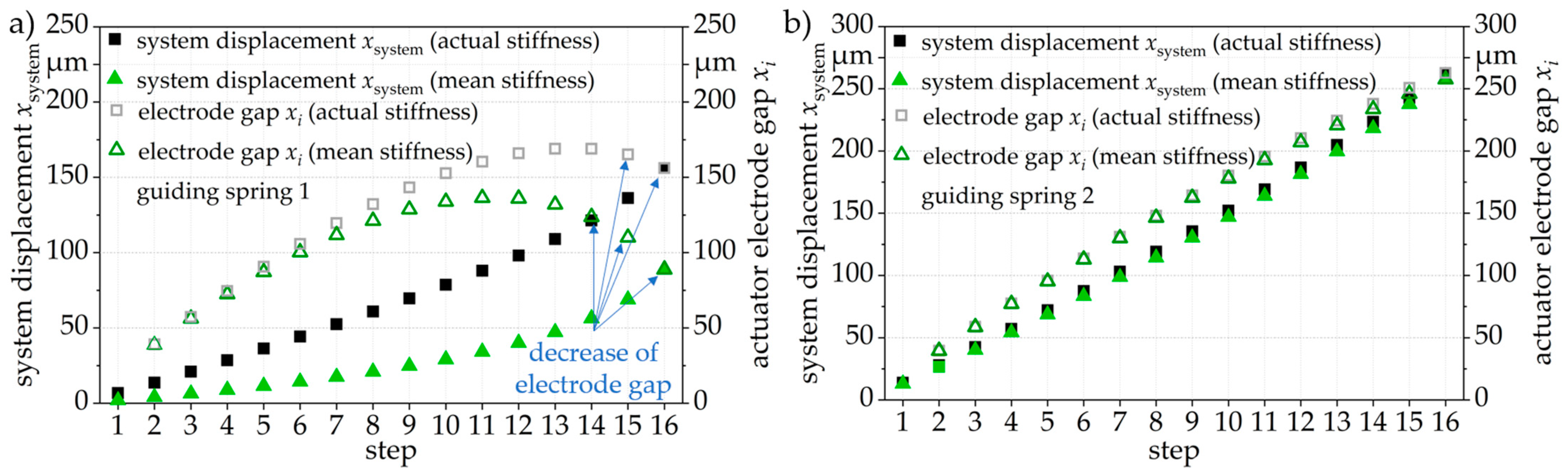
4.2.3. Step-by-Step Actuation of the 5-Step Systems
4.2.4. Comparison of Step-by-Step and Collective Actuation
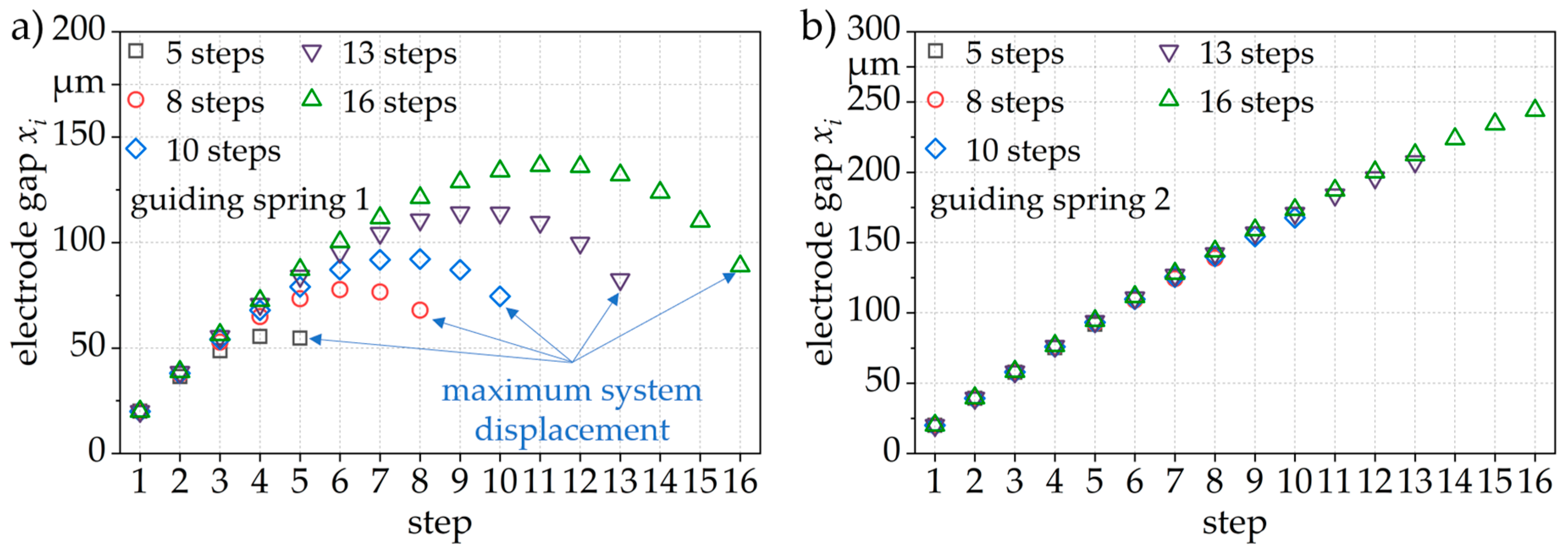
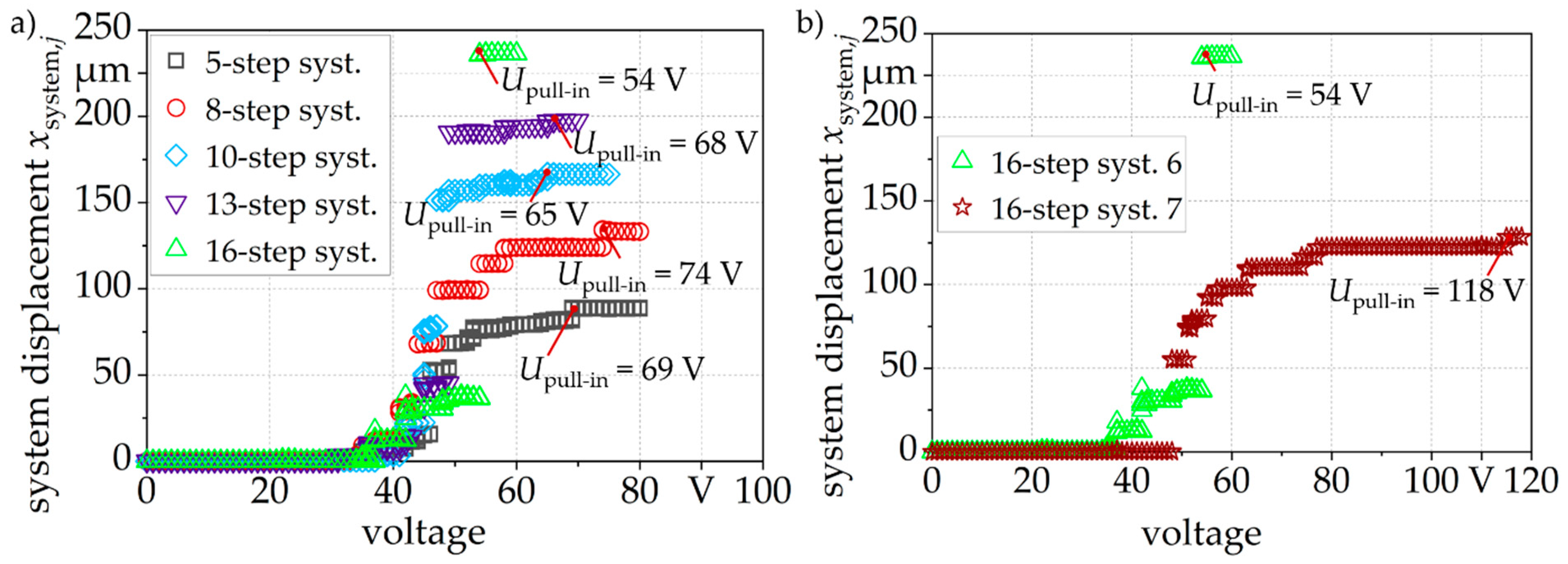
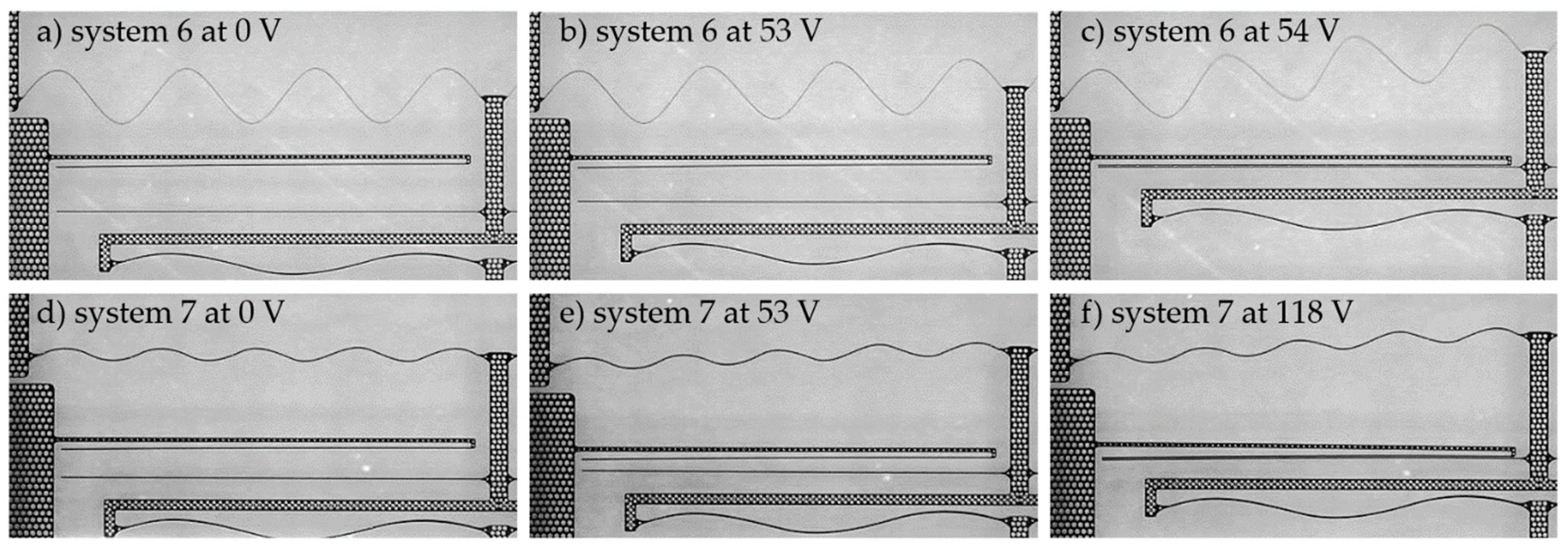
4.2.5. Characterization of Microsystems with 5 to 16 Steps
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, X.; Yang, F.; Liu, C.; Wu, X.; Cui, T.J. Terahertz Beam Steering Technologies: From Phased Arrays to Field-Programmable Metasurfaces. Adv. Opt. Mater. 2020, 8, 1900628. [Google Scholar] [CrossRef]
- Grade, J.D.; Jerman, H.; Kenny, T.W. Design of large deflection electrostatic actuators. J. Micromech. Syst. 2003, 12, 335–343. [Google Scholar] [CrossRef]
- Preetham, B.S.; Lake, M.A.; Hoelzle, D.J. A curved electrode electrostatic actuator designed for large displacement and force in an underwater environment. J. Micromech. Microeng. 2017, 27, 095009. [Google Scholar] [CrossRef]
- Burugupally, S.P.; Perera, W.R. Dynamics of a parallel-plate electrostatic actuator in viscous dielectric media. In Sensors and Actuators A: Physical; Elsevier: Amsterdam, The Netherlands, 2019; Volume 295, pp. 366–373. [Google Scholar]
- Liu, X.; Samfaß, L.; Kolpatzeck, K.; Häring, L.; Balzer, J.C.; Hoffmann, M.; Czylwik, A. Terahertz Beam Steering Concept Based on a MEMS-Reconfigurable Reflection Grating. Sensors 2020, 20, 2874. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.; Nüsse, D.; Voges, E. Electrostatic parallel-plate actuators with large deflections for use in optical moving-fibre switches. J. Micromech. Microeng. 2001, 11, 323. [Google Scholar] [CrossRef]
- Bakri-Kassem, M.; Mansour, R.R. High tuning range parallel plate MEMS variable capacitors with arrays of supporting beams. In Proceedings of the 19th IEEE International Conference on Micro Electro Mechanical Systems, Istanbul, Turkey, 22–26 January 2006; pp. 666–669. [Google Scholar]
- Zhang, J.; Zhang, Z.; Lee, Y.C.; Bright, V.M.; Neff, J. Design and invention of multi-level digitally positioned micromirror for open-loop controlled applications. In Sensors and Actuators A: Physical; Elsevier: Amsterdam, The Netherlands, 2003; Volume 103, pp. 271–283. [Google Scholar]
- Velosa-Moncada, L.A.; Aguilera-Cortés, L.A.; González-Palacios, M.A.; Raskin, J.P.; Herrera-May, A.L. Design of a novel MEMS microgripper with rotatory electrostatic comb-drive actuators for biomedical applications. Sensors 2018, 18, 1664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leroy, E.; Hinchet, R.; Shea, H. Multimode hydraulically amplified electrostatic actuators for wearable haptics. Adv. Mater. 2020, 32, 2002564. [Google Scholar] [CrossRef] [PubMed]
- Legtenberg, R.; Groeneveld, A.W.; Elwenspoek, M. Comb-drive actuators for large displacements. J. Micromech. Microeng. 1996, 6, 320. [Google Scholar] [CrossRef] [Green Version]
- Korvink, J.; Oliver, P. MEMS: A Practical Guide of Design, Analysis, and Applications; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Dean, R.N.; Wilson, C.; Brunsch, J.P.; Hung, J.Y. A synthetic voltage division controller to extend the stable operating range of parallel plate actuators. In Proceedings of the 2011 IEEE International Conference on Control Applications (CCA), Denver, CO, USA, 28–30 September 2011; pp. 1068–1074. [Google Scholar] [CrossRef]
- Chiou, J.C.; Lin, Y.C. A novel capacitance control design of tunable capacitor using multiple electrostatic driving electrodes. In Proceedings of the IEEE-NANO 2001, M3.1 Nanoelectronics and Giga-Scale Systems, Maui, HI, USA, 28–30 October 2001; pp. 319–324. [Google Scholar]
- Seeger, J.I.; Boser, B.E. Charge control of parallel-plate, electrostatic actuators and tip-in instability. J. Micromech. Syst. 2003, 12, 656–671. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.C.; Fedder, G.K. Position control of parallel-plate microactuators for probe based data storage. J. Micromech. Syst. 2004, 13, 759–769. [Google Scholar] [CrossRef]
- Maithripala, D.H.S.; Berg, J.M.; Dayawansa, W.P. Nonlinear dynamic output feedback stabilization of electrostatically actuated MEMS. In Proceedings of the IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; Volume 1, pp. 61–66. [Google Scholar]
- Schmitt, L.; Schmitt, P.; Hoffmann, M. 3-Bit Digital-to-Analog Converter with Mechanical Amplifier for Binary Encoded Large Displacements. Actuators 2021, 10, 182. [Google Scholar] [CrossRef]
- Schmitt, L.; Schmitt, P.; Barowski, J.; Hoffmann, M. Stepwise Electrostatic Actuator System for THz Reflect Arrays. In Proceedings of the International Conference and Exhibition on New Actuator Systems and Applications, Online, 17–19 February 2021; 2021. [Google Scholar]
- Schmitt, P.; Schmitt, L.; Tsivin, N.; Hoffmann, M. Highly Selective Guiding Springs for Large Displacements in Surface MEMS. J. Micromech. Syst. 2021. [Google Scholar] [CrossRef]
- Overstolz, T.; Clerc, P.A.; Noell, W.; Zickar, M.; de Rooij, N.F. A clean wafer-scale chip-release process without dicing based on vapor phase etching. In Proceedings of the 17th IEEE International Conference on Micro Electro Mechanical Systems. Maastricht MEMS 2004 Technical Digest, Maastricht, The Netherlands, 25–29 January 2004. [Google Scholar]
- Sari, I.; Zeimpekis, I.; Kraft, M. A dicing free SOI process for MEMS devices. Microelectron. Eng. 2012, 95, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Schmitt, L.; Schmitt, P.; Liu, X.; Czylwik, A.; Hoffmann, M. Micromechanical Reflect-Array for THz Radar Beam Steering based on a Mechanical D/A Converter and a Mechanical Amplifier. In Proceedings of the 2020 Third International Workshop on Mobile Terahertz Systems (IWMTS), Essen, Germany, 1–2 July 2020. [Google Scholar]





| System | Number of Steps | Activation | Design/ Stiffness Value | Guiding Spring | Max. Calculated Displacement | Chip Size [µm × µm] | Presented in Figure |
|---|---|---|---|---|---|---|---|
| 1 | 5 | step-by-step and collective | mean | 1 | 80 µm | 6945 × 10,253 | 6a |
| 2 | 5 | step-by-step and collective | actual | 2 | 94 µm | 6945 × 10,253 | 3a |
| 3 | 8 | collective | mean | 2 | 143 µm | 8865 × 9157 | 6b |
| 4 | 10 | collective | mean | 2 | 171 µm | 10,255 × 9157 | 6b |
| 5 | 13 | collective | mean | 2 | 212 µm | 12,392 × 9157 | 6b |
| 6 | 16 | collective | mean | 2 | 242 µm | 14,407 × 9157 | 3b, 5b, 6b |
| 7 | 16 | collective | actual | 1 | 156 µm | 14,407 × 9157 | 5a |
| System | Max. Experimental Displacement | Voltage for Max. Displacement | System Properties |
|---|---|---|---|
| 1 | xsystem,5 = 71.9 ± 0.5 µm | 82 V (step-by-step) 71 V (collective) | xsystem,1 = 5.9 µm, xsystem,2 = 22.0 µm, xsystem,3 = 38.5 µm, xsystem,4 = 55.4 µm, oscillation during step-by-step actuation |
| 2 | xsystem,5 = 89.4 ± 0.8 µm | 97 V (step-by-step) 69 V (collective) | xsystem,1 = 10.6 µm, xsystem,2 = 27.9 µm, xsystem,3 = 47.3 µm, xsystem,4 = 61.4 µm, oscillation during step-by-step actuation |
| 3 | xsystem,8 = 138.4 ± 2.3 µm | 74 V | pull-in order: a1 + a2, a3 + a4, a5, a6, a7, a8 |
| 4 | xsystem,10 = 168.3 ± 3.1 µm | 65 V | pull-in order: a1, a2–a7, a8, a9, a10 |
| 5 | xsystem,13 = 202.7 ± 3.6 µm | 68 V | pull-in order: a1, a2–a4, a5–a8, a9, a10–a12, a13 |
| 6 | xsystem,16 = 230.7 ± 0.9 µm | 54 V | pull-in order: a1, a2, a3, a4, a5–a16 |
| 7 | xsystem,16 = 138.9 ± 1.7 µm | 118 V | pull-in order: a1, a2 + a3, a4–a6, a7, a8, a9–a12, a13, a14, a15, a16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitt, L.; Hoffmann, M. Large Stepwise Discrete Microsystem Displacements Based on Electrostatic Bending Plate Actuation. Actuators 2021, 10, 272. https://doi.org/10.3390/act10100272
Schmitt L, Hoffmann M. Large Stepwise Discrete Microsystem Displacements Based on Electrostatic Bending Plate Actuation. Actuators. 2021; 10(10):272. https://doi.org/10.3390/act10100272
Chicago/Turabian StyleSchmitt, Lisa, and Martin Hoffmann. 2021. "Large Stepwise Discrete Microsystem Displacements Based on Electrostatic Bending Plate Actuation" Actuators 10, no. 10: 272. https://doi.org/10.3390/act10100272






