Design of Four-DoF Compliant Parallel Manipulators Considering Maximum Kinematic Decoupling for Fast Steering Mirrors

Abstract

Laser beams can fluctuate in four directions, which requires active compensation by a fast steering mirror (FSM) motion system. This paper deals with the design of four-degrees-of-freedom (DoF) compliant parallel manipulators, for responding to the requirements of the FSM. In order to simplify high-precision control in parallel manipulators, maximum kinematic decoupling is always desired. A constraint map method is used to propose the four required DoF with the consideration of maximum kinematic decoupling. A specific compliant mechanism is presented based on the constraint map, and its kinematics is estimated analytically. Finite element analysis demonstrates the desired qualitative motion and provides some initial quantitative analysis. A normalization-based compliance matrix is finally derived to verify and demonstrate the mobility of the system clearly. In a case study, the results of normalization-based compliance matrix modelling show that the diagonal entries corresponding to the four DoF directions are about 10 times larger than those corresponding to the two-constraint directions, validating the desired mobility.

1. Introduction

Laser light sources have been widely used in various domains [1,2,3], with particular applications in high-quality and high-value products. Studies have shown that the geometric fluctuations of the laser light beam are not only affected by environmental conditions but also by the input and its structure, and by thermal issues [4,5,6,7,8,9]. Therefore, an optical device called a fast steering mirror (FSM) was invented to steer the laser beam, for stabilization and other applications [10,11]. The FSM consists of a mirror, an actuator, and a flexure structure which is required to compensate for the two in-plane translations and two out-of-plane rotations related to the fluctuations of laser beams, i.e., four degrees of freedom (DoF) [12,13].

A traditional FSM has two-piece two-axis actuators, and it has defects associated with an overlong optical path length, many elements, and difficulty in the set-up process. In [14], an FSM compensation system with double Porro prisms was reported to address the issues of the traditional FSM. Double Porro prisms are variants of 90° prisms that are used as a pair to displace and invert a beam, and they are widely employed in binoculars and beam rotators. The 90° prism can tilt and shift the laser path when it is rotated and shifted. When a pair of 90° prisms are put together vertically (called double Porro prisms), they have the ability to achieve 4-DoF steering [14]. This optical design was implemented and verified by a commercial 6-DoF Stewart parallel kinematic platform without designing a special 4-DoF mechanism for it. A compact 5-DoF motion system was presented in [15] for an optical anti-vibration mobile camera which can be used for FSM purposes. It consists of eight voice coil motors and a 5-DoF compliant mechanism. However, there are too many actuators for controlling only the four desired DoFs, and the other two DoFs of the compliant mechanism are not desired/constrained.

Based on the above advances, this paper aims to propose a framework for designing 4-DoF manipulators for FSM applications. Nowadays, manipulators with high precision and multiple functions play a more and more important role in various applications, such as surgery, grab operations, and positioning [16,17,18]. Ranzani et al. in [19] presented a bioinspired soft manipulator for minimally invasive surgery. They achieved similar motion capabilities to the octopus’s arm in order to reach the surgical target while exploiting its whole length to actively interact with the biological structures. Mishra et al. in [20] presented a hybrid approach for robotics-integrated manufacturing by utilizing the capability of both soft and rigid robotics. The whole manipulator is able to perform specific and delicate tasks such as pouring water, grasping eggs, or instant bending for obstacle avoidance. Li et al. in [21] presented a decoupled XY flexure parallel kinematic manipulator. The output decoupling is allowed by employing compound parallelogram flexure, and the input decoupling is implemented by actuation isolation. Nakshatharana et al. in [22] presented a 3-DoF manipulator which is a novel ionically driven soft, flat, parallel manipulator with a minimal footprint. They demonstrated the application of the 3-DoF manipulator via a four-way laser steering application. Xiao et al. in [23] presented a novel compliant flexure-based micro-parallel positioning stage for micro active vibration isolation applications. The designed manipulator is used as a high-accuracy 3-DOF micro/nano positioning stage for bio-engineering or micro-assembly applications. In [24] multi-DOF compliant parallel manipulators were presented using a new kinematic substitution method. The proposed design approach is a straightforward method for designing the multi-axis compliant manipulators by replacing the traditional kinematic sub-chain with appropriate multi-DOF compliant building blocks.

Because compliant parallel manipulators have many advantages, such as eliminated backlash, simplified manufacture, and low parts count [25,26,27,28], this study aimed to design a 4-DoF parallel manipulator for an FSM using compliant mechanisms. In order to simplify high-precision control in parallel manipulators, maximum kinematic decoupling was pursued in this study.

This paper is organized as follows. Section 2 proposes a general constraint map for manipulator design, considering maximum kinematic decoupling. A specific compliant parallel manipulator is presented in Section 3, with a kinematics approximation. Section 4 simulates the design and provides some initial quantitative results, followed by a mobility analysis using a normalization method in Section 5. Conclusions are finally drawn in Section 6.

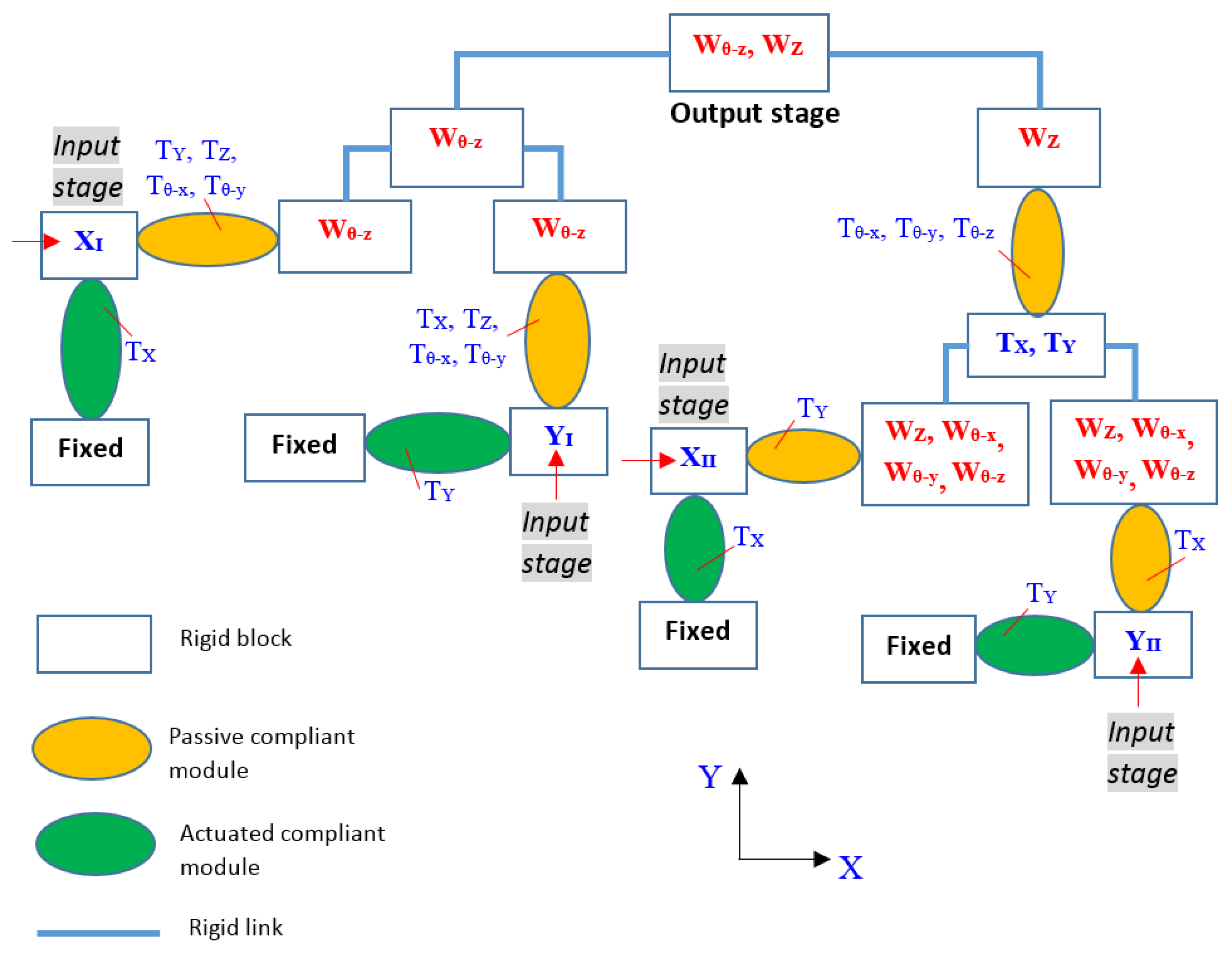
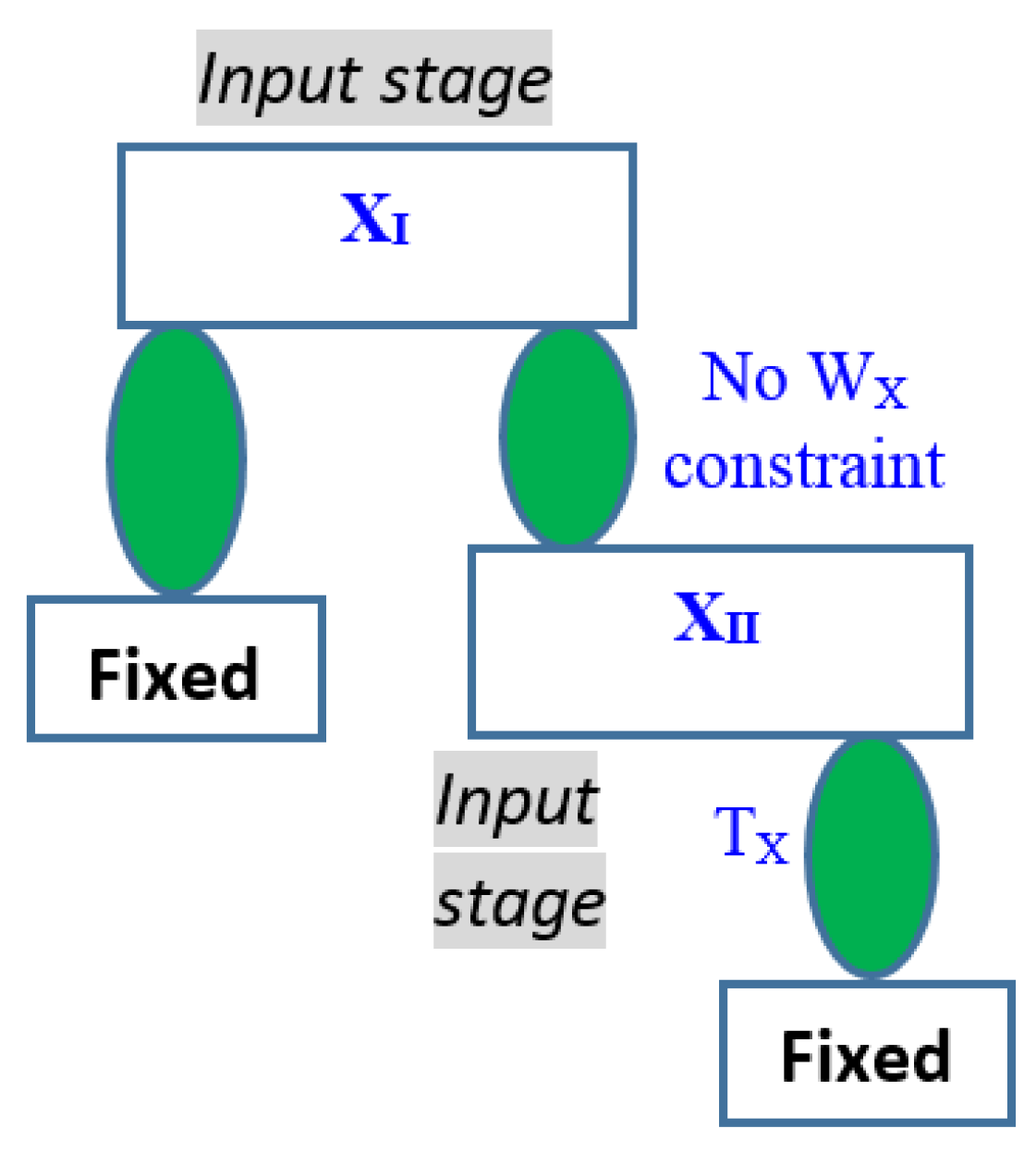
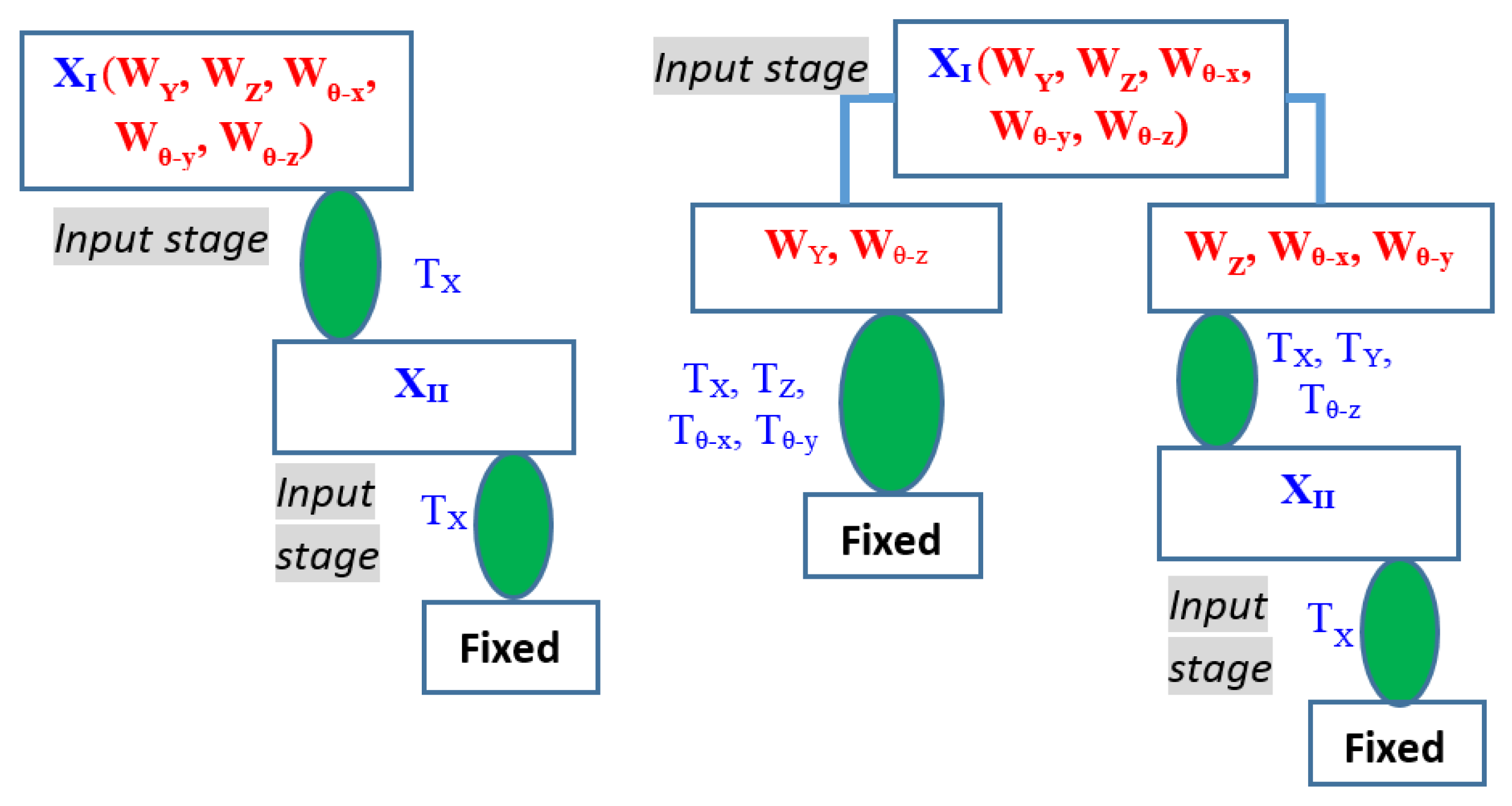
2. Constraint Map of Parallel Manipulators

Aiming at obtaining a manipulator for two in-plane translations and two our-of-plane rotations, this section proposes a basic constraint map (qualitatively) [29,30], which adheres to the following two general rules:

• Rule of a parallel mechanism: the wrench (or constraint denoted by W with a subscript for direction) of the end-effector of a parallel mechanism is the union of constraints from all legs in parallel;
• Rule of a serial mechanism/leg: the twist (or desired motion denoted by T with a subscript for direction) of the end-effector of a serial mechanism is the union of twists from all components in series.

Note that the corresponding wrench and twist follow a reciprocal relation.

Figure 1 demonstrates the details of the constraint map with maximum kinematic decoupling. The overall configuration is a parallel mechanism with two legs (Leg I and Leg II) connected at the output stage (rigid motion stage), one constraining the in-plane output rotation (W_θ-Z) and the other constraining the out-of-plane output translation (W_Z). Each leg has its own sub-leg system as shown in Figure 1, with two input stages (rigid): one for the X-axis actuation (X_I or X_II) and the other for the Y-axis actuation (Y_I or Y_II). Four actuators in total are needed to actuate the four input stages, which are all connected to base (ground). Leg I aims to produce two out-of-plane output rotations via two translational inputs/actuations, while Leg II aims to yield two in-plane output translations via two translational actuations. The actuation and the output motion are demonstrated in Section 4.

For Leg II, we can also constrain both the in-plane rotation and the out-of-plane translation. In the next section, we present a compliant parallel manipulator based on the constraint map in Figure 1.

Each of the two input stages for actuation in the same direction can also be interconnected using a compliant module, as shown in Figure 2 [30]. Two examples of the interconnection constraint are shown in Figure 3.

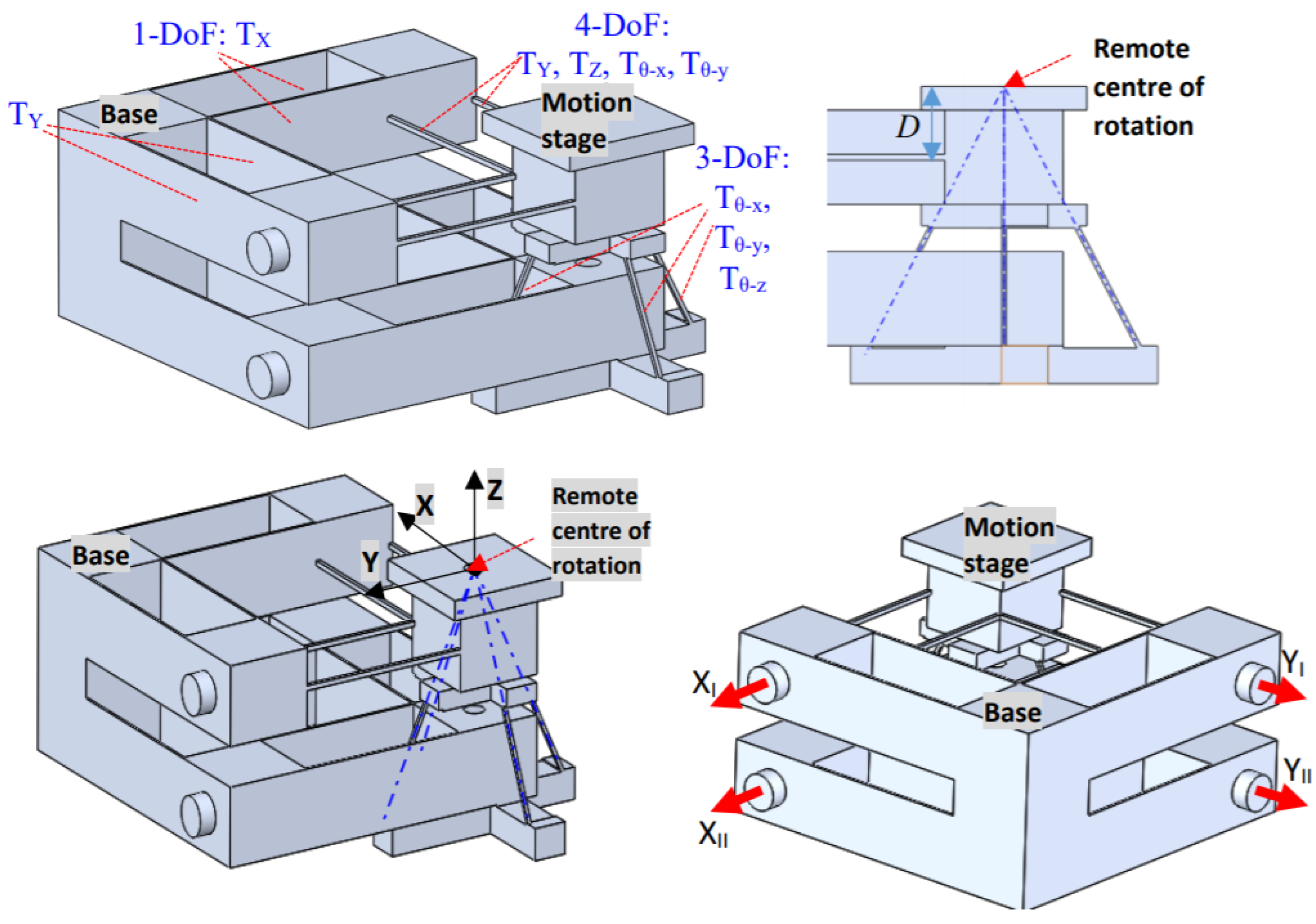
3. Design of a Compliant Parallel Manipulator

A four-DoF compliant parallel manipulator (Figure 4) is obtained by specifying each compliant module in Figure 3 and making appropriate structure arrangements. It has two layers coupled by the three-DoF rotational compliant module with a remote center of rotation (indicated at the center of the motion stage). The 1-DoF actuated compliant prismatic module uses the traditional parallelogram mechanism composed of two leaf beams. The 4-DoF passive compliant module uses the parallelogram mechanism composed of two wire (symmetrical) beams. The 3-DoF passive compliant rotational module consists of four wire beams with a common intersection point as the remote center of rotation. The top layer constrains the in-plane rotation of the motion stage and the bottom layer, along with the 3-DOF rotational module, constrains the out-of-plane translation.

Let the displacements of the motion stage at the center (specified in Figure 4) in the four DOF directions be S_X, S_Y, θ_X, and θ_Y, which can be approximately calculated based on the four actuation displacements as shown below:

S_X = X_II

(1)

S_Y = Y_II

(2)

θ_X = (Y_I − Y_II)/D

(3)

θ_Y = −(X_I − X_II)/D

(4)

where S_X and S_Y denote the translational displacements along the X- and Y-axes, respectively, and θ_X and θ_Y denote the rotational displacements about the X- and Y-axes, respectively. D is the geometrical parameter, as indicated in Figure 4.

Equations (1) through (4) show the maximum kinematic decoupling in principle. In reality, there is inherent kinematic coupling between the inputs and desired outputs due to parasitic motions in each compliant module. There are also parasitic motions in the other two non-DOF directions.

4. Simulations and Initial Performance Analysis

Finite element analysis (fine meshing) is used to simulate the compliant manipulator with the main parameter D = 15 mm (Figure 4). The qualitative simulation results in two actuation scenarios, and a 3D-printed prototype, are shown in Figure 5. For the actuation scenario as shown in Figure 5b, X_I = 1mm and X_II = Y_I = Y_II = 0, and we can see the clear difference between the ideal and simulation results in

Table 1. Comparison between simulation and ideal results for translational case.

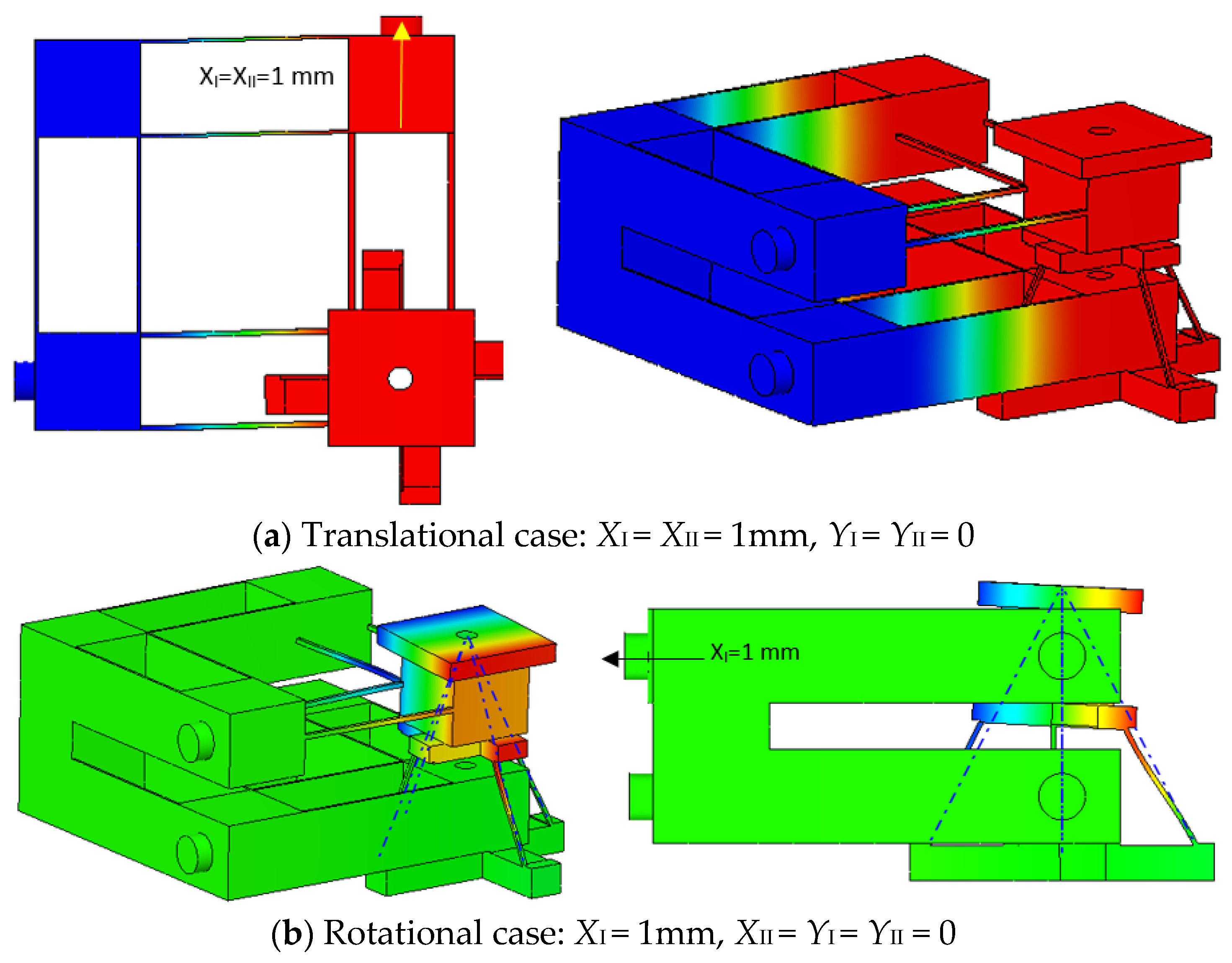
Actuations: XI = XII = 1 mm, YI = YII = 0	In Principle/Ideal Output	FEA Simulation Output
Translation along X: SX	1	9.9 × 10−1 mm
Translation along Y: SY	0	−4.5 × 10−5 mm
Translation along Z (parasitic): SZ	0	3.7 × 10−5 mm
Rotation about X: θX	0	9.9 × 10−5 rad
Rotation about Y: θY	0	−5.6 × 10−6 rad
Rotation about Z (parasitic): θZ	0	−3.3 × 10−4 rad

and

Table 2. Comparison between simulation and ideal results for rotational case.

Actuations:	In Principle/Ideal Output	FEA Simulation Output
XI = 1 mm, XII = YI = YII = 0
Translation along X: SX	0	1.9 × 10−1 mm
Translation along Y: SY	0	3 × 10−2 mm
Translation along Z (parasitic): SZ	0	5.2 × 10−2 mm
Rotation about X: θX	0	1.9 × 10−3 rad
Rotation about Y: θY	−5.2 × 10−2 rad	−6 × 10−2 rad
Rotation about Z (parasitic): θZ	0	1 × 10−4 rad

, indicating the kinematic coupling and the parasitic motions in the two constrained directions of the motion stage.

There is considerable room for improvement in the proposed design (at the compliant module level) in terms of kinematic coupling and parasitic motions. We can either optimize the geometric parameters of each currently used compliant module (including optimizing the position space of each compliant module [31]), or we can use a better (different) compliant module [32]. In addition, we can also improve the constraint map (at the topology level) by adding redundant legs for creating symmetry so that the motion stage shows better behavior.

5. Mobility Analysis

The mobility or DOF of the proposed design (Figure 4) can be verified by its analytical compliance matrix. In this section, the compliance matrix of the proposed design is derived in terms of the global coordinate frame XYZ.

The motion of the design is enabled by the deformation of its constituent compliant elements, i.e., strip beams and wire (bisymmetrical) beams. Therefore, the stiffness matrices of strip beams and wire beams are essential for the derivation of the compliance matrix of the design. Let all beams have the same length and the same thickness. The beam length is considered as the characteristic length for normalization in this paper. The normalized stiffness matrices of a wire beam and a strip beam can be expressed as shown in Equations (5) and (6) in their local coordinate frames, respectively [33].

$${\mathrm{K}}_{\mathrm{w}}=\left(\begin{array}{cccccc}\frac{12}{{\left(t\right)}^2}& 0& 0& 0& 0& 0\\ 0& 12& 0& 0& 0& -6\\ 0& 0& 12& 0& 6& 0\\ 0& 0& 0& \frac{1}{\mu +1}& 0& 0\\ 0& 0& 6& 0& 4& 0\\ 0& -6& 0& 0& 0& 4\end{array}\right)$$

(5)

$${\mathrm{K}}_{\mathrm{s}}=\left(\begin{array}{cccccc}\frac{12\left(1-{\mu }^2\right)}{t^2}& 0& 0& 0& 0& 0\\ 0& 12& 0& 0& 0& -6\\ 0& 0& \frac{12w^2\left(1-{\mu }^2\right)}{t^2}& 0& \frac{6w^2\left(1-{\mu }^2\right)}{t^2}& 0\\ 0& 0& 0& 2\left(1-\mu \right)& 0& 0\\ 0& 0& \frac{6w^2\left(1-{\mu }^2\right)}{t^2}& 0& \frac{4w^2\left(1-{\mu }^2\right)}{t^2}& 0\\ 0& -6& 0& 0& 0& 4\end{array}\right)$$

(6)

Here, w is the normalized width of the strip beam, t is the normalized thickness of the strip/wire beam, and µ represents the Poisson ratio of the material.

If the normalized stiffness matrices of all the wire beams and strip beams of the design are transformed from their local coordinate frames to the global coordinate frame, the normalized stiffness matrix of the whole design, denoted K_whole, can be obtained by combining all the transformed normalized stiffness matrices together. Such combinations are subject to the following two rules:

• The combined stiffness matrix of the compliant elements, placed in parallel, is the sum of all the stiffness matrices of the compliant elements;
• The combined stiffness matrix of compliant elements, placed in series, is the inverse of the combined compliance matrix, where the combined compliance matrix is the sum of the inverse of the stiffness matrices of the compliant elements.

Once the normalized stiffness matrix of the design is obtained, its normalized compliance matrix equals the inverse of the normalized stiffness matrix. Equation (7) shows the results of the system compliance matrix, where the following parameters are used: (identical) beam length L = 50 mm, E = 69,000 MPa, w (W/L) = 0.4, t (T/L) = 0.015, µ = 0.3, and d (D/L) = 0.2, and the height of the output stage h (H/L) = 0.1.

It can be seen that the normalized entries in the diagonal associated with the motions along and about the X- and Y-axes are 1.12 × 10⁻², 1.13 × 10⁻², 1.56 × 10⁻², and 1.53 × 10⁻², which are much larger than the other values. Therefore, the normalized compliance matrix indicates that the directions along and about the X- and Y-axes are the DOF directions of the design.

$${\mathrm{C}}_{\mathrm{whole}}={\left({\mathrm{K}}_{\mathrm{whole}}\right)}^{-1}=\left(\begin{array}{cccccc}1.12\times 10^{-2}& 0& 0& 0& 2.9\times {10}^{-3}& 0\\ 0& 1.13\times 10^{-2}& 0& -3.09\times {10}^{-3}& 0& 0\\ 0& 0& 1.61\times 10^{-3}& -1.08\times {10}^{-3}& 0& 0\\ 0& -3.09\times {10}^{-3}& -1.08\times {10}^{-3}& 1.56\times 10^{-2}& 0& 0\\ 2.9\times {10}^{-3}& 0& 0& 0& 1.53\times 10^{-2}& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right)$$

(7)

6. Conclusions

In this paper, we presented a general framework for the design of a kinematically decoupled parallel mechanism, based on a constraint map method. We designed a compliant parallel manipulator and subjected it to a preliminary analysis. There is considerable future work to be done in improving the work in this paper, including developing an accurate kinematic and kinetostatic model, developing a comprehensive optimization method, prototype manufacture, and experimental testing, as well as integration into the FSM.