Contactless Picking of Objects Using an Acoustic Gripper †
Abstract
:1. Introduction
2. Acoustic Levitation Using Transducer Arrays
2.1. Pressure and Force Generation
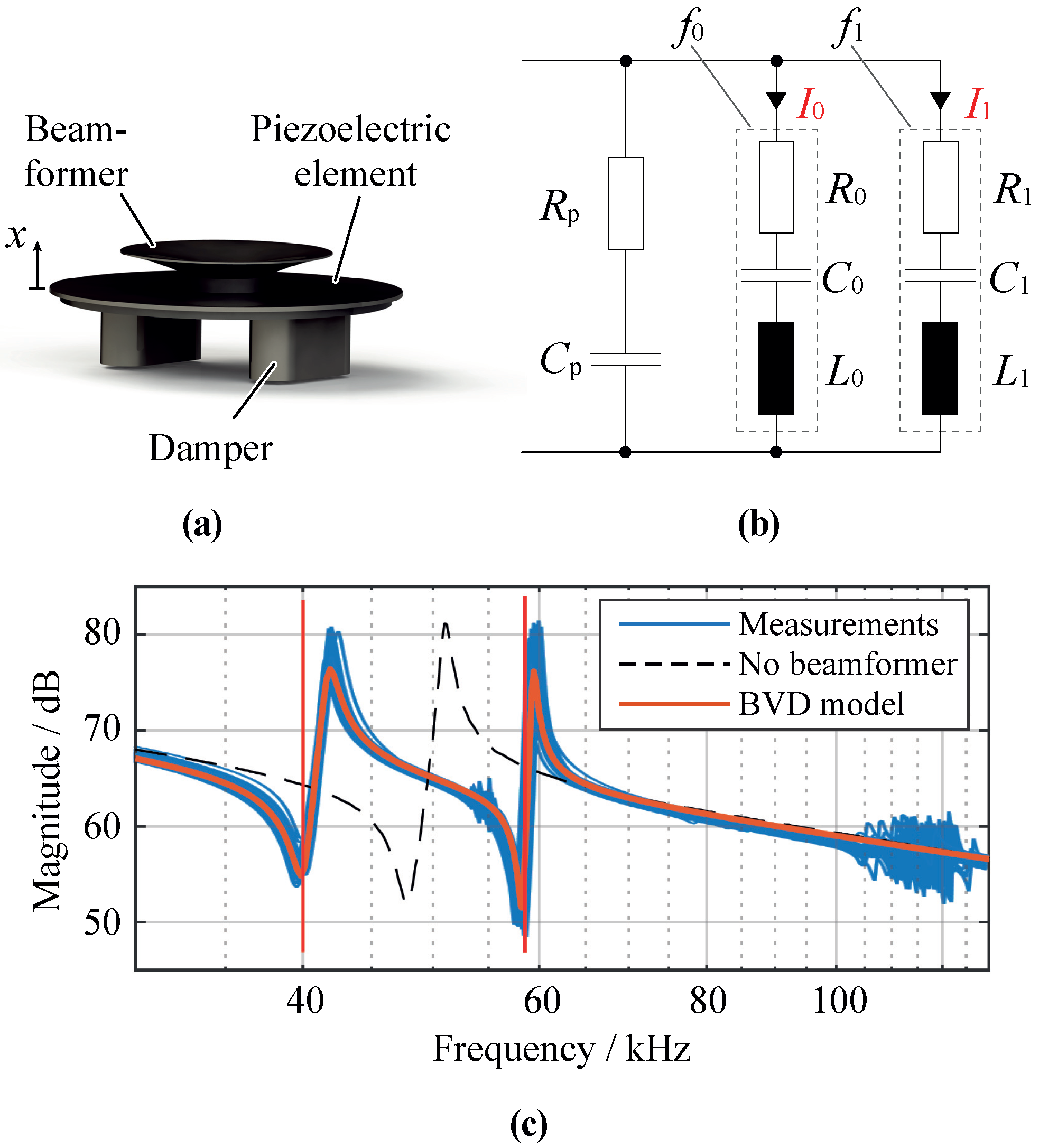
2.2. Transducer Characterization
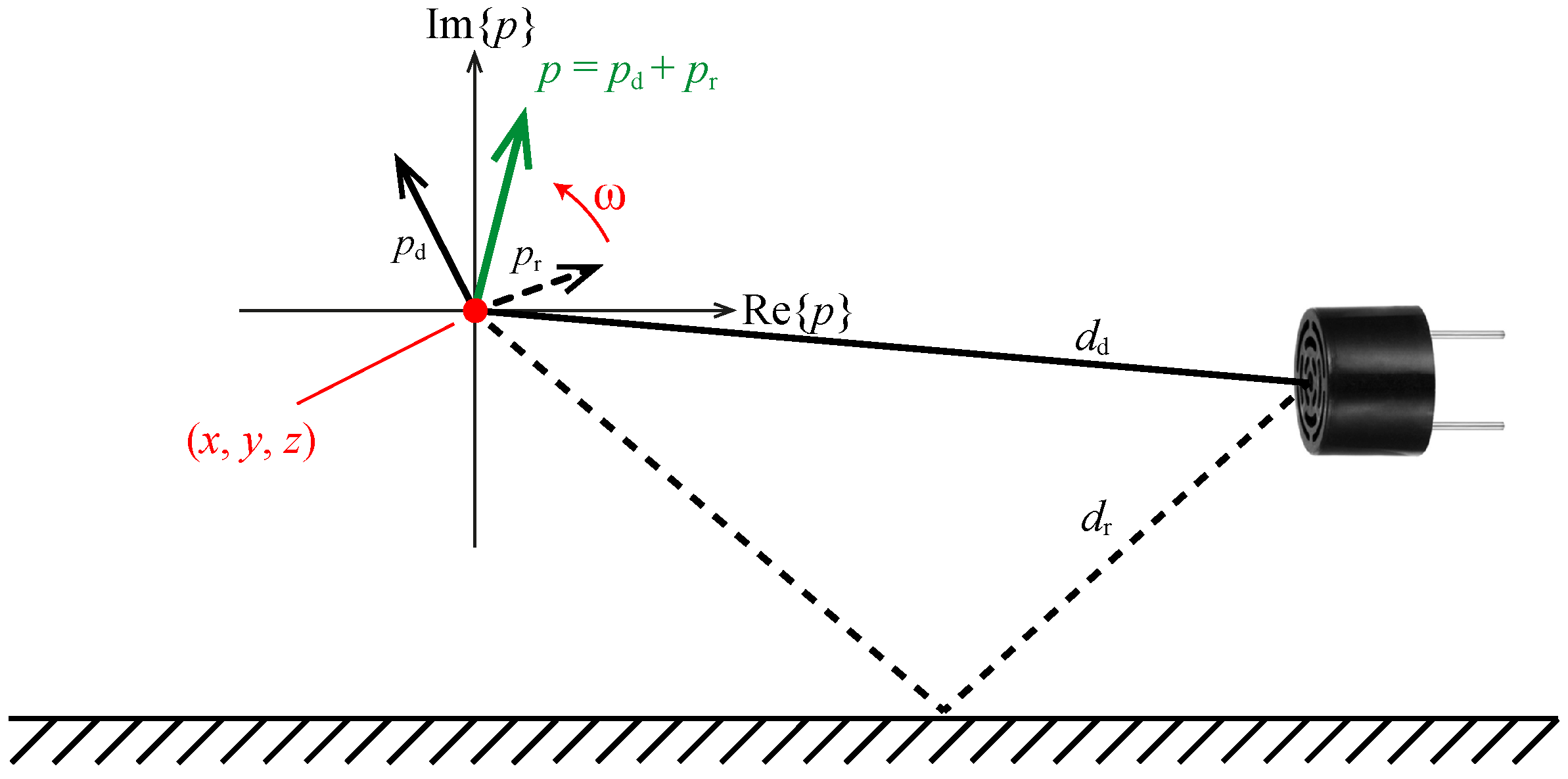
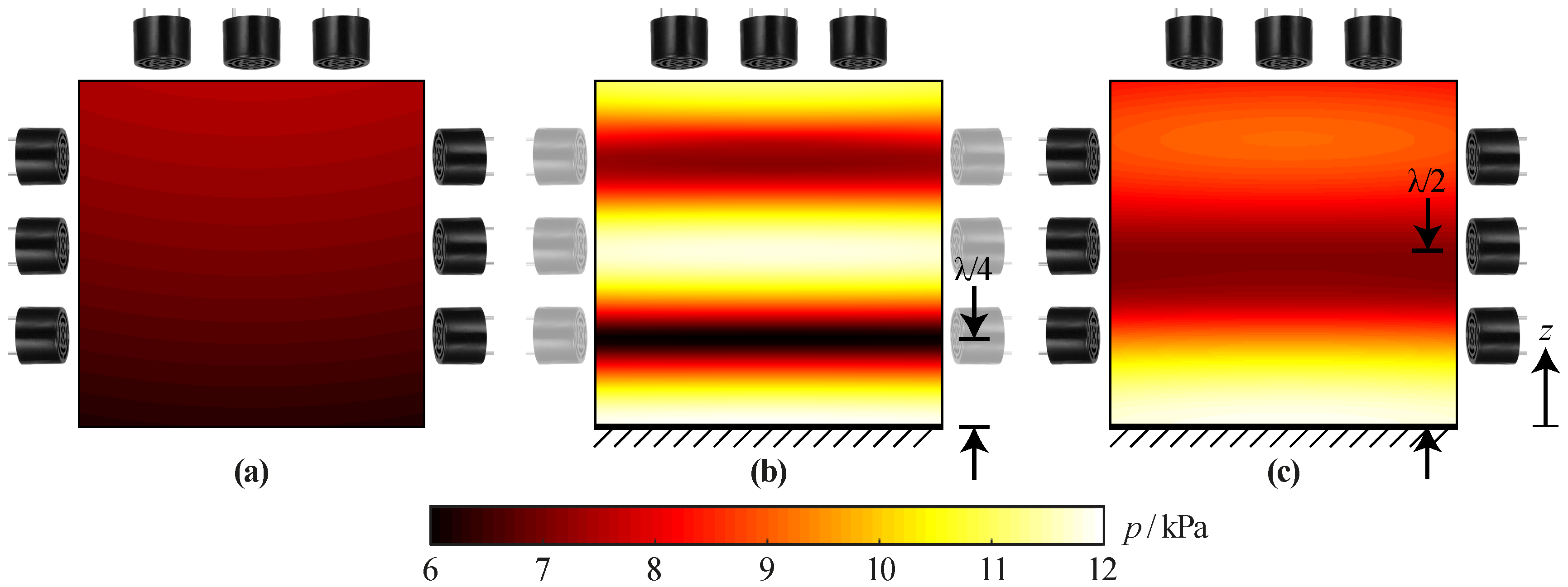
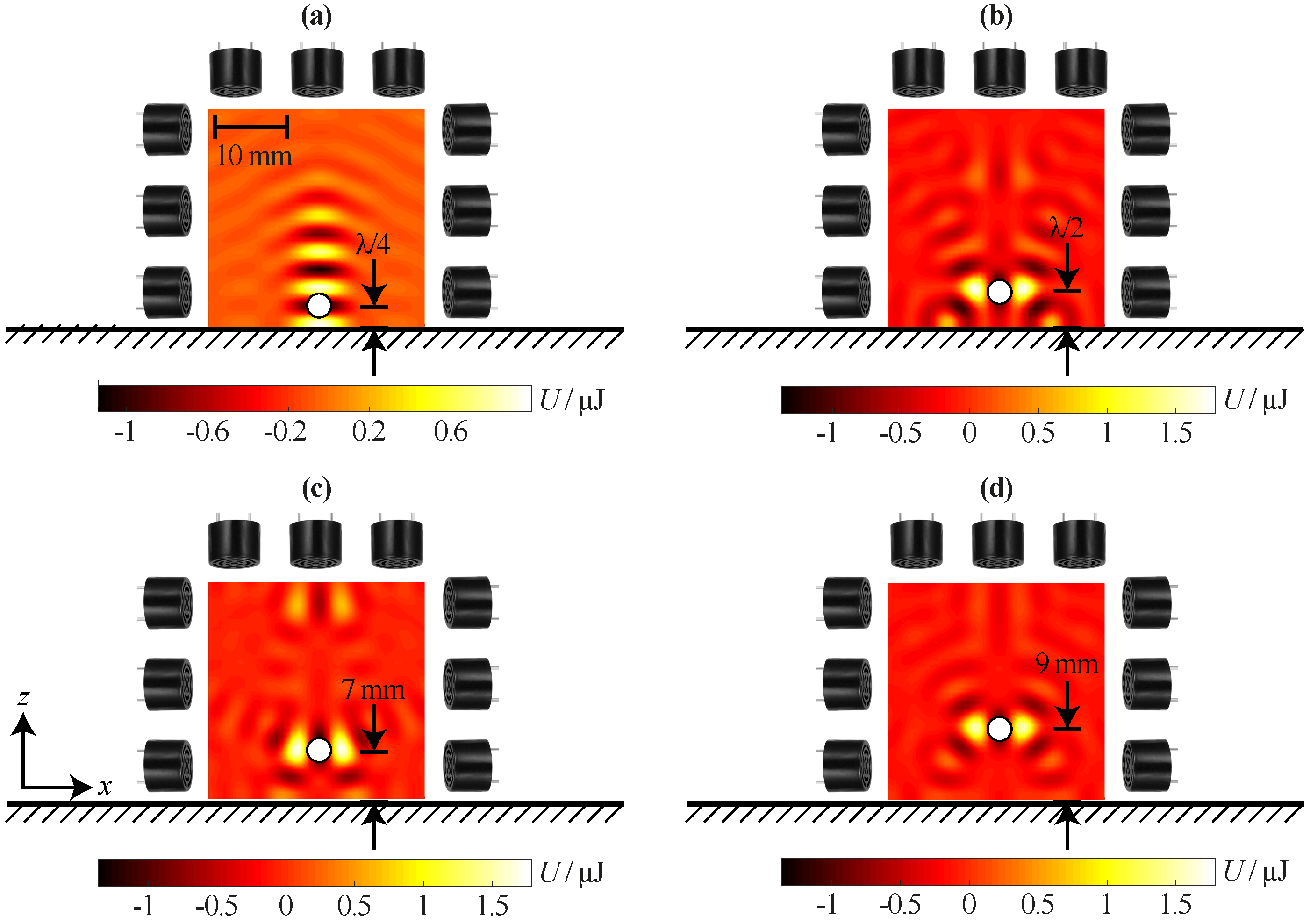
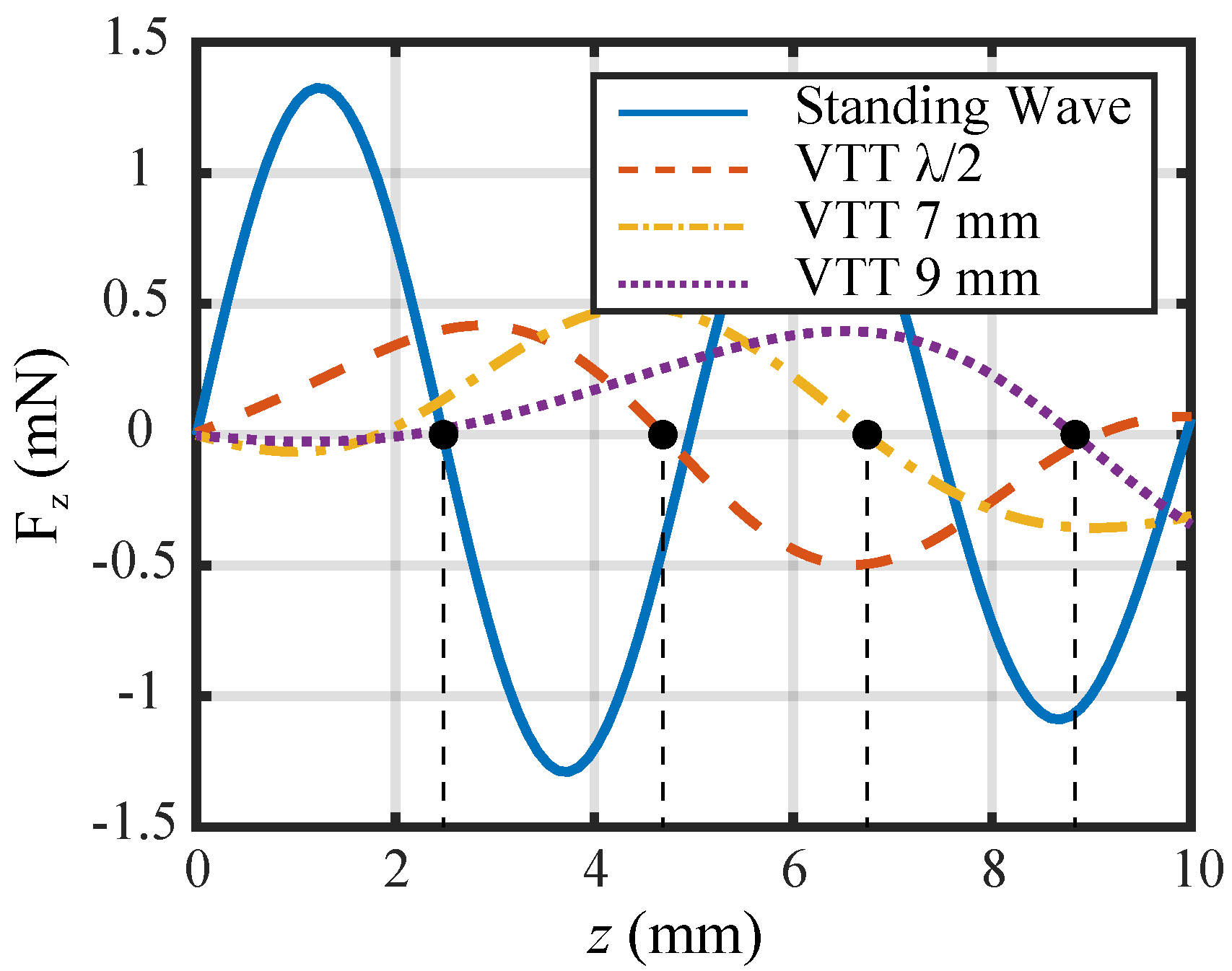
2.3. Acoustic Traps
2.4. Distribution of the Maximum Attainable Pressure
3. Experimental Setup
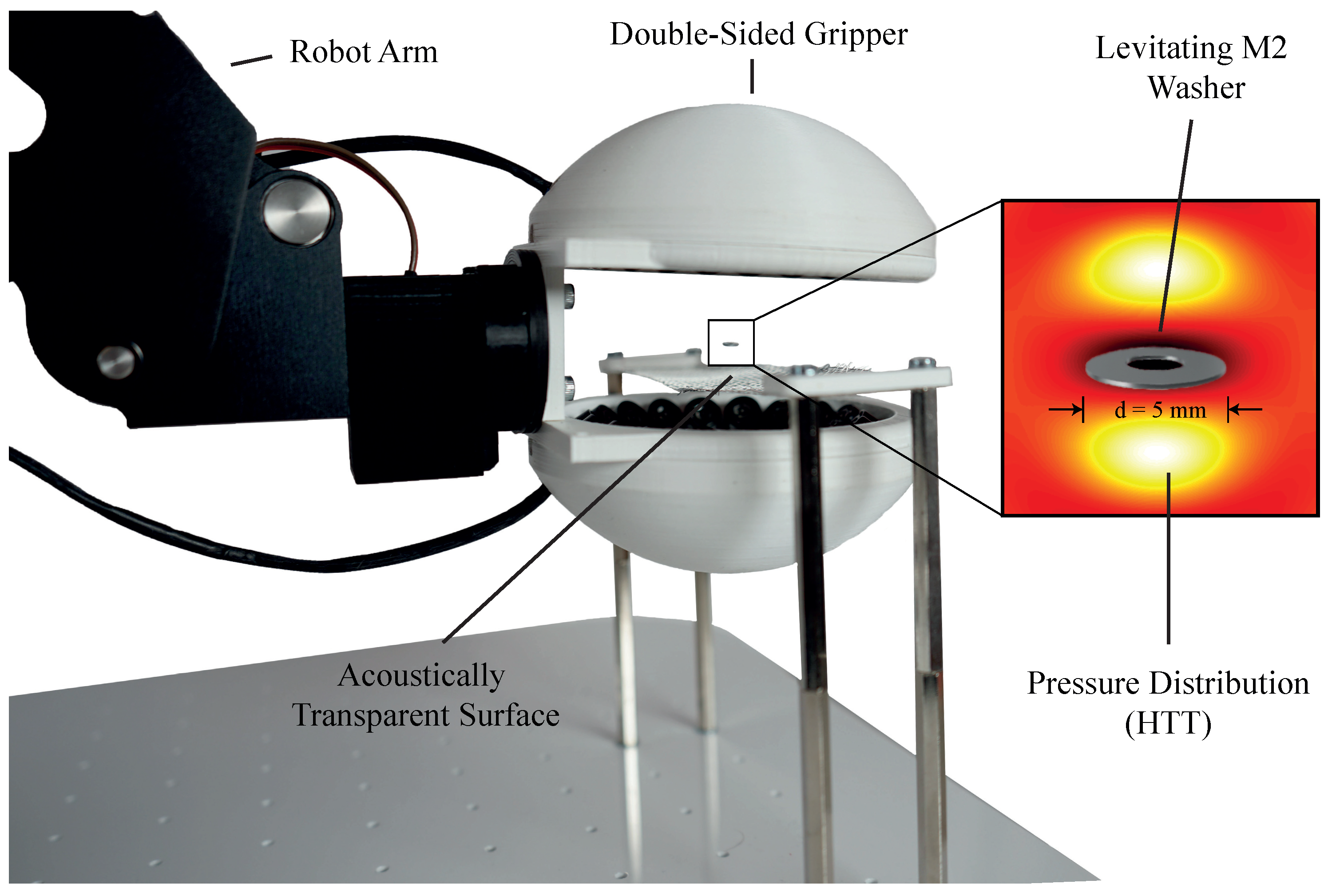
3.1. Transducer Arrays
- A double-sided array consisting of two pole caps of a sphere with a diameter , each equipped with 36 transducers arranged in three rings of 6, 12, and 18 transducers. All transducers are oriented such that they point towards the center of the sphere. This arrangement is shown in Figure 1.
- A cylindrical single-sided array with a height , an inner diameter , and an outer diameter , as depicted in Figure 2. Three rings of 6, 12, and 18 vertically oriented transducers are located at the horizontal top face of the arrangement. On the side walls of the cylinder, three rings of 20 horizontally oriented transducers each are located.
- A reflector array consisting of one half of the double-sided array and an additional thin reflector, which can be moved relative to the transducers. Depending on the application, a movable second half of the double-sided array is added.
3.2. Control System
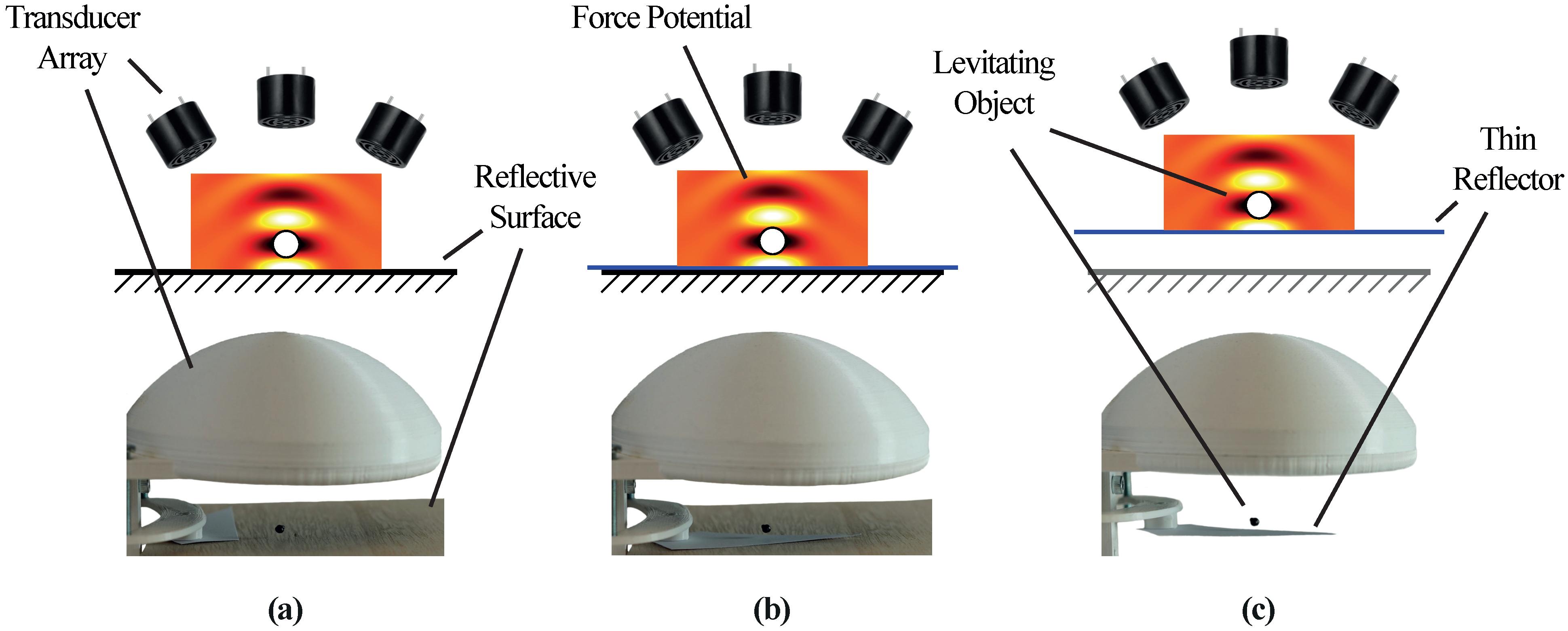
4. Automated Insertion
4.1. Acoustically Transparent Surface
4.2. Acoustically Reflective Surface
5. Gripper Using an Additional Reflector
5.1. Single-Sided Reflector Gripper
5.2. Double-Sided Reflector Gripper
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Symbols
| A | amplitude of the pressure wave |
| a | radius of the levitating particle |
| speed of sound in air | |
| d | distance of a considered point to the transducer |
| inner diameter of the single-sided arrangement | |
| outer diameter of the single-sided arrangement | |
| distance between the transducer and focal point for the direct acoustic wave | |
| distance between the transducer and focal point for the reflected acoustic wave | |
| F | acoustic force |
| h | cylinder height of the single-sided arrangement |
| i | current flowing through the transducer |
| Bessel function of order zero | |
| k | wave number |
| M | distribution of maximum attainable pressure (DMAP) |
| p | pressure |
| factor depending on the transducer type | |
| incident pressure wave | |
| reflected pressure wave | |
| Q | charge stored in the transducer |
| R | reflection coefficient |
| r | radius of the transducer |
| T | transmission coefficient |
| t | time |
| V | excitation voltage |
| v | particle velocity |
| Z | impedance of the transducer |
| phase of the transducer excitation signal | |
| acoustic wavelength | |
| density | |
| beam angle | |
| angular frequency |
Abbreviations
| VTT | Vertical Twin Trap |
| HTT | Horizontal Twin Trap |
| DMAP | Distribution of Maximum Attainable Pressure |
| FPGA | Field Programmable Gate Array |
| UART | Universal Asynchronous Receiver Transmitter |
| IC | Integrated Circuit |
| PC | Personal Computer |
| BVD | Butterworth-Van Dyke |
References
- Santesson, S.; Nilsson, S. Airborne chemistry: Acoustic levitation in chemical analysis. Anal. Bioanal. Chem. 2004, 378, 1704–1709. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.J.; Cao, C.D.; Lü, Y.J.; Hong, Z.Y.; Wei, B. Acoustic method for levitation of small living animals. Appl. Phys. Lett. 2006, 89, 214102. [Google Scholar] [CrossRef]
- Weber, J.K.R.; Benmore, C.; Tumber, S.; Tailor, A.; Rey, C.; Taylor, L.; Byrn, S. Acoustic levitation: Recent developments and emerging opportunities in biomaterials research. Eur. Biophys. J. EBJ 2011, 41, 397–403. [Google Scholar] [CrossRef]
- Puskar, L.; Tuckermann, R.; Frosch, T.; Popp, J.; Ly, V.; McNaughton, D.; Wood, B.R. Raman acoustic levitation spectroscopy of red blood cells and Plasmodium falciparum trophozoites. Lab Chip 2007, 7, 1125–1131. [Google Scholar] [CrossRef]
- Sundvik, M.; Nieminen, H.J.; Salmi, A.; Panula, P.; Hæggström, E. Effects of acoustic levitation on the development of zebrafish, Danio rerio, embryos. Sci. Rep. 2015, 5, 13596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seddon, A.M.; Richardson, S.J.; Rastogi, K.; Plivelic, T.S.; Squires, A.M.; Pfrang, C. Control of Nanomaterial Self-Assembly in Ultrasonically Levitated Droplets. J. Phys. Chem. Lett. 2016, 7, 1341–1345. [Google Scholar] [CrossRef] [Green Version]
- Foresti, D.; Sambatakakis, G.; Bottan, S.; Poulikakos, D. Morphing Surfaces Enable Acoustophoretic Contactless Transport of Ultrahigh-Density Matter in Air. Sci. Rep. 2013, 3, 3176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nordine, P.C.; Merkley, D.; Sickel, J.; Finkelman, S.; Telle, R.; Kaiser, A.; Prieler, R. A levitation instrument for containerless study of molten materials. Rev. Sci. Instrum. 2012, 83, 125107. [Google Scholar] [CrossRef] [Green Version]
- Yan, N.; Hong, Z.Y.; Geng, D.; Wei, B. A comparison of acoustic levitation with microgravity processing for containerless solidification of ternary Al–Cu–Sn alloy. Appl. Phys. A 2015, 120. [Google Scholar] [CrossRef]
- Ohsaka, K.; Trinh, E. Three-Lobed Shape Bifurcation of Rotating Liquid Drops. Phys. Rev. Lett. 2000, 84, 1700–1703. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Xie, W.; Wei, B. Parametrically excited sectorial oscillation of liquid drops floating in ultrasound. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 81, 46305. [Google Scholar] [CrossRef] [PubMed]
- Bleuler, H.; Cole, M.; Keogh, P.; Larsonneur, R.; Maslen, E.; Okada, Y.; Schweitzer, G.; Traxler, A. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Jin, J.; Higuchi, T. Direct electrostatic levitation and propulsion. IEEE Trans. Ind. Electron. 1997, 44, 234–239. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Stability of optical levitation by radiation pressure. Appl. Phys. Lett. 1974, 24, 586–588. [Google Scholar] [CrossRef]
- Kundt, A. Über eine neue Art akustischer Staubfiguren und über die Anwendung derselben zur Bestimmung der Schallgeschwindigkeit in festen Körpern und Gasen. Ann. Phys. 1866, 203, 497–523. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Holt, R.G.; Apfel, R.E. A new method for measuring liquid surface tension with acoustic levitation. Rev. Sci. Instrum. 1995, 66, 3349–3354. [Google Scholar] [CrossRef]
- Whymark, R. Acoustic field positioning for containerless processing. Ultrasonics 1975, 13, 251–261. [Google Scholar] [CrossRef]
- Marzo, A.; Seah, S.A.; Drinkwater, B.W.; Sahoo, D.R.; Long, B.; Subramanian, S. Holographic acoustic elements for manipulation of levitated objects. Nat. Commun. 2015, 6, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Drinkwater, B.W. Dynamic-field devices for the ultrasonic manipulation of microparticles. Lab Chip 2016, 16, 2360–2375. [Google Scholar] [CrossRef] [Green Version]
- Marzo, A.; Corkett, T.; Drinkwater, B.W. Ultraino: An Open Phased-Array System for Narrowband Airborne Ultrasound Transmission. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2018, 65, 102–111. [Google Scholar] [CrossRef] [Green Version]
- Omirou, T.; Marzo, A.; Seah, S.; Subramanian, S. LeviPath: Modular Acoustic Levitation for 3D Path Visualisations. In Proceedings of the CHI ’15: Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems, Seoul, Korea, 19–23 April 2015. [Google Scholar] [CrossRef] [Green Version]
- Nakahara, J.; Yang, B.; Smith, J.R. Contact-less Manipulation of Millimeter-scale Objects via Ultrasonic Levitation. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 264–271. [Google Scholar] [CrossRef]
- Andrade, M.A.B.; Ramos, T.S.; Adamowski, J.C.; Marzo, A. Contactless pick-and-place of millimetric objects using inverted near-field acoustic levitation. Appl. Phys. Lett. 2020, 116, 054104. [Google Scholar] [CrossRef]
- Gor’kov, L.P. On the Forces Acting on a Small Particle in an Acoustical Field in an Ideal Fluid. Sov. Phys. Dokl. 1962, 6, 773. [Google Scholar]
- King, L.V. On the Acoustic Radiation Pressure on Spheres. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1934, 147, 212–240. [Google Scholar]
- Fabijanski, P.; Lagoda, R. Modeling and Identification of Parameters the Piezoelectric Transducers in Ultrasonic Systems, Advances in Ceramics - Electric and Magnetic Ceramics, Bioceramics, Ceramics and Environment. IntechOpen 2011. [Google Scholar] [CrossRef] [Green Version]
- Uzunov, I.S.; Terzieva, M.D.; Nikolova, B.M.; Gaydazhiev, D.G. Extraction of modified butterworth—Van Dyke model of FBAR based on FEM analysis. In Proceedings of the 2017 26th International Scientific Conference Electronics, ET 2017—Proceedings, Sozopol, Bulgaria, 13–15 September 2017. [Google Scholar] [CrossRef]
- Andrade, M.A.B.; Marzo, A.; Adamowski, J.C. Acoustic levitation in mid-air: Recent advances, challenges, and future perspectives. Appl. Phys. Lett. 2020, 116, 250501. [Google Scholar] [CrossRef]
- Nichols, M.K.; Kumar, R.K.; Bassindale, P.G.; Tian, L.; Barnes, A.C.; Drinkwater, B.W.; Patil, A.J.; Mann, S. Fabrication of Micropatterned Dipeptide Hydrogels by Acoustic Trapping of Stimulus-Responsive Coacervate Droplets. Small 2018, 14, e1800739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ochiai, Y.; Hoshi, T.; Rekimoto, J. Pixie Dust: Graphics Generated by Levitated and Animated Objects in Computational Acoustic-Potential Field. ACM Trans. Graph. 2014, 33. [Google Scholar] [CrossRef]
- Gesellchen, F.; Bernassau, A.L.; Déjardin, T.; Cumming, D.R.S.; Riehle, M.O. Cell patterning with a heptagon acoustic tweezer—Application in neurite guidance. Lab Chip 2014, 14, 2266–2275. [Google Scholar] [CrossRef] [Green Version]
- Courtney, C.R.P.; Demore, C.E.M.; Wu, H.; Grinenko, A.; Wilcox, P.D.; Cochran, S.; Drinkwater, B.W. Independent trapping and manipulation of microparticles using dexterous acoustic tweezers. Appl. Phys. Lett. 2014, 104, 154103. [Google Scholar] [CrossRef]
- Seah, S.A.; Drinkwater, B.W.; Carter, T.; Malkin, R.; Subramanian, S. Correspondence: Dexterous ultrasonic levitation of millimeter-sized objects in air. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1233–1236. [Google Scholar] [CrossRef]
- Norasikin, M.A.; Martinez Plasencia, D.; Polychronopoulos, S.; Memoli, G.; Tokuda, Y.; Subramanian, S. SoundBender: Dynamic Acoustic Control Behind Obstacles. In Proceedings of the 31st Annual ACM Symposium on User Interface Software and Technology; UIST ’18; Association for Computing Machinery: New York, NY, USA, 2018; pp. 247–259. [Google Scholar] [CrossRef] [Green Version]
- Marzo, A.; Barnes, A.; Drinkwater, B.W. TinyLev: A multi-emitter single-axis acoustic levitator. Rev. Sci. Instrum. 2017, 88. [Google Scholar] [CrossRef]
- Marzo, A.; Caleap, M.; Drinkwater, B.W. Acoustic Virtual Vortices with Tunable Orbital Angular Momentum for Trapping of Mie Particles. Phys. Rev. Lett. 2018, 120, 044301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Savioja, L.; Svensson, U.P. Overview of geometrical room acoustic modeling techniques. J. Acoust. Soc. Am. 2015, 138, 708–730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rathnayake, A.; Wanniarachchi, W.K. Image Source Method Based Acoustic Simulation For 3-D Room Environment. Int. J. Sci. Technol. Res. 2019, 8, 222–228. [Google Scholar]
- Kandemir, M.H.; Çalışkan, M. Standing wave acoustic levitation on an annular plate. J. Sound Vib. 2016, 382, 227–237. [Google Scholar] [CrossRef]
- Zhao, S.; Wallaschek, J. A standing wave acoustic levitation system for large planar objects. Arch. Appl. Mech. 2011, 81, 123–139. [Google Scholar] [CrossRef]



| g/cm | g/cm | Environment | Applications | |
|---|---|---|---|---|
| Double-Sided | 7.8 | - | Accessible from both sides | Gripping of high-density objects |
| Single-Sided | 0.25 | 0.25 | - | Gripping low-density objects from reflective and transparent surfaces |
| Reflector | - | 1 | Sufficient space for moving the reflector | Gripping medium-density objects from reflective surfaces, gripping multiple objects, insertion of objects located on reflective surfaces into double-sided grippers |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Röthlisberger, M.; Schuck, M.; Kulmer, L.; Kolar, J.W. Contactless Picking of Objects Using an Acoustic Gripper. Actuators 2021, 10, 70. https://doi.org/10.3390/act10040070
Röthlisberger M, Schuck M, Kulmer L, Kolar JW. Contactless Picking of Objects Using an Acoustic Gripper. Actuators. 2021; 10(4):70. https://doi.org/10.3390/act10040070
Chicago/Turabian StyleRöthlisberger, Marc, Marcel Schuck, Laurenz Kulmer, and Johann W. Kolar. 2021. "Contactless Picking of Objects Using an Acoustic Gripper" Actuators 10, no. 4: 70. https://doi.org/10.3390/act10040070
APA StyleRöthlisberger, M., Schuck, M., Kulmer, L., & Kolar, J. W. (2021). Contactless Picking of Objects Using an Acoustic Gripper. Actuators, 10(4), 70. https://doi.org/10.3390/act10040070






