Road Roughness Estimation Based on the Vehicle Frequency Response Function
Abstract
:1. Introduction
2. Road Roughness Estimation
2.1. Vehicle Motion Equation
2.2. Theoretical Reduction
2.3. Simplification of the Estimation Using Time Shift Property of Fourier Transform
3. Estimation of the Vehicle FRF with Regard to Road Roughness
3.1. Direct Estimation of the Vehicle FRF
3.2. Updating the Estimated FRF Based on the Shape Function Method
3.3. On-Line Estimation of Road Roughness
4. Numerical Simulation
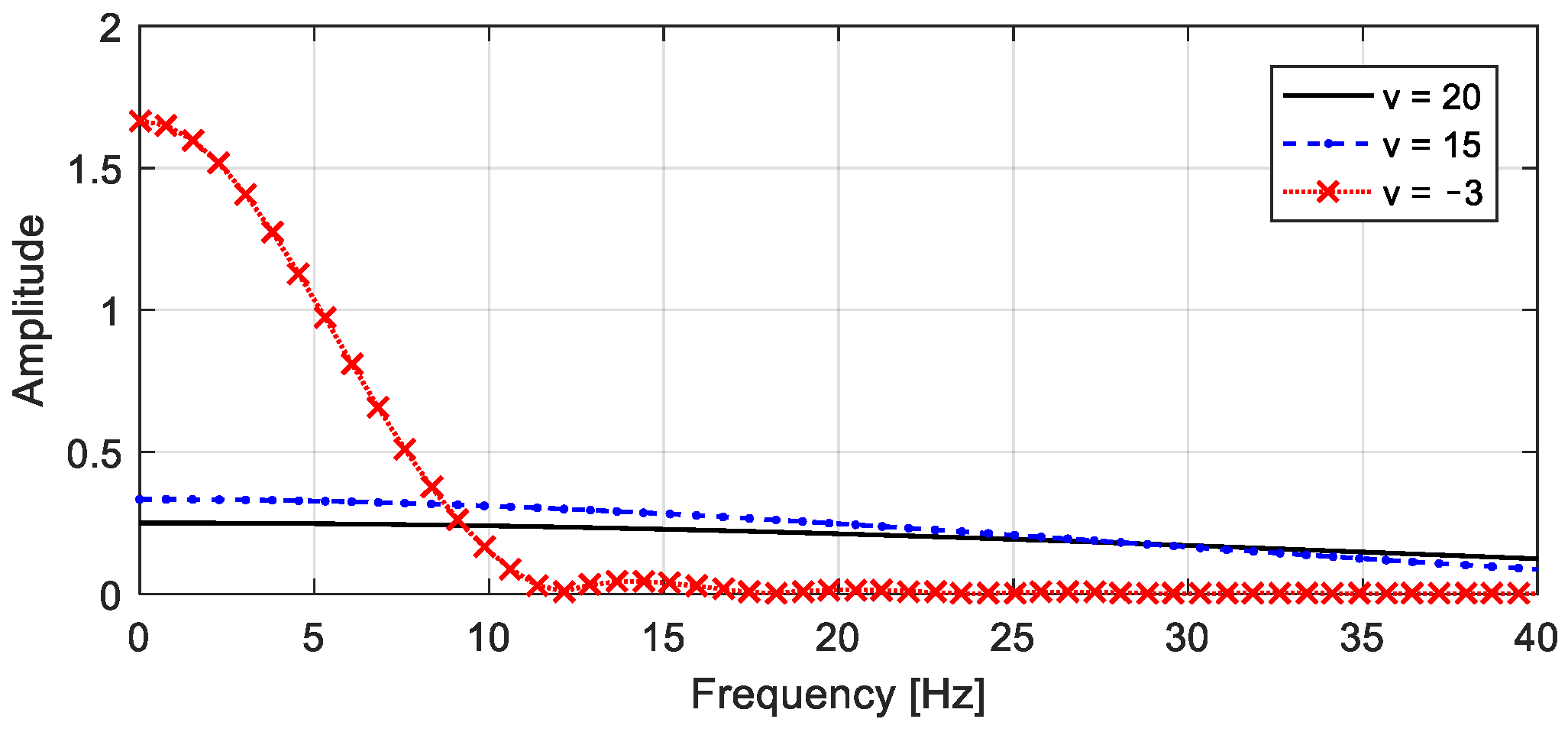
4.1. Characteristic Analysis of the Vehicle FRF
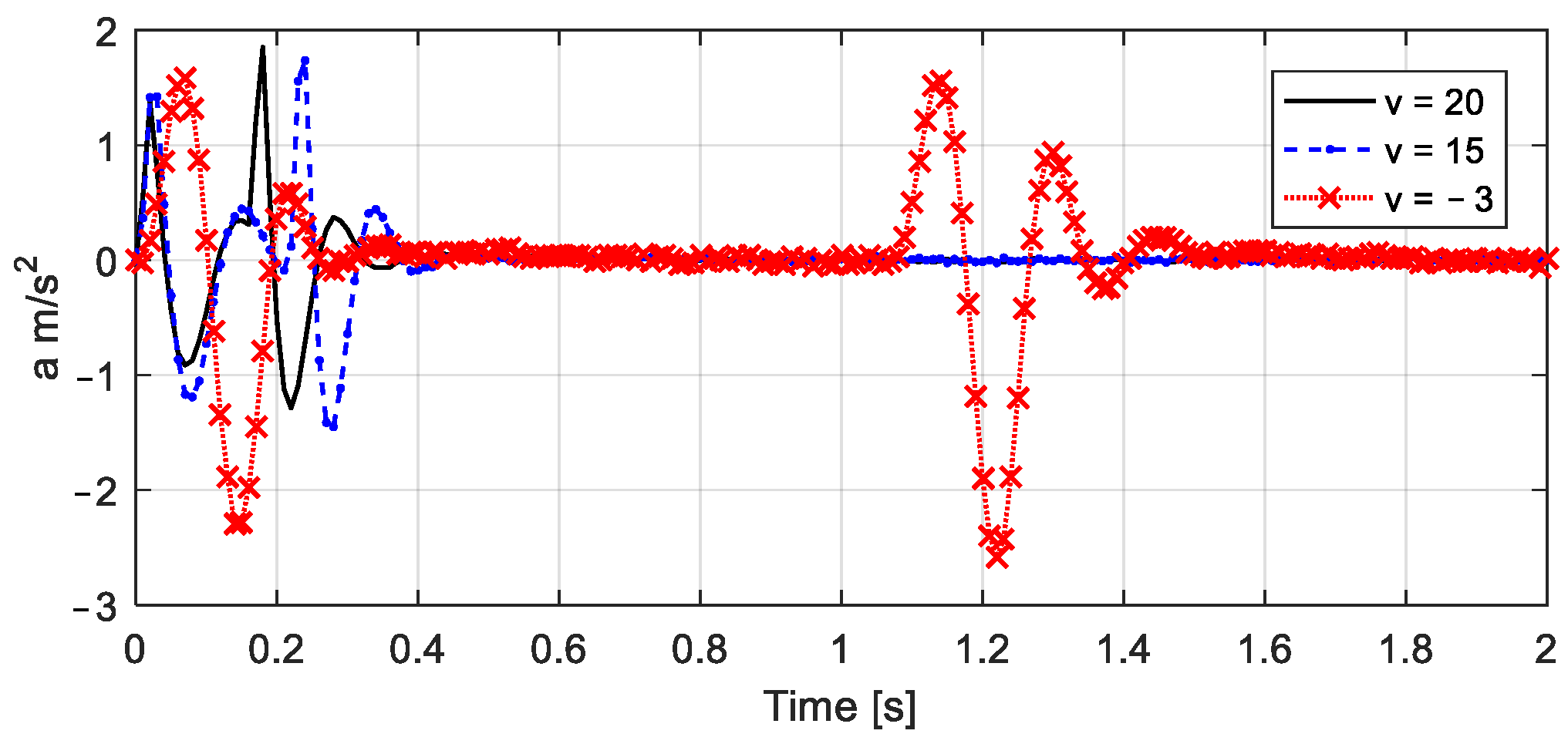
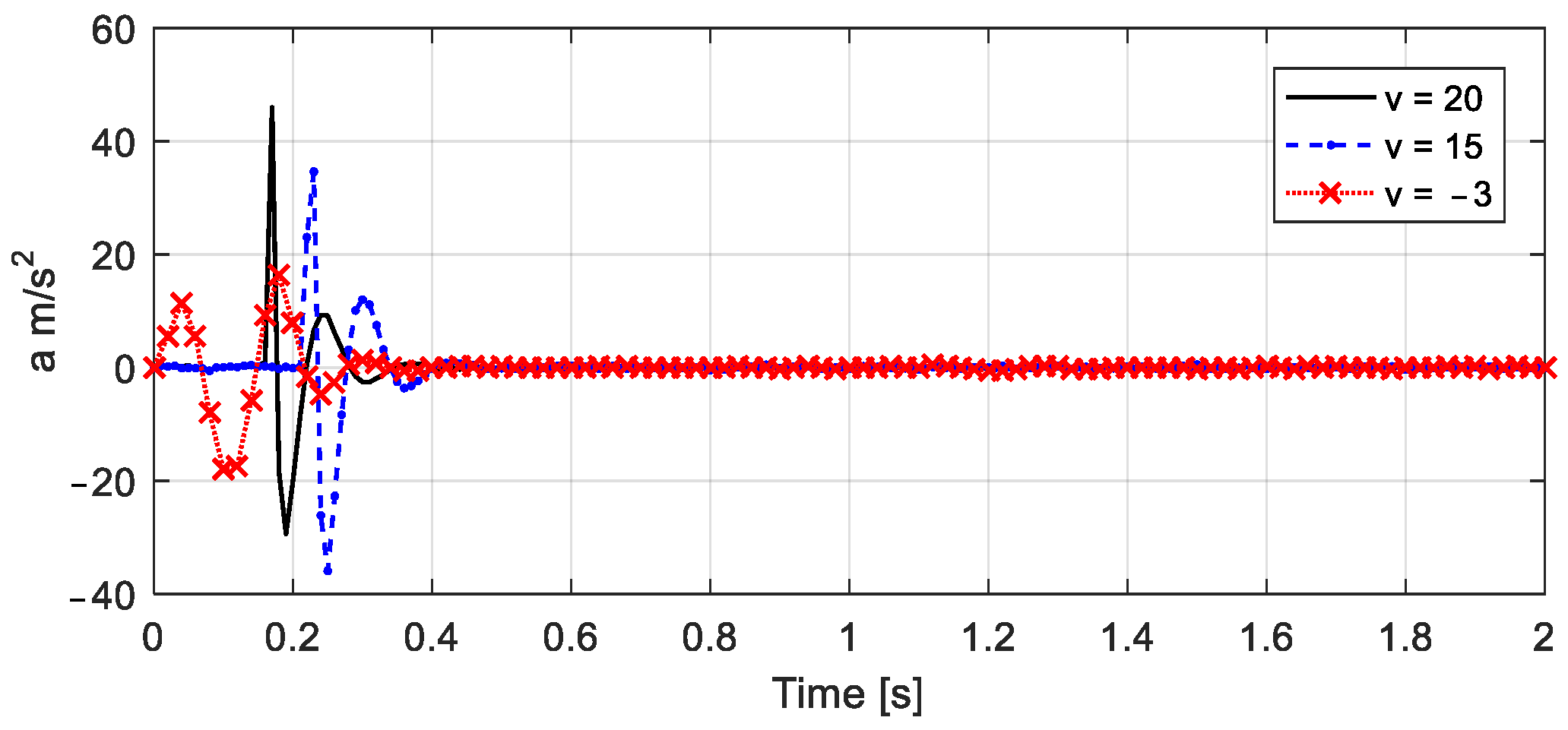
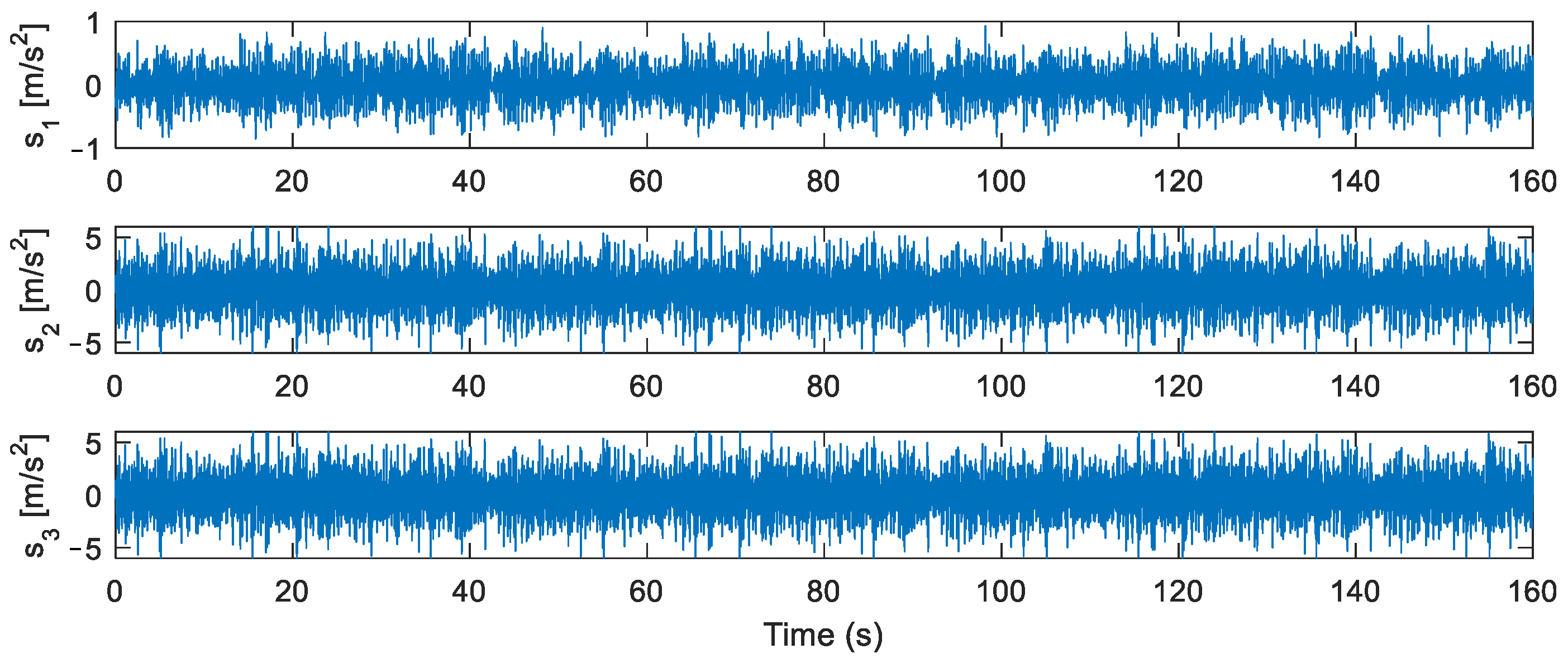
4.2. Simulation of the Measured Vehicle Accelerations
4.3. Estimation of Vehicle FRF
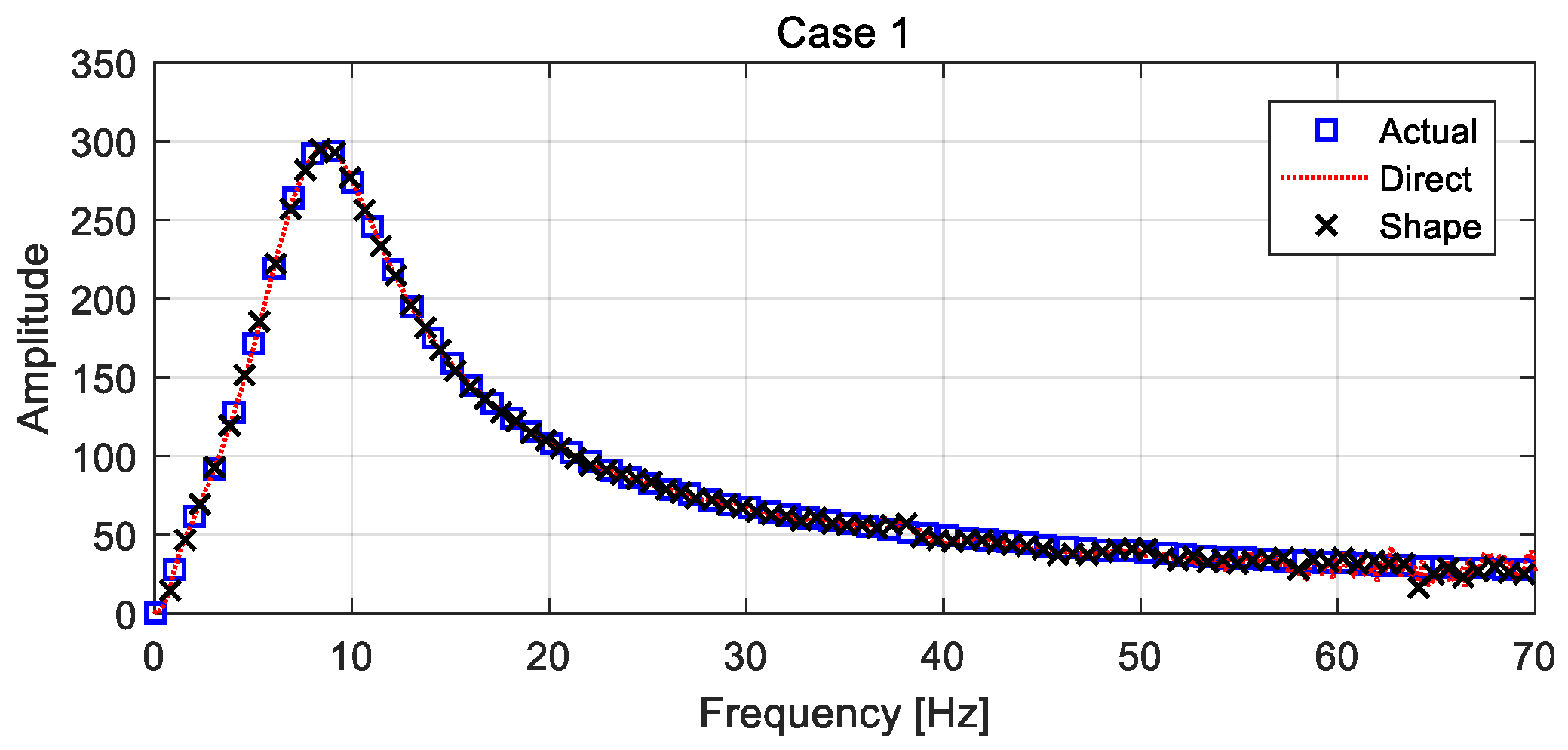
4.3.1. Direct Estimation Using Measured Responses
4.3.2. Updating the Vehicle FRF
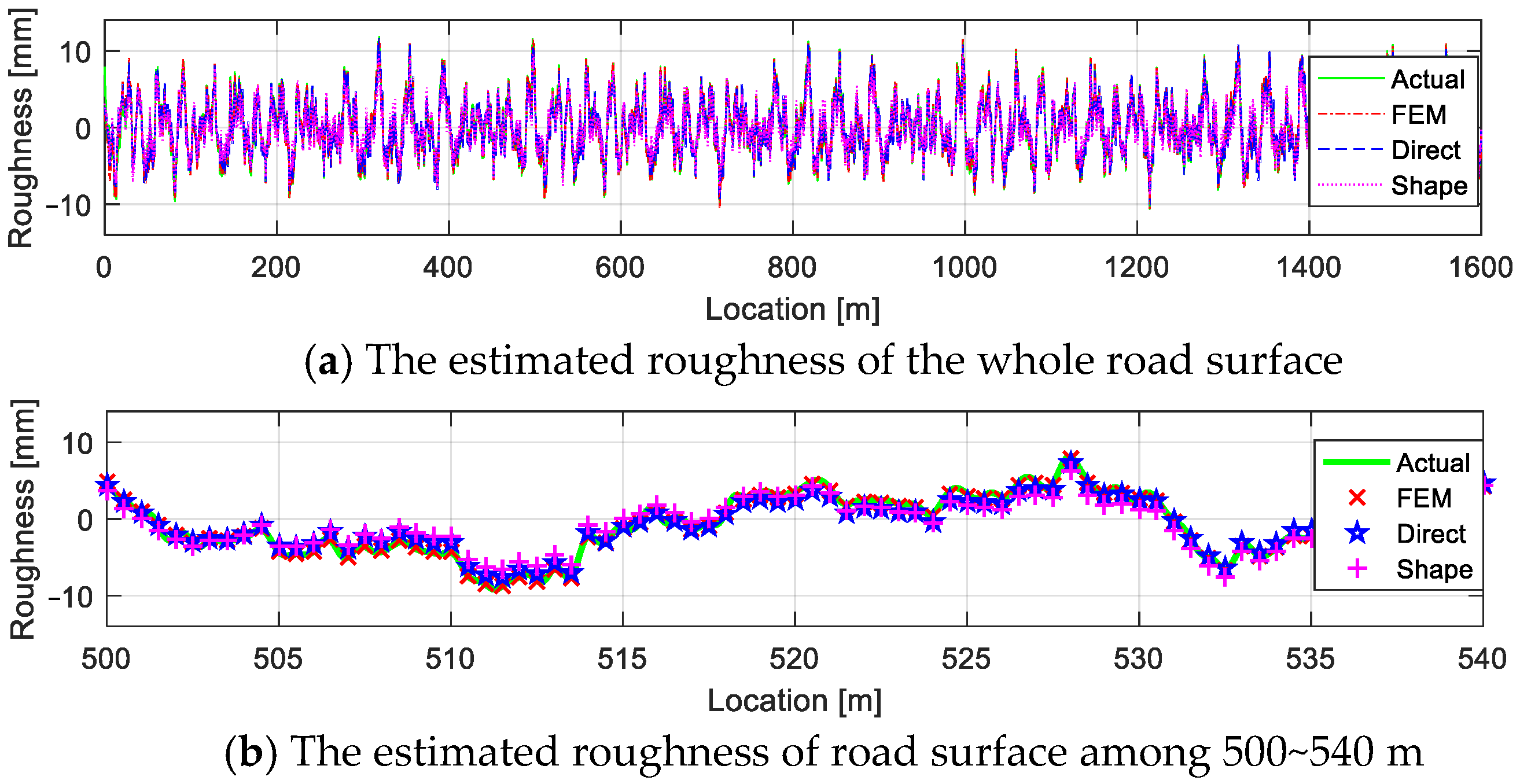
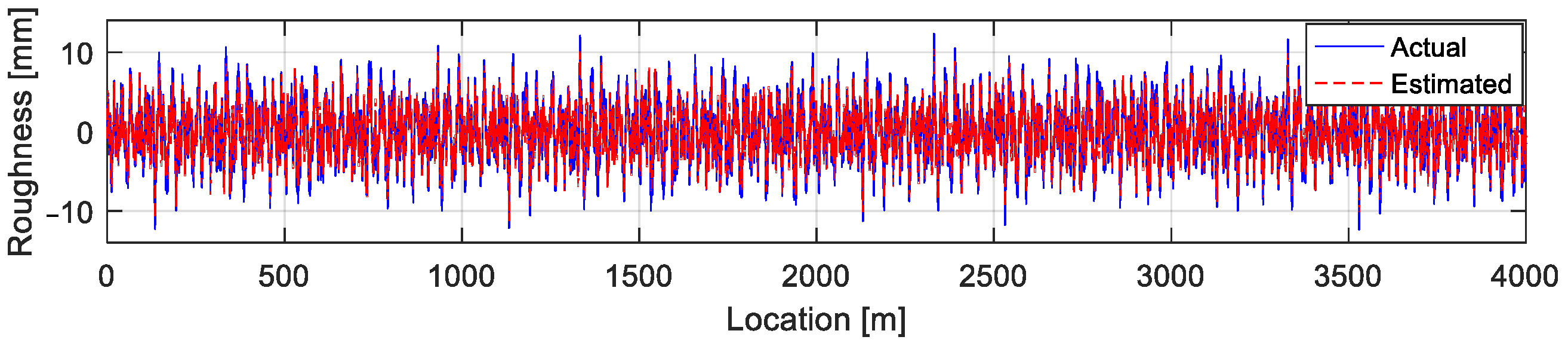
4.4. Road Roughness Estimation
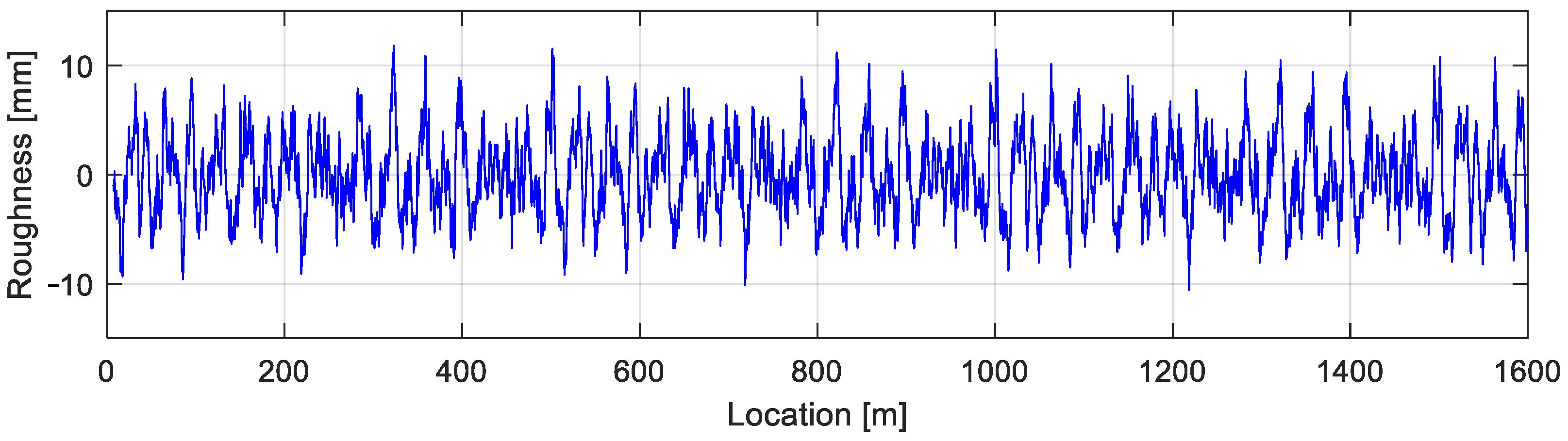
4.4.1. Road Roughness and Vehicle Response
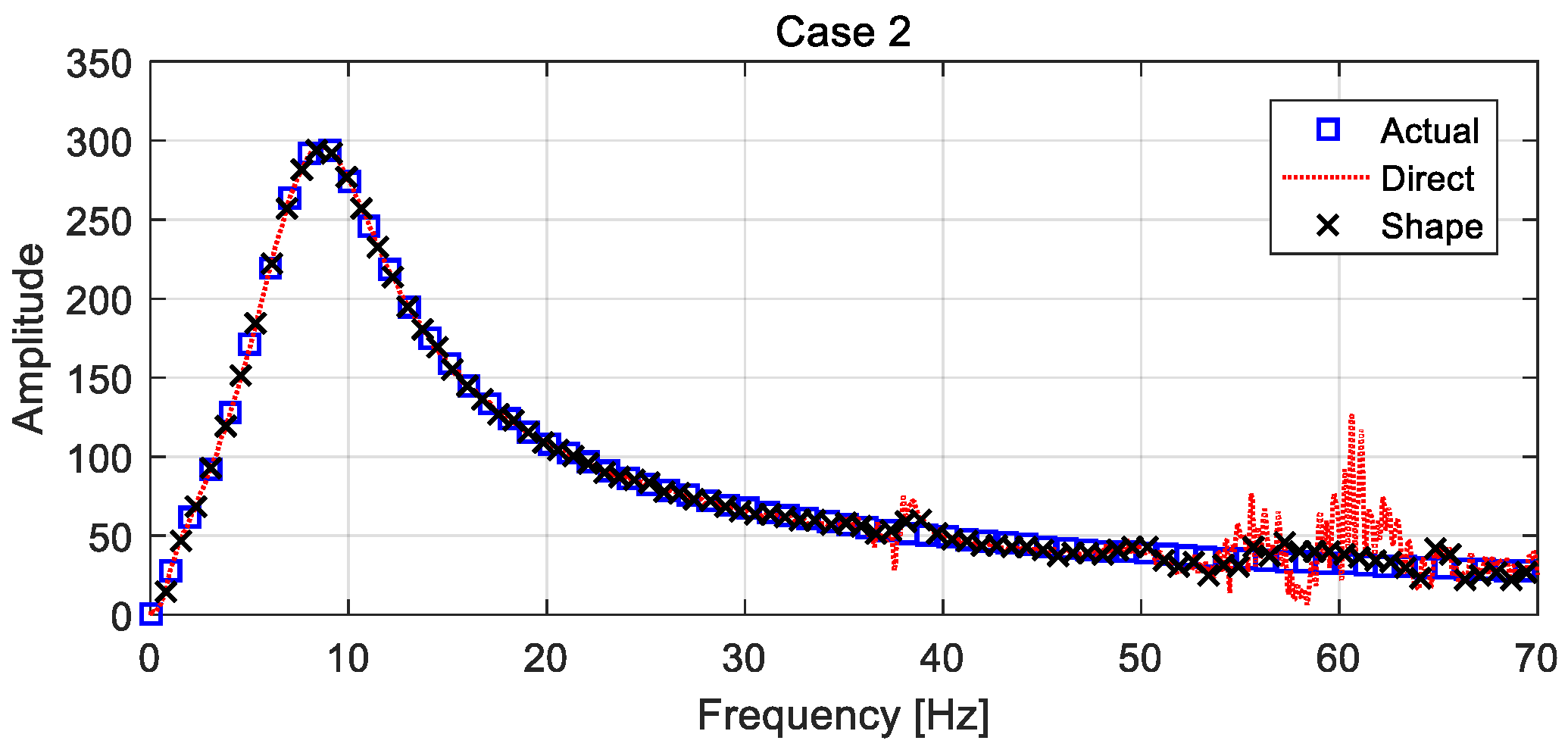
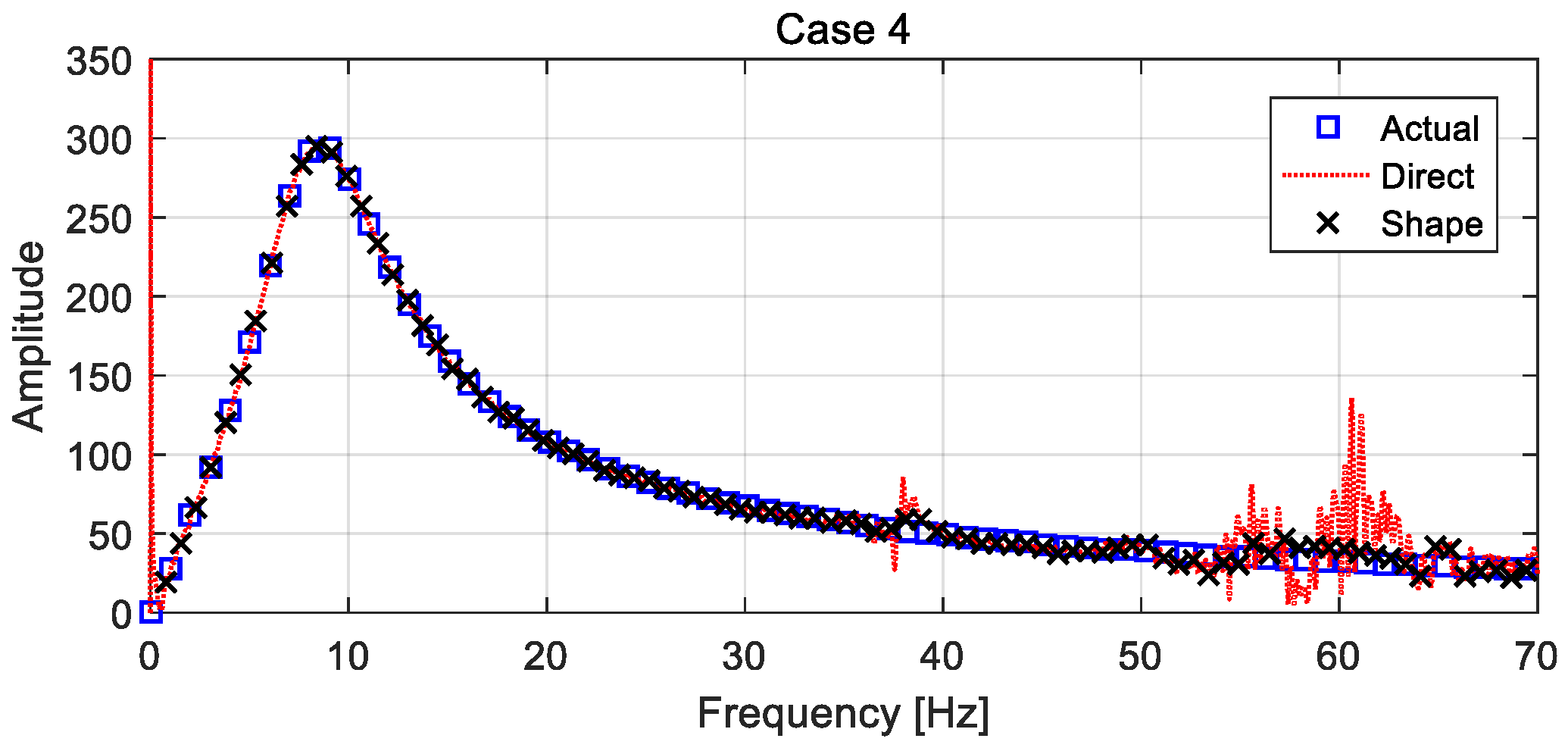
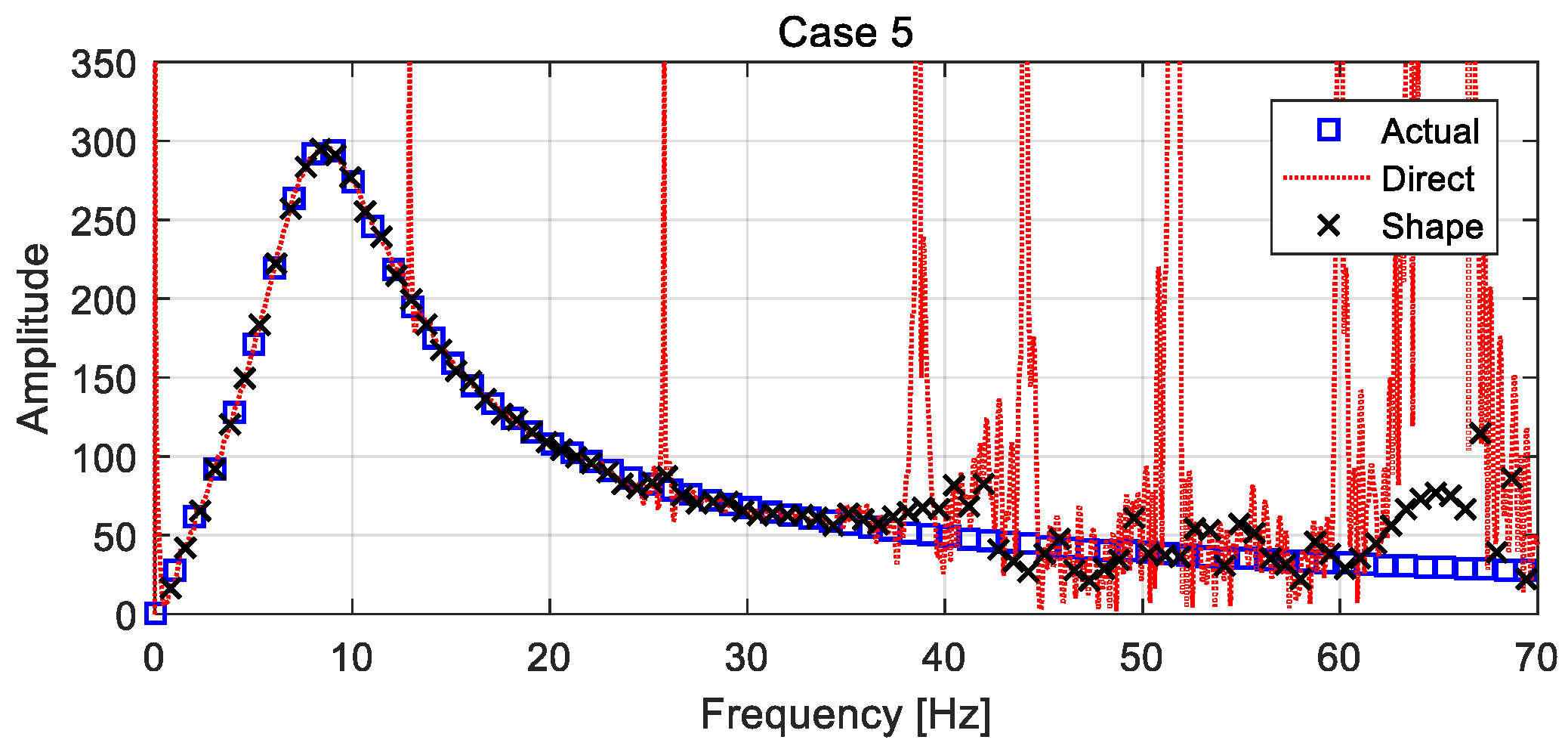
4.4.2. Different Case Estimations
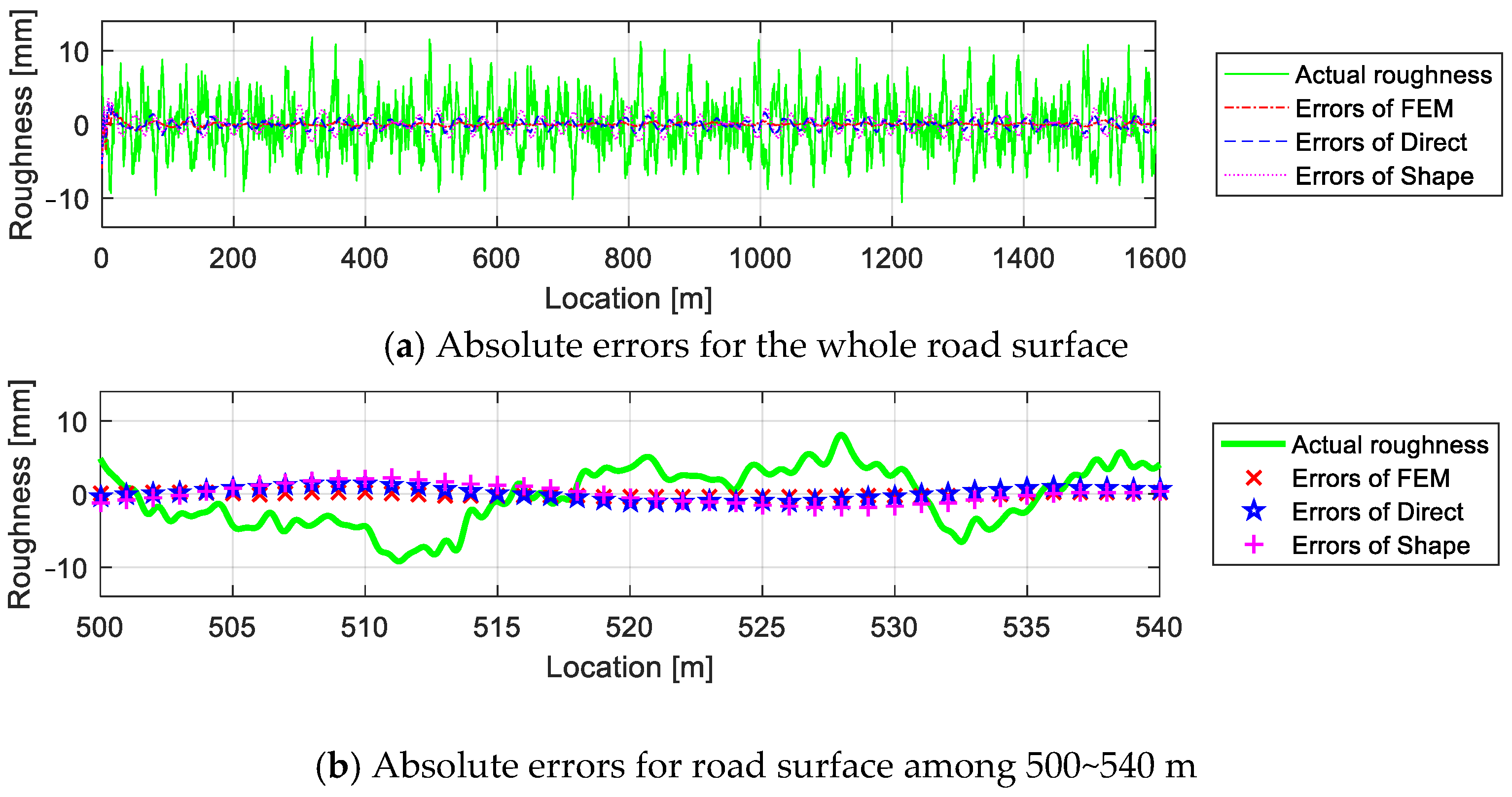
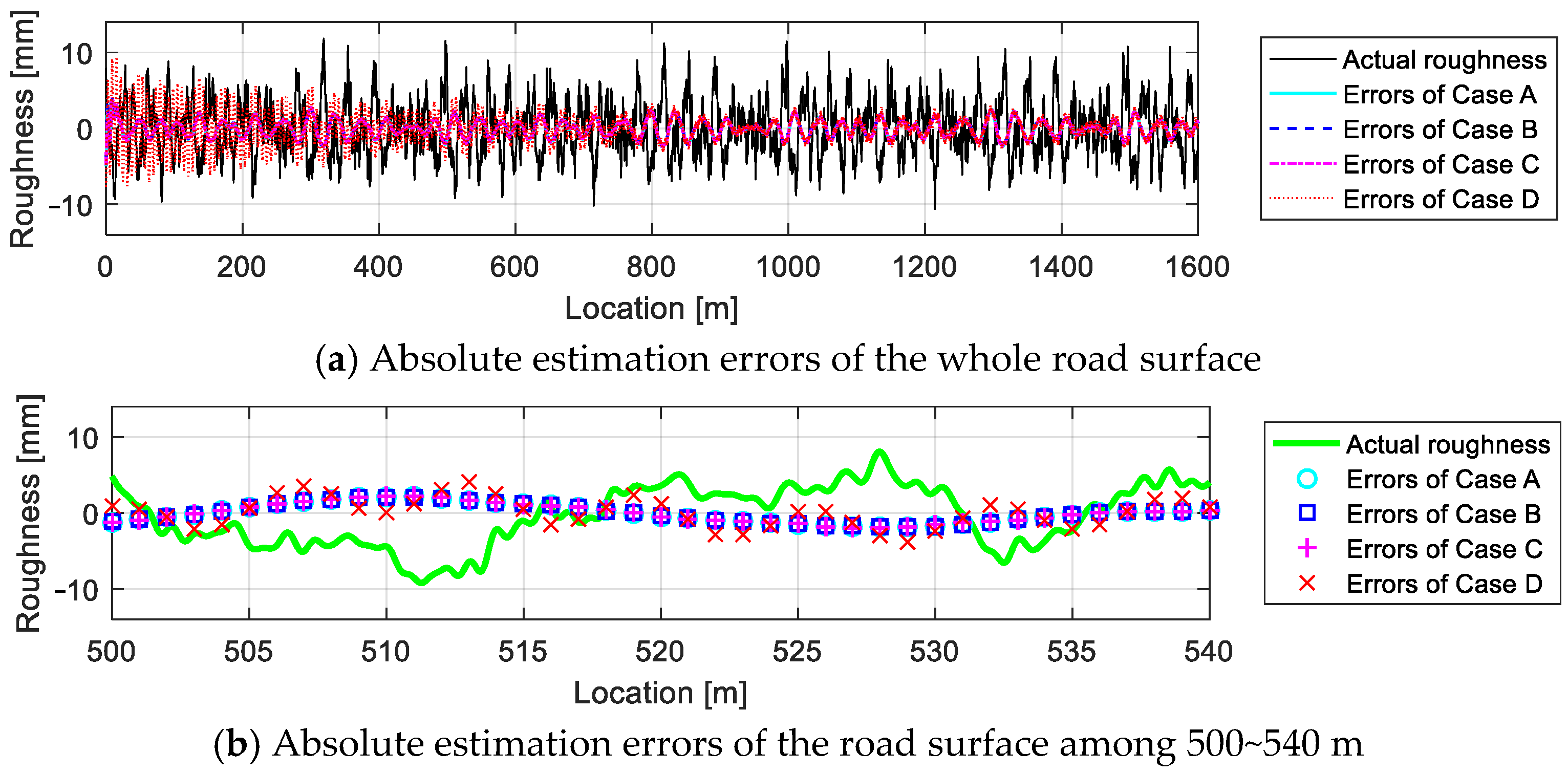
4.4.3. Error Analysis
4.4.4. On-Line Estimation of Road Roughness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ihs, A. The influence of road surface condition on traffic safety and ride comfort. In Proceedings of the 6th International Conference on Managing Pavements, Brisbane, Australian, 19–24 October 2004. [Google Scholar]
- Hanafi, D.; Huq, M.S.; Suid, M.S.; Rahmat, M. A Quarter Car ARX Model Identification Based on Real Car Test Data. J. Telecommun. Electron. Comput. Eng. 2017, 9, 135–138. [Google Scholar]
- Otremba, F.; Navarrete, J.A.R.; Guzmán, A.A.L. Modelling of a partially loaded road tanker during a braking-in-a-turn maneuver. Actuators 2018, 7, 45. [Google Scholar] [CrossRef] [Green Version]
- Qinghua, M.; Huifeng, Z.; Fengjun, L. Fatigue failure fault prediction of truck rear axle housing excited by random road roughness. Int. J. Phys. Sci. 2011, 6, 1563–1568. [Google Scholar] [CrossRef]
- Reza-Kashyzadeh, K.; Ostad-Ahmad-Ghorabi, M.J.; Arghavan, A. Investigating the effect of road roughness on automotive component. Eng. Fail. Anal. 2014, 41, 96–107. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y.; Long, X.; Wang, Y. Optimizing rail profiles to improve metro vehicle-rail dynamic performance considering worn wheel profiles and curved tracks. Struct. Multidiscip. Optim. 2021, 63, 419–438. [Google Scholar] [CrossRef]
- Ngwangwa, H.M. Calculation of road profiles by reversing the solution of the vertical ride dynamics forward problem. Cogent Eng. 2020, 7, 1833819. [Google Scholar] [CrossRef]
- Yang, Y.; Cheng, Q.; Zhu, Y.; Wang, L.; Jin, R. Feasibility study of tractor-test vehicle technique for practical structural condition assessment of beam-like bridge deck. Remote Sens. 2020, 12, 114. [Google Scholar] [CrossRef] [Green Version]
- Burger, M. Calculating road input data for vehicle simulation. Multibody Syst. Dyn. 2014, 31, 93–110. [Google Scholar] [CrossRef]
- Kumar, P.; Lewis, P.; Mcelhinney, C.P.; Rahman, A.A. An algorithm for automated estimation of road roughness from mobile laser scanning data. Photogramm. Rec. 2015, 30, 30–45. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Nagayama, T.; Xue, K. Road profile estimation, and its numerical and experimental validation, by smartphone measurement of the dynamic responses of an ordinary vehicle. J. Sound Vib. 2019, 457, 92–117. [Google Scholar] [CrossRef]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Identification of coexistent load and damage. Struct. Multidiscip. Optim. 2010, 41, 243–253. [Google Scholar] [CrossRef]
- Xu, Z.D.; Huang, X.H.; Xu, F.H.; Yuan, J. Parameters optimization of vibration isolation and mitigation system for precision platforms using non-dominated sorting genetic algorithm. Mech. Syst. Signal Process. 2019, 128, 191–201. [Google Scholar] [CrossRef]
- Guo, S.S.; Shi, Q. Transient influence of correlation between excitations on system responses. Commun. Nonlinear Sci. Numer. Simul. 2020, 80. [Google Scholar] [CrossRef]
- Imine, H.; Delanne, Y.; M’Sirdi, N.K. Road profile input estimation in vehicle dynamics simulation. Veh. Syst. Dyn. 2006, 44, 285–303. [Google Scholar] [CrossRef]
- Ngwangwa, H.M.; Heyns, P.S.; Labuschagne, F.J.J.; Kululanga, G.K. Reconstruction of road defects and road roughness classification using vehicle responses with artificial neural networks simulation. J. Terramech. 2010, 47, 97–111. [Google Scholar] [CrossRef] [Green Version]
- Doumiati, M.; Victorino, A.; Charara, A.; Lechner, D. Estimation of road profile for vehicle dynamics motion: Experimental validation. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011. [Google Scholar]
- Fauriat, W.; Mattrand, C.; Gayton, N.; Beakou, A.; Cembrzynski, T. Estimation of road profile variability from measured vehicle responses. Veh. Syst. Dyn. 2016, 54, 585–605. [Google Scholar] [CrossRef]
- Kang, S.W.; Kim, J.S.; Kim, G.W. Road roughness estimation based on discrete Kalman filter with unknown input. Veh. Syst. Dyn. 2019, 57, 1530–1544. [Google Scholar] [CrossRef]
- Kim, G.W.; Kang, S.W.; Kim, J.S.; Oh, J.S. Simultaneous estimation of state and unknown road roughness input for vehicle suspension control system based on discrete Kalman filter. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1610–1622. [Google Scholar] [CrossRef]
- Jiang, J.; Seaid, M.; Mohamed, M.S.; Li, H. Inverse algorithm for real-time road roughness estimation for autonomous vehicles. Arch. Appl. Mech. 2020, 90, 1333–1348. [Google Scholar] [CrossRef]
- Jeong, J.H.; Jo, H.; Ditzler, G. Convolutional neural networks for pavement roughness assessment using calibration-free vehicle dynamics. Comput. Civ. Infrastruct. Eng. 2020, 35, 1209–1229. [Google Scholar] [CrossRef]
- Bhowmik, B.; Tripura, T.; Hazra, B.; Pakrashi, V. First-Order Eigen-Perturbation Techniques for Real-Time Damage Detection of Vibrating Systems: Theory and Applications. Appl. Mech. Rev. 2019, 71. [Google Scholar] [CrossRef]
- Panda, S.; Tripura, T.; Hazra, B. First-Order Error-Adapted Eigen Perturbation for Real-Time Modal Identification of Vibrating Structures. J. Vib. Acoust. Trans. ASME 2021, 143. [Google Scholar] [CrossRef]
- Andrén, P. Power spectral density approximations of longitudinal road profiles. Int. J. Veh. Des. 2006, 40, 2–14. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Shan, Y.; He, T. Construction of road roughness in left and right wheel paths based on PSD and coherence function. Mech. Syst. Signal Process. 2015, 60, 668–677. [Google Scholar] [CrossRef]
- González, A.; O’Brien, E.J.; Li, Y.Y.; Cashell, K. The use of vehicle acceleration measurements to estimate road roughness. Veh. Syst. Dyn. 2008, 46, 483–499. [Google Scholar] [CrossRef]
- Qin, Y.; Guan, J.; Gu, L. The research of road profile estimation based on acceleration measurement. Appl. Mech. Mater. 2012, 226–228, 1614–1617. [Google Scholar] [CrossRef]
- Akcay, H.; Turkay, S. Cramer-Rao bounds for road profile estimation. In Proceedings of the 2017 IEEE 3rd Colombian Conference on Automatic Control (CCAC), Cartagena, Colombia, 18 October 2017. [Google Scholar]
- Türkay, S.; Akçay, H. Modelling of road roughness for full-car models: A spectral factorization approach. In Proceedings of the 20th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 13–15 October 2016. [Google Scholar]
- Turkay, S.; Akcay, H. Road roughness modelling by using spectral factorization methods. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Korea, 16–19 October 2016. [Google Scholar]
- Zhao, B.; Nagayama, T. IRI Estimation by the Frequency Domain Analysis of Vehicle Dynamic Responses. Procedia Eng. 2017, 188, 9–16. [Google Scholar] [CrossRef]
- Zhao, B.; Nagayama, T.; Toyoda, M.; Makihata, N.; Takahashi, M.; Ieiri, M. Vehicle model calibration in the frequency domain and its application to large-scale IRI estimation. J. Disaster Res. 2017, 12, 446–455. [Google Scholar] [CrossRef]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion; SIAM: Philadelphia, PA, USA, 1998; pp. 175–206. [Google Scholar]
- Pan, C.D.; Yu, L.; Liu, H.L. Identification of moving vehicle forces on bridge structures via moving average Tikhonov regularization. Smart Mater. Struct. 2017, 26, 085041. [Google Scholar] [CrossRef]
- Zhang, Q.; Dduan, Z.; Jankowski, Ł. Experimental validation of a fast dynamic load identification method based on load shape function. J. Vib. Shock 2011, 9, 98–102. [Google Scholar] [CrossRef]
- GB/T7031-2005/ISO 8608. Mechanical Vibration-Road Surface Profiles-Reporting of Measured Data of National Standard of the People’s Republic of China; International Organization for Standardization: Geneva, Switzerland, 1995. [Google Scholar]


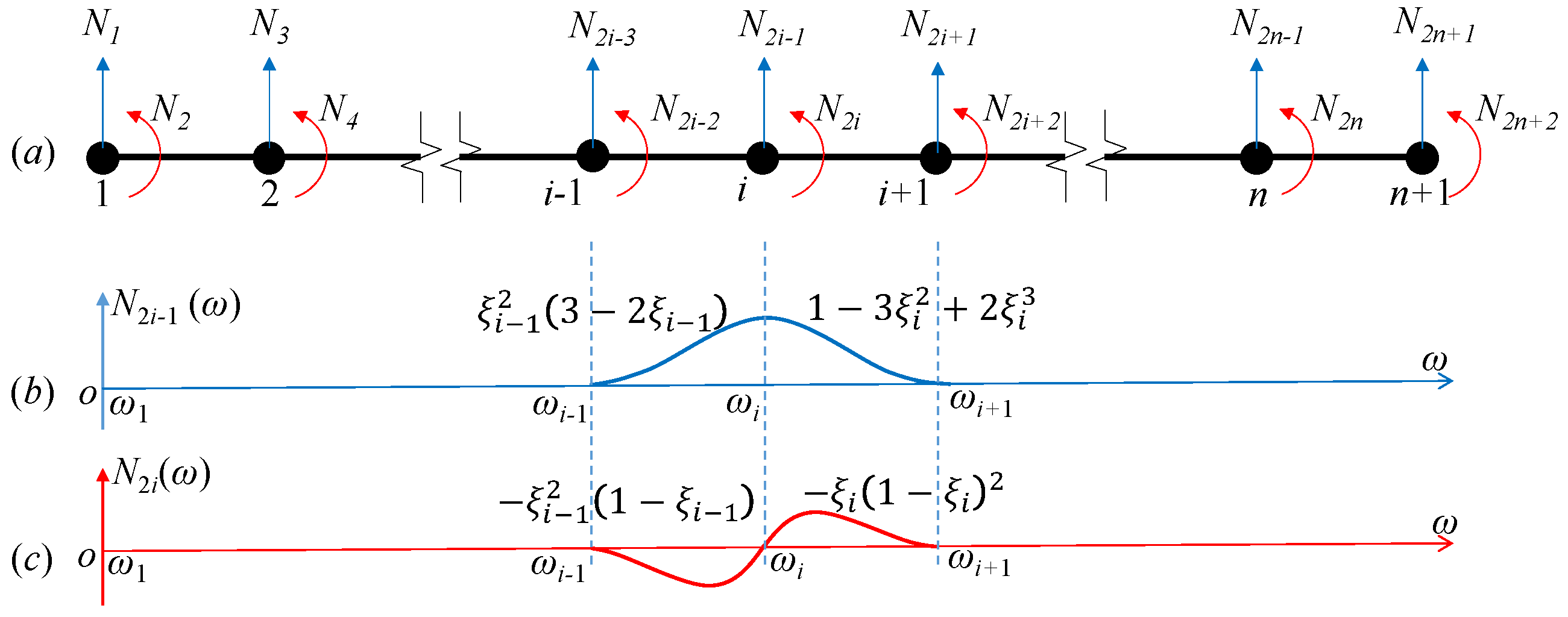
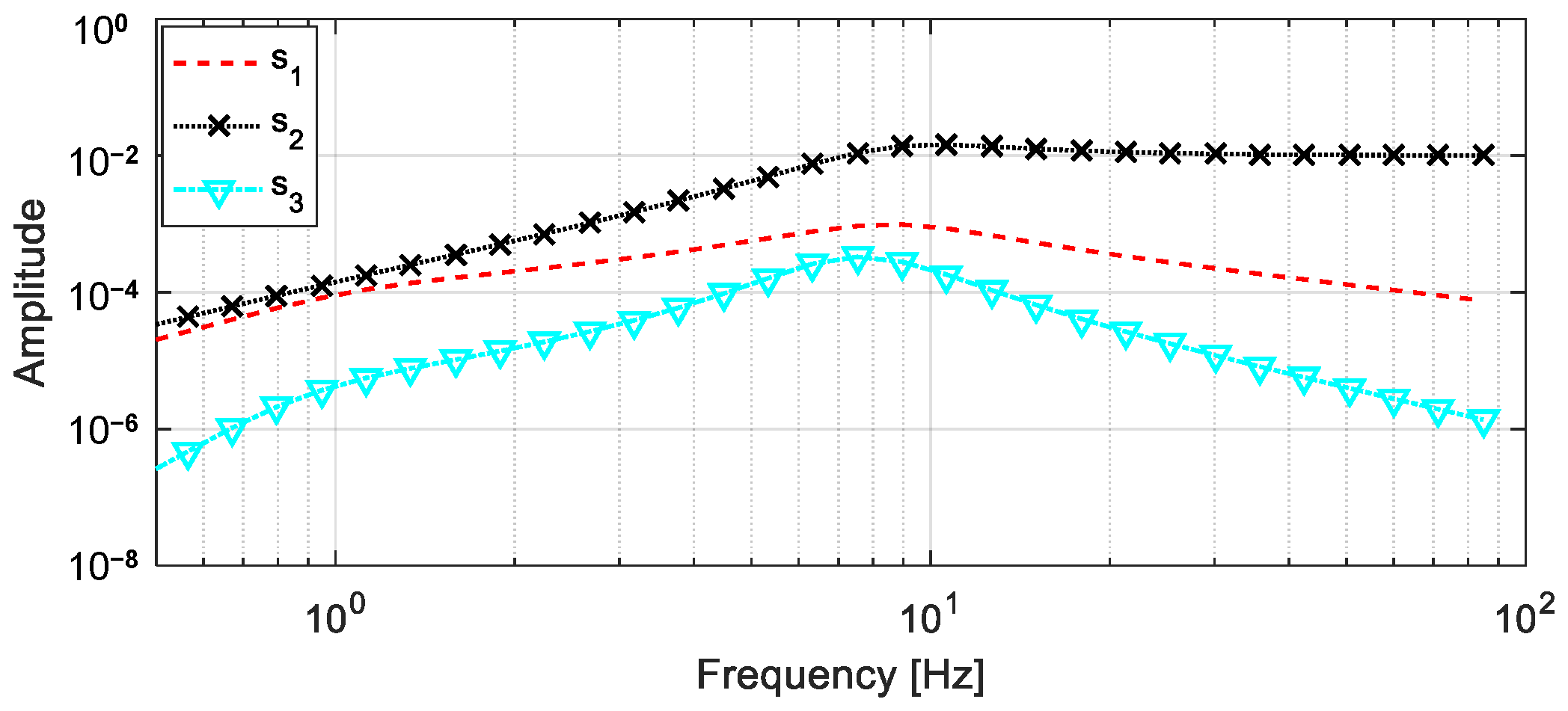
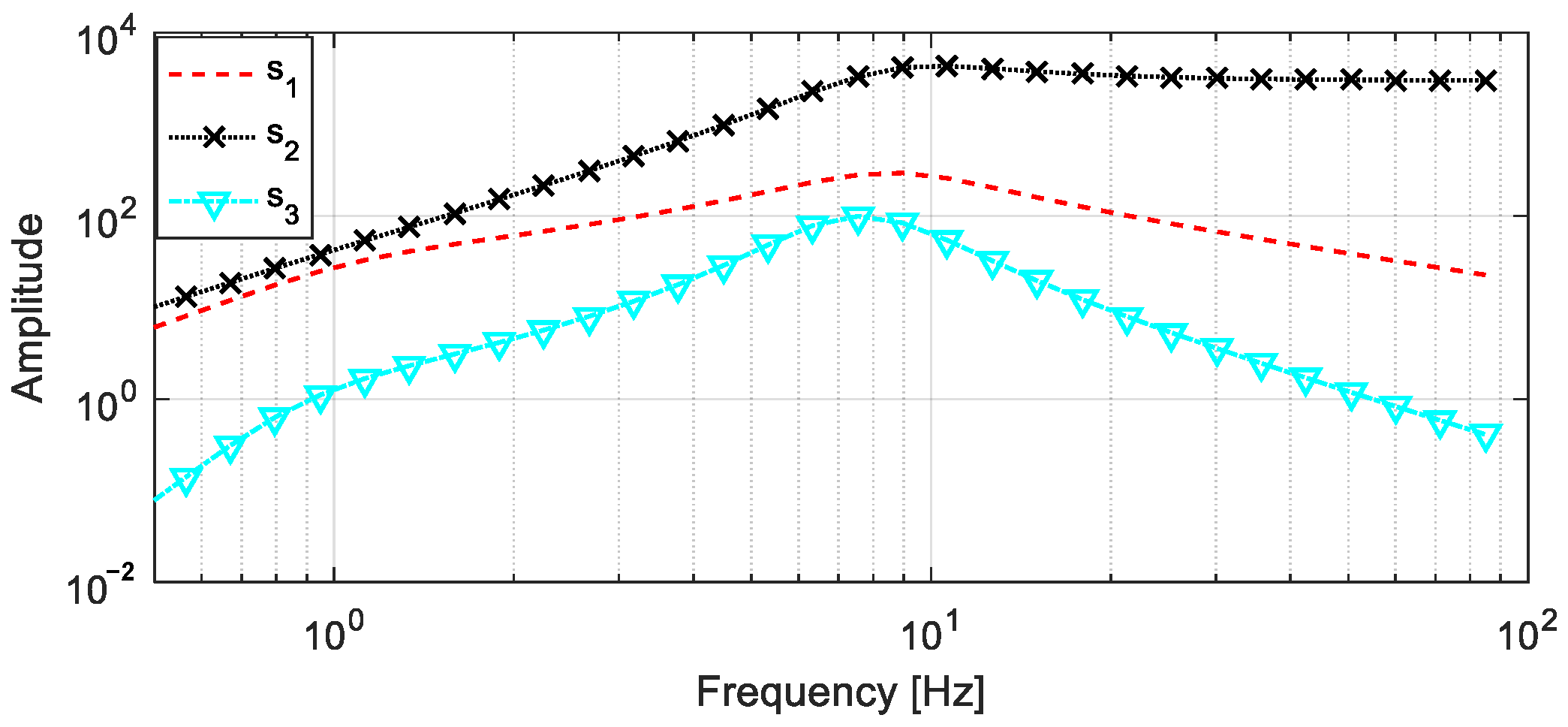

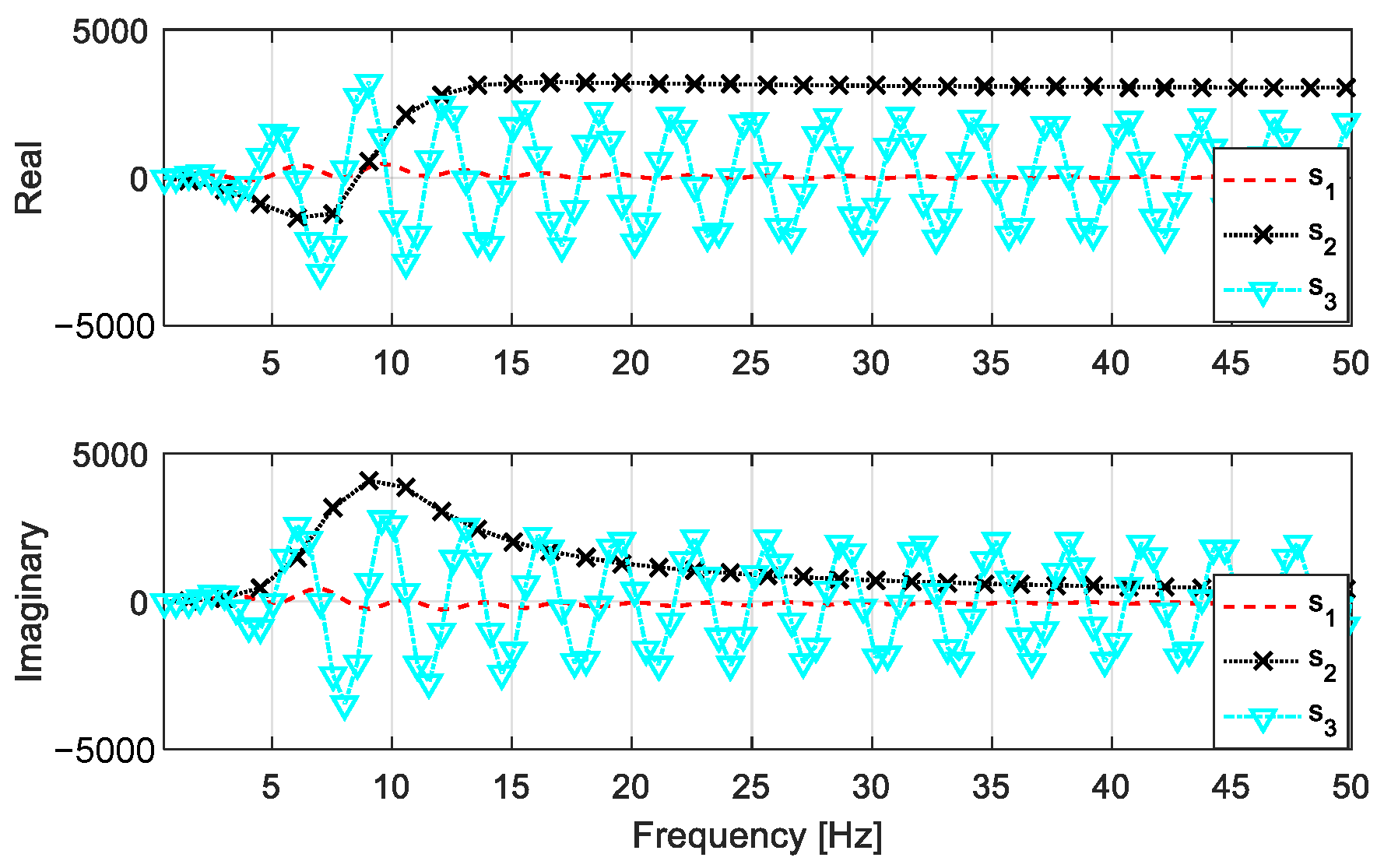





| m1 (kg) | m2 (kg·m2) | m3 (kg) | m4 (kg) | k1 = k2 (N/m) | k3 = k4 (N/m) | c1 = c2 (N·s /m) | e1 (m) | e2 (m) |
|---|---|---|---|---|---|---|---|---|
| 1000 | 4000 | 100 | 150 | 20,000 | 300,000 | 4000 | 1.6 | 1.6 |
| Order | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| natural frequency | 0.779 | 0.974 | 7.355 | 9.006 |
| Case | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| Sets of velocity (m/s) | 20, 17, 15, 13, 11, 7, 5, −3 | 20, 15, 11, 5, −3 | 20, 15, 11, 5 | 20,15, 1 | 15, 11 |
| Case A | Case B | Case C | Case D | |
|---|---|---|---|---|
| Case 1 | 17.02% | 16.82% | 16.07% | 31.10% |
| Case 2 | 24.67% | 22.67% | 20.17% | 47.71% |
| Case 3 | 23.21% | 23.16% | 16.73% | 38.03% |
| Case 4 | 54.33% | 35.60% | 53.53% | 48.09% |
| Case 5 | 54.85% | 42.51% | 53.49% | 52.85% |
| Case A | Case B | Case C | Case D | |
|---|---|---|---|---|
| Case 1 | 10.26% | 10.43% | 10.50% | 28.76% |
| Case 2 | 11.67% | 11.63% | 11.57% | 45.66% |
| Case 3 | 15.29% | 12.68% | 13.72% | 33.36% |
| Case 4 | 59.89% | 41.05% | 57.57% | 36.70% |
| Case 5 | 61.70% | 46.58% | 60.14% | 42.95% |
| Case A | Case B | Case C | Case D | |
|---|---|---|---|---|
| Errors | 8.55% | 8.75% | 8.88% | 16.39% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Hou, J.; Duan, Z.; Jankowski, Ł.; Hu, X. Road Roughness Estimation Based on the Vehicle Frequency Response Function. Actuators 2021, 10, 89. https://doi.org/10.3390/act10050089
Zhang Q, Hou J, Duan Z, Jankowski Ł, Hu X. Road Roughness Estimation Based on the Vehicle Frequency Response Function. Actuators. 2021; 10(5):89. https://doi.org/10.3390/act10050089
Chicago/Turabian StyleZhang, Qingxia, Jilin Hou, Zhongdong Duan, Łukasz Jankowski, and Xiaoyang Hu. 2021. "Road Roughness Estimation Based on the Vehicle Frequency Response Function" Actuators 10, no. 5: 89. https://doi.org/10.3390/act10050089
APA StyleZhang, Q., Hou, J., Duan, Z., Jankowski, Ł., & Hu, X. (2021). Road Roughness Estimation Based on the Vehicle Frequency Response Function. Actuators, 10(5), 89. https://doi.org/10.3390/act10050089






