Factors Affecting the Dependency of Shear Strain of LRB and SHDR: Experimental Study
Abstract
:1. Introduction
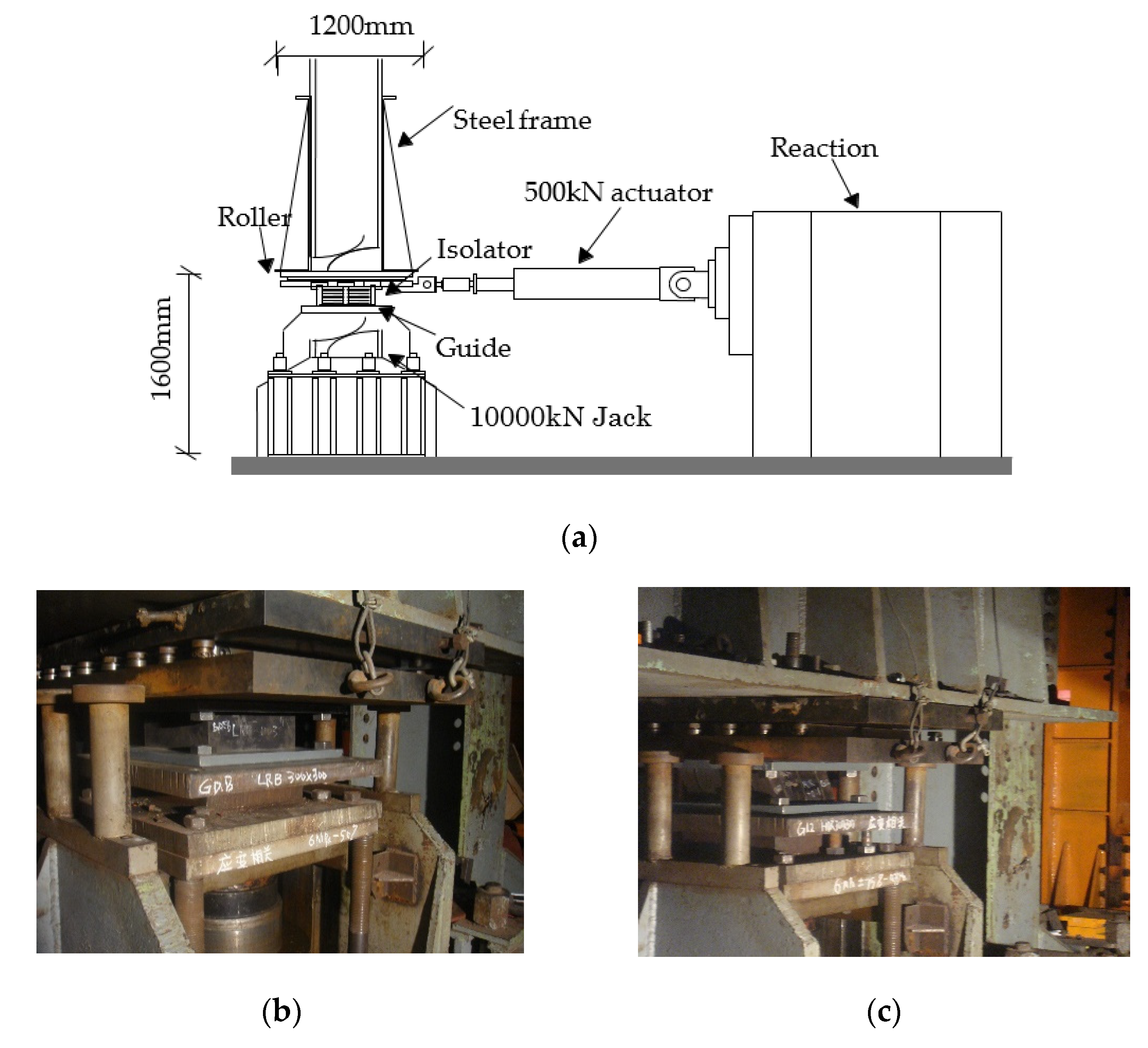
2. Experimental Setup
3. General Observation of Tests
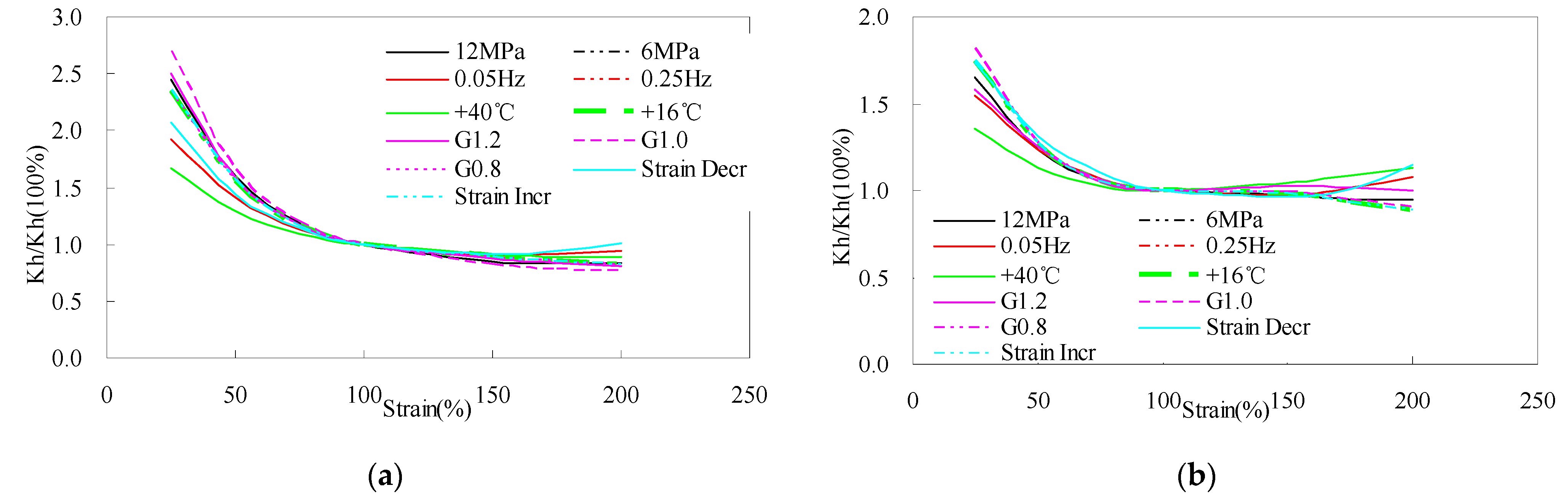
3.1. Post-Yield Stiffness
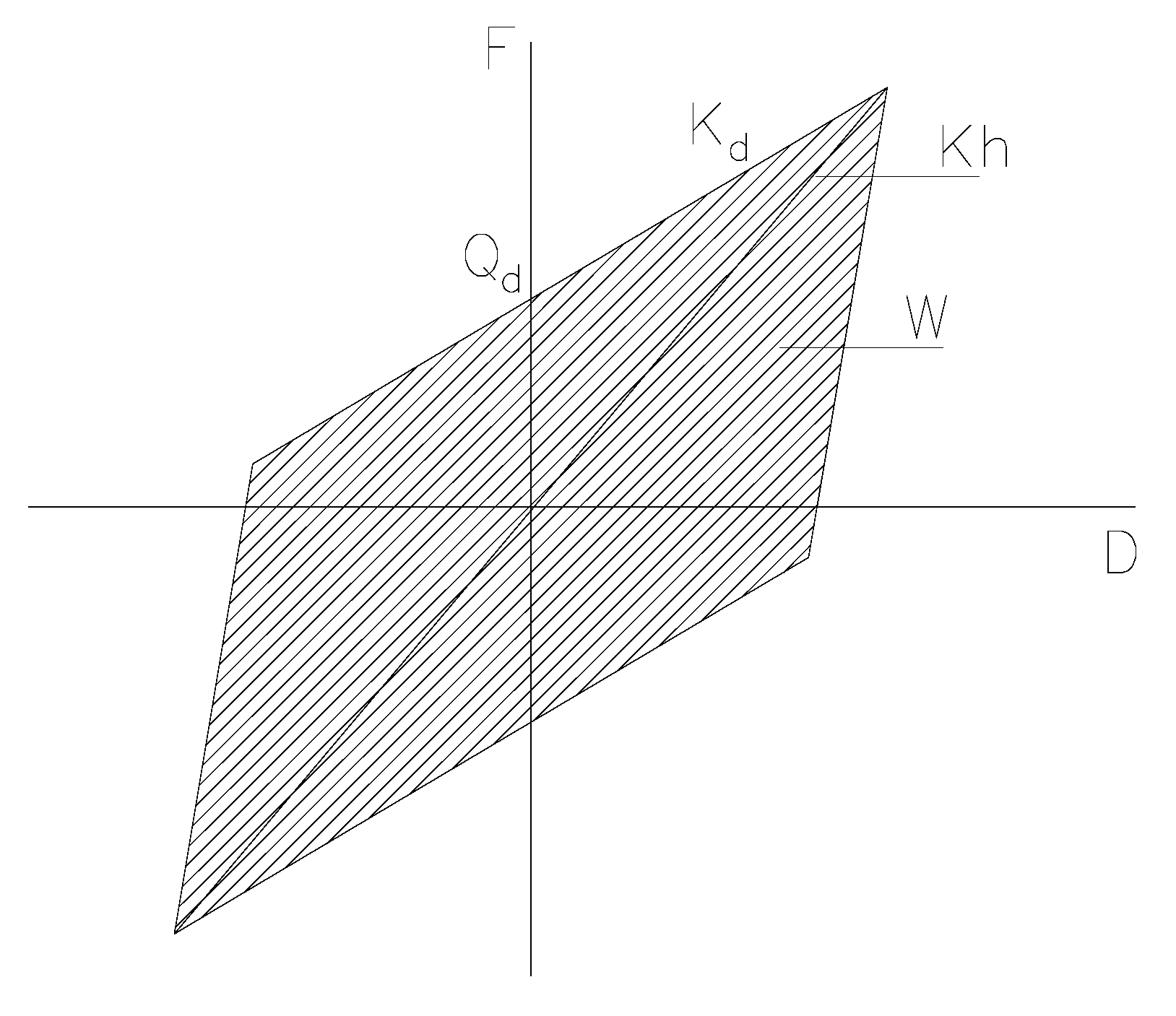
3.2. Characteristic Strength
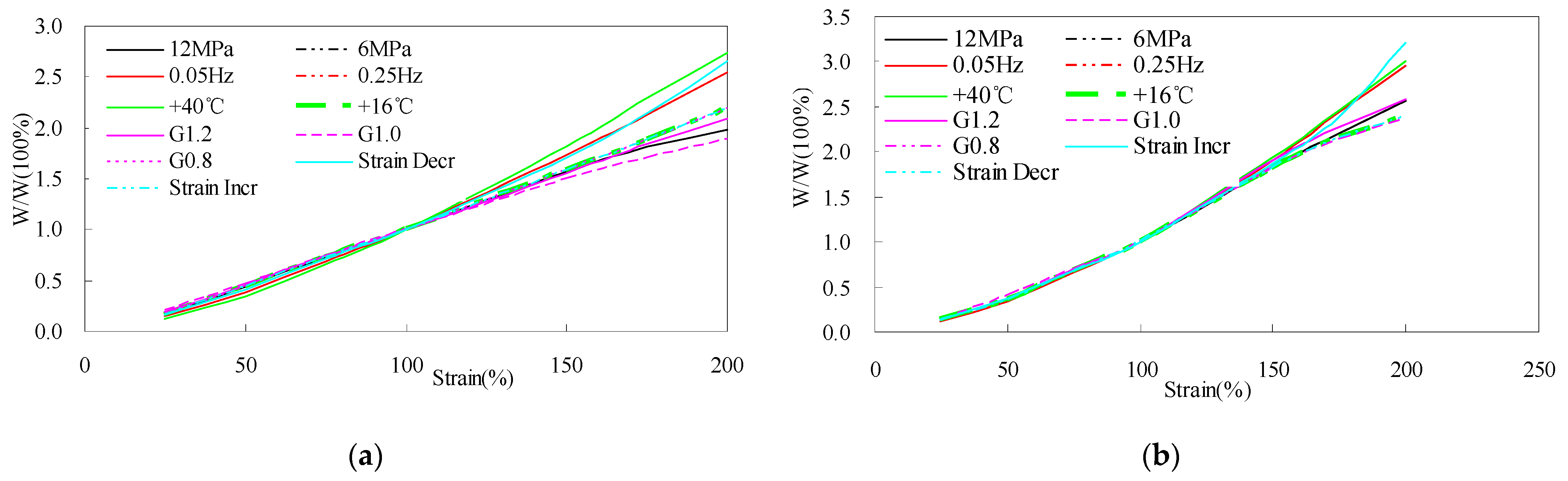
3.3. Area of Single Cycle of Hysteretic Loop
3.4. Equivalent Stiffness
3.5. Equivalent Damping Ratio
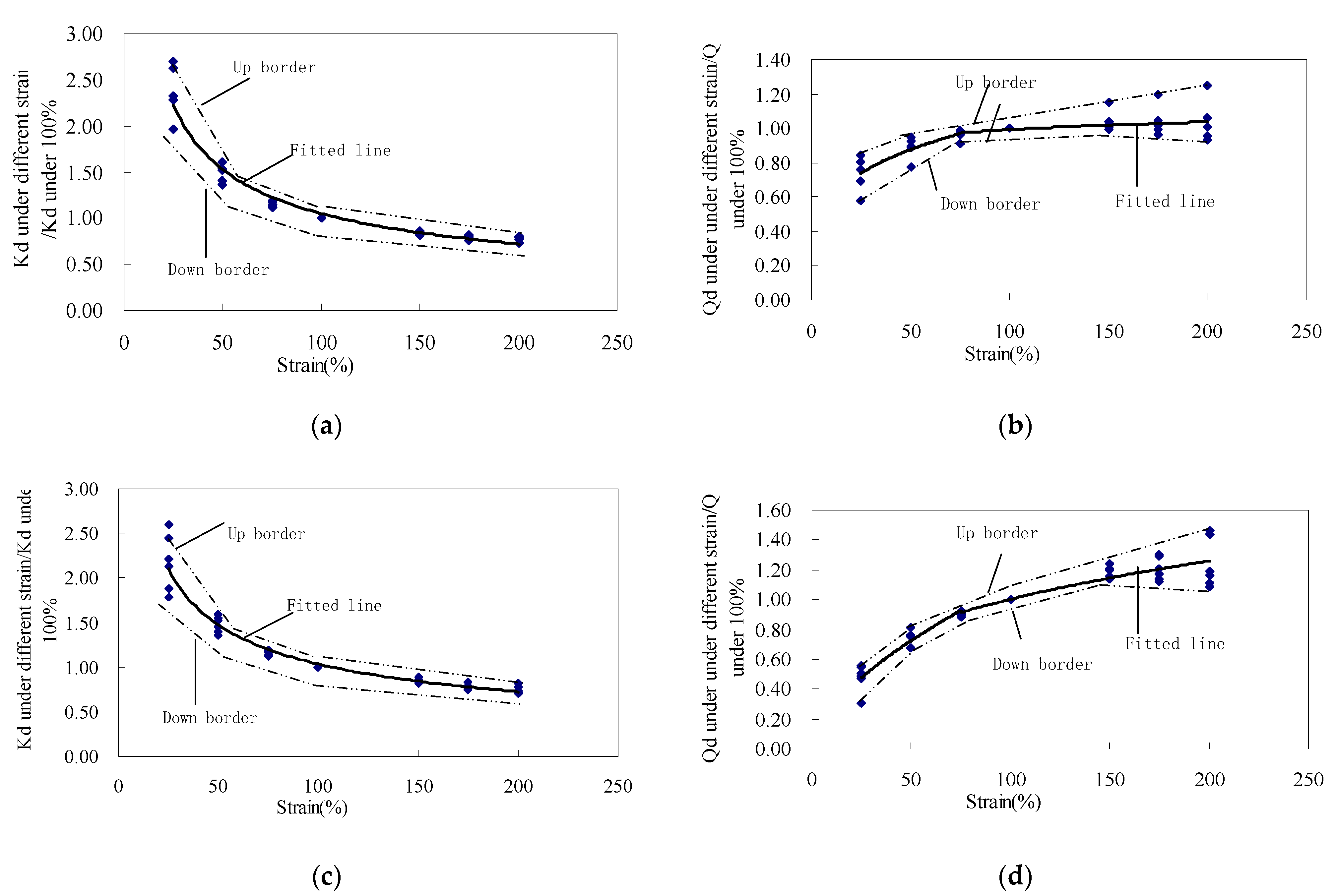
3.6. Fitted Curve
4. Discussion on Special Experimental Results
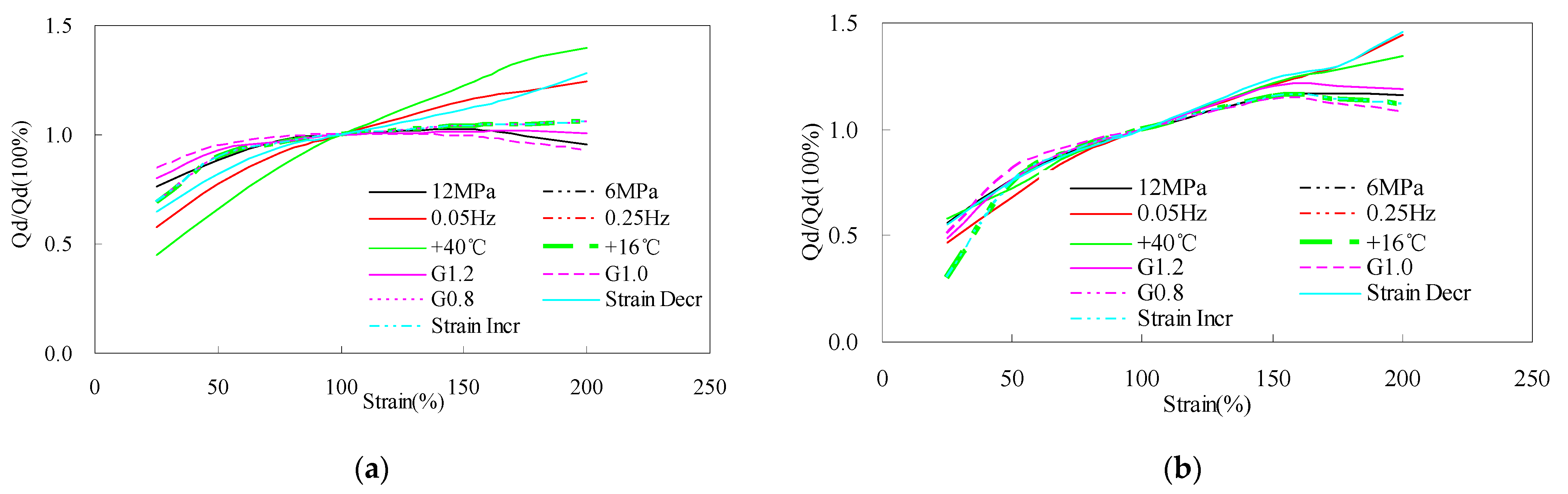
4.1. Comparing Slope of for LRB under Low and High Temperatures
4.2. Normalized Value of of LRB at Low Strain under Low Temperature Being Greather than That under High Temperature
5. Conclusions
- In most of the conditions, the temperature may be the most significant factor in the shear strain dependency of LRB or SHDR.
- The G value and pressure may be the least impactful factors, especially the G value, whose effect can be neglected, whether for LRB or SHDR.
- For the loading frequency and loading sequence, there are certain impacts; in most of the conditions, their level of effect is found between the temperature and G value.
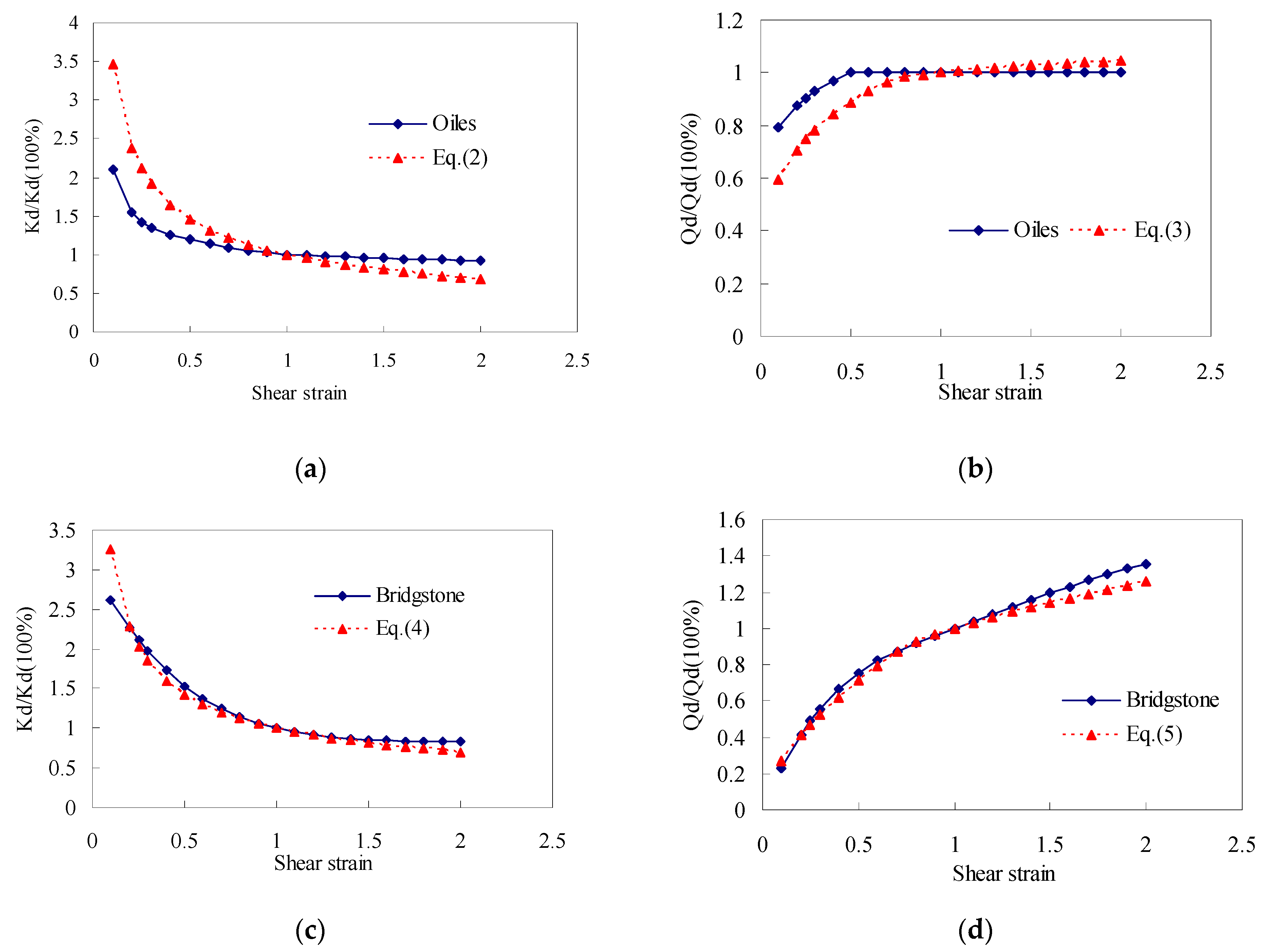
- For LRB, excluding the temperature, the fitted curves of the post-yielded stiffness and the characteristic strength were given. By comparing them with those given by Olies, a little difference is found at small shear strains.
- For SHDR, the corresponding fitted curves fit well with those given by Bridgestone.
- For LRB, during all the shear strains, the change of the characteristic strength is very little under low temperature. However, the slope of characteristic strength versus the shear strain under high temperature is large.
- For LRB, the post-yielded stiffness at 25% is larger than that at 100% under low temperature; however, the increase shows a significant reduction under high temperature. The reason is caused by the high yield strength of lead at low temperature and its incompletely yielded state.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, F.L. Earthquake Energy Absorbing Control on Engineering Structure; Seismological Press: Beijing, China, 1997. [Google Scholar]
- Li, A.Q. Investigation and consideration of seismic isolation and energy dissipation structures in Tohoku earthquake. Eng. Mech. 2012, 29, 69–77. [Google Scholar]
- Yutaka, N.; Tetsuya, H.; Masanobu, H. Report on the effects of seismic isolation methods from the 2011 Tohoku-Pacific Earthquake. Seism. Isol. Prot. Syst. 2011, 2, 57–74. [Google Scholar]
- China Ministry of Transport. High Damper Rubber Bearings for Bridges on Road, JT/T 842-2012; China Communications Press: Beijing, China, 2012.
- Roeder, C.; Stanton, J.; Feller, T. Low-temperature performance of elastomeric bearings. J. Cold Reg. Eng. 1990, 4, 113–132. [Google Scholar] [CrossRef]
- Nakano, O.; Nishi, H.; Shirono, T. Temperature-dependency of base-isolated bearings. In Proceedings of the Second U.S-Japan Workshop on Earthquake Protective Systems for Bridges, Technical Memorandum, Tsukuba Science City, Japan, 7–8 December 1992; Public Works Research Institute: Tsukuba Science City, Japan, 1993. [Google Scholar]
- Kim, D.K.; Mander, J.; Chen, S. Temperature and strain rate effects on the seismic performance of elastomeric and lead-rubber bearings. In Proceedings of the Fourth World Congress on Joint Sealants and Bearing Systems for Concrete Structures, Sacramento, CA, USA, 29 September–3 October 1996. [Google Scholar]
- Liu, W.G.; Zhuang, X.Z.; Zhou, F.L.; Feng, D.T.; Kato, Y. Dependence and durability properties of Chinese lead plug rubber bearings. Earthq. Eng. Eng. Vib. 2002, 22, 114–120. [Google Scholar]
- Yakut, A.; Yura, J.A. Evaluation of Elastomeric Bearing Performance at Low Temperatures. J. Struct. Eng. 2002, 128, 995–1002. [Google Scholar] [CrossRef]
- Yakut, A.; Yura, J.A. Parameters Influencing Performance of Elastomeric Bearings at Low Temperatures. J. Struct. Eng. 2002, 128, 986–994. [Google Scholar] [CrossRef]
- Li, H.; Du, Y.F.; Di, S.K.; Tu, J.M.; Yang, W.X.; Li, Q.F. Cyclic test of laminated rubber damping bearing at low temperature and calculation of equivalent viscous damping ratio. J. Lanzhou Univ. Technol. 2006, 32, 116–119. [Google Scholar]
- Li, L.; Ye, K.; Jiang, Y.C. Thermal effect on the mechanical behavior of Lead-Rubber Bearing. J. Hua Zhong Univ. Sci. Technol. 2009, 26, 1–3. [Google Scholar]
- Fuller, K.; Gough, J.; Thomas, A.G. The effect of low temperature crystallization on the mechanical behavior of rubber. J. Polym. Sci. Part B Polym. Phys. 2010, 42, 2181–2190. [Google Scholar] [CrossRef]
- Shirazi, A. Thermal degradation of the performance of elastomeric bearings for seismic isolation. Ph.D. Thesis, University of California, San Diego, CA, USA, 2010. [Google Scholar]
- Cardone, D.; Gesualdi, G.; Nigro, D. Effects of air temperature on the cyclic behavior of Elastomeric seismic isolators. Bull. Earthq. Eng. 2011, 9, 1227–1255. [Google Scholar] [CrossRef]
- Shen, C.Y.; Zhou, F.L.; Cui, J.; Huang, X.; Zhuang, X.; Ma, Y. Dependency test research of mechanical performance of HDR and its parametric value analysis. Earthq. Eng. Eng. Vib. 2012, 32, 95–103. [Google Scholar]
- Shen, C.Y.; Tan, P.; Cui, J.; Ma, Y.H.; Huang, X.Y.; Wang, C. Experimental study on dependency of the horizontal mechanical property of elastomeric isolators with ultralow hardness. Earthq. Eng. Eng. Vib. 2014, 34, 204–216. [Google Scholar]
- Basit, Q. Low temperature performance of elastomeric bearings in a full size field experience bridge. Master’s Thesis, State University of New York at Buffalo, Buffalo, NY, USA, 2016. [Google Scholar]
- Wang, J.Q.; Xin, W.; Li, Z.; Zhao, Z. Experimental study on vertical pressure dependency about shear properties of lead rubber bearing. Earthq. Eng. Eng. Vib. 2016, 36, 200–206. [Google Scholar]
- Wang, J.Q.; Zhang, Z.Y.; Li, Z. Experimental research on the vertical pressure dependency about shear properties of High Damping Rubber Bearing. J. Railw. Eng. Soc. 2017, 220, 47–117. [Google Scholar]
- Rohola, R.; Rovert, J.T. Numerical evaluation of steel-rubber isolator with single and multiple rubber cores. Eng. Struct. 2019, 198, 1–15. [Google Scholar]
- Zhang, R.J.; Li, A.Q. Experimental study on temperature dependence of mechanical properties of scaled high-performance rubber bearings. Compos. Part B 2020, 190, 107932. [Google Scholar] [CrossRef]
- Rohola, R.; Helder, D.C.; Rbecc, N. Static and dynamic stability analysis of a steel-rubber isolator with rubber cores. Structures 2020, 26, 441–455. [Google Scholar]
- Javad, S.; Mojtaba, F. Natural Rubber Bearing Incorporated with Steel Ring Damper. Int. J. Steel Struct. 2020, 20, 23–34. [Google Scholar]
- Radkia, S.; Rahnavard, R.; Tuwair, H.; Gandomkar, F.A.; Napolitano, R. Investigating the effects of seismic isolators on steel asymmetric structures considering soil-structure interaction. Structures 2020, 27, 1029–1040. [Google Scholar] [CrossRef]
- Sheikhi, J.; Fathi, M.; Rahnavard, R.; Napolitano, R. Numerical analysis of natural rubber bearing equipped with steel and shape memory alloys dampers. Structures 2021, 32, 1839–1855. [Google Scholar] [CrossRef]
- Masahiko, H.; Shin, O. Response Control. and Seismic Isolation of Buildings; Taylor & Francis Press: London, UK; New York, NY, USA, 2005. [Google Scholar]
- Bridgestone Corporation Seismic Isolation Products & Engineering Development. In Technical Report: High.-Damping Rubber Bearings for Base Isolation; Product Code: HDR-X0.6R; Yokohama, Japan, 2010.
- International Standardization Organization. Elastomeric Seismic-Protection Isolators-Part. 1: Test. Methods. ISO 22762-1; ISO: Geneva, Switzerland, 2005. [Google Scholar]
- The Society of Architecture of Japan. Recommendation for the Design of Base Isolated Buildings; Gihodo Shuppan Co., Ltd.: Tokyo, Japan, 2001. [Google Scholar]
- Shen, C.Y.; Ma, Y.H.; Zhuang, X.Z.; Chen, Y.Y.; Lin, J.; Wang, S.B. Experimental Research on dependencies of mechanical property of elastomeric isolator with lower hardness and parameters analysis. Appl. Mech. Mater. 2012, 166–169, 2982–2994. [Google Scholar] [CrossRef]
- International Standardization Organization. Elastomeric Seismic-Protection Isolators-Part 3: Applications for Buildings—Specifications. ISO 22762-3; ISO: Geneva, Switzerland, 2005. [Google Scholar]
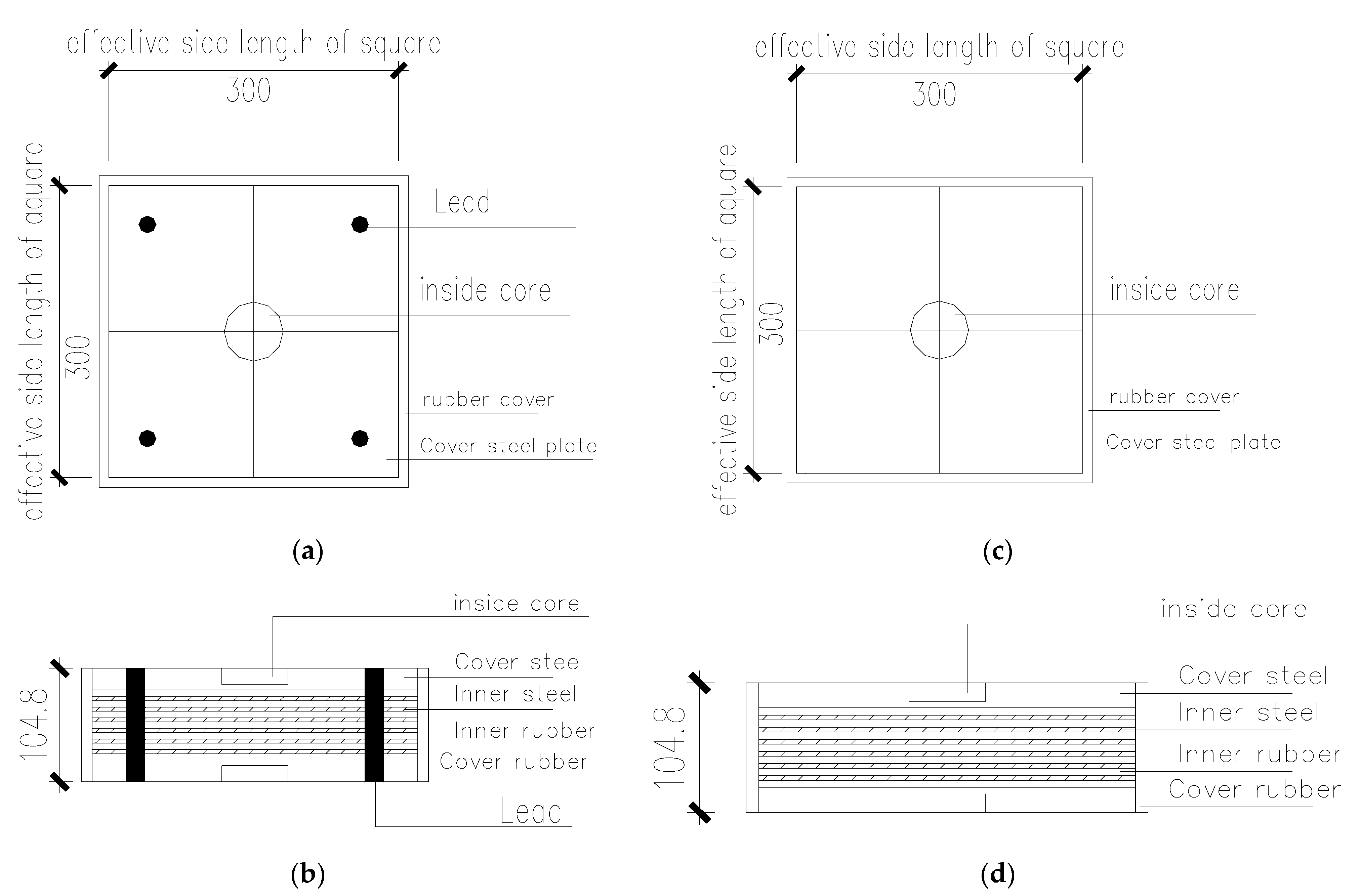




| Effective Side Length of Square (mm) | Shear Modulus of Inner Rubber (MPa) | Diameter of Lead (mm) | Number of Layers of Inner Rubber | Thickness of Single Inner Rubber (mm) | Thickness of Single Inner Steel (mm) | Thickness of Cover Rubber (mm) | Thickness of Cover Steel (mm) |
|---|---|---|---|---|---|---|---|
| 300 | 0.8/1.0/1.2 | 4 × 42.5 | 7 | 6 | 3.8 | 10 | 20 |
| Test Case | Specimen | Values Used for Factors | |
|---|---|---|---|
| LRB | SHDR | ||
| Different frequency of loading | 300 × 300 (G0.8) | 300 × 300 (G0.8) | 0.05 Hz, 0.25 Hz |
| Different sequence of loading | 300 × 300 (G0.8) | 300 × 300 (G0.8) | Shear strain increasing or decreasing |
| Different pressure | 300 × 300 (G0.8) | 300 × 300 (G0.8) | 6 MPa, 12 MPa |
| Different shear modulus of inner rubber | 300 × 300 (G0.8/G1.0/G1.2) | 300 × 300 (G0.8/G1.0/G1.2) | 0.8 MPa, 1.0 Mpa, 1.2 MPa |
| Different temperature | 300 × 300 (G0.8) | 300 × 300 (G0.8) | 16 °C, 40 °C |
| Shear strain | 25%, 50%, 100%, 150%, 175%, 200% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, C.-Y.; Huang, X.-Y.; Chen, Y.-Y.; Ma, Y.-H. Factors Affecting the Dependency of Shear Strain of LRB and SHDR: Experimental Study. Actuators 2021, 10, 98. https://doi.org/10.3390/act10050098
Shen C-Y, Huang X-Y, Chen Y-Y, Ma Y-H. Factors Affecting the Dependency of Shear Strain of LRB and SHDR: Experimental Study. Actuators. 2021; 10(5):98. https://doi.org/10.3390/act10050098
Chicago/Turabian StyleShen, Chao-Yong, Xiang-Yun Huang, Yang-Yang Chen, and Yu-Hong Ma. 2021. "Factors Affecting the Dependency of Shear Strain of LRB and SHDR: Experimental Study" Actuators 10, no. 5: 98. https://doi.org/10.3390/act10050098
APA StyleShen, C.-Y., Huang, X.-Y., Chen, Y.-Y., & Ma, Y.-H. (2021). Factors Affecting the Dependency of Shear Strain of LRB and SHDR: Experimental Study. Actuators, 10(5), 98. https://doi.org/10.3390/act10050098





