Design and Experimental Validation of a Fuzzy Cascade Controller for a Zero-Power Permanent Magnetic Suspension System with Variable Flux Path Control
Abstract
:1. Introduction
2. Structure and Working Principle
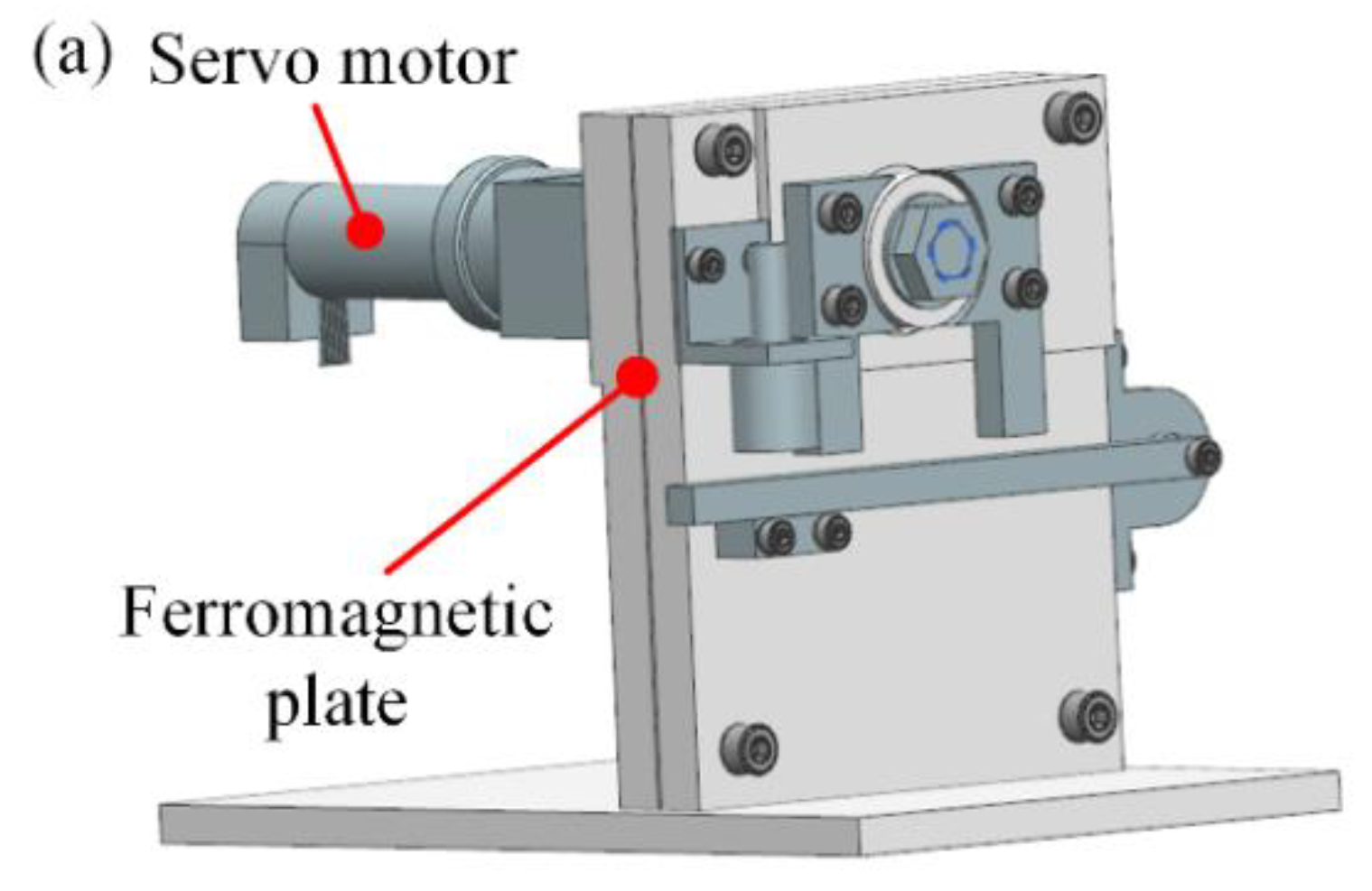
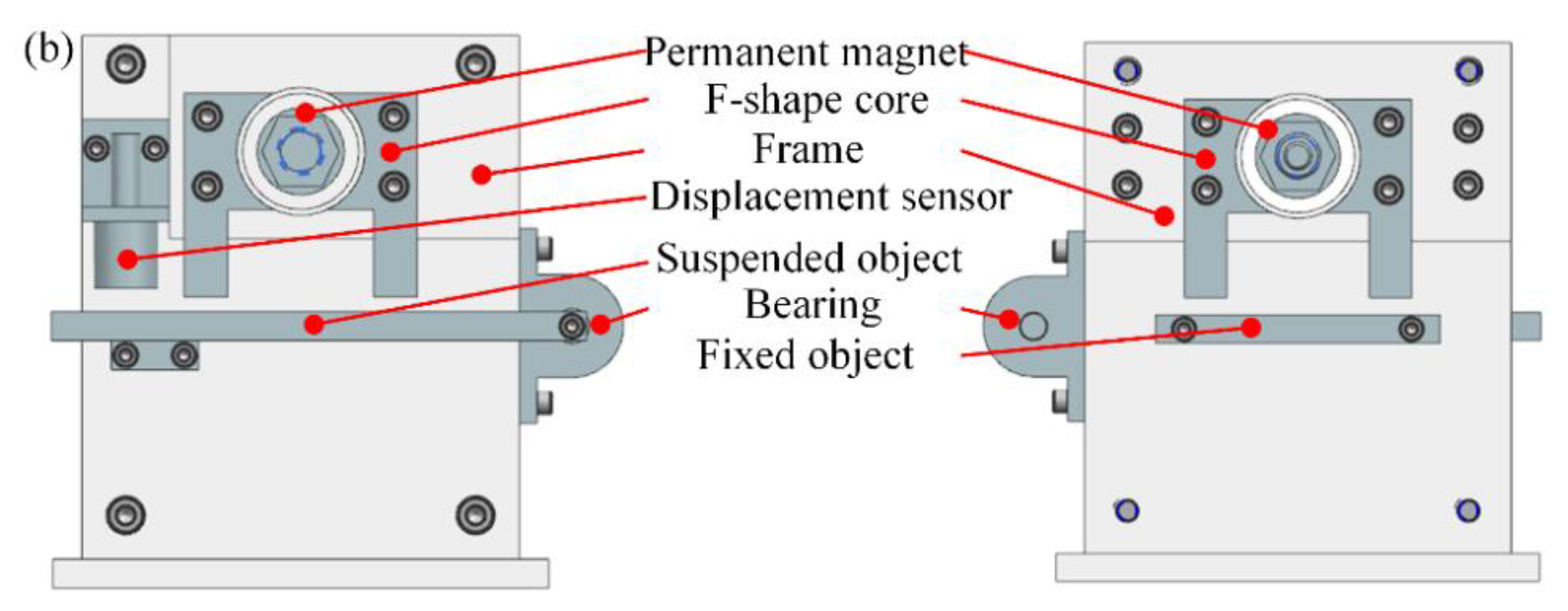
2.1. Structure
2.2. Working Principle
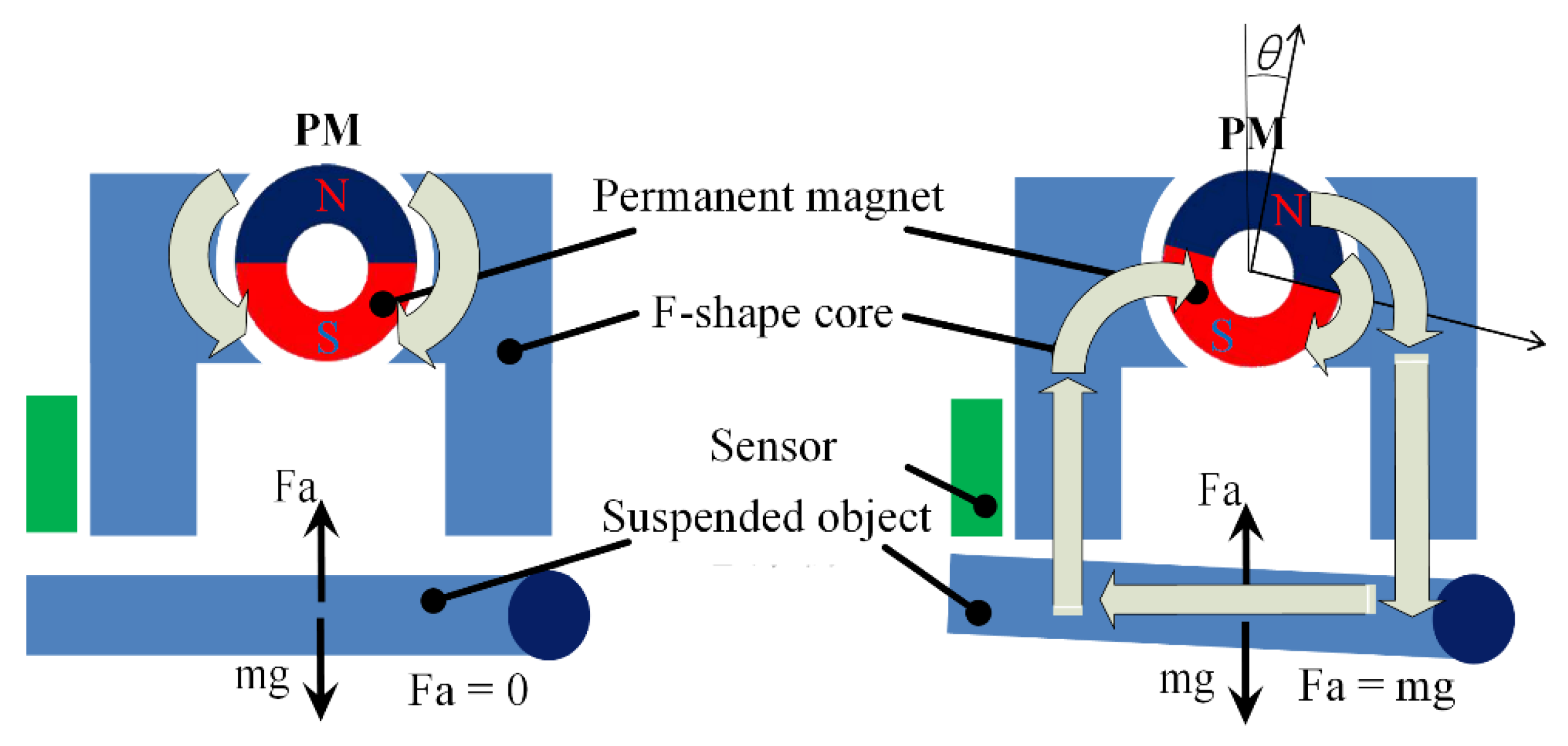
2.2.1. Suspension Principle
2.2.2. Zero Power Principle
2.3. Novelty of the Proposed Magnetic Suspension Device
3. Theoretical Modeling and Controller Design
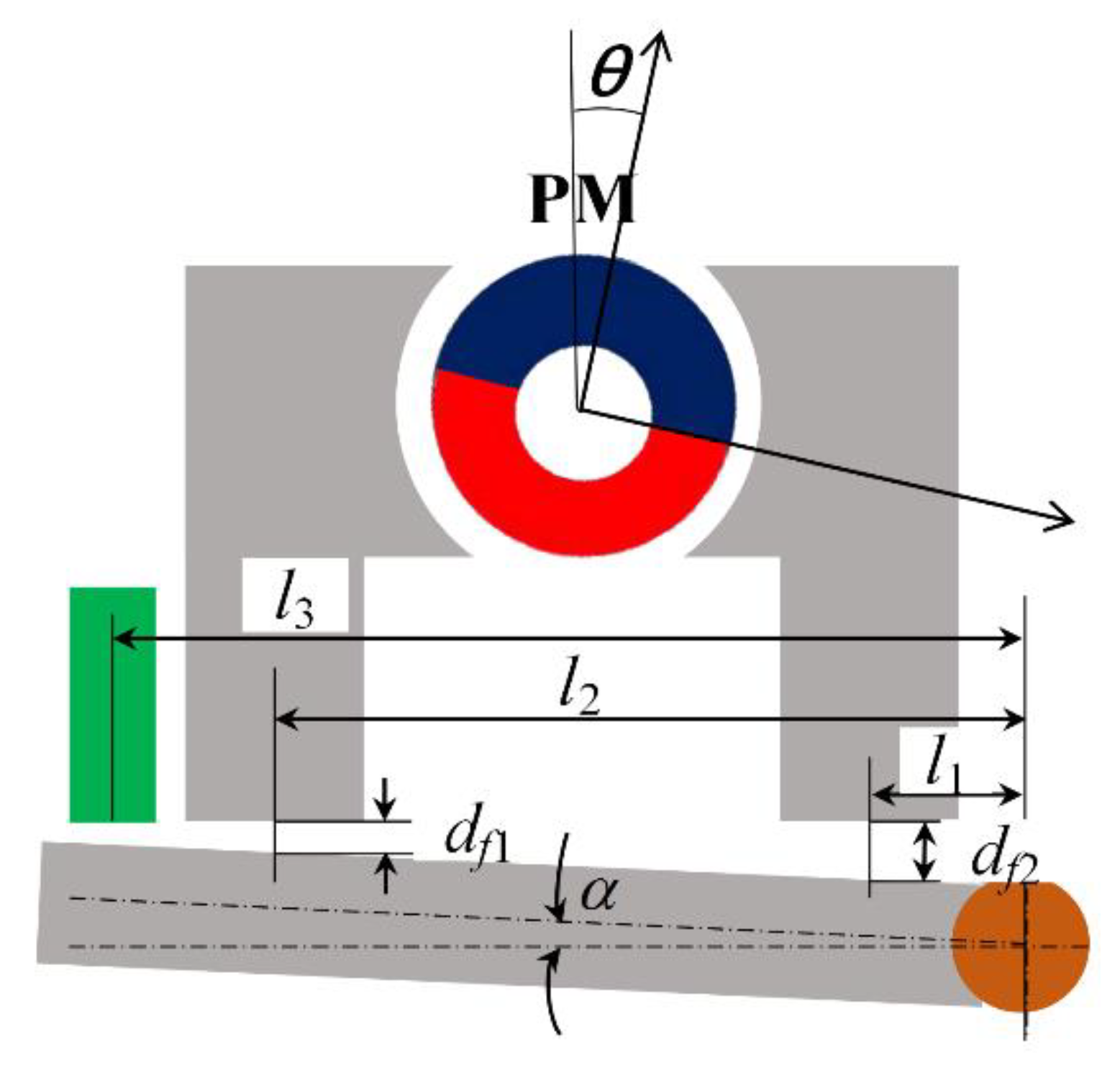
3.1. Theoretical Modeling
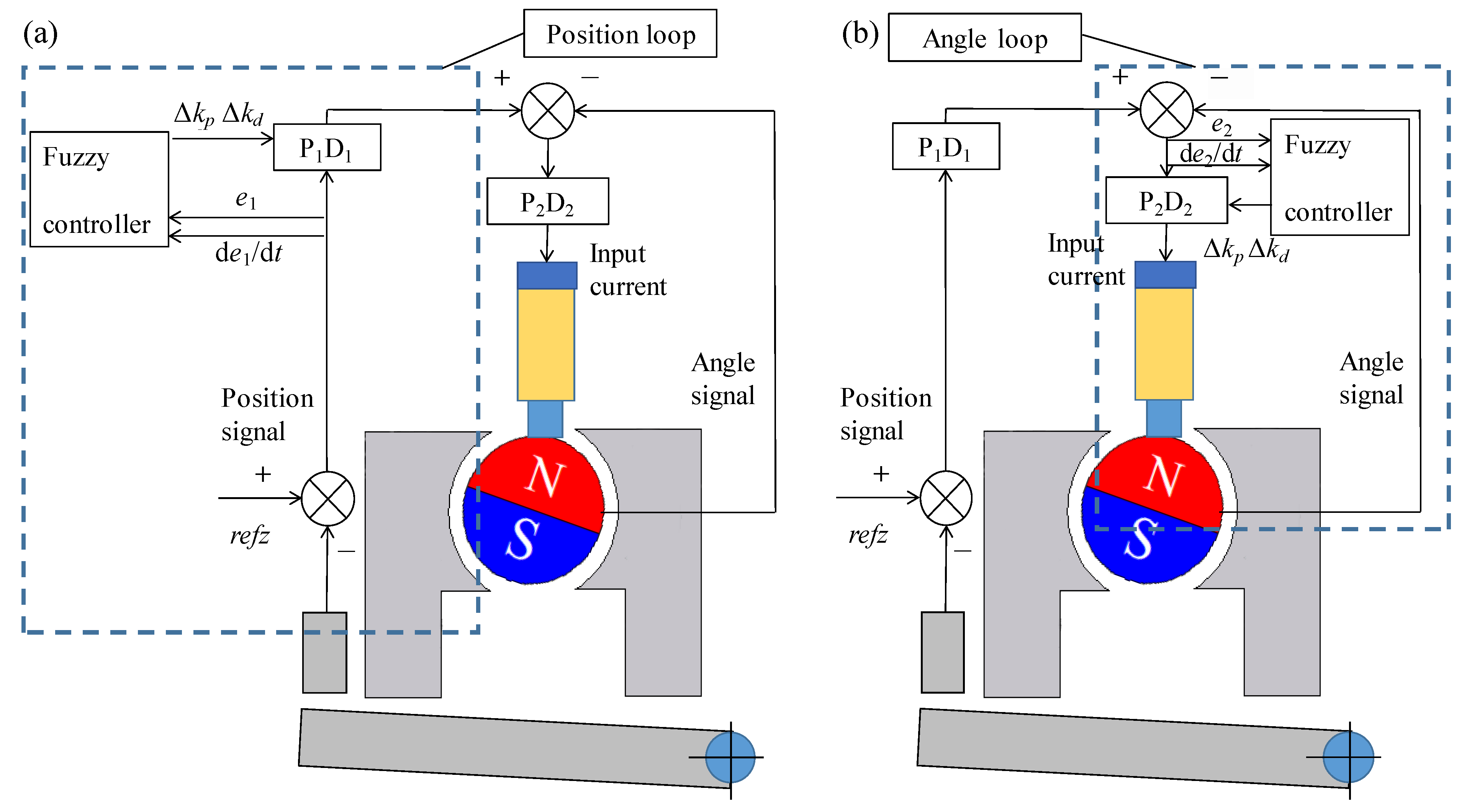
3.2. Controller Design
3.2.1. Design of Domains and Membership Functions
3.2.2. Fuzzy Control Rules
4. Simulation Analysis
4.1. Simulation Results of the Displacement Disturbance
4.2. Simulation Results of the Force Disturbance
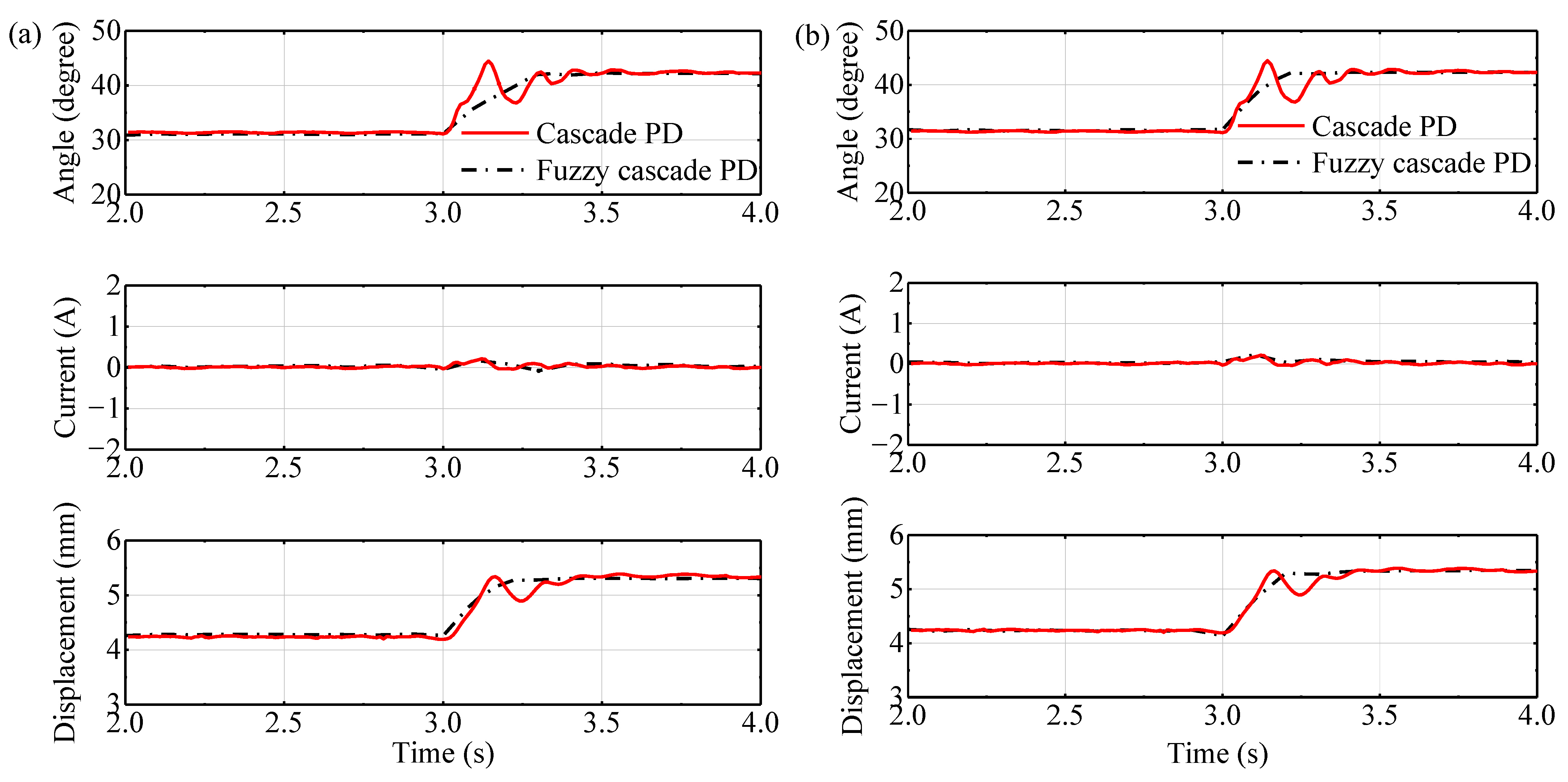
5. Experiment Verification
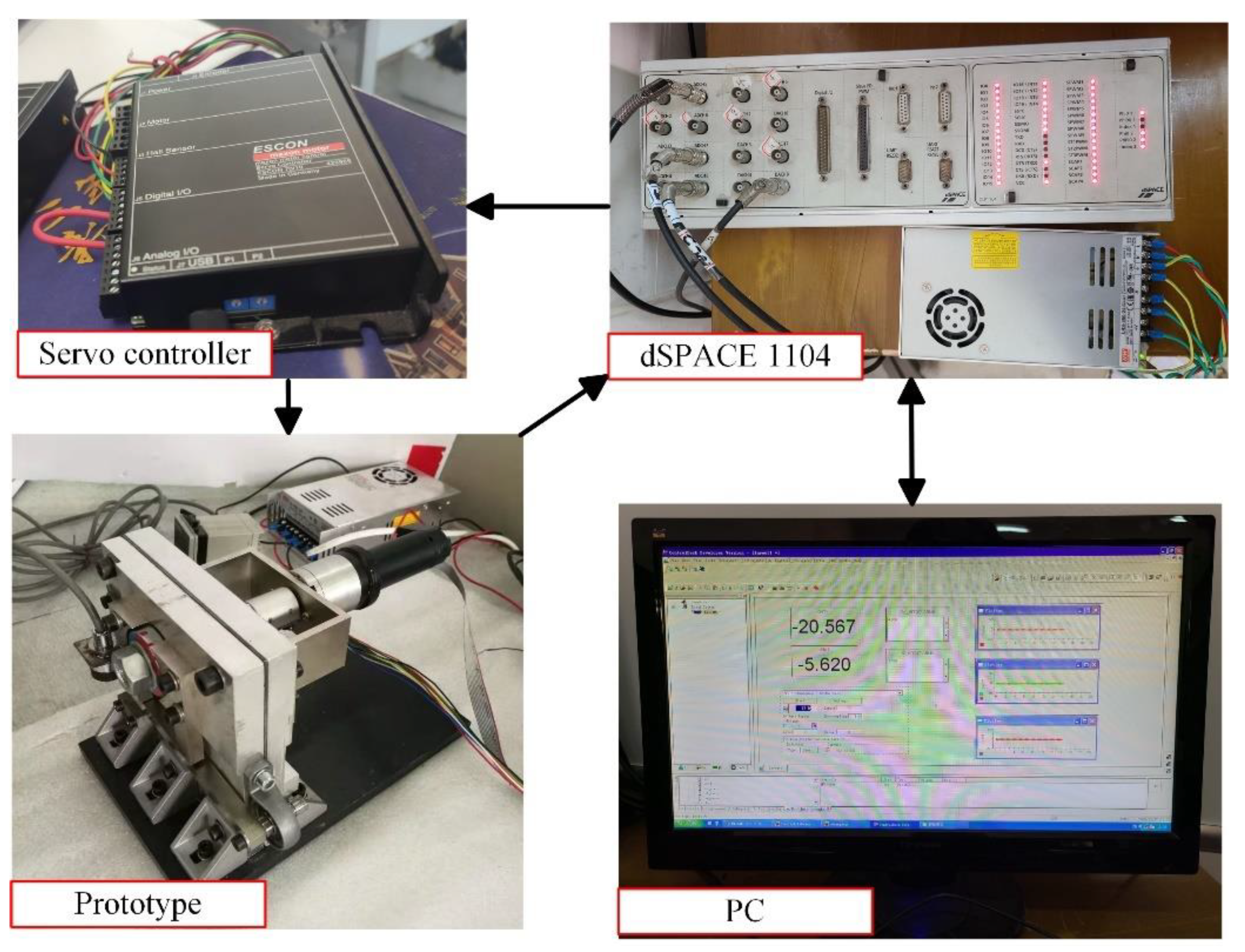
5.1. Experimental Setup
5.2. Experimental Results
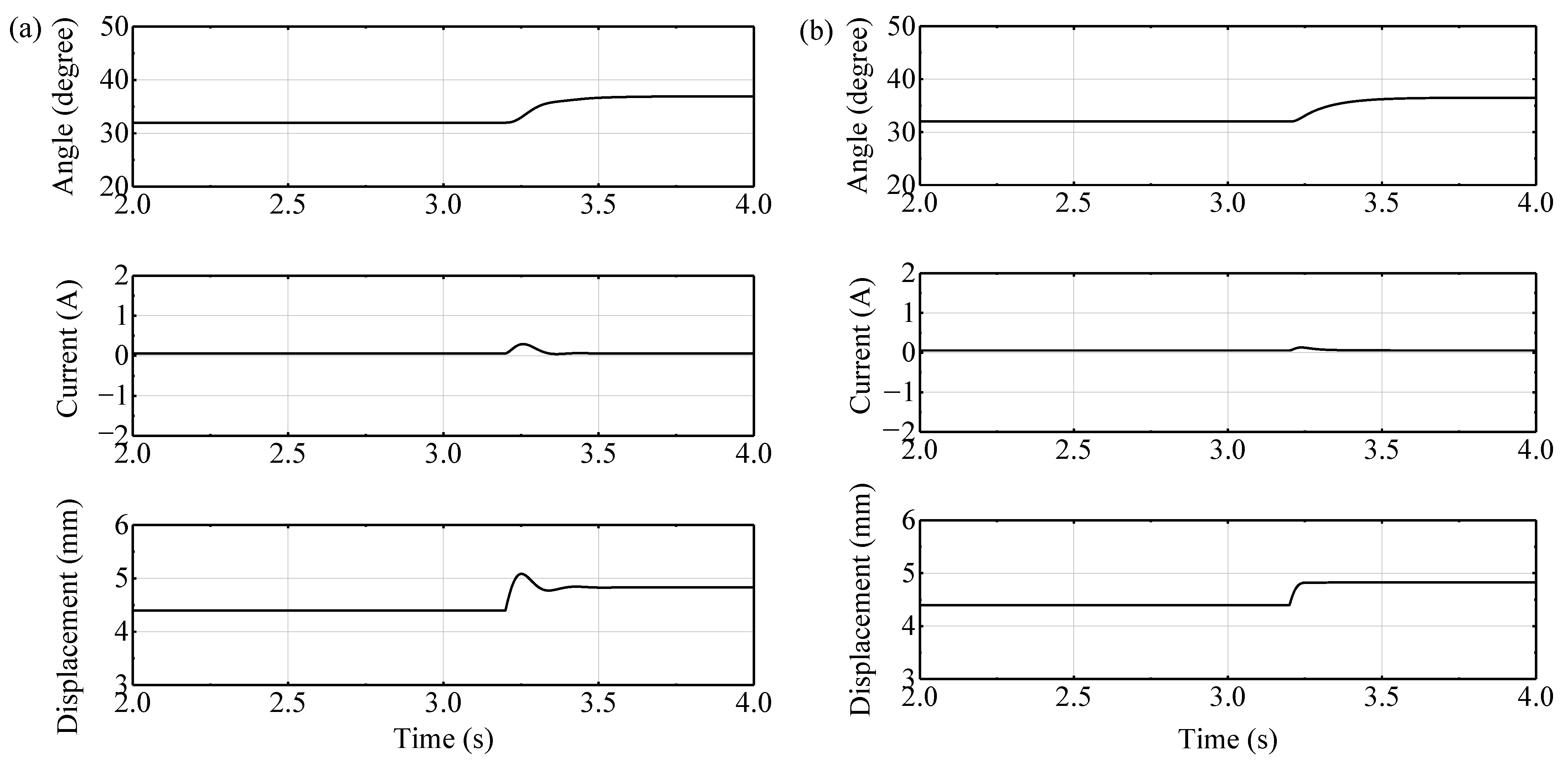
5.2.1. Experimental Results of the Displacement Disturbance
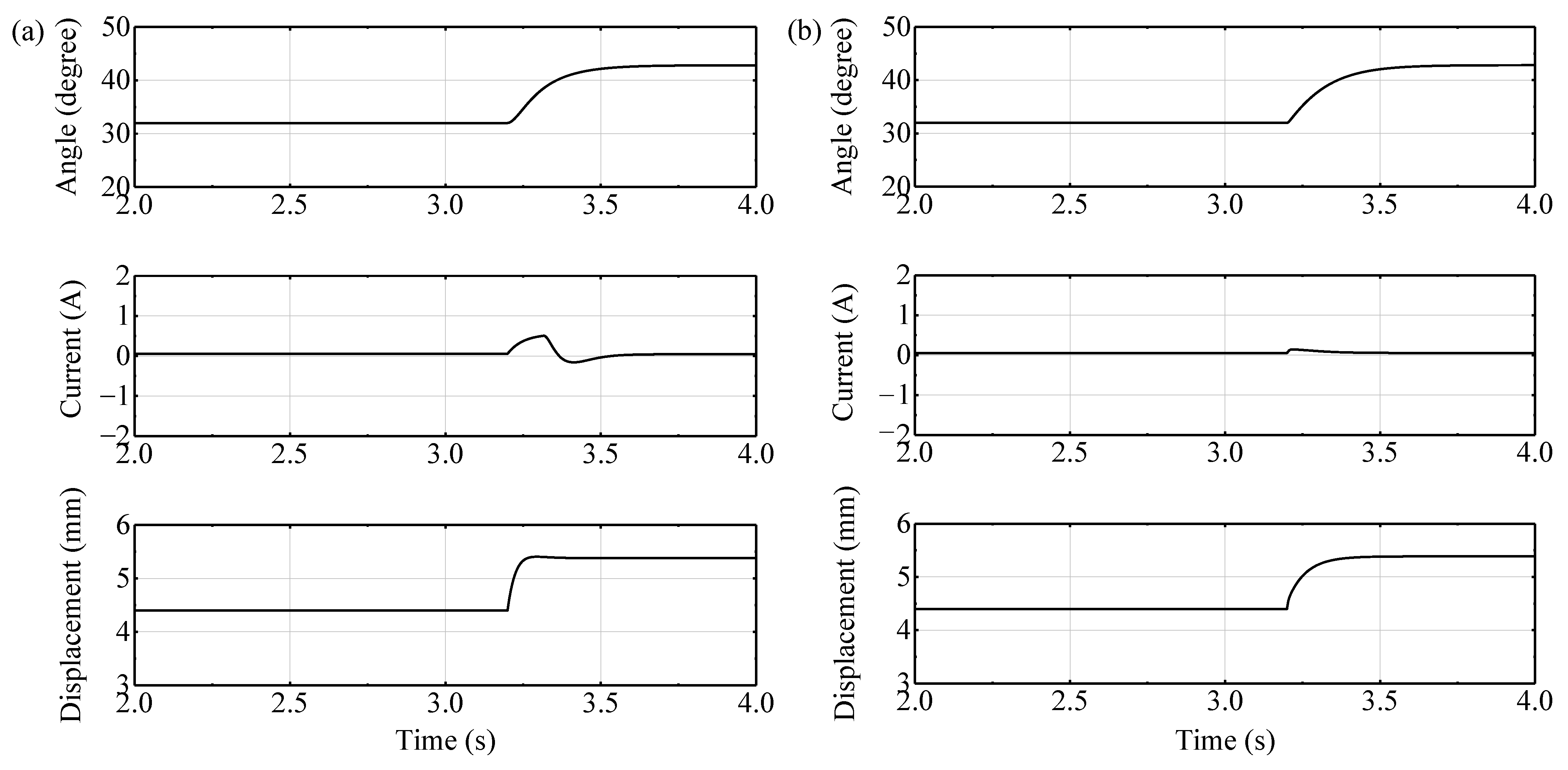
5.2.2. Experimental Results of the Force Disturbance
5.2.3. Comparison Analysis
5.3. Discussion
6. Conclusions
- (1)
- The proposed ZPPMSS-VFPC can realize the stable suspension at the external disturbance by the designed fuzzy cascade controller.
- (2)
- Compared with the cascade controller, the response times of the designed fuzzy cascade controller at the displacement disturbance and the force disturbance are 0.50 s and 0.60 s faster, respectively, and the suspension system with the fuzzy cascade controller has better robustness and smaller overshoot.
- (3)
- The response times of the PLFCC at the displacement disturbance and the force disturbance are 0.10 s faster than that of the ALFCC, respectively.
- (4)
- The response time difference of the experimental results for the two control methods is 0.10 s, which is less than that of the simulated results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| The rotation angle of the PM | |
| The horizontal distance from the bearing to the right F-shape core | |
| The horizontal distance from the bearing to the left F-shape core | |
| The horizontal distance from the bearing to the displacement sensor | |
| Distance from the suspended object to the bottom of the left F-shape core | |
| Distance from the suspended object to the bottom of the right F-shape core | |
| The angle between the suspended object and the horizontal line | |
| Torque coefficient of the system | |
| Suspension force coefficient of the system | |
| Leakage flux compensation coefficients of the torque | |
| Leakage flux compensation coefficients of the suspension force | |
| Distance from the suspended object to the bottom of the left F-shape core | |
| Damping coefficients of the PM | |
| Damping coefficients of the suspended object | |
| Moments of inertia of the motor | |
| Moments of inertia of the suspended object | |
| Torque coefficient of the servo motor | |
| The input current of the servo motor | |
| The external disturbing force acting on the system | |
| Length of the suspended object | |
| Suspension forces generated by the left F-shape core | |
| Suspension forces generated by the right F-shape core |
References
- Chen, S.Y.; Lin, F.J. Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system. IEEE Trans. Control Syst. Technol. 2011, 19, 636–643. [Google Scholar] [CrossRef]
- Chamroon, C.; Cole, M.O.T.; Fakkaew, W. Linearizing control of a distributed actuation magnetic bearing for thin-walled rotor systems. Actuators 2020, 9, 99. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Qiang, H.; Lin, G. Adaptive Neural-fuzzy robust position control scheme for maglev train systems with experimental verification. IEEE Trans. Ind. Electron. 2019, 66, 8589–8599. [Google Scholar] [CrossRef]
- Li, M.; Luo, S.H.; Ma, W.H.; Li, T.; Gao, D.G.; Xu, Z.Q. Experimental and numerical investigations of the dynamic responses of low and medium speed maglev train-track-bridge coupled system. Veh. Syst. Dyn. 2020, 5, 1–24. [Google Scholar] [CrossRef]
- Shi, C.; Sun, F.; Dou, R.T.; Ren, H.Z.; Li, Q.; Xu, F.C.; Zhang, X.Y. Modeling and simulation analysis of oil-free scroll compressor driven by magnetic force. Int. J. Appl. Electromagn. Mech. 2020, 64, 1269–1278. [Google Scholar] [CrossRef]
- Zhu, J.; Song, D.D.; Han, Q.L.; Li, S.L.; Wang, J.M.; Li, G.H.; Cao, D. Multi objective optimization on suspension characteristics of vertical axis wind turbine. Int. J. Appl. Electromagn. Mech. 2018, 58, 215–226. [Google Scholar] [CrossRef]
- Yu, Y.J.; Zhang, W.Y.; Sun, Y.X.; Xu, P.F. Basic Characteristics and Design of a Novel Hybrid Magnetic Bearing for Wind Turbines. Energies 2016, 9, 905. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.Y.; Ahn, D. Analysis of high force voice coil motor for magnetic levitation. Actuators 2020, 9, 133. [Google Scholar] [CrossRef]
- Zhou, R.; Sun, F.; Yan, M.Y.; Jin, J.J.; Li, Q.; Xu, F.C.; Zhang, X.Y.; Nakano, K. Design, analysis and prototyping of a magnetic energy-harvesting suspension for vehicles. Smart Mater. Struct. 2020, 29, 105034. [Google Scholar] [CrossRef]
- Gu, C.; Wang, X.L.; Deng, Z.Q. Evaluation of three improved space-vector-modulation strategies for the high-speed permanent magnet motor fed by a SiC/Si hybrid inverter. IEEE Trans. Power Electron. 2021, 36, 4399–4409. [Google Scholar] [CrossRef]
- Kawase, Y.; Ota, T.; Fukunaga, H. 3-D eddy current analysis in permanent magnet of interior permanent magnet motors. IEEE Trans. Magn. 2002, 36, 1863–1866. [Google Scholar] [CrossRef]
- Park, S.Y.; Lee, D.Y.; Song, B.C.; Baek, Y.S. Analysis and modeling of attractive force using an electropermanent magnet and electromagnetic in a novel wobble gripper. Actuators 2020, 9, 116. [Google Scholar] [CrossRef]
- Wang, Z.; Long, Z.; Li, X. Levitation control of permanent magnet electromagnetic hybrid suspension maglev train. Proc. Inst. Mech. Eng. Part I J. Syst Control Eng. 2018, 232, 315–323. [Google Scholar] [CrossRef]
- Park, S.U.; Mok, H.S.; Lim, J.W.; Seo, H.U.; Oh, S.H. Efficiency improvement by deriving the optimal operating slip frequency of a linear-induction-style maglev train. Energies 2020, 13, 6544. [Google Scholar] [CrossRef]
- Chaban, A.; Lukasik, Z.; Lis, M.; Szafraniec, A. Mathematical modeling of transient processes in magnetic suspension of maglev trains. Energies 2020, 13, 6642. [Google Scholar] [CrossRef]
- Han, J.W.; Kim, J.D.; Song, S.Y. Fatigue strength evaluation of a bogie frame for urban maglev train with fatigue test on full-scale test rig. Eng. Fail. Anal. 2013, 31, 412–420. [Google Scholar] [CrossRef]
- Zhou, D.F.; Yu, P.C.; Wang, L.C.; Li, J. An adaptive vibration control method to suppress the vibration of the maglev train caused by track irregularities. J. Sound Vibr. 2017, 408, 331–350. [Google Scholar] [CrossRef]
- Spece, H.; Fittro, R.; Knospe, C. Optimization of axial magnetic bearing actuators for dynamic performance. Actuators 2018, 7, 66. [Google Scholar] [CrossRef] [Green Version]
- Bonfitto, A.; Castellanos Molina, L.M.; Tonoli, A.; Amati, N. Offset-free model predictive control for active magnetic bearing systems. Actuators 2018, 7, 46. [Google Scholar] [CrossRef] [Green Version]
- Schuhmann, T.; Hofmann, W.; Werner, R. Improving operational performance of active magnetic bearings using kalman filter and state feedback control. IEEE Trans. Ind. Electron. 2011, 59, 821–829. [Google Scholar] [CrossRef]
- Sun, F.; Oka, K. Development of noncontact suspension mechanism using flux path control by disk magnet rotation. Trans. Jpn. Soc. Mech. Eng. 2010, 76, 2916–2922. [Google Scholar] [CrossRef] [Green Version]
- Sun, F.; Oka, K.; Saibara, Y. Magnetic suspension system by flux path control using rotary actuator. Int. J. Appl. Electromagn. Mech. 2010, 33, 769–776. [Google Scholar] [CrossRef]
- Sun, F.; Zhou, R.; Jin, J.; Li, Q.; Oka, K. Optimal design for quasi-zero power performance of a permanent magnetic suspension system. Int. J. Appl. Electromagn. Mech. 2018, 59, 607–616. [Google Scholar] [CrossRef]
- Xu, F.C.; Guo, Y.Q.; Zhou, R.; Jin, J.J.; Zhao, C.; Zhang, X.Y.; Sun, F. Analysis of structure factors affecting suspension force of permanent magnet system with variable magnetic flux path control. Int. J. Appl. Electromagn. Mech. 2020, 64, 1495–1504. [Google Scholar] [CrossRef]
- Mercado-Uribe, A.; Moreno, J.A. Homogeneous integral controllers for a magnetic suspension system. Control Eng. Pract. 2020, 97, 104325. [Google Scholar] [CrossRef]
- Pesch, A.H.; Sawicki, J.T. Active magnetic bearing online levitation recovery through μ-synthesis robust control. Actuators 2017, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.S.; Soffker, D. Optimization strategy for PID-controller design of AMB rotor systems. IEEE Trans. Control Syst. Technol. 2016, 24, 788–803. [Google Scholar] [CrossRef]
- Wei, W.; Xue, W.C.; Li, D.H. On disturbance rejection in magnetic levitation. Control Eng. Pract. 2019, 82, 24–35. [Google Scholar] [CrossRef]
- Anantachaisilp, P.; Lin, Z.L. Fractional order PID control of rotor suspension by active magnetic bearings. Actuators 2017, 6, 4. [Google Scholar] [CrossRef] [Green Version]
- Zhou, R.; Yan, M.Y.; Guo, Y.Q.; Jin, J.J.; Sun, F.; Zhang, X.Y.; Oka, K. Suspension characteristics of a zero-power permanent magnetic suspension system with flux path control. Int. J. Appl. Electromagn. Mech. 2020, 63, 187–198. [Google Scholar] [CrossRef]
- Sun, X.W.; Lu, Y.Y.; Sun, F.; Jin, J.J.; Wang, K. Research on dynamics performance of permanent magnet suspension system with variable magnetic circuitJ. China Mech. Eng. 2014, 25, 2782–2787. [Google Scholar] [CrossRef]


| ec | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| e | ||||||||
| NB | NB | NB | NM | NM | NS | ZO | ZO | |
| NM | NB | NB | NM | NS | NS | ZO | PS | |
| NS | NM | NM | NM | NS | ZO | PS | PS | |
| ZO | NM | NM | NS | ZO | PS | PM | PM | |
| PS | NS | NS | ZO | PS | PM | PM | PM | |
| PM | NS | ZO | PS | PM | PM | PB | PB | |
| PB | ZO | ZO | PM | PM | PM | PB | PB | |
| ec | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| e | ||||||||
| NB | NB | NS | NS | NM | NM | NM | NB | |
| NM | NB | NS | NS | NS | NS | NS | NB | |
| NS | NS | ZO | ZO | ZO | PS | PS | ZO | |
| ZO | ZO | PS | PS | PS | PM | PM | ZO | |
| PS | ZO | PS | PS | PM | PM | PS | PS | |
| PM | ZO | PS | PM | PM | PB | PS | NS | |
| PB | NS | PM | PB | PB | PB | PS | NS | |
| Parameters | Description | Value |
|---|---|---|
| m | Quality of the suspended object | 0.142 kg |
| Δdτ | Magnetic leakage compensation constant of the torque | 21 mm |
| Δdf | Magnetic leakage compensation constant of the suspension force | 2 mm |
| c1 | Damping coefficient of the PM | 0.5 N·m·s−1 |
| c2 | Damping coefficient of the suspended object | 10 N·m·s−1 |
| J1 | Moment of inertia of the PM | 1.856 × 10−5 kg·m2 |
| J2 | Moment of inertia of the suspended object | 1.108 × 10−3 kg·m2 |
| kt | Torque constant of the servo motor | 0.69 Nm/A |
| kτ | Torque constant of the PM | 8.726 × 10−3 Nm2 |
| km | Constant of the suspension force | 6.277 × 10−5 Nm2 |
| Description | Simulated Response Time | Experimental Response Time |
|---|---|---|
| PLFCC for the displacement disturbance | 0.26 s | 0.20 s |
| ALFCC for the displacement disturbance | 0.13 s | 0.30 s |
| PLFCC for the force disturbance | 0.19 s | 0.20 s |
| ALFCC for the force disturbance | 0.38 s | 0.30 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhou, R.; Guo, Y.; Jin, J.; Yu, S.; Sun, F. Design and Experimental Validation of a Fuzzy Cascade Controller for a Zero-Power Permanent Magnetic Suspension System with Variable Flux Path Control. Actuators 2021, 10, 118. https://doi.org/10.3390/act10060118
Zhao H, Zhou R, Guo Y, Jin J, Yu S, Sun F. Design and Experimental Validation of a Fuzzy Cascade Controller for a Zero-Power Permanent Magnetic Suspension System with Variable Flux Path Control. Actuators. 2021; 10(6):118. https://doi.org/10.3390/act10060118
Chicago/Turabian StyleZhao, Haining, Ran Zhou, Yongquan Guo, Junjie Jin, Shenbo Yu, and Feng Sun. 2021. "Design and Experimental Validation of a Fuzzy Cascade Controller for a Zero-Power Permanent Magnetic Suspension System with Variable Flux Path Control" Actuators 10, no. 6: 118. https://doi.org/10.3390/act10060118
APA StyleZhao, H., Zhou, R., Guo, Y., Jin, J., Yu, S., & Sun, F. (2021). Design and Experimental Validation of a Fuzzy Cascade Controller for a Zero-Power Permanent Magnetic Suspension System with Variable Flux Path Control. Actuators, 10(6), 118. https://doi.org/10.3390/act10060118








