Disturbance Observer-Based Backstepping Control of Tail-Sitter UAVs
Abstract
:1. Introduction
- a robust controller for tail-sitter UAVs development using the backstepping technique;
- a nonlinear disturbance observer for both periodic and wind-gust-type disturbances.
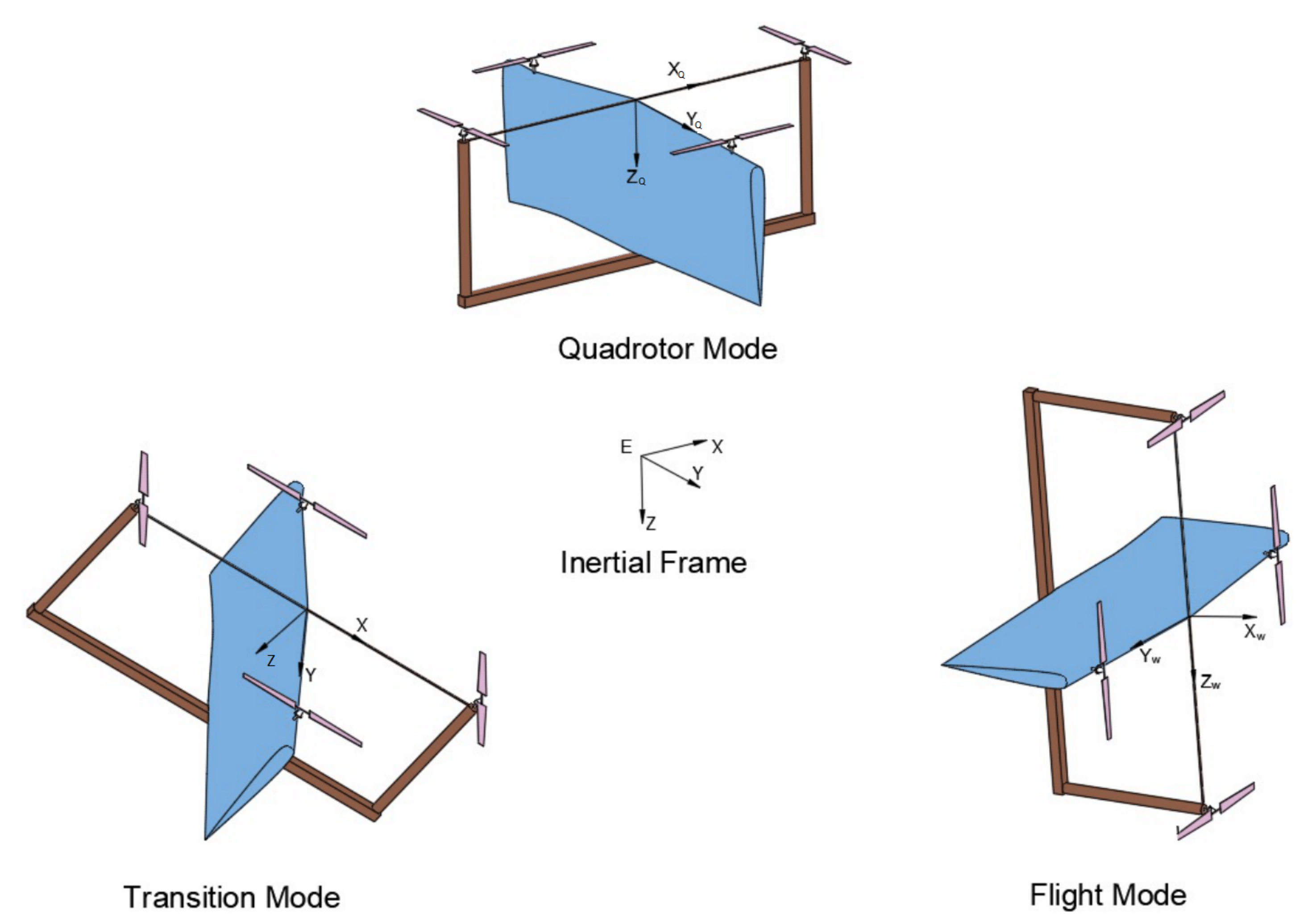
2. Problem Formulation
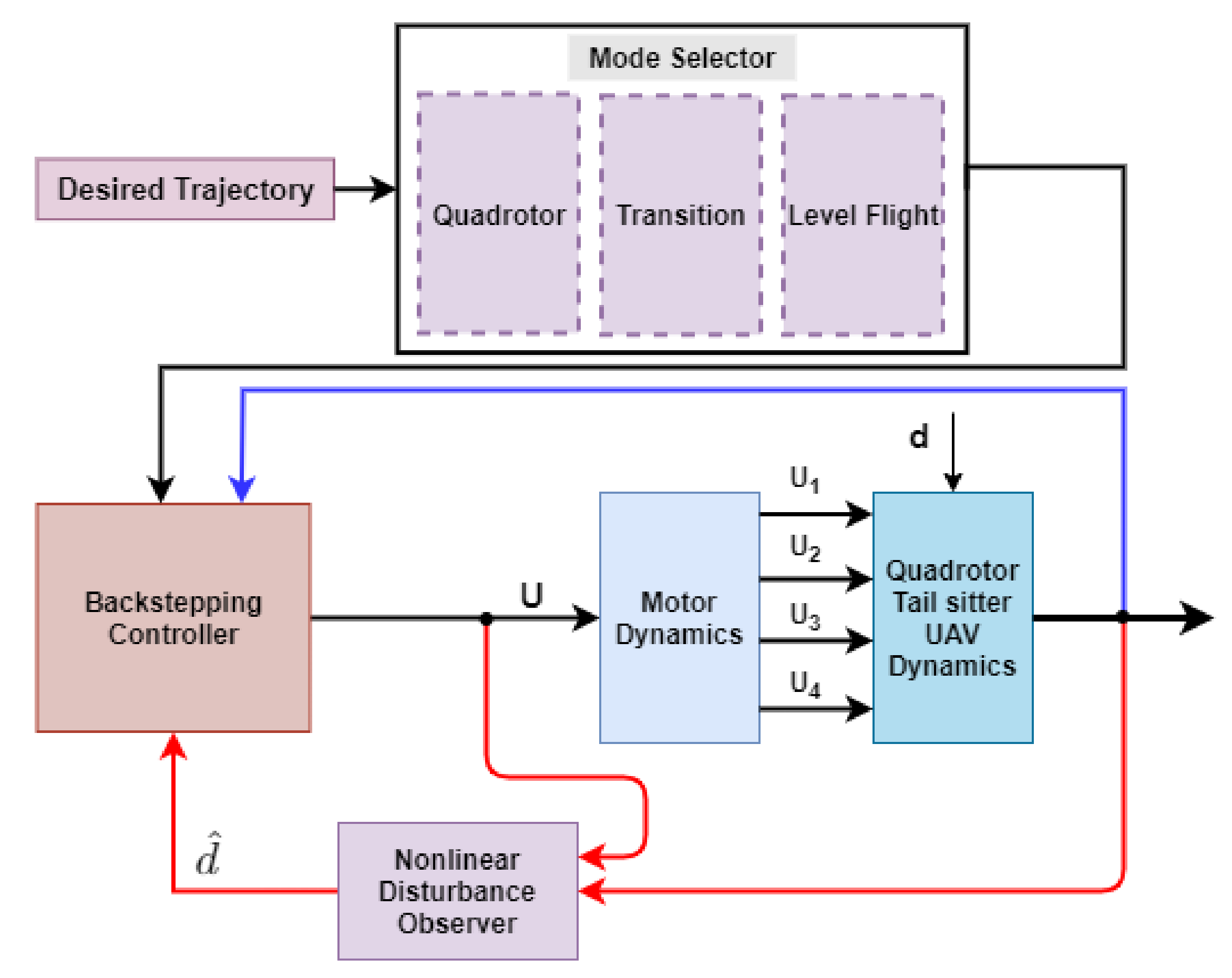
- Design a nonlinear disturbance observer for model uncertainty as well as wind gust (external) disturbances while in takeoff phase, hovering mode and landing phase.
- To design control laws using backstepping technique for quadrotor tail-sitter UAVs to track the given trajectory.
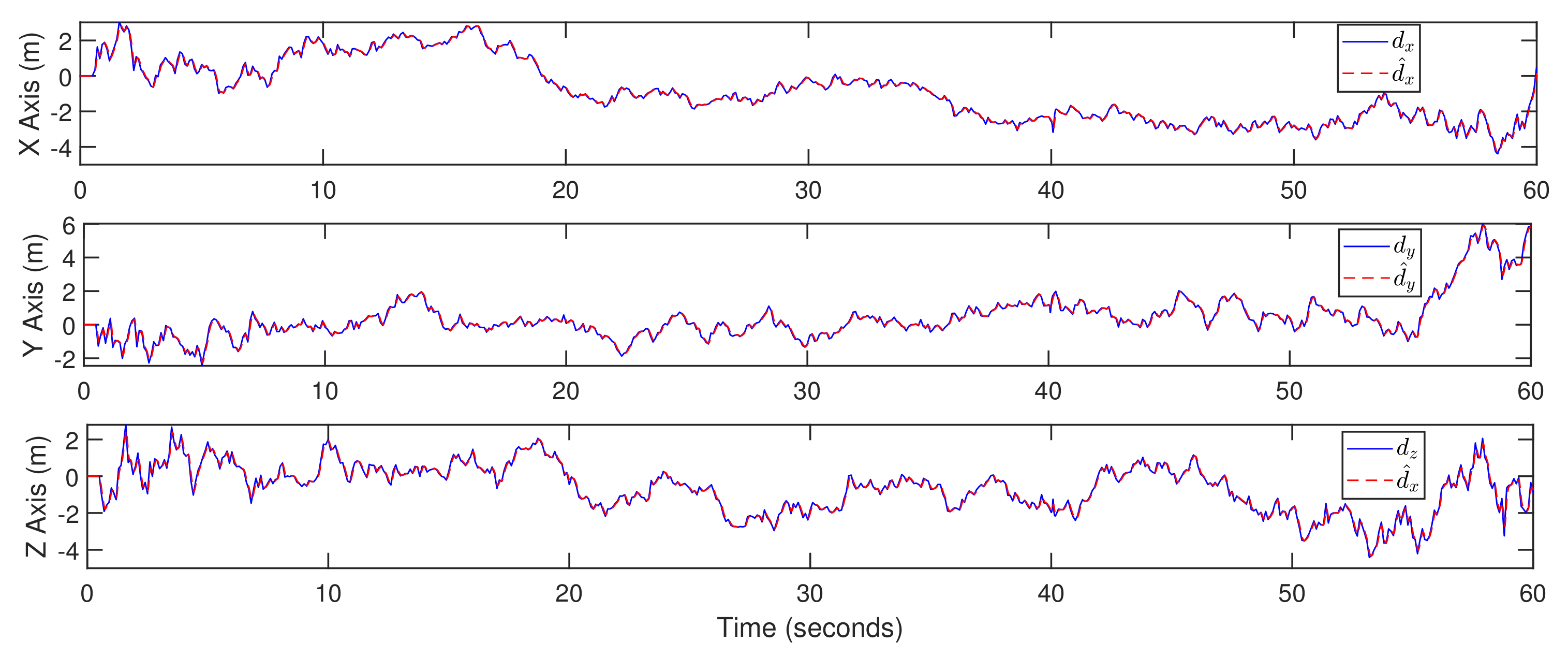
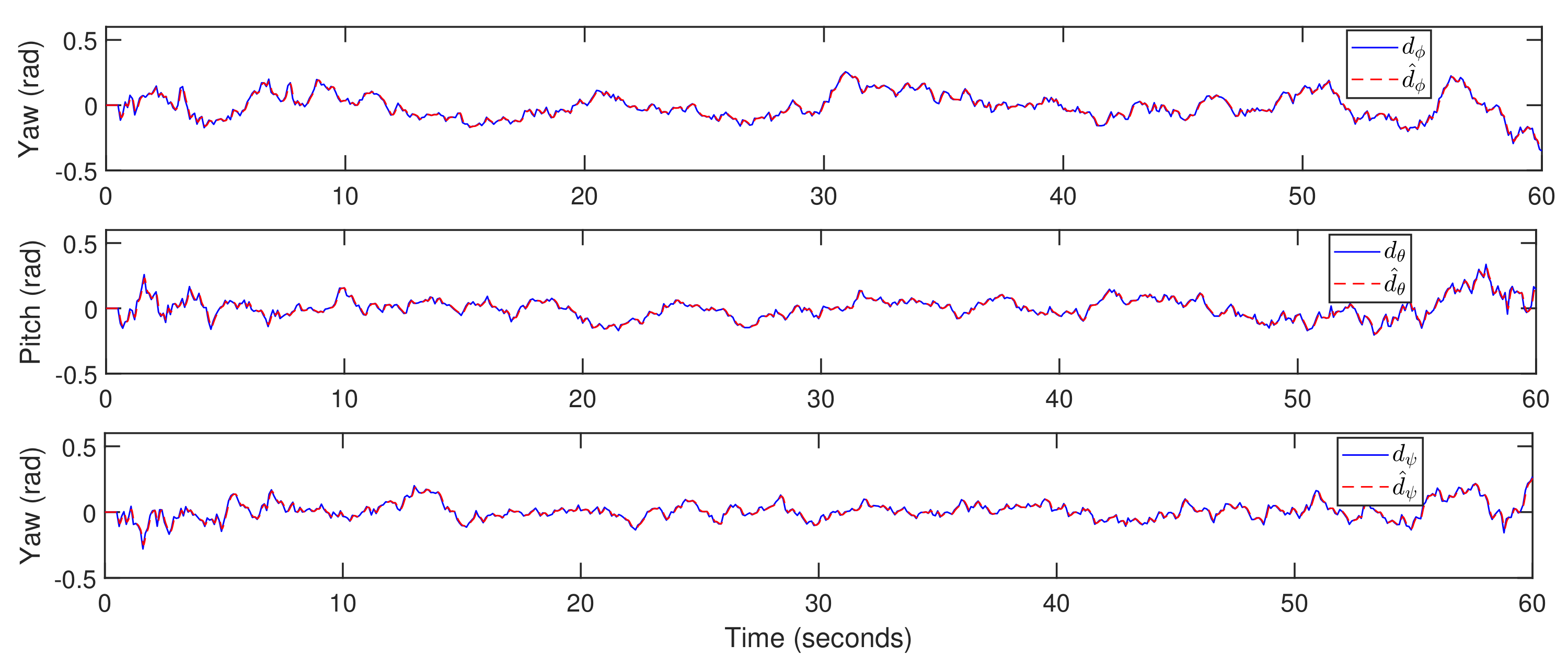
3. Nonlinear Observer Design
4. Backstepping Control Design
4.1. Quadrotor Mode
4.2. Transition Mode
4.3. Level-Flight Mode
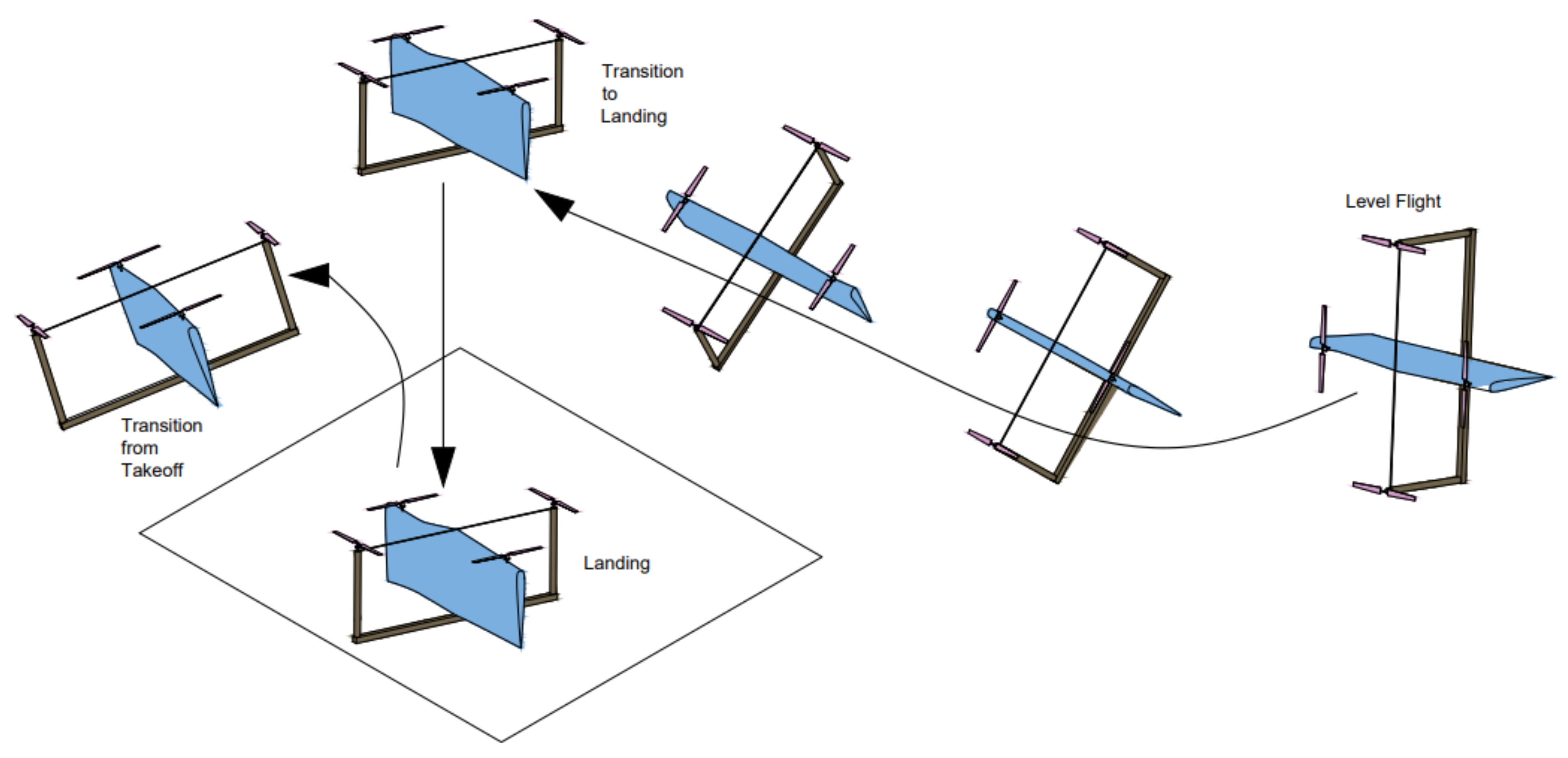
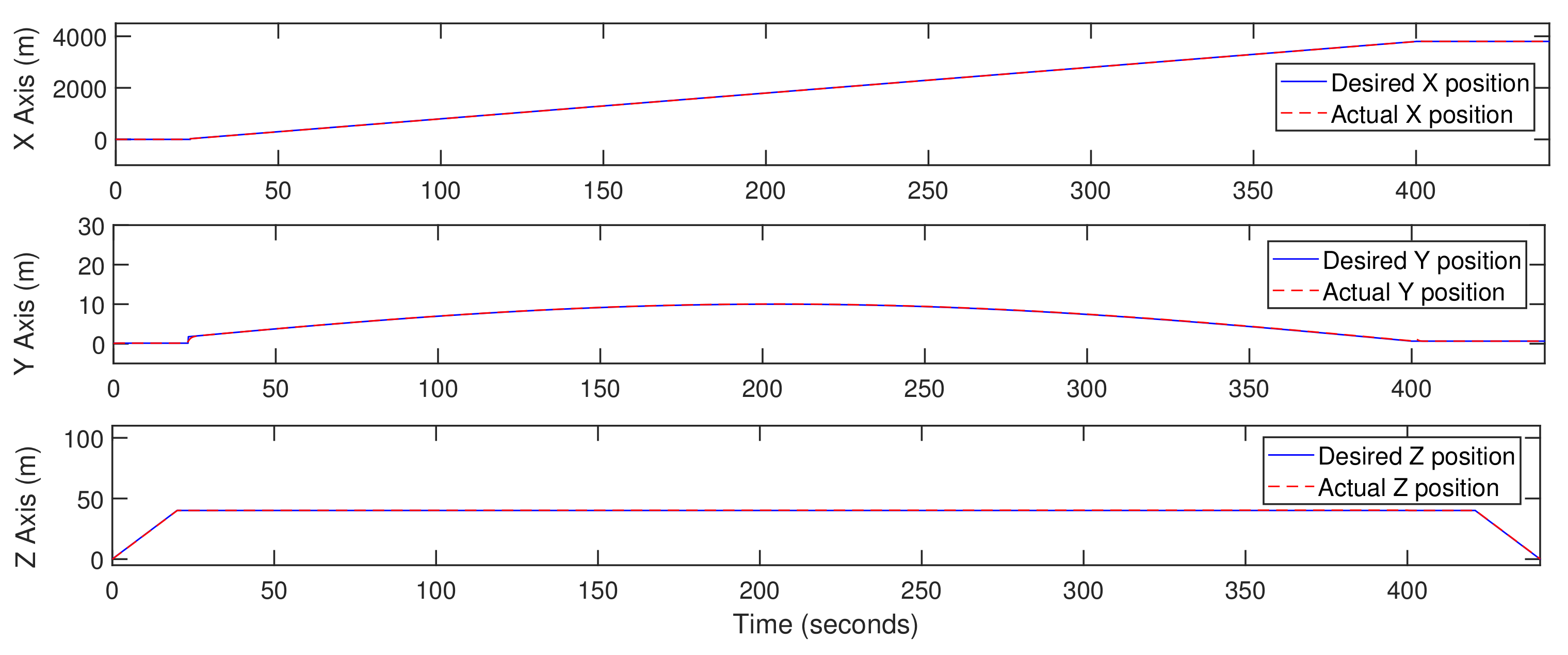
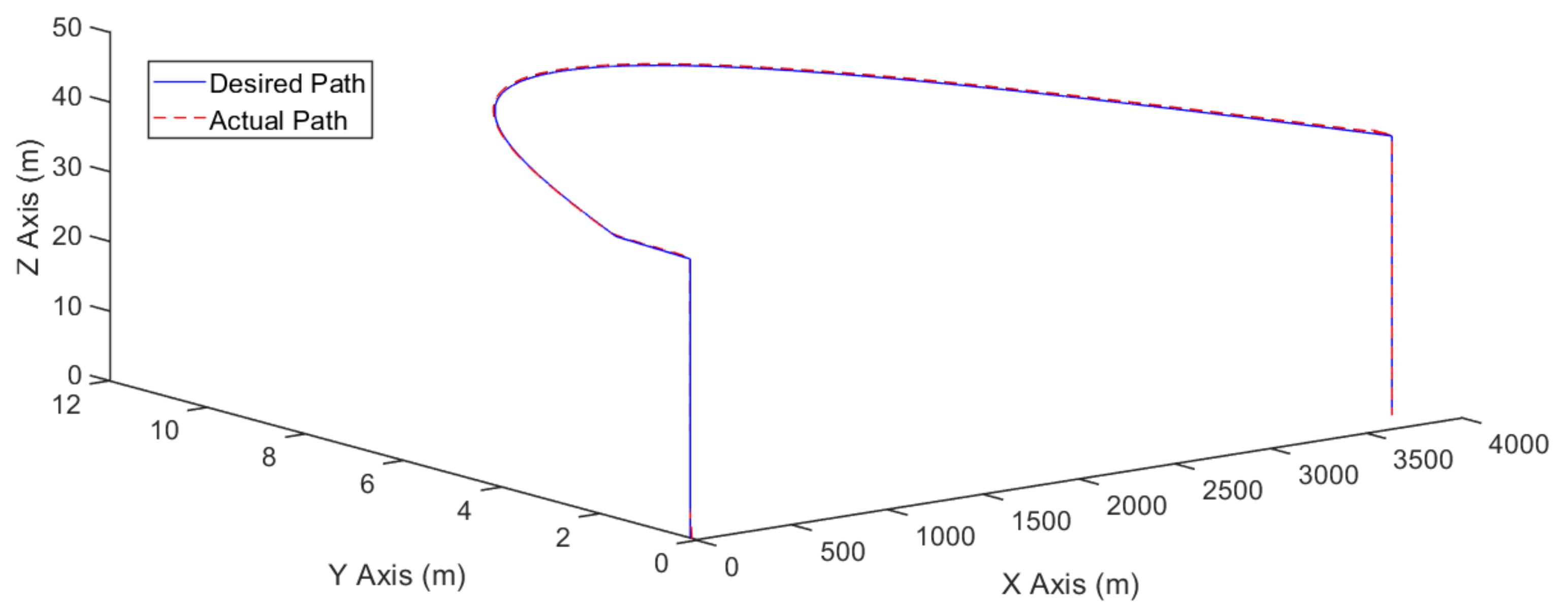
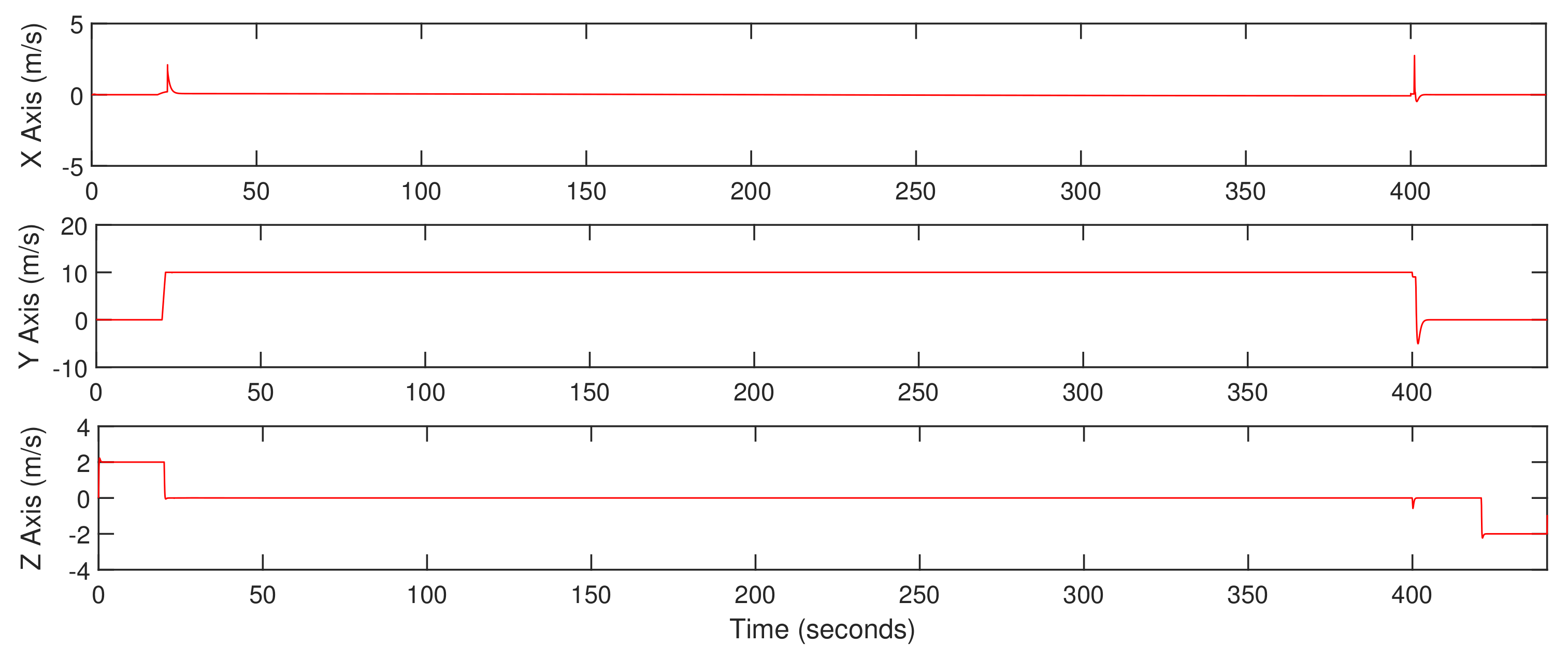
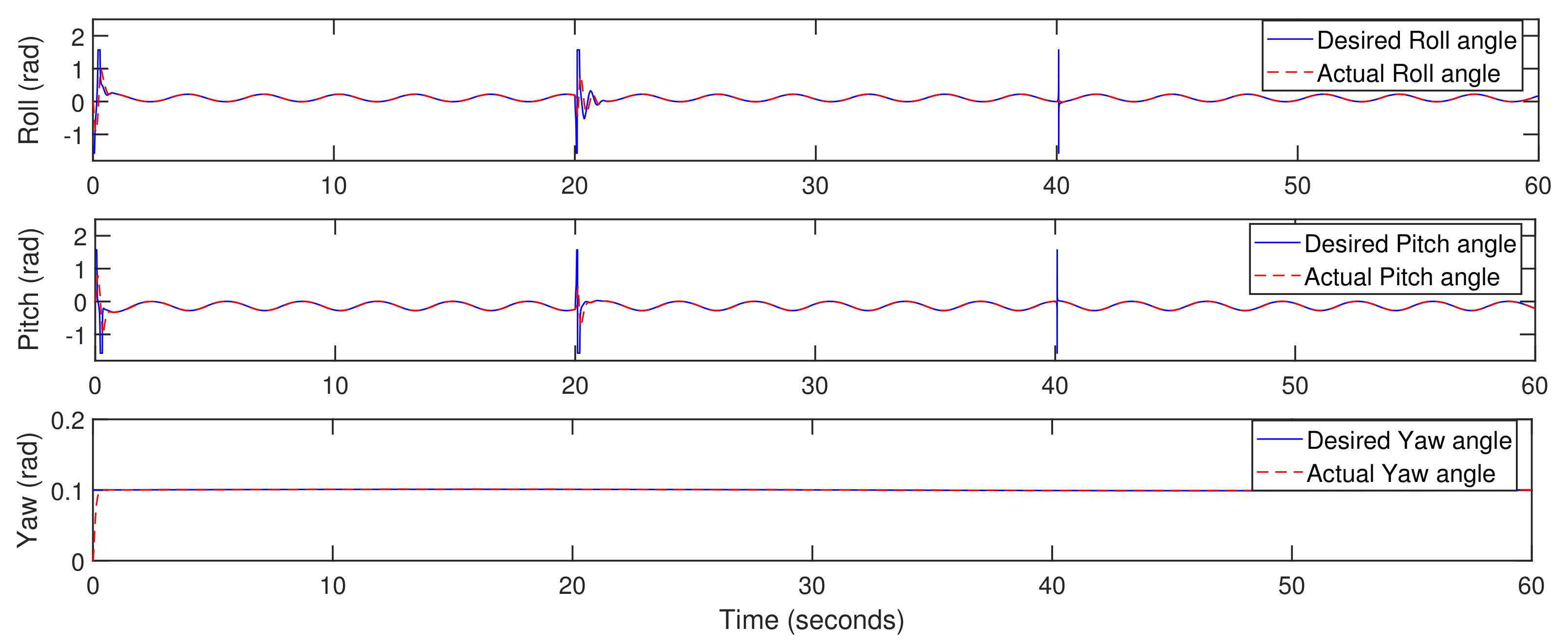
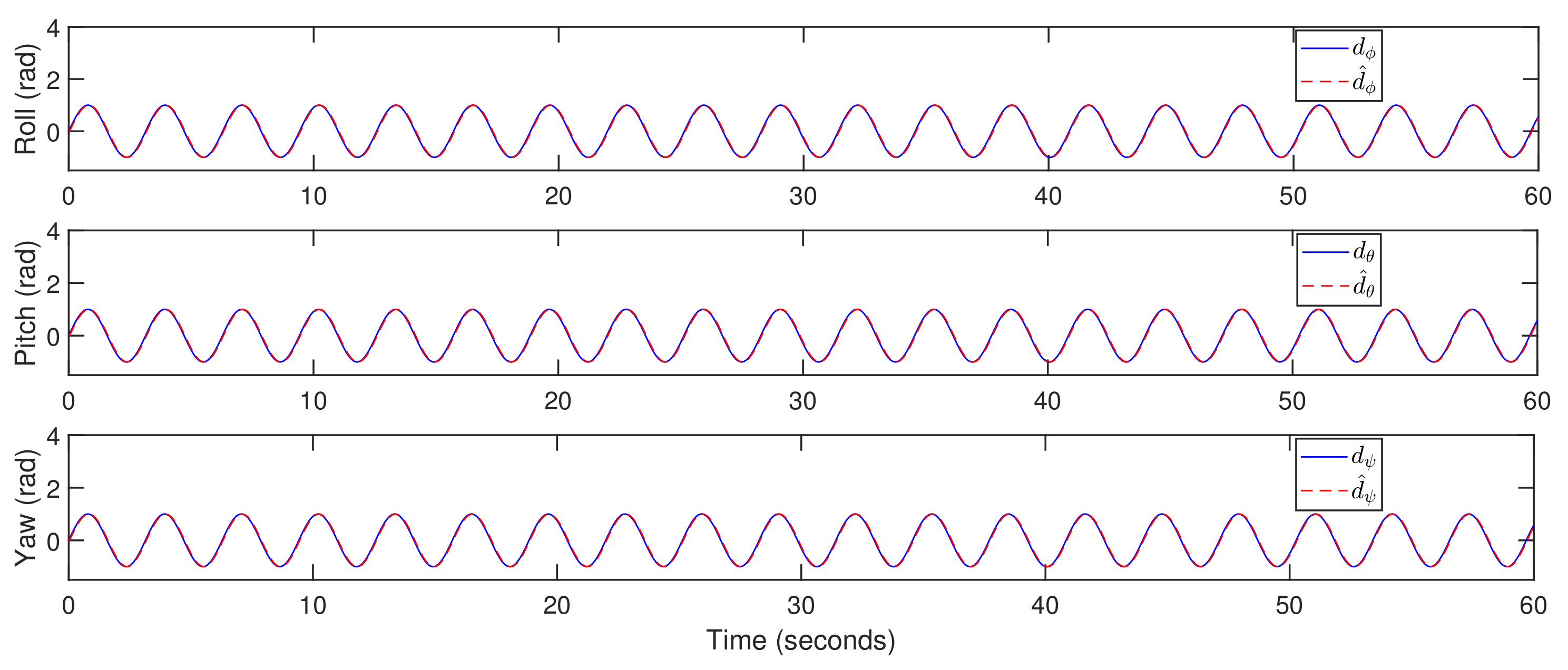
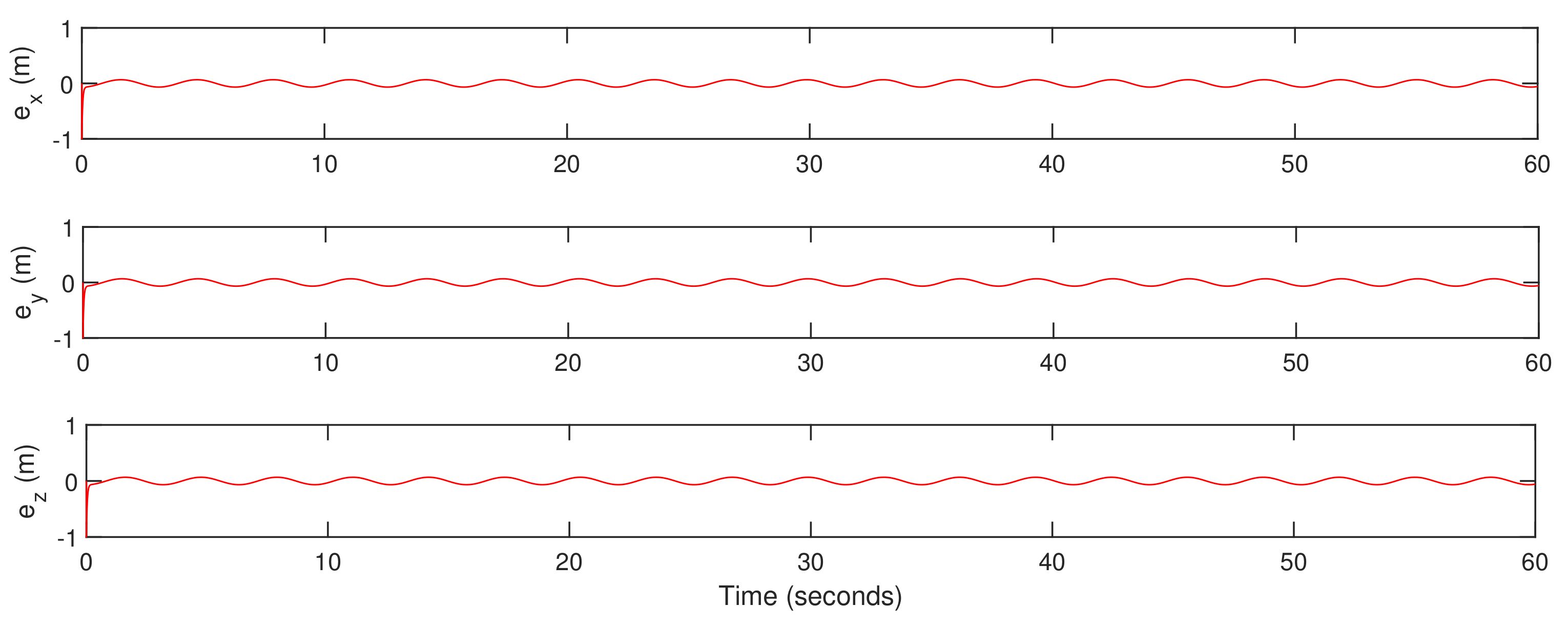
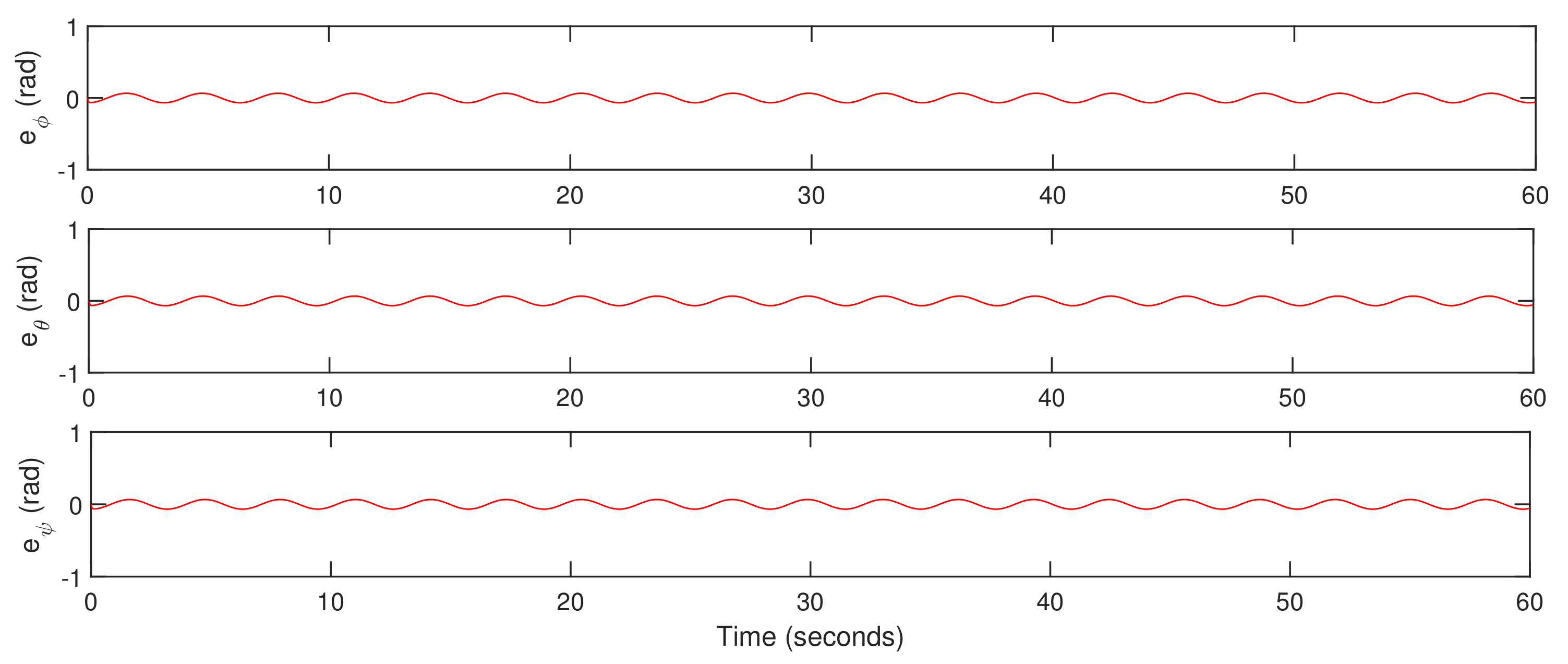
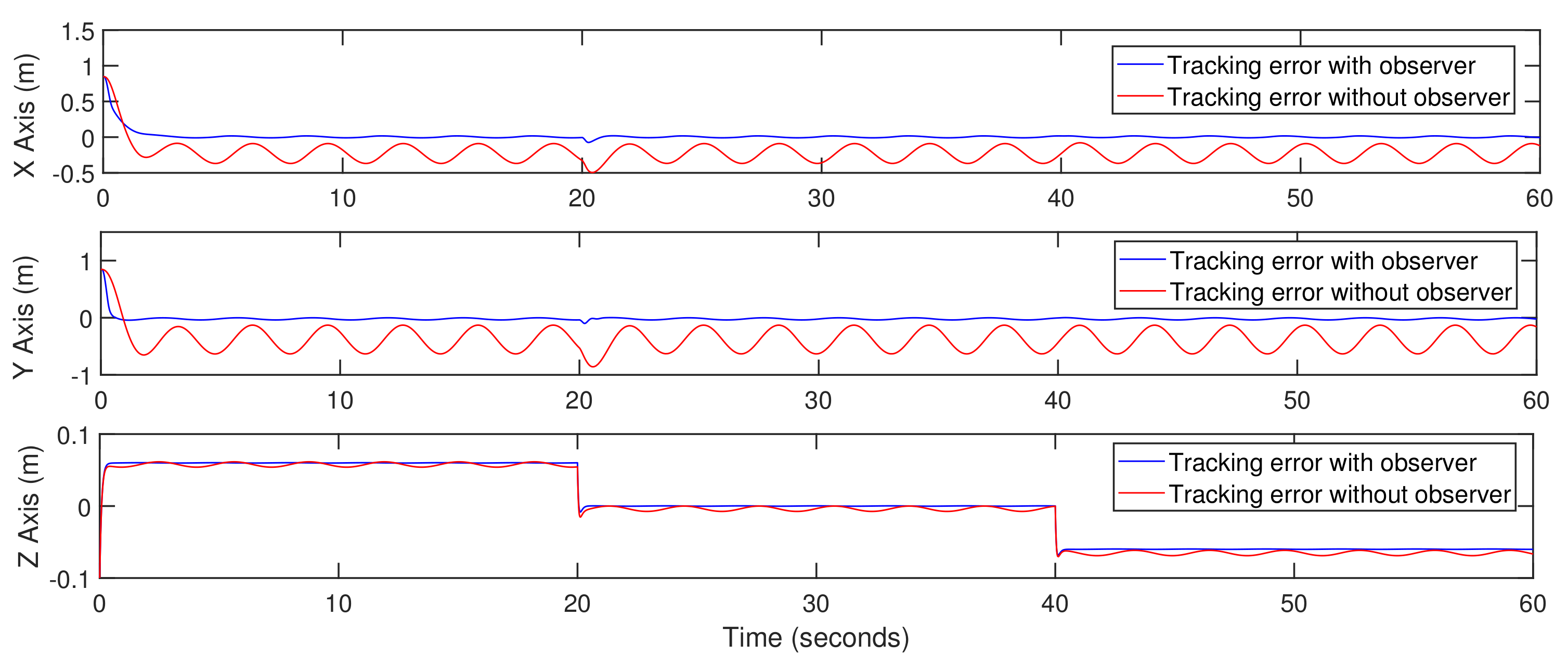
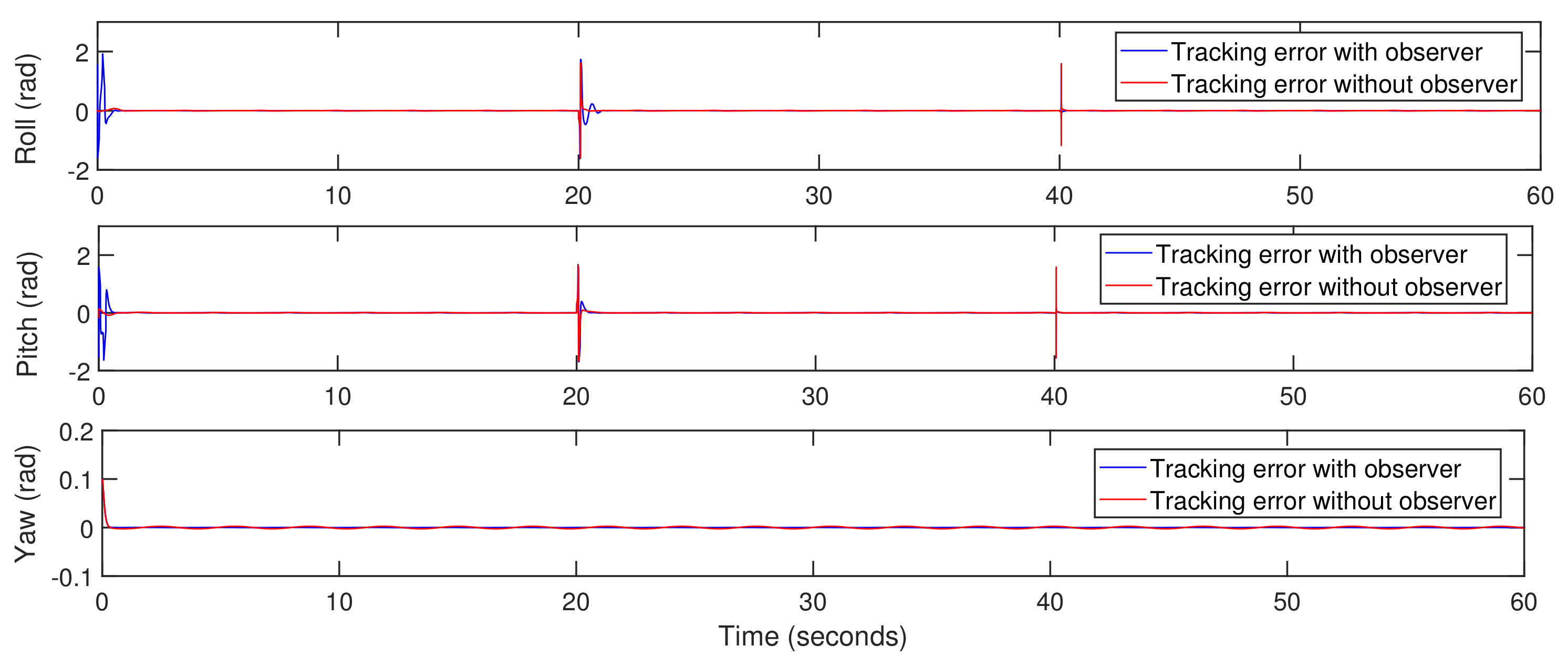
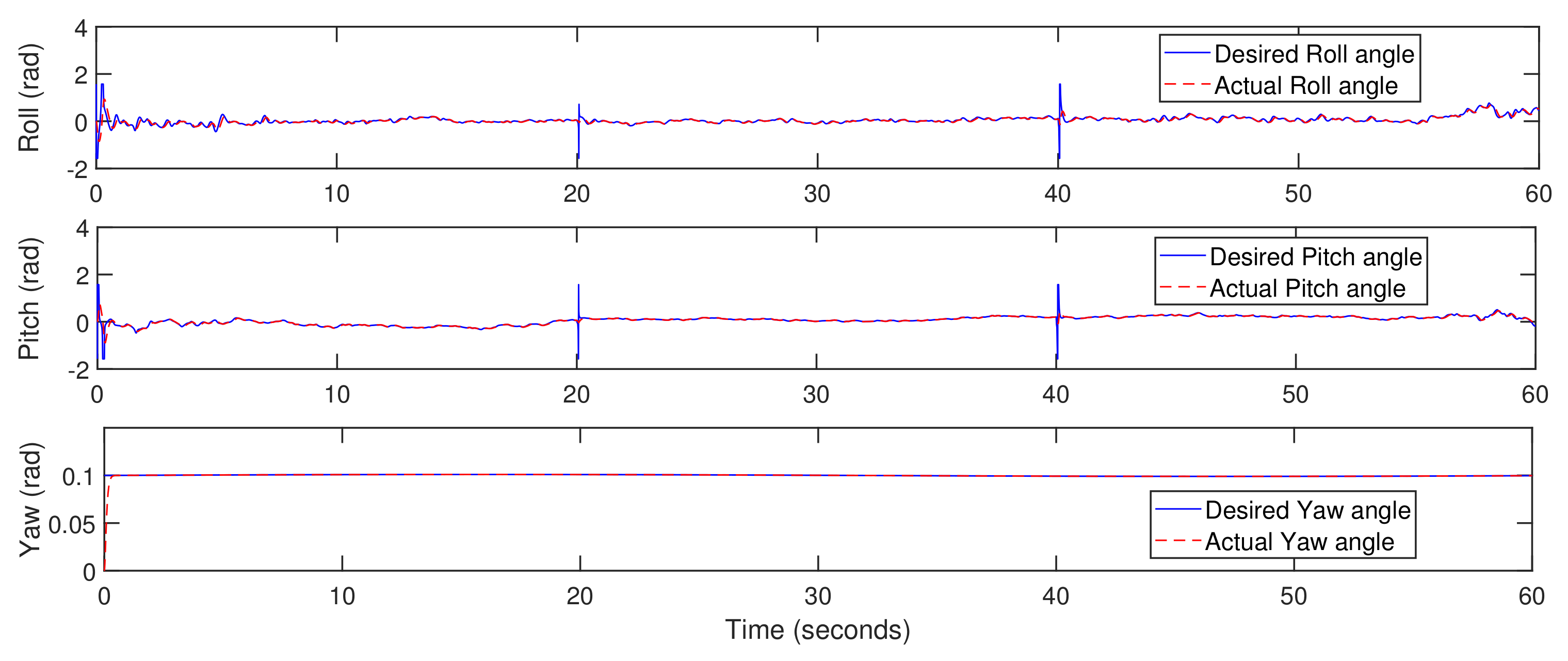
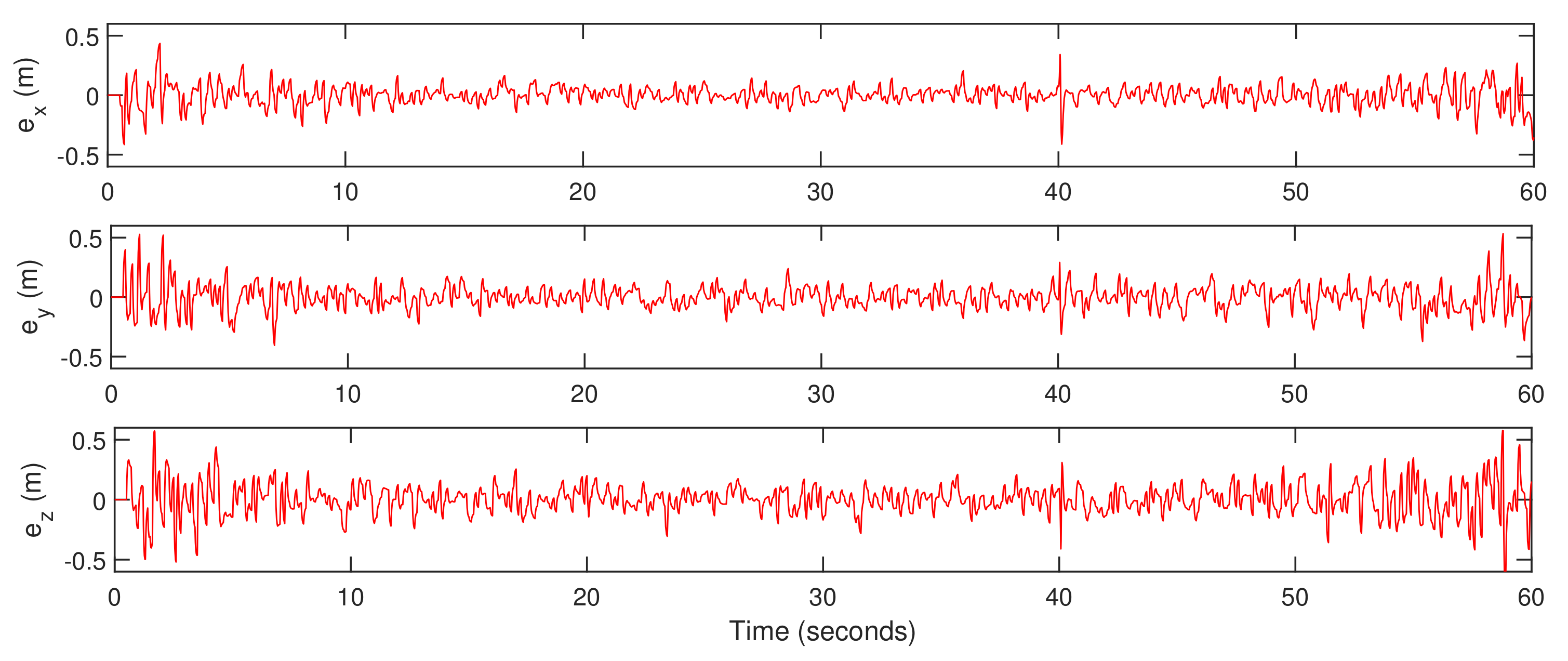
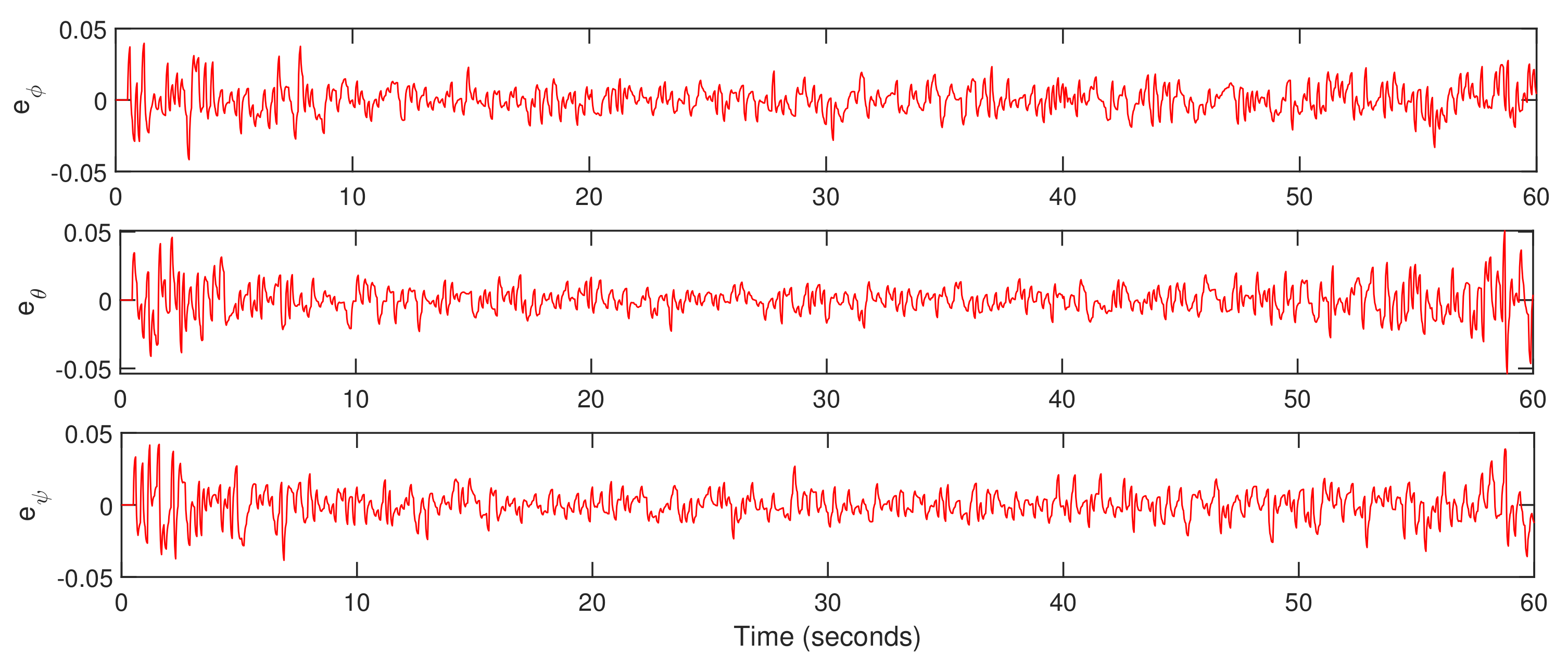
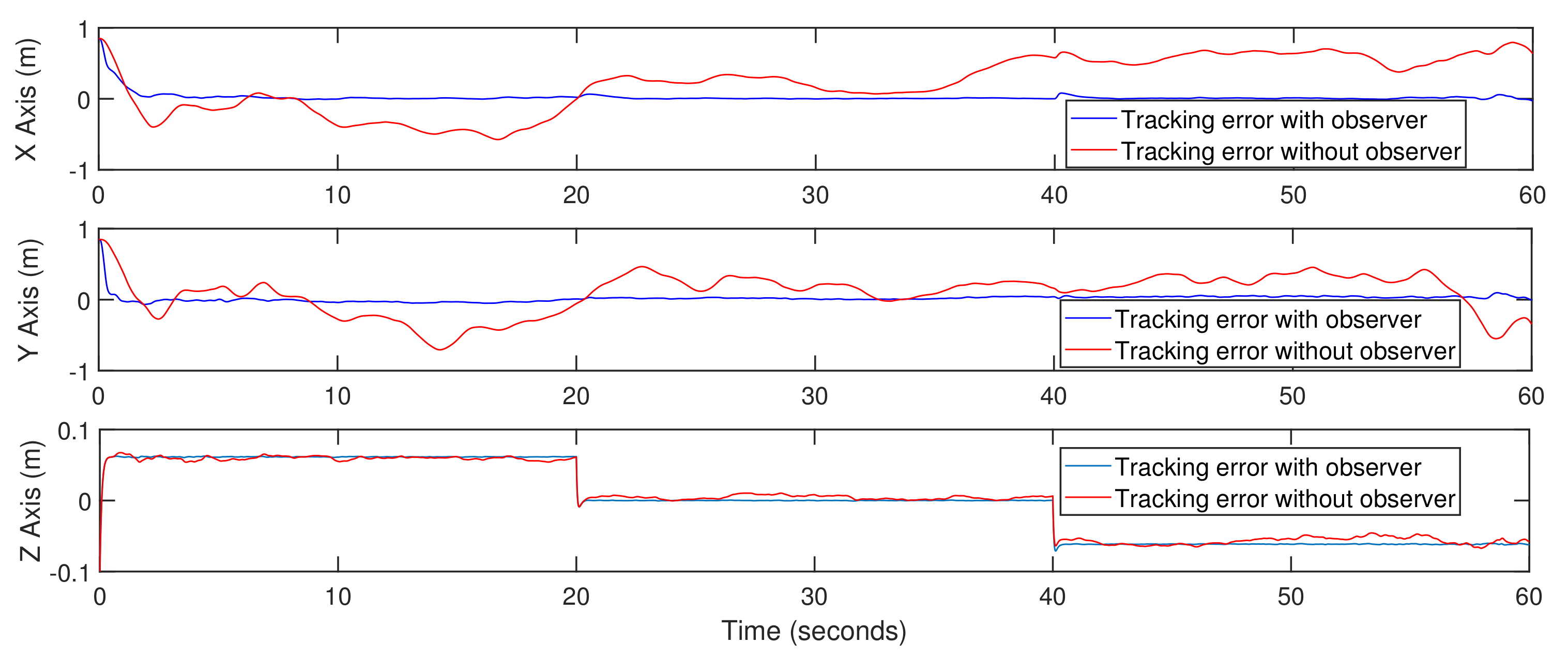
5. Simulation Results
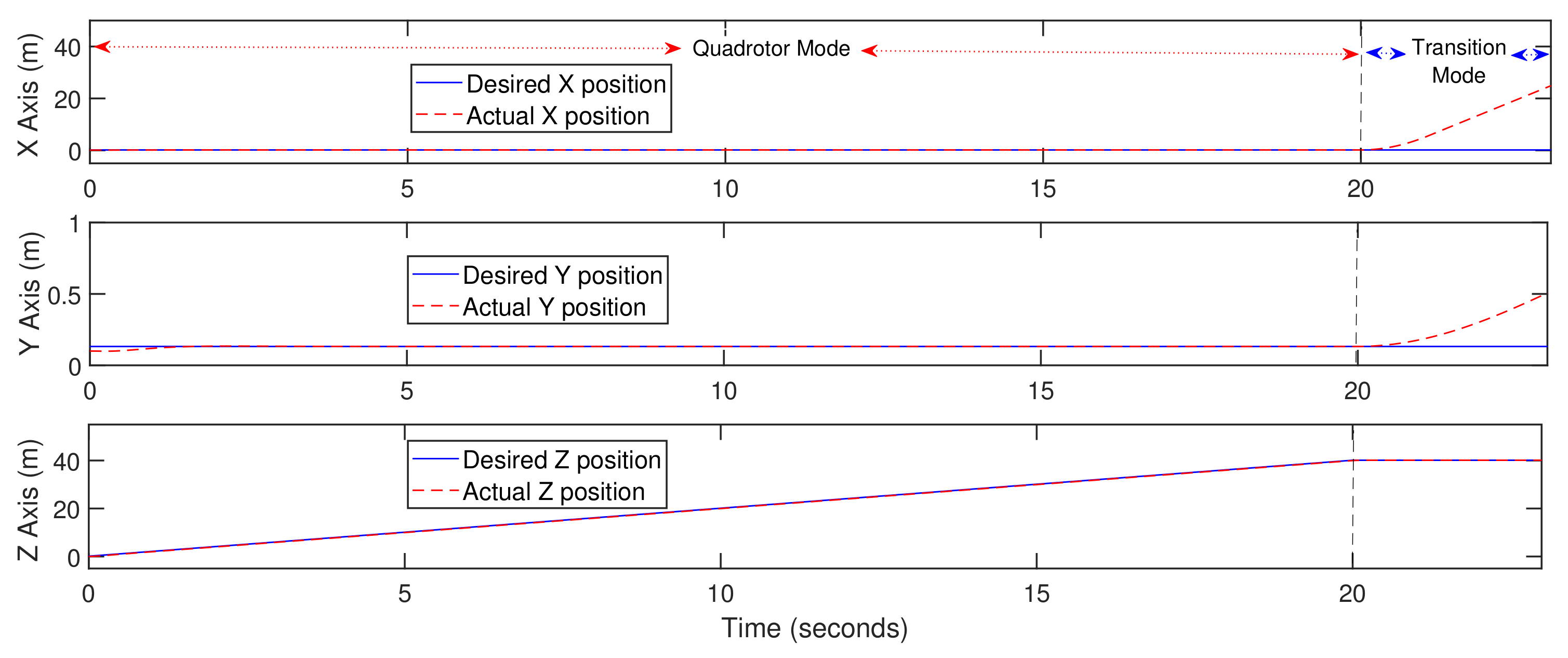
5.1. Trajectory-Tracking
5.2. Quadrotor Mode with External Disturbance
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kita, K.; Konno, A.; Uchiyama, M. Transition between Level Flight and Hovering of a Tail-Sitter Vertical Takeoff and Landing Aerial Robot. Adv. Robot. 2010, 24, 763–781. [Google Scholar] [CrossRef]
- Zhang, F.; Lyu, X.; Wang, Y.; Gu, H.; Li, Z. Modeling and Flight Control Simulation of a Quadrotor Tailsitter VTOL UAV. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Bapst, R.; Ritz, R.; Meier, L.; Pollefeys, M. Design and implementation of an unmanned tail-sitter. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; IEEE: New York City, NY, USA, 2015; pp. 1885–1890. [Google Scholar]
- Forshaw, J.L.; Lappas, V.J. Architecture and systems design of a reusable Martian twin rotor tailsitter. Acta Astronaut. 2012, 80, 166–180. [Google Scholar] [CrossRef]
- Verling, S.; Weibel, B.; Boosfeld, M.; Alexis, K.; Burri, M.; Siegwart, R. Full Attitude Control of a VTOL tailsitter UAV. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: New York City, NY, USA, 2016; pp. 3006–3012. [Google Scholar]
- Oosedo, A.; Abiko, S.; Konno, A.; Koizumi, T.; Furui, T.; Uchiyama, M. Development of a quad rotor tail-sitter VTOL UAV without control surfaces and experimental verification. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: New York City, NY, USA, 2013; pp. 317–322. [Google Scholar]
- Oosedo, A.; Abiko, S.; Konno, A.; Uchiyama, M. Optimal transition from hovering to level-flight of a quadrotor tail-sitter UAV. Auton. Robot. 2016, 41, 1143–1159. [Google Scholar] [CrossRef]
- Wang, Y.; Lyu, X.; Gu, H.; Shen, S.; Li, Z.; Zhang, F. Design, implementation and verification of a quadrotor tail-sitter VTOL UAV. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; IEEE: New York City, NY, USA, 2017; pp. 462–471. [Google Scholar]
- Hochstenbach, M.; Notteboom, C.; Theys, B.; Schutter, J.D. Design and Control of an Unmanned Aerial Vehicle for Autonomous Parcel Delivery with Transition from Vertical Take-off to Forward Flight – VertiKUL, a Quadcopter Tailsitter. Int. J. Micro Air Veh. 2015, 7, 395–405. [Google Scholar] [CrossRef] [Green Version]
- Máthé, K.; Buşoniu, L. Vision and Control for UAVs: A Survey of General Methods and of Inexpensive Platforms for Infrastructure Inspection. Sensors 2015, 15, 14887–14916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trotta, A.; Andreagiovanni, F.D.; Felice, M.D.; Natalizio, E.; Chowdhury, K.R. When UAVs Ride A Bus: Towards Energy-efficient City-scale Video Surveillance. In Proceedings of the IEEE INFOCOM 2018—IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018; IEEE: New York City, NY, USA, 2018. [Google Scholar] [CrossRef]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; D’Andreagiovanni, F.; Liu, W.; Gutierrez, J.; Blefari-Melazzi, N.; Choo, K.K.R.; Alouini, M.S. Multi-Area Throughput and Energy Optimization of UAV-aided Cellular Networks Powered by Solar Panels and Grid. IEEE Trans. Mob. Comput. 2020, 1. [Google Scholar] [CrossRef]
- Li, B.; Zhou, W.; Sun, J.; Wen, C.; Chen, C. Model Predictive Control for Path Tracking of a VTOL Tailsitter UAV in an HIL Simulation Environment. In Proceedings of the 2018 AIAA Modeling and Simulation Technologies Conference, Kissimmee, FL, USA, 8–12 January 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Lyu, X.; Gu, H.; Zhou, J.; Li, Z.; Shen, S.; Zhang, F. A hierarchical control approach for a quadrotor tail-sitter VTOL UAV and experimental verification. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: New York City, NY, USA, 2017; pp. 5135–5141. [Google Scholar]
- Li, Z.; Zhang, L.; Liu, H.; Zuo, Z.; Liu, C. Nonlinear robust control of tail-sitter aircrafts in flight mode transitions. Aerosp. Sci. Technol. 2018, 81, 348–361. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Xiong, H.L.; Liu, Y.; Tan, N.D.; Chen, L. Trajectory Planning Algorithm of UAV Based on System Positioning Accuracy Constraints. Electronics 2020, 9, 250. [Google Scholar] [CrossRef] [Green Version]
- Flores, G.R.; Escareño, J.; Lozano, R.; Salazar, S. Quad-Tilting Rotor Convertible MAV: Modeling and Real-Time Hover Flight Control. J. Intell. Robot. Syst. 2011, 65, 457–471. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Lyu, X.; Li, Z.; Shen, S.; Zhang, F. A unified control method for quadrotor tail-sitter UAVs in all flight modes: Hover, transition, and level flight. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: New York City, NY, USA, 2017; pp. 4835–4841. [Google Scholar]
- Swarnkar, S.; Parwana, H.; Kothari, M.; Abhishek, A. Biplane-Quadrotor Tail-Sitter UAV: Flight Dynamics and Control. J. Guid. Control Dyn. 2018, 41, 1049–1067. [Google Scholar] [CrossRef]
- Flores, G.; Lugo-Cárdenas, I.; Lozano, R. A nonlinear path-following strategy for a fixed-wing MAV. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; IEEE: New York City, NY, USA, 2013; pp. 1014–1021. [Google Scholar]
- Brezoescu, A.; Espinoza, T.; Castillo, P.; Lozano, R. Adaptive Trajectory Following for a Fixed-Wing UAV in Presence of Crosswind. J. Intell. Robot. Syst. 2012, 69, 257–271. [Google Scholar] [CrossRef] [Green Version]
- Hajiloo, A.; Rodrigues, L. Modeling and backstepping control of under-actuated spherical UAV. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017; IEEE: New York City, NY, USA, 2017; pp. 2069–2074. [Google Scholar]
- Espinoza, T.; Dzul, A.E.; Lozano, R.; Parada, P. Backstepping—Sliding Mode Controllers Applied to a Fixed-Wing UAV. J. Intell. Robot. Syst. 2013, 73, 67–79. [Google Scholar] [CrossRef]
- Sartori, D.; Quagliotti, F.; Rutherford, M.J.; Valavanis, K.P. Implementation and Testing of a Backstepping Controller Autopilot for Fixed-wing UAVs. J. Intell. Robot. Syst. 2014, 76, 505–525. [Google Scholar] [CrossRef] [Green Version]
- Lungu, M. Auto-landing of fixed wing unmanned aerial vehicles using the backstepping control. ISA Trans. 2019, 95, 194–210. [Google Scholar] [CrossRef] [PubMed]
- Rubí, B.; Pérez, R.; Morcego, B. A Survey of Path Following Control Strategies for UAVs Focused on Quadrotors. J. Intell. Robot. Syst. 2019, 98, 241–265. [Google Scholar] [CrossRef] [Green Version]
- Lyu, X.; Zhou, J.; Gu, H.; Li, Z.; Shen, S.; Zhang, F. Disturbance Observer Based Hovering Control of Quadrotor Tail-Sitter VTOL UAVs Using Synthesis. IEEE Robot. Autom. Lett. 2018, 3, 2910–2917. [Google Scholar] [CrossRef]
- Kikkawa, H.; Uchiyama, K. Nonlinear flight control with an extended state observer for a fixed-wing UAV. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; IEEE: New York City, NY, USA, 2017. [Google Scholar] [CrossRef]
- Guo, K.; Jia, J.; Yu, X.; Guo, L.; Xie, L. Multiple observers based anti-disturbance control for a quadrotor UAV against payload and wind disturbances. Control Eng. Pract. 2020, 102, 104560. [Google Scholar] [CrossRef]
- Oosedo, A.; Konno, A.; Matumoto, T.; Go, K.; Masuko, K.; Abiko, S.; Uchiyama, M. Design and simulation of a quad rotor tail-sitter unmanned aerial vehicle. In Proceedings of the 2010 IEEE/SICE International Symposium on System Integration, Sendai, Japan, 21–22 December 2010; IEEE: New York City, NY, USA, 2011; pp. 254–259. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Siegwart, R. Backstepping and Sliding-mode Techniques Applied to an Indoor Micro Quadrotor. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; IEEE: New York City, NY, USA, 2006; pp. 2247–2252. [Google Scholar]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Chen, W.H.; Andrews, J. Tracking control of small-scale helicopters using explicit nonlinear MPC augmented with disturbance observers. Control Eng. Pract. 2012, 20, 258–268. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Li, S.; Yu, X. Sliding-Mode Control for Systems With Mismatched Uncertainties via a Disturbance Observer. IEEE Trans. Ind. Electron. 2013, 60, 160–169. [Google Scholar] [CrossRef]
- Viswanath, D.; Deb, D. Disturbance Observer based Sliding Mode Control for Proportional Navigation Guidance. IFAC Proc. Vol. 2012, 45, 163–168. [Google Scholar] [CrossRef]
- Fethalla, N.; Saad, M.; Michalska, H.; Ghommam, J. Robust Observer-Based Dynamic Sliding Mode Controller for a Quadrotor UAV. IEEE Access 2018, 6, 45846–45859. [Google Scholar] [CrossRef]
- Patel, R.; Deb, D.; Modi, H.; Shah, S. Adaptive backstepping control scheme with integral action for quanser 2-dof helicopter. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; IEEE: New York City, NY, USA, 2017. [Google Scholar] [CrossRef]
- Patel, R.; Deb, D. Parametrized control-oriented mathematical model and adaptive backstepping control of a single chamber single population microbial fuel cell. J. Power Sources 2018, 396, 599–605. [Google Scholar] [CrossRef]
- Patel, R.; Deb, D. Adaptive Backstepping Control of Single Chamber Microbial Fuel Cell. IFAC-PapersOnLine 2018, 51, 319–322. [Google Scholar] [CrossRef]








| Parameters | Value |
|---|---|
| g | 9.8 m·s |
| Mass (m) | 1.2 kg |
| length (l) | 1 m |
| kg·m2 | |
| kg·m2 | |
| kg·m2 | |
| drag coefficient (d) | |
| lift coefficient (b) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalwadi, N.; Deb, D.; Kothari, M.; Ozana, S. Disturbance Observer-Based Backstepping Control of Tail-Sitter UAVs. Actuators 2021, 10, 119. https://doi.org/10.3390/act10060119
Dalwadi N, Deb D, Kothari M, Ozana S. Disturbance Observer-Based Backstepping Control of Tail-Sitter UAVs. Actuators. 2021; 10(6):119. https://doi.org/10.3390/act10060119
Chicago/Turabian StyleDalwadi, Nihal, Dipankar Deb, Mangal Kothari, and Stepan Ozana. 2021. "Disturbance Observer-Based Backstepping Control of Tail-Sitter UAVs" Actuators 10, no. 6: 119. https://doi.org/10.3390/act10060119
APA StyleDalwadi, N., Deb, D., Kothari, M., & Ozana, S. (2021). Disturbance Observer-Based Backstepping Control of Tail-Sitter UAVs. Actuators, 10(6), 119. https://doi.org/10.3390/act10060119







