Cold Sintering of PZT 2-2 Composites for High Frequency Ultrasound Transducer Arrays
Abstract
:1. Introduction
1.1. Design Considerations
1.2. Processing
2. Materials and Methods
2.1. Design and Fabrication of PZT–ZnO 3-0 Composites
2.2. Fabrication and Characterization of PZT–Polymer 2-2 Composites
2.3. Electrical Characterization
3. Results and Discussion
3.1. PZT–ZnO 3-0 Composite
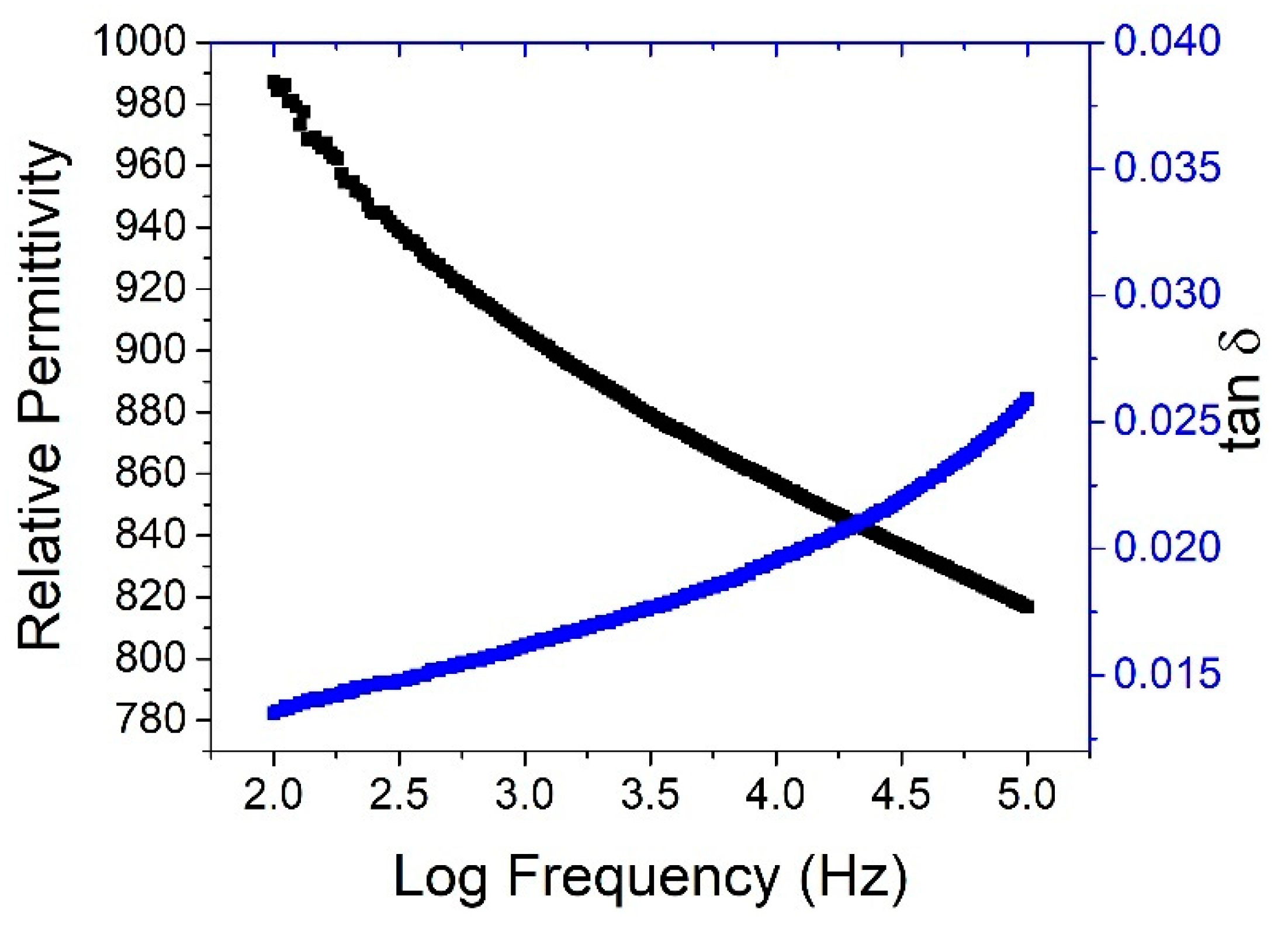
3.2. Electrical Measurements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shung, K.K. Diagnostic ultrasound: Past, present, and future. J. Med. Biol. Eng. 2011, 31, 371–374. [Google Scholar] [CrossRef]
- Shung, K.K. High frequency ultrasonic imaging. J. Med. Ultrasound 2009, 17, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Szabo, T.L.; Lewin, P.A. Ultrasound transducer selection in clinical imaging practice. J. Ultrasound Med. 2013, 32, 573–582. [Google Scholar] [CrossRef]
- Jiang, X.; Snook, K.; Walker, T.; Portune, A.; Haber, R.; Geng, X.; Welter, J.; Hackenberger, W.S. Single crystal piezoelectric composite transducers for ultrasound NDE applications. Int. Soc. Opt. Photonics 2008, 6934, 69340D. [Google Scholar] [CrossRef]
- Shung, K.K. Diagnostic Ultrasound: Imaging and Blood Flow Measurements; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Song, L.; Maslov, K.I.; Bitton, R.; Shung, K.K.; Wang, L.V. Fast 3-D dark-field reflection-mode photoacoustic microscopy in vivo with a 30-MHz ultrasound linear array. J. Biomed. Opt. 2008, 13, 054028. [Google Scholar] [CrossRef]
- Giannelli, P.; Bulletti, A.; Capineri, L. Multifunctional piezopolymer film transducer for structural health monitoring applications. IEEE Sens. J. 2017, 17, 4583–4586. [Google Scholar] [CrossRef]
- Smith, W.A. Piezocomposite materials for acoustical imaging transducers. In Acoustical Imaging; Jones, J.P., Ed.; Springer: Boston, MA, USA, 1995; pp. 121–138. [Google Scholar] [CrossRef]
- Lockwood, G.R.; Turnbull, D.H.; Christopher, D.A.; Foster, F.S. Beyond 30 MHz [applications of high-frequency ultrasound imaging]. IEEE Eng. Med. Biol. Mag. 1996, 15, 60–71. [Google Scholar] [CrossRef]
- Passmann, C.; Ermert, H. A 100-MHz ultrasound imaging system for dermatologic and ophthalmologic diagnostics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 545–552. [Google Scholar] [CrossRef]
- Mina, I.G. High Frequency Transducers from PZT Thin Films. Master’s Thesis, Pennsylvania State University, University Park, PA, USA, 2007. [Google Scholar]
- Safari, A. Development of piezoelectric composites for transducers. J. Phys. III 1994, 4, 1129–1149. [Google Scholar] [CrossRef]
- Newnham, R.E.; Skinner, D.P.; Cross, L.E. Connectivity and piezoelectric-pyroelectric composites. Mater. Res. Bull. 1978, 13, 525–536. [Google Scholar] [CrossRef]
- Newnham, R.E. Composite electroceramics. Ferroelectrics 1986, 68, 1–32. [Google Scholar] [CrossRef]
- Turnbull, D.H.; Foster, F.S. Beam steering with pulsed two-dimensional transducer arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1991, 38, 320–333. [Google Scholar] [CrossRef]
- Gururaja, T.R.; Schulze, W.A.; Cross, L.E.; Newnham, R.E.; Auld, B.A.; Wang, Y.J. Piezoelectric composite materials for ultrasonic transducer applications. Part I: Resonant modes of vibration of PZT rod-polymer composites. IEEE Trans. Sonics Ultrason. 1985, 32, 481–498. [Google Scholar] [CrossRef] [Green Version]
- Akdogan, E.K.; Allahverdi, M.; Safari, A. Piezoelectric composites for sensor and actuator applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 746–775. [Google Scholar] [CrossRef]
- Jaffe, B.; Cook, W.R., Jr.; Jaffe, H. Piezoelectric Ceramics; Academic Press: London, UK; New York, NY, USA, 1971. [Google Scholar]
- Corker, D.; Whatmore, R.; Ringgaard, E.; Wolny, W. Liquid-phase sintering of PZT ceramics. J. Eur. Ceram. Soc. 2000, 20, 2039–2045. [Google Scholar] [CrossRef]
- International Standard: IEEE Standards on Piezoelectricity, ANSI/IEEE Std 176–1987; The Institute of Electrical and Electronics Engineers, Inc.: Manhattan, NY, USA, 1987; p. 66. [CrossRef]
- Cain, M.G.; Stewart, M. Measurement Good Practice Guide No. 33. Piezoelectric Resonance 2001. Available online: https://www.npl.co.uk/special-pages/guides/gpg33_resonance.aspx?ext= (accessed on 5 March 2021).
- Ritter, T.A.; Shrout, T.R.; Tutwiler, R.; Shung, K.K. A 30-MHz piezo-composite ultrasound array for medical imaging applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 217–230. [Google Scholar] [CrossRef]
- Lee, H.J.; Zhang, S. Design of low-loss 1-3 piezoelectric composites for high-power transducer applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 1969–1975. [Google Scholar] [CrossRef]
- Hayward, G.; Bennett, J. Assessing the influence of pillar aspect ratio on the behavior of 1-3 connectivity composite transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 98–108. [Google Scholar] [CrossRef]
- Wang, S.H.; Tsai, M.C. Dynamic modeling of thickness-mode piezoelectric transducer using the block diagram approach. Ultrasonics 2011, 51, 617–624. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, T. Fundamentals of Piezoelectricity; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Klicker, K.A.; Newnham, R.E.; Cross, L.E.; Biggers, J.V. PZT Composite and A Fabrication Method Thereof. U.S. Patent 4,412,148, 25 October 1983. [Google Scholar]
- Sliwa, J.W.; Ayter, S.; Mohr, J.P., III. Acuson Corp, Method for Making Piezoelectric Composites. U.S. Patent 5,239,736, 31 August 1993. [Google Scholar]
- Savakus, H.P.; Klicker, K.A.; Newnham, R.E. PZT-epoxy piezoelectric transducers: A simplified fabrication procedure. Mater. Res. Bull. 1981, 16, 677–680. [Google Scholar] [CrossRef]
- Cannata, J.M.; Williams, J.A.; Zhou, Q.; Ritter, T.A.; Shung, K.K. Development of a 35-MHz piezo-composite ultrasound array for medical imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 224–236. [Google Scholar] [CrossRef]
- Safari, A.; Janas, V.F. Processing of fine-scale piezoelectric ceramic/polymer composites for transducer applications. Ferroelectrics 1997, 196, 187–190. [Google Scholar] [CrossRef]
- Günther, P.A.; Neumeister, P.; Neubert, H.; Gebhardt, S. Development of 40-MHz ultrasonic transducers via soft mold process. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1497–1503. [Google Scholar] [CrossRef]
- Safari, A.; Janas, V.; Panda, R.K. Fabrication of fine-scale 1-3 Pb(Zrx,Ti1−x)O3/ceramic/ polymer composites using a modified lost mold method. Int. Soc. Opt. Photonics 1996, 2721, 251–262. [Google Scholar] [CrossRef]
- Hackenberger, W.; Pan, M.J.; Kuban, D.; Ritter, T.; Shrout, T. Novel method for producing high frequency 2-2 composites from PZT ceramic. IEEE Int. Ultrason. Symp. Proc. 2000, 2, 969–972. [Google Scholar] [CrossRef]
- Kwon, S.; Hackenberger, W.; Rehrig, P.; Snook, K.; Rhee, S.; Shrout, T.R.; Geng, X. Ceramic/polymer 2-2 composites for high frequency transducers by tape casting. IEEE Symp. Ultrason. 2003, 1, 366–369. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.; Lin, X.; Xie, R.; Zhou, K.; Button, T.W.; Zhang, D. Fine-scaled piezoelectric ceramic/polymer 2-2 composites for high-frequency transducer. J. Am. Ceram. Soc. 2014, 97, 1060–1064. [Google Scholar] [CrossRef]
- Stevenson, J.W.; Reidmeyer, M.R.; Huebner, W. Fabrication and characterization of PZT/thermoplastic polymer composites for high-frequency phased linear arrays. J. Am. Ceram. Soc. 1994, 77, 2481–2484. [Google Scholar] [CrossRef]
- Livneh, S.S.; Janas, V.F.; Safari, A. Development of fine scale PZT ceramic fiber/polymer shell composite transducers. J. Am. Ceram. Soc. 1995, 78, 1900–1906. [Google Scholar] [CrossRef]
- Ohara, Y.; Miyayama, M.; Koumoto, K.; Yanagida, H. PZT-polymer composites fabricated with YAG laser cutter. Sens. Actuators A Phys. 1994, 40, 187–190. [Google Scholar] [CrossRef]
- Ohara, Y.; Miyayama, M.; Koumoto, K.; Yanagida, H. Partially stabilized zirconia-polymer composites fabricated with an ultrasonic cutter. J. Mater. Sci. Lett. 1993, 12, 1279–1282. [Google Scholar] [CrossRef]
- Hoy, C.V.; Barda, A.; Griffith, M.; Halloran, J.W. Microfabrication of ceramics by co-extrusion. J. Am. Ceram. Soc. 1998, 81, 152–158. [Google Scholar] [CrossRef]
- Lubitz, K.; Wolff, A.; Preu, G.; Stoll, R.; Schulmeyer, B. PcI2: New piezoelectric composites for ultrasonic transducers. Ferroelectrics 1992, 133, 21–26. [Google Scholar] [CrossRef]
- Zhou, Q.; Lau, S.; Wu, D.; Shung, K.K. Piezoelectric films for high frequency ultrasonic transducers in biomedical applications. Prog. Mater. Sci. 2011, 56, 139–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Safari, A.; Allahverdi, M.; Akdogan, E.K. Solid freeform fabrication of piezoelectric sensors and actuators. Front. Ferroelectr. 2006, 41, 177–198. [Google Scholar] [CrossRef]
- Zhen, Y.; Li, J.F. Preparation and electrical properties of fine-scale 1–3 lead zirconium titanate/epoxy composite thick films for high-frequency ultrasonic transducers. J. Appl. Phys. 2008, 103, 084119. [Google Scholar] [CrossRef]
- Lee, H.J.; Zhang, S.; Bar-Cohen, Y.; Sherrit, S. High temperature, high power piezoelectric composite transducers. Sensors 2014, 14, 14526–14552. [Google Scholar] [CrossRef] [Green Version]
- Chabok, H.; Zhou, C.; Chen, Y.; Eskandarinazhad, A.; Zhou, Q.; Shung, K. Ultrasound transducer array fabrication based on additive manufacturing of piezocomposites. In Proceedings of the International Symposium on Flexible Automation, St. Louis, MO, USA, 18–20 June 2012; Volume 45110, pp. 433–444. [Google Scholar] [CrossRef]
- Hackenberger, W.S.; Kim, N.; Randall, C.A.; Cao, W.; Shrout, T.R.; Pickrell, D.P. Processing and structure-property relationships for fine grained PZT ceramics. In Proceedings of the Tenth IEEE International Symposium on Applications of Ferroelectrics, ISAF’96, East Brunswick, NJ, USA, 18–21 August 1996; Volume 2, pp. 903–906. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, T.; Ou-Yang, J.; Yang, X.; Wu, D.; Zhu, B. PIN-PMN-PT single crystal 1-3 composite-based 20 MHz ultrasound phased array. Micromachines 2020, 11, 524. [Google Scholar] [CrossRef]
- Bowen, L.J.; Gentilman, R.L.; Pham, H.T.; Fiore, D.F.; French, K.W. Injection molded fine-scale piezoelectric composite transducers. In Proceedings of the 1993 Proceedings IEEE Ultrasonics Symposium, Baltimore, MD, USA, 31 October–3 November 1993; pp. 499–503. [Google Scholar] [CrossRef]
- Cesarano, J., III; Calvert, P.D. National Technology, Engineering Solutions of Sandia LLC. Freeforming Objects with Low-Binder Slurry. U.S. Patent 6,027,326, 22 February 2000. [Google Scholar]
- Rittenmyer, K.; Shrout, T.; Schulze, W.A.; Newnham, R.E. Piezoelectric 3–3 composites. Ferroelectrics 1982, 41, 189–195. [Google Scholar] [CrossRef]
- Pan, M.-J.; Randall, C.A. A brief introduction to ceramic capacitors. IEEE Electr. Insul. Mag. 2010, 26, 44–50. [Google Scholar] [CrossRef]
- Lee, W.; Lyon, C.K.; Seo, J.H.; Lopez-Hallman, R.; Leng, Y.; Wang, C.Y.; Hickner, M.A.; Randall, C.A.; Gomez, E.D. Ceramic–salt composite electrolytes from cold sintering. Adv. Funct. Mater. 2019, 29, 1807872. [Google Scholar] [CrossRef]
- Funahashi, S.; Guo, H.; Guo, J.; Baker, A.L.; Wang, K.; Shiratsuyu, K.; Randall, C.A. Cold sintering and co-firing of a multilayer device with thermoelectric materials. J. Am. Ceram. Soc. 2017, 100, 3488–3496. [Google Scholar] [CrossRef]
- Baker, A.; Guo, H.; Guo, J.; Randall, C.A. Utilizing the cold sintering process for flexible–printable electroceramic device fabrication. J. Am. Ceram. Soc. 2016, 99, 3202–3204. [Google Scholar] [CrossRef]
- Guo, J.; Guo, H.; Baker, A.L.; Lanagan, M.T.; Kupp, E.R.; Messing, G.L.; Randall, C.A. Cold sintering: A paradigm shift for processing and integration of ceramics. Angew. Chem. 2016, 128, 11629–11633. [Google Scholar] [CrossRef]
- Ndayishimiye, A.; Sengul, M.Y.; Sada, T.; Dursun, S.; Bang, S.H.; Grady, Z.A.; Tsuji, K.; Funahashi, S.; van Duin, A.C.; Randall, C.A. Roadmap for densification in cold sintering: Chemical pathways. Open Ceram. 2020, 2, 100019. [Google Scholar] [CrossRef]
- Wang, D.; Guo, H.; Morandi, C.S.; Randall, C.A.; Trolier-McKinstry, S. Cold sintering and electrical characterization of lead zirconate titanate piezoelectric ceramics. APL Mater. 2018, 6, 016101. [Google Scholar] [CrossRef] [Green Version]
- Linder, V.; Gates, B.D.; Ryan, D.; Parviz, B.A.; Whitesides, G.M. Water-soluble sacrificial layers for surface micromachining. Small 2005, 1, 730–736. [Google Scholar] [CrossRef]
- Peeni, B.A.; Lee, M.L.; Hawkins, A.R.; Woolley, A.T. Sacrificial layer microfluidic device fabrication methods. Electrophoresis 2006, 27, 4888–4895. [Google Scholar] [CrossRef]
- Lee, J.D. Concise Inorganic Chemistry, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Liu, T.; Wallace, M.; Trolier-McKinstry, S.; Jackson, T.N. High-temperature crystallized thin-film PZT on thin polyimide substrates. J. Appl. Phys. 2017, 122, 164103. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, J.; Marquina, J.; Rodriguez, F.; Valiente, R. Nanocrystals of ZnO formed by the hot isostatic pressure method. High Press. Res. 2009, 29, 594–599. [Google Scholar] [CrossRef]
- Butt, Z.; Pasha, R.A.; Qayyum, F.; Anjum, Z.; Ahmad, N.; Elahi, H. Generation of electrical energy using lead zirconate titanate (PZT-5A) piezoelectric material: Analytical, numerical and experimental verifications. J. Mech. Sci. Technol. 2016, 30, 3553–3558. [Google Scholar] [CrossRef] [Green Version]
- Wang, D. Low Temperature Processing of Electro-Ceramic Materials and Devices. Ph.D. Thesis, Pennsylvania State University, University Park, PA, USA, 2020. [Google Scholar]
- Guo, J.; Pfeiffenberger, N.; Beese, A.; Rhoades, A.; Gao, L.; Baker, A.; Wang, K.; Bolvari, A.; Randall, C.A. Cold sintering Na2Mo2O7 ceramic with poly (ether imide)(PEI) polymer to realize high-performance composites and integrated multilayer circuits. ACS Appl. Nano Mater. 2018, 1, 3837–3844. [Google Scholar] [CrossRef]
- ASTM E112-13, Standard Test Methods for Determining Average Grain Size; ASTM International: West Conshohocken, PA, USA, 2013; Available online: http://www.astm.org (accessed on 1 September 2018).
- Wang, D.; Dursun, S.; Gao, L.; Morandi, C.S.; Randall, C.A.; Trolier-McKinstry, S. Fabrication of bimorph lead zirconate titanate thick films on metal substrates via the cold sintering-assisted process. Acta Mater. 2020, 195, 482–490. [Google Scholar] [CrossRef]
- Banerjee, A.; Bandyopadhyay, A.; Bose, S. Influence of La2O3, SrO, and ZnO addition on PZT. J. Am. Ceram. Soc. 2006, 89, 1594–1600. [Google Scholar] [CrossRef]
- Trolier-McKinstry, S.; Newnham, R.E. Materials Engineering: Bonding, Structure, and Structure-Property Relationships; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Wu, Y.; Zhao, X.; Li, F.; Fan, Z. Evaluation of mixing rules for dielectric constants of composite dielectrics by MC-FEM calculation on 3D cubic lattice. J. Electroceramics 2003, 11, 227–239. [Google Scholar] [CrossRef]



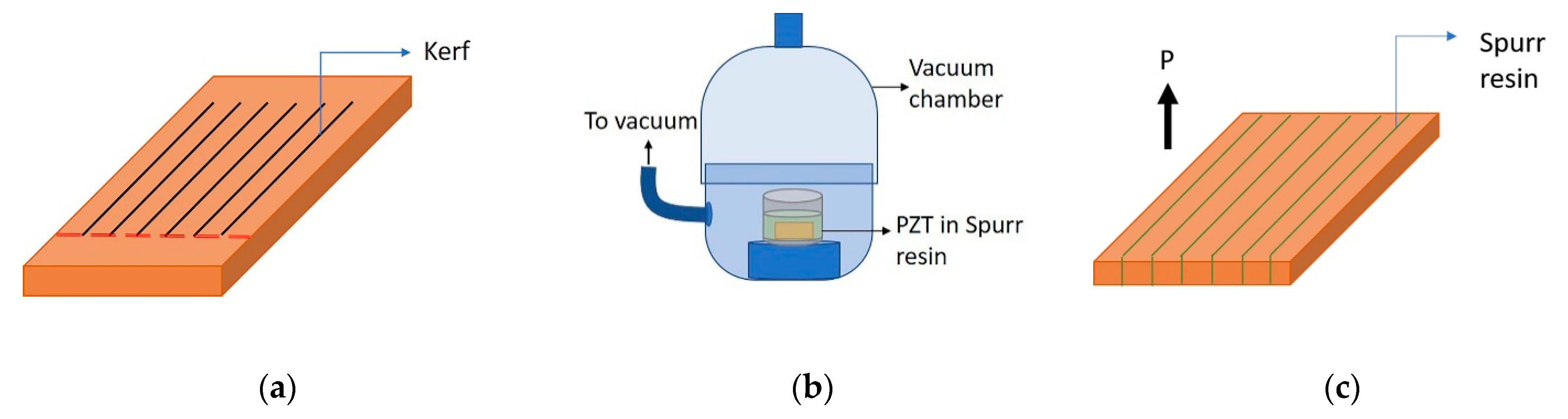




| Dice and Fill | Injection Molding | Solid Freeform Fabrication | Lost Mold Technique | |
|---|---|---|---|---|
| Advantages | Can achieve kerfs above 12 µm. Utilizes inexpensive tooling. | Rapid production and flexibility in transducer design. | Can process different shapes. Overcomes problems with dimensional tolerances. | Can be used to fabricate 30 µm beam sizes with 10 µm kerfs. |
| Disadvantages | Fails for arrays >~10–20 MHz. Piezoelectric elements can crack at very low widths. Limited element patterns. | Requires expensive precision molds. Ceramic green body is prone to deformation on sintering. | Limited in fine feature sizes and achievable densities. | At very fine feature sizes, the structure deforms upon firing. |
| PZT | Polymer | |
|---|---|---|
| Type | PZT-5A (PKI-509, PiezoKinetics Inc., Bellefonte, PA, UK) | Spurr resin (Polyscience Inc., Warrington, PA, UK) |
| (GPa) | 121 Ref. [65] | 5.28 Ref. [23] |
| Density (kg/m3) ♣ | 7600 | 1135 |
| Velocity (m/s) | = 3938 | = 976 Ref. [23] |
| Width (µm) | ≤34 | ≤8 |
| Layer | Green Tape Thickness (μm) | Layer Width (μm) | Standard Deviation in Layer Width | |
|---|---|---|---|---|
| 16 elements | PZT | 125 | 39 | 0.7 |
| ZnO/kerf | 17 | 5.4 | 0.2 | |
| 32 elements | PZT | 112 | 35 | 1.1 |
| ZnO/kerf | 19 | 6.2 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, S.; Wang, D.; Shetty, S.; Meddeb, A.; Dursun, S.; Randall, C.A.; Trolier-McKinstry, S. Cold Sintering of PZT 2-2 Composites for High Frequency Ultrasound Transducer Arrays. Actuators 2021, 10, 235. https://doi.org/10.3390/act10090235
Gupta S, Wang D, Shetty S, Meddeb A, Dursun S, Randall CA, Trolier-McKinstry S. Cold Sintering of PZT 2-2 Composites for High Frequency Ultrasound Transducer Arrays. Actuators. 2021; 10(9):235. https://doi.org/10.3390/act10090235
Chicago/Turabian StyleGupta, Shruti, Dixiong Wang, Smitha Shetty, Amira Meddeb, Sinan Dursun, Clive A. Randall, and Susan Trolier-McKinstry. 2021. "Cold Sintering of PZT 2-2 Composites for High Frequency Ultrasound Transducer Arrays" Actuators 10, no. 9: 235. https://doi.org/10.3390/act10090235
APA StyleGupta, S., Wang, D., Shetty, S., Meddeb, A., Dursun, S., Randall, C. A., & Trolier-McKinstry, S. (2021). Cold Sintering of PZT 2-2 Composites for High Frequency Ultrasound Transducer Arrays. Actuators, 10(9), 235. https://doi.org/10.3390/act10090235






