Port-Hamiltonian Modeling and IDA-PBC Control of an IPMC-Actuated Flexible Beam
Abstract
:1. Introduction
2. Port-Hamiltonian Formulation for IPMC Actuated Flexible Beam
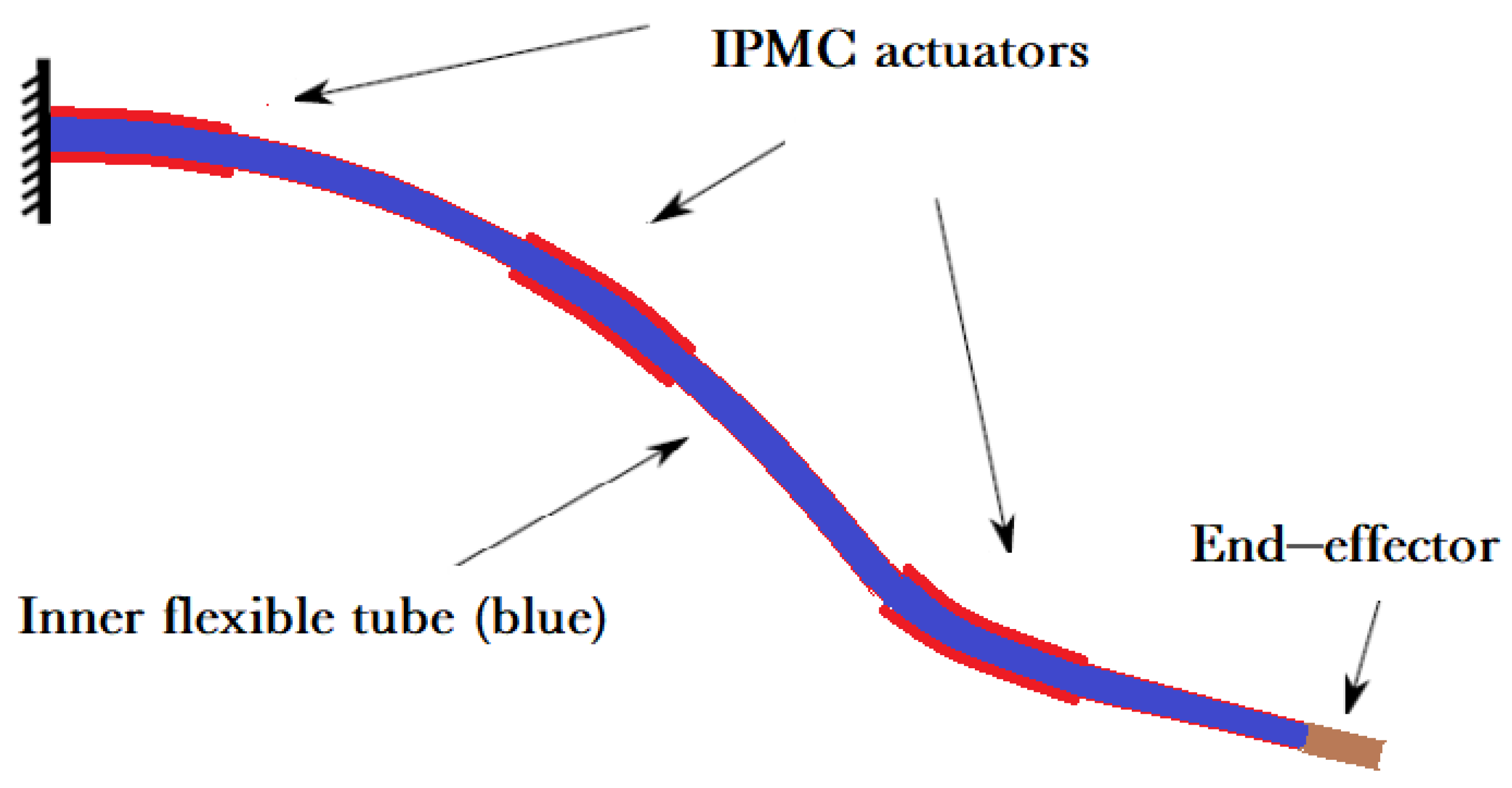
2.1. Flexible Beam with Distributed Control
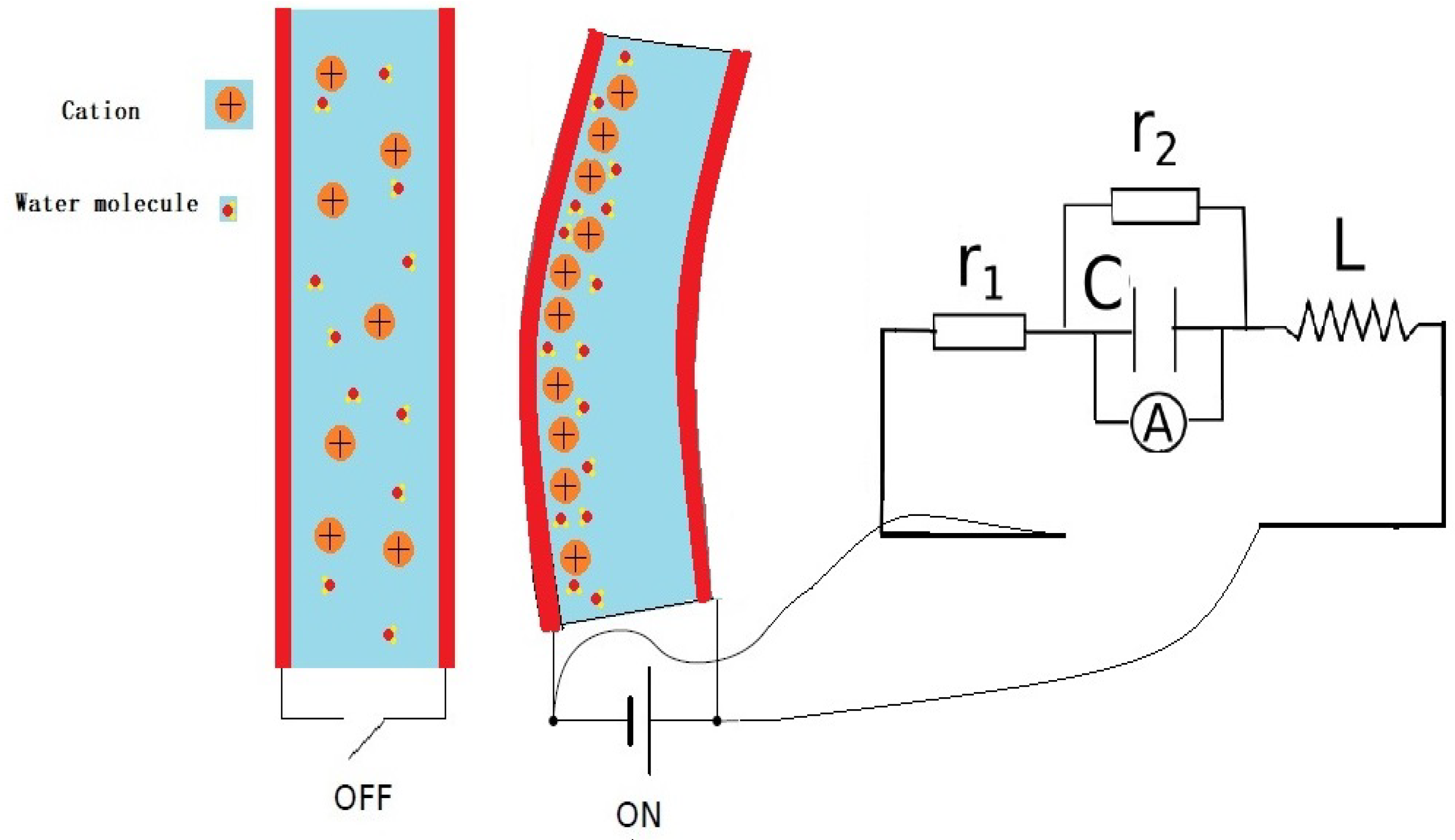
2.2. The IPMC Actuator Model
3. Control Design via IDA-PBC
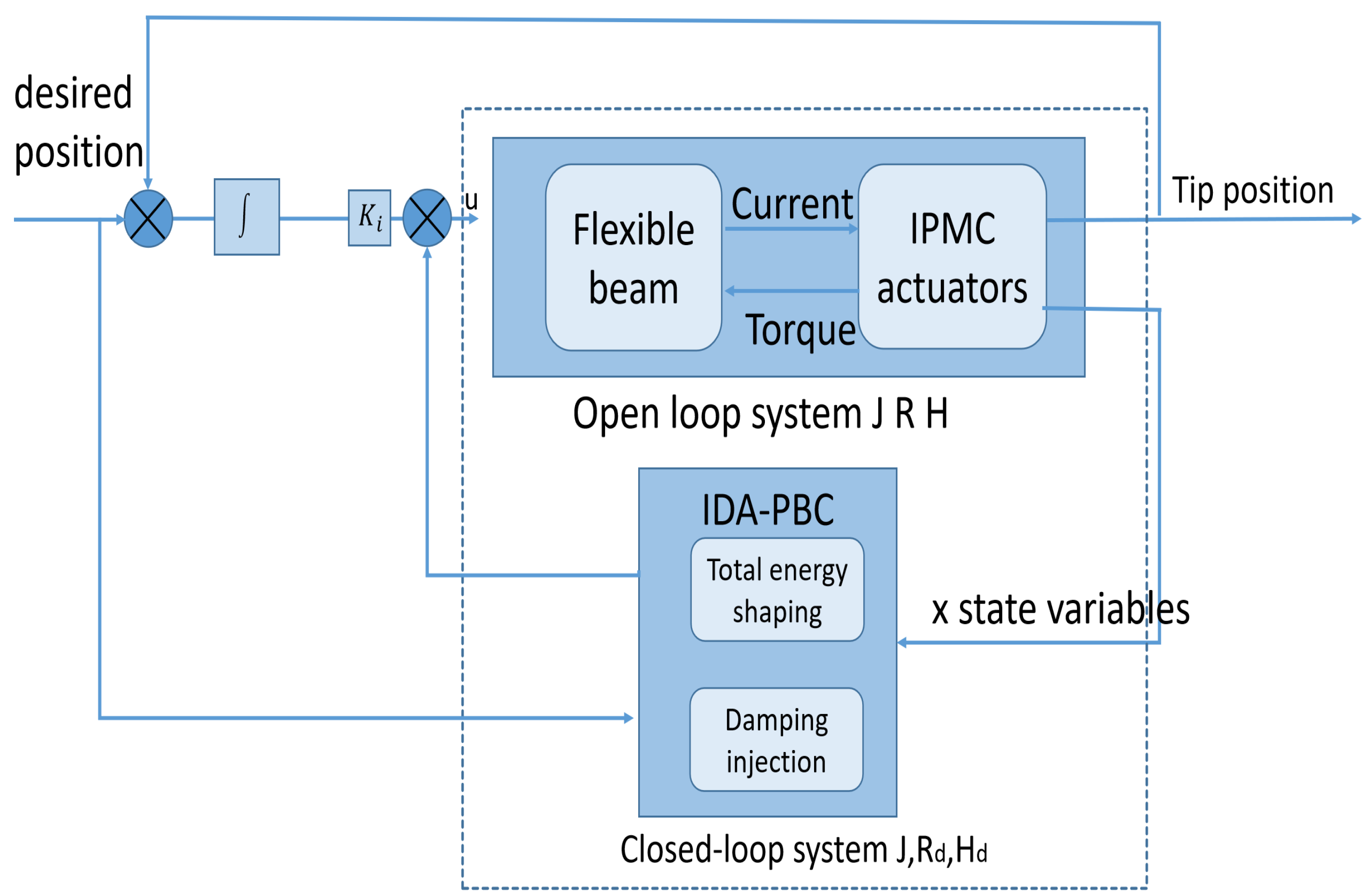
3.1. Ida-Pbc Control Method
3.2. Control Design
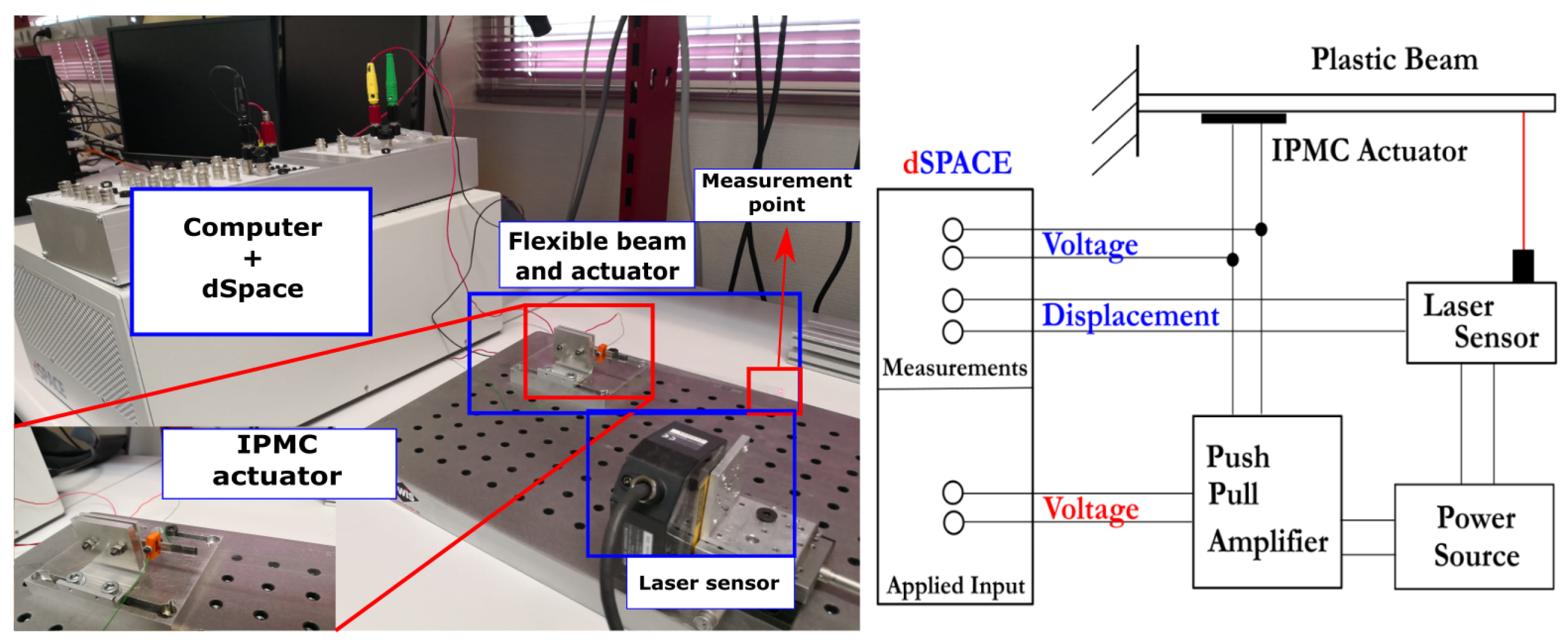
4. Control Validation by Experimentation and Simulation
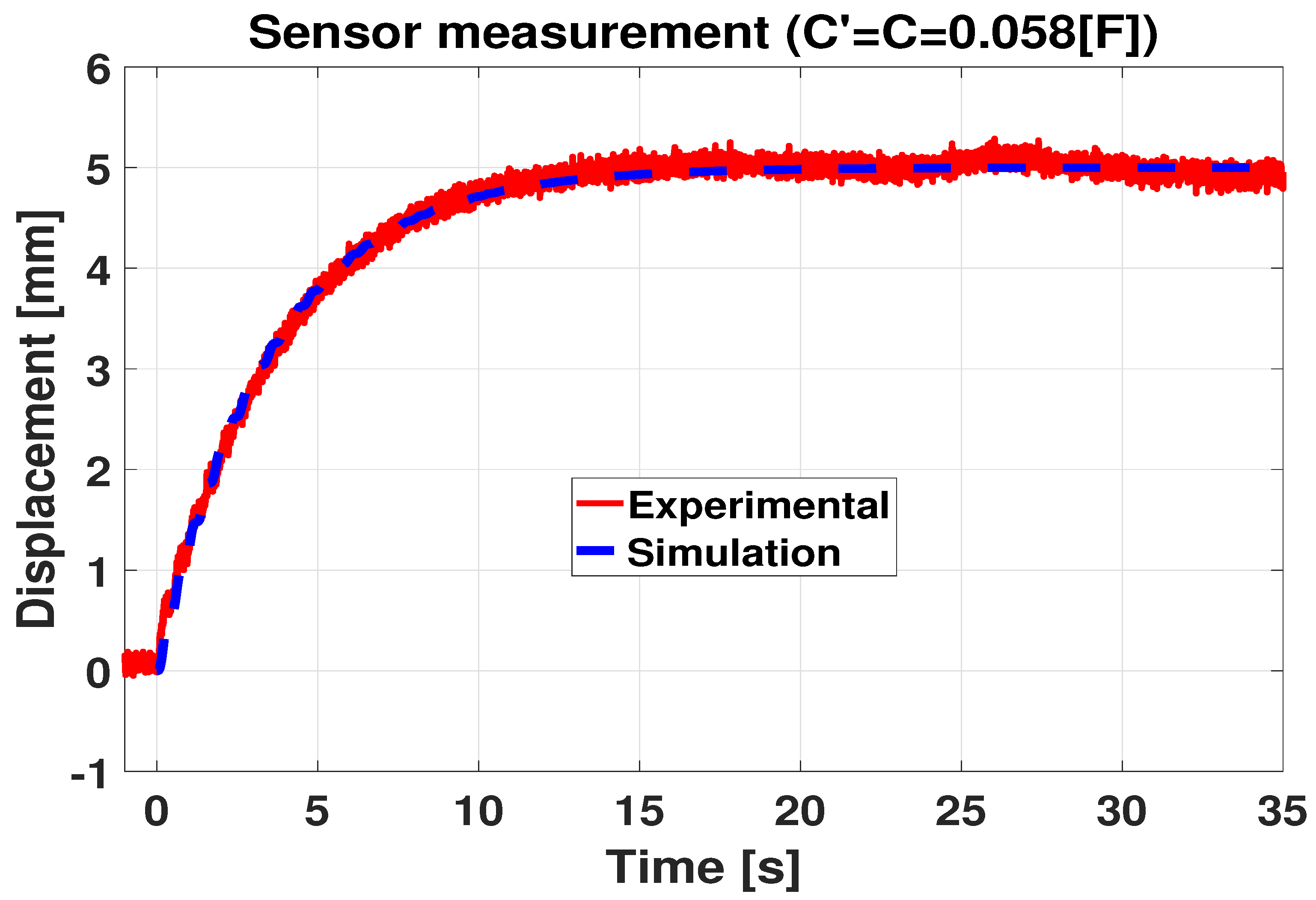
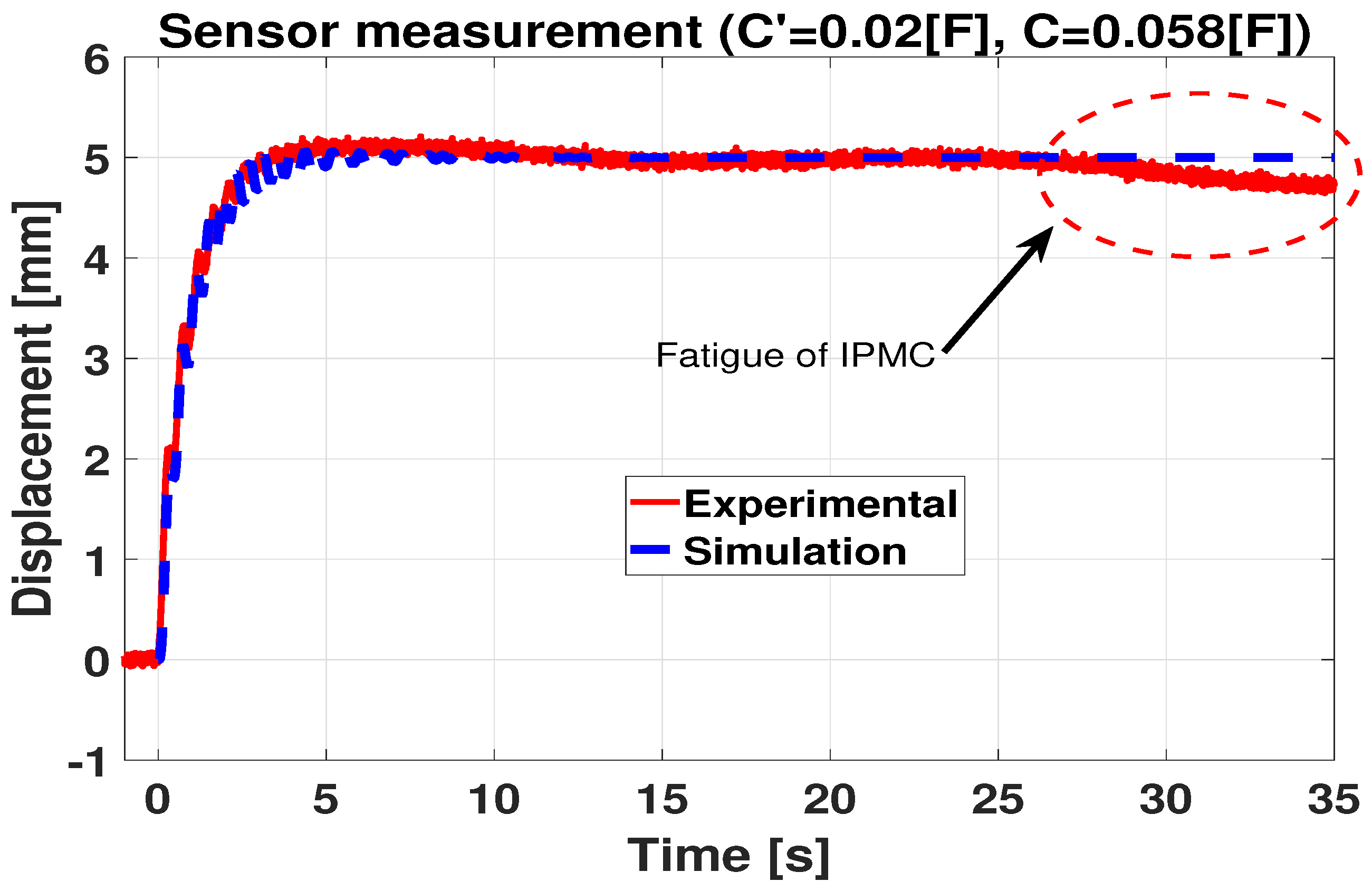
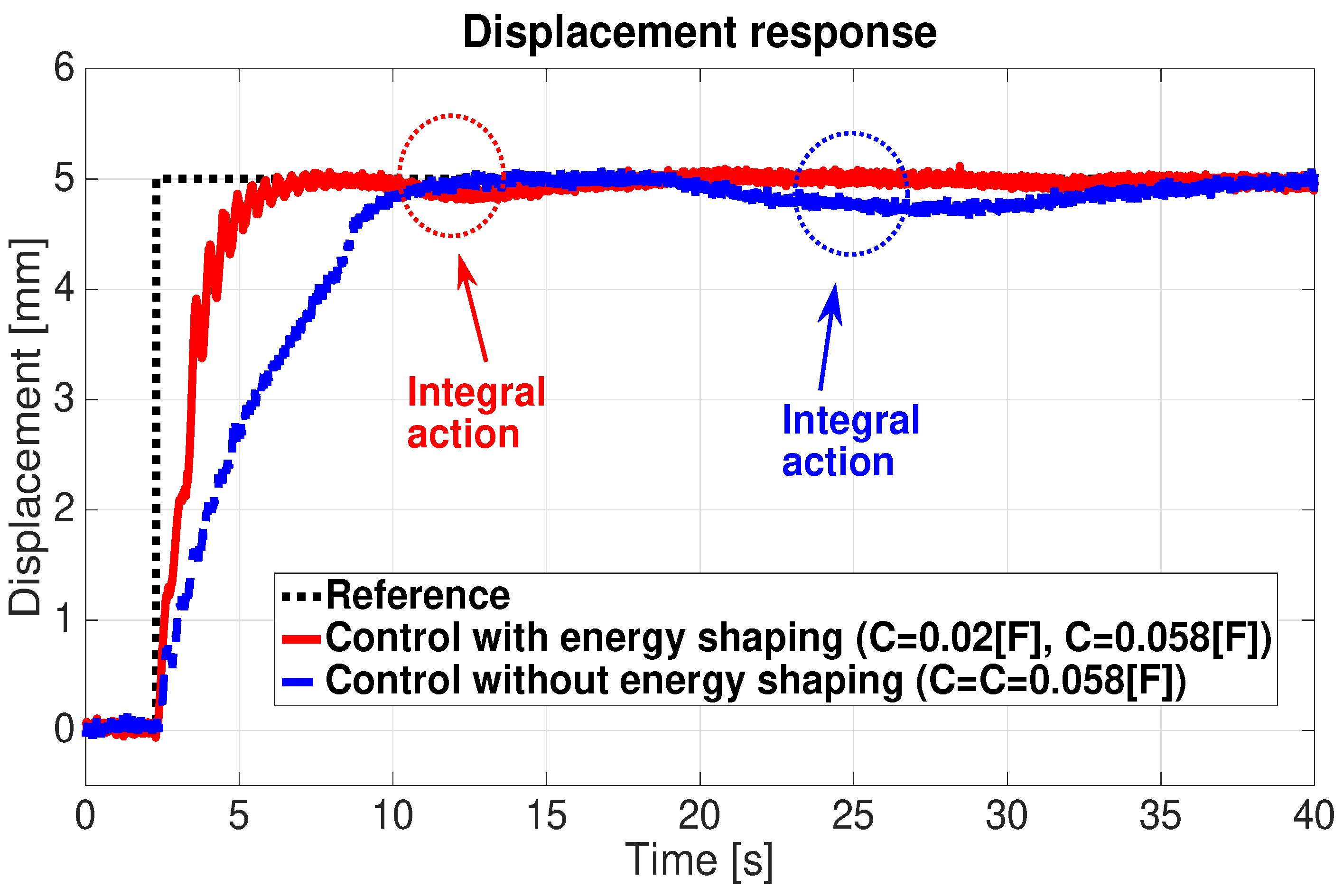
4.1. Control of a Single IPMC-Actuated Flexible Beam
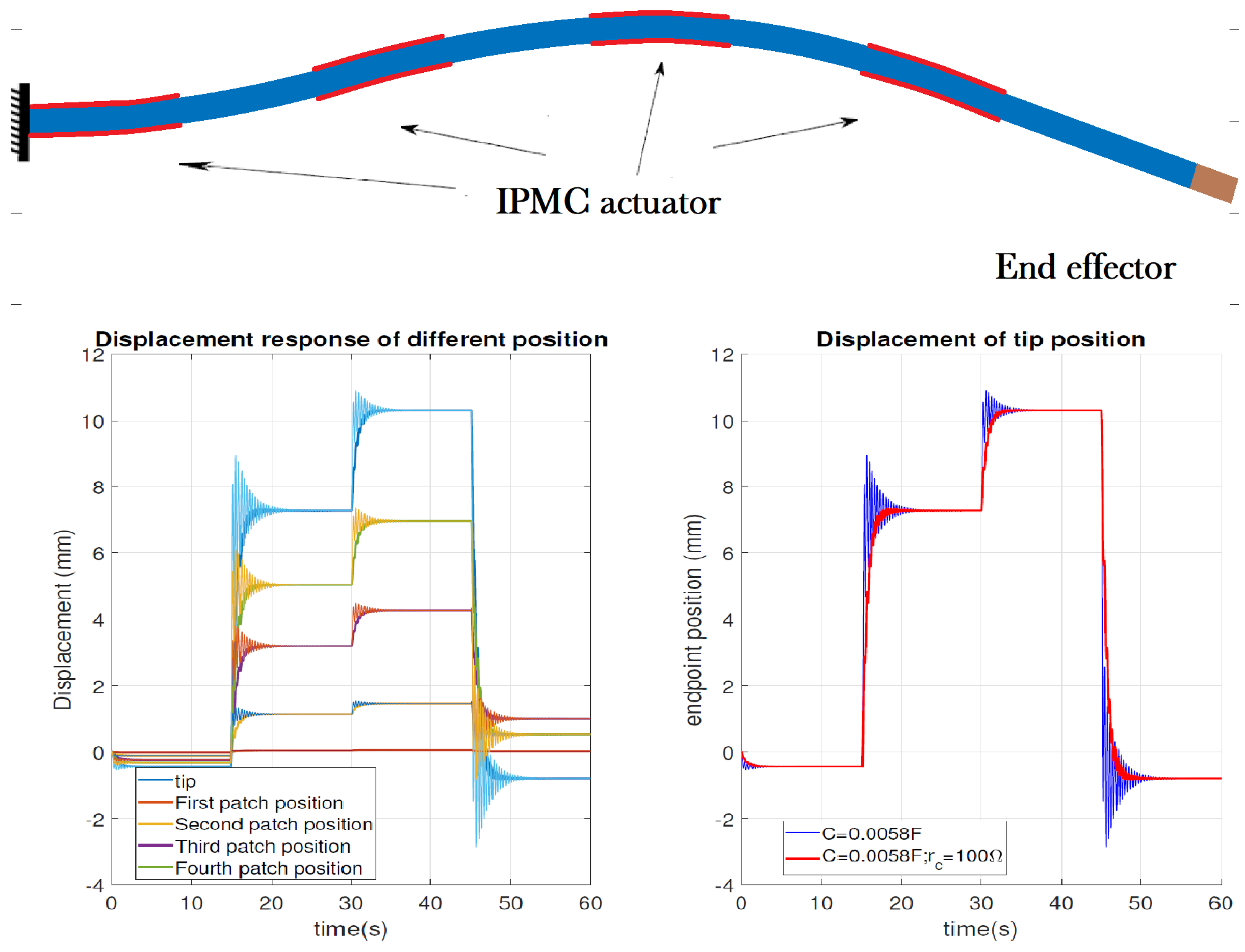
4.2. Multi-Actuation of a Flexible Beam
5. Conclusion and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Chikhaoui, M.T.; Rabenorosoa, K.; Andreff, N. Kinematic modeling of an EAP actuated continuum robot for active micro-endoscopy. In Advances in Robot Kinematics; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 457–465. [Google Scholar]
- Shahinpoor, M.; Kim, K.J. Ionic polymer-metal composites: I. Fundamentals. Smart Mater. Struct. 2001, 10, 819. [Google Scholar] [CrossRef]
- Maschke, B.; van der Schaft, A. Port Controlled Hamiltonian Systems: Modeling Origins and System Theoretic Properties; IFAC Nonlinear Control Systems Design: Bordeaux, France, 1992. [Google Scholar]
- Mattioni, A.; Wu, Y.; Le Gorrec, Y. Infinite dimensional model of a double flexible-link manipulator: The Port-Hamiltonian approach. Appl. Math. Model. 2020, 83, 59–75. [Google Scholar] [CrossRef]
- Monshizadeh, P.; Machado, J.E.; Ortega, R.; van der Schaft, A. Power-controlled Hamiltonian systems: Application to electrical systems with constant power loads. Automatica 2019, 109, 108527. [Google Scholar] [CrossRef] [Green Version]
- Hoang, H.; Couenne, F.; Jallut, C.; Le Gorrec, Y. The port Hamiltonian approach to modeling and control of Continuous Stirred Tank Reactors. J. Process. Control 2011, 21, 1449–1458. [Google Scholar] [CrossRef] [Green Version]
- Maschke, B.; van der Schaft, A. Hamiltonian representation of distributed parameter systems with boundary energy flow. In Nonlinear Control in the Year 2000; Springer: London, UK, 2000; pp. 137–142. [Google Scholar]
- Le Gorrec, Y.; Zwart, H.; Maschke, B. Dirac structures and boundary control systems associated with skew-symmetric differential operators. SIAM J. Control Optim. 2005, 44, 1864–1892. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Hamroun, B.; Couenne, F.; Le Gorrec, Y. Distributed port-Hamiltonian modelling for irreversible processes. Math. Comput. Model. Dyn. Syst. 2017, 23, 3–22. [Google Scholar] [CrossRef]
- Nishida, G.; Takagi, K.; Maschke, B.; Osada, T. Multi-scale distributed parameter modeling of ionic polymer-metal composite soft actuator. Control. Eng. Pract. 2011, 19, 321–334. [Google Scholar] [CrossRef]
- Liu, N.; Wu, Y.; Le Gorrec, Y. Energy based modeling of ionic polymer metal composite actuators dedicated to the control of flexible structures. IEEE/ASME Trans. Mechatronics 2021. [Google Scholar] [CrossRef]
- Macchelli, A. Energy shaping of distributed parameter port-Hamiltonian systems based on finite element approximation. Syst. Control Lett. 2011, 60, 579–589. [Google Scholar] [CrossRef]
- Ramírez, H.; Le Gorrec, Y.; Macchelli, A.; Zwart, H. Exponential stabilization of boundary controlled port-Hamiltonian systems with dynamic feedback. IEEE Trans. Autom. Control 2014, 59, 2849–2855. [Google Scholar] [CrossRef] [Green Version]
- Ortega, R.; van der Schaft, A.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef] [Green Version]
- Ortega, R.; van der Schaft, A.J.; Mareels, I.; Maschke, B. Putting energy back in control. IEEE Control Syst. Mag. 2001, 21, 18–33. [Google Scholar]
- Mattioni, A.; Wu, Y.; Ramirez, H.; Le Gorrec, Y.; Macchelli, A. Modelling and control of an IPMC actuated flexible structure: A lumped port Hamiltonian approach. Control Eng. Pract. 2020, 101, 104498. [Google Scholar] [CrossRef]
- Wu, Y.; Lamoline, F.; Winkin, J.; Le Gorrec, Y. Modeling and control of an IPMC actuated flexible beam under the port-Hamiltonian framework. IFAC-PapersOnline 2019, 52, 108–113. [Google Scholar] [CrossRef]
- Jacob, B.; Zwart, H.J. Linear Port-Hamiltonian Systems on Infinite-Dimensional Spaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 223. [Google Scholar]
- Macchelli, A.; Melchiorri, C. Modeling and control of the Timoshenko beam. The distributed port Hamiltonian approach. SIAM J. Control Optim. 2004, 43, 743–767. [Google Scholar] [CrossRef] [Green Version]
- Gutta, S.; Lee, J.S.; Trabia, M.B.; Yim, W. Modeling of ionic polymer metal composite actuator dynamics using a large deflection beam model. Smart Mater. Struct. 2009, 18, 115023. [Google Scholar] [CrossRef]
- Golo, G.; Talasila, V.; van der Schaft, A.; Maschke, B. Hamiltonian discretization of boundary control systems. Automatica 2004, 40, 757–771. [Google Scholar] [CrossRef] [Green Version]
- Moulla, R.; Lefèvre, L.; Maschke, B. Pseudo-Spectral Methods for the Spatial Symplectic Reduction of Open Systems of Conservation Laws. J. Comput. Phys. 2011, 231, 1272–1292. [Google Scholar] [CrossRef] [Green Version]
- Trenchant, V.; Ramirez, H.; Le Gorrec, Y.; Kotyczka, P. Finite differences on staggered grids preserving the port-Hamiltonian structure with application to an acoustic duct. J. Comput. Phys. 2018, 373, 673–697. [Google Scholar] [CrossRef]
- Kotyczka, P. Finite Volume Structure-Preserving Discretization of 1D Distributed-Parameter Port-Hamiltonian Systems. IFAC-PapersOnLine 2016, 49, 298–303. [Google Scholar] [CrossRef] [Green Version]
- Rashad, R.; Califano, F.; van der Schaft, A.J.; Stramigioli, S. Twenty years of distributed port-Hamiltonian systems: A literature review. IMA J. Math. Control Inf. 2020, 37, 1400–1422. [Google Scholar] [CrossRef]
- Ortega, R.; Garcia-Canseco, E. Interconnection and damping assignment passivity-based control: A survey. Eur. J. Control 2004, 10, 432–450. [Google Scholar] [CrossRef]
- Lei, H.; Lim, C.; Tan, X. Humidity-dependence of IPMC sensing dynamics: Characterization and modeling from a physical perspective. Meccanica 2015, 50, 2663–2673. [Google Scholar] [CrossRef]


| L | Length | m |
|---|---|---|
| W | Width | m |
| T | Thickness | m |
| Mass density | 936 kgm | |
| I | Inertia moment of area | m |
| Angular moment of inertia | kg | |
| E | Young’s modulus | Pa |
| K | shear modulus | Pa |
| Traversal viscous fraction | kgm/s | |
| Angular viscous fraction | kgm/s | |
| C | Capacitance | F |
| Resistance | 29.75 | |
| Resistance | 700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Wu, Y.; Hu, H.; Li, Y.; Wang, Y. Port-Hamiltonian Modeling and IDA-PBC Control of an IPMC-Actuated Flexible Beam. Actuators 2021, 10, 236. https://doi.org/10.3390/act10090236
Zhou W, Wu Y, Hu H, Li Y, Wang Y. Port-Hamiltonian Modeling and IDA-PBC Control of an IPMC-Actuated Flexible Beam. Actuators. 2021; 10(9):236. https://doi.org/10.3390/act10090236
Chicago/Turabian StyleZhou, Weijun, Yongxin Wu, Haiqiang Hu, Yanjun Li, and Yu Wang. 2021. "Port-Hamiltonian Modeling and IDA-PBC Control of an IPMC-Actuated Flexible Beam" Actuators 10, no. 9: 236. https://doi.org/10.3390/act10090236
APA StyleZhou, W., Wu, Y., Hu, H., Li, Y., & Wang, Y. (2021). Port-Hamiltonian Modeling and IDA-PBC Control of an IPMC-Actuated Flexible Beam. Actuators, 10(9), 236. https://doi.org/10.3390/act10090236






