A New Method for Identifying Kinetic Parameters of Industrial Robots

Abstract

Identifying the kinetic parameters of an industrial robot is the basis for designing a controller for it. To solve the problems of the poor accuracy and easy premature convergence of common bionic algorithms for identifying the dynamic parameters of such robots, this study proposed simulated annealing with similar exponential changes based on the beetle swarm optimization (SEDSABSO) algorithm. Expressions for the dynamics of the industrial robot were first obtained through the SymPyBotics toolkit in Python, and the required trajectories of excitation were then designed to identify its dynamic parameters. Following this, the search pattern of the global optimal solution for the beetle swarm optimization algorithm was improved in the context of solving for these parameters. The global convergence of the algorithm was improved by improving the iterative form of the number N of skinks in it by considering random perturbations and the simulated annealing algorithm, whereas its accuracy of convergence was improved through the class exponential change model. The improved beetle swarm optimization algorithm was used to identify the kinetic parameters of the Zhichang Kawasaki RS010N industrial robot. The results of experiments showed that the proposed algorithm was fast and highly accurate in identifying the kinetic parameters of the industrial robot.

1. Introduction

Kinetic parameters are the main factor influencing the control of fast and highly precise movements of industrial robots [1]. The process of identifying of their kinetic parameters is usually divided into a number of steps, such as kinetic modeling, designing the excitation trajectory, data acquisition, and identifying and verifying the kinetic parameters [2]. Gautier et al. used a two degree-of-freedom (DOF) robot as the object of study and applied the extended Kalman filter and the least-squares method to identify its parameters. Memar used the SCHUNK Powerball LWA 4P as an experimental object, constructed a dynamics model for it, and implemented the least-squares method to identify the dynamic parameters of the industrial robot [3]. However, the least-squares method is susceptible to measurement noise that lowers its accuracy [4]. Fu et al. [5] used the particle swarm optimization (PSO) algorithm with least squares to identify the kinetic parameters of a seven-DOF collaborative robot in Xinsong, but PSO can easily fall into the local optimum owing to poor population diversity in the late stage of processing that reduces the accuracy of identification of the parameters. Ding et al. [6] identified the dynamics of the robot by using the genetic algorithm, but the process of coding of the algorithm is cumbersome.

Summarizing the existing research, it is found that the identification of robot dynamics parameters is a high-dimensional function problem. Common algorithms are either the PSO accuracy is not high enough, or the genetic algorithm coding is more complicated, so a simple programming, strong anti-interference ability, and convergence accuracy are needed. High algorithm. BSO is a bionic algorithm recently proposed, which mainly uses the principles of PSO and the Beetle Antenna Search (BAS) algorithm, so it has the advantage of simple programming [7,8,9]. This article proposes SEDSABSO on the basis of BSO.SEDSABSO combined random perturbation-based behavior and the simulated annealing (SA) algorithm with the global optimal solution of the BSO [10,11] to improve its ability to search for global optimal particles as well as the manner of changes in N particles through an exponential decay model. This improved the convergence of BSO without affecting its computational complexity. Therefore, using the SEDSABSO algorithm for robot dynamic parameter identification will have the advantages of simple programming, high convergence accuracy, and fast iteration speed.

The rest of the paper is organized as follows. Section 2 describes the D-H and the dynamic parameters of the RS010N robot and then linearized them through the SymPyBotics toolkit in Python. In Section 3, the genetic algorithm toolbox in MATLAB was used to design the excitation trajectories required to identify the dynamic parameters of the robot. Section 4 describes the principle of the SEDSABSO algorithm and its process for the identification of robot dynamics parameters. In Section 5, the minimum set of parameters for the dynamics of the RS010N robot was identified and was used to compare the per-formance of the SEDSABSO, BSO, and LDWPSO algorithms. The results verified the accuracy and effectiveness of the proposed algorithm [12].

2. Robotic arm Dynamics Model

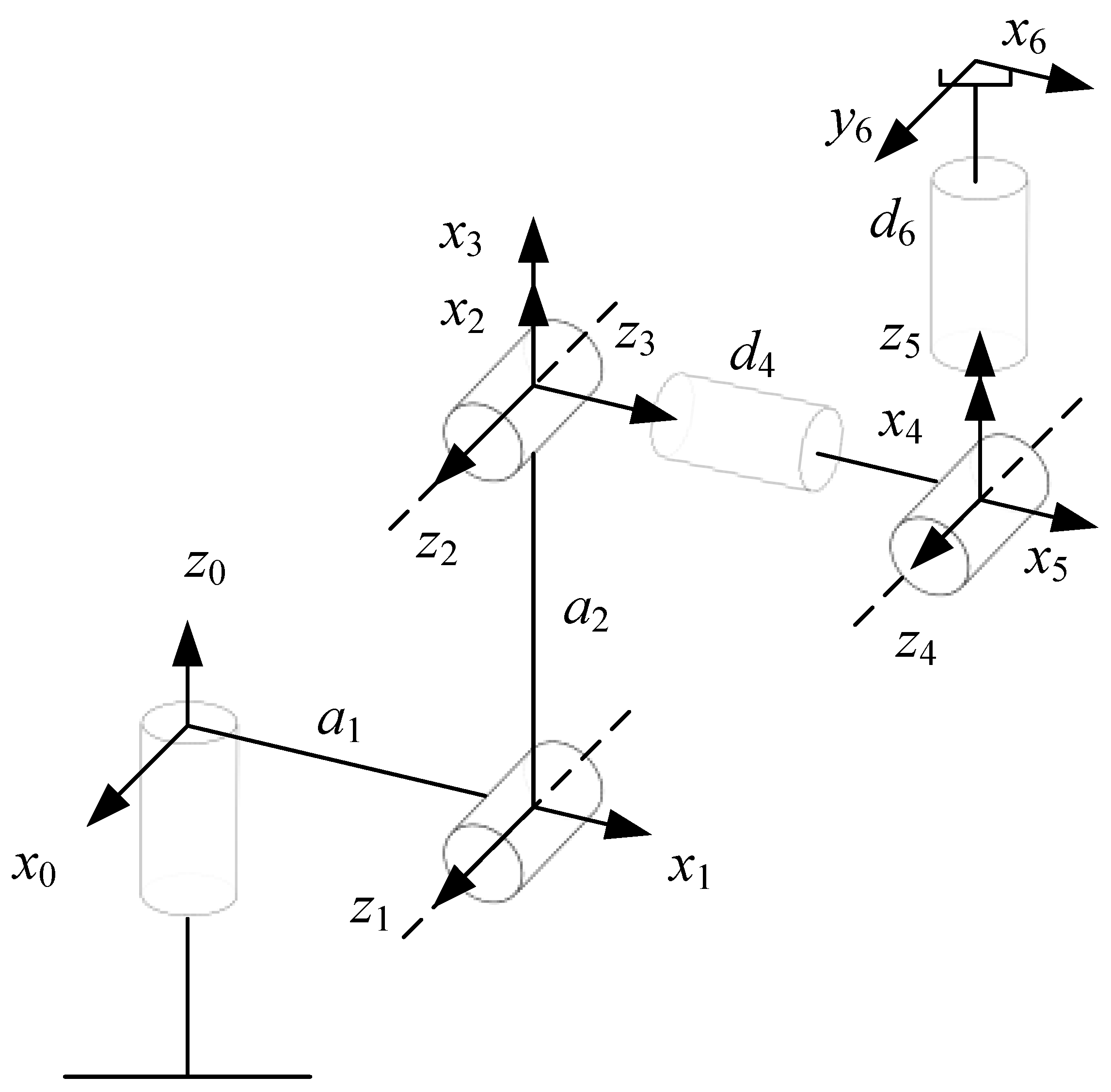
2.1. RS010N Industrial Robots

In this paper, we used the Zhichang Kawasaki RS010N robot as the research object. Figure 1 shows its structural configuration, and Figure 2 shows the configuration of its DH coordinates. The RS010N robot is a typical six-DOF industrial robot. Because the kinetic parameters of its three rear joints are much smaller than those of its three front joints, the former have a smaller influence on the accuracy of control of the robot’s motion. Thus, we considered only the first three joints of the RS010N industrial robot here [13].

2.2. Dynamics Modeling

For an n-link robotic arm, the dynamics as modeled by the Newton-Euler method can be described as

$$\tau =D(q)\cdot \ddot{q}+C(q,\dot{q})+G(q)$$

(1)

In Equation (1), τ denotes the driving moment, q denotes the vector of the position of the joints, and $\dot{q}$ and $\ddot{q}$ denote vectors of the velocity and acceleration of the joints, respectively. D(q) denotes the inertial matrix, C(q,$\dot{q}$) denotes the Koch and centrifugal force terms, respectively, and G(q) denotes the gravitational force term [14].

According to the improved Newtonian–Eulerian dynamics, the above equation can be transformed into

$$\tau =\Phi (q,\dot{q},\ddot{q})P$$

(2)

where Φ is the observation matrix with a size of n ∗ 12n, and P denotes the vector of the inertial parameters of the robot arm.

2.3. Minimum Set of Parameters for the Dynamical Model

The parameters of the first three joint linkages of the RS010N six-freedom robot are shown in

Table 1. RS010N connecting rod parameters.

i	αi−1/rad	ai−1/mm	di/mm	θi/rad
1	pi/2	a0	0	θ1
2	−pi/2	a1	0	θ2
3	0	0	0	θ3

below. a₀ = 350 mm, a₁ = 1035 mm.

The kinetic parameters are shown in

Table 2. Actual kinetic parameters.

Member Number	1	2	3
Ixx/(kg·m2)	36.33	−10.02	7.74
Iyy/(kg·m2)	40.61	7.05	1.02
Izz/(kg·m2)	36.33	11.61	9.81
Ixy/(kg·m2)	0.00	6.14	3.34
Ixz/(kg·m2)	0.00	5.93	−3.42
Iyz/(kg·m2)	0.00	−7.82	−0.29
m/(kg)	18.33	25.18	20.47
x/(mm)	0.00	122.41	152.34
y/(mm)	110.11	163.81	90.24
z/(mm)	0.00	73.36	−34.21
Fc (N·m)	0.00	0.00	0.00
Fv (N·m)	0.00	0.00	0.00

.

We obtained the minimum set of parameters and related expressions for them through the SymPyBotics toolkit in Python.

$$\left[\begin{array}{c}{I}_{1xx}\\ I_{1yy}\\ I_{1zz}\\ I_{1xy}\\ I_{1xz}\\ I_{1yz}\\ m_1\\ x_1\\ y_1\\ z_1\\ F_{1c}\\ F_{1v}\\ I_{2xx}\\ I_{2yy}\\ I_{2zz}\\ I_{2xy}\\ I_{2xz}\\ I_{2yz}\\ m_2\\ x_2\\ y_2\\ z_2\\ F_{2c}\\ F_{2v}\\ I_{3xx}\\ I_{3yy}\\ I_{3zz}\\ I_{3xy}\\ I_{3xz}\\ I_{3yz}\\ m_3\\ x_3\\ y_3\\ z_3\\ F_{3c}\\ F_{3v}\end{array}\right]\stackrel{\mathrm{Linearization}}{\to }\left[\begin{array}{c}{I}_{1zz}+I_{2zz}+I_{3zz}+2*a1*I_{1x}+m_1{*a}_1{}^2-\\ (m_2+m_3{)*(a}_2{}^2{-a}_1{}^2)\\ F_{1c}\\ F_{1v}\\ I_{2xx}-I_{2yy}-(m_2+m_3)*a_2{}^2\\ I_{2xy}\\ I_{2x}-a^2*(I_{2z}-I_{3y})\\ I_{2yz}\\ I_{2zz}-(m_2+m_3)*a_2{}^2\\ I_{2x}+(m_2+m_3)*a_2\\ I_{2y}\\ F_{2c}\\ F_{2v}\\ I_{3xx}-I_{3zz}\\ I_{3xy}\\ I_{3xz}\\ I_{3yy}\\ I_{3yz}\\ I_{3x}\\ I_{3z}\\ F_{3c}\\ F_{3v}\end{array}\right]$$

(3)

According to Equation (3) above, the 36 kinetic parameters of the robot were linearized to 21, and the kinetic model can be written in the following form

$$\tau ={\Phi }_b(q,\dot{q},\ddot{q})p_b$$

(4)

where Φ_b is the full-rank observation matrix and P_b denotes the underlying parameter vector of the robotic arm.

3. Incentive Track Design

The commonly used excitation trajectory when identifying the kinetic parameters of industrial robots is the finite-term Fourier series [15,16]. It can be expressed in the following form:

$${\ddot{\theta }}_i(t)=-{\displaystyle \sum _{n=1}^N{a}_{n}n{w}_f}\sin (n{w}_{f}t)-b_{n}n{w}_f\cos (n{w}_{f}t)$$

(5)

$${\dot{\theta }}_i(t)={\displaystyle \sum _{n=1}^N{a}_n}\cos (n{w}_{f}t)-b_n\sin (n{w}_{f}t)$$

(6)

$${\theta }_i(t)={\theta }_0+{\displaystyle \sum _{n=1}^N\frac{a_n}{n{w}_f}}\sin (n{w}_{f}t)-\frac{b_n}{n{w}_f}\cos (n{w}_{f}t)$$

(7)

w_f denotes the fundamental frequency of the Fourier series. Each Fourier series contains a_n, b_n, and θ₀. N represents the number of harmonic terms of the Fourier series. Because each Fourier series has 2N + 1 parameters, n represents the number of 1 … 2N + 1.

The constraints on the RS010N robot are shown in

Table 3. RS010N robot joint constraints.

Parameter	Joint i	Min	Max
	1	−180	180
Angle	2	−60	140
	3	−180	80
	1	−125	125
Angle velocity	2	−100	100
	3	−165	165
	1	−45	45
Angle acceleration	2	−40	40
	3	−75	75

.

When the robot moved, the observation matrix w was obtained by recording the angle, velocity, and acceleration of the joints of the robot in Φ_b. n denotes the nth sample.

$$w=\left[\begin{array}{c}{\Phi }_b(q_1,{\dot{q}}_1,{\ddot{q}}_1)\\ \dots \\ {\Phi }_b(q_n,{\dot{q}}_n,{\ddot{q}}_n)\end{array}\right]$$

(8)

Adaptation function of the incentive trajectory.

$$y=Cond(w)+P$$

(9)

where P denotes a penalty function and Cond denotes the number of conditions of the acquisition matrix. When the trajectory of the industrial robot satisfies the above constraint, P = 0, and P = 10⁸ otherwise. The excitation of the first three joints of the RS010N was obtained by the genetic algorithm toolbox in MATLAB as shown in Figure 3.

4. SEDSABSO for the Identification of Industrial Robot Dynamics Parameters

4.1. Improving Global Optimal Search

Owing to the large number of dynamic parameters of the industrial robot that needed to be identified, their solution was a high-dimensional function optimization problem with certain constraints. The BSO used to obtain the kinetic parameter identification of industrial robots easily falls into the premature phenomenon, so the global optimal solution search mode of BSO and the iterative change form of the number N of tennies in the iterative process of BSO are improved in this paper.

BSO

BSO was proposed by Wang et al. based on the PSO and the Aspen whisker algorithm. The position of a body in BSO represents a feasible solution to the optimization problem. The formula to update BSO is:

$$x_{ij}\left(t+1)=x_{ij}\right(t)+\lambda v_{ij}\left(t+1)+(1-\lambda \right){\xi }_{ij}\left(t\right)$$

(10)

where t denotes the number of iterations of the skink, i denotes the number of skinks in the skink population, j denotes the dimensionality of the problem to be solved, λ denotes x_ij(t + 1) denotes the position of skink i in the skink population at t + 1 iterations, ξ_ij(t) denotes the position of the ith skink moving autonomously, and v_ij(t + 1) denotes the velocity of the ith skink. It is expressed as:

$$v_{ij}\left(t+1)=w{v}_{ij}\right(t)+c_1{r}_1\left(p_{ij}\right(t)-x_{ij}\left(t\left)\right)+c_2{r}_2\right(g_{ij}\left(t)-x_{ij}\right(t\left)\right)$$

(11)

w denotes inertial weight, p_ij(t) denotes the optimal position of individual i after t iterations of the Aspen population, x_ij(t) denotes the given position of i after t iterations, g_ij(t) denotes the optimal position of the Aspen population after t iterations, c₁ and c₂ denote adjustment factors, and r₁ and r₂ denote random numbers within the interval [0,1]

$${\xi }_{ij}\left(t+1)=\delta \right(t)*V_{ij}\left(t)*sign\right(f\left(x_{lj}\right(t\left)\right)-f\left(x_{rj}\right(t\left)\right))$$

(12)

In Equation (12), sign(.) denotes the sign function, ξ_ij(t + 1) denotes the t + 1th motion position searched by Aspen autonomously, δ(t) denotes the step size of the Aspen individual after t iterations, and f(x_lj(t)) and f(x_rj(t)) denote the fitness values of the left and right whiskers of the Aspen, respectively.

The positions of the left and right whiskers of the Aspen are indicated by:

$$\begin{array}{l}{x}_{lj}\left(t+1)=x_{lj}\right(t)+V_{ij}\left(t\right)d_0/2\\ x_{rj}\left(t+1)=x_{rj}\right(t)-V_{ij}\left(t\right)d_0/2\end{array}$$

(13)

x_lj(t + 1) denotes the position of the left whisker in iteration t + 1, x_rj(t + 1) is the t + 1 right whisker position, and d₀ denotes the distance between the whiskers.

4.2. Improving BSO

4.2.1. Improved Global Optimal Solution

The global optimal particle P_g of BSO is randomly perturbed. Then, the new solution after perturbation is selected by the metropolis criterion of SA to improve the global convergence of BSO.

(1)

Simulated annealing algorithm

The simulated annealing algorithm controls the probability of jumping out of the local optimum by setting the temperature. The algorithm evaluates whether to jump out of the worse solution by the metropolis criterion. The procedure is as follows:

• The algorithm is initialized, and an initial solution x is randomly generated as the optimal solution.
• A new solution x_t is obtained in the vicinity of the initial solution, denoted by ∆f = f(x_t) − f(x).
• The new solution x_t is accepted according to min{1,exp(−∆f/T_k)}>random. T_k denotes the temperature and exp denotes the exponential function, with natural number e as the base.

(2)

Random behavior

Stochastic behavior is a search behavior that can improve the diversity of algorithmic populations and is widely used in a variety of intelligent algorithms, such as in the foraging behavior within the fish swarm algorithm to search for food and the wandering behavior of the wolf pack algorithm to sense the scent of prey in the air in a random pattern [17,18]. Inspired by this, we incorporated stochastic behavior into BSO, and the optimal particles in it were randomly perturbed during each iteration to enhance its ability to escape from the local optimal solution to improve global convergence:

P_g^new = P_g ∗ (1 + rand)

(14)

where P_g^new denotes the new solution after the random perturbation of the optimal particle of the Aspen swarm, and rand represents a random number from zero to one. The fitness value of the optimal particle p_g of BSO was compared with that of the global optimal particle P_g^new for random perturbation; then, the new solution was accepted according to the metropolis criterion of SA. BSO performed q random perturbations of its global optimal solution in each iteration.

4.2.2. Improved Iterative Approach to N Particles of the Aspen Swarm

Each skyline of BSO represents a potential solution to the problem. Assuming that the number of skylines in each iteration of BSO is N, the maximum number of its iterations is Maxdt, and the duration of the iteration of a single skyline is t, the total complexity of iterations of BSO is N*Maxdt*t [19]. In solving a high-dimensional function problem, similar to determining the dynamic parameters of the industrial robot, the number of particles N at the moment of each iteration of BSO is constant. BSO is based on PSO, and a larger number of particles in PSO yields a higher accuracy of the convergence, but the time needed for convergence also increases.

For example, in previous work, we proposed a two-stage dynamic PSO that changed the number of particles in the swarm by linearly reducing the number of iterations. The experimental results showed that the accuracy of convergence of the algorithm was similar to that of the classical PSO algorithm, which also reflects a side-effect of the latter. The algorithm proposed here also had this property of a high initial accuracy of convergence [20]. Inspired by this, the number N of skinks in the skink swarm was changed dynamically. The number was larger in the early stage of the skink swarm algorithm and smaller in the later stage, such that the total number of skinks did not differ by much and the gap in the durations of their iterations was not large. We fully exploited the high efficiency of the early iterations of the skink swarm algorithm for the accuracy of its solution. The exponentially decreasing rate of curtailment was used for the number of cows N of the Aspen swarm algorithm by drawing on the idea proposed by Wang et al. [21]. That is, the particle swarm algorithm used a larger number of particles to search in the initial stage. With the increase of the number of iterations, the exponentially decreasing number of particle was used to reduce the Aspen number, so as to improve the search efficiency, and the improved iterative formula for the Aspen number is as follows:

$$N=round(e^{\alpha }*N_{start})$$

(15)

$$\alpha =t\frac{In{f}_{max}-In{f}_{min}}{Maxdt}-In{f}_{max}$$

(16)

where N_start denotes the initial number of skinks of the improved skink herd, i denotes the number of iterations of the skink herd algorithm, Maxdt denotes the maximum number of iterations, and f_max and f_min are the respective maximum and minimum values of the search factor set used to control the number of skinks N.

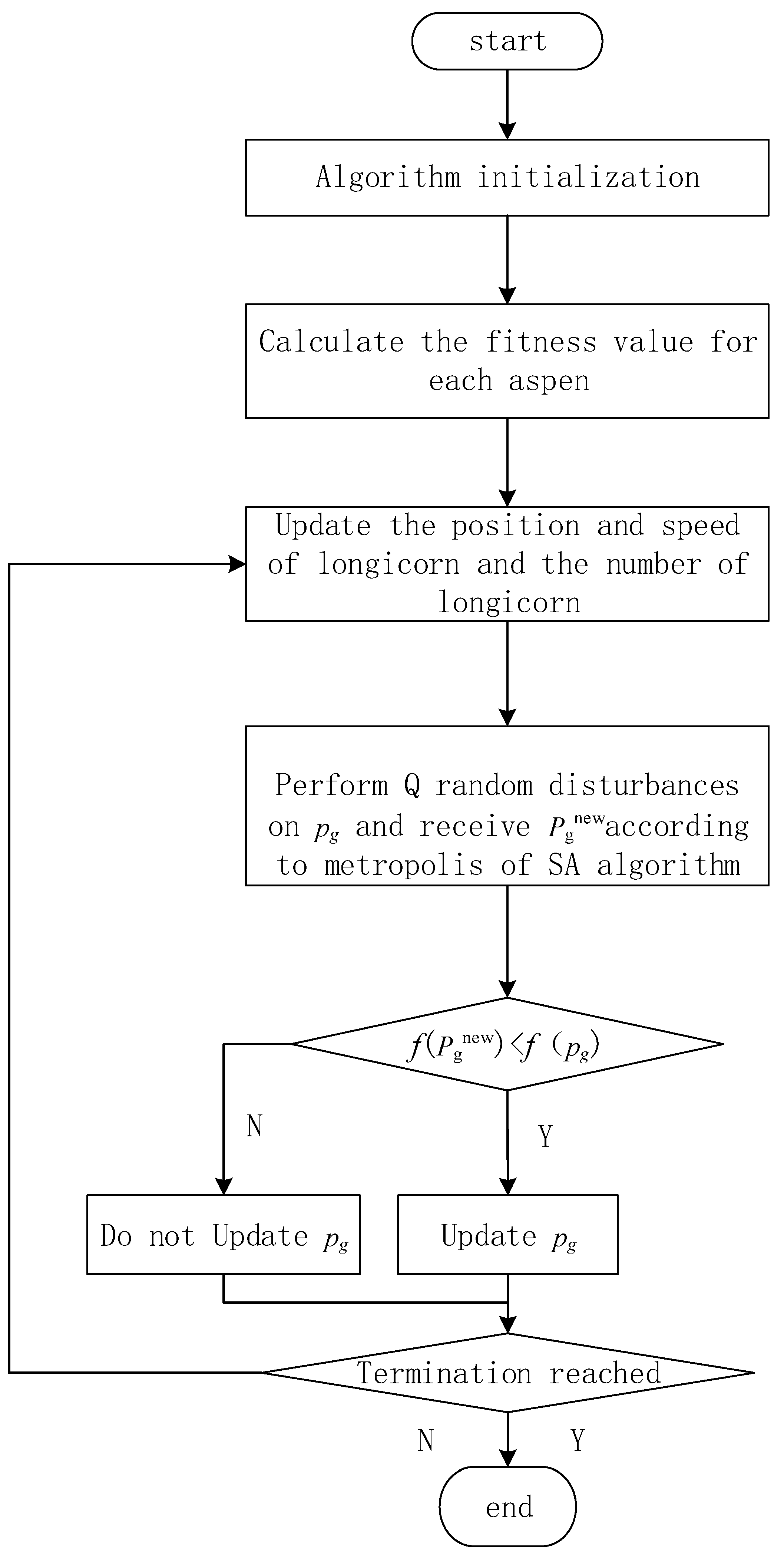
4.3. Robot Dynamic Parameter Identification Based on SEDSABSO

The SEDSABSO process is illustrated below:

From Figure 4, the flow of SEDSABSO for industrial robot dynamics parameter identification is:

(1)

Initialization of the algorithm.

(2)

Obtain SEDSABSO individual and group best-fit values.

(3)

Update the position, velocity, and number of skinks N

(4)

Perform a random perturbation search for the global optimal solution and then accept the searched solution with SA’s Metropolis criterion and cycle through q searches.

(5)

Compare with the global optimal solution obtained in step 3 after passing q times of search and proceed to the next step of the search by merit.

(6)

Determine whether the algorithm ends, and if the termination condition is not satisfied, return to step 3. If it is satisfied, the global optimal solution is output. In turn, the parameters related to industrial robot dynamics are obtained.

5. Simulation Experiments and Results Analysis

5.1. Adaptation Function

The sum of the absolute values of the difference between the torque of joint recognition and the theoretical torque of the RS010N robot when sampled i times was used as the objective function, as in Equation (17)

$${\displaystyle \sum _{i=1}^{N}abs(f_{k}1(i)}-f1(i))+abs(f_{k}2(i)-f2(i))+abs(f_{k}3(i)-f3(i))$$

(17)

i = 1, 2, …, N denotes the ith sample of the robot, f_k1(i), f_k2(i), and f_k3(i) denote values of the first, second, and third moments of the joints values for the i robot recognition f1(i), f2(i), f3(i) denotes the theoretical value of the three joint moments sampled by the robot.

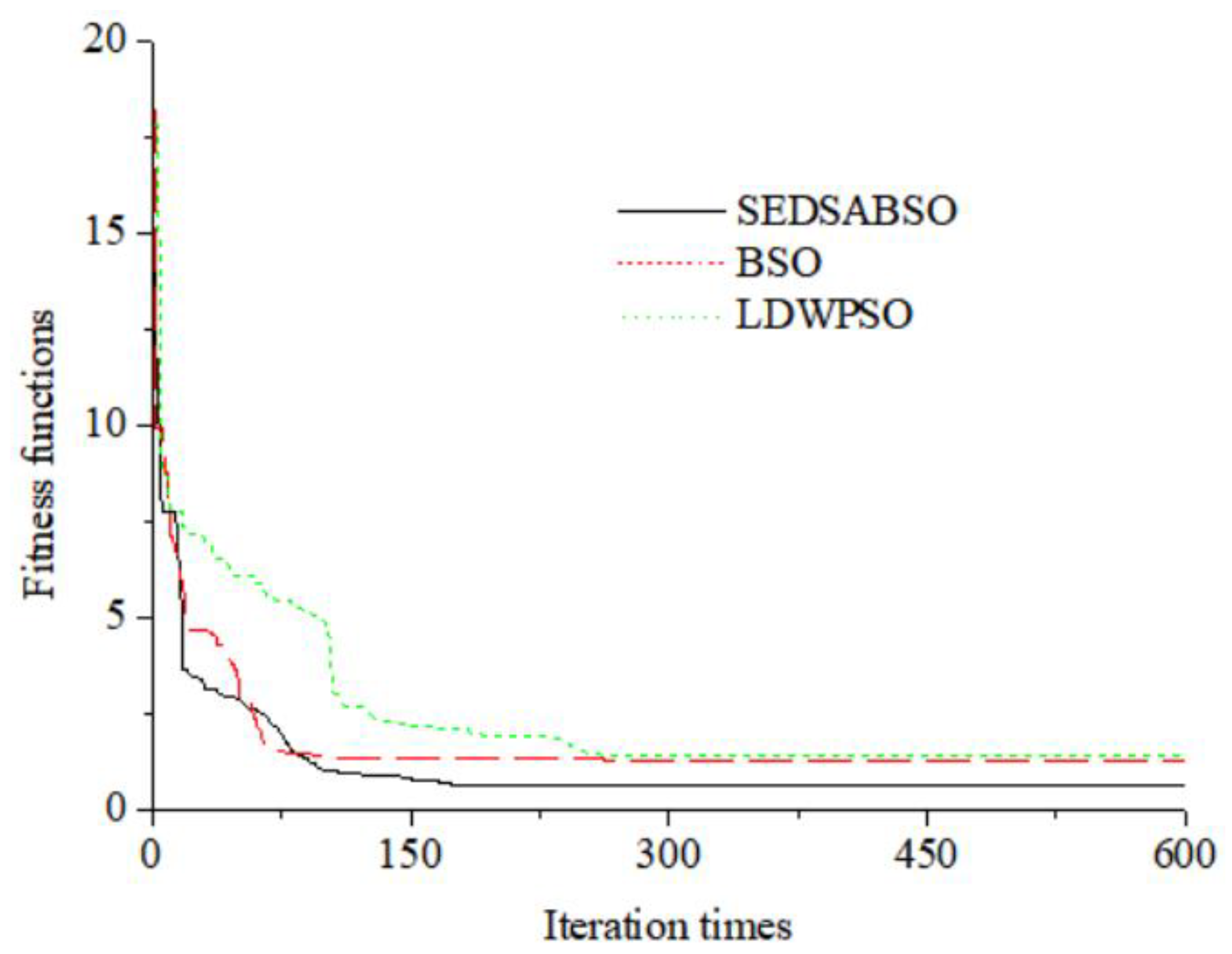
5.2. Analysis of Experimental Results

Experimental Parameter Setting

To improve the accuracy of identification of the kinetic parameters, the individual algorithms were initialized uniformly by using a small interval [22]. Then, the dynamic parameters of the robot were solved for by using the SEDSABSO algorithm, BSO algorithm, and linearly decreasing particle swarm algorithm (LDWPSO), where the number of particles N was set to 50 for the BSO and LDWPSO algorithms. The initial population N_start for SEDSABSO was set to 90, the learning factor was c₁ = c₂ = 2.0, and the inertial weight w was 0.8. The maximum number of iterations was set to 600. The initial temperature T for simulated annealing was set to 10,000, the decay scale of the annealing coefficient was set to 0.93, the step δ(t) was set to a constant value of 0.05, the adjustment factor λ was 0.9, and the ratio of the Aspen step to the distance between the whiskers, c, was set to two. After many trials, the optimal number of particle perturbations for the population was set to q = 3, f_max was 0.9, and f_min was 0.3. The iteration curves of the Aspen number for SEDSABSO and BSO are shown below:

Figure 5 shows that the number of particles N was constant during iterations of the BSO algorithm. Assuming that the maximum number of iterations was Maxdt and the duration of iteration of each particle was t, the total duration of iterations of BSO was N∗Maxdt∗t, and N∗Maxdt is equal to Area1+Area2 in the figure. For the SEDSABSO algorithm, the total iteration time was approximately the product of Figure 5. For the SEDSABSO algorithm, the total iteration time was approximately the product of the area of the class trapezoid enclosed by the dash and the horizontal axis and the time t, i.e., (Area3 + Area1) ∗ t, and since the area of Area3 was not much different from that of Area2, the computational complexity of the improved Amanita group algorithm was approximately the same as that of the standard Amanita group algorithm.

Figure 6 below shows the adaptation iteration curves of each algorithm on an Intel(R) Core(TM) i7-8550U main frequency 4.00 GHz computer with 600 iterations through Matlab 9.1:

From Figure 6, we can see that the SEDSABSO algorithm proposed in this paper converges faster and has smaller fitness values than the BSO and LDWPSO algorithms. It is clear that the SEDSABSO algorithm proposed in this paper performs best.

In order to further verify the advanced level of the SEDSABSO algorithm, this paper ran each of the above three algorithms ten times and found the average fitness and average time as follows in

Table 4. Comparison of average fitness values.

Algorithm	Average Fitness	Average Time/s
SDESABSO	0.95	16.93
BSO	1.12	17.31
LDWPSO	1.18	12.73

:

From Table 4, we can see that the average fitness values of the three algorithms after ten runs were only 0.95 for SEDSABSO, 1.12 for BSO, and 1.18 for LDWPSO, further confirming the stability and effectiveness of the proposed SEDSABSO algorithm. It can be seen that the average time of SEDSABSO was better than that of BSO, further proving the analysis in Figure 5. The difference with LDWPSO was not significant, and combined with the average fitness value, it can be seen that SEDSABSO performed optimally.

The linearized kinetic parameters of the RS010N industrial robot had a total of 21 minimum parameter sets, and the results of the kinetic parameters identified by SEDSABSO, BSO, and LDWPSO are shown in

Table 5. Identification of dynamic parameters.

Dynamic Minimum Parameters	Theoretica Value	SEDSABSO Identification Value	BSO Identification Value	LDWPSO Identification Value	SEDSABSO Absolute Error	BSO Absolute Error	LDWPSO Absolute Error
I1yy + I2yy + I3zz + 2 ∗ a1 ∗ I1x + m1 ∗ a12 − (m2 + m3) ∗ a22	16.41	16.80	16.89	16.82	−0.39	−0.48	−0.41
F1c	0	0.01	0.35	−0.20	−0.01	−0.35	0.2
F1v	0	−0.07	−0.21	0.22	0.07	0.21	−0.22
I2xx − I2yy + (m2 + m3) ∗ a22	31.83	31.77	31.92	32.21	0.06	−0.09	−0.38
I2xy	6.14	5.78	5.12	6.12	0.36	1.02	0.02
I2x − a2 ∗ (I2z − I3y)	5.76	5.54	6.22	5.83	0.22	−0.46	−0.07
I2yz	−7.82	−7.84	−7.72	−8.10	0.02	−0.1	0.28
I2zz − (m2 + m3) ∗ a22	−37.29	−37.11	−37.30	−37.94	−0.18	0.01	0.65
I2x + (m2 + m3) ∗ a22	47.37	47.29	47.52	47.27	0.08	−0.15	0.1
I2y	0.16	0.13	0.09	0.27	0.03	0.07	−0.11
F2c	0	0.14	−0.02	−0.08	−0.14	0.02	0.08
F2v	0	−0.21	−0.23	−0.03	0.21	0.23	0.03
I3xx − I3zz	−2.07	−2.20	−2.40	−1.51	0.13	0.33	−0.56
I3xy	3.34	3.24	3.25	4.57	0.10	0.09	−1.23
I3xz	−3.42	−3.34	−2.95	−4.10	−0.08	−0.47	0.68
I3yy	1.02	0.77	1.12	−0.85	0.25	−0.1	1.87
I3yz	−0.29	0.10	−0.34	−1.42	−0.39	0.05	1.13
I3x	0.15	0.11	0.12	−0.04	0.04	0.03	0.19
I3z	−0.034	0.00	−0.16	0.04	−0.034	0.126	−0.074
F3c	0	0.18	−0.13	−1.20	−0.18	0.13	1.2
F3v	0	0.06	−0.34	−0.1	−0.06	0.34	0.1

below; the absolute errors between the identified kinetic parameters and the actual parameters were also obtained.

Taking the second parameter F_1c of the set of minimum parameters of the industrial robot in Table 5 as an example, the absolute errors identified by BSO and LDWPSO were −0.35 and 0.2, respectively, while the absolute error of SEDSABSO was −0.01. On the whole, the SEDSABSO algorithm yielded the smallest error in identifying the kinetic parameters of the industrial robot, while BSO and LDWPSO The kinetic parameters identified by the SEDSABSO algorithm deviated from the theoretical kinetic parameter values, which further reflects the superiority of the SEDSABSO algorithm. The maximum absolute error in the kinetic parameters as identified by the SEDSABSO algorithm was −0.39. The overall error in identification was thus small. The SEDSABSO algorithm can thus identify the kinetic parameters of the robot.

6. Conclusions

(1)

In this paper, a new improved Beetle Antennae Search-QEDSABSO is proposed, which makes a class exponential change to the number of skinks in the iterative process of Beetle Antennae Search and effectively improved the utilization rate of Beetle Antennae Search skinks while the total number of skinks was basically unchanged. Simulation experiments showed that the proposed algorithm is more accurate and faster than the common particle swarm and Beetle Antennae Search in identifying the dynamics parameters of robots. The simulations showed that the proposed algorithm can identify the dynamical parameters of the robot with higher accuracy and faster speed than the common particle swarm and Beetle Antennae Search.

(2)

The difficulty in identifying the kinetic parameters of industrial robots lies in the sheer number of variables that need to be determined and the selection of reasonable excitation trajectories. This paper designed the relevant excitation trajectories by using the genetic algorithm and linearized the kinetic parameters of the industrial robot to improve the accuracy of their recognition.

(3)

The work provided the foundation for experiments compensating for the kinetic moments of the industrial robot. The minimum set of parameters of the kinetics could first be obtained by SymPyBotics. Then, the excitation trajectory of the industrial robot was designed by using the genetic algorithm, the data on its kinetic moments were collected, and the moments were identified by the SEDSABSO algorithm. Following this, the theoretical kinetic moments of the robot were calculated and compared with empirically sampled moments to obtain the error. Finally, this error was used to compensate for the kinetic moment of the robot.