High-Precision Displacement and Force Hybrid Modeling of Pneumatic Artificial Muscle Using 3D PI-NARMAX Model
Abstract
:1. Introduction
2. The Hysteresis and Couplings of the PAM
2.1. Testbench for PAM Characterization
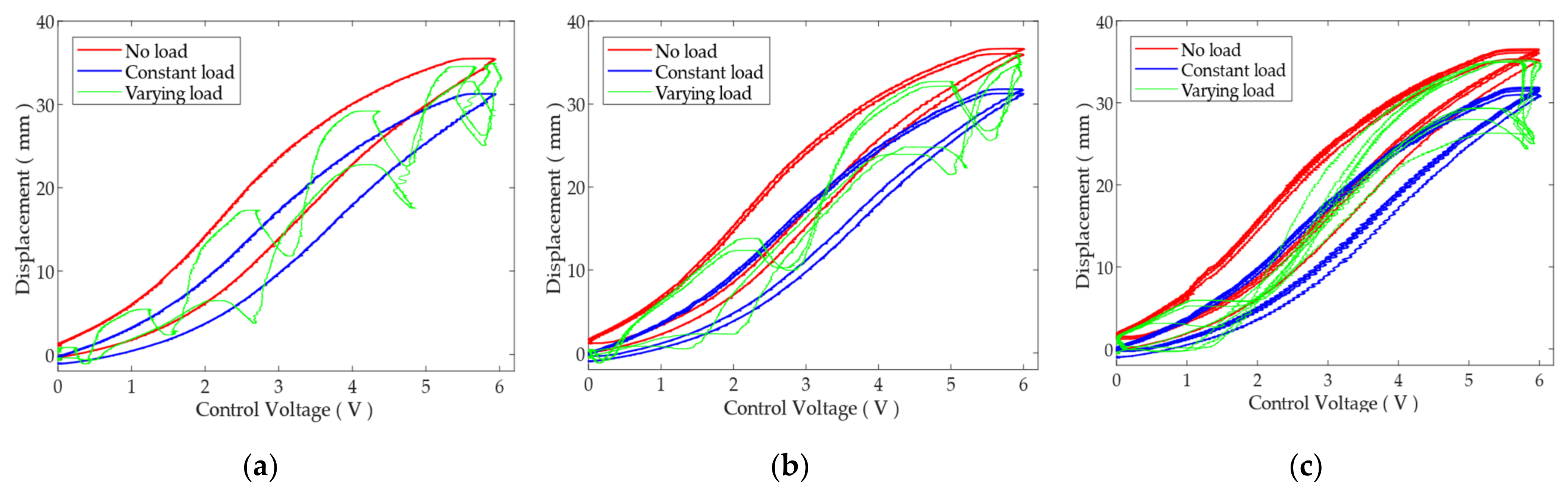
2.2. The Input-Displacement Hysteresis of the PAM
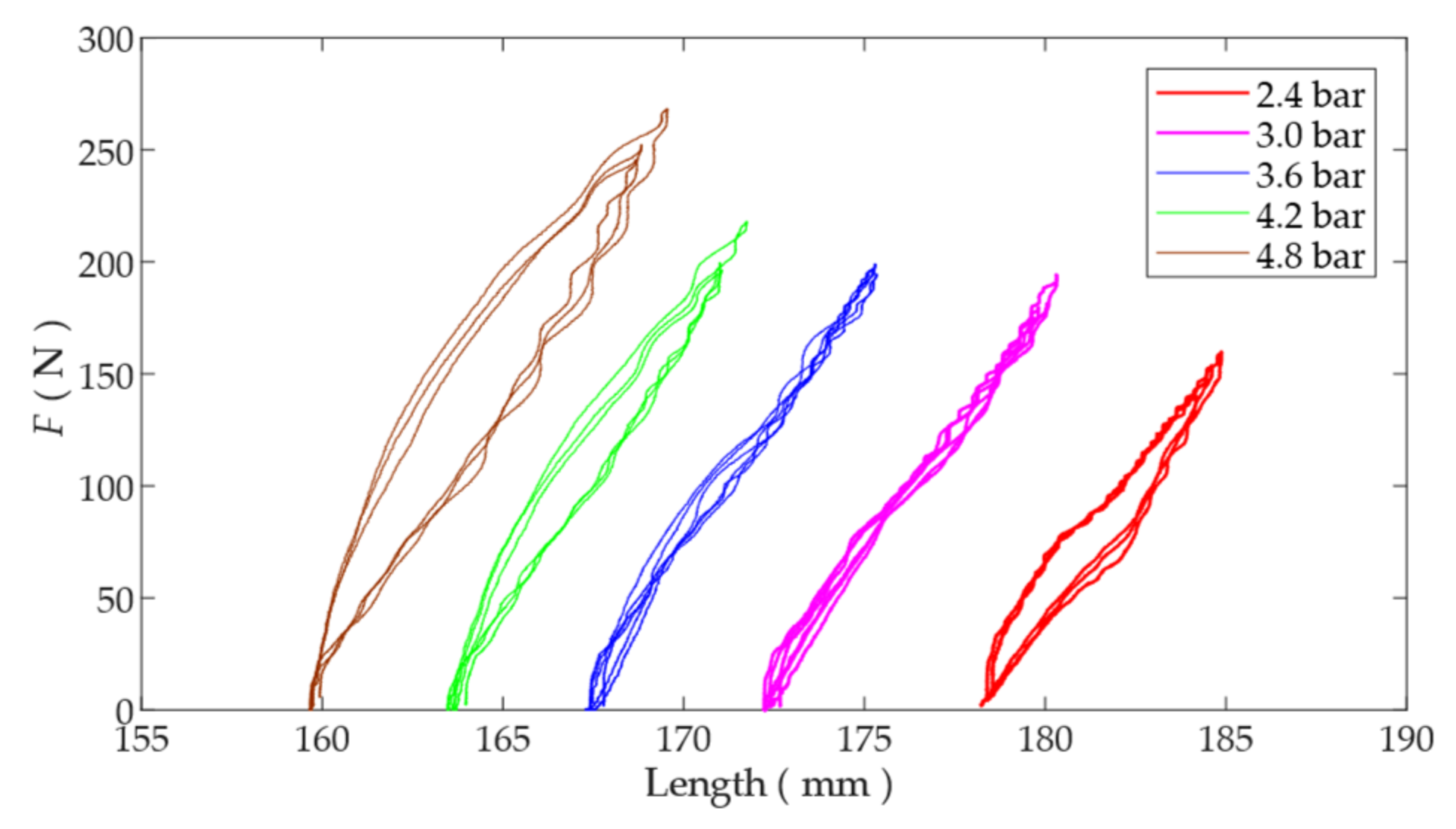
2.3. The Couplings between the Output Force and Displacement
3. MPI-NARMAX Hysteresis Model
3.1. The MPI Model
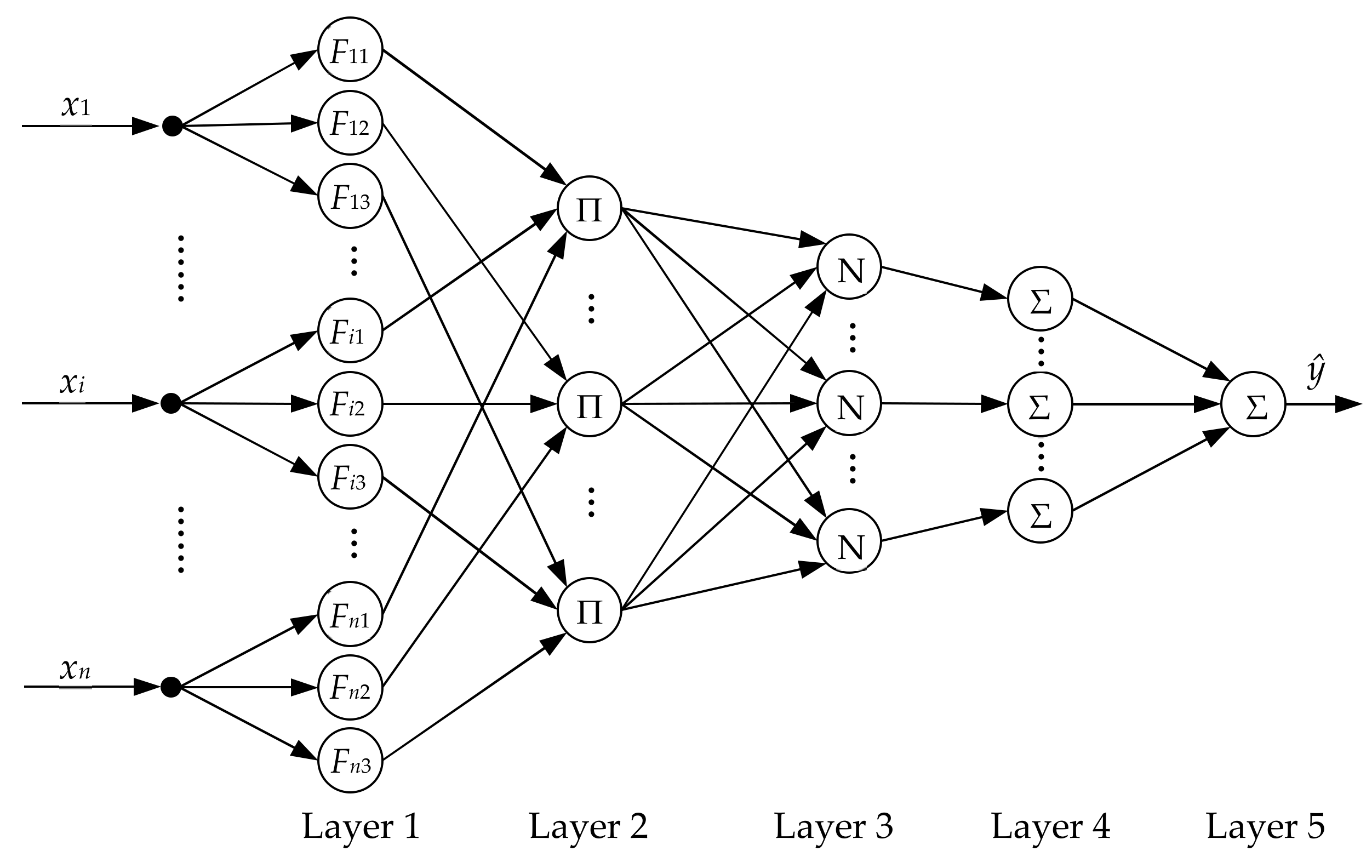
3.2. NARMAX Model Based on RFNN
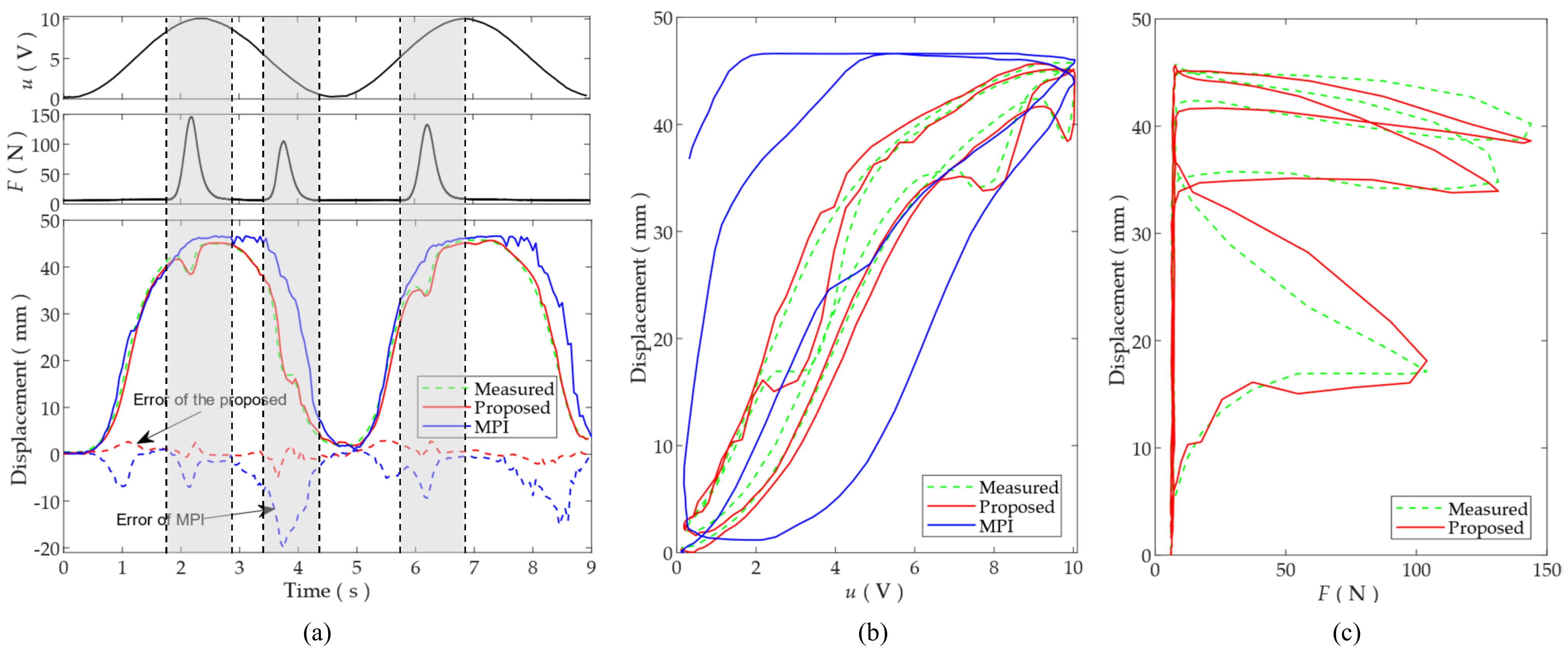
4. Experimental Results
4.1. Parameter Identification of MPI Model
4.2. Training of RFNN
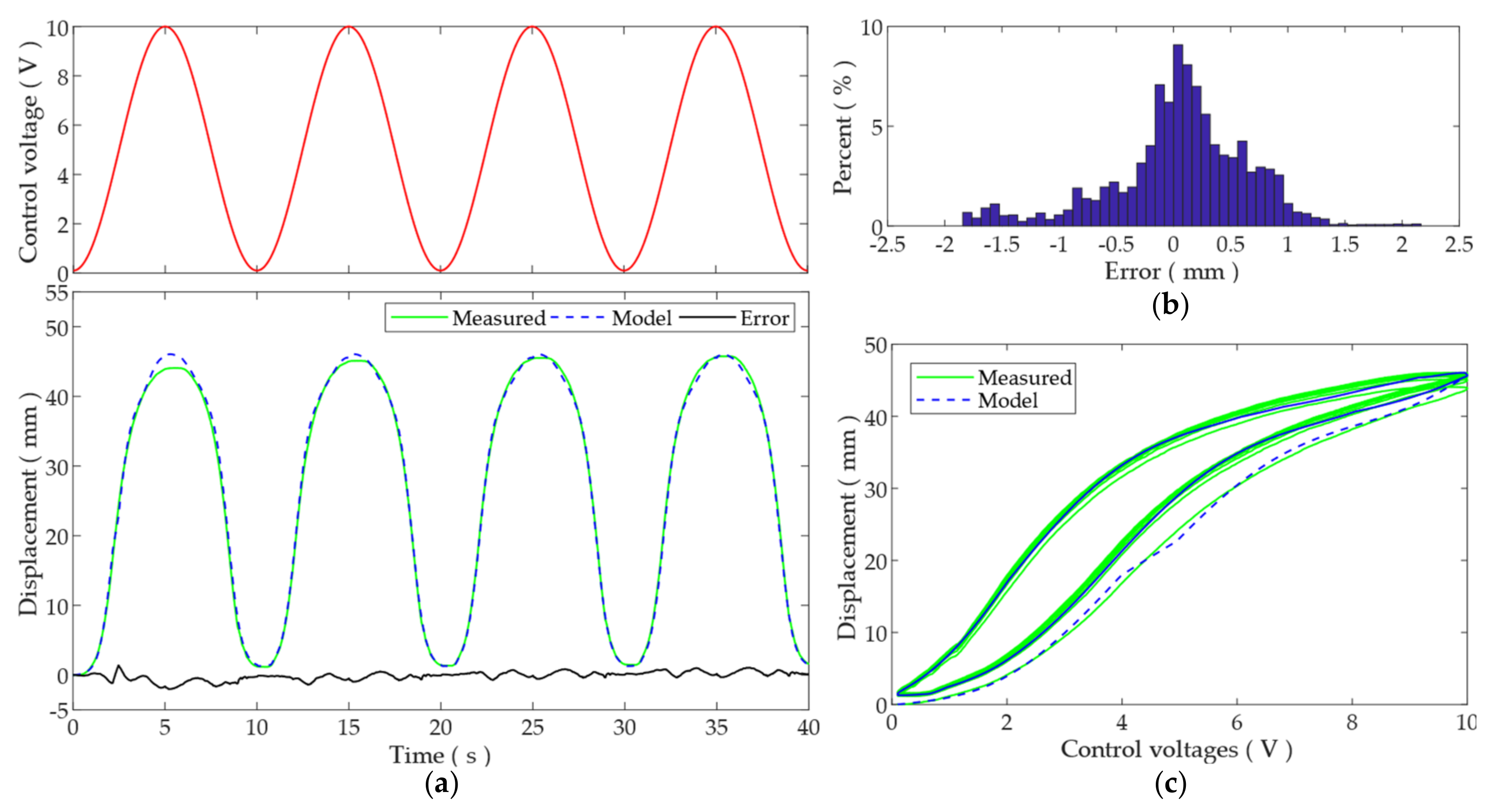
4.3. The Results of MPI-NARMAX Model
4.3.1. Varying Load
4.3.2. Cross-Checking with Different Load Statuses
- Status 1:
- 0.1 Hz sinusoidal signal actuation without load.
- Status 2:
- 0.2 Hz sinusoidal actuation with a constant load of 10.04 kg.
- Status 3:
- 0.2 Hz sinusoidal actuation with a constant load of 21.75 kg.
- Status 4:
- 0.22 Hz sinusoidal actuation with varying load, as investigated in Figure 8.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tondu, B. Modelling of the McKibben artificial muscle: A review. J. Intell. Mater. Syst. Struct. 2012, 23, 225–253. [Google Scholar] [CrossRef]
- Vo-Minh, T.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. A new approach to modeling hysteresis in a pneumatic artificial muscle using the Maxwell-slip model. IEEE/ASME Trans. Mechatron. 2011, 16, 177–186. [Google Scholar] [CrossRef]
- Tsagarakis, N.G.; Caldwell, D.G. Development and control of a ‘soft-actuated’ exoskeleton for use in physiotherapy and training. Auton. Robot. 2003, 15, 21–33. [Google Scholar] [CrossRef]
- Liu, Y.; Zang, X.; Lin, Z.; Li, W.; Zhao, J. Position control of a bio-inspired semi-active joint with direct inverse hysteresis modeling and compensation. Adv. Mech. Eng. 2016, 8, 168781401667722. [Google Scholar] [CrossRef] [Green Version]
- Meng, W.; Liu, Q.; Zhang, M.; Ai, Q.; Xie, S.Q. Compliance adaptation of an intrinsically soft ankle rehabilitation robot driven by pneumatic muscles. In Proceedings of the 2017 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Munich, Germany, 3–7 July 2017; pp. 82–87. [Google Scholar]
- Yang, H.; Xiang, C.; Hao, L.; Zhao, L.; Xue, B. Research on PSA-MFAC for a novel bionic elbow joint system actuated by pneumatic artificial muscles. J. Mech. Sci. Technol. 2017, 31, 3519–3529. [Google Scholar] [CrossRef]
- Minh, T.V.; Kamers, B.; Ramon, H.; Van Brussel, H. Modeling and control of a pneumatic artificial muscle manipulator joint—Part I: Modeling of a pneumatic artificial muscle manipulator joint with accounting for creep effect. Mechatronics 2012, 22, 923–933. [Google Scholar] [CrossRef]
- Minh, T.V.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. Cascade position control of a single pneumatic artificial muscle-mass system with hysteresis compensation. Mechatronics 2010, 20, 402–414. [Google Scholar] [CrossRef]
- Sofla, M.S.; Sadigh, M.J.; Zareinejad, M. Design and dynamic modeling of a continuum and compliant manipulator with large workspace. Mech. Mach. Theory 2021, 164, 104413. [Google Scholar] [CrossRef]
- Shakiba, S.; Ourak, M.; Poorten, E.V.; Ayati, M.; Yousefi-Koma, A. Modeling and compensation of asymmetric rate-dependent hysteresis of a miniature pneumatic artificial muscle-based catheter. Mech. Syst. Signal Processing 2021, 154, 107532. [Google Scholar] [CrossRef]
- Liang, D.; Sun, N.; Wu, Y.; Chen, Y.; Fang, Y.; Liu, L. Energy-based Motion Control for Pneumatic Artificial Muscle-Actuated Robots With Experiments. IEEE Trans. Ind. Electron. 2021, 2021, 3095788. [Google Scholar] [CrossRef]
- Qin, Y.; Xu, Y.; Han, J. Hysteresis Compensation of Pneumatic Artificial Muscle ActuatedAssistive Robot for the Elbow Joint. Jiqiren/Robot 2021, 43, 453–462. (In Chinese) [Google Scholar] [CrossRef]
- Qin, Y.; Tian, Y.; Zhang, D.; Shirinzadeh, B.; Fatikow, S. A novel direct inverse modeling approach for hysteresis compensation of piezoelectric actuator in feedforward applications. IEEE/ASME Trans. Mechatron. 2013, 18, 981–989. [Google Scholar] [CrossRef]
- Mohareb, S.A.; Alsharkawi, A.; Zgoul, M. Hysteresis modeling of a pam system using anfis. Actuators 2021, 10, 280. [Google Scholar] [CrossRef]
- Kogiso, K.; Sawano, K.; Itto, T.; Sugimoto, K. Identification procedure for McKibben pneumatic artificial muscle systems. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 3714–3721. [Google Scholar]
- Sofla, M.S.; Sadigh, M.J.; Zareinejad, M. Precise dynamic modeling of pneumatic muscle actuators with modified Bouw-Wen hysteresis model. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 1449–1457. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Ma, T.; Hao, L.; Li, Z. A comprehensive dynamic model for pneumatic artificial muscles considering different input frequencies and mechanical loads. Mech. Syst. Signal Processing 2021, 148, 107133. [Google Scholar] [CrossRef]
- Konda, R.; Zhang, J. Hysteresis with lonely stroke in artificial muscles: Characterization, modeling, and inverse compensation. Mech. Syst. Signal Processing 2022, 164, 108240. [Google Scholar] [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems Part I: Deterministic non-linear systems. Int. J. Control 1985, 41, 303–328. [Google Scholar] [CrossRef]
- Gu, Y.; Li, B.; Meng, Q. Hybrid interpretable predictive machine learning model for air pollution prediction. Neurocomputing 2022, 468, 123–136. [Google Scholar] [CrossRef]
- Araluce, J.; Bergasa, L.M.; Ocaña, M.; López-Guillén, E.; Revenga, P.A.; Felipe Arango, J.; Pérez, O. Gaze focalization system for driving applications using openface 2.0 toolkit with NARMAX algorithm in accidental scenarios. Sensors 2021, 21, 6262. [Google Scholar] [CrossRef]
- Lee, C.H.; Teng, C.C. Identification and control of dynamic systems using recurrent fuzzy neural networks. IEEE Trans. Fuzzy Syst. 2000, 8, 349–366. [Google Scholar] [CrossRef]



| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| ri | 0 | 0.0101 | 0.0296 | 0.2596 | 0.4318 | 0.8309 | 1.6003 | 1.9544 | 3.9537 | 4.95 |
| ki | 3.5838 | −3.8779 | 0.3084 | 0.1117 | −0.0887 | −0.0033 | −0.0116 | −0.0208 | −0.0429 | 0.0315 |
| di | −0.3435 | 0.643 | −0.1711 | 0.1878 | −0.0425 | 0.0359 | 0.046 | 0.0461 | −0.0298 | 0.0698 |
| ai | −8.97e-04 | 0 | 0.0411 | 0 | −0.6712 | 0 | 4.4945 | 0 | 2.3917 | 0 |
| Status 1 | Status 2 | Status 3 | Status 4 | |
|---|---|---|---|---|
| MPI-1 | 0.5675 | 6.8589 | 10.0609 | 3.8926 |
| MPI-2 | 4.6434 | 0.1716 | 3.2333 | 3.6108 |
| MPI-3 | 7.8112 | 3.2266 | 0.1628 | 6.7443 |
| MPI-NARMAX | 0.3094 | 0.2887 | 0.3676 | 0.9304 |
| Status 1 | Status 2 | Status 3 | Status 4 | |
|---|---|---|---|---|
| MPI-1 | 0.6577 | 5.4060 | 6.5387 | 4.4845 |
| MPI-2 | 2.9424 | 0.2348 | 1.9331 | 2.3808 |
| MPI-3 | 4.5439 | 1.9357 | 0.2146 | 3.8913 |
| MPI-NARMAX | 0.3997 | 0.3887 | 0.4668 | 1.2138 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Xu, Y.; Shen, C.; Han, J. High-Precision Displacement and Force Hybrid Modeling of Pneumatic Artificial Muscle Using 3D PI-NARMAX Model. Actuators 2022, 11, 51. https://doi.org/10.3390/act11020051
Qin Y, Xu Y, Shen C, Han J. High-Precision Displacement and Force Hybrid Modeling of Pneumatic Artificial Muscle Using 3D PI-NARMAX Model. Actuators. 2022; 11(2):51. https://doi.org/10.3390/act11020051
Chicago/Turabian StyleQin, Yanding, Yuankai Xu, Chenyu Shen, and Jianda Han. 2022. "High-Precision Displacement and Force Hybrid Modeling of Pneumatic Artificial Muscle Using 3D PI-NARMAX Model" Actuators 11, no. 2: 51. https://doi.org/10.3390/act11020051
APA StyleQin, Y., Xu, Y., Shen, C., & Han, J. (2022). High-Precision Displacement and Force Hybrid Modeling of Pneumatic Artificial Muscle Using 3D PI-NARMAX Model. Actuators, 11(2), 51. https://doi.org/10.3390/act11020051






