Development of a Parallel Dual-Stage Compliant Nanopositioning System
Abstract
1. Introduction
2. Design of PDCNS
3. Analytical Modelling
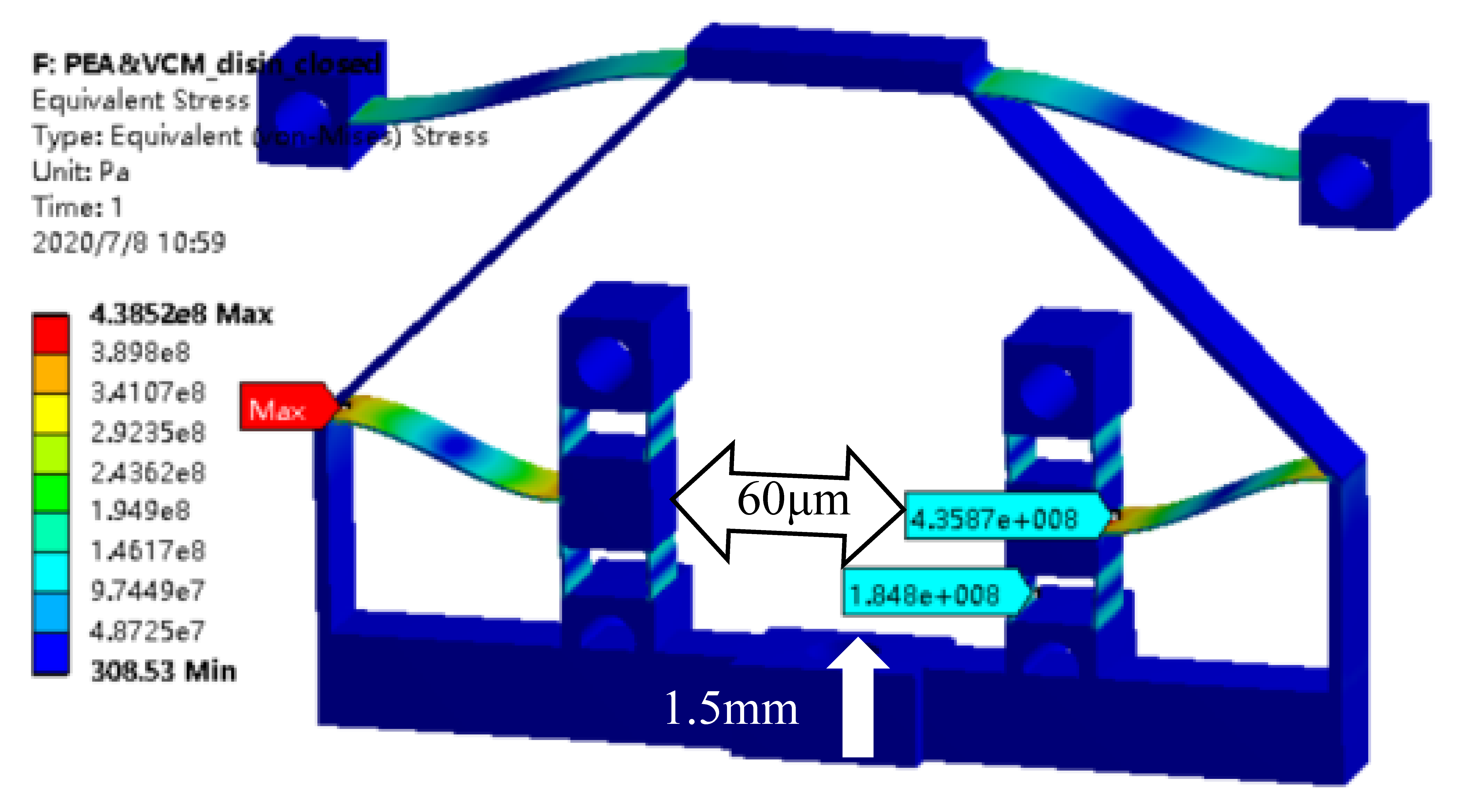
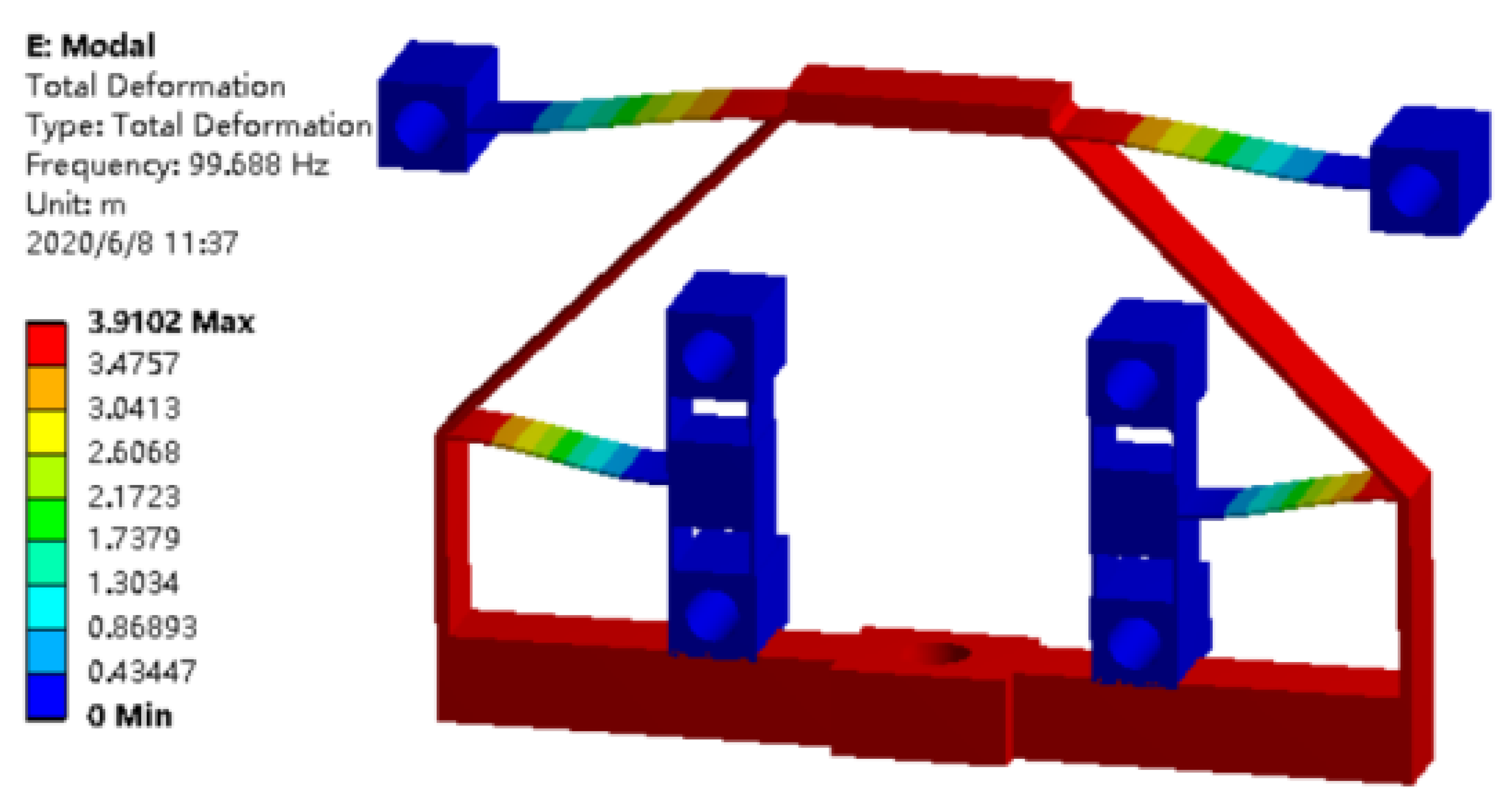
4. Simulation Analysis
5. Experimental Analysis
5.1. Kinematic Investigation
5.2. Stroke and Hysteresis Investigation
5.3. Motion Resolution Investigation
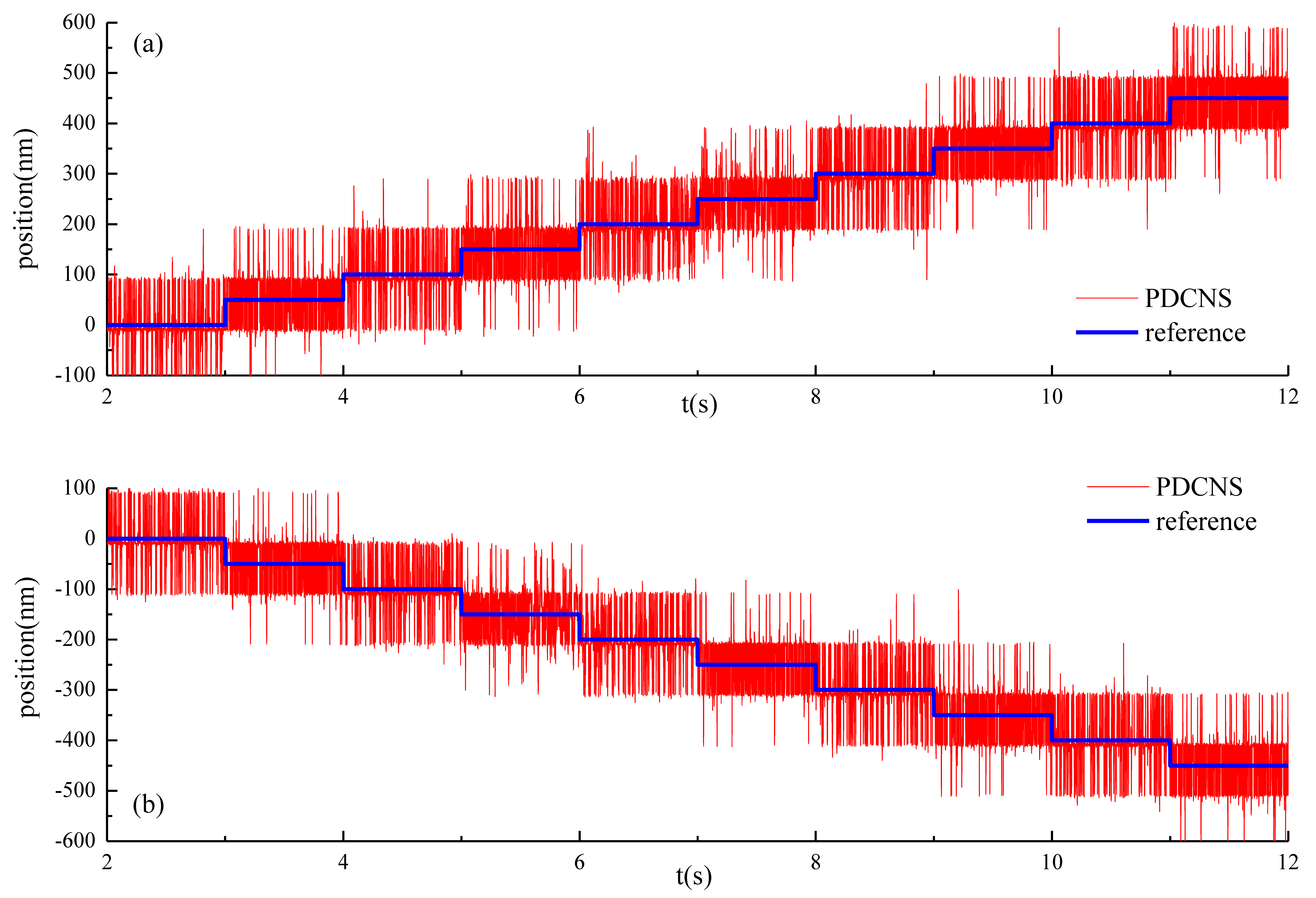
5.4. Closed-Loop Motion Investigation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nikooienejad, N.; Maroufi, M.; Moheimani, S.O.R. Iterative Learning Control for Video-Rate Atomic Force Microscopy. IEEE/ASME Trans. Mechatron. 2021, 26, 2127–2138. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, X.; Duan, F.; Zhu, Z.; Ju, B. Design and Adaptive Terminal Sliding Mode Control of a Fast Tool Servo System for Diamond Machining of Freeform Surfaces. IEEE Trans. Ind. Electron. 2019, 66, 4912–4922. [Google Scholar] [CrossRef]
- Wan, N.; Wen, J.; Hu, Y.; Kan, J.; Li, J. A Parasitic Type Piezoelectric Actuator with an Asymmetrical Flexure Hinge Mechanism. Microsyst. Technol. 2020, 26, 917–924. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Q. A Survey of Force-Assisted Robotic Cell Microinjection Technologies. IEEE Trans. Automat. Sci. Eng. 2019, 16, 931–945. [Google Scholar] [CrossRef]
- Chen, X.; Deng, Z.; Hu, S.; Gao, J.; Gao, X. Designing a Novel Model of 2-DOF Large Displacement with a Stepwise Piezoelectric-Actuated Microgripper. Microsyst. Technol. 2020, 26, 2809–2816. [Google Scholar] [CrossRef]
- Eleftheriou, E. Nanopositioning for Storage Applications. Annu. Rev. Control 2012, 36, 244–254. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, W.; Zhu, Z.; Zhu, L. Design, Assessment, and Trajectory Control of a Novel Decoupled Robotic Nanomanipulator. IEEE/ASME Trans. Mechatron. 2022, 1–12. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, W.; Zhu, Z.; Zhu, L. Development of a New Compliant Active-Force Support System. IEEE/ASME Trans. Mechatron. 2022, 27, 372–382. [Google Scholar] [CrossRef]
- Tao, Y.; Li, H.; Zhu, L. Time/Space-Separation-Based Gaussian Process Modeling for the Cross-Coupling Effect of a 2-DOF Nanopositioning Stage. IEEE/ASME Trans. Mechatron. 2021, 26, 2186–2194. [Google Scholar] [CrossRef]
- Fleming, A.J.; Aphale, S.; Moheimani, S.O.R. A New Method for Robust Damping and Tracking Control of Scanning Probe Microscope Positioning Stages. IEEE Trans. Nanotechnol. 2010, 9, 438–448. [Google Scholar] [CrossRef]
- Yong, Y.K.; Moheimani, S.O.R.; Kenton, B.J.; Leang, K.K. Invited review article: High-Speed Flexure-Guided Nanopositioning: Mechanical Design and Control Issues. Rev. Sci. Instrum. 2012, 83, 121101. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.K.; Lee, T.H.; Zhou, H.X. Micro-Positioning of Linear-Piezoelectric Motors Based on a Learning Nonlinear PID Controller. IEEE/ASME Trans. Mechatron. 2001, 6, 428–436. [Google Scholar] [CrossRef]
- Ho, S.T.; Jan, S.J. A Piezoelectric Motor for Precision Positioning Applications. Precis. Eng. 2016, 43, 285–293. [Google Scholar] [CrossRef]
- Li, J.P.; Huang, H.; Morita, T. Stepping Piezoelectric Actuators with Large Working Stroke for Nano-positioning Systems: A Review. Sens. Actuators A Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Delibas, B.; Koc, B. A Method to Realize Low Velocity Movability and Eliminate Friction Induced Noise in Piezoelectric Ultrasonic Motors. IEEE/ASME Trans. Mechatron. 2020, 25, 2677–2687. [Google Scholar] [CrossRef]
- Mamun, A.A.; Mareels, I.; Lee, T.H.; Tay, A. Dual Stage Actuator Control in Hard Disk Drive—A review. In Proceedings of the Industrial Electronics Conference, Roanoke, VA, USA, 2–6 November 2003. [Google Scholar]
- Zhu, Z.; Du, H.; Zhou, R.; Huang, P.; Zhu, W.; Guo, P. Design and Trajectory Tracking of a Nanometric Ultra-Fast Tool Servo. IEEE Trans. Ind. Electron. 2020, 67, 432–441. [Google Scholar] [CrossRef]
- Gutierrez, H.M.; Ro, P.I. Sliding-Mode Control of a Nonlinear-Input System: Application to a Magnetically Levitated Fast-Tool Servo. IEEE Trans. Ind. Electron. 1998, 45, 921–927. [Google Scholar] [CrossRef][Green Version]
- Yang, X.; Zhu, W. Design, Analysis and Test of a Novel Self-Sensing Fast Tool Servo. IEEE Trans. Ind. Informat. 2020, 16, 4447–4455. [Google Scholar] [CrossRef]
- Wang, G.; Xu, Q. Design and Precision Position/Force Control of a Piezo-Driven Microinjection System. IEEE/ASME Trans. Mechatron. 2017, 22, 1744–1754. [Google Scholar] [CrossRef]
- Permana, S.; Grant, E.; Walker, G.M.; Yoder, J.A. A Review of Automated Microinjection Systems for Single Cells in the Embryogenesis Stage. IEEE/ASME Trans. Mechatron. 2016, 21, 2391–2404. [Google Scholar] [CrossRef]
- Xu, Q. Design and Development of Flexure-Based Dual-Stage Nanopositioning System with Minimum Interference Behavior. IEEE Trans. Autom. Sci. Eng. 2012, 9, 554–563. [Google Scholar] [CrossRef]
- Michellod, Y.; Mullhaupt, P.; Gillet, D. Strategy for the Control of a Dual-Stage Nano-Positioning System with a Single Metrology. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006; pp. 1–8. [Google Scholar]
- Dong, W.; Tang, J.; ElDeeb, Y. Design of a Linear-Motion Dual-Stage Actuation System for Precision Control. Smart Mater. Struct. 2009, 18, 095035. [Google Scholar] [CrossRef]
- Zhu, H.; Pang, C.K.; Teo, T.J. Integrated Servo-Mechanical Design of a Fine Stage for a Coarse/Fine Dual-Stage Positioning System. IEEE/ASME Trans. Mechatron. 2016, 21, 329–338. [Google Scholar] [CrossRef]
- Long, Y.Q.; Bao, S.H.; Yuan, S. Structural Mechanics, 3rd ed.; The Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Zhu, W.; Zhu, Z.; Shi, Y.; Wang, X.; Guan, K.; Ju, B. Design, Modeling, Analysis and Testing of a Novel Piezo-Actuated XY Compliant Mechanism for Large Workspace Nano-Positioning. Smart Mater. Struct. 2016, 25, 115033. [Google Scholar] [CrossRef]
- Koseki, Y.; Tanikawa, T.; Koyachi, N.; Arai, T. Kinematic Analysis of Translational 3-DOF Micro Parallel Mechanism Using Matrix Method. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems, Takamatsu, Japan, 31 October–5 November 2000; pp. 786–792. [Google Scholar]
- Ling, M.; Cao, J.; Li, Q.; Zhuang, J. Design, Pseudo-Static Model and PVDF-Based Motion Sensing of a Piezo-Actuated XYZ Flexure Manipulator. IEEE/ASME Trans. Mechatron. 2018, 23, 2837–2848. [Google Scholar] [CrossRef]
- Zhu, W.; Zhu, Z.; To, S.; Liu, Q.; Ju, B.; Zhou, X. Redundantly Piezo-Actuated XYθz Compliant Mechanism for Nano-Positioning Featuring Simple Kinematics, Bi-Directional Motion and Enlarged Workspace. Smart Mater. Struct. 2016, 25, 125002. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, Y.; Liu, C.; Wang, F.; Liu, X.; Shirinzadeh, B.; Zhang, D. Design and Control Methodology of a 3-DOF Flexure-Basedmechanism for Micro/Nano Positioning. Robot. Comput-Integr. Manuf. 2015, 32, 93–105. [Google Scholar] [CrossRef]
- Chen, M. Research on Mechanical Properties Test and Dynamic Material Model of TC4 Titanium Alloy. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2012. [Google Scholar]
- Wang, D.; Yang, Q.; Dong, H. A Monolithic Compliant Piezoelectric-Driven Microgripper: Design, Modeling, and Testing. IEEE/ASME Trans. Mechatron. 2013, 18, 138–147. [Google Scholar] [CrossRef]




mm | mm | mm | mm | mm | mm | mm | mm | mm | mm | mm |
| 43.98 | 10 | 22.75 | 1.5 | 25 | 0.5 | 5 | 0.5 | 55.13 | 1 | 35 |
mm | mm | mm | mm | mm | r ° | mm | E ×1011 Pa | μ | ρ kg/m3 | |
| 0.5 | 15 | 3.5 | 10 | 10 | 45° | 10 | 1.167 | 0.36 | 4414 | |
| Amplification Ratio |
Input Stiffness (N/μm) |
Stress Coefficient (Mpa/μm) | ||||
|---|---|---|---|---|---|---|
| anal. | 0.514 | 0.997 | 2.41 | 0.0249 | 3.49 | 0.279 |
| ANSYS | 0.524 | 0.993 | 2.02 | 0.0256 | 3.11 | 0.287 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Ji, L.; Shang, Y.; Zhu, W.; Li, S. Development of a Parallel Dual-Stage Compliant Nanopositioning System. Actuators 2022, 11, 136. https://doi.org/10.3390/act11050136
Yang X, Ji L, Shang Y, Zhu W, Li S. Development of a Parallel Dual-Stage Compliant Nanopositioning System. Actuators. 2022; 11(5):136. https://doi.org/10.3390/act11050136
Chicago/Turabian StyleYang, Xu, Lichao Ji, Ying Shang, Wule Zhu, and Shizhen Li. 2022. "Development of a Parallel Dual-Stage Compliant Nanopositioning System" Actuators 11, no. 5: 136. https://doi.org/10.3390/act11050136
APA StyleYang, X., Ji, L., Shang, Y., Zhu, W., & Li, S. (2022). Development of a Parallel Dual-Stage Compliant Nanopositioning System. Actuators, 11(5), 136. https://doi.org/10.3390/act11050136






