Development of a Novel Dual Servo Magnetic Levitation Stage
Abstract
1. Introduction
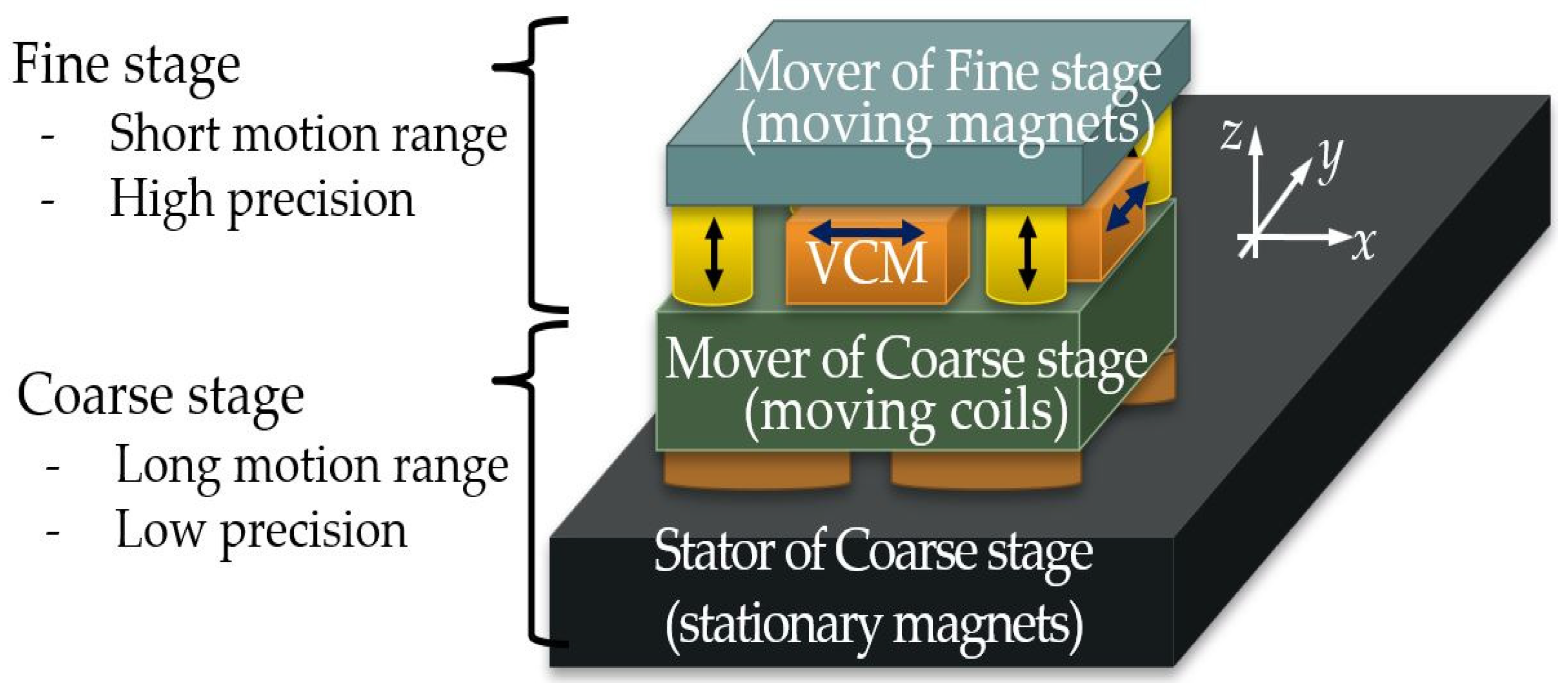
2. Structure of the Dual Servo Maglev Stage
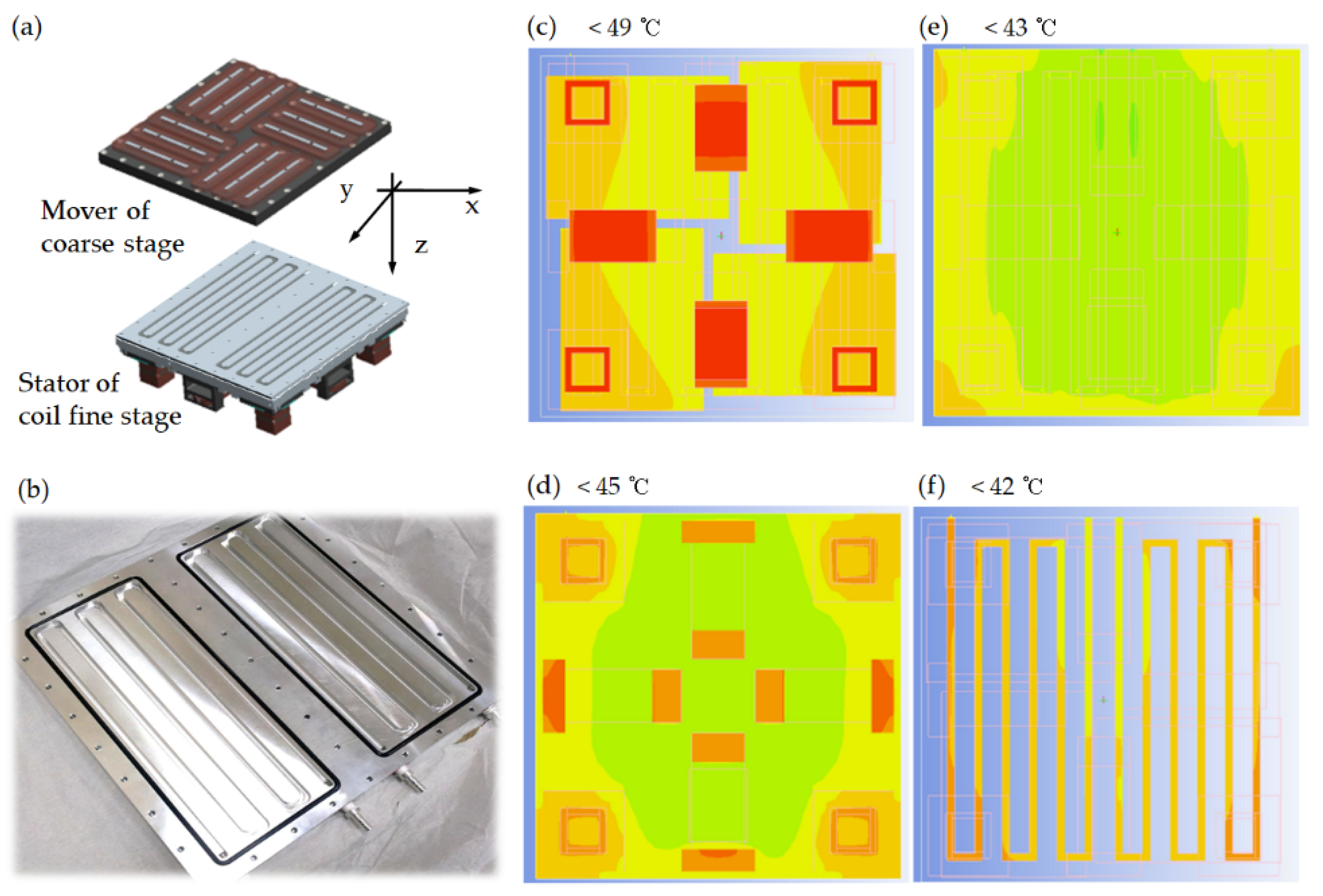
2.1. Fine Stage
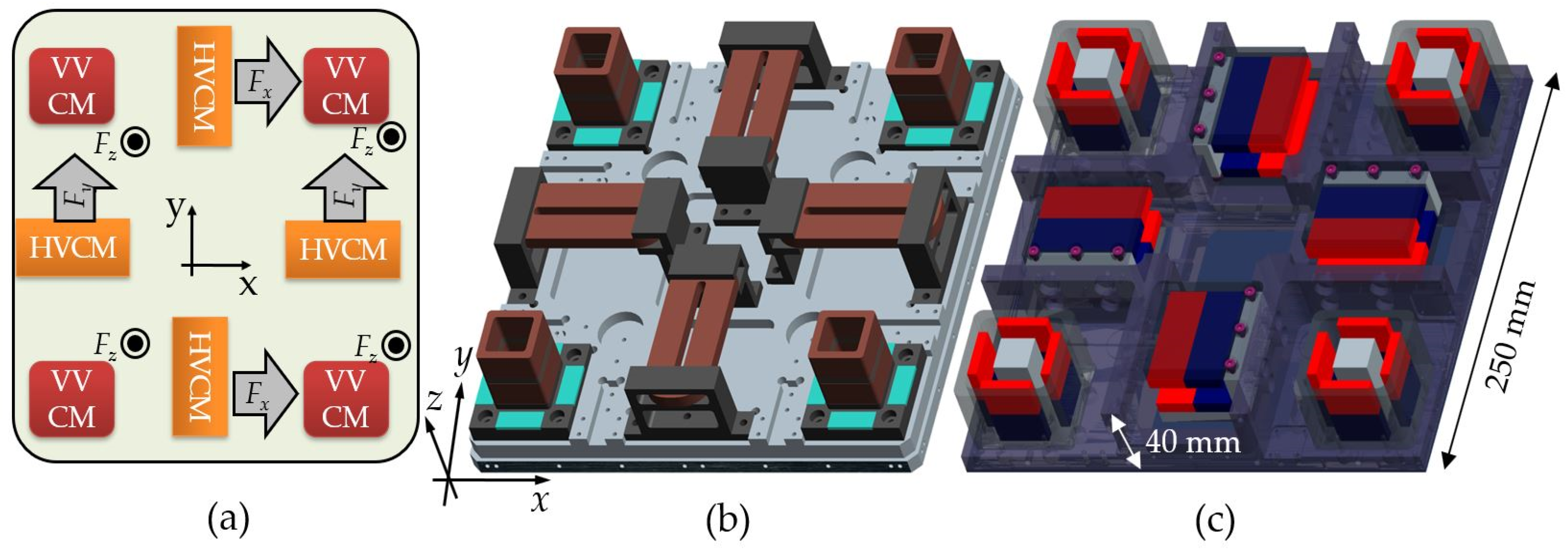
2.2. Coarse Stage
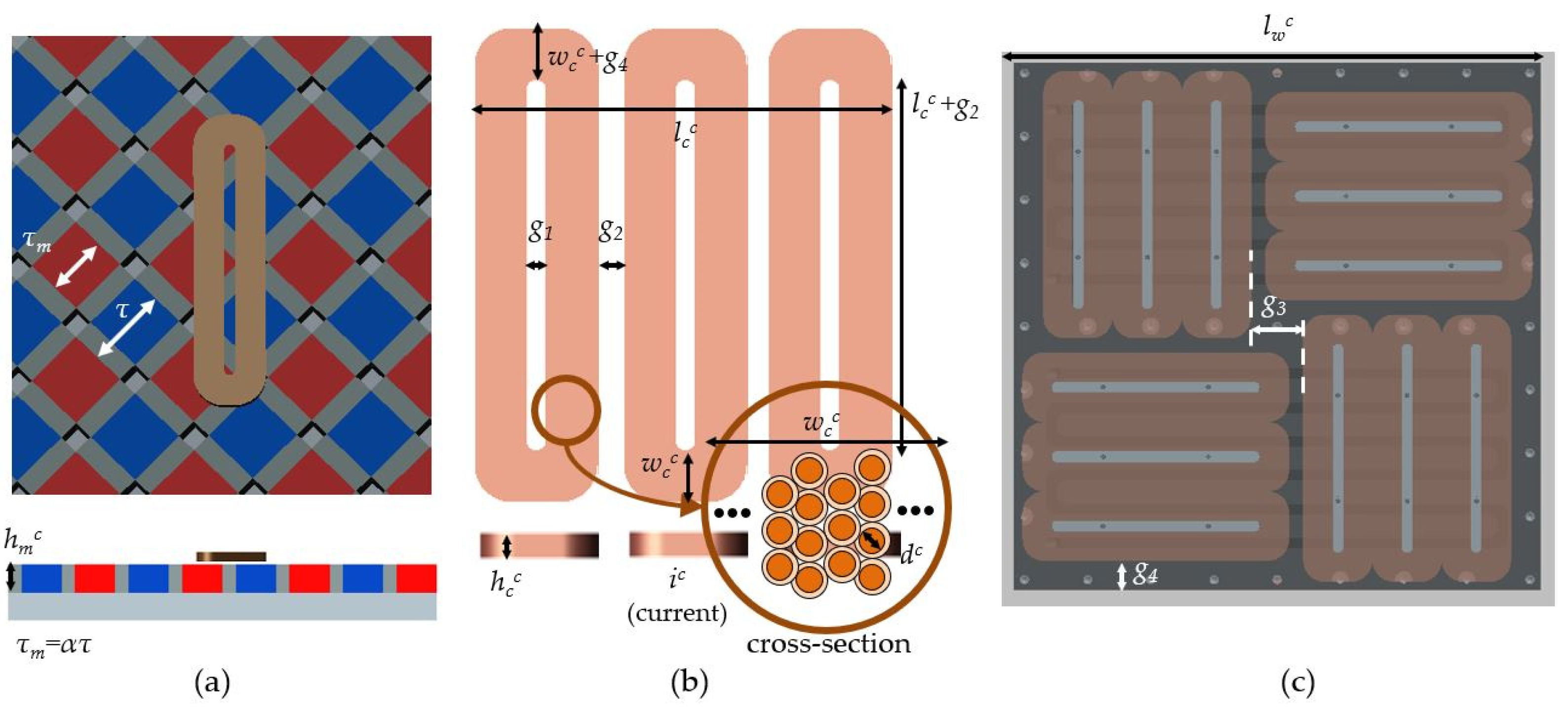
2.2.1. Coil and Magnet Array Topology
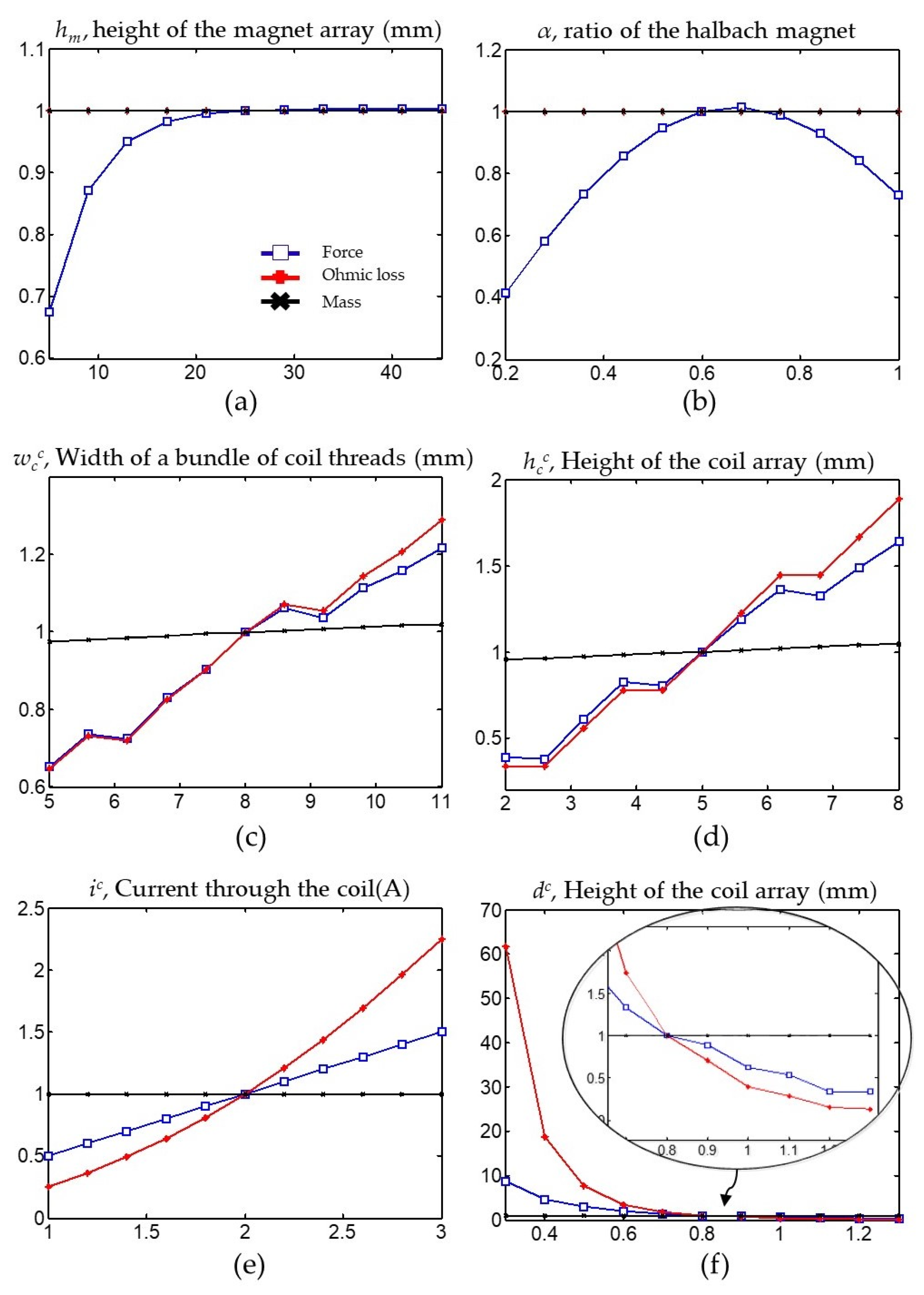
2.2.2. Design Parameter Analysis
2.2.3. Optimization
3. Realization of the Dual Servo Maglev Stage
3.1. Heat Exchanger
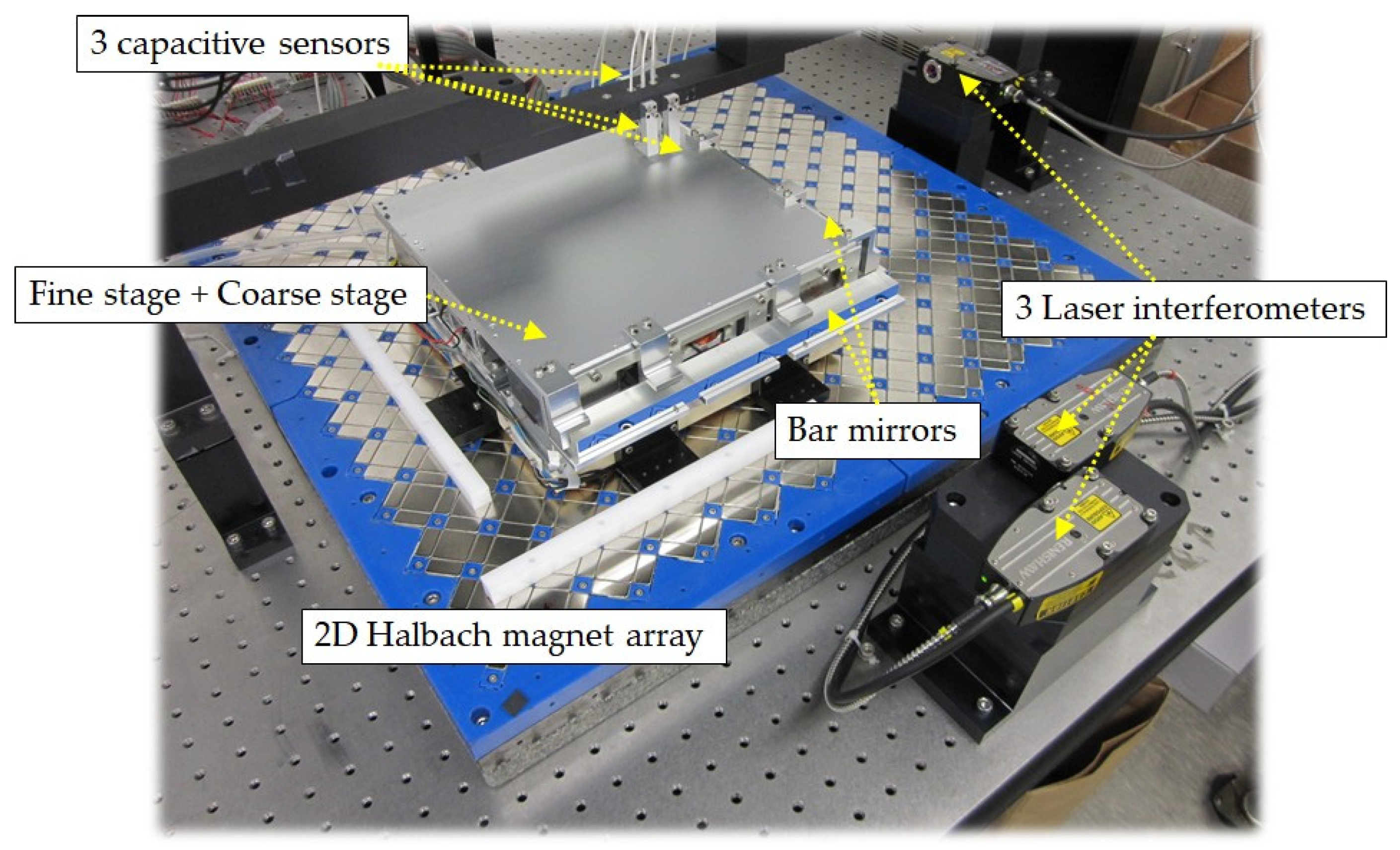
3.2. Experiment Setup
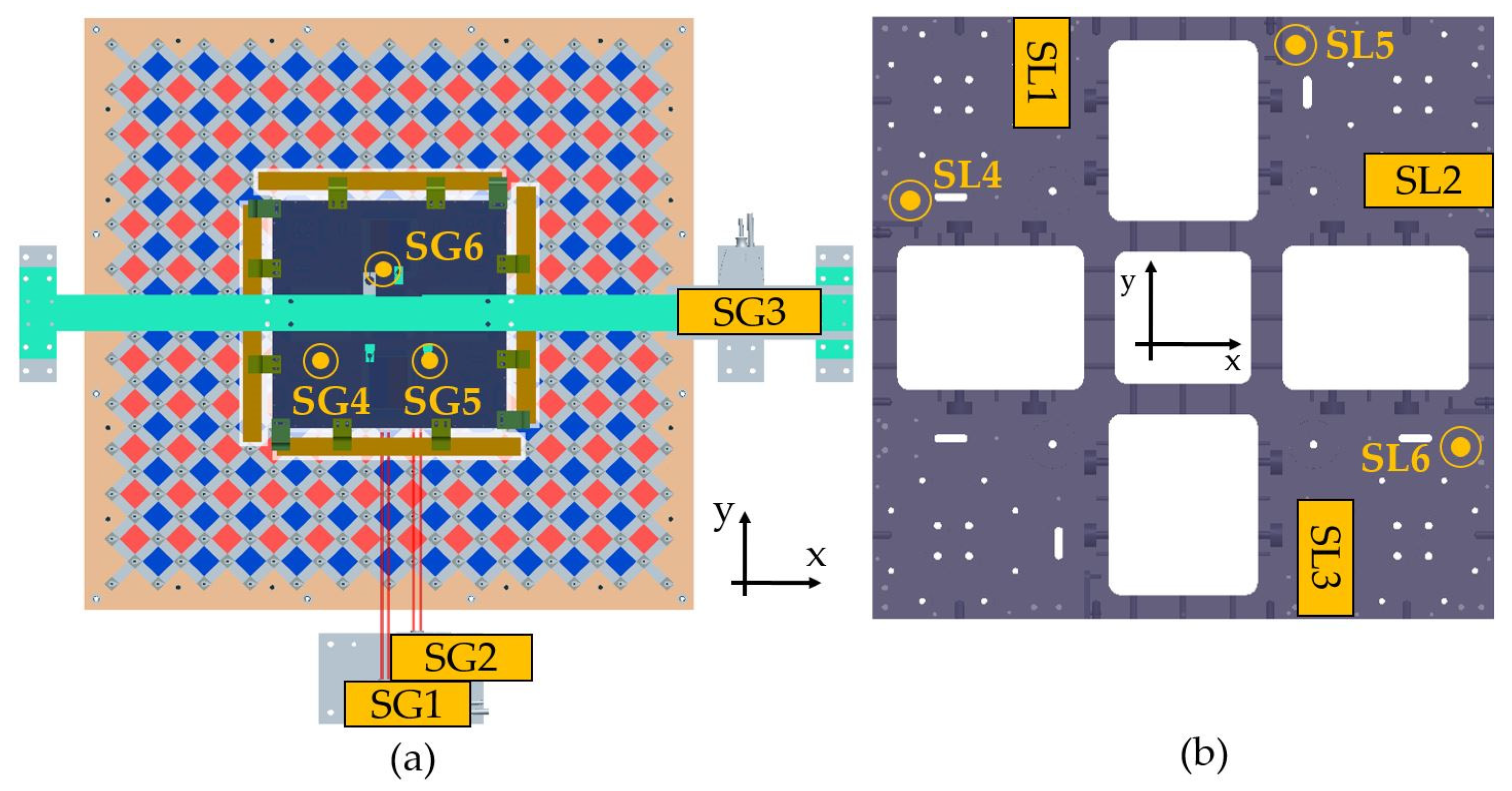
3.2.1. Sensors
3.2.2. Electric Devices and Data Acquisition
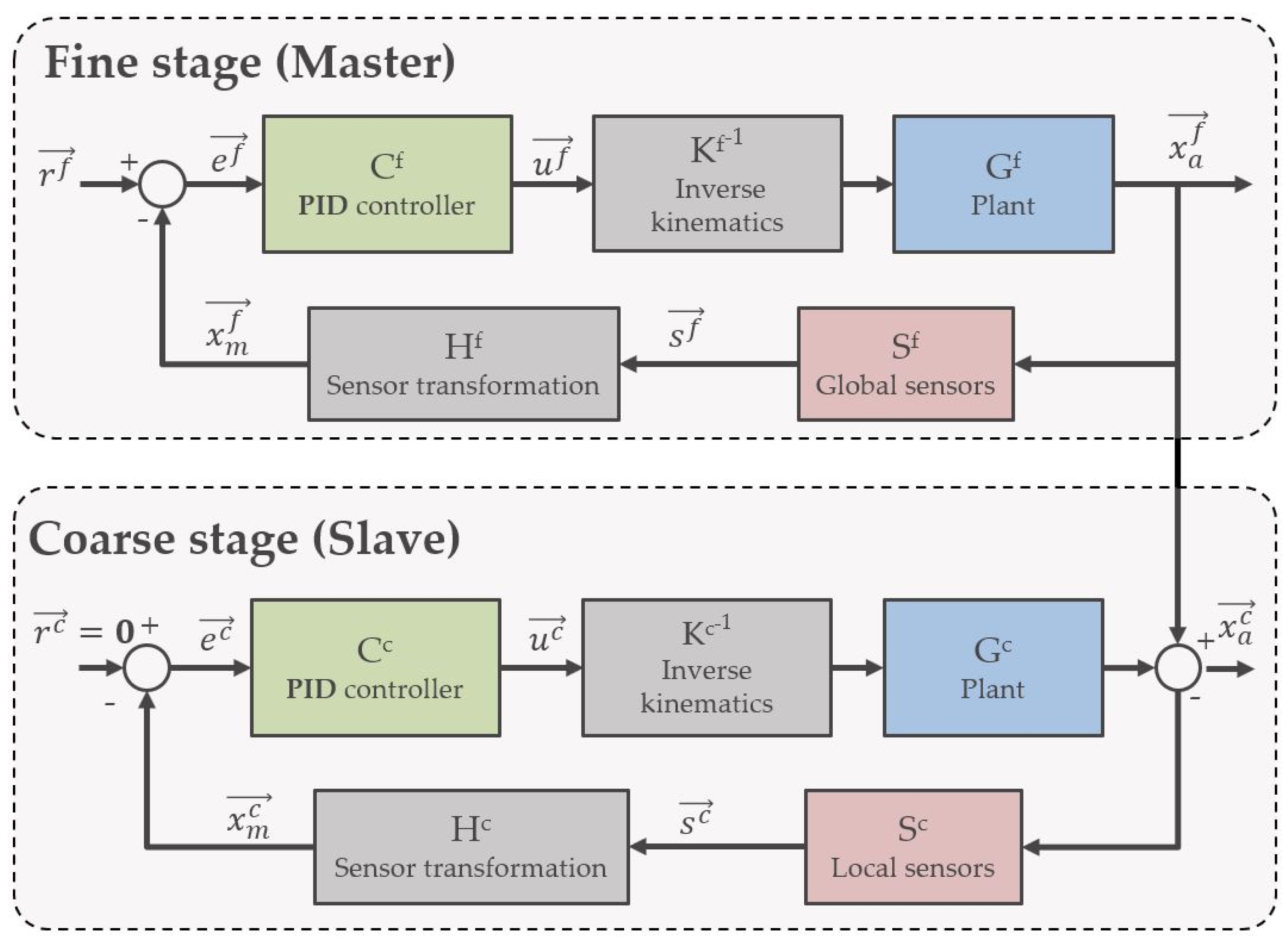
3.2.3. Control Strategy
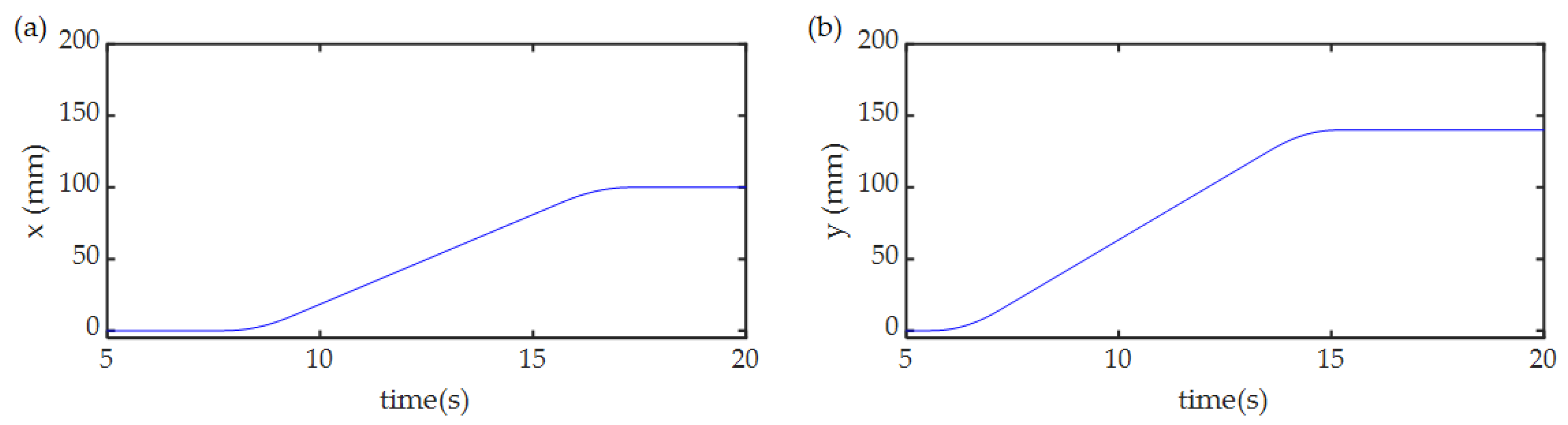
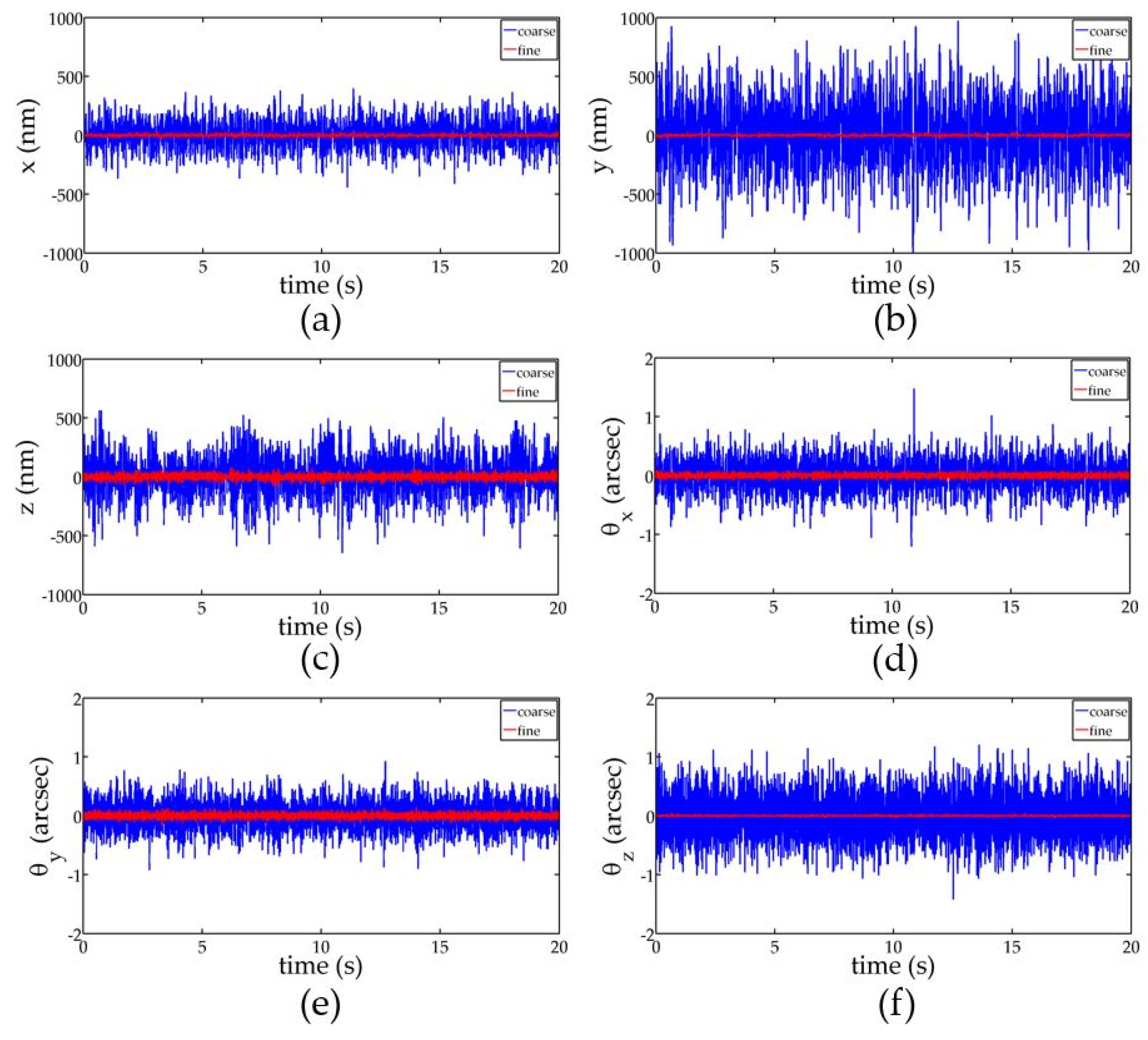
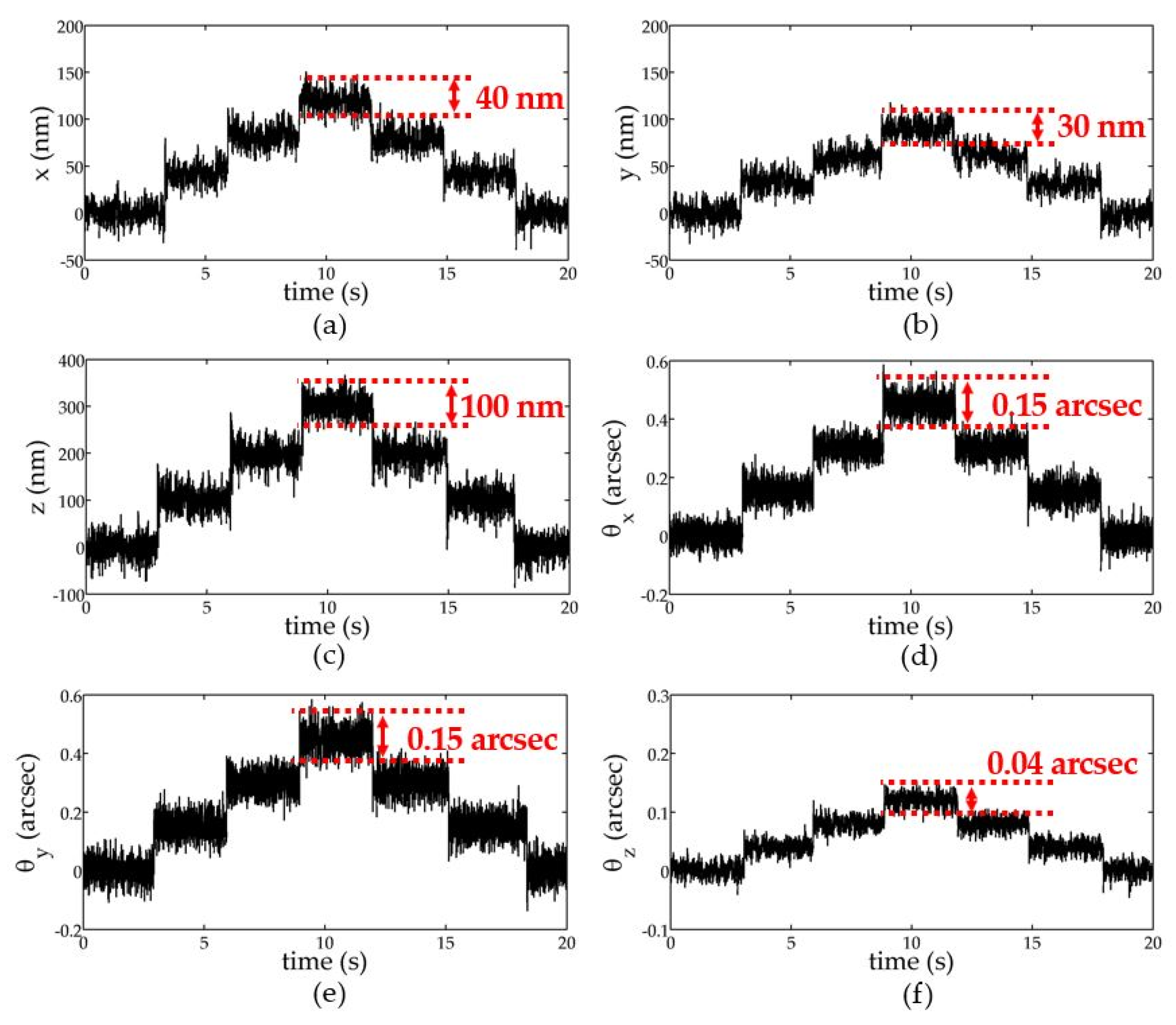
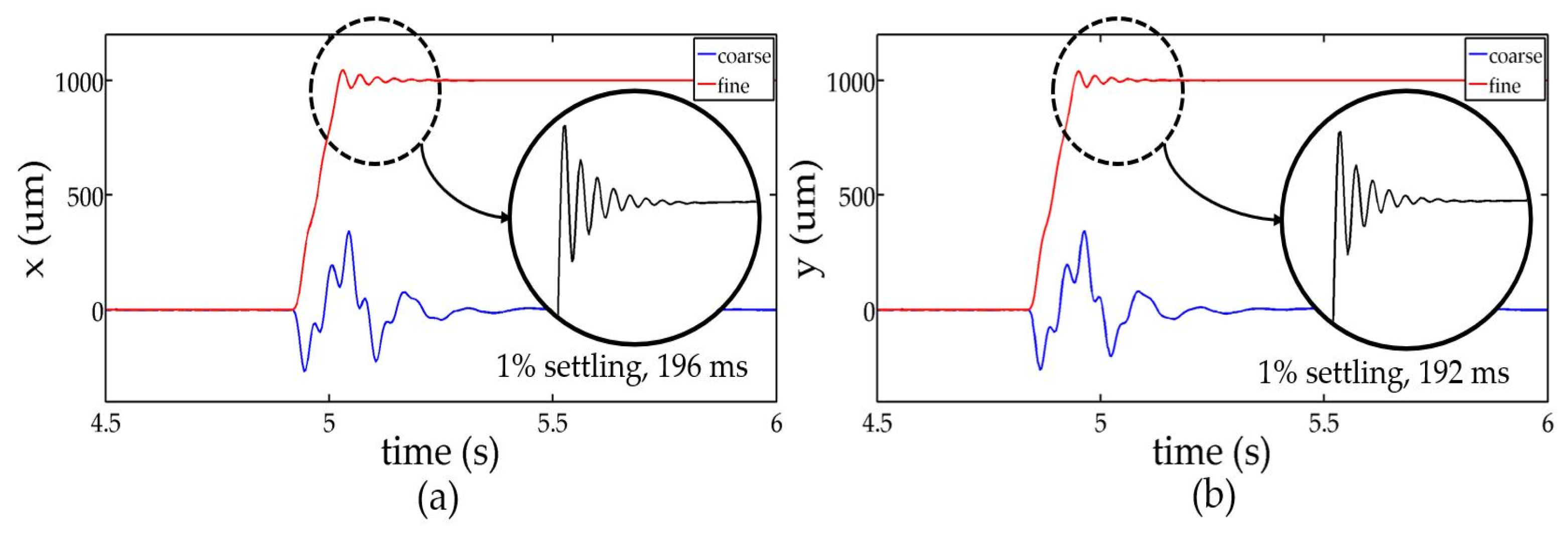
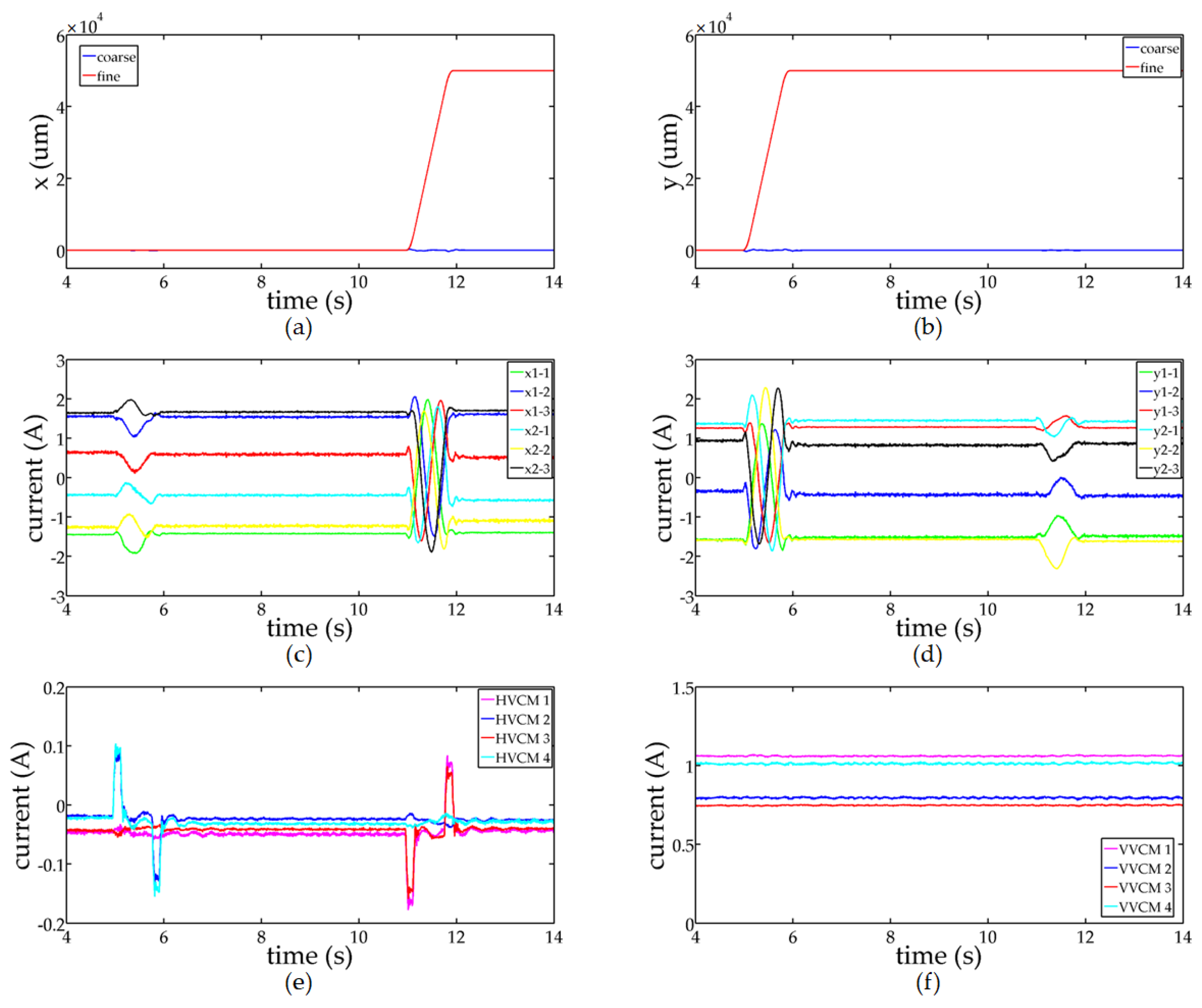
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Otsuka, J. Nanometer level positioning using three kinds of lead screws. Nanotechnology 1992, 3, 29–36. [Google Scholar] [CrossRef]
- Futami, S.; Furutani, A.; Yoshida, S. Nanometer positioning and its micro-dynamics. Nanotechnology 1990, 1, 31–37. [Google Scholar] [CrossRef]
- Ro, S.-K.; Park, J.-K. Development of a Miniature Air-bearing Stage with a Moving-magnet Linear Motor. Int. J. Precis. Eng. Manuf. 2008, 9, 19–24. [Google Scholar]
- Ro, S.-K.; Kim, S.; Kwak, Y.; Park, C.H. A linear air bearing stage with active magnetic preloads for ultraprecise straight motion. Precis. Eng. 2010, 34, 186–194. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X. Input coupling analysis and optimal design of a 3-DOF compliant micro-positioning stage. Mech. Mach. Theory 2008, 32, 400–410. [Google Scholar] [CrossRef]
- Kim, H.Y.; Ahn, D.H.; Gweon, D.G. Development of a novel 3-degrees of freedom flexure based positioning system. Rev. Sci. Instrum. 2012, 83, 055114. [Google Scholar] [CrossRef]
- Kim, K.H.; Gweon, D.G.; Jung, H.S.; Lee, S.H.; Hong, M.S.; Lee, M.-G. A Stage Based on Voice Coil Motor with High Speed and Long Range for Laser Micro/Nano Fabrication. Key Eng. Mat. 2007, 345, 757–760. [Google Scholar] [CrossRef]
- Kim, K.H.; Choi, Y.M.; Nam, B.-U.; Lee, M.-G. Dual servo stage without mechanical coupling for process of manufacture and inspection of flat panel displays via modular design approach. Int. J. Precis. Eng. Manuf. 2012, 13, 407–412. [Google Scholar] [CrossRef]
- Compter, J.C. Electro-dynamic planar motor. Precis. Eng. 2004, 28, 171–180. [Google Scholar] [CrossRef]
- Peijnenburg, A.T.A.; Vermeulen, J.P.M.; van Eijk, J. Magnetic levitation systems compared to conventional bearing systems. Microelectron. Eng. 2006, 83, 1372–1375. [Google Scholar] [CrossRef]
- Jansen, J.W.; van Lierop, C.M.M.; Lomonova, E.A.; Vandenput, A.J.A. Ironless magnetically levitated planar actuator. J. Appl. Phys. 2008, 103, 07E905. [Google Scholar] [CrossRef]
- Boeij, J.D.; Lomonova, E. Experimental verification of look-up table based real-time commutation of 6-DOF planar actuators. J. Syst. Des. Dyn. 2009, 3, 563–571. [Google Scholar] [CrossRef][Green Version]
- Ueda, Y.; Ohsaki, H. Six-Degree-of-Freedom Motion Analysis of a Planar Actuator with a Magnetically Levitated Mover by Six-Phase Current Controls. IEEE Trans. Magn. 2008, 44, 4301–4304. [Google Scholar] [CrossRef]
- Kim, J.J.; Lee, M.G.; Jeong, J.; Gweon, D.G. Design of a magnetically levitated six degrees-of-freedom planar motor using T-shape halbach magnet array. In Proceedings of the Euspen International Conference, Delft, The Netherland, 31 May 2010. [Google Scholar]
- Jansen, J.W. Magnetically Levitated Planar Actuator with Moving Magnets: Electromechanical Analysis and Design. Ph.D. Thesis, Technical University Eindhoven, Eindhoven, The Netherlands, 2007. [Google Scholar]
- Zhu, H.; Pang, C.K.; Law, T.L.; Teo, T.J. Design and Control of a Six Degrees-of-Freedom Magnetically Levitated Positioning System. IFAC Pap. 2016, 49, 127. [Google Scholar] [CrossRef]
- Zhu, H.; Teo, T.J.; Pang, C. K, Conceptual design and modeling of a six degrees-of-freedom unlimited stroke magnetically levitated positioner. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besacon, France, 8–11 July 2014. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.; Zhang, H.; Guo, S. Characteristic Analysis of a Long-Stroke Synchronous Permanent Magnet Planar Motor. IEEE Trans. Magn. 2012, 48, 4658–4661. [Google Scholar] [CrossRef]
- Lu, X.; Usman, I.U.R. 6D direct-drive technology for planar motion stages. CIRP Ann. 2012, 61, 359–362. [Google Scholar] [CrossRef]
- Rovers, J.M.M.; Janse, J.W.; Lomonova, E.A. Design and measurements of the Double Layer Planar Motor. In Proceedings of the International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, H.; Galea, M.; Li, J.; Lu, W.; Gerada, C. Analysis and Design of a Magnetically Levitated Planar Motor with Novel Multilayer Windings. IEEE Trans. Magn. 2015, 51, 8106909. [Google Scholar] [CrossRef]
- Kou, B.; Xing, F.; Zhang, C.; Zhang, L.; Zhou, Y.; Wang, T. Improved ADRC for a Maglev Planar Motor with a Concentric Winding Structure. Appl. Sci. 2016, 6, 419. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.; Xing, F.; Zhang, H. Analysis and comparison of two two-dimensional Halbach permanent magnet arrays for magnetically levitated planar motor. J. Appl. Phys. 2014, 115, 17E704. [Google Scholar] [CrossRef]
- Zhang, L.; Kou, B.; Li, L.; Zhao, B. Modeling and design of an integrated winding synchronous permanent magnet planar motor. In Proceedings of the 16th International Symposium on Electromagnetic Launch Technology, Beijing, China, 15–19 May 2012. [Google Scholar] [CrossRef]
- Usman, I.U.R.; Lu, X. Force Ripple Attenuation of 6-DOF Direct Drive Permanent Magnet Planar Levitating Synchronous Motors. IEEE Trans. Magn. 2015, 51, 8208708. [Google Scholar] [CrossRef]
- Xing, F.; Kou, B.; Zhang, L.; Yin, X.; Zhou, Y. Design of a Control System for a Maglev Planar Motor Based on Two-Dimension Linear Interpolation. Energies 2017, 10, 1132. [Google Scholar] [CrossRef]
- Ahn, D.; Kim, H.; Choi, K.; Choi, Y.-M.; Lim, J.-Y. Design process of square column-shaped voice coil motor design for magnetic levitation stage. Int. J. Appl. Electrom. 2020, 62, 517–540. [Google Scholar] [CrossRef]

| Design Results | HVCM | VVCM |
|---|---|---|
| Size | 95 × 50 × 40 mm3 | 55 × 55 × 40 mm3 |
| Wire diameter | 0.6 mm | 0.4 mm |
| Number of turns | 297 turns | 738 turns |
| Electric resistance | 3.29 Ω | 11.29 Ω |
| Max. voltage | 26.5 V | 36.9 V |
| Max. current | 3.43 A | 1.24 A |
| Max. power | 17.5 W | 17.5 W |
| Max. Force | 52.4 N | 28.2 N |
| Force constant | 15.6 N/A | 22.3 N/A |
| Design Parameters | Description | |
|---|---|---|
| Independent parameters | Height of the magnet array | |
| Ratio of the length of the main magnet to the half-pitch of the magnet array | ||
| Width of a bundle of coil threads with the same current direction | ||
| Height of the coil array | ||
| Current through the coil | ||
| Diameter of the core of the coil (without sheath) | ||
| Dependent parameters | Half-pitch of the magnet array | |
| Length of the main magnet | ||
| Effective length of the coil | ||
| Center gap of the coil winding | ||
| Distance between the coil sets which generate forces in the same direction | ||
| Pre-defined parameters | Pre-defined to match the phase of the current and the magnetic flux density: 0 mm | |
| Pre-defined to consider manufacturing the tolerance of coil winding: 8 mm | ||
| Pre-defined by the size of the mover of the coarse stage: 250 mm | ||
| Materials | Magnet | NdFeB, N-38H, magnetization of 8.99 × 105 A/m |
| Coil | Copper wire, resistivity of 1.793 × 10−8 Ωm | |
| Yoke | AISI 1020 | |
| Independent Design Parameters | Nominal Value | Variation |
|---|---|---|
| 25 mm | 5 mm–45 mm | |
| 0.6 | 0.2–1 | |
| 8 mm | 5 mm–11 mm | |
| 5 mm | 2 mm–8 mm | |
| 2 A | 1 A–3 A | |
| 0.8 mm | 0.3 mm–1.3 mm |
| Objective | ||
|---|---|---|
| Constraints | Vertical force | >50 N |
| Horizontal force | >100 N | |
| Ohmic loss | <130 W | |
| Design Parameters | Constraints | ||||||
|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (A) | (mm) | ||||
| 0.668 | 13.9 | 5.98 | 5.17 | 0.5 | 154.9 | 130 | 19.17 |
| 0.671 | 13.9 | 6.06 | 7.44 | 0.6 | 155.8 | 130 | 19.20 |
| 0.672 | 13.9 | 6.63 | 9.68 | 0.7 | 154.2 | 130 | 19.23 |
| 0.646 | 13.9 | 5.83 | 13.62 | 0.8 | 151.3 | 130 | 19.11 |
| 0.671 | 13.9 | 8.08 | 14.54 | 0.9 | 160.0 | 130 | 19.97 |
| Sensors | Measurement Range | Theoretical Resolution (16-bit A/D) | |
|---|---|---|---|
| Laser interferometers | RLE10 | 1 m | 38.63 pm |
| Capacitive sensors | C5S | 10 μm | 150 pm |
| C9.5R | 1250 μm | 19.07 nm | |
| C8S | 2000 μm | 30.52 nm | |
| (RMS Value) | x (nm) | y (nm) | z (nm) | θx (arcsec) | θy (arcsec) | θz (arcsec) |
|---|---|---|---|---|---|---|
| Fine stage | 9.29 | 7.85 | 23.2 | 0.0323 | 0.0400 | 0.0106 |
| Coarse stage | 115.94 | 275.87 | 170.73 | 0.3640 | 0.2662 | 0.2435 |
| Fine-to-coarse ratio (%) | 8.01 | 2.85 | 13.59 | 8.87 | 15.03 | 4.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, D.; Jin, J.-W.; Yun, H.; Jeong, J. Development of a Novel Dual Servo Magnetic Levitation Stage. Actuators 2022, 11, 147. https://doi.org/10.3390/act11060147
Ahn D, Jin J-W, Yun H, Jeong J. Development of a Novel Dual Servo Magnetic Levitation Stage. Actuators. 2022; 11(6):147. https://doi.org/10.3390/act11060147
Chicago/Turabian StyleAhn, Dahoon, Ji-Won Jin, Hyeeun Yun, and Jaeheon Jeong. 2022. "Development of a Novel Dual Servo Magnetic Levitation Stage" Actuators 11, no. 6: 147. https://doi.org/10.3390/act11060147
APA StyleAhn, D., Jin, J.-W., Yun, H., & Jeong, J. (2022). Development of a Novel Dual Servo Magnetic Levitation Stage. Actuators, 11(6), 147. https://doi.org/10.3390/act11060147







