Novel Magnetic Circuit Design and Acceleration Calculation of Horizontal Linear Vibration Motor

Abstract

This study proposes a novel magnetic circuit design to reduce the size of horizontal linear vibration motors (HLVMs) used in vehicle touchscreens. The HLVM prototype uses two thick permanent magnets to create a magnetic circuit below the voice coil; however, the novel design places four thin permanent magnets above and below the voice coil. Moreover, the coil position has been changed to a yoke center to create an effective magnetic circuit with short magnets. Compared with the vertical linear vibration motor, the force calculation method of the HLVM is significantly different. In this study, a new force calculation method is used to analyze the electromagnetic–mechanical coupling of the HLVM. As a prototype, the novel design is small in size (−28.85%) but possesses similar acceleration. The experimental results verify the analysis results of the HLVM in the displacement and acceleration on a dummy jig.

1. Introduction

Rotational motors with an eccentric mass were previously widely used to provide continuous vibration in mobile devices. Chung et al. introduced a new brushless and sensor-less vibration motor to increase the lifetime of motor and manufacturing cost [1]. Won et al. developed a new method to analyze a flat-type vibration motor to obtain the load torque and rising time [2]. However, most of those motors showed slow response time (more than 100 ms) and short lifetime due to the inertia, making it difficult to provide fast haptic feedback. Hwang et al. introduced a novel design of a solenoid type with a shaker vibration algorithm to increase the lifetime and reliability [3]. Fukumoto et al. used a small actuator attached to the backside of a touch panel to generate fast haptic feedback; the actuator is similar to a magnetic speaker that provides a linear motion of voice coil to reduce the response time and extend the lifetime [4]. Choi et al. introduced a linear vibration motor, equipping a voice coil and permanent-magnet springs to increase the lifetime [5]. At that time, people were focusing on improving the response time and lifetime of rotational motors by using linear vibration motors, but not performance. In recent years, linear vibration motors have become increasingly popular and are used to improve the haptic performance of some devices, which are included in smartwatches, handheld game players and in-vehicle touchscreens that require haptic feedback or vibration alert.

With the rapid development of electric cars, the number of in-vehicle touchscreens has drastically increased to enhance multimedia entertainment, which replaces traditional instrument clusters. It is extremely dangerous for drivers to operate some functions on the touchscreen while driving. Bernard et al. figured out that gradient haptic feedback can guide the user to adjust settings on the touchscreen without vision [6]. In addition, he conducted many studies on gradual surface haptic feedback and proposed a new haptic touchpad to control the setting value [7]. The demand of linear vibration motor used for the touchscreen in electric cars is also increasing. Linear vibration motors can be classified into two types based on the direction of vibration: VLVM (vertical linear vibration motor) and HLVM (horizontal linear vibration motor), as shown in Figure 1. The reason to distinguish the VLVM and HLVM is to establish the main differences between HLVM and VLVM, which can help people to decide what kind of motor type (VLVM or HLVM) is more suitable to be used in specific application conditions.

VLVM vibrates along the height of the device (z-direction), which is the smallest dimension, while the HLVM vibrates along the length and width dimensions (x- or y-direction). There are many linear vibration motors that have been developed to obtain the best haptic feedback. However, due to the physical constraints of devices or touchscreens, the motor should be lightweight and small.

In most cases, the height is limited owing to design targets, e.g., smartphones and smartwatches. Thus, it is difficult to reduce the height of the device and maintain the same performance using the VLVM. HLVM has a spatial advantage over VLVM in the era of thinner touchscreens, which can be used in some applications instead of VLVM.

Lee et al. proposed a horizontal vibration motor to improve motor performance considering smaller thickness; the finite element method and mathematical vibration modeling were used to calculate the magnetic force [8]. A new electromagnetic actuator using permanent magnet and solenoid coil was proposed to generate higher magnetic force in order to provide a higher vibration acceleration. The experimental results showed that the proposed actuator can generate more than 2.5 G vibration over a wide frequency range from 0 Hz to 100 Hz [9]. Pyo et al. proposed a novel linear impact-resonant actuator for mobile devices to improve acceleration by using stronger magnetic force. Based on the experiment, a sufficient vibration intensity (above 2.0 G) is generated over a broad frequency range of 1 Hz to 210 Hz [10]. These papers only discuss force analysis results and experimental acceleration, as there is no results comparison between analysis and experiment.

In previous studies, the electromagnetic–mechanical coupling model was used to obtain the displacement of tubular linear stepping motors by using the finite element method and Newton–Raphson algorithm [11]. Kim et al. introduced the electromagnetic–mechanical coupling method and numerical iteration method to obtain the current, displacement and impedance value of vertical linear actuator, considering nonlinear parameters [12]. The above papers conducted research on linear motors to obtain the magnetic force and displacement by using the electromagnetic–mechanical coupling method. However, they did not include the analysis of motor acceleration on a dummy jig. A dummy jig is used to simulate a test environment for smartphones or other electronic devices.

Nowadays, the HLVM has been mainly used to replace the VLVM in several applications to provide better haptic feedback. The prototype of the HLVM used for in-vehicle infotainment is shown in Figure 2. Haptic feedback provides touch sense and allows drivers to know that the input has been registered by the infotainment system without glancing at the touchscreen.

Usually, the mechanical volume of a linear vibration motor is proportional to the motor performance. Thus, it is always a significate issue to maintain a similar performance with size reduction. This study proposes a new design of a small-volume HLVM with a novel and optimized magnetic circuit using a 3D (three-dimensional) FEM (finite element method). Moreover, the E-M (electromagnetic–mechanical) coupling method is employed to obtain the displacement and acceleration of the HLVM on a 100 g dummy jig with a new spring design. The sample of the novel HLVM is developed, and the experimental results agree well with the analysis results.

2. Analysis Method

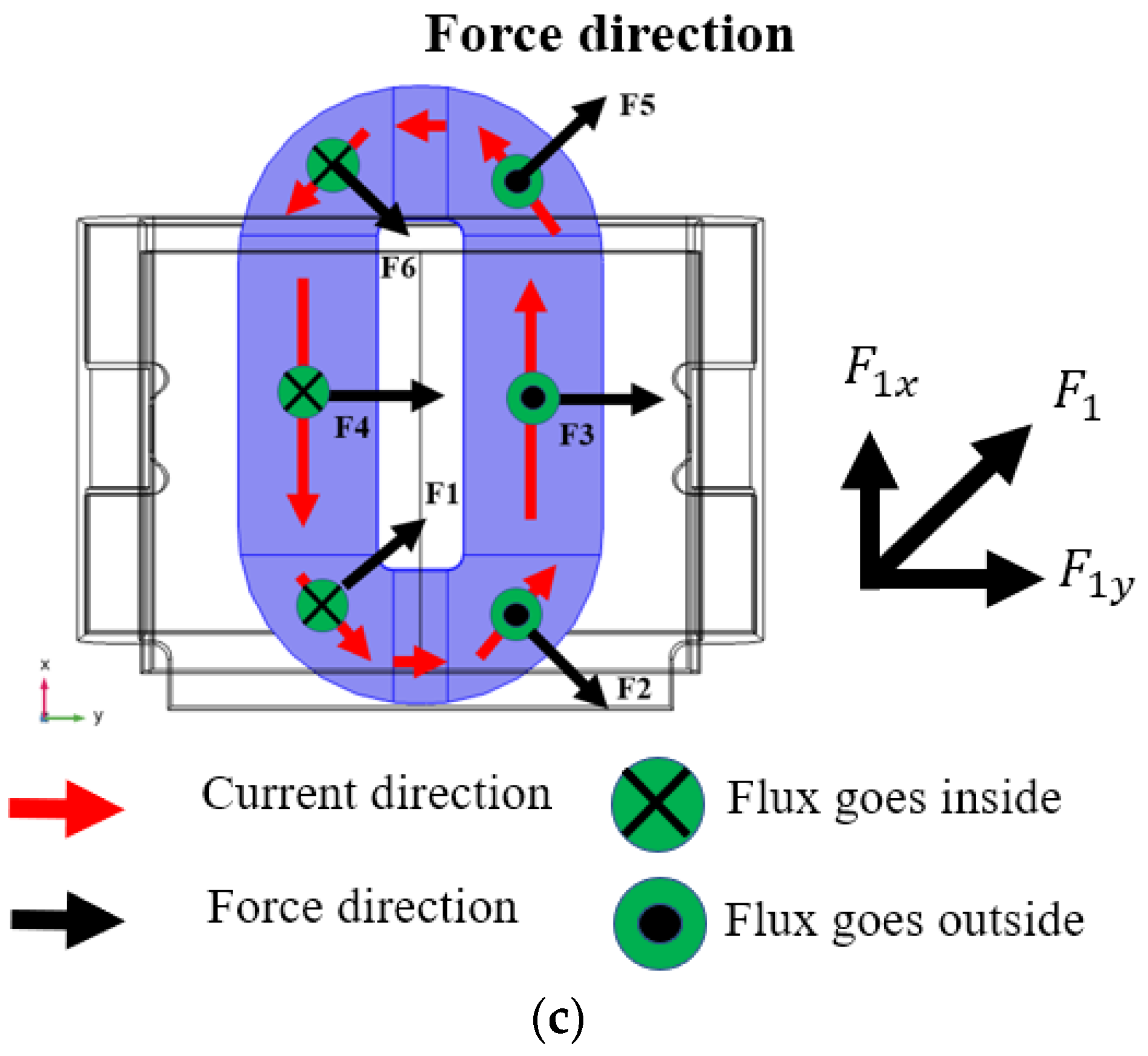
The HLVM includes an electromagnetic domain and a mechanical domain. The Lorentz force calculation of the HLVM is different from that of the VLVM due to different magnetic circuits and coil positions. In previous research, the magnetic flux passed through the entire coil, thereby generating the Lorentz force on every section of the coil [13]. The magnetic circuit of the prototype and magnetic flux direction are shown in Figure 3a. However, the force calculation method of the HLVM is not the same, as shown in Figure 3b. The coil is divided into eight parts based on the directions of the current and magnetic flux, and only six parts of the coil can generate the Lorentz force along the x–y plane, as shown in Figure 3c.

The force calculation method is expressed by the equations mentioned below. The HLVM only vibrates along the y-direction.

$$F_{ky}=B_{kz}{L}_{k}i, L_k=\frac{V_k{L}_{total}}{V_{total}},k=1\mathrm{to}6,$$

(1)

$$F_{total}={\sum }_{k=1}^6{F}_{ky},\mathrm{and}$$

(2)

$$Bl=\frac{F_{total}}{i}.$$

(3)

$F_{ky}$ (N) is the Lorentz force on each coil part, of which calculation along the y-direction depends on the flux density, where $B_{kz}$ (T), $L_k\left(\mathrm{m}\right)$, $i \left(\mathrm{A}\right)$, $V_{total}$ (m³), $V_k$ (m³), $L_{total}$ (m) and $k$ represent z-direction magnetic flux density passing through the coil, length of each coil part, current applied to the coil, total coil volume, coil volume of each part, total coil length and the coil part number, which ranges from 1 to 6, respectively.

Equation (2) expresses the total force calculation of the coil, which is the summation of the Lorentz force on each coil part. Furthermore, the total force factor is defined using Equation (3), where $F_{total}$ (N) and $Bl \left(\mathrm{N}/\mathrm{A}\right)$ are total force of coil and total force factor, respectively.

The voltage equation of the motor is defined by Equation (4), where $R \left(\mathrm{ohm}\right)$, $\left\{i\right\}$, $L_e\left(\mathrm{mH}\right)$,$\left\{V_{backemf}\right\}\left(\mathrm{V}\right)$, $\left\{V_{input}\right\}\left(\mathrm{V}\right)$, $e$, $\omega \left(\mathrm{rad}/\mathrm{s}\right)$ and $t$ (s) are coil DCR (direct current resistance), current vector, inductance, back electromotive force (back emf) vector, input voltage vector, Euler’s number, angular frequency and time, respectively.

Equation (5) expresses the relationship between the back emf, force factor and mechanical velocity. The vibration of the motor under Lorentz force is defined by Equation (6). The moving mass of the motor includes the yoke, top plate and magnets, where $[M_{motor}] \left(\mathrm{kg}\right)$, $[C_{motor}] \left(\mathrm{Ns}/\mathrm{m}\right)$, $[K_{motor}] \left(\mathrm{N}/\mathrm{m}\right)$, $\left\{\frac{d^{2}y}{d{t}^2}\right\}\left(\mathrm{m}/{\mathrm{s}}^2\right)$ and $\left\{y\right\}\left(\mathrm{m}\right)$ are the mass matrix, damping matrix, stiffness matrix, acceleration vector and displacement vector, respectively. The E–M coupling method is shown in Figure 4a. The total force $Bl\left\{i\right\}$ is applied to the moving mass. Figure 4b describes the acceleration calculation on the dummy jig and the accelerometer is on the side of the dummy jig.

$$R\left\{i\right\}+L_e\left\{\frac{di}{dt}\right\}+\left\{V_{backemf}\right\}=\left\{V_{input}\right\}{e}^{j\omega t},$$

(4)

$$\left\{V_{backemf}\right\}=Bl\left\{\frac{dy}{dt}\right\},\mathrm{and}$$

(5)

$$[M_{motor}]\left\{\frac{d^{2}y}{d{t}^2}\right\}+[C_{motor}]\left\{\frac{dy}{dt}\right\}+[K_{motor}]\left\{y\right\}=Bl\left\{i\right\}.$$

(6)

The material properties of the mechanical domain are the density, Young’s modulus and Poisson’s ratio, as shown in

Table 1. Mechanical material properties.

Parts	Material	Density [kg/m3]	Young’s Modulus [GPa]	Poison’s Ratio
Cases	Stainless steel	7859	166	0.25
Coil	DHT	6101	126	0.34
Yoke	SPCC	7821	207	0.29
Magnet	N42H	7551	160	0.30
Dummy jig	POM	1417	3.15	0.30

. The coil is made of a DHT wire (Daikoku high tension). The top plate and yoke are made of the same magnetic material, named SPCC (commercial quality cold-rolled steel), which exhibits high nonlinear magnetic permeability. SPCC is defined in JIS G 3141 (Japanese material standard for cold rolled steel). The magnetic material possesses neodymium iron boron with an N42H magnetic grade. The motor spring and dummy jig spring possess the same material as the cases. POM is the short name for polyoxymethylene, which is an engineering thermoplastic.

3. Novel Magnetic Circuit Design

The prototype places two thick magnets below the coil. Type 1 is designed considering four pieces of thin magnets, which are placed above and below the coil to improve the flux density passing through the coil; the coil can generate high Lorentz force. From types 1 to 2, the outer dimension has been changed to consider a smaller volume from 9867 mm³ to 7020 mm³, as shown in Figure 5a.

To improve the Lorentz force as much as possible, the coil is positioned at the center of the magnets. The yoke shape is designed as an x-axial symmetry. The prototype coil plate is connected to the upper case using the welding process, whereas the type 2 design uses a newly structured coil plate fixed on the lower case with a silicon supporter to improve the stability of the coil. Owing to the coil plate, the coil comes closer to the upper magnet, which implies that the upper air gap is smaller than the lower air gap in the type 2 design.

Furthermore, coil DCR, FPCB (flexible printed circuit board) and spring dimensions are redesigned to produce a resonance frequency similar to that of the prototype. The position of the type 2 coil is shown in Figure 5b.

For the magnetic field analysis, the 3D FEM is used to obtain the magnetic flux density on the coil. The magnetic field of the HLVM can be assumed to be a magnetostatic field, which is a quasi-static magnetic field with the assumption that magnetic fields produced by the permanent magnet, or the current, are not significantly affected by other dynamic effects.

The magnetic flux density of the coil is shown in Figure 6. The magnetic flux density distribution of the prototype and type 1 are not uniform, as only four parts of the coil can generate the Lorentz force. However, type 2 exhibits a uniform and high magnetic flux density distribution on the six parts of the coil.

The magnet length (one piece) is selected as the optimization parameter. The magnet length of Type 2 is 7.75 mm, and the magnetic flux saturation levels of the yoke are 1.55 T and 1.75 T. The saturation level of the magnetic material implies that when the external magnetic field intensity increases, the magnetic flux density of the material asymptotically reaches a maximum value. When the material becomes saturated, the magnetic flux density more or less levels off. The material saturation level is about 1.25 T.

According to Figure 7 and

Table 2. Force factor and force comparison.

Model	DCR [ohm]	Magnet Length [mm]	Total Force Factor [N/A]	Total Force [N]
Prototype	12.4	8.63	3.102	0.444
Type 1	12.4	8.63	3.514	0.503 (+13.29%)
Type 2-0	8.0	7.75	2.262	0.503
Type 2-1	8.0	7.25	2.291	0.509
Type 2-2	8.0	6.75	2.309	0.513 (+15.54%)
Type 2-3	8.0	6.25	2.303	0.512
Type 2-4	8.0	5.75	2.292	0.510
Type 2-5	8.0	5.25	2.239	0.498

, type 2-2 has a maximum total force factor compared with those of the other type 2 designs, and its saturation levels (1.00 T and 1.35 T) is significantly closer to the saturation level of the material. Thus, type 2-2 is selected as an optimized model to manufacture samples and process experiments. Compared with the prototype, the total force of type 2-2 exhibits an improvement of 15.54%.

4. Experiments and Results

4.1. Samples and Experimental Setups

Type 2-2 is defined as the final type. The voice coil specification comparison between prototype and final type are shown in

Table 3. Voice coil specification comparison.

Model	Prototype	Final Type
Coil diameter [mm]	0.141	0.117
DCR [ohm]	12.4	8.0
Coil inductance [mH]	0.560	0.153
Coil total length [m]	10.31	4.58
Coil turn	269	125

. The sample comparison between the prototype and final type is shown in Figure 8a. The parts of type 2-2 are shown in Figure 8b. The input voltage is 1.78 V with a sinusoidal signal of 50–500 Hz. The Klippel measurement system includes a monitor for Klippel motor control, power amplifier, Klippel motor and laser head, shown in Figure 8c. The displacement on the spring from the vibration motor can be obtained by using laser of Klippel setup. The acceleration measurement setups include the monitor, vibration analyzer, dummy jig and accelerometer. The vibration motor is set on the center of the dummy jig and acceleration is attached on the side to obtain the acceleration, shown in Figure 8d.

4.2. Experimental Results and Analysis Results

The displacement and acceleration comparisons between the prototype and final type are illustrated in Figure 9. Due to the size reduction, the moving mass of the final type is less than that of the prototype. Compared to the prototype, the final type has a higher force factor, which causes a higher displacement in the motor around the resonance frequency. The higher displacement of the motor offsets the moving mass reduction in the final type and provides a similar acceleration on the dummy jig as that of the prototype. The analysis results match well with the experimental results.

5. Conclusions

In this paper, a small-volume horizontal linear vibration motor that used a novel magnetic circuit, new coil position magnet, length optimization, new coil plate and new spring size was proposed to obtain a similar performance as the prototype. Moreover, this study clearly described the magnetic circuit of HLVM and developed a force calculation method based on the coil position to obtain the Lorentz force on the coil. To overcome the space limitation of the display, the height of the prototype was reduced from 13.0 mm to 9.0 mm. The novel magnetic circuit with four pieces of permanent magnets has been proposed to generate more magnetic flux density passing through the voice coil. The new coil supporters were used to simplify the mechanical structure and improve the stability of the coil plate. The E–M coupled analysis method was used on the HLVM to calculate displacement and acceleration on a 100 g dummy jig. The final type exhibited a similar displacement and acceleration as those of the prototype, verified by the experimental results.